Abstract
We approach scalability and cold start problems of collaborative recommendation in this paper. An intelligent hybrid filtering framework that maximizes feature engineering and solves cold start problem for personalized recommendation based on deep learning is proposed in this paper. Present e-commerce sites mainly recommend pertinent items or products to a lot of users through personalized recommendation. Such personalization depends on large extent on scalable systems which strategically responds promptly to the request of the numerous users accessing the site (new users). Tensor Factorization (TF) provides scalable and accurate approach for collaborative filtering in such environments. In this paper, we propose a hybrid-based system to address scalability problems in such environments. We propose to use a multi-task approach which represent multiview data from users, according to their purchasing and rating history. We use a Deep Learning approach to map item and user inter-relationship to a low dimensional feature space where item-user resemblance and their preferred items is maximized. The evaluation results from real world datasets show that, our novel deep learning multitask tensor factorization (NeuralFil) analysis is computationally less expensive, scalable and addresses the cold-start problem through explicit multi-task approach for optimal recommendation decision making.
1. Introduction
The era of big data has led to the information overload problem as a result of the fact that, information abounds in volume, variety and veracity and velocity on the internet and e-commerce sites. Cichocki et al. [1] posit that big data is characterized not only by big Volume but also by other specific “V” challenges: Veracity, Variety, Velocity and Value highlight big data characteristics for information filtering related problems [2,3]. High Volume implies the need for algorithms that are scalable; high Velocity is related to the processing of stream of data in near real-time; high Veracity calls for robust and predictive algorithms for noisy, incomplete and/or inconsistent data, high Variety require integration across different kind of data for instance, genetic and behavior data. Such attributes pose complexity in such a manner that, existing standard methods and algorithms become woefully inadequate for the processing and optimization of such data. In the big data world, machine learning algorithms which provide efficient and innovative solutions and technologies to enhance feature engineering and memorization is critical for better analytics for development. A recommender system purposely provide users with personalized online products or services recommendations to handle the increasing massive information to enhance customer relationship management and decision making process [4,5]. Various recommender system techniques have been proposed since the mid-1990s and many sorts of recommender system software have been developed recently for a variety of applications as a result of the cold start problem of users and items [6,7]. Researchers and managers recognize that recommender systems offer great opportunities and challenges for business, government, education and other domains with more recent successful developments of recommender systems for real-world applications. According to [8], Multi-task learning on the other hand, is an approach designed to improve predictive performance by learning from multiple related tasks simultaneously, taking into account the relationships and information shared among the different tasks [9]. The multi-task learning paradigm activates a great deal of model interpretability and it is able to provide explicit information for further analysis on user behavior patterns according to current research in information filtering [10]. In this paper, we focus on explicit feedback, through user’s auxiliary data which directly depicts users’ preference through ratings and sentiments expressed [11]. A radial basis function [12] is used to filter the complex interactions between the items, users and sentiments scores of users of an e-commerce site. Compared to implicit feedback, this paper explores user information in more than two dimensions and treats it as a tensor model. Deep neural network model for the existing relationships is then formulated in a Multilayer Perceptron (MPL) model. Regarding the key content filtering effectiveness, MF when used to fuse item and user characteristics with inner product sometimes hinders better performance as a result of the cross product normally counted as cost. This paper mitigates the just mentioned research constraints with a multi-modal data and models it as a multi-task algorithm, which is hybrid in real sense. Therefore, a hybrid recommendation based on multi-task learning framework for solving cold start and scalability problems is proposed for collaborative filtering in this paper. The main contributions of this paper are:
- (i)
- A novel tensor factorization strategy, which adapts radial basis of Gaussian type to solve the cold start problem is proposed.
- (ii)
- A hybrid collaborative system using the speed of the multilayer perceptron and the simplicity and accuracy of Tensor Factorization to produce fast and accurate model for improved performance to ensure a scalable processing of big data is proposed.
- (iii)
- Our novelty lies in the fact that, our proposed models; MLP and MTF which are jointly trained promotes feature engineering and memorization which could be used as basis for future learning through our special tweaking strategy. We wish to draw readers attention to the fact that, our model is not an ensemble where each model is trained disjointly and then combining their predictions in the final stage. We train a deep neural network over the corresponding user information over the latent factors from the user matrix via tensor factorization which is innovative.
2. Review of Related Works
In recent times, there has been a hype in academia and industry about Artificial Intelligence (AI) [13] and its associated technologies enhancing industry and academia. AI which encapsulates Machine learning (ML) [14] and Deep leaning (DNN) [15] show up in countless articles out of the technology motivated ones. A Deep neural network as proposed by [15,16] has the potential of estimating both continuous and discrete function. Recently, various application areas such as speech recognition, computer vision and text processing [17] among other fields have experienced the potency of deep neural networks. However, few publications have employed tensor factorization for filtering information with the subject matter considering the numerous amount of literature on MF methods. Notwithstanding the fact that, some recent advances [18,19] used DNNs for filtering tasks and shown encouraging consequences, auxiliary information of users were modelled, for instance, in audio and images. From literature [20], the massive data generated in recent times is as a result of generations from multi-modal, multi-dimensional datasets from current Recommender Systems (Rss) Hybrid algorithms [21] as proposed in this paper and being represented are used to optimize real-world implementations of algorithms and have received significant interest in recent years and are increasingly used to solve real-world problems as propounded by [22]. These hybrid models could include combination of two or more algorithms such as particle swarm optimization (PSO) [23], matrix factorization [24], genetic algorithms (GA) [25] and other computational strategies like artificial intelligence or deep neural networks [26] including but not limited to fuzzy logic systems [27], simulation, sigmoid functions or MLP [28], radial basis functions [29], just to mention a few. Deep neural networks (DNNs) are techniques of artificial intelligence (AI) that have the capability to learn from experiences, it is robust [30] and improves performance by adapting to the changes in the environment [22]. The underlying advantages of Deep Neural Networks are the possibility of efficient operation of large amounts of data and its ability to generalize the outcome [19,31] proposed neural collaborating filtering which showed significant improvements but used matrix factorization approach which as far as we are concerned has additional computational burden.
In this paper, we wish to envisage hybrid models for real collaborative filtering environment in the same way as those writers though differently with our tensor strategy and multimodal data that is explicit in nature to solve the information overload problem. We prove that, DNNs have an excellent capability for user–item modelling, which to our knowledge has not been investigated to a large extent by researchers.
3. Materials and Methods
3.1. General Framework
Tensor factorization has emerged as a promising solution for the computational challenges of collaborative recommendation [32] and it is the basic framework for this paper, Figure 1. Tensor [33] as a multi-way array is multidimensional in nature and its order refers to the number of its dimensions. Various schemes have been proposed to decompose a tensor into factor matrices, which not only reduces dimensionality but also helps to discover latent factors in each modality and identify group-wise interactions. Typically, matrix factorization approaches concatenate multiple data modalities into a single second dimension of the matrix, thus disallowing explicit representation of interactions among these modalities [34]. This explains our choice for tensor modelling in this paper. Tensor integrates additional domain-specific prior knowledge to constraint the tensor structure [35]. Thus tensor factorizations can easily integrate multiple data modalities, reduce dimensionality and identify latent groups in each mode for meaningful summarization of both features and instances as propounded by [36] in medical data analysis. According to Nickel et al. [37] tensor as a factorization tool has a collective entity for filtering hidden factors related to massive data. In Reference [38], it is proven that, tensor-based methods is ideal for mitigating personalized tagging and link prediction recommendation. Tensor for efficient and simple parallelization [39], sentiment–based tensor factorization for big data [40] our previous works provide sufficient basis for tensor implementation in this paper. Regarding personalized tag recommendation system, singular vector decomposition (HOSVD) [41] are based on Tucker Decomposition (TD), while LFTF [42] is a Canonical Decomposition (CD) type. We now present the general framework of our model in Figure 1 explaining tensor and deep neural models for filtering customer interactions. U means user, I is Items whiles S is review sentiments expressed.
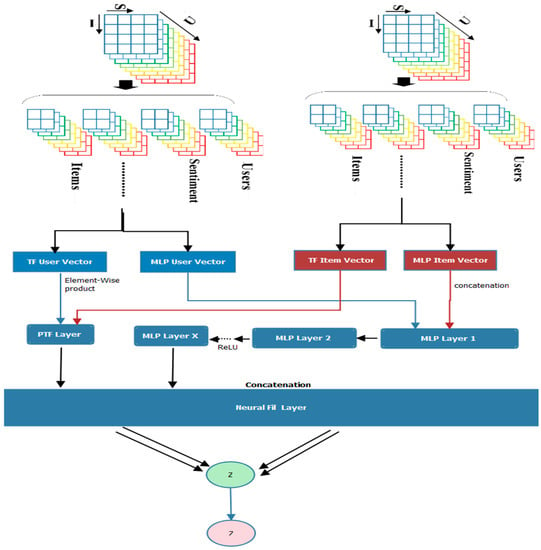
Figure 1.
General Framework.
3.2. Multi-Task Tensor Factorization
As in the case of MF in Recommender Systems (Rss), TF produces a predictive model by revealing patterns from the data. The major advantage of a tensor based approach is the ability to take into account a multifaceted nature of user-item interactions [43]. In the Google’s wide and deep model [44], a generalized linear model was used to capture latent features in the wide perspective. In this paper, tensor factorization model which is non-linear in nature is chosen to be a platform model as a result of the fact that it has appealing property to efficiently impose structure on the vector space representation of the data as propounded by [37]. We will regard an array of numbers with more than 2 dimensions as a tensor. This is a natural extension of matrices to a higher order case. A tensor with N distinct dimensions is called an N-way tensor or a tensor of order N. Tucker Decomposition (TD) factorizes a multi-dimensional array into a main tensor multiplied by a matrix [20]. Taking a 3rd-order tensor for instance,
In that, and are core tensors.
represent latent characteristics. However, CD factorizes a multi-way data which is a tensor into a summation of rank-one modes. Let be a tensor and it can be written as;
where and represents the number of features. in Equations (1) and (2) can be equated to the factor matrices SVD and core tensor C can be said to be the eigenvalues [45]. Probabilistic Tensor factorization is applied to model the reviews sentiment and rating scores with their item (IDs) which are the explicit user feedback [46] which are in line with [12]. We treat dataset as three-dimensional tensor structure. We adapt notations of [12,47] for the formulation of our model. If I is the set of items, is the set of users whiles is the set of review sentiments, then the process that reviewer of an item reviews or scores with sentiment s and how the user u rates an item is symbolized by a triple (). denotes the set of review history (Table 1). If a triplet () then the interactions between items, users and review sentiment for personalized tag recommendation can be represented by a three-order tensor, which is depicted in Figure 1. A ranking scheme propounded by [35] for personalized recommendation is employed in this paper. If denotes the item-user pairs () in then a multi-task tensor factorization (MTF) using Gaussian Kernel for the filtering job can be fitted. The triplicate interactions between items, users and review sentiment is presented by a 3rd-order tensor with |I| items, |U| users and |S| sentiment votes [40]. The tensor can then be factorized into three components, an item matrix , a user matrix and a sentiment matrix , where is the number of features. The entry of the i-th row of the matrix , matrix and matrix denotes the latent variables of the i = item, i-th user and i-th sentiment vote, respectively. The columns of matrices and could be referenced as a feature topic. Three paired relations are modelled with respect to this paper; user-sentiment, user-item and user ratings. It is assumed that, if sentiment and item are relevant with the k-th topic, then is a Gaussian pair of and the same is true with the other variables. Readers must note here that, represents k-th characteristics of the sentiment whiles is the k-th characteristic of item i. Thus, the k-th character of the sentiment as well as the k-th character of item depicts a Gaussian-like feature. Therefore,
whiles represents the standard deviation of the distribution. Three pairs of the dimensions items, users and sentiments are respectively deduced assuming that,

Table 1.
Notations.
Based on this assumption, a triplet (u; i; t) as well as its potential score (u; i; t) is deduced as;
Here, represents the k-th feature for the item-user features. Again, and represent the value of the k-th topic for item-sentiment and user-sentiment interactions.
The matrices and columns feature topic are fused into a feed-forward MLP layer of the deep model. On top of the input, the embedding layer maps the sparse representation to a deep vector. The resultant item or user embedding labelled as the item or user feature vector in the field of feature modelling. The item and user embedding are directly inputted into the multi-layer neural model, we name it as; deep neural filtering layer which maps the feature vectors to a recommendation field. The dimension layer explains the potency of the model. A fully connected multilayer feed-forward networks have nodal transfer function activation flows from the input layer through a hidden layer to the output layer [48]. This is expressed as;
where is one of the N inputs nodes for processing node j, denotes the weight of the connection node, is the bias for node y and is the output node. Each neuron is connected to each other in the forward direction within the network.
3.3. Proposed Deep Neural Filtering Model
The general NeuralFil framework Figure 1, explains the learning propensity of NeuralFil with a probabilistic concept which dwells on tensor factorization for explicit learning. Learning via tensor factorizations is based on the idea of explaining an observed tensor Y through a set of latent factors. We then show that multi-task tensor factorization (MTF) can be expressed and discretized as a generalization under Neuralfil. We explore the use of deep neural networks for information filtering with multi-layer perceptron (MLP) to learn the item- user interaction in this paper. Importantly, a unique tensor factorization model with deep learning, which is jointly trained (MTF and MLP) under the NeuralFil framework is revealed; The model brings a unification through the potency and effectiveness of the Tensor Framework and non-linearity of Multi-Layer Perceptron (MLP) for modelling interrelated factors. The factors of the final hidden layer C shows the model’s potency. is the output the predicted and a point-wise loss algorithm is used to train the model of z and the target . Thus we formulate Neuralfil’s predictive model as
where , and signifies feature factor matrix for items, users, items and ratings whiles αH signifies parameter of H which is the association function of the model. Thus H is remains as the multi-layer neural network and it is re-formulated as;
where and represent the mapping of the output layer and the c-th neural filtering layer, with X in all.
3.4. Learning the Joint Model of Non-Linear Tensor Factorization and Multilayer Perceptron
The explicit data is not binarized so our model is learned adopting pointwise methods [49,50] which mainly implement a regression with squared loss:
where Z is the observed relationship in Z and denotes refers to the set of negativities and is a hyper-parameter representing weights of training (u, i). We explain squared loss on the mere assumption that, observations are as a result of multivariate Gaussian distribution. Given S, the learning task is to model parameter .
For the purpose of this work, the tensor model is then discretized by adopting the sigmoid function which is a Gaussian-like kernel, by freezing the power parameter as;
In a form;
and respectively. The objective is to explore and remove this power computation burden and apply it in a recommendation system through Tensor Factorization. The function MLP and MTF which is adopted as a Radial Basis Function is given as , . Here log sig (R) is the function for multilayer perceptron or sigmoid (SBF) and exp(−abs(R)) is the function for MTF, respectively.
3.5. Proposed Deep Neural Prediction Model
For a real neural network filtering model, we present a multi-layer algorithm such as [51] to model a user interaction . Here, the individual output stratum becomes the effort of the layer which is above it. The underlying input stratum comprises double dimensional vectors and that explains user and item on top of the input stratum. The dimensional features of the very last concealed stratum Y establishes the model’s efficacy. The last output stratum depicts the envisaged grade. We at the moment put together the NeuralFil’s prognostic model being referred to as ‘deep neural collaborative filtering (NeuralFil)’ layers that maps the vectors of latency in the prediction space. The dimensional feature Y of the last layer explains the efficacy of the model. The predicted score is the output and training is implemented by a point-wise minimization between and expected value . NeuralFil’s predictive model is then formulated as;
and signifying the latent feature matrix for items and users; represents model’s parameter of . f as a function is a multi-layer neural network and can be deduced that;
where and stands for the interaction function for the final phase and a deep neural collaborative filtering phase, where NeuralFil phases in length is available.
4. Model Integration
The two models of NeuralFil—MTF adapts a non-Gaussian kernel as a model that that learns feature relations and MLP which adapts a non-linear kernel to learn the interaction function from massive datasets have been developed, Figure 2. This is for MTF and MLP to reinforce each other so as to improve the user-item interactions. We also want to identify most parameter combinations in order to determine the one that will give the right fusion to reduce the error, to maintain the speed if not to increase it and to improve accuracy, to optimize various parameters well in a one-time engineering complexity strategy. In this paper, it is assumed that, MTF and MLP share a similar embedding layer, whiles their outputs are fused or jointly trained to enhance its generalization potential which is crucial element in machine learning. Same idea as propounded in Neural Tensor Network (NTN) [52] and NCF [19]. For issues of tractability and adaptability of the integrated model, MTF and MLP are made to be trained as isolated stratums which are thereafter combined by lashing the final hidden stratum as depicted in Figure 1. We therefore formulate our model as follows; similar to [19].

Figure 2.
Integrating a non-linear with MLP.
, , represent the user ingrain of MTF and the MLP side as in the case of [22]; ReLU is used as the activation function of the MLP stratum. This model effectively joints the effectiveness of MTF and efficiency of DNNs harnessing the propensity of multimodal datasets of users of a recommender system hence; “NeuralFil,” is short for Neural Tensor Filtering.
Pre-Training
We believe in the initialization of deep neural networks as pertinent as to the convergence and performance of the model [53]. Because NeuralFil is a mutation of MTF and MLP, we present initialization of NeuralFil using pre-trained MLP and MTF. We train MTF and MLP with initializations randomly for quick merging criteria. The model parameters are used to initialize. where and is the m-th vector of the user stratum of MLP and MTF, when tweaked; is the trade-off hyper parameters of the pre-trained paradigms. Training MTF and MLP from beginning, a mini-batch training model is adopted. The rate of learning for each parameter updates are done and are applicable via online and offline trainings. The mini-batch algorithm provides faster convergence for both models.
5. Results
5.1. Data Preparation
Two recommendation available accessible datasets: Amazon datasets, MovieLens (Table 2). The movie rating dataset is an explicit feedback data containing one million ratings, We intentionally chose this to investigate the performance of learning from the multimodal data [54]. The second datasets, Amazon contains product reviews and metadata from Amazon, including 142.8 million review [55]. This dataset includes reviews (ratings, text and helpfulness votes), product metadata (descriptions, category information, price, brand and image features) and links. In order to study MTF’s parallel performance, we process it into three 3-order tensors, where each mode correspond to users, movies and calendar month, respectively. The rates range from 0.5 to 5. The hyper-parameters are all determined by cross validation. The ratings of amazon datasets range from 1 to 5. NeuralFil models are pre-trained and are inadvertently initialized with parameters of zero meaan and a deviation of 0.01, then optimized with mini-batch inference. A rate of 0.0001, 0.0005, 0.001, 0.005 is used for learning the parameters. Based on the fact that of the last hidden layer revealing the efficacy of the model, the factors of {4, 8, 16, 32, 64} were evaluated. Large values might have brought about outliers and hamper the proper efficiency thereby employing 3 hidden layers for MLP as proposed by [19] for a predictive value of 4, the structure of the NeuralFil layers is 64→32→16→8→4, whiles the stratum would be 8. İn the NeuralFil’s pre-training strategy, tuned around 0.5, permitting the pre-trained values to work well in NeuralFil’s strategy.

Table 2.
Evaluation datasets.
The actual data is massive and sparsely distributed. So, the dataset is preprocessed in the same way as the MovieLens data and maintained only users with at least 20 rating scores. Each relationship signifies if a user rated an item or reviewed it.
5.2. Evaluation
The Normalized Discounted Cumulative Gain (NDCG) sorts all relevant documents in the corpus by their relative relevance. This produces the maximum possible Discounted Cumulative Gain (DCG) through position p, also called Ideal DCG (IDCG). For the quality of the proposed algorithm, the normalized discounted cumulative gain or NDCG, is computed as;
Thus
NDCG value of (1) was obtained from the MTF algorithm which shows a degree of relevance of the algorithm.
The model had an NDCG value of (0.0311926404933), showing the competitiveness of the MTF model. In evaluating the effectiveness of the proposed model, the Normalized Discounted Cumulative Gain (NDCG) as well as the Hit Ratio are used as the metric for that purpose [11]. The rank list is concatenated at 8 for both metrics. The HR actually calculates the extent of the test item on the top-8 list, whiles NDCG measures the position of hit allocating massive values to the top rank hits [19]. The two metrics were calculated as applicable to each test and weighted values are reported.
5.3. Efficiency of NeuralFil
Figure 3 shows the efficiency of HR@8 and NDCG@8 with respect to the number of predictive factors. We can infer that, NeuralFil’s performs best on both datasets, significantly outperforming the state of the-art methods GMF, NeuMF, NNMF by a relatively appreciable margin. This indicates the high expressiveness of NeuralFil ‘s fusion strategy of MTF and non-linear MLP models. In the small predictive factors, MTF outperforms GMF on both datasets; although MTF suffers from overfitting for large factors, its best performance obtained is better. Lastly, MTF shows consistent improvements over NNMF, admitting the effectiveness of the log loss for collaborative recommendation task.

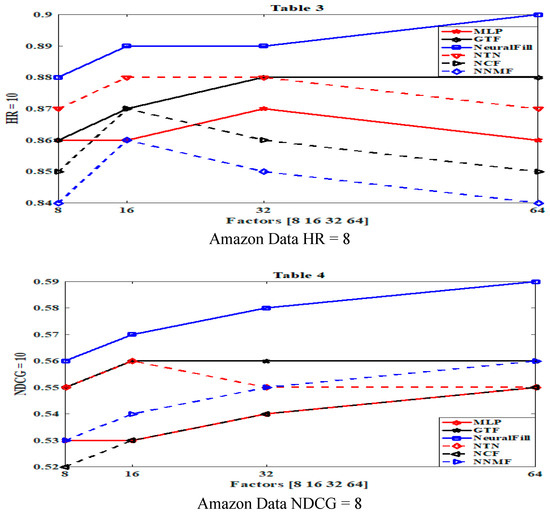
Figure 3.
Performance of NDCG and HR with their respective predictive factors on the datasets.
5.4. Pre-Training Strategy
In demonstrating the benefits of pre-training the NeuralFil, the performance of two scenarios of NeuralFil with pre-training as well as no pre-training is implemented. As shown in Figure 4, the NeuralFil with pretraining attained better prediction performance in most cases as depicted. This result proves the effectiveness of our pre-training method for NeuralFil’s initialization strategy.
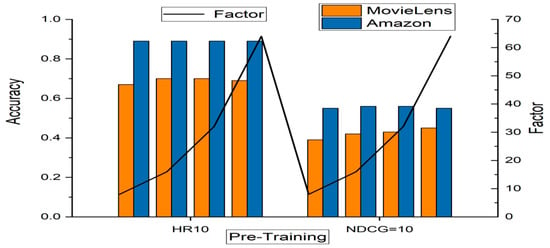
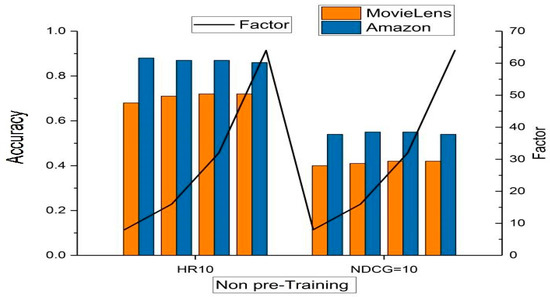
Figure 4.
Deep Learning Performance.
5.5. The Efficacy of DNN for modelling User-Item Interaction
Research on item-user association modelling bluredwith deep learning is trivial. It is therefore worth researching to prove whether using a deep network model is prudent on recommendation systems. Working towards that objective, MLP with different hidden layers were further experimented. Results are depicted in Figure 5. This result is highly encouraging, indicating the efficiency of using deep models for collaborative filtering prediction task.
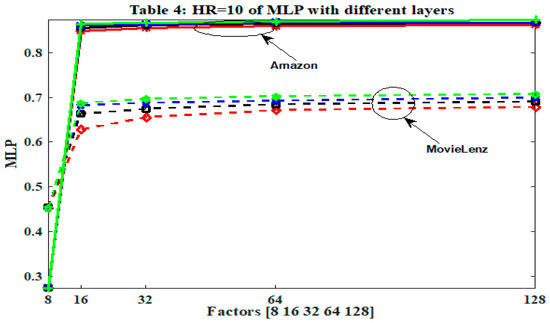
Figure 5.
Performance of MLP.
5.6. Computational Complexity Analysis
NeuralFil needs two steps to update all variables once. The first step updates . For each value the computational complexity of an update is . Since the total number of observed entries in each process is about |Ω|/N, the time complexity of step one is O(|Ω|R/N). The next step has to update a matrix of size (J × R) and another of size (K × R) in every process, thus the computational complexity is O(max{J,K}R). In all, the computational complexity of NeuralFil in each iteration could run down to O(|Ω|R/N + max{J,K}R). We compare our proposed NeuralFil strategies: ‘MTF and MLP’ with the following methods: Neural Collaborative Filtering(NCF) [19]: This method optimizes the MTF model of Equation (2) with a pairwise ranking loss, which is geared towards learning from implicit feedback. It is a highly competitive baseline for item recommendation.
Neural Network Matrix Factorization (NNMF) [56]: This method alternates between optimizing the network for fixed latent features and optimizing the latent features for a fixed network. We used a fixed learning rate, varying it and reporting the best performance. Neural Tensor Networks (NTN) [52]; an expressive neural tensor network suitable for reasoning over relationships between two entities. Figure 3 and Figure 4 depicts the results.
6. Conclusions
In this work, we present deep neural network modelling with multimodal datasets for collaborative recommendation system. The general framework NeuralFil is proposed with two different models—MTF, MLP—for modelling item-user associations in a novel way. Our framework is simple and generalizes well [57]; it is not limited to the models presented in this paper but is designed to serve as a basis for developing deep learning methods for recommendation. Our model networks can generalize better to unseen feature combinations through low-dimensional dense embedding learned for the sparse features through little dimensional re-engineering. In this paper, we have applied a tensor-based deep neural network framework which propagates gradients from the output to both the nonlinear tensor and MLP using a mini-batch stochastic algorithm which is novel. In this paper, we have illuminated that tensor factorization, are very promising tools for big data optimization problems. High Volume implies the need for algorithms that are scalable. We have used tensor factorization as a framework which is scalable. Value refers to extracting high quality and consistent data which could lend themselves to meaningful and interpretable results and in this paper, neural networks has been used to achieve value associated with big data. High Volume implies the need for algorithms that are scalable. We have used tensor factorization as a framework which is scalable. One of the novel strategies implemented in this paper are pre-training initialization and mini-batch stochastic gradient propagation strategies and our efficient tensor strategy makes this particular paper distinct. In the future, temporal dynamics for parallel processing for social would be envisaged. This novel multi-task learning which a hybrid transfer is shows outstanding performance and is competitive over other existing models. It is robust as a result of the evidence from the baseline comparisons.
Author Contributions
The following statements should be used “conceptualization, E.O.A. methodology, E.O.A.; software, R.K.; validation, E.O.A. and R.K., formal analysis; R.K., investigation, E.O.A.; resources, E.O.A.; data curation, R.K.; writing—original draft preparation, E.O.A.; writing—review and editing, E.O.A.; visualization, E.O.A.; supervision, E.O.A.
Funding
This work was supported in part by the programs of International Science and Technology Cooperation and Exchange of Sichuan Province under Grant 2017HH0028 and Grant 2018HH0102, in part by the Fundamental Research Funds for the Central Universities under Grant ZYGX2016J152 and Grant ZYGX2016J170, in part by the Key Research and Development Projects of High and New Technology Development and Industrialization of Sichuan Province under Grant 2017GZ0007, in part by the National Key Research and Development Program of China under Grant 2016QY04WW0802, Grant 2016QY04W0800 and Grant 2016QY04WW0803 and in part by the National Engineering Laboratory for Big data application on improving government governance capabilities.
Acknowledgments
I wish to acknowledge the direction and the supervision of Gee James, Jianbin Gao and Qi Xia of University of Science and Technology, Chengdu, China.
Conflicts of Interest
Authors declare no conflict of interest in this paper.
References
- Cichocki, A. Era of Big Data Processing: A New Approach via Tensor Networks and Tensor Decompositions. arXiv, 2014; arXiv:1403.2048. [Google Scholar]
- Mujawar, S. Big Data: Tools and Applications. Int. J. Comput. Appl. 2015, 115, 7–11. [Google Scholar] [CrossRef]
- Cichocki, A. Tensor networks for big data analytics and large-scale optimization problems. arXiv, 2014; arXiv:1407.3124. [Google Scholar]
- Park, D.H.; Kim, H.K.; Choi, I.Y.; Kim, J.K. A literature review and classification of recommender systems research. Expert Syst. Appl. 2012, 39, 10059–10072. [Google Scholar] [CrossRef]
- Zheng, L.; Noroozi, V.; Yu, P.S. Joint Deep Modeling of Users and Items Using Reviews for Recommendation. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; pp. 425–433. [Google Scholar]
- Zhang, Q.; Wu, D.; Lu, J.; Liu, F.; Zhang, G. A cross-domain recommender system with consistent information transfer. Decis. Support Syst. 2017, 104, 49–63. [Google Scholar] [CrossRef]
- Sun, M.; Li, F.; Zhang, J. A Multi-Modality Deep Network for Cold-Start Recommendation. Big Data Cogn. Comput. 2018, 2, 7. [Google Scholar]
- Han, H.; Jain, A.K.; Shan, S.; Chen, X. Heterogeneous Face Attribute Estimation: A Deep Multi-Task Learning Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 2597–2609. [Google Scholar] [CrossRef] [PubMed]
- Suphavilai, C.; Bertrand, D.; Nagarajan, N. Predicting Cancer Drug Response using a Recommender System. Bioinformatics 2018, 34, 3907–3914. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Tan, P.-N.; Zhou, J.; Luo, L. Online Multi-task Learning Framework for Ensemble Forecasting. IEEE Trans. Knowl. Data Eng. 2017, 29, 1268–1280. [Google Scholar] [CrossRef]
- Brodén, B.; Hammar, M.; Nilsson, B.J.; Paraschakis, D. Ensemble Recommendations via Thompson Sampling: An Experimental Study within e-Commerce. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2018; Volume 74, pp. 19–29. [Google Scholar]
- Fang, X.; Pan, R.; Cao, G.; He, X.; Dai, W. Personalized Tag Recommendation through Nonlinear Tensor Factorization Using Gaussian Kernel. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–29 January 2015; pp. 439–445. [Google Scholar]
- Zahraee, S.M.; Assadi, M.K.; Saidur, R. Application of Artificial Intelligence Methods for Hybrid Energy System Optimization. Renew. Sustain. Energy Rev. 2016, 66, 617–630. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine learning. In Burr Ridge; McGraw Hill: New York, NY, USA, 1997; Volume 45, pp. 870–877. [Google Scholar]
- Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Niemi, J.; Tanttu, J. Deep Learning Case Study for Automatic Bird Identification. Appl. Sci. 2018, 8, 2089. [Google Scholar] [CrossRef]
- Zheng, X.; Luo, Y.; Sun, L.; Zhang, J.; Chen, F. A tourism destination recommender system using users’ sentiment and temporal dynamics. J. Intell. Inf. Syst. 2018, 51, 557–578. [Google Scholar] [CrossRef]
- Abdi, M.H.; Okeyo, G.O.; Mwangi, R.W. Matrix Factorization Techniques for Context-Aware Collaborative Filtering Recommender Systems: A Survey. Comput. Inf. Sci. 2018, 11, 1. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.-S. Neural Collaborative Filtering. In Proceedings of the 26th International Conference on World Wide Web (WWW ’17), Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
- Chen, H.; Dou, Q.; Yu, L.; Qin, J.; Heng, P.A. VoxResNet: Deep voxelwise residual networks for brain segmentation from 3D MR images. NeuroImage 2017, 170, 446–455. [Google Scholar] [CrossRef]
- Arshad, S.; Shah, M.A.; Wahid, A.; Mehmood, A.; Song, H. SAMADroid: A Novel 3-Level Hybrid Malware Detection Model for Android Operating System. IEEE Access 2018, 6, 4321–4339. [Google Scholar] [CrossRef]
- Ansong, M.O.; Huang, J.S.; Yeboah, M.A.; Dun, H.; Yao, H. Non-Gaussian Hybrid Transfer Functions: Memorizing Mine Survivability Calculations. Math. Probl. Eng. 2015, 2015, 623720. [Google Scholar] [CrossRef]
- Shi, Z.; Zuo, W.; Chen, W.; Yue, L.; Han, J.; Feng, L. User Relation Prediction Based on Matrix Factorization and Hybrid Particle Swarm Optimization. In Proceedings of the 26th International Conference on World Wide Web Companion, Perth, Australia, 3–7 April 2017; pp. 1335–1341. [Google Scholar]
- Zitnik, M.; Zupan, B. Data Fusion by Matrix Factorization. Pattern Anal. Mach. Intell. IEEE Trans. 2015, 37, 41–53. [Google Scholar] [CrossRef]
- Kumar, R.S.; Sathyanarayana, B. Adaptive Genetic Algorithm Based Artificial Neural Network for Software Defect Prediction. Glob. J. Comput. Sci. Technol. 2015, 15. [Google Scholar]
- Opoku, E.; James, G.C.; Kumar, R.; Opoku, E.; James, G.C.; Kumar, R. ScienceDirect ScienceDirect Evaluating the Performance of Deep Neural Networks for Health Evaluating the Performance of Deep Neural Networks for Health Decision Making Decision Making. Procedia Comput. Sci. 2018, 131, 866–872. [Google Scholar]
- Yera, R.; Mart, L. Fuzzy Tools in Recommender Systems: A Survey. Int. J. Comput. Intell. Syst. 2017, 10, 776–803. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer Perceptron (MLP). In Geomatic Approaches for Modelling Land Change Scenarios; Springer: Berlin, Germany, 2018; pp. 451–455. [Google Scholar]
- Zare, M.; Pourghasemi, H.R.; Vafakhah, M.; Pradhan, B. Landslide susceptibility mapping at Vaz Watershed (Iran) using an artificial neural network model: A comparison between multilayer perceptron (MLP) and radial basic function (RBF) algorithms. Arab. J. Geosci. 2013, 6, 2873–2888. [Google Scholar] [CrossRef]
- Li, S.; Xing, J.; Niu, Z.; Shan, S.; Yan, S. Shape driven kernel adaptation in Convolutional Neural Network for robust facial trait recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 222–230. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. Proc. IEEE Int. Conf. Comput. Vis. 2017, 115, 4278–4284. [Google Scholar]
- Xu, Z.; Yan, F.; Qi, Y. Bayesian nonparametric models for multiway data analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 475–487. [Google Scholar] [CrossRef] [PubMed]
- Aboagye, E.O.; James, G.C.; Jianbin, G.; Kumar, R.; Khan, R.U. Probabilistic Time Context Framework for Big Data Collaborative Recommendation. In Proceedings of the 2018 International Conference on Computing and Artificial Intelligence, ICCAI, Chengdu, China, 12–14 March 2018; pp. 118–121. [Google Scholar]
- Chen, W.; Hsu, W.; Lee, M.L. Making recommendations from multiple domains. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’13, Chicago, IL, USA, 11–14 August 2013; p. 892. [Google Scholar]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Vervliet, N.; Debals, O.; Sorber, L.; De Lathauwer, L. Breaking the curse of dimensionality using decompositions of incomplete tensors: Tensor-based scientific computing in big data analysis. IEEE Signal Process. Mag. 2014, 31, 71–79. [Google Scholar] [CrossRef]
- Nickel, M.; Tresp, V. An Analysis of Tensor Models for Learning on Structured Data. Mach. Learn. Knowl. Discov. Databases 2013, 8189, 272–287. [Google Scholar]
- Karatzoglou, A.; Amatriain, X.; Baltrunas, L.; Oliver, N. Multiverse recommendation: N-dimensional tensor factorization for context-aware collaborative filtering. In Proceedings of the fourth ACM Conference on Recommender Systems, RecSys ’10, Barcelona, Spain, 26–30 September 2010; p. 79. [Google Scholar]
- Li, G.; Xu, Z.; Wang, L.; Ye, J.; King, I.; Lyu, M. Simple and efficient parallelization for probabilistic temporal tensor factorization. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1–8. [Google Scholar]
- Opoku, A.E.; Jianbin, G.; Xia, Q.; Tetteh, N.O.; Eugene, O.M. Efficient Tensor Strategy for Recommendation. ASTES J. 2017, 2, 111–114. [Google Scholar] [CrossRef]
- Liu, X.; De Lathauwer, L.; Janssens, F.; De Moor, B. Hybrid clustering of multiple information sources via HOSVD. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2010; Volume 6064 LNCS, pp. 337–345. [Google Scholar]
- Yang, F.; Shang, F.; Huang, Y.; Cheng, J.; Li, J.; Zhao, Y.; Zhao, R. Lftf: A framework for efficient tensor analytics at scale. Proc. VLDB Endow. 2017, 10, 745–756. [Google Scholar] [CrossRef]
- Frolov, E.; Oseledets, I. Tensor Methods and Recommender Systems. arXiv, 2016; arXiv:1603.06038. [Google Scholar]
- Cheng, H.T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.; Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.; et al. Wide & Deep Learning for Recommender Systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, Boston, MA, USA, 15 September 2016. [Google Scholar]
- Dhillon, I.S.; Guan, Y.; Kulis, B. Kernel k-means, Spectral Clustering and Normalized Cuts. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004; pp. 551–556. [Google Scholar]
- Sohangir, S.; Wang, D.; Pomeranets, A.; Khoshgoftaar, T.M. Big Data: Deep Learning for financial sentiment analysis. J. Big Data 2018, 5, 3. [Google Scholar] [CrossRef]
- Gantner, Z.; Drumond, L.; Freudenthaler, C.; Schmidt-Thieme, L. Bayesian Personalized Ranking for Non-Uniformly Sampled Items. In Proceedings of the KDD Cup 2011, San Diego, CA, USA, 21–24 August 2011; Volume 18, pp. 231–247. [Google Scholar]
- Liu, M.; Li, S.; Shan, S.; Chen, X. AU-inspired Deep Networks for Facial Expression Feature Learning. Neurocomputing 2015, 159, 126–136. [Google Scholar] [CrossRef]
- Hong, R.; Hu, Z.; Liu, L.; Wang, M.; Yan, S.; Tian, Q. Understanding Blooming Human Groups in Social Networks. IEEE Trans. Multimed. 2015, 17, 1980–1988. [Google Scholar] [CrossRef]
- Wang, M.; Fu, W.; Hao, S.; Liu, H.; Wu, X. Learning on Big Graph: Label Inference and Regularization with Anchor Hierarchy. IEEE Trans. Knowl. Data Eng. 2017, 29, 1101–1114. [Google Scholar] [CrossRef]
- Parkhi, O.M.; Vedaldi, A.; Zisserman, A. Deep Face Recognition. BMVC 2015, 1, 6. [Google Scholar]
- Socher, R.; Chen, D.; Manning, C.; Chen, D.; Ng, A. Reasoning with Neural Tensor Networks for Knowledge Base Completion; Neural Information Processing Systems: La Jolla, CA, USA, 2013; pp. 926–934. [Google Scholar]
- Rauber, P.E.; Fadel, S.G.; Falcão, A.X.; Telea, A.C. Visualizing the Hidden Activity of Artificial Neural Networks. IEEE Trans. Vis. Comput. Graph. 2017, 23, 101–110. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Yuan, L.; Liao, J.; Yu, N.; Hua, G. Stylebank: An explicit representation for neural image style transfer. arXiv, 2017; arXiv:1703.09210. [Google Scholar]
- McAuley, J.; Pandey, R.; Leskovec, J. Inferring Networks of Substitutable and Complementary Products. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; p. 12. [Google Scholar]
- Covington, P.; Adams, J.; Sargin, E. Deep Neural Networks for YouTube Recommendations. In Proceedings of the 10th ACM Conference on Recommender Systems, RecSys ’16, Boston, MA, USA, 15–19 September 2016. [Google Scholar]
- Boaz, A.; Gough, D. Deep and wide: New perspectives on evidence and policy. Evid. Policy 2012, 8, 139–140. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).