Joint Uplink and Downlink Resource Allocation for D2D Communications System
Abstract
1. Introduction
2. System Model and Problem Formulation
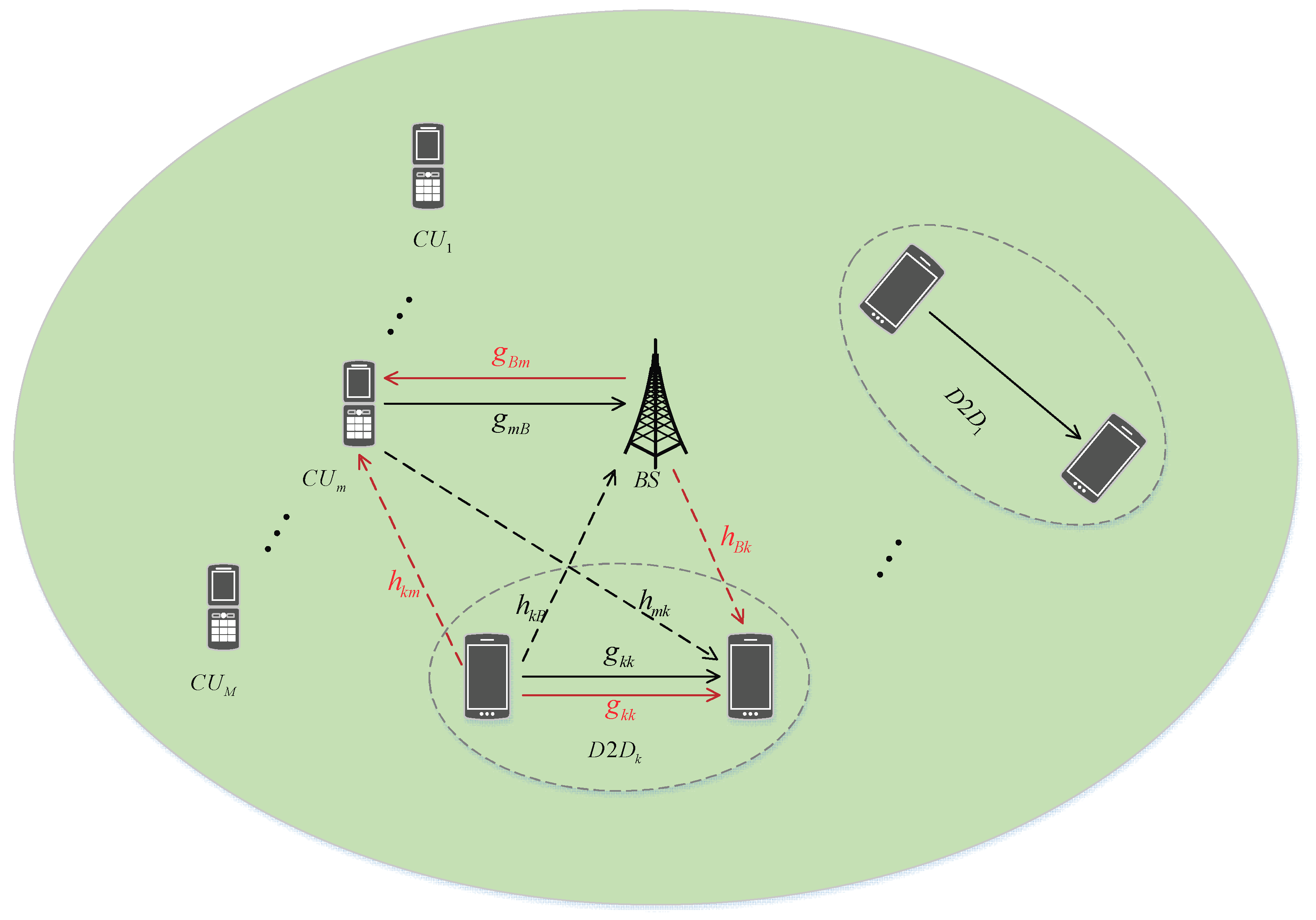
2.1. System Model
2.2. System Capacity
2.2.1. Uplink Phase
2.2.2. Downlink Phase
2.3. Problem Formulation
3. Resource Allocation Algorithm
3.1. Power Allocation
3.2. Channel Assignment
| Algorithm 1. Optimal Resource Hungarian Algorithm |
| 1: : The set of CU users : The set of D2D pairs |
| 2: Using the Power allocation scheme to derive the optimal transmission power |
| 3: for |
| 4: for |
| 5: calculate |
| 6: end |
| 7: end |
| 8: The big-value matrix |
| 9: |
| 10: Returns the assigned channel value using the Hungarian algorithm function |
| 11: system capacity after returning the 1st Hungarian algorithm |
| 12: store the conflicting channel |
| 13: if the 1st Hungarian algorithm did not allocate all channels |
| 14: |
| 15: |
| 16: |
| 17: |
| 18: else |
| 19: |
| 20: end |
| 21: Allocate resources using the Hungarian algorithm until the number of conflicting channels is 0 |
| 22: The total system capacity is calculated by using the sum function |
| 23: Complete joint uplink and downlink Channel allocation |
4. Numerical Analysis
4.1. Simulation Parameters
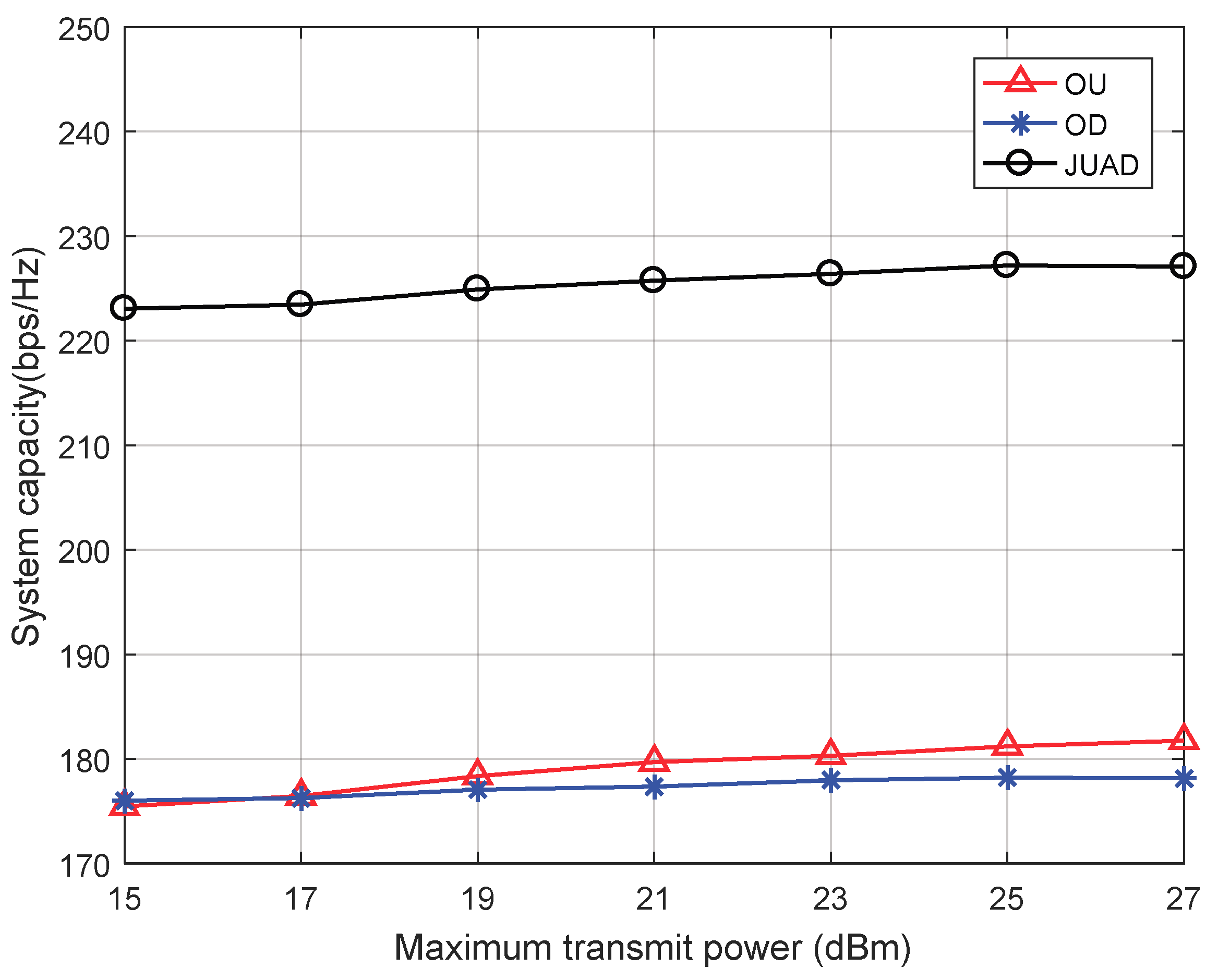
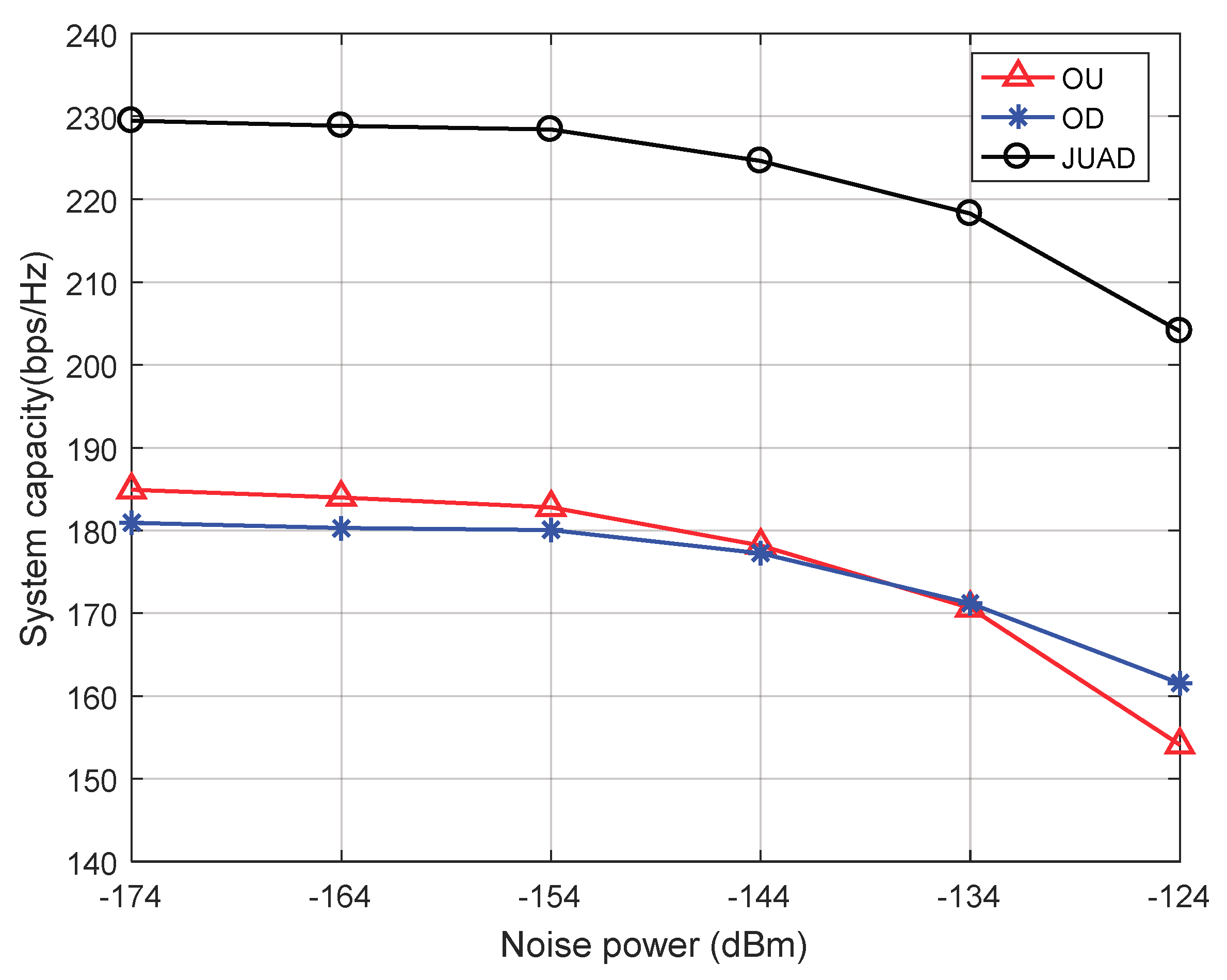
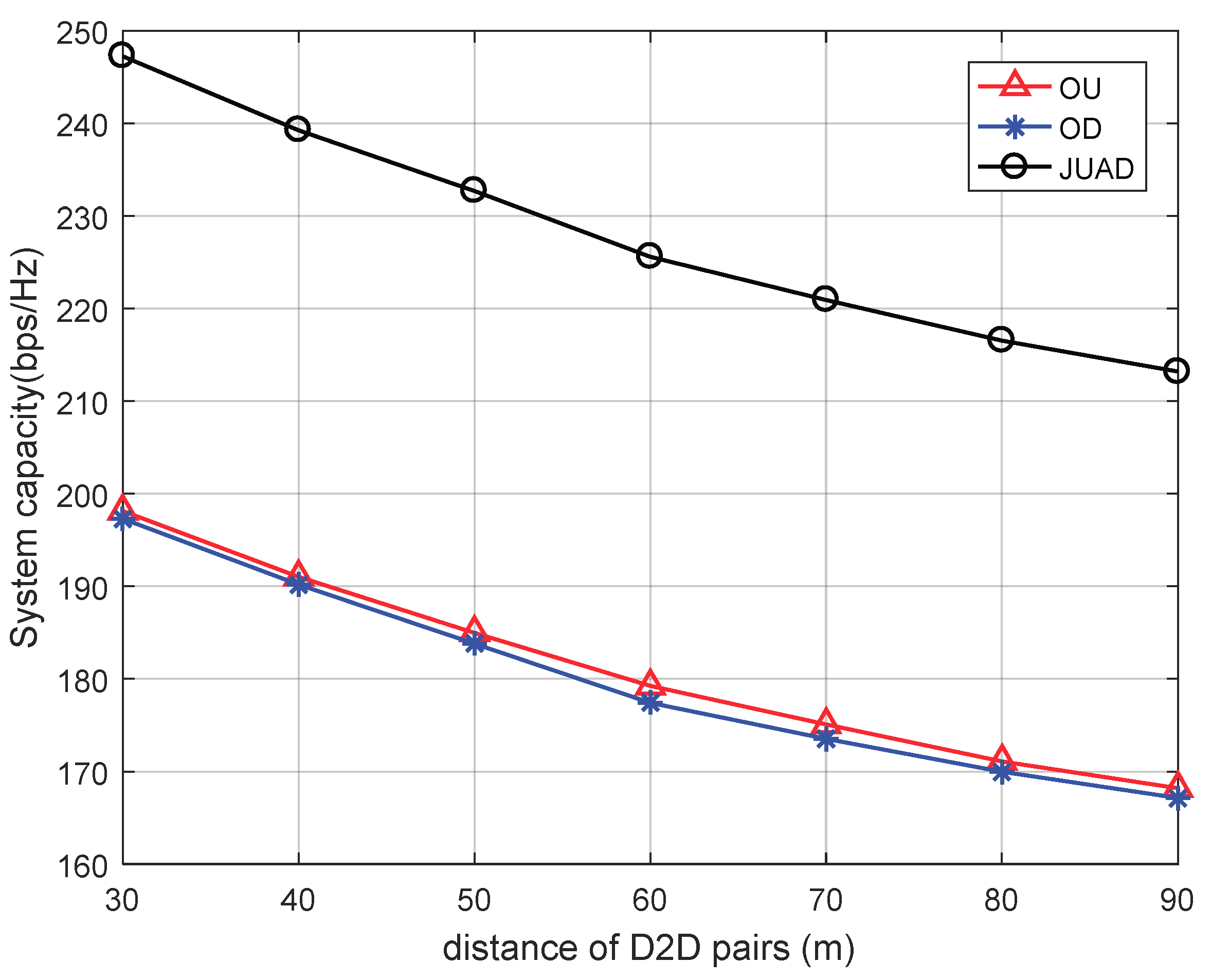
- OU: A two-step resource management scheme is proposed to optimize transmission power of D2D pairs and the spectrum efficiency of the network in [31]. Firstly, the interaction between BS and D2D pairs is modeled as a two-level Stackelberg game to get the best transmission power for each D2D. Secondly, the uplink resource allocation algorithm based on the Hungarian algorithm is proposed to assign spectrum to each D2D pair.
- OD: A social-aware jamming allocation for D2D multicast secure communication is proposed in reference [32]. Firstly, a novel D2D cluster and jammer formation scheme is designed, which takes account of the physical domain and the social domain. Secondly, a joint optimal power control and jamming allocation is obtained, and the Hungarian algorithm is introduced to provide the final solution.
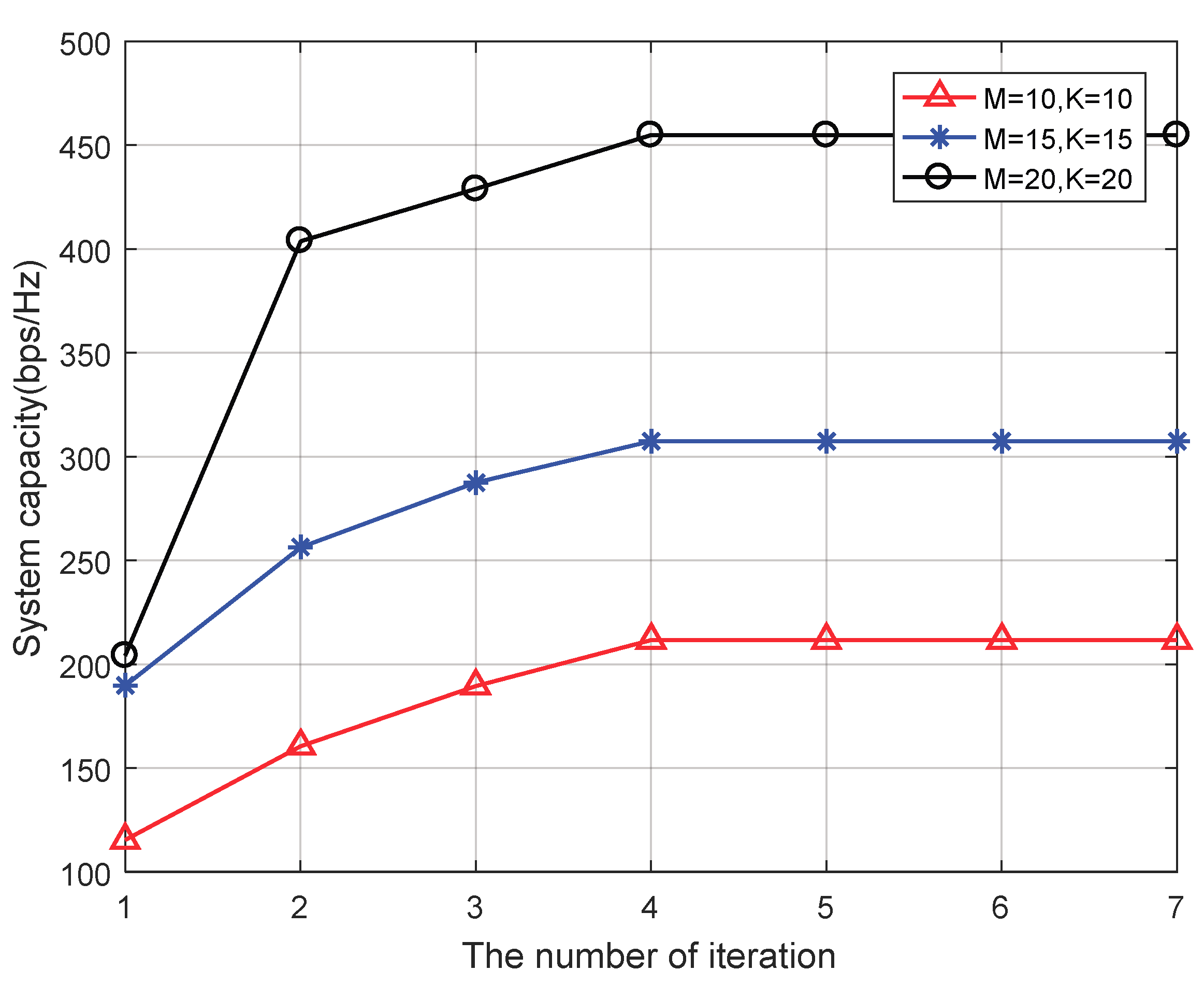
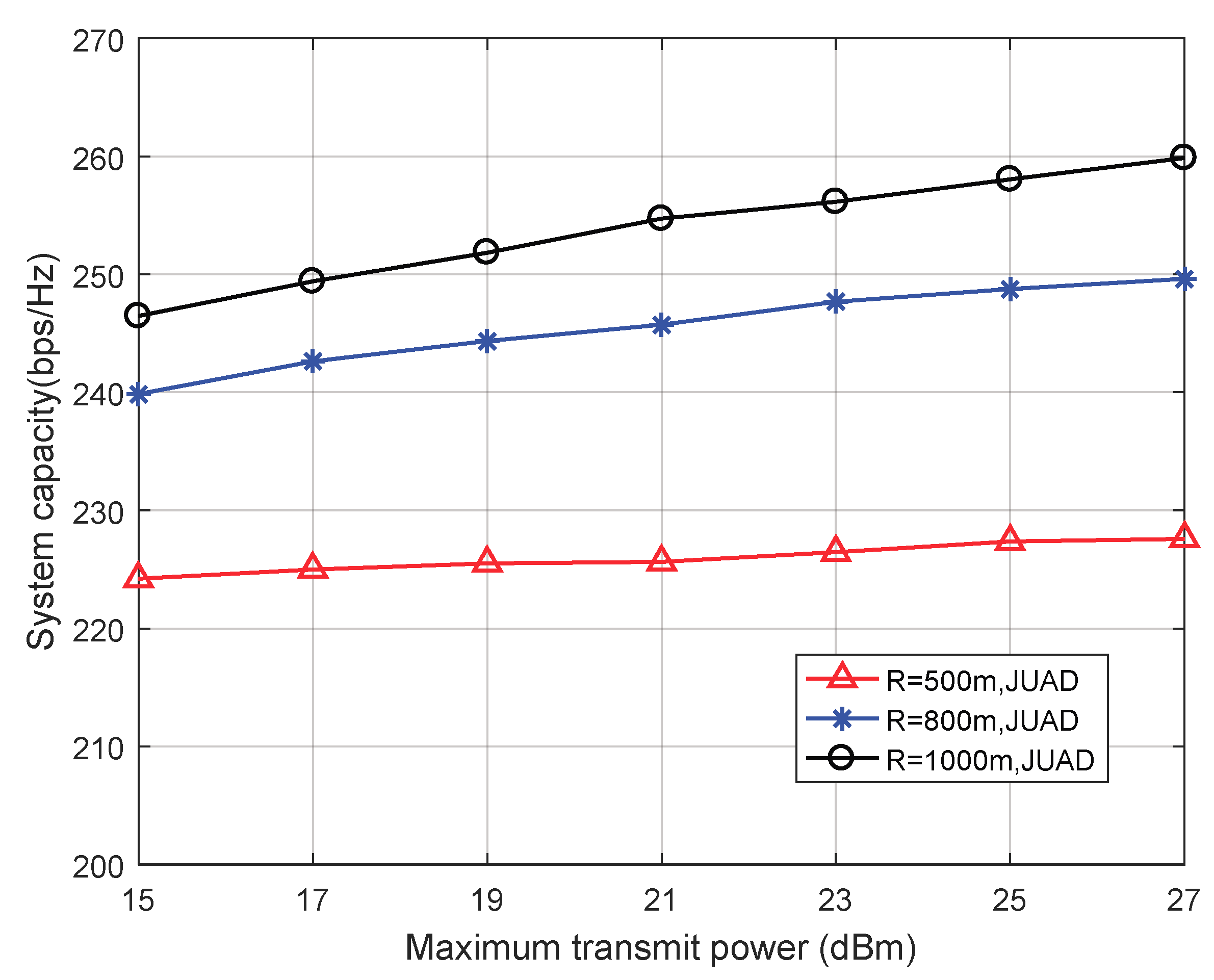
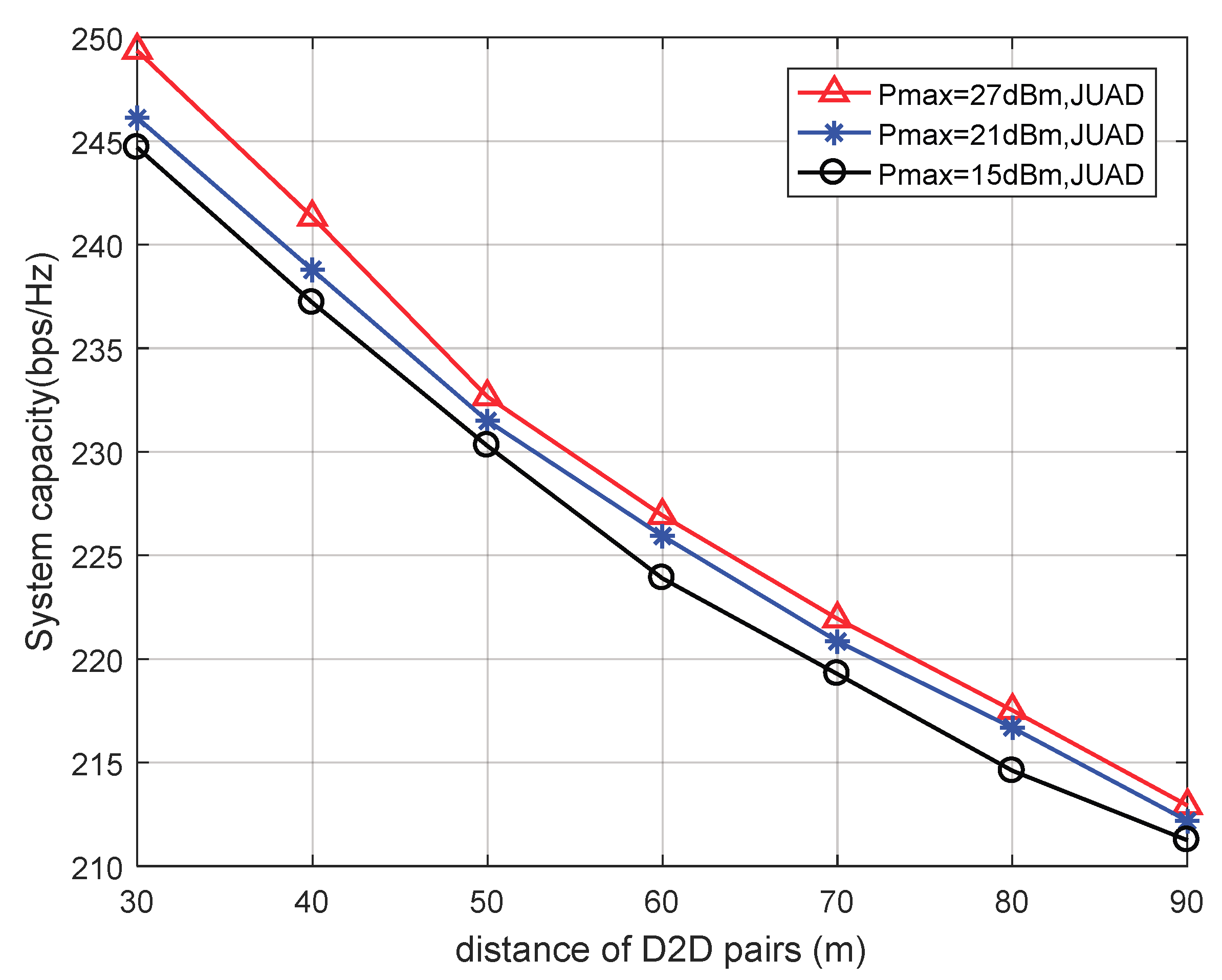
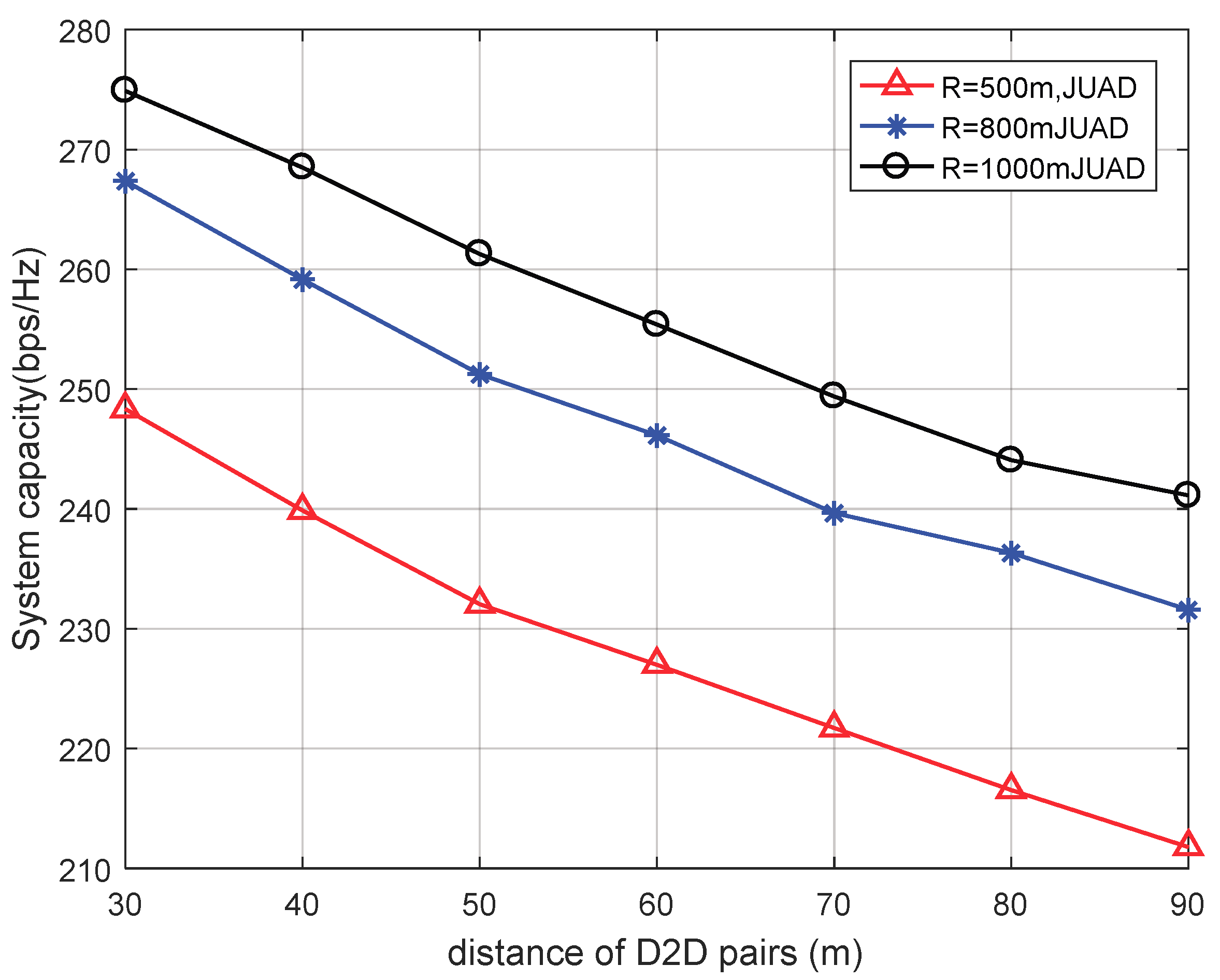
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Agiwal, M.; Roy, A.; Saxena, N. Next generation 5G wireless networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Chen, S.; Zhao, J. The requirements, challenges, and technologies for 5G of terrestrial mobile telecommunication. IEEE Commun. Mag. 2014, 52, 36–43. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, G.; Dong, M.; Ota, K.; Xu, C.; Jia, Y. Iterative Energy-Efficient Stable Matching Approach for Context-Aware Resource Allocation in D2D Communications. IEEE Access 2016, 4, 6181–6196. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, S. Resource Allocation for Device-to-Device Communication Underlaying Cellular Networks: An Alternating Optimization Method. IEEE Commun. Lett. 2015, 19, 1398–1401. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, R.; Cheng, X.; Yang, L. Graph coloring based resource sharing (GCRS) scheme for D2D communications underlaying full-duplex cellular networks. IEEE Trans. Veh. Technol. 2017, 66, 7506–7517. [Google Scholar] [CrossRef]
- Wu, D.; Cai, Y.; Hu, R.Q.; Qian, Y. Dynamic distributed resource sharing for mobile D2D communications. IEEE Trans. Wirel. Commun. 2015, 14, 5417–5429. [Google Scholar] [CrossRef]
- Feng, D.; Lu, L.; Yuan-Wu, Y.; Li, G.Y.; Feng, G.; Li, S. Device-to-device communications underlaying cellular networks. IEEE Trans. Commun. 2013, 61, 3541–3551. [Google Scholar] [CrossRef]
- Gurjar, D.S.; Upadhyay, P.K. Overlay Device-to-Device Communications in Asymmetric Two-Way Cellular Systems with Hybrid Relaying. IEEE Syst. J. 2017, 12, 3713–3724. [Google Scholar] [CrossRef]
- Katsinis, G.; Tsiropoulou, E.E.; Papavassiliou, S. Joint resource block and power allocation for interference Management in Device to device underlay cellular networks: A game theoretic approach. Mob. Netw. Appl. 2017, 22, 539–551. [Google Scholar] [CrossRef]
- Song, L.; Niyato, D.; Han, Z.; Hossain, E. Game-theoretic resource allocation methods for device-to-device communication. IEEE Wirel. Commun. 2014, 21, 136–144. [Google Scholar] [CrossRef]
- Asadi, A.; Wang, Q.; Mancuso, V. A survey on device-to-device communication in cellular networks. IEEE Commun. Surv. Tutor. 2014, 16, 1801–1819. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, Z.; Xing, C.; Xiao, H. Uplink Resource Allocation for Relay-Aided Device-to-Device Communication. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3883–3892. [Google Scholar] [CrossRef]
- Yu, G.; Xu, L.; Feng, D.; Yin, R.; Li, G.Y.; Jiang, Y. Joint mode selection and resource allocation for device-to-device communications. IEEE Trans. Commun. 2014, 62, 3814–3824. [Google Scholar] [CrossRef]
- Abedin, A.; Rasti, M. A distributed joint power control and mode selection scheme for D2D-enabled cellular systems. In Proceedings of the 2016 IEEE Symposium on Computers and Communication (ISCC), Messina, Italy, 27–30 June 2016; pp. 1284–1289. [Google Scholar]
- Han, X.; Song, X.; Li, D.; Wang, J. Uplink Resource Allocation in Device-to-Device Communication System. In Proceedings of the 2018 International Symposium on Water System Operations (ISWSO), Beijing, China, 16–20 October 2018. [Google Scholar]
- Gu, Y.; Zhang, Y.; Pan, M.; Han, Z. Matching and cheating in device to device communications underlying cellular networks. IEEE J. Sel. Areas Commun. 2015, 33, 2156–2166. [Google Scholar] [CrossRef]
- Xu, Y.; Yin, R.; Han, T.; Yu, G. Dynamic resource allocation for Device-to-Device communication underlaying cellular networks. Int. J. Commun. Syst. 2014, 27, 2408–2425. [Google Scholar] [CrossRef]
- Huang, J.; Sun, Y.; Chen, Q. GALLERY: A game-theoretic resource allocation scheme for multicell device-to-device communications underlaying cellular networks. IEEE Internet Things J. 2015, 2, 504–514. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Chai, K.K.; Elkashlan, M.; Chen, Y. Matching with peer effects for context-aware resource allocation in D2D communications. IEEE Commun. Lett. 2017, 21, 837–840. [Google Scholar] [CrossRef]
- Kai, C.; Li, H.; Xu, L.; Li, Y.; Jiang, T. Energy-Efficient Device-to-Device Communications for Green Smart Cities. IEEE Trans. Ind. Inform. 2018, 14, 1542–1551. [Google Scholar] [CrossRef]
- Chen, X.; Hu, R.Q.; Qian, Y. Distributed resource and power allocation for device-to-device communications underlaying cellular network. In Proceedings of the 2014 IEEE Global Communications Conference (GLOBECOM), Austin, TX, USA, 8–12 December 2014; pp. 4947–4952. [Google Scholar]
- Zhang, R.; Cheng, X.; Yang, L.; Jiao, B. Interference graph-based resource allocation (InGRA) for D2D communications underlaying cellular networks. IEEE Trans. Veh. Technol. 2015, 64, 3844–3850. [Google Scholar] [CrossRef]
- Lee, C.-H.; Chang, R.Y.; Lin, C.-T.; Cheng, S.-M. Sum-rate maximization for energy harvesting-aided D2D communications underlaid cellular networks. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017. [Google Scholar]
- Dominic, S.; Jacob, L. Distributed Resource Allocation for D2D Communications Underlaying Cellular Networks in Time-Varying Environment. IEEE Commun. Lett. 2018, 22, 388–391. [Google Scholar] [CrossRef]
- Hoang, T.D.; Le, L.B.; Le-Ngoc, T. Resource allocation for D2D communications under proportional fairness. In Proceedings of the 2014 IEEE Global Communications Conference (GLOBECOM), Austin, TX, USA, 8–12 December 2014; pp. 1259–1264. [Google Scholar]
- Wang, H.; Wang, J.; Ding, G.; Han, Z. D2D Communications Underlaying Wireless Powered Communication Networks. IEEE Trans. Veh. Technol. 2018, 67, 7872–7876. [Google Scholar] [CrossRef]
- Hu, J.; Heng, W.; Li, X.; Wu, J. Energy-efficient resource reuse scheme for D2D communications underlaying cellular networks. IEEE Commun. Lett. 2017, 21, 2097–2100. [Google Scholar] [CrossRef]
- Idris, F.; Tang, J.; So, D.K. Resource and energy efficient device to device communications in downlink cellular system. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018. [Google Scholar]
- Zhao, P.; Yu, P.; Feng, L.; Li, W.; Qiu, X. Gain-Aware Joint Uplink-Downlink Resource Allocation for Device-to-Device Communications. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, NSW, Australia, 4–7 June 2017. [Google Scholar]
- Huynh, T.; Onuma, T.; Kuroda, K.; Hasegawa, M.; Hwang, W.-J. Joint downlink and uplink interference management for device to device communication underlaying cellular networks. IEEE Access 2016, 4, 4420–4430. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Gao, M.; Zhang, Q.; Li, H.; Ahmad, I.; Feng, Z. Resource management in device-to-device underlaying cellular network. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015. [Google Scholar]
- Yan, S.; Shang, Y.; Huang, Y. Social-aware Jamming Allocation for Physical-layer Security in D2D Multicast Network. In Proceedings of the 2018 IEEE Conference on Communications and Network Security (CNS), Beijing, China, 30 May–1 June 2018. [Google Scholar]
| Parameter | Value |
|---|---|
| Cell radius | 500 m |
| Bandwidth | 0.5 MHz |
| Noise spectral density | −144 dBm |
| Path loss exponent | 4 |
| Path loss constant | 0.01 |
| Maximum transmission power of CU | 21 dBm |
| Maximum transmission power of D2D | 21 dBm |
| Maximum transmission power of BS | 27 dBm |
| SINR threshold of CU | 13 dB |
| SINR threshold of D2D | 13 dB |
| Number of CUs | 10 |
| Number of D2D pairs | 10 |
| Number of uplink (or downlink) channels | 10 |
| D2D distance | 30–90 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Han, X.; Ni, Y.; Dong, L.; Qin, L. Joint Uplink and Downlink Resource Allocation for D2D Communications System. Future Internet 2019, 11, 12. https://doi.org/10.3390/fi11010012
Song X, Han X, Ni Y, Dong L, Qin L. Joint Uplink and Downlink Resource Allocation for D2D Communications System. Future Internet. 2019; 11(1):12. https://doi.org/10.3390/fi11010012
Chicago/Turabian StyleSong, Xin, Xiuwei Han, Yue Ni, Li Dong, and Lei Qin. 2019. "Joint Uplink and Downlink Resource Allocation for D2D Communications System" Future Internet 11, no. 1: 12. https://doi.org/10.3390/fi11010012
APA StyleSong, X., Han, X., Ni, Y., Dong, L., & Qin, L. (2019). Joint Uplink and Downlink Resource Allocation for D2D Communications System. Future Internet, 11(1), 12. https://doi.org/10.3390/fi11010012





