Hybrid Approach with Improved Genetic Algorithm and Simulated Annealing for Thesis Sampling

Abstract

Sampling inspection uses the sample characteristics to estimate that of the population, and it is an important method to describe the population, which has the features of low cost, strong applicability and high scientificity. This paper aims at the sampling inspection of the master’s degree thesis to ensure their quality, which is commonly estimated by random sampling. Since there are disadvantages in random sampling, a hybrid algorithm combined with an improved genetic algorithm and a simulated annealing algorithm is proposed in this paper. Furthermore, a novel mutation strategy is introduced according to the specialty of Shanghai’s thesis sampling to improve the efficiency of sampling inspection; the acceleration of convergence of the algorithm can also take advantage of this. The new algorithm features the traditional genetic algorithm, and it can obtain the global optimum in the optimization process and provide the fairest sampling plan under the constraint of multiple sampling indexes. The experimental results on the master’s thesis dataset of Shanghai show that the proposed algorithm well meets the requirements of the sampling inspection in Shanghai with a lower time-complexity.

1. Introduction

The thesis is one of the essential prerequisites for the graduation of postgraduates. Accordingly, thesis sampling inspection has been regarded as a significant task for analyzing and controlling the quality. Such a quality inspection ensures the high-quality standards of postgraduate education. Most of the existing research still is focused on the double-blinded review process of the degree theses. Moreover, there exists no applied research of the problem that Ph.D. dissertations and master’s degree theses of the previous academic year must be sampled for inspection after [1] was issued.

In this paper, theses of the postgraduates who have achieved their degrees are used to carry out sampling inspection under the requirements of the Shanghai Academic Degrees Committee. The Shanghai Academic Degrees Committee builds the platform for provincial degree and postgraduate education, and the system is practically used in the Shanghai Postgraduate Education Quality Informatization Evaluation System [2].

To this end, this paper focuses on the sampling method that meets the actual need for quality inspection. The hybrid approach with the combination of the genetic algorithm and the simulated annealing algorithm automatically samples master’s theses from Shanghai in the previous year under the requirements of national sampling inspection of the Shanghai Academic Degree Committee. Development tools are used to implement the method to rebound the theoretical research and practical applications from the aspect of specific operations.

With the combination of the traditional genetic algorithm and the simulated annealing algorithm, a new mutation operation is also developed, leading to efficient and effective optimization for the sampling inspection of master’s degree theses. Under the process of the method, the sampling inspection of the master’s theses of provincial degree committees will be more standardized and institutionalized.

The rest of the paper is organized as follows: Section 2 introduces the background of paper quality sampling, sampling rules and related algorithms. The details of the hybrid algorithms with the improved genetic algorithm and the simulated annealing algorithm are given in Section 3. Experimental settings and dataset preprocessing are provided in Section 4. Section 5 presents the experimental results with the analysis. Section 6 draws the conclusion.

2. Background

2.1. Thesis Inspection via Sampling

Nearly 40,000 postgraduates graduate from Shanghai’s universities each year. Because of the importance of the thesis to the graduation mentioned above, the quality of their theses needs to be controlled. For this reason, the Academic Degrees Committee of the State Council and the Ministry of Education formally promulgated [1] on 29 January 2014, which stipulates that the state will sample the doctoral dissertations and master’s degree theses in the previous academic year nationwide. The sampling results would be used as an important indicator for the evaluation of degree authorization points. Rather than evaluating all items, sampling inspection aims to randomly select a small number of samples from a batch of individuals or a process according to an established sampling plan and judge whether the batch of individuals or the process meets the quality requirements [3]. It is an important method to describe the population, which has the features of low cost, strong applicability and high scientificity.

Compared o the national sampling after degree-granting, the Shanghai Academic Degree Commission has spent 300,000 to 400,000 RMB since 1997 for the random sampling and “double-blind” review of doctoral dissertations and master’s theses before degree granting. It has directly promoted the overall attention of graduate students and their supervisors to the quality of their theses or dissertations [4]. Jiangsu, Hunan, Shandong and other provinces and cities have also followed suit and thus have some achievements. To a certain extent, they have all together exerted a positive effect on rectifying academic plagiarism and other unhealthy academic tendencies, just as the saying goes, “If you want people to think correctly, the first thing is to eliminate academic misconducts. When faults occur, then right or wrong is reversed“ [5].

The primary purpose of this national sampling after degree-granting is not to influence the normal learning and employment of the applicants for degrees and the degree-granting of degree-cultivation units, but to promote the construction of professional disciplines and the training of talents. Emphasis is laid upon the performance of supervisors and the training quality of degree authorization institutions [6]. Moreover, [1] further clarified as the method for the sampling of master’s dissertations is determined by provincial degree committees and the People’s Liberation Army Academic Degree Committee.

Therefore, the correct understanding of the spirit of the national sampling method and how to implement it in the administrative area of Shanghai have become some of the critical tasks at the moment.

2.2. Sampling Rules

In the Shanghai sampling method, the sampling rules are listed as below.

(1)

The sampling rate of masters’ theses from each master degree conferring institution is about 5%.

(2)

About 10% of foreign masters’ theses need to be extracted for sampling inspection.

(3)

The sampling rate of theses of masters whose tutor guided ten or more postgraduates in the same year is about 10%.

2.3. Genetic Algorithm

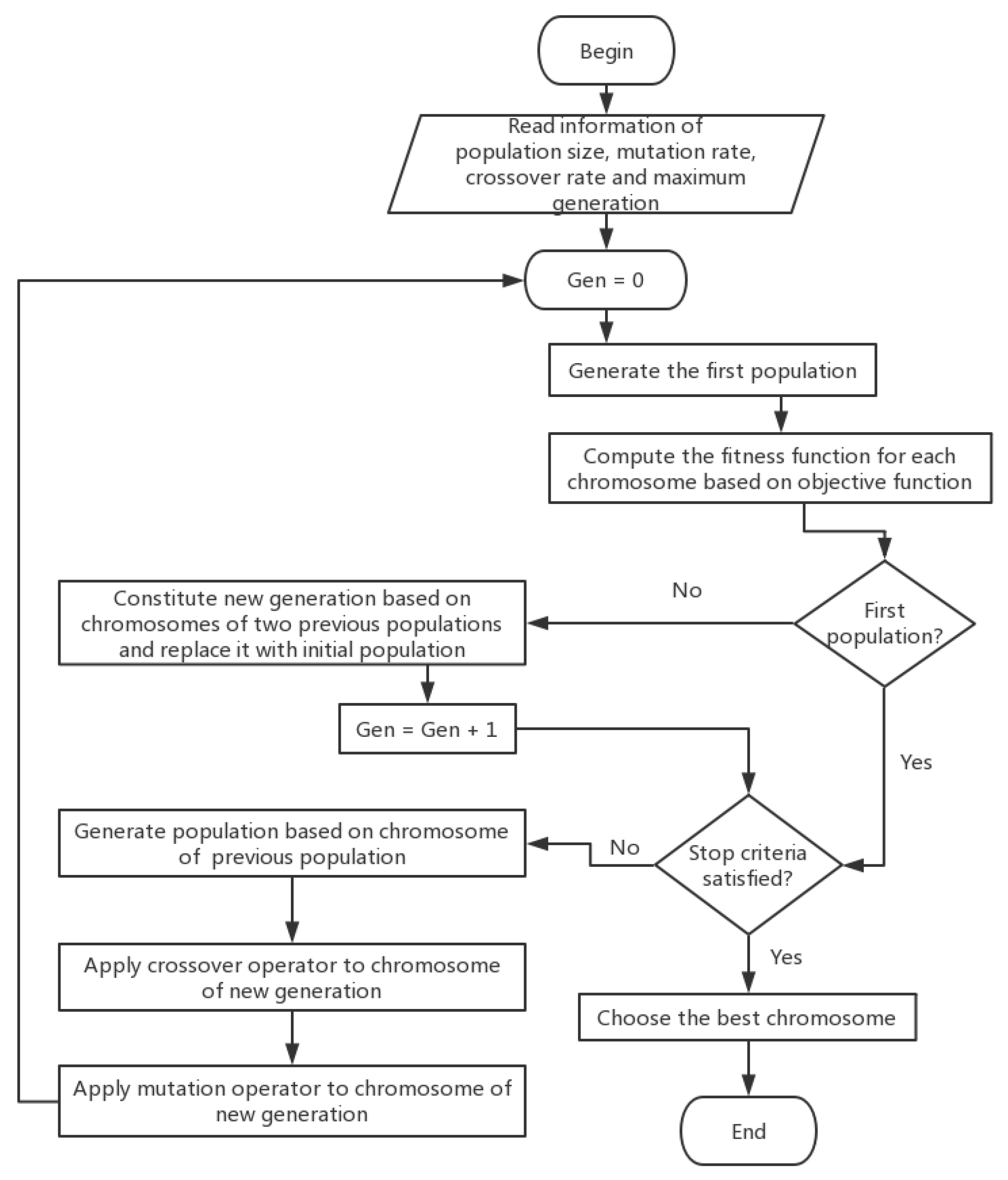
The genetic algorithm (GA) [7] is an evolutionary algorithm inspired by the principle process of natural selection and survival of the fittest. GA is commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operations such as mutation, crossover and selection [8]. As shown in Figure 1.

GA mainly borrows the principle of the survival of the fittest in biological evolution. First, the solution to the optimization problem is encoded. Here, the encoded solution is called a chromosome, and the elements that make up the encoding are called genes. Then, according to the objective function of the optimization problem, the corresponding fitness function is constructed, and the chromosome is selected by the probability distribution determined by the size of the fitness function. The survived chromosomes constitute a population, and at the same time, the parents are randomly generated according to the probability distribution. Then, the parents create offspring through mating between the codes, and consequently, the offspring mutate with a certain probability to form a new population. At this time, the decoding turns back to the solution to the optimization problem. Finally, the termination rule is applied. Through the above cycle, the solution of the optimization problem is obtained.

Common iterative methods tend to fall into a local minimum trap, and thus, a dead loop phenomenon emerges, which makes the iteration process unable to continue. To overcome this shortcoming, GA adopts a global optimization approach [8]. Compared with traditional optimization methods (like enumeration, heuristics, etc.), GA has good convergence due to the adaptation of the biological evolution model [9]. GA also has several advantages as follows.

• It has no bias for specific problem areas.
• It has the capacity to perform a fast and random search.
• It uses a simple search process with the evaluation function.
• It features randomness as the probabilistic mechanism used for the iteration.
• It is extensible and easy to integrate with other algorithms.

Many variants of GA and its applications were thoroughly studied by [10]. Recently, GA has been one of the widely-used algorithms in solving optimization problems such as for image processing and communications. In this paper, we use it to make a sampling inspection of 40,000 masters’ theses according to the three rules for thesis sampling in Shanghai mentioned in Section 2.2.

2.4. Simulated Annealing

Simulated annealing (SA) is a learning method that simulates the physical quenching process in thermodynamics. Its starting point is based on the similarity between the annealing process of solid materials in physics and general combinatorial optimization [11]. It is a greedy algorithm, but its search process introduces random factors. When iterating to update the feasible solution, a solution worse than the current solution is accepted with a certain probability, so it is possible to get the optimal global solution by jumping out of the local optimal solution [12]. In [13,14,15], the simulated annealing algorithm was improved or combined with other algorithms to achieve a better performance in experiments.

Figure 2 is an example. Assuming that the initial solution is the left blue point A, the simulated annealing algorithm will quickly search for the optimal local solution B, but after searching for the optimal local solution, it does not end there, but will move to the left with a certain probability. Maybe after a few of these non-locally optimal moves, the global optimum D is reached, and the local minimum jumps out.

According to the principle of thermodynamics, when the temperature is T, the probability of the temperature drop with the energy difference of $dE$ is $p\left(dE\right)$, which is expressed as:

$$p\left(dE\right)=\exp (\frac{dE}{kT}),$$

(1)

where k is the Boltzmann constant; the value is $1.3806488\times {10}^{-23}$, and $dE<0$. Therefore $dE/kT<0$, so the value range of the $p\left(dE\right)$ function is (0,1). In fact, the more intuitive meaning of this formula is: the higher the temperature, the greater the probability that the energy difference is $p\left(dE\right)$, and the lower the temperature, the lower the probability of temperature drop.

In practical problems, the calculation of “certain probability” here refers to the annealing process of metal smelting. Assuming that the currently feasible solution is x and the iteratively-updated solution is $x_{new}$, then the corresponding “energy difference” is defined as:

$$\Delta f=f\left(x_{new}\right)-f\left(x\right),$$

(2)

and its corresponding “certain probability” is:

$$p(\Delta f)=\left\{\begin{array}{cc}1,\hfill & \hfill if\Delta f>0\\ \exp (\frac{\Delta f}{kT}),\hfill & \hfill if\Delta f\le 0\end{array}\right.$$

(3)

Here, let k = 1. The simulated annealing algorithm can be described as below,

Step 1:

Initialization: initial temperature T (sufficiently large), original best solution x obtained after GA applied; solution obtained from the previous iteration $x_{new}$.

Step 2:

Calculate the increment $\Delta f=f\left(x_{new}\right)-f\left(x\right)$, where $f\left(x\right)$ is the optimization target. Here, it is the function that minimizes the mean absolute error $ϵ$ calculated according to the sampling rules after the sampling result is obtained by decoding the solution. We use the result of one minus $ϵ$ to represent the fitness function value; see Section 3.4.

Step 3:

If $\Delta f>0$, $x_{new}$ is accepted as the new current solution, otherwise $x_{new}$ is accepted as the new current solution with the probability $\exp (\frac{\Delta f}{kT})$.

Step 4:

If the termination condition is satisfied, the current solution is output as the optimal solution to terminate the program. Otherwise, wait for a new $x_{new}$ to go to Step 2.

3. The Proposed Algorithm

3.1. The Main Idea

The major steps of the proposed algorithm are:

Step 1:

Initialize the variables of GA and SA; determine the initial temperature of annealing $T_0$, temperature reduction parameter k, size of population s, crossover probability $pcross$ and mutation probability $pmutation$ by the result obtained from the experiment in Section 4.2;

Step 2:

Randomly generate initial population $p_0$, and encode each chromosome; the size of $p_0$ is 10;

Step 3:

Calculate the mean absolute error $ϵ$ of the sampling scheme corresponding to each chromosome according to the sampling rules, then the fitness of each chromosome is denoted as f; let $f=1-ϵ$. Determine the fitness function of each chromosome in the population ($f=1-ϵ$); see Section 3.4;

Step 4:

Roulette wheel method is used to select s chromosomes from $p_0$ to constitute new population p, the probability of choosing an individual depends directly on its fitness value f;

Step 5:

Randomly choose two chromosomes from p, and apply the crossover operator to them;

Step 6:

Apply the mutation operator described in Section 3.3 to the new population;

Step 7:

Let the current population be the new population;

Step 8:

If the mean absolute error $ϵ$ is less than 0.2%, then the convergence criterion is satisfied; stop. Otherwise, go to Step 4.

3.2. Coding and Initialization Methods

According to [16], the floating point representation is faster, more consistent and provides higher precision especially with large domains where binary coding would require prohibitively long representation. Compared with binary coding, the floating point coding has obvious advantages [17] as follows.

• The floating point coding does not require a decoding process.
• It represents a larger range of numbers in the genetic algorithm, which is convenient in larger spaces.
• It also simplifies the traditional genetic algorithm and improves the computational efficiency.
• Furthermore, the floating point encoding prevents the precision errors caused by the hexadecimal conversion.
• It is easy to mix it with classical optimization methods.

Thus, the floating point representation is used in this paper. After the master’s thesis dataset is preprocessed, the thesis number will participate in the coding operation.

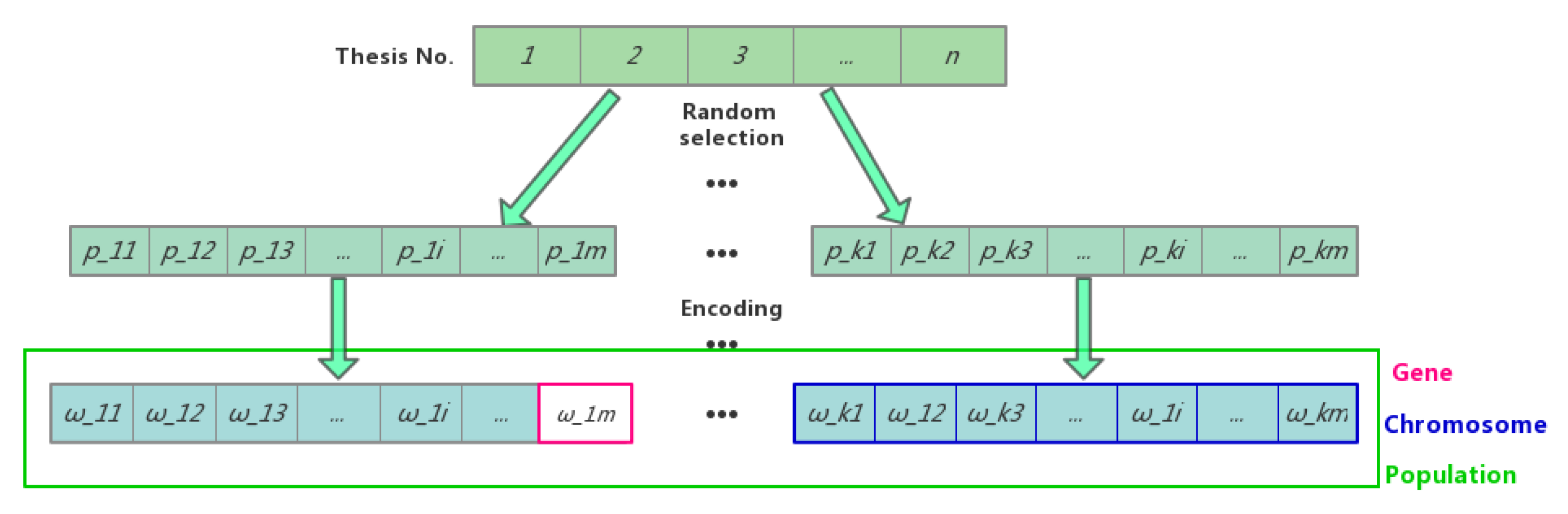
Figure 3 shows the chromosome coding scheme in this paper. n is the total number of thesis to be sampled. $p\_ij$ (1 ≤i≤ k, 1 ≤j≤ m) is the sequence number of the thesis taken from the thesis sample population randomly to generate the population in GA. Then, let $\omega \_ij$ = $p\_ij$/n to indicate the encoded value of the genes in chromosomes.

For example, for the first chromosome in Figure 3, assume n equals 10 and m equals 5: the theses with Serial Numbers 1, 3, 5, 7, 8 are selected. Accordingly, after encoding, the gene codes are 0.1, 0.3, 0.5, 0.7, 0.8.

3.3. Selection, Crossover and Mutation

The selection operator chooses some good individuals from the current population and transfers them to the next generation [18]. Methods used as the selection operator can be classified into two categories: proportional and elitist. The former category employs the probability of selection proportional to the fitness value of each individual. These methods allow maintaining a genetic diversity within the population of candidate solutions throughout the generations, which prevents GA from falling into local optima. However, these methods increase the time of convergence [19]. This paper uses the roulette wheel method making individuals with high-fitting values get a higher probability of survival. The basic idea under this method is that the probability of each individual being selected is proportional to its fitness value. The proportional selection method has enormous randomness and thus might be trapped in local extrema. The integration of simulated annealing factor into the genetic algorithm leads to avoid slow convergence rate and local extrema problem.

The crossover operator newly produces some better individual patterns [20], which is the main element of the search process in optimization. The encoding type used in GA is the major criteria for selecting the crossover. The global convergence and search space must be considered for selecting the crossover operators. the effect of crossover operators in GA is dependent on the application, as well as encoding [21]. Here, the two-point arithmetic crossover is used.

$${\omega }_1\left(t\right)=({\omega }_{11},{\omega }_{21},\dots ,{\omega }_{n1})$$

(4)

$${\omega }_2\left(t\right)=({\omega }_{12},{\omega }_{22},\dots ,{\omega }_{n2})$$

(5)

where ${\omega }_1\left(t\right)$ and ${\omega }_2\left(t\right)$ are two chromosomes at time t. Let two random numbers generated at time t be $i(1\le i\le n)$ and $j(0<j<1)$. Then, the two-point arithmetic crossover at the i-th locus of the above two chromosomes, respectively, as ${\omega }_1^{{}^{\prime }}\left(t\right)$ and ${\omega }_2^{{}^{\prime }}\left(t\right)$, is defined as follows:

$${\omega }_{i1}^{{}^{\prime }}=j\ast {\omega }_{i2}+(1-j)\ast {\omega }_{i1}$$

(6)

$${\omega }_{i2}^{{}^{\prime }}=j\ast {\omega }_{i1}+(1-j)\ast {\omega }_{i2}$$

(7)

The following descendants are propagated:

$${\omega }_1(t+1)=({\omega }_{11},{\omega }_{21},\dots ,{\omega }_{i1}^{{}^{\prime }},\dots ,{\omega }_{n1})$$

(8)

$${\omega }_2(t+1)=({\omega }_{12},{\omega }_{22},\dots ,{\omega }_{i2}^{{}^{\prime }},\dots ,{\omega }_{n2})$$

(9)

where, i is the locus involved in the crossover operation on the chromosome. n is the length of the chromosomes, that is, the number of genes. In this paper, it is the number of selected theses.

The mutation operator is employed to avoid establishing a uniform population unable to evolve [22]. According to [23], the NP-complete problems are intractable, i.e., they can be solved theoretically, but in practice, they take too long for their solutions to be useful.

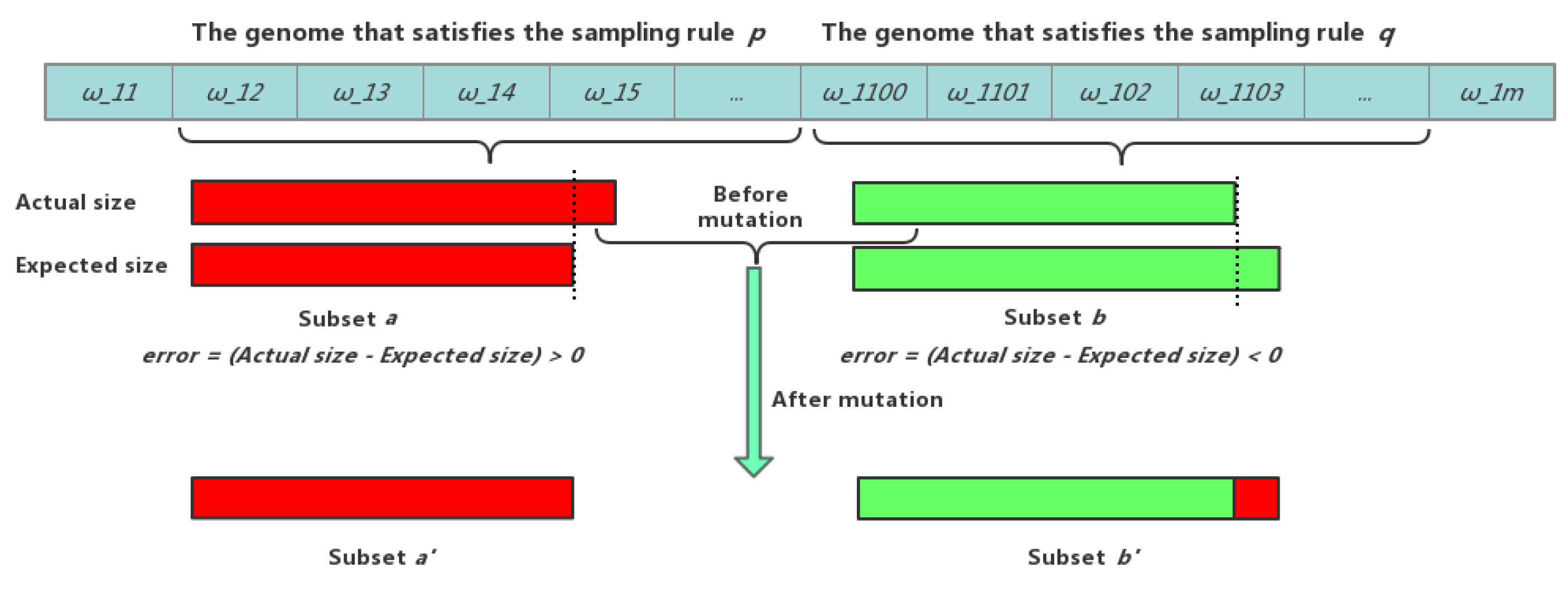
Once a new generation is created after the crossover operation, the genetic process is performed iteratively until an optimal result is found. We have used the traditional genetic algorithm to solve the thesis sampling problem. More than 30,000 iterations were carried out, which took nearly 3.5 h, and the sampling effect was not ideal. By analyzing the traditional genetic algorithm, we found that the whole algorithm was time consuming. Since the mutation operator is directionless, we believe that some modifications could be made to the mutation operator based on the traditional genetic algorithm to speed up the convergence of the algorithm. Thus, an improved mutation strategy is introduced as Algorithm 1.

Figure 4, provided below, is for easier understanding of the proposed mutation operation.

Algorithm 1: Mutation strategy.

1.   Input: Thesis data, mutation probability, chromosome length, number of chromosomes and the fitness

2.             value of each chromosome.

3.   Output: Mutated chromosomes

4.   Initialize parameter: $ϵ$

5.   for i = 1 to the size of the population

5.      do

6.         for k = 1 to the length of the chromosome

7.            do

8.               Denote the extracted thesis set (chromosome) as S, then calculate the error of the unique subset

9.                of S determined by the samplings rules according to the value of the genes.

10.         end for

11.         Assume that the subset a of set S has the maximum error, and subset b of set S has the minimum error.

12.                   On the current chromosome, a mutation operation is performed by randomly replacing a gene

13.                   corresponding to an element of set a with a gene that satisfies set b.

14.         Check whether the chromosome after the mutation meets the requirement that the same two genes

15.                   do not exist on the chromosome.

16.      if the mutated chromosome meets the requirements

17.         The mutated chromosomes are accepted according to Equation (3);

18.      else

19.         Undo the mutation operation.

20.      end if

21.   end for

3.4. The Definition of Fitness Function

According to the sampling rules introduced in Section 2.2, the fitness function is defined as follows:

$$f=1-\frac{1}{n}\sum _{i=1}^n\sqrt{{(P_i-E_i)}^2,}$$

(10)

it is equivalent to:

$$f=1-ϵ,$$

(11)

where n denotes the number of constrained conditions (sampling rules) and $P_i$ and $E_i$ indicate, respectively, the actual sampling rate and the expected sampling rate of the subset that satisfies the i-th sampling rule. $ϵ$ is the mean absolute error. Then, the objective function of our proposed algorithm is,

$$g=min(\frac{1}{n}\sum _{i=1}^n\sqrt{{(P_i-E_i)}^2}),$$

(12)

which is equivalent to the following equation,

$$h=max(1-\frac{1}{n}\sum _{i=1}^n\sqrt{{(P_i-E_i)}^2}).$$

(13)

4. Experimental Setup

This section describes the experimental setup for evaluating the proposed algorithm. The parameters used for the algorithm are also provided.

4.1. Experimental Setup

The improved GA was implemented in MATLAB and evaluated in the task for the sampling of Shanghai papers. For a fair comparison, the traditional GA and other comparison algorithms were also implemented in MATLAB. The evaluations were executed on a MacBook-Pro with 8 GB memory on a 2.7-GHz Intel Core i5 processor. The processed information of Shanghai municipal master’s degree theses submitted from Shanghai in 2014 was used as input data. In total, 39,779 theses were used for the evaluation. The number of sampled theses and error rates were analyzed and provided in Section 5.

4.2. Parameters

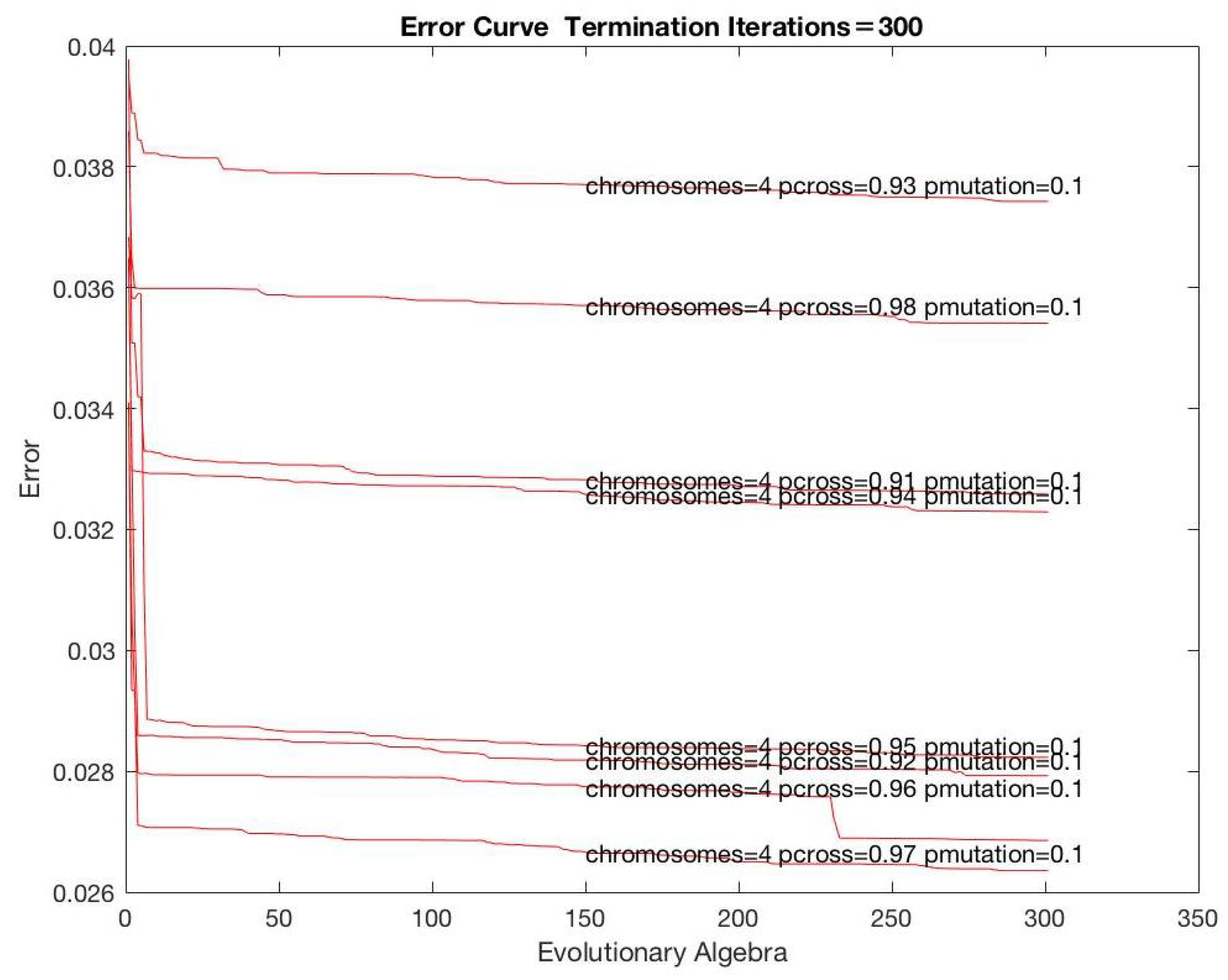
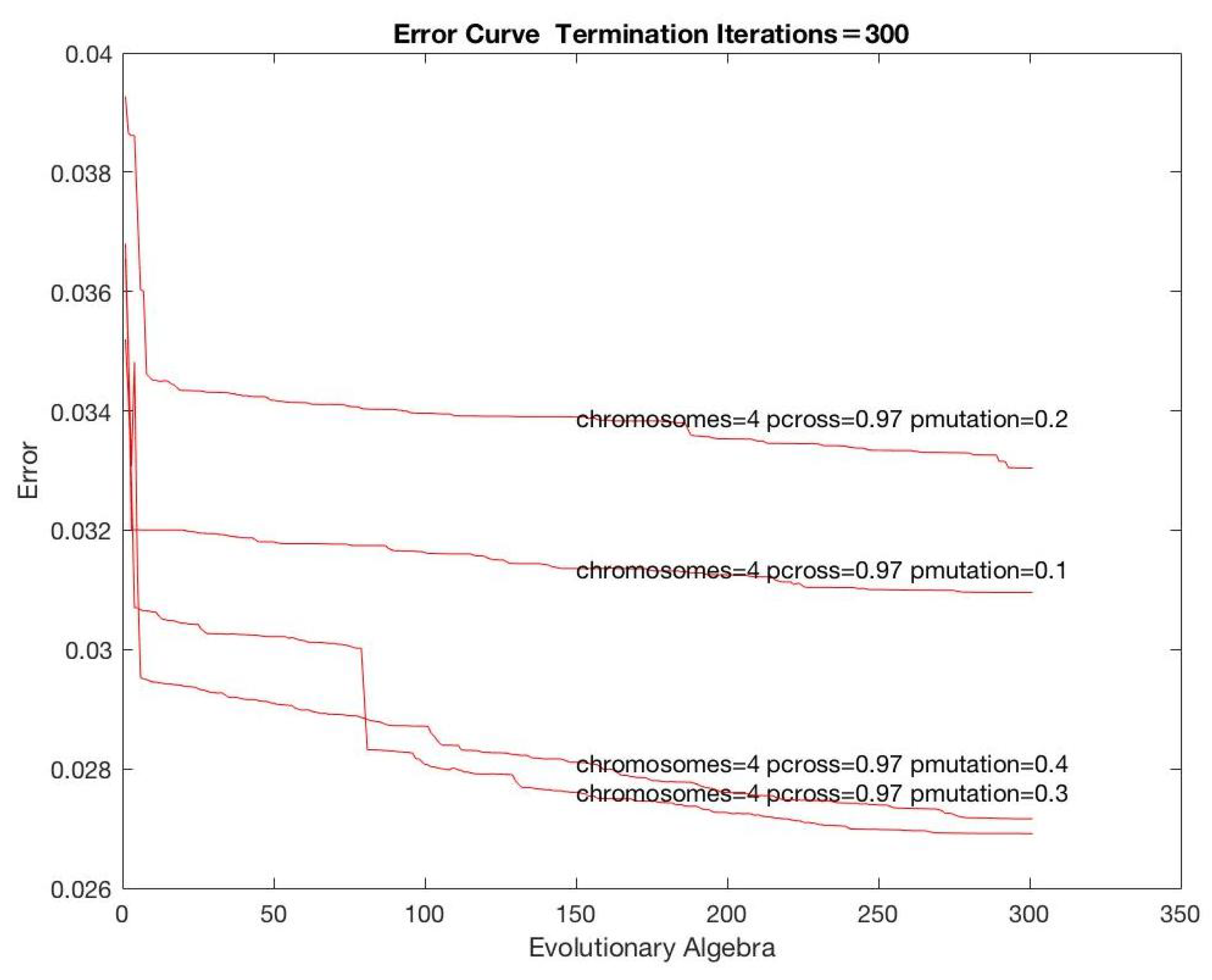
Figure 5, Figure 6 and Figure 7 show the analysis according to varying parameters. Based on the analysis and other information, the parameters were set as

Table 1. Experiment parameters.

Size of initial population is 10

Size of population $sizepop$ = 4

Probability of crossover $pcross$ = 0.97

Probability of mutation $pmutation$ = 0.3

Mode of selection $fselect$ = ‘roulette’

Method of coding $fcode$ = ‘float’

Mode of crossover $fcross$ = ‘float’

Temperature of annealing $T_0$ = 100

Temperature reduction parameter k = 0.98

.

4.3. Redundancy Reduction in Data

The source data shown as Figure 8a have too much redundant information relative to the data required for the experiment, so they need to be processed. The process mainly includes: adding missing data items, numbering the theses from 1 to 39,779 and adding attributes related to the sampling rules. To remove irrelevant data items, the processed data are as shown below.

In Figure 8b, the attribute $id$ of a thesis is used as a parameter in the encoding method, the attribute $school$ of the thesis is used to calculate the sampling rate of Sampling Rule No. 1, attribute $nation$ is used to calculate the sampling rate of Sampling Rule No. 2 and attribute $tutor$ is used to calculate the sampling rate of Sampling Rule No. 3.

5. Experimental Result Analysis

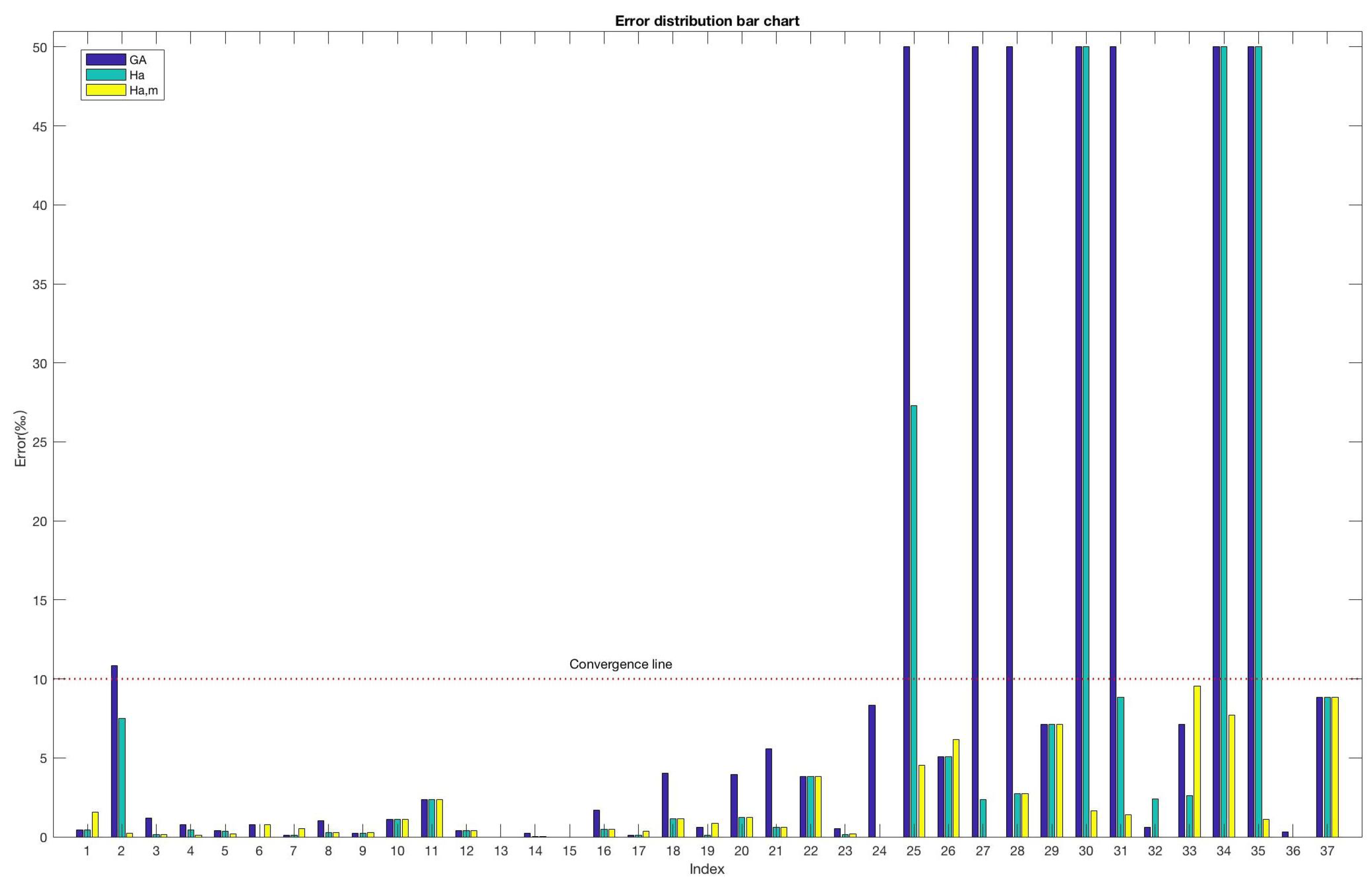
The three algorithms are solved by minimizing the objective function (Equation (12)). In order to verify the good effect of the hybrid algorithm proposed in this paper on solving the sampling scheme of the theses,

Table 2. Sampling results under each algorithm.

Index	P${}_{\mathit{e}}$	GA	H${}_{\mathit{a}}$	H${}_{\mathit{a},\mathit{m}}$
1	10%	10.044%	10.044%	10.156%
2	10%	8.917%	9.251%	10.022%
3	5%	5.117%	5.015%	5.015%
4	5%	4.921%	5.042%	4.991%
5	5%	4.960%	5.035%	5.017%
6	5%	5.078%	5.000%	5.078%
7	5%	4.990%	4.991%	5.053%
8	5%	5.103%	5.029%	5.029%
9	5%	4.979%	5.025%	5.026%
10	5%	5.109%	5.109%	5.109%
11	5%	4.762%	4.762%	4.762%
12	5%	4.962%	4.962%	4.962%
13	5%	5.000%	5.000%	5.000%
14	5%	4.978%	5.004%	5.004%
15	5%	5.000%	5.000%	5.000%
16	5%	5.168%	5.048%	5.048%
17	5%	4.991%	4.991%	5.035%
18	5%	4.598%	4.885%	4.885%
19	5%	4.938%	5.010%	5.085%
20	5%	4.607%	4.878%	4.878%
21	5%	5.556%	4.938%	4.938%
22	5%	4.615%	5.384%	5.384%
23	5%	4.947%	5.015%	4.981%
24	5%	4.167%	5.000%	5.000%
25	5%	0.000%	2.272%	4.545%
26	5%	4.494%	4.494%	5.617%
27	5%	0.000%	4.764%	5.000%
28	5%	0.000%	5.274%	5.274%
29	5%	4.286%	4.286%	4.286%
30	5%	0.000%	0.000%	5.166%
31	5%	0.000%	5.882%	5.142%
32	5%	4.938%	4.761%	5.000%
33	5%	5.714%	5.263%	3.947%
34	5%	0.000%	0.000%	5.769%
35	5%	0.000%	0.000%	5.111%
36	5%	4.968%	5.000%	5.000%
37	5%	5.882%	5.882%	5.882%

and

Table 3. Comparisons on iterations, time cost and mean absolute errors.

	GA	H${}_{\mathit{a}}$	H${}_{\mathit{a},\mathit{m}}$
Iterations	31,568	32,594	287
Time (min)	324.37	341.64	2.96
Mean absolute error (%)	1.155	0.644	0.164

respectively analyze the experimental results from the perspective of local and general, while Figure 8 depicts the experimental results from the perspective of visualization.

In Table 2, $P_e$ means expected sampling rate, $GA$ is the traditional genetic algorithm, $H_a$ is hybrid approach with annealing algorithm $H_{a,m}$ is the hybrid approach with annealing algorithm and the proposed mutation method.

In Table 2, Index 1 represents the sampling index of nationality mentioned in Sampling Rule No. 2; Index 2 represents the sampling index of tutor mentioned in Sampling Rule No. 3; Indices 3 to 37 correspond to 35 degree grant points, respectively; and the probability of sampling at these point grants reaches about 5% as mentioned in Sampling Rule No. 1.

Table 2 shows that the traditional genetic algorithm can generally meet the sampling requirements of Shanghai, but a significant drawback is that the sampling probability of some degree-granting units is zero. This is caused by the fact that these degree-granting units have fewer degree theses and traditional GA has considerable instability. After combining the simulated annealing algorithm, this situation can be improved and then mixed with the new mutation strategy; the results were satisfactory and met the requirements of Shanghai thesis sampling.

In Table 3, $GA$ is the traditional genetic algorithm, $H_a$ is the hybrid approach with the annealing algorithm and $H_{a,m}$ is the hybrid approach with the annealing algorithm and the proposed mutation method.

In Table 3, the proposed method is compared to the traditional GA in time complexity and mean absolute errors. The analysis shows that adopting the annealing algorithm led to a locally optimal solution, but not to the globally optimal solution. The time consumption was still high, which might lead to a long time to solve the problem, especially for the huge amount of data. Comparing the two methods, the proposed hybrid approach ${\mathit{H}}_{\mathit{a},\mathit{m}}$ was greatly improved with the new mutation strategy regarding time and errors.

We can analyze the convergence characteristics of these algorithms according to Figure 9. Here, we assume that when the absolute error of a sampling index is less than 1%, then we can say that the convergence criterion of this sampling index is satisfied. If the mean absolute error of all these sampling indices is less than 0.2%, it satisfies the convergence criterion of the whole algorithm well.

6. Conclusions and Future Work

The sampling of the master’s degree thesis in Shanghai municipality is formulated as a problem of permutation and combination. The number of combinations of $\mathit{n}$ theses taken $\mathit{m}$ at a time is denoted by ${\mathit{C}}_{\mathit{n}}^{\mathit{r}}$. In this paper, $\mathit{n}$ equals 39,779 and $\mathit{m}$ equals about 2000. The number of combinations is too large, and meanwhile, it needs to satisfy three sampling rules. To address this problem, we proposed to combine the genetic algorithm and simulated annealing. The experimental results showed that the proposed algorithm outperformed the conventional genetic algorithm, providing hundreds of times lower complexity and satisfactory results. Furthermore, the proposed method satisfied the sampling requirements of Shanghai. In the future, we will expand the proposed algorithm to cope with the dynamic development of the demand for sampling in Shanghai. For example, sampling rules can also make relevant requirements for the attributes $\mathit{ethnicity}$ and $\mathit{origin}$ of the master’s thesis.

Furthermore, since the initial parameters are obtained by experiments roughly and they are fixed, both good individuals and inferior individuals undergo the same probability of crossover and mutation operations. This can cause two very serious problems:

(1)

With the same probability, it can be said to be unfair, because, for good individuals, we should reduce the probability of cross mutation so that it can be preserved as much as possible; and for inferior individuals, we should increase the probability of crossover and mutation so that the inferior condition can be changed as much as possible.

(2)

The same probability cannot meet the needs of the evolution process of the population. For example, in the early iteration, the population needs a higher crossover and mutation probability, which has reached the goal of quickly finding the optimal solution. In the later stage of convergence, the population needs to be smaller. The crossover and mutation probability can help the population converge quickly after finding the optimal solution.

Therefore, the constant cross mutation probability affects the efficiency of the algorithm. Then, compared to traditional genetic algorithms, an adaptive genetic algorithm (AGA) is more suitable to solve this kind of multi-constraint problem.