The Optimization of Marine Diesel Engine Rotational Speed Control Process by Fuzzy Logic Control Based on Particle Swarm Optimization Algorithm
Abstract
:1. Introduction
2. Methodology
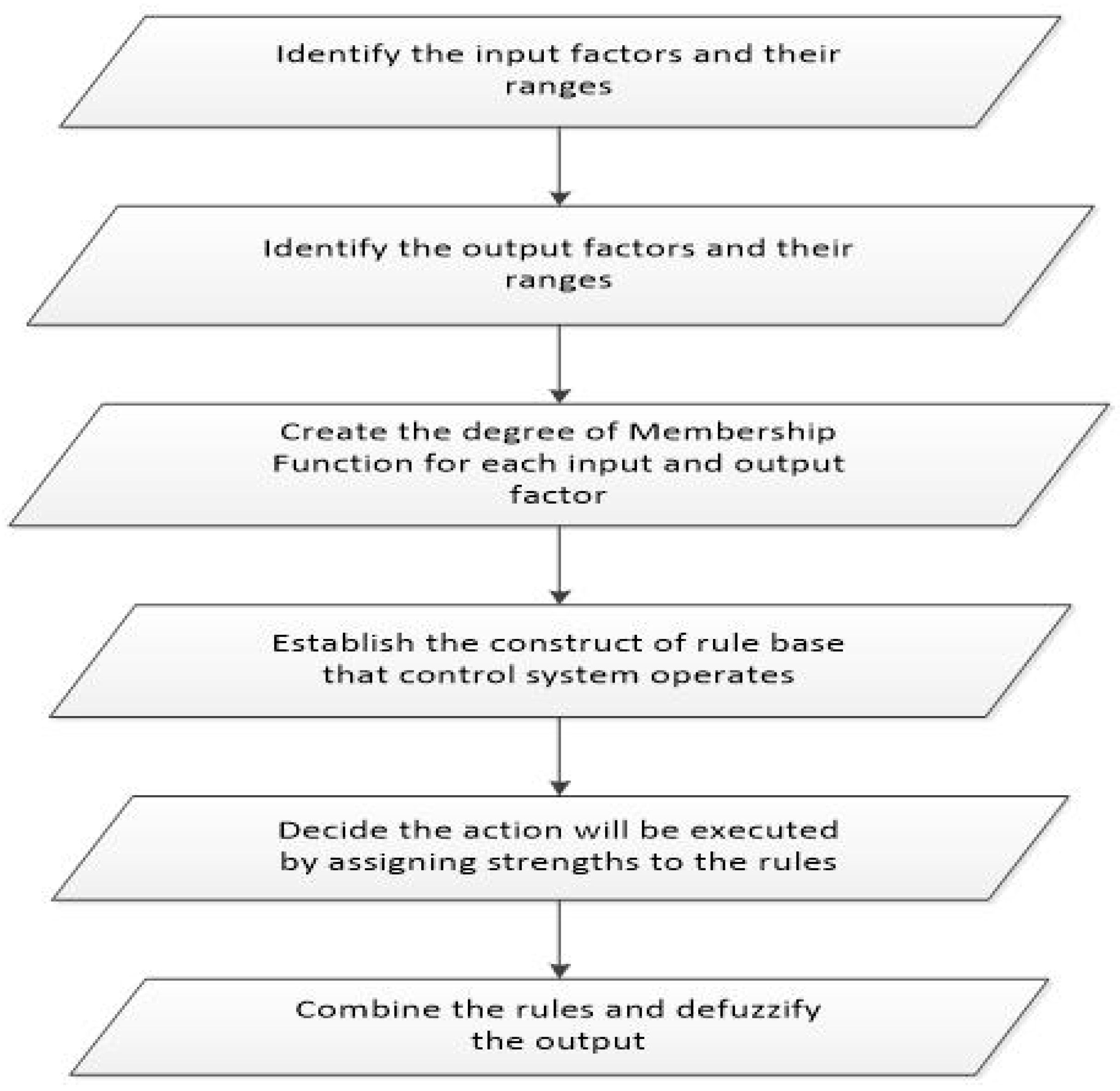
2.1. Fuzzy Logic Control Theory
2.1.1. Fuzzification
2.1.2. Rule Base
2.1.3. Inference Engine
2.1.4. Defuzzification
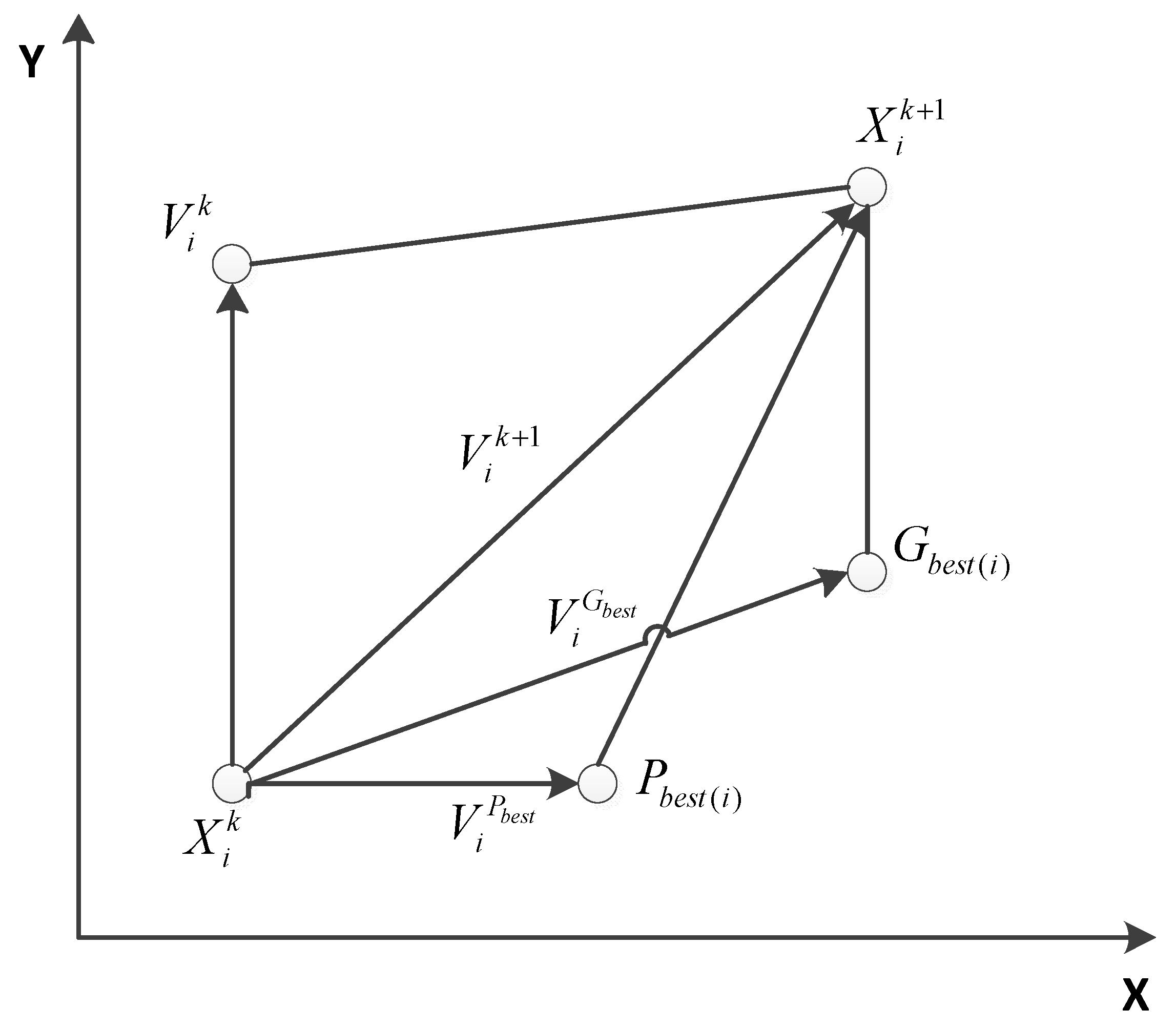
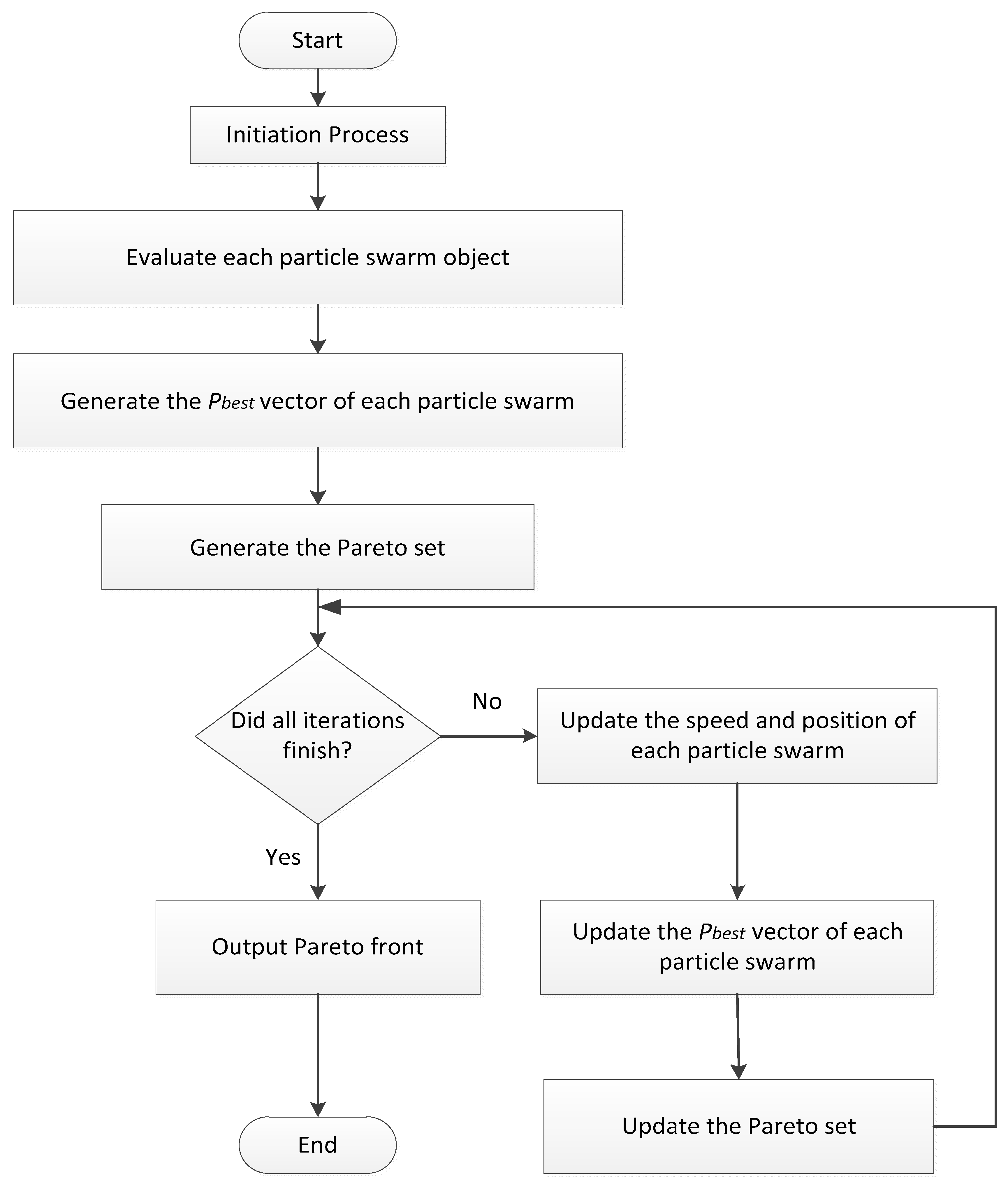
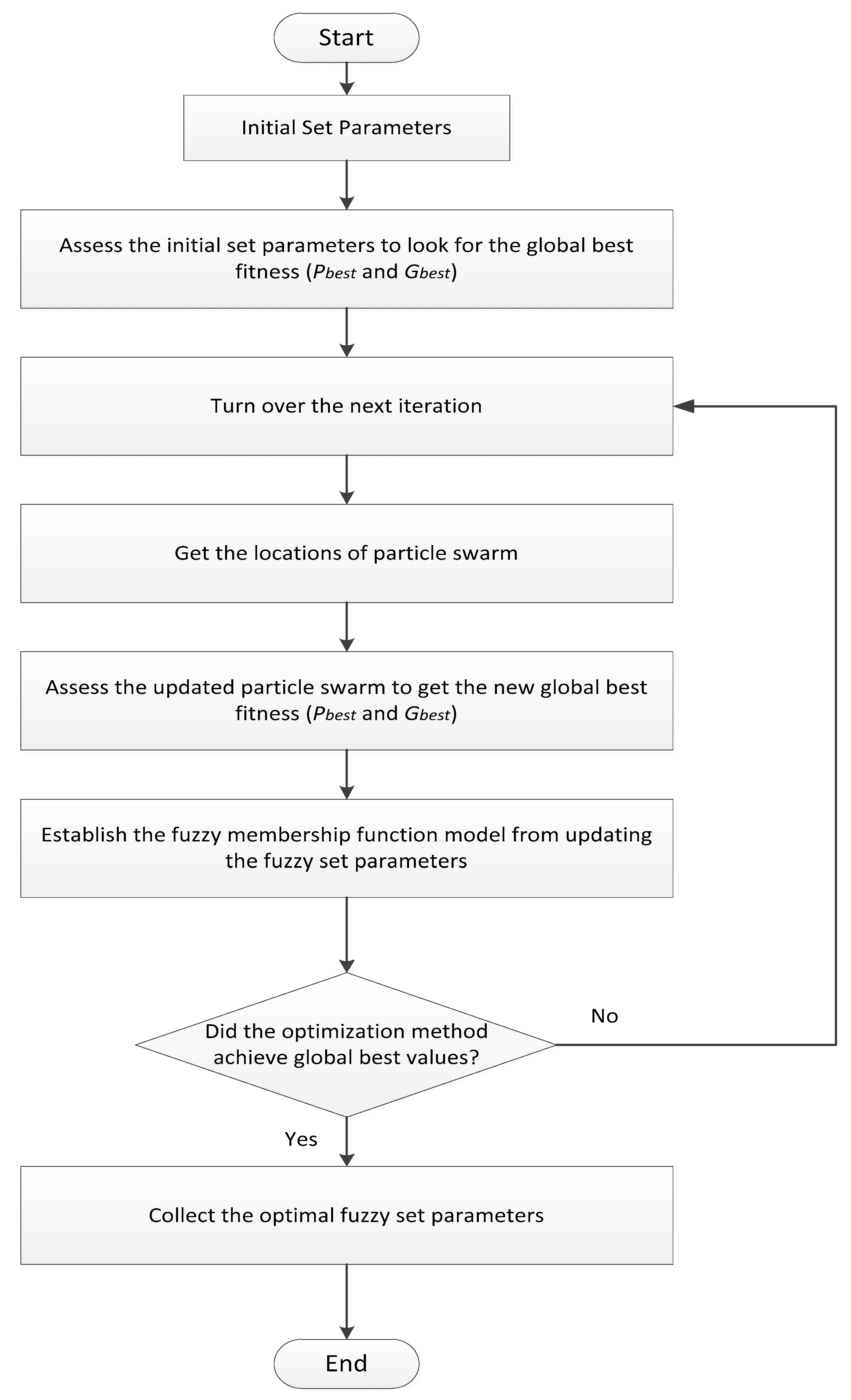
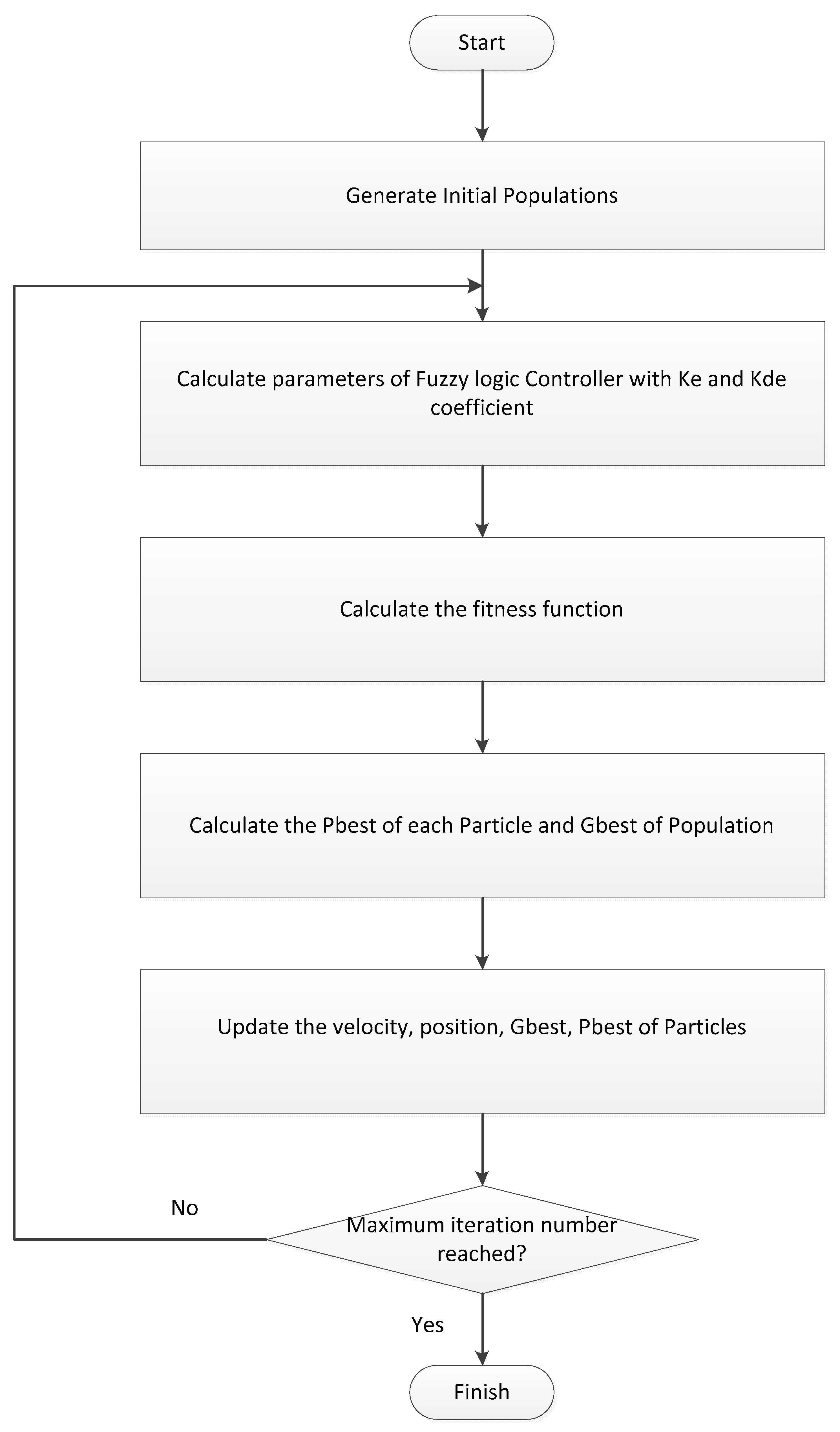
2.2. Particle Swarm Optimization Algorithm
- ➢
- Initialization process: Generate a population of particles and allocate a velocity to each particle randomly.
- ➢
- Ø Evaluation process: Update the best locations of particles and calculate the optimization fitness function.
- ➢
- Velocity and location update: Change the location of each particle by means of updating its own velocity as well as the particle will be adjusted dramatically.
- ➢
- The updating process of velocity and location at each particle can be realized through Equations (1) and (2).
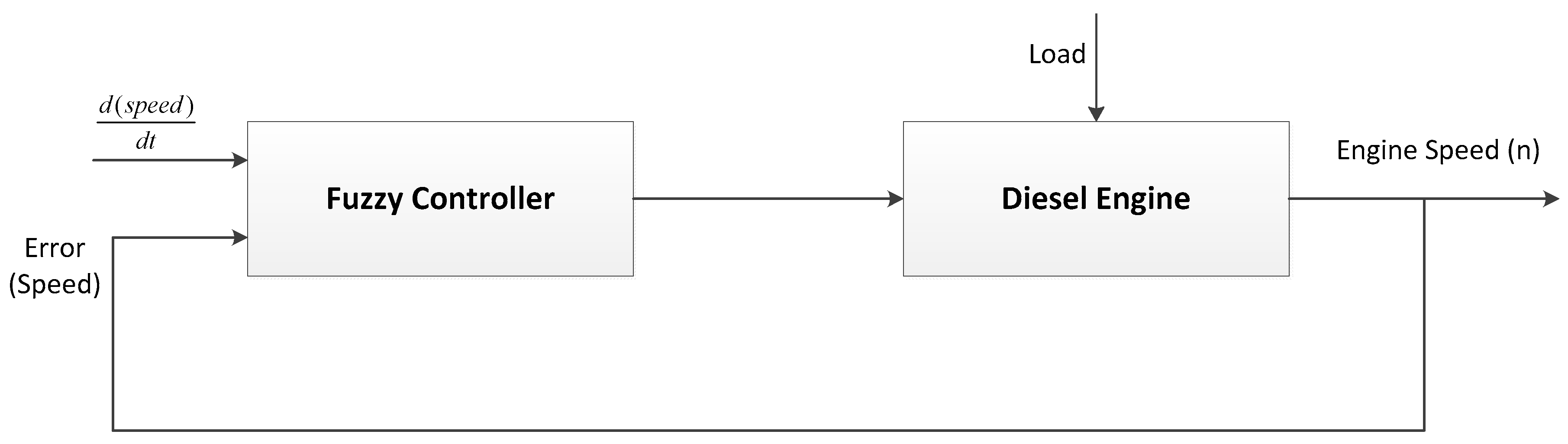
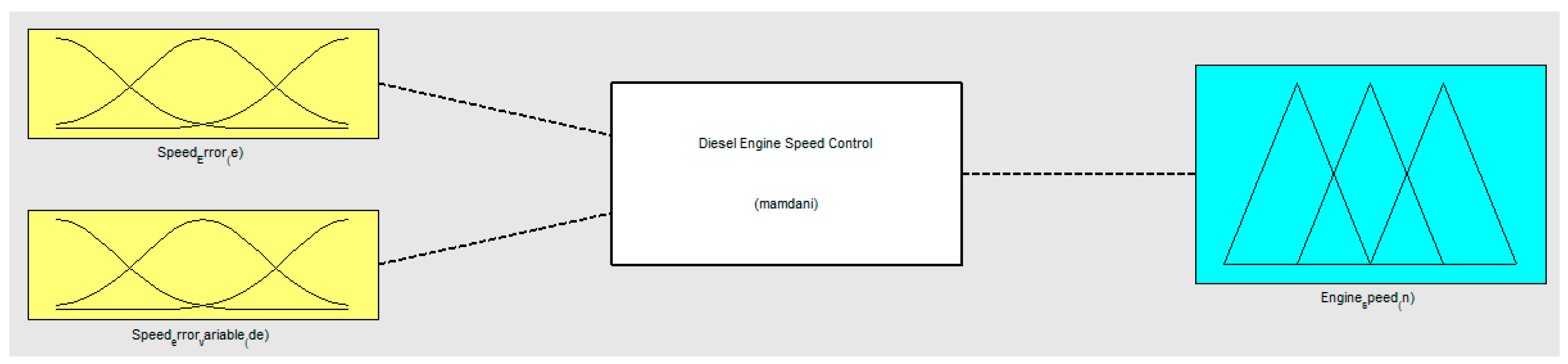
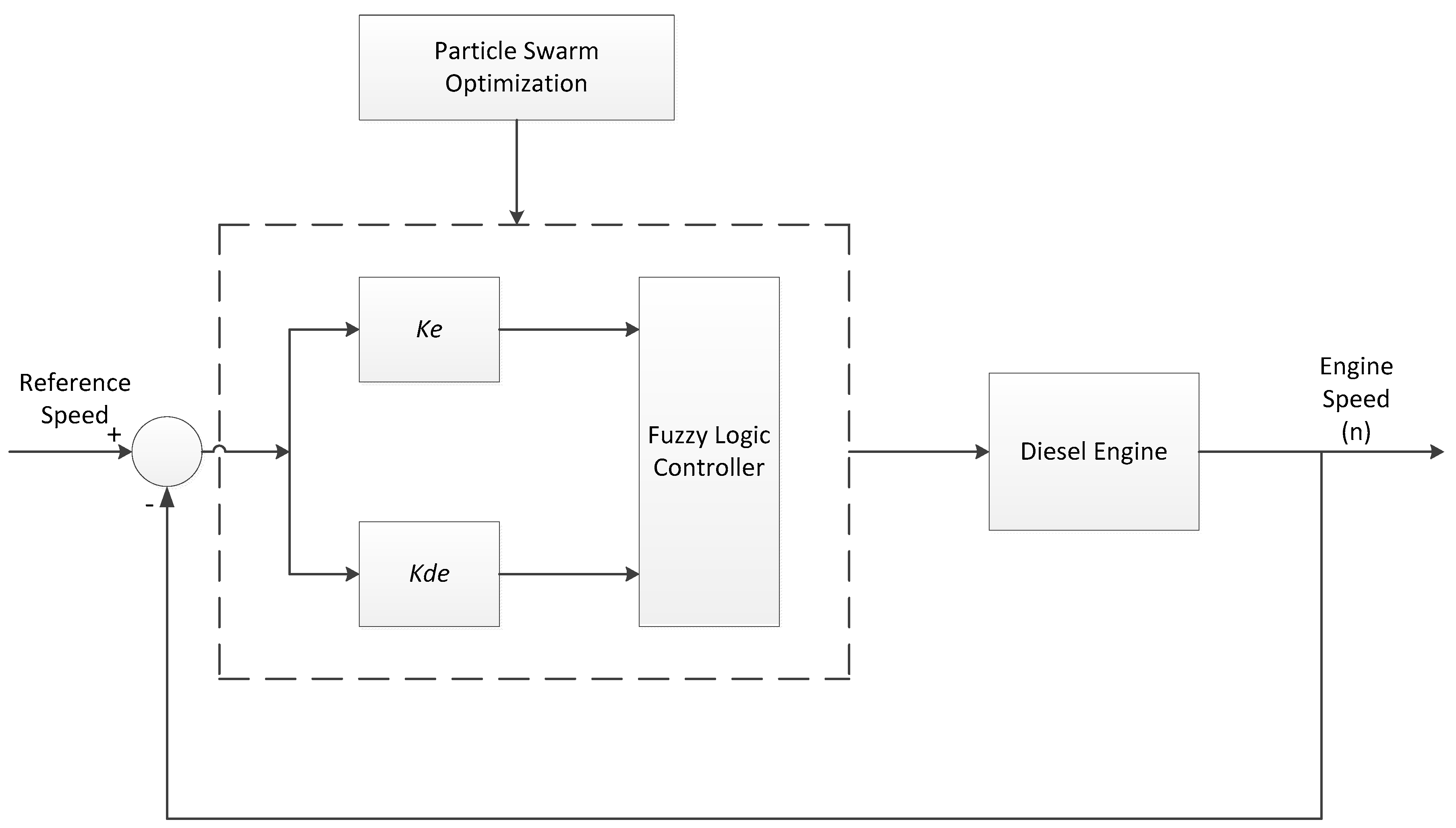
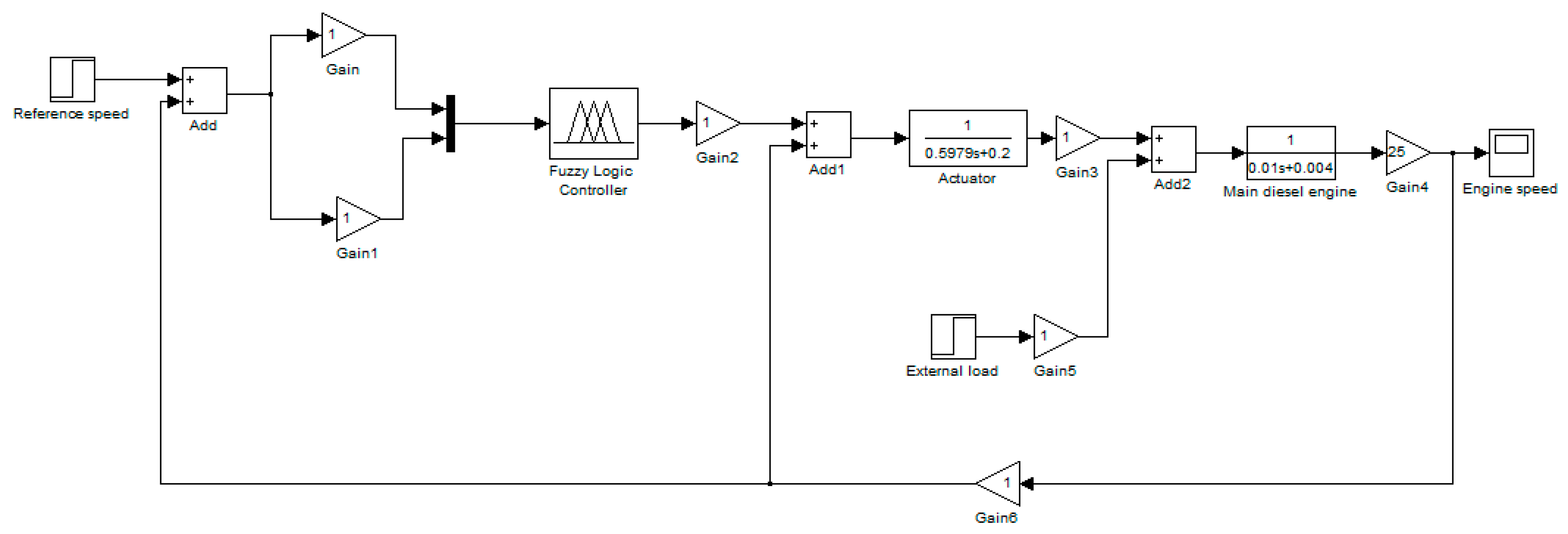
3. Case Study
Modeling of Main Diesel Engine Rotational Speed Control by Fuzzy Logic Control Theory
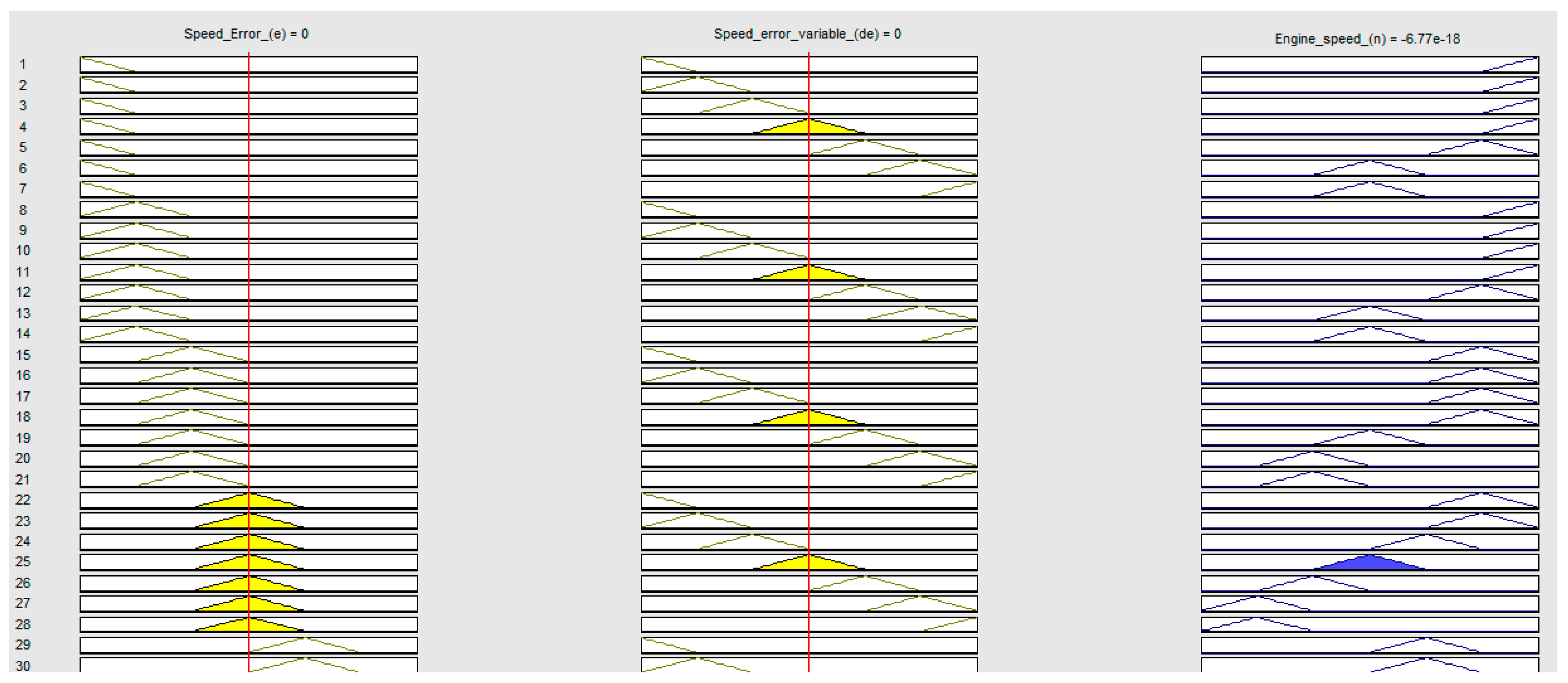
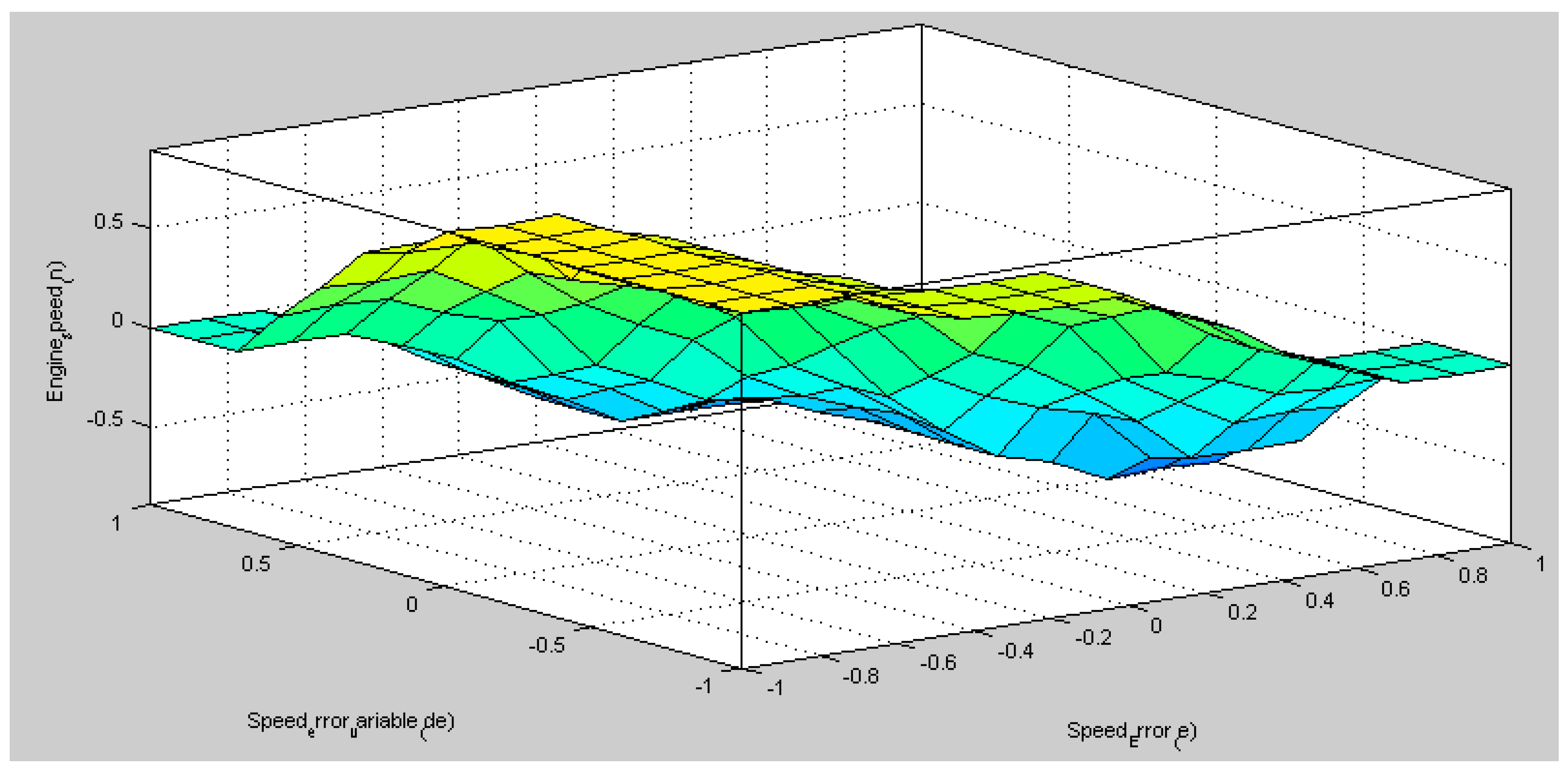
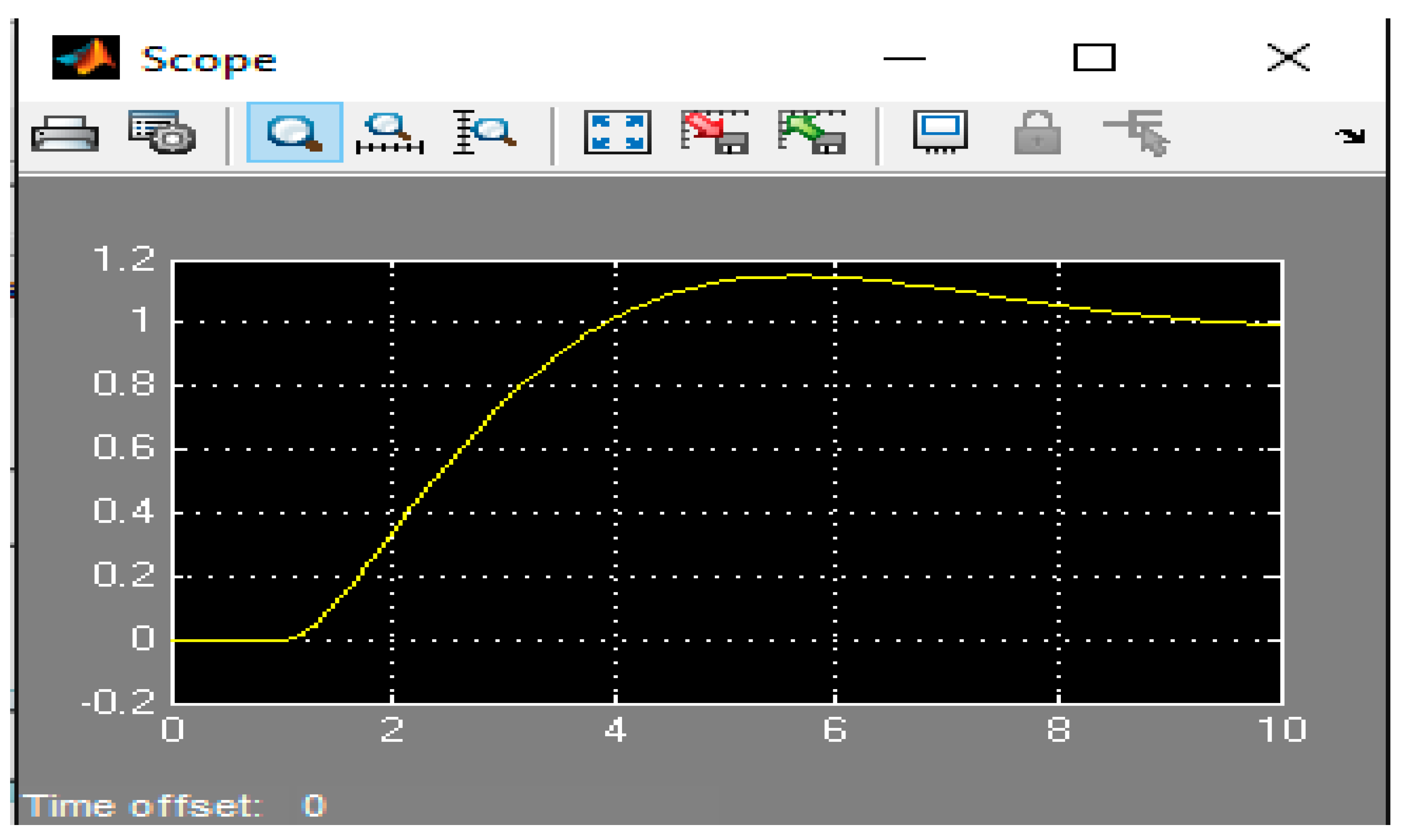
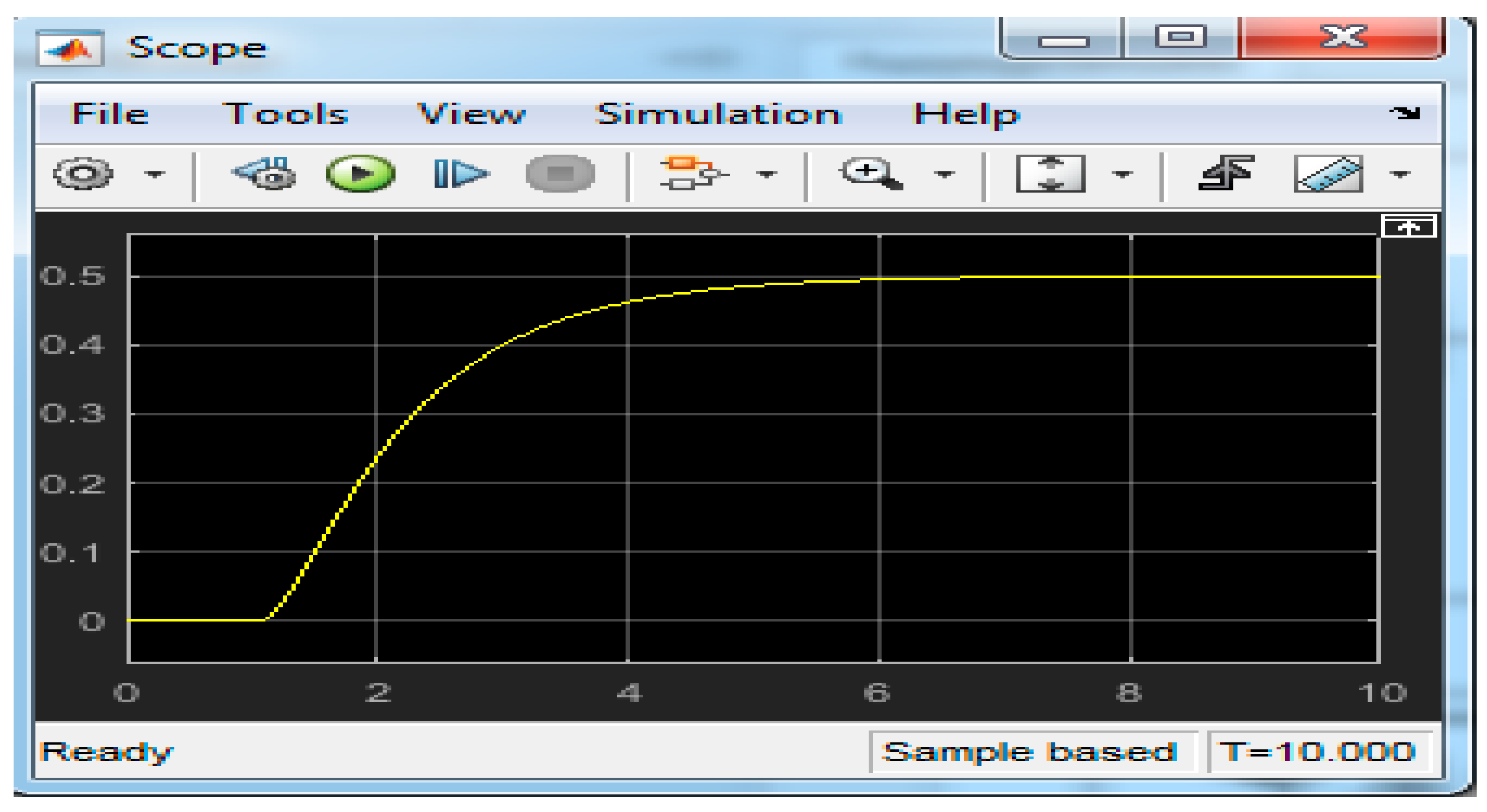
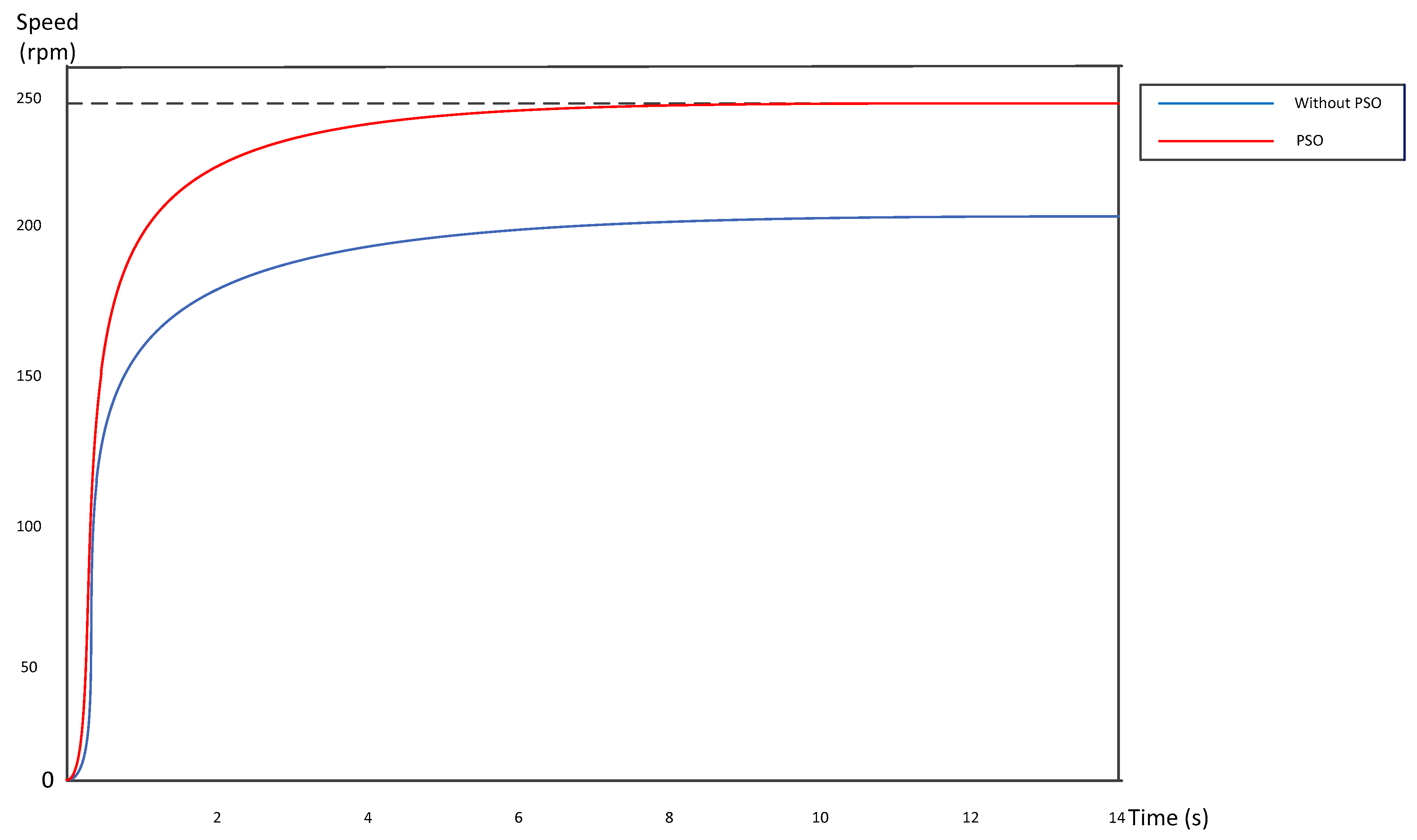
4. Results
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Yen, J.; Langari, R. Fuzzy Logic: Intelligence, Control, and Information; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Zhou, Y.S.; Lai, L.Y. Optimal Design for Fuzzy Controllers by Genetic Algorithms. IEEE Trans. Ind. Appl. 2000, 36, 93–97. [Google Scholar] [CrossRef]
- Jiang, J. Optimal Gain Scheduling Controller for a Diesel Engine. In Proceedings of the IEEE Conference on Control Applications, Vancouve, BC, Canada, 13–16 September 1994. [Google Scholar]
- Astrom, K.; Hagglund, T. PID Controllers: Theory, Design and Tuning, Instrument Society; ISA: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Wei, H.; Min, R.; Yingqi, T. A Fuzzy Control System of Diesel Generator Speed. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar]
- Simani, S.; Bonfe, M. Fuzzy Modelling and Control of the Air System of a Diesel Engine. Adv. Fuzzy Syst. 2009, 2009, 450259. [Google Scholar] [CrossRef]
- McGowan, D.J.; Morrow, D.J.; Fox, B. Integrated Governor Control for a Diesel—Generating Set. IEEE Trans. Energy Convers. 2006, 21, 476–483. [Google Scholar] [CrossRef]
- Tran, T.A.; Yan, X.; Yuan, Y. Marine Engine Rotational Speed Control Automatic System Based on Fuzzy PID Logic Control. In Proceedings of the 4th International Conference on Transportation Information and Safety (ICTIS 2017), Banff, AB, Canada, 8–10 August 2017; pp. 1099–1104. [Google Scholar]
- Jafari, R.; Yu, W.; Li, X.; Razvarz, S. Numerical Solution of Fuzzy Differential Equations with Z-numbers Using Bernstein Neural Networks. Int. J. Comput. Intell. Syst. 2017, 10, 1226–1237. [Google Scholar] [CrossRef]
- Jafari, R.; Li, X.; Yu, W. Numerical Solution of Fuzzy Equations with Z-numbers Using Neural Networks. Intell. Autom. Soft Comput. 2017, 85, 1–7. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the International Conference on Evolutionary Computation—The IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Clerc, M.; Kennedy, J. The Particle Swarm-explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Trans. Evolut. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Valdez, F.; Melin, P.; Castillo, O. Evolutionary Method Combining Particle Swarm Optimization and Genetic Algorithms using Fuzzy Logic for Decision Making. In Proceedings of the IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009. [Google Scholar]
- Zadeh, A.L. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, A.L. Outline of a New Approach to the Analysis of Complex Systems and Decision Processes. IEEE Trans. Syst. Man Cybern. 1973, 1, 28–44. [Google Scholar] [CrossRef]
- Aissaoui, A.G.; Tahour, A. Application of Fuzzy Logic in Control of Electrical Machines. Available online: http://www.intechopen.com/books/fuzzy-logic-controls-conceptstheories-andapplications/-application-of-fuzzy-logic-in-control-ofelectrical-machines (accessed on 28 March 2012).
- Uddin, M.N.; Huang, Z.R.; Chy, M.M.I. A Simplified Self-Tuned Neuro-Fuzzy Controller Based Speed Control of an Induction Motor Drive. In Proceedings of the 2007 IEEE International Conference on Industrial Technology, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Pundaleek, B.H.; Manish, G.R.; Vijay Kumar, M.G. Speed Control of Induction Motor: Fuzzy Logic Controller v/s PI Controller. IJCSNS Int. J. Comput. Sci. Netw. Secur. 2010, 10, 10. [Google Scholar]
- Vas, P. Artificial Intelligence Based Drives. In Power Electronics Handbook. Rashid, M.H., Ed.; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Bai, Y.; Zhuang, H.; Wang, D. Advanced Fuzzy Logic Technologies in Industrial Applications; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rubaai, A. Fuzzy Logic in Electric Drives. In Power Electronics Handbook; Rashid, M.H., Ed.; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Piscataway, NJ, USA, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Allaoua, B.; Abderrahmani, A.; Brahim, G.; Nasri, A. The Efficiency of Particle Swarm Optimization Applied on Fuzzy Logic DC Motor Speed Control. Serb. J. Electr. Eng. 2008, 5, 247–262. [Google Scholar] [CrossRef]
- Wang, K.; Yan, X.; Yuan, Y. Optimizing Ship Energy Efficiency: Application of Particle Swarm Optimization Algorithm. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 1–13. [Google Scholar] [CrossRef]

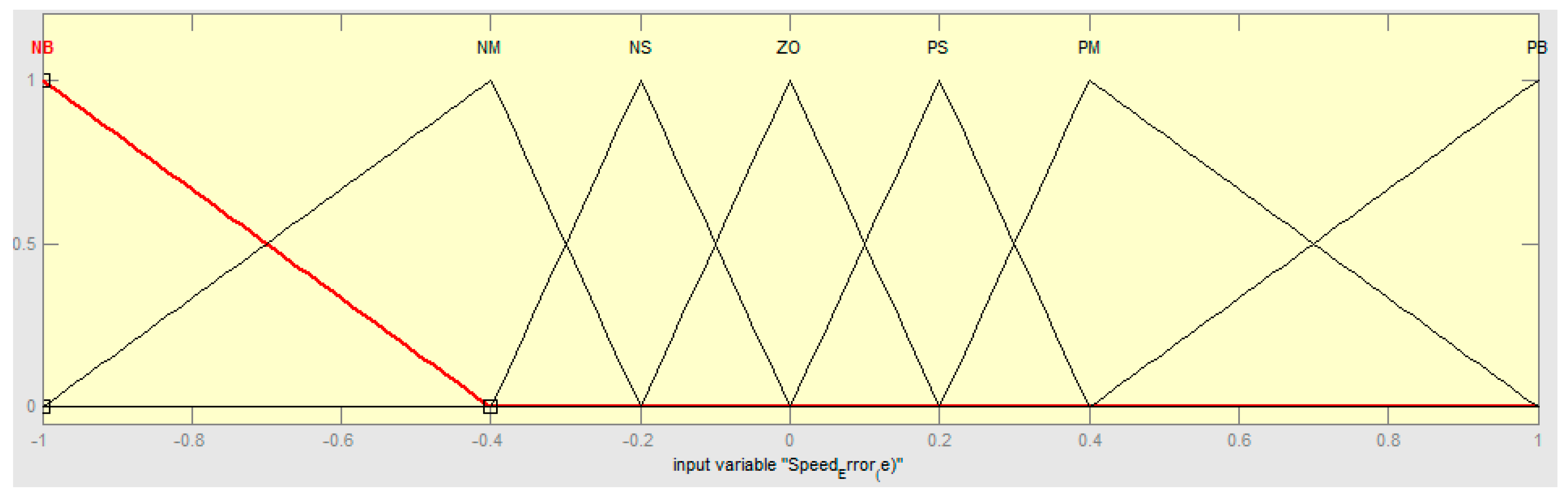
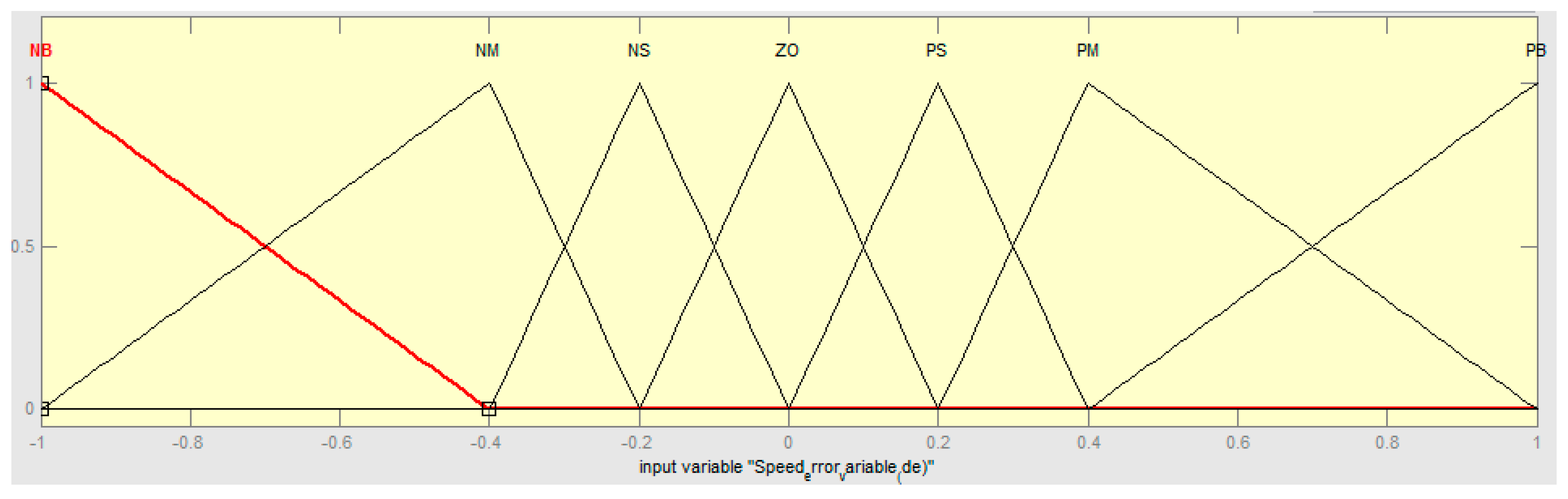
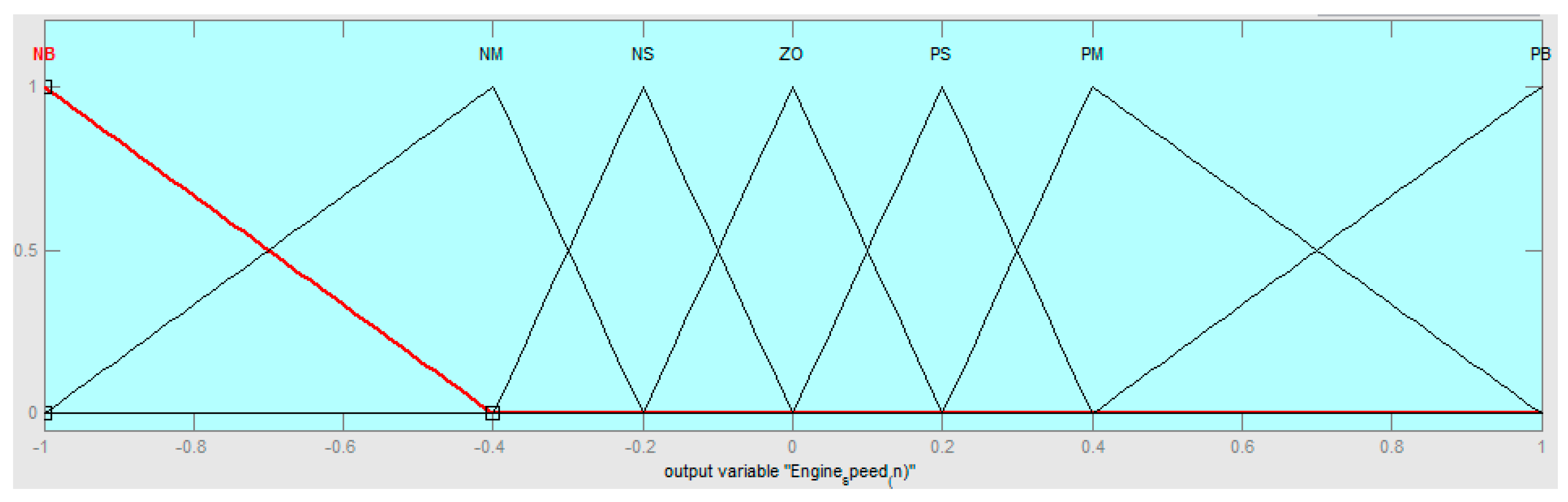
| e | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| de | ||||||||
| NB | PB | PB | PM | PM | PS | ZO | ZO | |
| NM | PB | PB | PM | PM | PS | ZO | ZO | |
| NS | PB | PB | PM | PS | ZO | NM | NM | |
| ZO | PB | PB | PM | ZO | NM | NB | NB | |
| PS | PM | PM | ZO | NS | NM | NB | NB | |
| PM | ZO | ZO | NS | NM | NM | NB | NB | |
| PB | ZO | ZO | NS | NM | NM | NB | NB | |
| e | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| de | ||||||||
| NB | r1 | r8 | r15 | r22 | r29 | r36 | r43 | |
| NM | r2 | r9 | r16 | r23 | r30 | r37 | r44 | |
| NS | r3 | r10 | r17 | r24 | r31 | r38 | r45 | |
| ZO | r4 | r11 | r18 | r25 | r32 | r39 | r46 | |
| PS | r5 | r12 | r19 | r26 | r33 | r40 | r47 | |
| PM | r6 | r13 | r20 | r27 | r34 | r41 | r48 | |
| PB | r7 | r14 | r21 | r28 | r35 | r42 | r49 |
| Population Size | 50 | e1, de1 and n1 | [−1, −1, −0.4] |
| Number of Iteration | 100 | e2, de2 and n2 | [−1, −0.4, −0.2] |
| wmax | 0.6 | e3, de3 and n3 | [−0.4, −0.2, 0] |
| wmin | 0.1 | e4, de4 and n4 | [−0.2, 0, 0.2] |
| c1 = c2 | 1.5 | e5, de5 and n5 | [0, 0.2, 0.4] |
| Min-offset | 200 | e6, de6 and n6 | [0.2, 0.4, 1] |
| Ke and Kde | [0.001, 0.005] | e7, de7 and n7 | [0.4, 1, 1] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, T.A. The Optimization of Marine Diesel Engine Rotational Speed Control Process by Fuzzy Logic Control Based on Particle Swarm Optimization Algorithm. Future Internet 2018, 10, 99. https://doi.org/10.3390/fi10100099
Tran TA. The Optimization of Marine Diesel Engine Rotational Speed Control Process by Fuzzy Logic Control Based on Particle Swarm Optimization Algorithm. Future Internet. 2018; 10(10):99. https://doi.org/10.3390/fi10100099
Chicago/Turabian StyleTran, Tien Anh. 2018. "The Optimization of Marine Diesel Engine Rotational Speed Control Process by Fuzzy Logic Control Based on Particle Swarm Optimization Algorithm" Future Internet 10, no. 10: 99. https://doi.org/10.3390/fi10100099
APA StyleTran, T. A. (2018). The Optimization of Marine Diesel Engine Rotational Speed Control Process by Fuzzy Logic Control Based on Particle Swarm Optimization Algorithm. Future Internet, 10(10), 99. https://doi.org/10.3390/fi10100099





