Physiologically Based Pharmacokinetic Modeling of Biologic Case Studies in Monkeys and Humans Reveals the Necessity of an Additional Clearance Term
Abstract
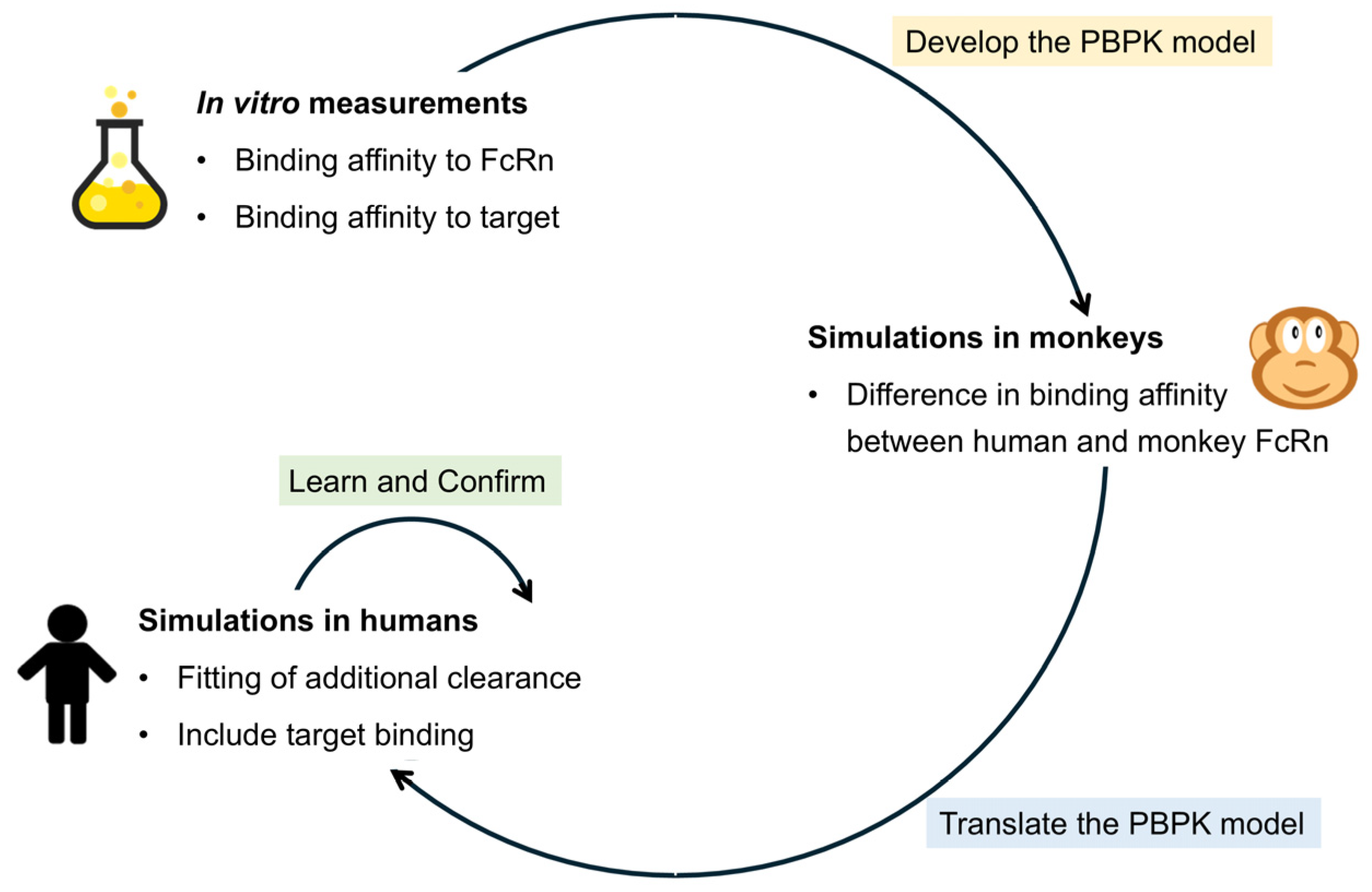
1. Introduction
2. Materials and Methods
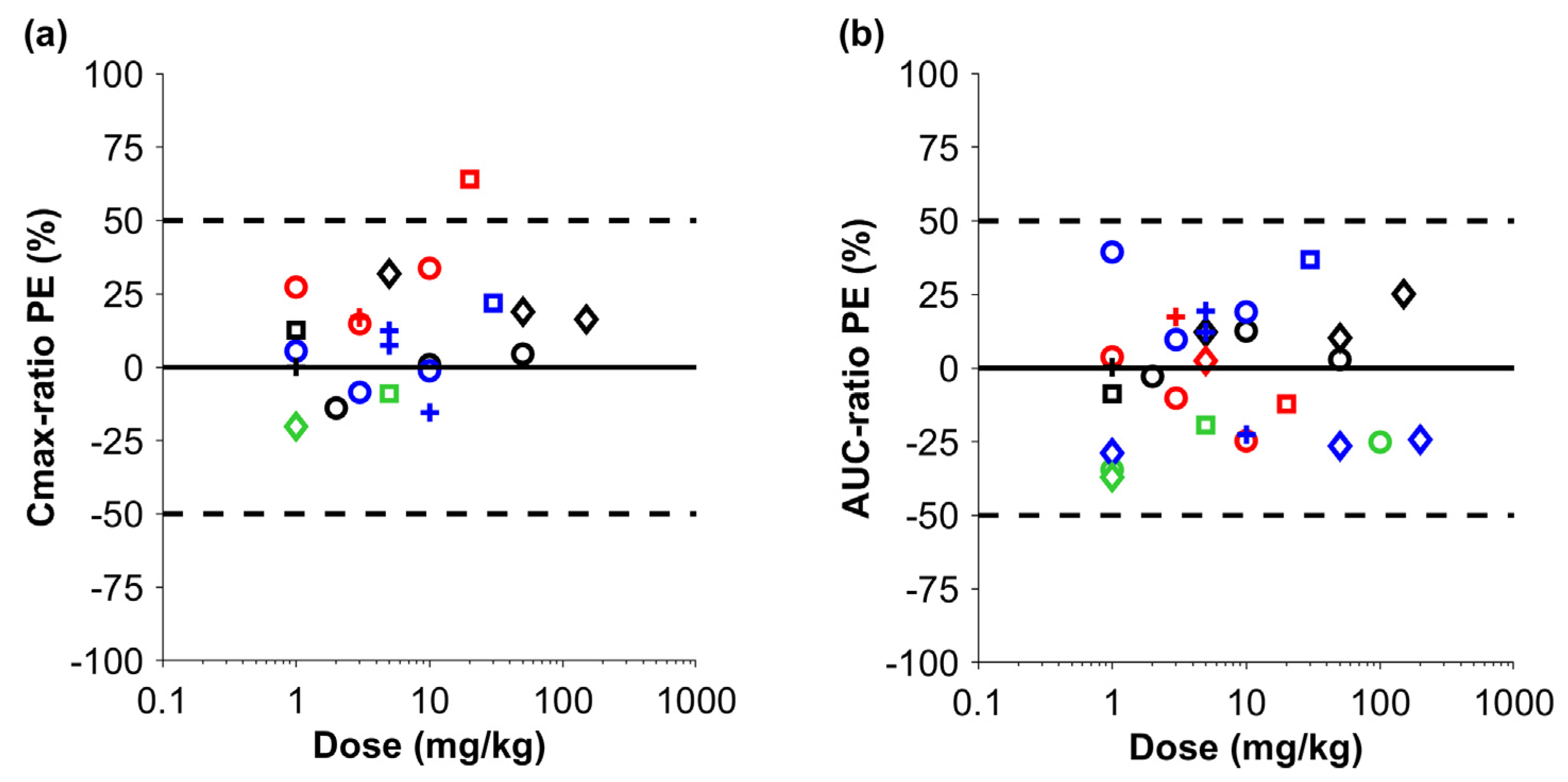
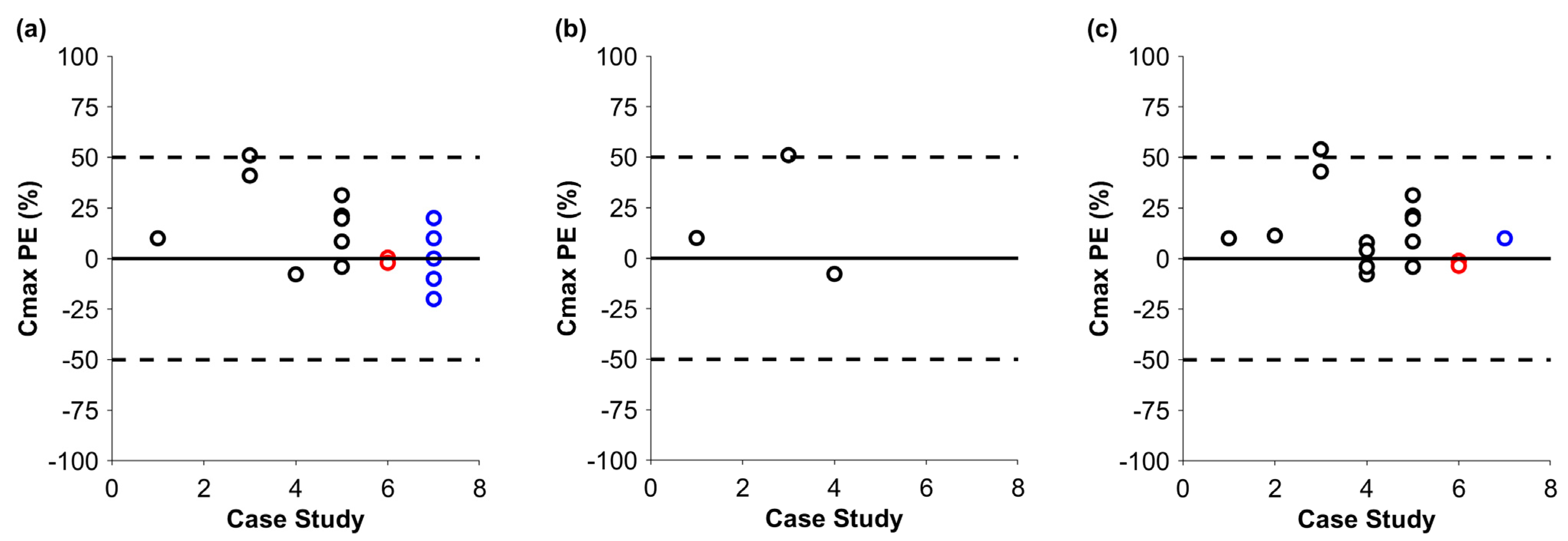
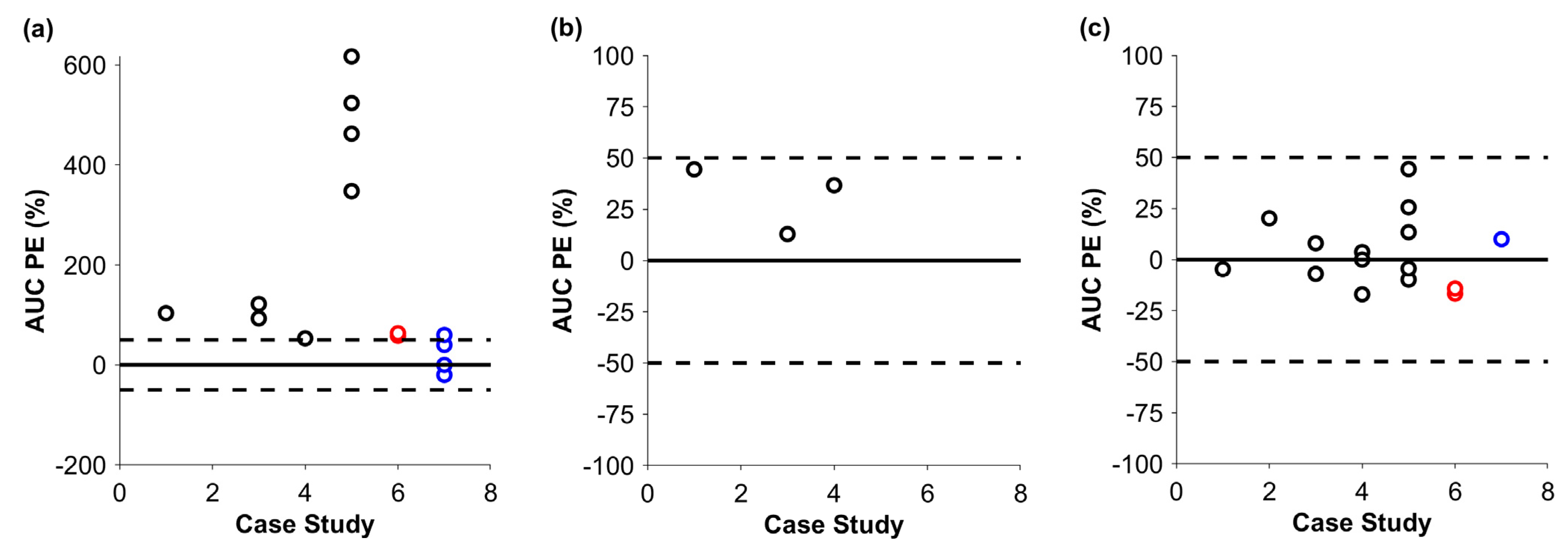
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PBPK | Physiologically-based pharmacokinetic modeling |
| Cmax | Peak concentration |
| AUC | Area under the curve |
| APC | Antigen-presenting cells |
| mAb | Monoclonal antibody |
| ADC | Antibody–drug conjugate |
| BI-TCE | Bispecific T-cell engager |
| TMDD | Target-mediated drug disposition |
| FcRn | Neonatal Fc receptor |
References
- Sepp, A.; Muliaditan, M. Application of Quantitative Protein Mass Spectrometric Data in the Early Predictive Analysis of Membrane-Bound Target Engagement by Monoclonal Antibodies. mAbs 2024, 16, 2324485. [Google Scholar] [CrossRef]
- Stader, F.; Liu, C.; Derbalah, A.; Momiji, H.; Pan, X.; Gardner, I.; Jamei, M.; Sepp, A. A Physiologically Based Pharmacokinetic Model Relates the Subcutaneous Bioavailability of Monoclonal Antibodies to the Saturation of Fcrn-Mediated Recycling in Injection-Site-Draining Lymph Nodes. Antibodies 2024, 13, 70. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Stader, F.; Chan, P.; Shemesh, C.S.; Chen, Y.; Gill, K.L.; Jones, H.M.; Li, L.; Rossato, G.; Wu, B.; et al. Development of a Pediatric Physiologically-Based Pharmacokinetic Model to Support Recommended Dosing of Atezolizumab in Children with Solid Tumors. Front. Pharmacol. 2022, 13, 974423. [Google Scholar] [CrossRef]
- Choules, M.P.; Zuo, P.; Otsuka, Y.; Garg, A.; Tang, M.; Bonate, P. Physiologically Based Pharmacokinetic Model to Predict Drug–Drug Interactions with the Antibody–Drug Conjugate Enfortumab Vedotin. J. Pharmacokinet. Pharmacodyn. 2023, 51, 417–428. [Google Scholar] [CrossRef]
- Rippe, B.; Haraldsson, B. Fluid and Protein Fluxes Across Small and Large Pores in the Microvasculature. Application of Two-Pore Equations. Acta Physiol. Scand. 1987, 131, 411–428. [Google Scholar] [CrossRef]
- Ober, R.J.; Martinez, C.; Vaccaro, C.; Zhou, J.; Ward, E.S. Visualizing the Site and Dynamics of Igg Salvage by the Mhc Class I-Related Receptor, FcRn. J. Immunol. 2004, 172, 2021–2029. [Google Scholar] [CrossRef] [PubMed]
- Shah, D.K.; Betts, A.M. Towards a Platform PBPK model to Characterize the Plasma and Tissue Disposition of Monoclonal Antibodies in Preclinical Species and Human. J. Pharmacokinet. Pharmacodyn. 2012, 39, 67–86. [Google Scholar] [CrossRef] [PubMed]
- Abdiche, Y.N.; Yeung, Y.A.; Chaparro-Riggers, J.; Barman, I.; Strop, P.; Chin, S.M.; Pham, A.; Bolton, G.; McDonough, D.; Lindquist, K.; et al. The Neonatal Fc Receptor (FcRn) Binds Independently to Both Sites of the Igg Homodimer with Identical Affinity. mAbs 2015, 7, 331–343. [Google Scholar] [CrossRef] [PubMed]
- Gill, K.L.; Gardner, I.; Li, L.; Jamei, M. A Bottom-up Whole-Body Physiologically Based Pharmacokinetic Model to Mechanistically Predict Tissue Distribution and the Rate of Subcutaneous Absorption of Therapeutic Proteins. AAPS J. 2016, 18, 156–170. [Google Scholar] [CrossRef]
- Li, L.; Gardner, I.; Dostalek, M.; Jamei, M. Simulation of Monoclonal Antibody Pharmacokinetics in Humans Using a Minimal Physiologically Based Model. AAPS J. 2014, 16, 1097–1109. [Google Scholar] [CrossRef]
- Haigler, H.T.; McKanna, J.A.; Cohen, S. Rapid Stimulation of Pinocytosis in Human Carcinoma Cells A-431 by Epidermal Growth Factor. J. Cell Biol. 1979, 83, 82–90. [Google Scholar] [CrossRef]
- Fan, Y.Y.; Farrokhi, V.; Caiazzo, T.; Wang, M.; O’Hara, D.M.; Neubert, H. Human FcRn Tissue Expression Profile and Half-Life in PBMCs. Biomolecules 2019, 9, 373. [Google Scholar] [CrossRef]
- Challacombe, S.; Russell, M. Estimation of the Intravascular Half-Lives of Normal Rhesus Monkey Igg, Iga and Igm. Immunology 1979, 36, 331. [Google Scholar]
- Waldmann, T.A.; Strober, W.; Blaese, R.M. Metabolism of Immunoglobulins. Prog. Immunol. 1971, 13, 891–903. [Google Scholar]
- Eigenmann, M.J.; Karlsen, T.V.; Krippendorff, B.F.; Tenstad, O.; Fronton, L.; Otteneder, M.B.; Wiig, H. Interstitial Igg Antibody Pharmacokinetics Assessed by Combined in Vivo-and Physiologically-Based Pharmacokinetic Modelling Approaches. J. Physiol. 2017, 595, 7311–7330. [Google Scholar] [CrossRef]
- Eigenmann, M.; Fronton, L.; Grimm, H.; Otteneder, M.; Krippendorff, B. Quantification of Igg Monoclonal Antibody Clearance in Tissues. mAbs 2017, 9, 1007–1015. [Google Scholar] [CrossRef]
- Zhang, X.; Lumen, A.; Wong, H.; Connarn, J.; Dutta, S.; Upreti, V.V. A Mechanistic Physiologically-Based Pharmacokinetic Platform Model to Guide Adult and Pediatric Intravenous and Subcutaneous Dosing for Bispecific T Cell Engagers. Clin. Pharmacol. Ther. 2024, 115, 457–467. [Google Scholar] [CrossRef]
- Lin, Y.S.; Nguyen, C.; Mendoza, J.-L.; Escandon, E.; Fei, D.; Meng, Y.G.; Modi, N.B. Preclinical Pharmacokinetics, Interspecies Scaling, and Tissue Distribution of a Humanized Monoclonal Antibody against Vascular Endothelial Growth Factor. J. Pharmacol. Exp. Ther. 1999, 288, 371–378. [Google Scholar] [CrossRef]
- Han, C.; Gunn, G.R.; Marini, J.C.; Shankar, G.; Hsu, H.H.; Davis, H.M. Pharmacokinetics and Immunogenicity Investigation of a Human Anti-Interleukin-17 Monoclonal Antibody in Non-Naïve Cynomolgus Monkeys. Drug Metab. Dispos. 2015, 43, 762–770. [Google Scholar] [CrossRef] [PubMed]
- Nnane, I.P.; Xu, Z.; Zhou, H.; Davis, H.M. Non-Clinical Pharmacokinetics, Prediction of Human Pharmacokinetics and First-in-Human Dose Selection for Cnto 5825, an Anti-Interleukin-13 Monoclonal Antibody. Basic Clin. Pharmacol. Toxicol. 2015, 117, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Vugmeyster, Y.; Szklut, P.; Tchistiakova, L.; Abraham, W.; Kasaian, M.; Xu, X. Preclinical Pharmacokinetics, Interspecies Scaling, and Tissue Distribution of Humanized Monoclonal Anti-Il-13 Antibodies with Different Il-13 Neutralization Mechanisms. Int. Immunopharmacol. 2008, 8, 477–483. [Google Scholar] [CrossRef] [PubMed]
- Halpern, W.G.; Lappin, P.; Zanardi, T.; Cai, W.; Corcoran, M.; Zhong, J.; Baker, K.P. Chronic Administration of Belimumab, a Blys Antagonist, Decreases Tissue and Peripheral Blood B-Lymphocyte Populations in Cynomolgus Monkeys: Pharmacokinetic, Pharmacodynamic, and Toxicologic Effects. Toxicol. Sci. 2006, 91, 586–599. [Google Scholar] [CrossRef] [PubMed]
- Deng, R.; Loyet, K.M.; Lien, S.; Iyer, S.; DeForge, L.E.; Theil, F.-P.; Lowman, H.B.; Fielder, P.J.; Prabhu, S. Pharmacokinetics of Humanized Monoclonal Anti-Tumor Necrosis Factor-A Antibody and Its Neonatal Fc Receptor Variants in Mice and Cynomolgus Monkeys. Drug Metab. Dispos. 2010, 38, 600–605. [Google Scholar] [CrossRef] [PubMed]
- Davis, C.B.; Hepburn, T.W.; Urbanski, J.J.; Kwok, D.C.; Hart, T.K.; Herzyk, D.J.; Demuth, S.G.; Leland, M.; Rhodes, G.R. Preclinical Pharmacokinetic Evaluation of the Respiratory Syncytial Virus-Specific Reshaped Human Monoclonal Antibody Rshz19. Drug Metab. Dispos. 1995, 23, 1028–1036. [Google Scholar] [CrossRef]
- Hinton, P.R.; Johlfs, M.G.; Xiong, J.M.; Hanestad, K.; Ong, K.C.; Bullock, C.; Keller, S.; Tang, M.T.; Tso, J.Y.; Vásquez, M. Engineered Human Igg Antibodies with Longer Serum Half-Lives in Primates. J. Biol. Chem. 2004, 279, 6213–6216. [Google Scholar] [CrossRef]
- Hinton, P.R.; Xiong, J.M.; Johlfs, M.G.; Tang, M.T.; Keller, S.; Tsurushita, N. An Engineered Human Igg1 Antibody with Longer Serum Half-Life. J. Immunol. 2006, 176, 346–356. [Google Scholar] [CrossRef]
- Ferrant, J.L.; Benjamin, C.D.; Cutler, A.H.; Kalled, S.L.; Hsu, Y.-M.; Garber, E.A.; Hess, D.M.; Shapiro, R.I.; Kenyon, N.S.; Harlan, D.M.; et al. The Contribution of Fc Effector Mechanisms in the Efficacy of Anti-Cd154 Immunotherapy Depends on the Nature of the Immune Challenge. Int. Immunol. 2004, 16, 1583–1594. [Google Scholar] [CrossRef]
- Dall’Acqua, W.F.; Kiener, P.A.; Wu, H. Properties of Human Igg1s Engineered for Enhanced Binding to the Neonatal Fc Receptor (FcRn). J. Biol. Chem. 2006, 281, 23514–23524. [Google Scholar] [CrossRef]
- Yeung, Y.A.; Wu, X.; Reyes, A.E.; Vernes, J.-M.; Lien, S.; Lowe, J.; Maia, M.; Forrest, W.F.; Meng, Y.G.; Damico, L.A.; et al. A Therapeutic Anti–Vegf Antibody with Increased Potency Independent of Pharmacokinetic Half-Life. Cancer Res. 2010, 70, 3269–3277. [Google Scholar] [CrossRef]
- Henne, K.R.; Ason, B.; Howard, M.; Wang, W.; Sun, J.; Higbee, J.; Tang, J.; Matsuda, K.C.; Xu, R.; Zhou, L.; et al. Anti-PCSK9 Antibody Pharmacokinetics and Low-Density Lipoprotein-Cholesterol Pharmacodynamics in Nonhuman Primates Are Antigen Affinity–Dependent and Exhibit Limited Sensitivity to Neonatal Fc Receptor–Binding Enhancement. J. Pharmacol. Exp. Ther. 2015, 353, 119–131. [Google Scholar] [CrossRef]
- Köck, K.; Pan, W.J.; Gow, J.M.; Horner, M.J.; Gibbs, J.P.; Colbert, A.; Goletz, T.J.; Newhall, K.J.; Rees, W.A.; Sun, Y.; et al. Preclinical Development of Amg 139, a Human Antibody Specifically Targeting Il-23. Br. J. Pharmacol. 2015, 172, 159–172. [Google Scholar] [CrossRef] [PubMed]
- Steinman, R.M.; Brodie, S.E.; Cohn, Z.A. Membrane Flow During Pinocytosis. A Stereologic Analysis. J. Cell Biol. 1976, 68, 665–687. [Google Scholar] [CrossRef] [PubMed]
- Richter, W.F.; Christianson, G.J.; Frances, N.; Grimm, H.P.; Proetzel, G.; Roopenian, D.C. Hematopoietic Cells as Site of First-Pass Catabolism after Subcutaneous Dosing and Contributors to Systemic Clearance of A Monoclonal Antibody in Mice. mAbs 2018, 10, 803–813. [Google Scholar] [CrossRef]
- Challa, D.K.; Wang, X.; Montoyo, H.P.; Velmurugan, R.; Ober, R.J.; Ward, E.S. Neonatal Fc Receptor Expression in Macrophages is Indispensable for Igg Homeostasis. mAbs 2019, 11, 848–860. [Google Scholar] [CrossRef]
- Jiménez Morales, A.; Maldonado-Montoro, M.; Martínez de la Plata, J.E.; Pérez Ramírez, C.; Daddaoua, A.; Alarcón Payer, C.; Expósito Ruiz, M.; García Collado, C. FCGR2A/FCGR3A Gene Polymorphisms and Clinical Variables as Predictors of Response to Tocilizumab and Rituximab in Patients with Rheumatoid Arthritis. J. Clin. Pharmacol. 2019, 59, 517–531. [Google Scholar] [CrossRef]
- Bruhns, P.; Iannascoli, B.; England, P.; Mancardi, D.A.; Fernandez, N.; Jorieux, S.; Daëron, M. Specificity and Affinity of Human Fcγ Receptors and Their Polymorphic Variants for Human Igg Subclasses. Blood 2009, 113, 3716–3725. [Google Scholar] [CrossRef] [PubMed]
- Foti, R.S.; Biswas, K.; Aral, J.; Be, X.; Berry, L.; Cheng, Y.; Conner, K.; Falsey, J.R.; Glaus, C.; Herberich, B.; et al. Use of Cryopreserved Hepatocytes as Part of an Integrated Strategy to Characterize in Vivo Clearance for Peptide-Antibody Conjugate Inhibitors of Nav1.7 in Preclinical Species. Drug Metab. Dispos. 2019, 47, 1111–1121. [Google Scholar] [CrossRef]
- Kumar, M.; Lanke, S.; Yadav, A.; Ette, M.; Mager, D.E.; Shah, D.K. Inter-Antibody Variability in the Clinical Pharmacokinetics of Monoclonal Antibodies Characterized Using Population Physiologically Based Pharmacokinetic Modeling. Antibodies 2024, 13, 54. [Google Scholar] [CrossRef]
- Liu, S.; Shah, D.K. Physiologically Based Pharmacokinetic Modeling to Characterize the Effect of Molecular Charge on Whole-Body Disposition of Monoclonal Antibodies. AAPS J. 2023, 25, 48. [Google Scholar] [CrossRef]
- Basset; Devauchelle; Durand; Jamin; Pennec; Youinou; Dueymes. Glycosylation of Immunoglobulin a Influences Its Receptor Binding. Scand. J. Immunol. 1999, 50, 572–579. [Google Scholar] [CrossRef]
- Avery, L.B.; Wang, M.; Kavosi, M.S.; Joyce, A.; Kurz, J.C.; Fan, Y.Y.; Dowty, M.E.; Zhang, M.; Zhang, Y.; Cheng, A.; et al. Utility of a Human Fcrn Transgenic Mouse Model in Drug Discovery for Early Assessment and Prediction of Human Pharmacokinetics of Monoclonal Antibodies. mAbs 2016, 8, 1064–1078. [Google Scholar] [CrossRef]
- Betts, A.; Keunecke, A.; van Steeg, T.J.; van der Graaf, P.H.; Avery, L.B.; Jones, H.; Berkhout, J. Linear Pharmacokinetic Parameters for Monoclonal Antibodies Are Similar within a Species and across Different Pharmacological Targets: A Comparison between Human, Cynomolgus Monkey and Hfcrn Tg32 Transgenic Mouse Using a Population-Modeling Approach. mAbs 2018, 10, 751–764. [Google Scholar] [CrossRef]
- Valente, D.; Mauriac, C.; Schmidt, T.; Focken, I.; Beninga, J.; Mackness, B.; Qiu, H.; Vicat, P.; Kandira, A.; Radošević, K.; et al. Pharmacokinetics of Novel Fc-Engineered Monoclonal and Multispecific Antibodies in Cynomolgus Monkeys and Humanized Fcrn Transgenic Mouse Models. mAbs 2020, 12, 1829337. [Google Scholar] [CrossRef]
| Performed Simulations | Case 1: mAb | Case 2: mAb | Case 3: mAb | Case 4: mAb | Case 5: mAb | Case 6: ADC | Case 7: Bi-TCE |
|---|---|---|---|---|---|---|---|
| Monkey |  |  |  |  |  |  |  |
| Human without CLadd |  |  |  |  |  |  |  |
| Human with allometrically scaled CLadd |  |  |  |  |  |  |  |
| Human with optimized CLadd |  |  |  |  |  |  |  |
| Parameter | mAb | ADC | Bi-TCE |
|---|---|---|---|
| Molecular weight (g/mol) |  |  |  |
| KD to FcRn (µM) |  |  |  |
| Additional systemic clearance (L/h) |  |  |  |
| Renal filtration clearance |  |  |  |
| Deconjugation |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stader, F.; Sharma, P.; Huang, W.; Choules, M.P.; Willemin, M.-E.; Zhang, X.; Yau, E.; Derbalah, A.; Zyla, A.; Liu, C.; et al. Physiologically Based Pharmacokinetic Modeling of Biologic Case Studies in Monkeys and Humans Reveals the Necessity of an Additional Clearance Term. Pharmaceutics 2025, 17, 560. https://doi.org/10.3390/pharmaceutics17050560
Stader F, Sharma P, Huang W, Choules MP, Willemin M-E, Zhang X, Yau E, Derbalah A, Zyla A, Liu C, et al. Physiologically Based Pharmacokinetic Modeling of Biologic Case Studies in Monkeys and Humans Reveals the Necessity of an Additional Clearance Term. Pharmaceutics. 2025; 17(5):560. https://doi.org/10.3390/pharmaceutics17050560
Chicago/Turabian StyleStader, Felix, Pradeep Sharma, Weize Huang, Mary P. Choules, Marie-Emilie Willemin, Xinwen Zhang, Estelle Yau, Abdallah Derbalah, Adriana Zyla, Cong Liu, and et al. 2025. "Physiologically Based Pharmacokinetic Modeling of Biologic Case Studies in Monkeys and Humans Reveals the Necessity of an Additional Clearance Term" Pharmaceutics 17, no. 5: 560. https://doi.org/10.3390/pharmaceutics17050560
APA StyleStader, F., Sharma, P., Huang, W., Choules, M. P., Willemin, M.-E., Zhang, X., Yau, E., Derbalah, A., Zyla, A., Liu, C., & Sepp, A. (2025). Physiologically Based Pharmacokinetic Modeling of Biologic Case Studies in Monkeys and Humans Reveals the Necessity of an Additional Clearance Term. Pharmaceutics, 17(5), 560. https://doi.org/10.3390/pharmaceutics17050560






