Kinetics of Drug Release from Clay Using Enhanced Sampling Methods
Abstract
1. Introduction
2. Methods
- GAMBES
- OPES
2.1. The Model
2.1.1. The Surface Model System
2.1.2. Model System for the Case of the Interlayer Adsorbed Drug
2.2. Computational Details
3. Results and Discussion
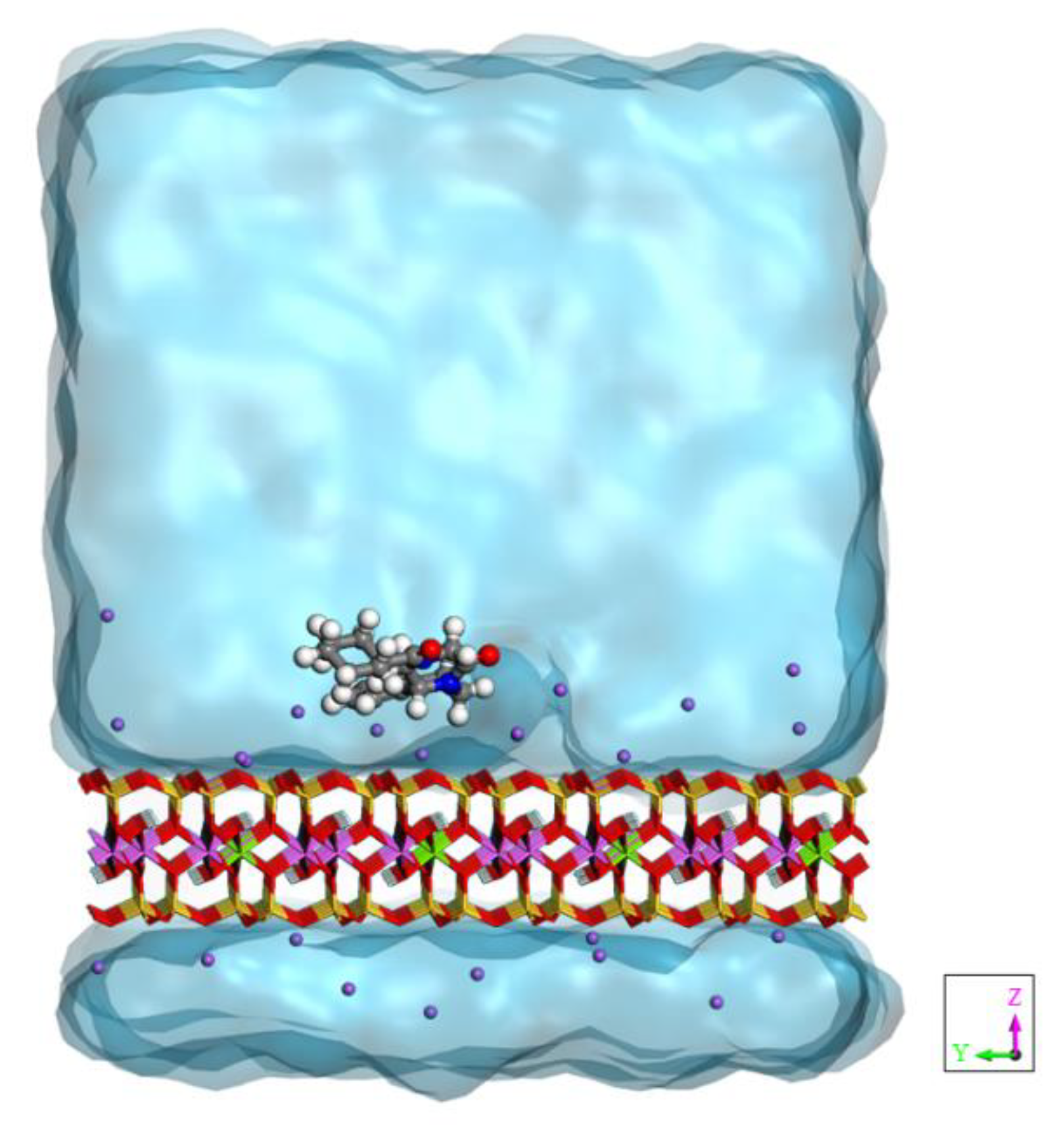
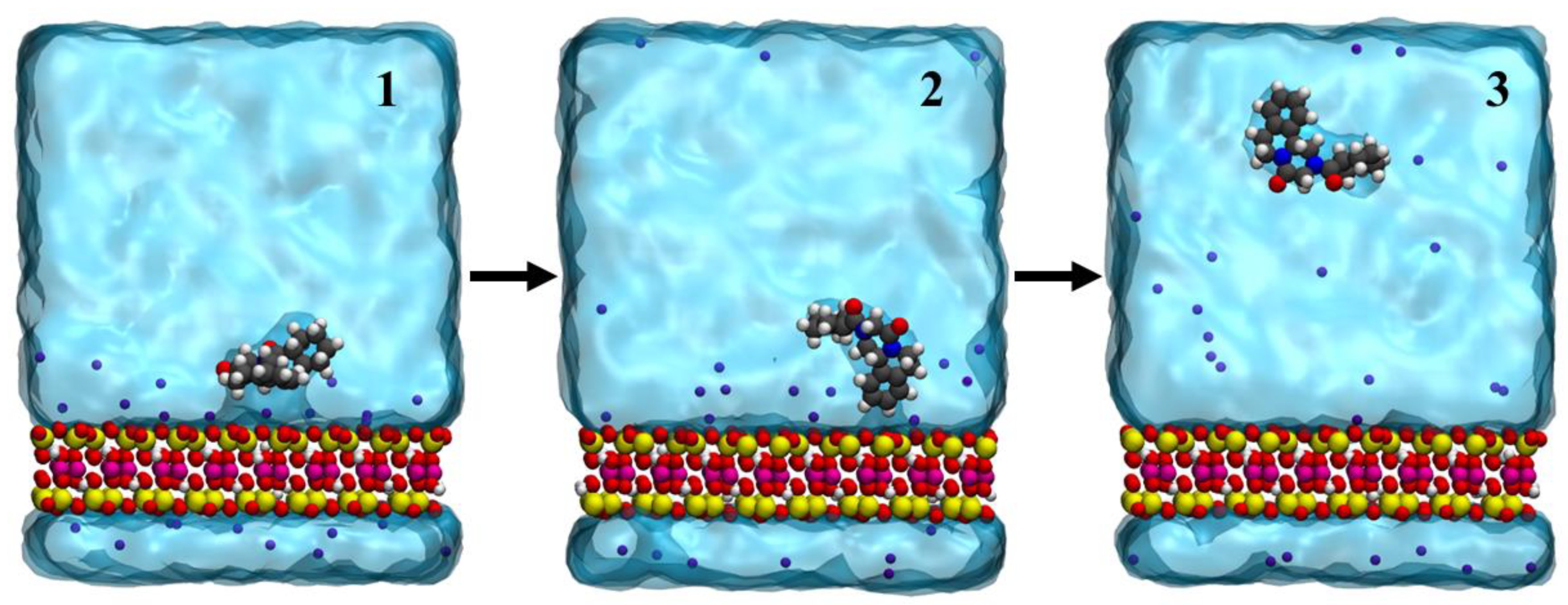
3.1. Drug Adsorbed on the Clay’s Surface
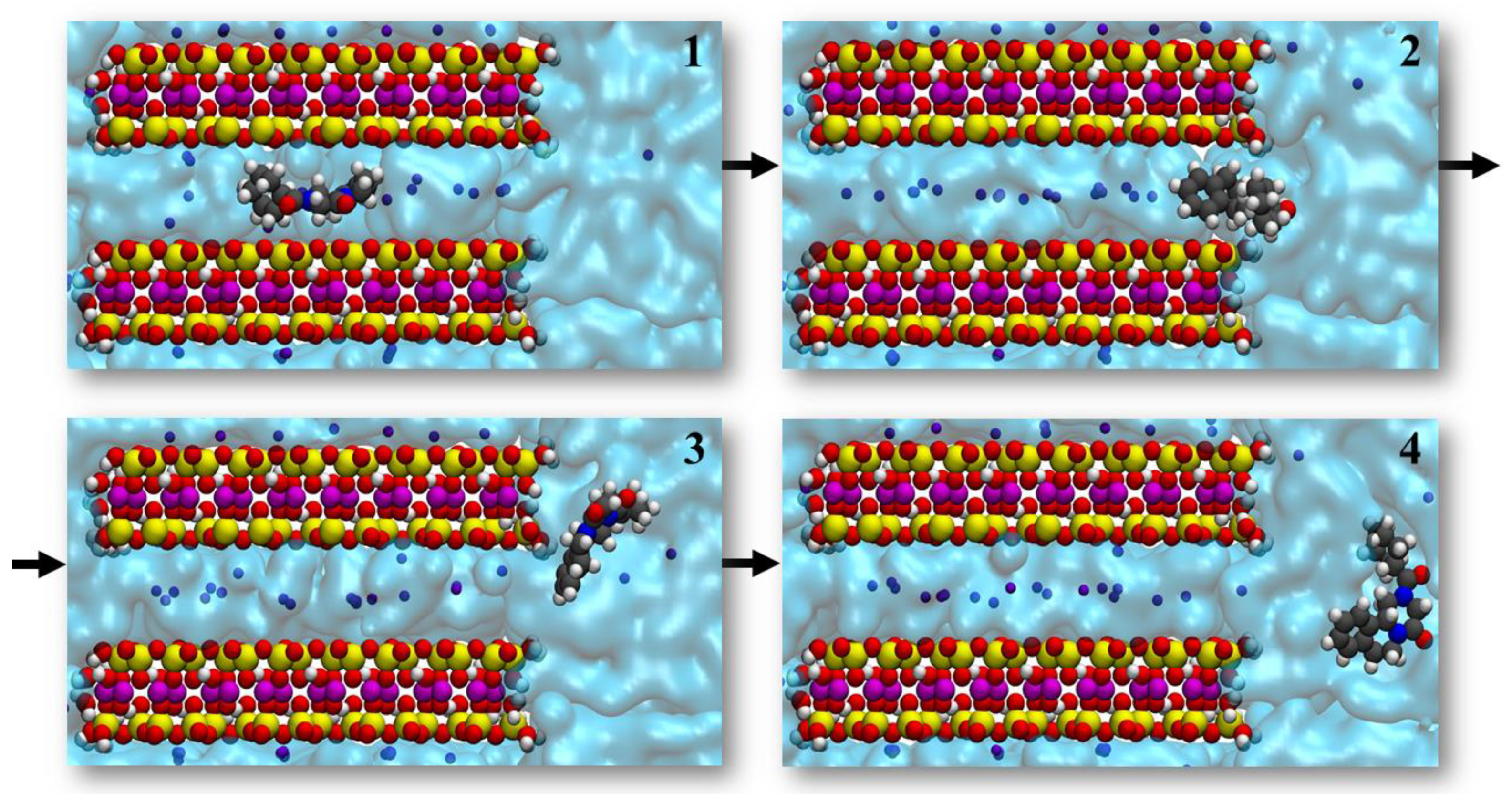
3.2. Drug Adsorbed in the Clay’s Interlayer Space
4. Conclusions
Supplementary Materials
Author Contributions
Funding
 ) 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 895355.
) 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 895355.Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WHO (World Health Organization). Available online: https://www.who.int/health-topics/schistosomiasis. (accessed on 10 December 2021).
- Colley, D.G.; Bustinduy, A.L.; Secor, W.E.; King, C.H. Human schistosomiasis. Lancet 2014, 383, 2253–2264. [Google Scholar] [CrossRef] [PubMed]
- Gryseels, B.; Polman, K.; Clerinx, J.; Kestens, L. Human schistosomiasis. Lancet 2006, 368, 1106–1118. [Google Scholar] [CrossRef]
- Steinmann, P.; Keiser, J.; Bos, R.; Tanner, M.; Utzinger, J. Schistosomiasis and water resources development: Systematic review, meta-analysis, and estimates of people at risk. Lancet Infect. Dis. 2006, 6, 411–425. [Google Scholar] [CrossRef] [PubMed]
- Chitsulo, L.; Engels, D.; Montresor, A.; Savioli, L. The global status of schistosomiasis and its control. Acta Trop. 2000, 77, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Andrews, P. Praziquantel: Mechanisms of anti-schistosomal activity. Pharmacol. Ther. 1985, 29, 129–156. [Google Scholar] [CrossRef] [PubMed]
- Lindenberg, M.; Kopp, S.; Dressman, J.B. Classification of orally administered drugs on the World Health Organization model list of essential medicines according to the biopharmaceutics classification system. Eur. J. Pharm. Biopharm. 2004, 58, 265–278. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.; Deng, Z.; Xu, Y.; Yan, G.; Deng, X.; Wu, L.; Liang, Q.; Fang, F.; Feng, X.; Yu, M.; et al. Preparation and In Vitro/In Vivo Evaluation of Orally Disintegrating/Modified-Release Praziquantel Tablets. Pharmaceutics 2021, 13, 1567. [Google Scholar] [CrossRef]
- Boniatti, J.; Januskaite, P.; da Fonseca, L.B.; Viçosa, A.L.; Amendoeira, F.C.; Tuleu, C.; Basit, A.W.; Goyanes, A.; Ré, M.-I. Direct Powder Extrusion 3D Printing of Praziquantel to Overcome Neglected Disease Formulation Challenges in Paediatric Populations. Pharmaceutics 2021, 13, 1114. [Google Scholar] [CrossRef] [PubMed]
- Zanolla, D.; Hasa, D.; Arhangelskis, M.; Schneider-Rauber, G.; Chierotti, M.R.; Keiser, J.; Voinovich, D.; Jones, W.; Perissutti, B. Mechanochemical Formation of Racemic Praziquantel Hemihydrate with Improved Biopharmaceutical Properties. Pharmaceutics 2020, 12, 289. [Google Scholar] [CrossRef]
- Cioli, D.; Pica-Mattoccia, L. Praziquantel. Parasitol. Res. 2003, 90, S3–S9. [Google Scholar] [CrossRef]
- Wang, W.; Wang, L.; Liang, Y.-S. Susceptibility or resistance of praziquantel in human schistosomiasis: A review. Parasitol. Res. 2012, 111, 1871–1877. [Google Scholar] [CrossRef] [PubMed]
- Aguzzi, C.; Cerezo, P.; Viseras, C.; Caramella, C. Use of clays as drug delivery systems: Possibilities and limitations. Appl. Clay Sci. 2007, 36, 22–36. [Google Scholar] [CrossRef]
- Viseras, C.; Cerezo, P.; Sánchez, R.; Salcedo, I.; Aguzzi, C. Current challenges in clay minerals for drug delivery. Appl. Clay Sci. 2010, 48, 291–295. [Google Scholar] [CrossRef]
- De Sousa Rodrigues, L.A.; Figueiras, A.; Veiga, F.; Mendes de Freitas, R.; Nunes, L.C.C.; Da Silva Filho, E.C.; Da Silva Leite, C.M. The systems containing clays and clay minerals from modified drug release: A review. Colloids Surf. B 2013, 103, 642–651. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.-H.; Lee, J.-H.; Ryu, H.-J.; Elzatahry, A.A.; Alothman, Z.A.; Choy, J.-H. Drug–clay nanohybrids as sustained delivery systems. Appl. Clay Sci. 2016, 130, 20–32. [Google Scholar] [CrossRef]
- Meirelles, L.M.A.; Raffin, F.N. Clay and Polymer-Based Composites Applied to Drug Release: A Scientific and Technological Prospection. J. Pharm. Pharm. Sci. 2017, 20, 115–134. [Google Scholar] [CrossRef] [PubMed]
- Massaro, M.; Colletti, C.G.; Lazzara, G.; Riela, S. The Use of Some Clay Minerals as Natural Resources for Drug Carrier Applications. J. Funct. Biomater. 2018, 9, 58. [Google Scholar] [CrossRef]
- Borrego-Sánchez, A.; Carazo, E.; Aguzzi, C.; Viseras, C.; Sainz-Díaz, C.I. Biopharmaceutical improvement of praziquantel by interaction with montmorillonite and sepiolite. Appl. Clay Sci. 2018, 160, 173–179. [Google Scholar] [CrossRef]
- Borrego-Sánchez, A.; Sánchez-Espejo, R.; García-Villén, F.; Viseras, C.; Sainz-Díaz, C.I. Praziquantel–Clays as Accelerated Release Systems to Enhance the Low Solubility of the Drug. Pharmaceutics 2020, 12, 914. [Google Scholar] [CrossRef] [PubMed]
- Borrego-Sánchez, A.; Sainz-Díaz, C.I. Natural phyllosilicates as excipientes of drugs: Computational approaches. In Computational Modeling in Clay Mineralogy; Sainz-Díaz, C.I., Fiore, S., Eds.; Digilabs: Bari, Italy, 2021; Volume 3, pp. 255–270. [Google Scholar]
- Debnath, J.; Parrinello, M. Gaussian Mixture-Based Enhanced Sampling for Statics and Dynamics. J. Phys. Chem. Lett. 2020, 11, 5076–5080. [Google Scholar] [CrossRef]
- Ray, D.; Ansari, N.; Rizzi, V.; Invernizzi, M.; Parrinello, M. Rare Event Kinetics from Adaptive Bias Enhanced Sampling. J. Chem. Theory Comput. 2022, 18, 6500–6509. [Google Scholar] [CrossRef]
- Ansari, N.; Rizzi, V.; Parrinello, M. Water regulates the residence time of Benzamidine in Trypsin. Nat. Comm. 2022, 13, 5438. [Google Scholar] [CrossRef] [PubMed]
- Torrie, G.; Valleau, J. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Mezei, M. Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias. J. Comput. Phys. 1987, 68, 237–248. [Google Scholar] [CrossRef]
- Marsili, S.; Barducci, A.; Chelli, R.; Procacci, P.; Schettino, V. Self-healing umbrella sampling: A non-equilibrium approach for quantitative free energy calculations. J. Phys. Chem. B. 2006, 110, 14011–14013. [Google Scholar] [CrossRef] [PubMed]
- Babin, V.; Roland, C.; Sagui, C. Adaptively biased molecular dynamics for free energy calculations. J. Chem. Phys. 2008, 128, 134101. [Google Scholar] [CrossRef]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Maragakis, P.; van der Vaart, A.; Karplus, M. Gaussian-mixture umbrella sampling. J. Phys. Chem. B. 2009, 113, 4664–4673. [Google Scholar] [CrossRef]
- Fort, G.; Jourdain, B.; Lelièvre, T.; Stoltz, G. Self-healing umbrella sampling: Convergence and efficiency. Stat. Comput. 2017, 27, 147–168. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A. Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2020, 2, 200–212. [Google Scholar] [CrossRef]
- Parrinello, M. Breviarium de Motu Simulato Ad Atomos Pertinenti. Isr. J. Chem. 2022, 62, e202100105. [Google Scholar] [CrossRef]
- Grubmüller, H. Predicting slow structural transitions in macromolecular systems: Conformational flooding. Phys. Rev. E 1995, 52, 2893–2906. [Google Scholar] [CrossRef] [PubMed]
- Voter, A.F. A method for accelerating the molecular dynamics simulation of infrequent events. Chem. Phys. 1997, 106, 4665–4677. [Google Scholar] [CrossRef]
- McCarty, J.; Valsson, O.; Tiwary, P.; Parrinello, M. Variationally Optimized Free-Energy Flooding for Rate Calculation. Phys. Rev. Lett. 2015, 115, 070601. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Statist. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- Heinz, H.; Vaia, R.A.; Farmer, L. Interaction energy and surface reconstruction between sheets of layered silicates. J. Chem. Phys. 2006, 124, 224713. [Google Scholar] [CrossRef]
- Heinz, H.; Lin, T.-J.; Mishra, R.K.; Emami, F.S. Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The INTERFACE Force Field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef]
- Heinz, H.; Suter, U.W. Atomic charges for classical simulations of polar systems. J. Phys. Chem. B 2004, 108, 18341–18352. [Google Scholar] [CrossRef]
- Rebitski, E.P.; Alcântara, A.C.S.; Darder, M.; Cansian, R.L.; Gómez-Hortigüela, L.; Pergher, S.B.C. Functional Carboxymethylcellulose/Zein Bionanocomposite Films Based on Neomycin Supported on Sepiolite or Montmorillonite Clays. ACS Omega 2018, 3, 13538–13550. [Google Scholar] [CrossRef] [PubMed]
- Francisco-Márquez, M.; Soriano-Correa, C.; Sainz-Díaz, C.I. Adsorption of Sulfonamides on Phyllosilicate Surfaces by Molecular Modeling Calculations. J. Phys. Chem. C 2017, 121, 2905–2914. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Dutournié, P.; Bruneau, M.; Brendlé, J.; Limousy, L.; Pluchon, S. Mass transfer modelling in clay-based material: Estimation of apparent diffusivity of a molecule of interest. C. R. Chim. 2019, 22, 250–257. [Google Scholar] [CrossRef]
- De Jesus, M.B.; Pinto, L.M.A.; Fraceto, L.F.; Magalhães, A.; Zanotti-Magalhães, E.M.; De Paula, E. Improvement of the oral praziquantel anthelmintic effect by cyclodextrin complexation. J. Drug Target 2010, 18, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Špehar, T.K.; Pocrnić, M.; Klarić, D.; Bertoša, B.; Čikoš, A.; Jug, M.; Padovan, J.; Dragojević, S.; Galić, N. Investigation of Praziquantel/Cyclodextrin Inclusion Complexation by NMR and LC-HRMS/MS: Mechanism, Solubility, Chemical Stability, and Degradation Products. Mol. Pharm. 2021, 18, 4210–4223. [Google Scholar] [CrossRef]
- Tournassat, C.; Steefel, C.I. Ionic transport in nano-porous clays with consideration of electrostatic effects. Rev. Mineral. Geochem. 2015, 80, 287–329. [Google Scholar] [CrossRef]
- Uddin, F. Montmorillonite: An Introduction to Properties and Utilization. In Current Topics in the Utilization of Clay in Industrial and Medical Applications; Zoveidavianpoor, M., Ed.; IntechOpen: London, UK, 2018; Volume 1, pp. 3–23. [Google Scholar] [CrossRef]
- Krupskaya, V.V.; Zakusin, S.V.; Tyupina, E.A.; Dorzhieva, O.V.; Zhukhlistov, A.P.; Belousov, P.E.; Timofeeva, M.N. Experimental Study of Montmorillonite Structure and Transformation of Its Properties under Treatment with Inorganic Acid Solutions. Minerals 2017, 7, 49. [Google Scholar] [CrossRef]
- Lagaly, G.; Ogawa, M.; Dékány, I. Chapter 7.3—Clay Mineral Organic Interactions. In Developments in Clay Science, Handbook of Clay Science; Bergaya, F., Theng, B.K.G., Lagaly, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 1, pp. 309–377. [Google Scholar] [CrossRef]
- Zhang, J.; Manias, E.; Wilkie, C.A. Polymerically Modified Layered Silicates: An Effective Route to Nanocomposites. J. Nanosci. Nanotechnol. 2008, 8, 1597–1615. [Google Scholar] [CrossRef]
- He, H.; Tao, Q.; Zhu, J.; Yuan, P.; Shein, W.; Yang, S. Silylation of clay mineral surfaces. Appl. Clay Sci. 2013, 71, 15–20. [Google Scholar] [CrossRef]
- Chiu, C.-W.; Huang, T.-K.; Wang, Y.-C.; Alamani, B.G.; Lin, J.J. Intercalation strategies in clay/polymer hybrids. Prog. Polym. Sci. 2014, 39, 443–485. [Google Scholar] [CrossRef]
- Cypes, S.H.; Saltzman, W.M.; Giannelis, E.P. Organosilicate-polymer drug delivery systems: Controlled release and enhanced mechanical properties. J. Control. Release 2003, 90, 163–169. [Google Scholar] [CrossRef] [PubMed]
- Odom, I.E. Smectite Clay Minerals: Properties and Uses. Phil. Trans. R. Soc. Lond. A 1984, 311, 391–409. [Google Scholar] [CrossRef]
- Kevan, L. Microporous materials: Zeolites, clays, and aluminophosphates. In Encyclopedia of Physical Science and Technology, 3rd ed.; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2003; pp. 755–764. [Google Scholar] [CrossRef]
- Bleam, W.F. Chapter 3—Clay mineralogy and Clay Chemistry. In Soil and Environmental Chemistry; Bleam, W.F., Ed.; Academic Press: New York, NY, USA, 2012; pp. 85–115. [Google Scholar] [CrossRef]
- Dong, J.; Cheng, Z.; Tan, S.; Zhu, Q. Clay nanoparticles as pharmaceutical carriers in drug delivery systems. Expert Opinion on Drug Delivery 2021, 18, 695–714. [Google Scholar] [CrossRef]
- Invernizzi, M.; Parrinello, M. Rethinking Metadynamics: From Bias Potentials to Probability Distributions. J. Phys. Chem. Lett. 2020, 11, 2731–2736. [Google Scholar] [CrossRef]


| τ (10−12 s) | k (109 s−1) | p-Value | µ ± σ (10−12 s) | |
|---|---|---|---|---|
| Surface, MD | 363 | 2.76 | 0.76 | 344 ± 218 |
| k (106 s−1) | p-Value | µ ± σ (10−6 s) | ||
|---|---|---|---|---|
| A, OPESf | 200.0 | 0.005 | 0.76 | 198.0 ± 176.0 |
| B, OPESf | 54.4 | 0.018 | 0.41 | 55.4 ± 64.5 |
| C, MD | 0.00547 | 182.8 | 0.42 | 0.00536 ± 0.00393 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borrego-Sánchez, A.; Debnath, J.; Parrinello, M. Kinetics of Drug Release from Clay Using Enhanced Sampling Methods. Pharmaceutics 2022, 14, 2586. https://doi.org/10.3390/pharmaceutics14122586
Borrego-Sánchez A, Debnath J, Parrinello M. Kinetics of Drug Release from Clay Using Enhanced Sampling Methods. Pharmaceutics. 2022; 14(12):2586. https://doi.org/10.3390/pharmaceutics14122586
Chicago/Turabian StyleBorrego-Sánchez, Ana, Jayashrita Debnath, and Michele Parrinello. 2022. "Kinetics of Drug Release from Clay Using Enhanced Sampling Methods" Pharmaceutics 14, no. 12: 2586. https://doi.org/10.3390/pharmaceutics14122586
APA StyleBorrego-Sánchez, A., Debnath, J., & Parrinello, M. (2022). Kinetics of Drug Release from Clay Using Enhanced Sampling Methods. Pharmaceutics, 14(12), 2586. https://doi.org/10.3390/pharmaceutics14122586






