A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation
Abstract
1. Introduction
1.1. Twin Screw Wet Granulation
1.2. Objectives
2. Materials and Methods
3. Theory and Metrics
3.1. Theory behind Equation Development
3.2. Formulation of the Equations for the Metrics
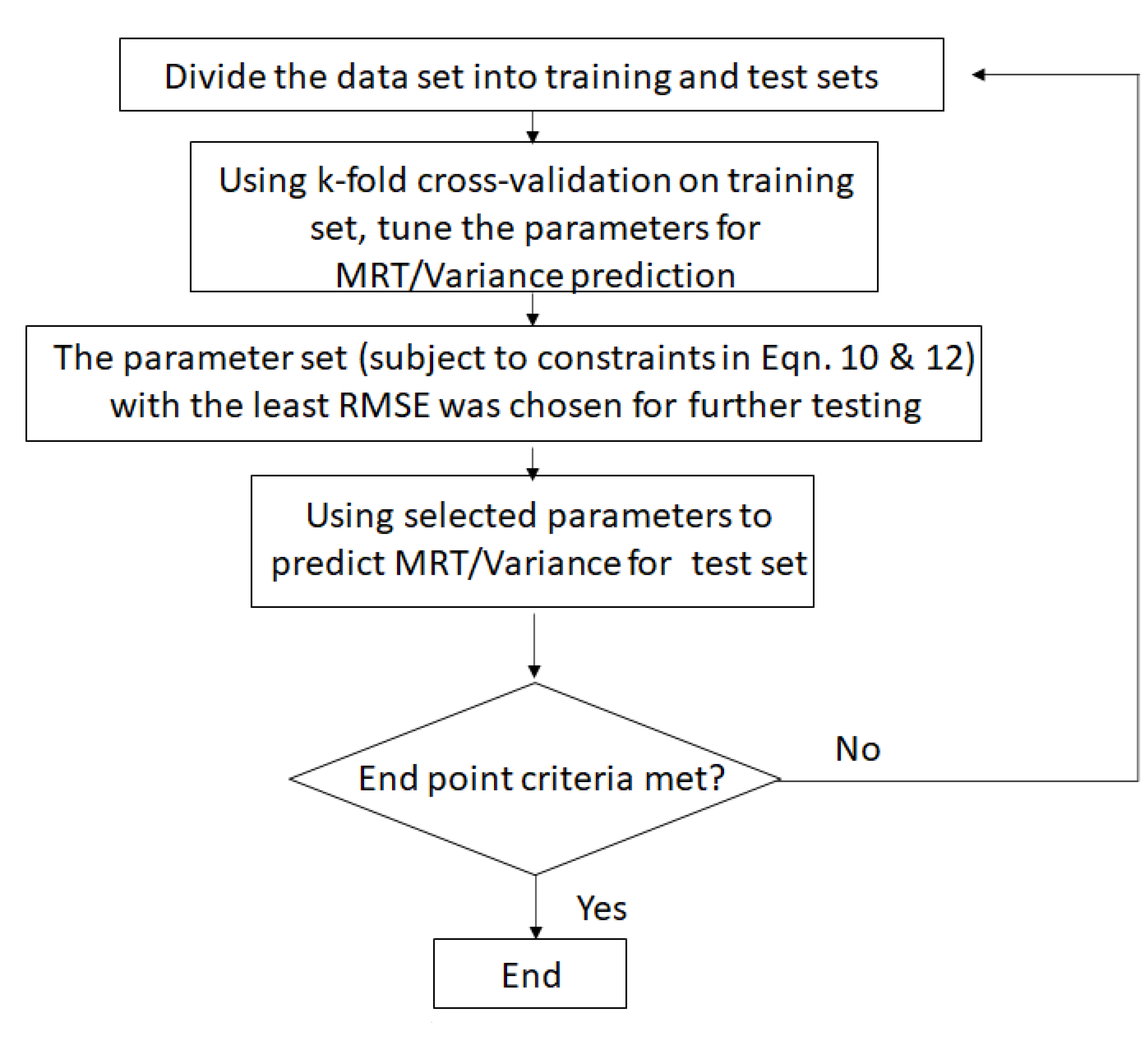
3.3. Algorithm Development
- i
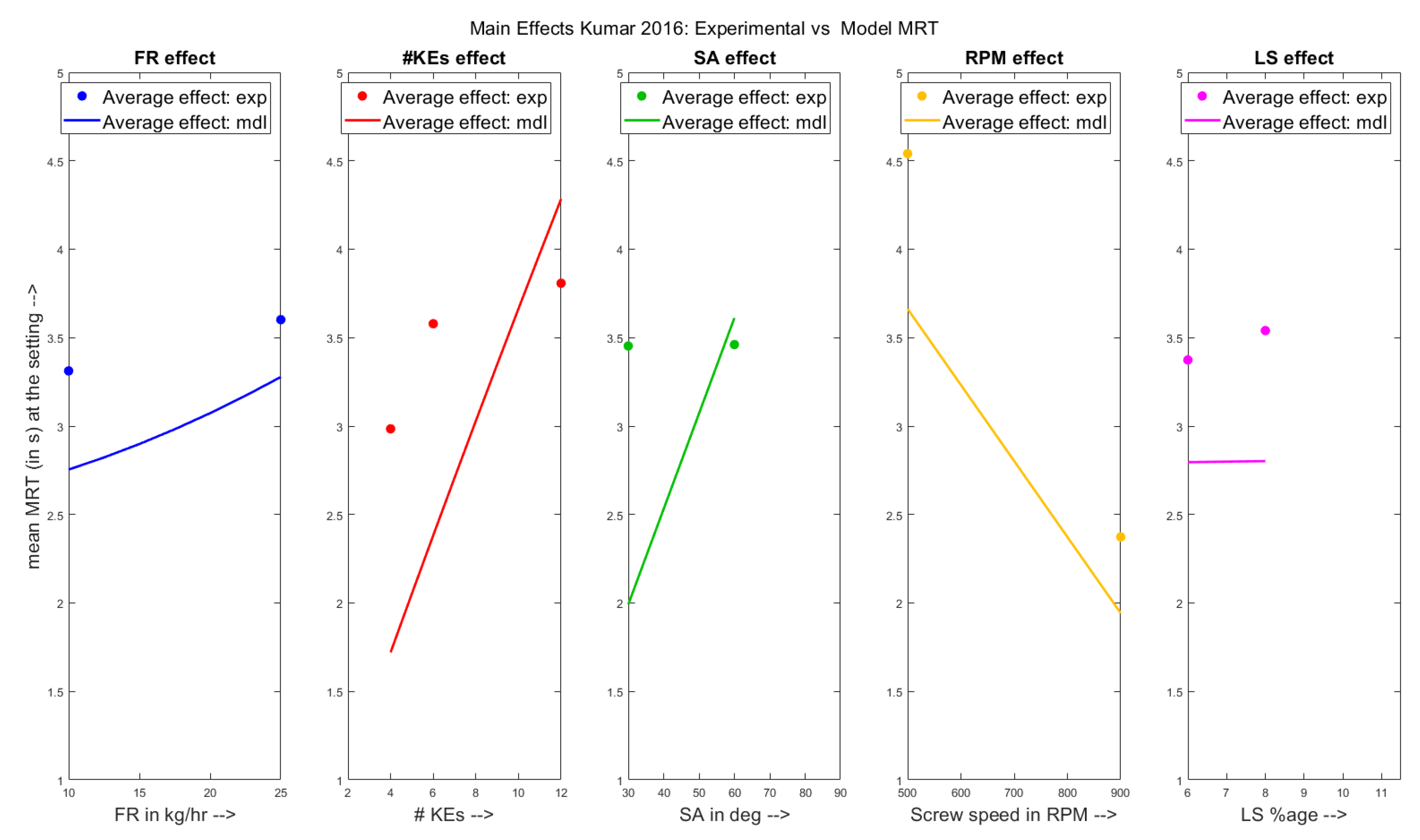
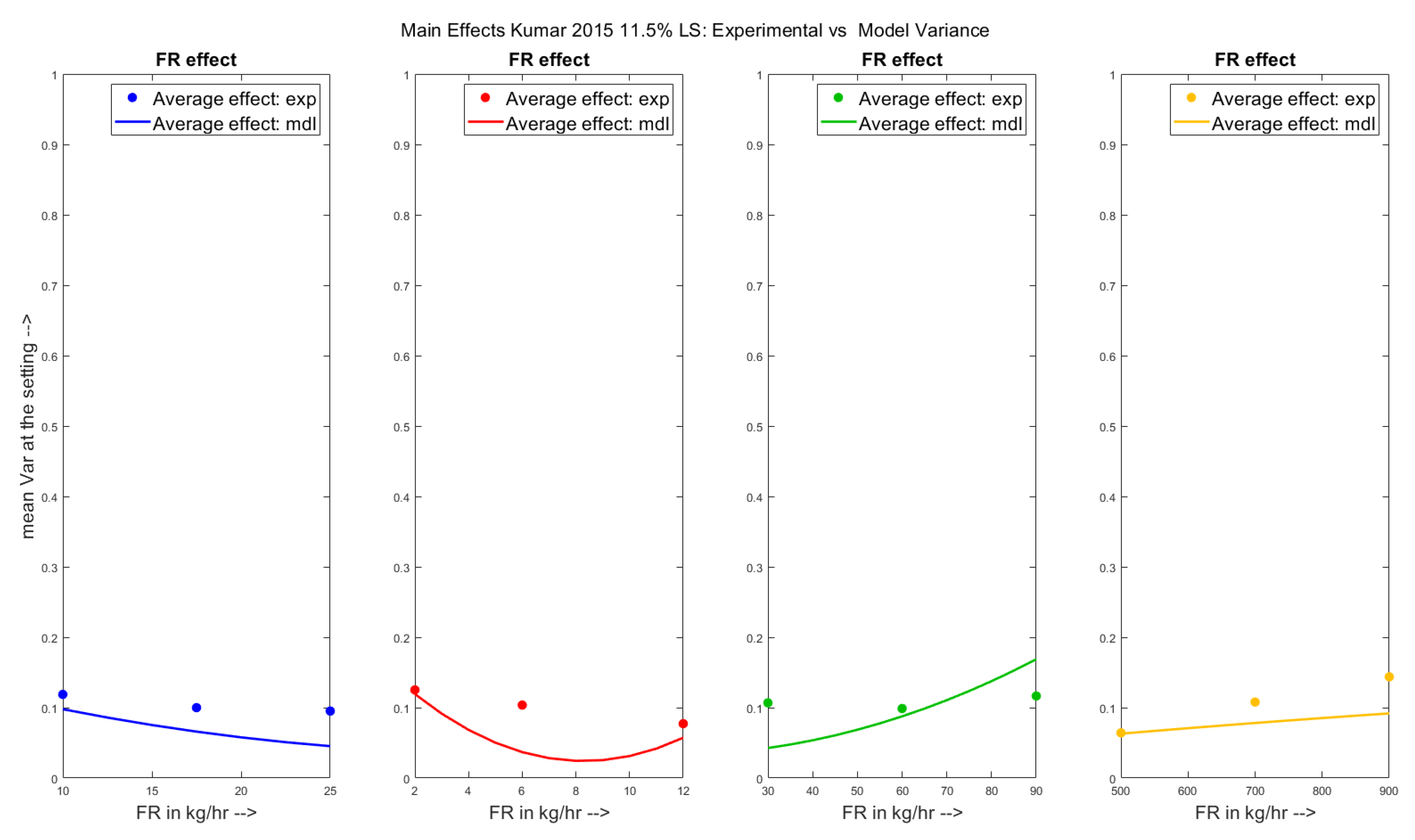
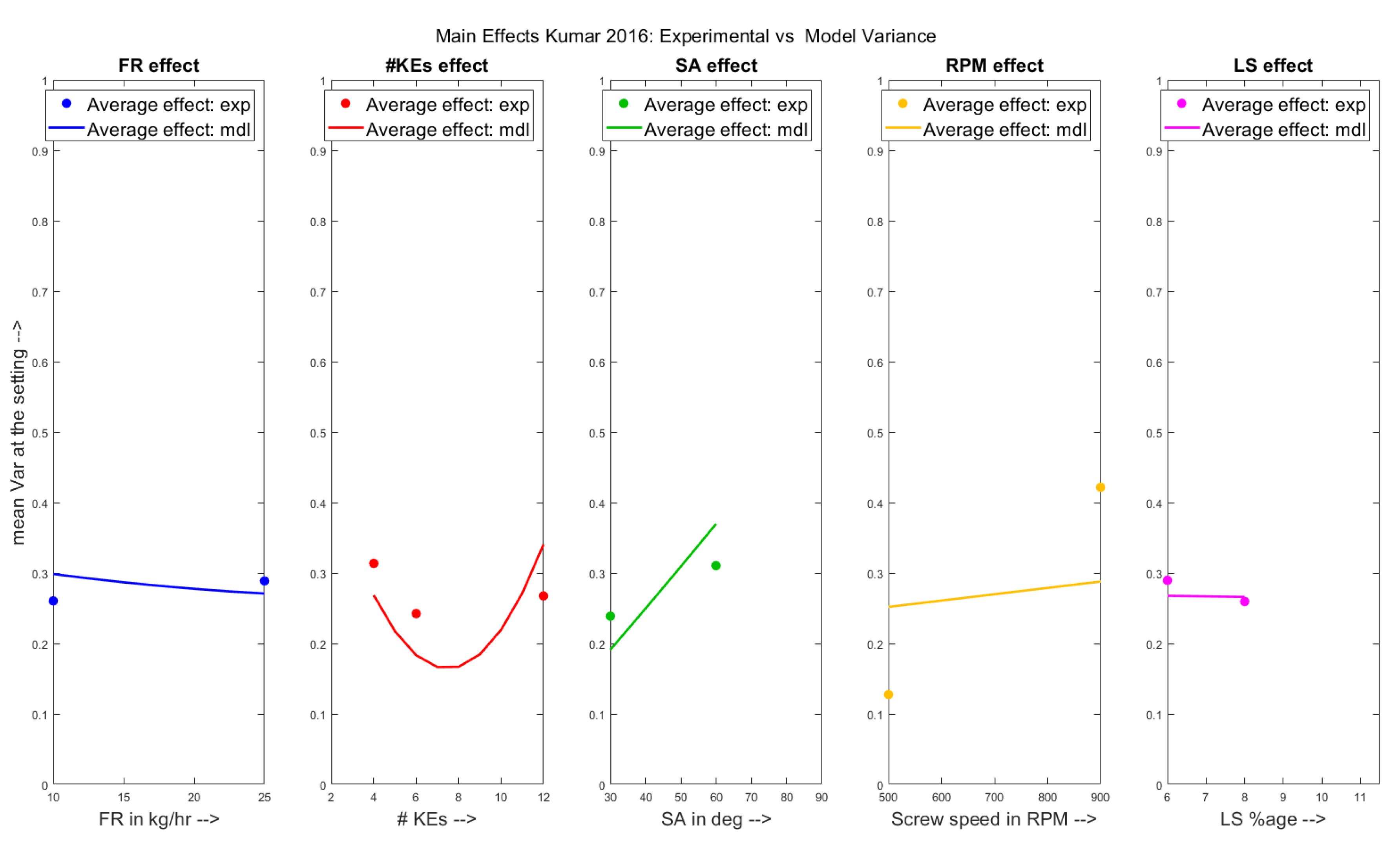
- Comparison between main effects plot of the experiments and that of the model
- ii
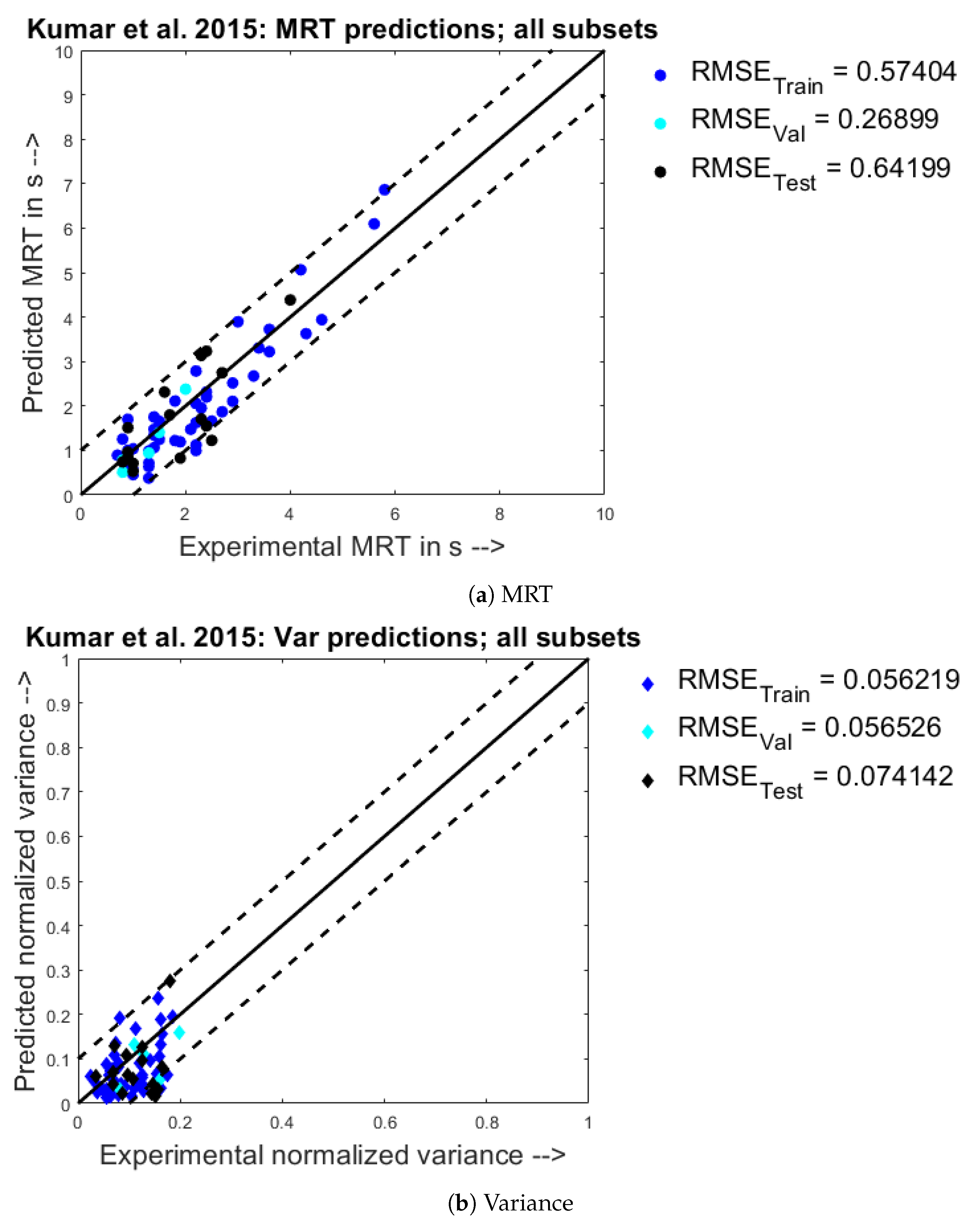
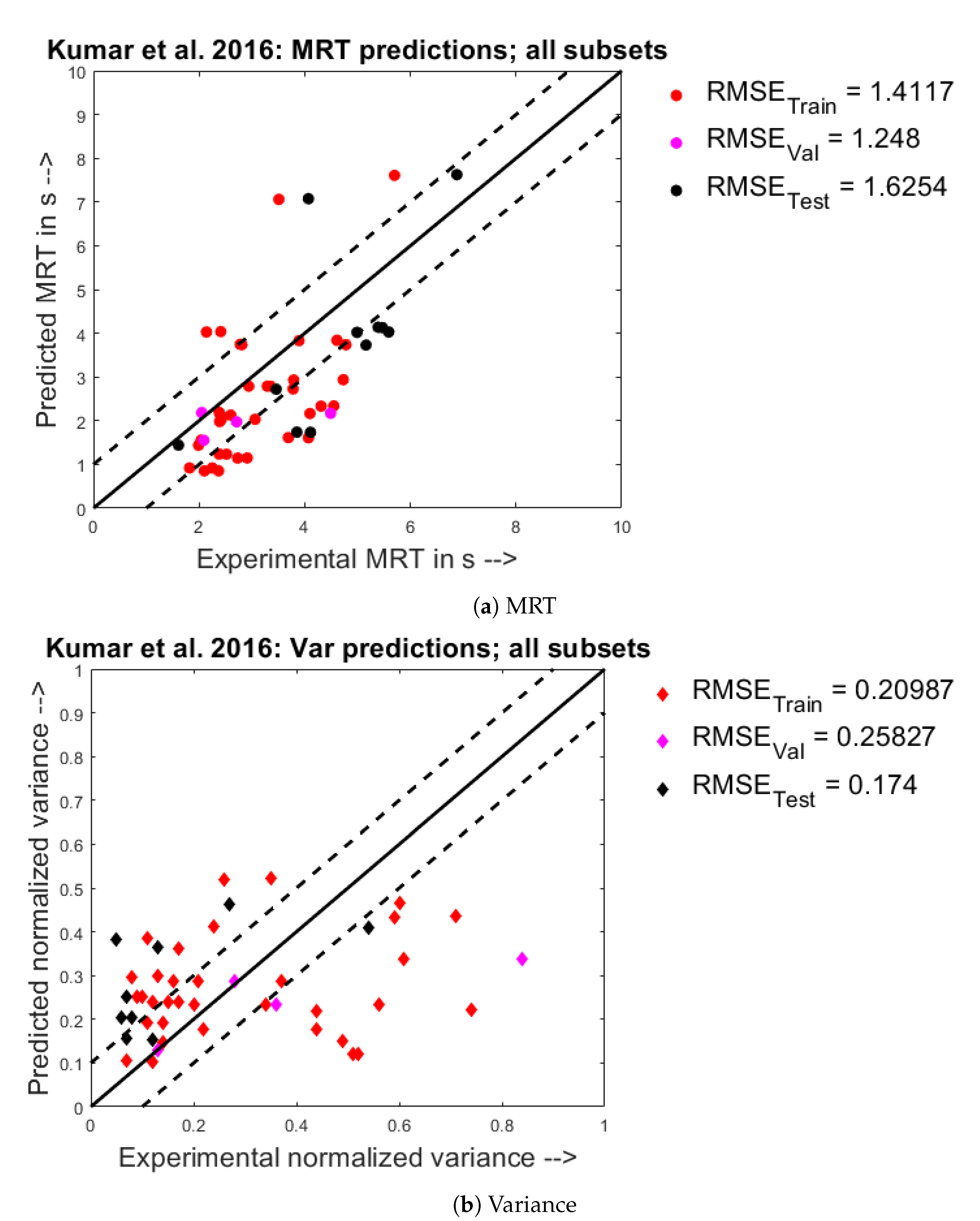
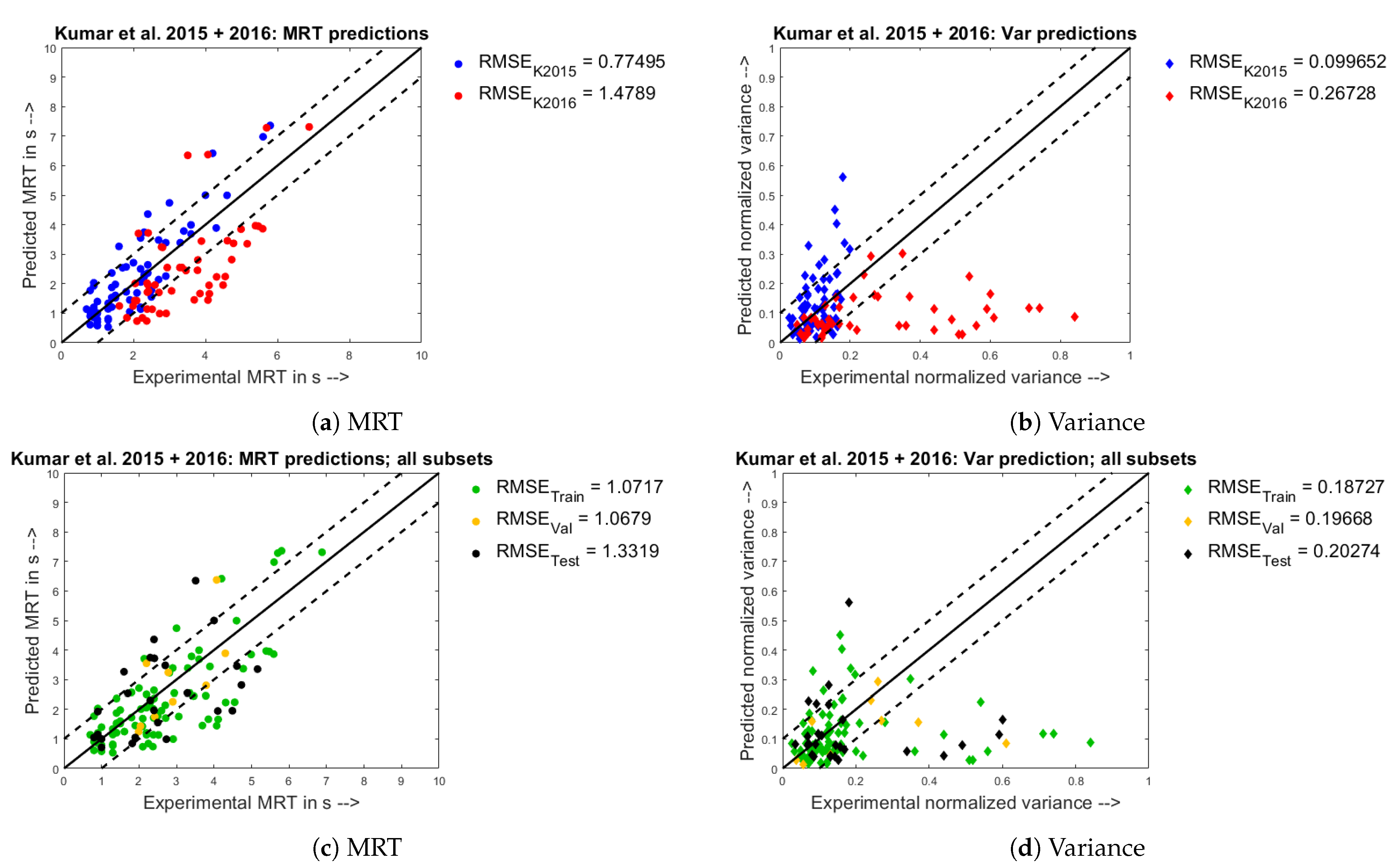
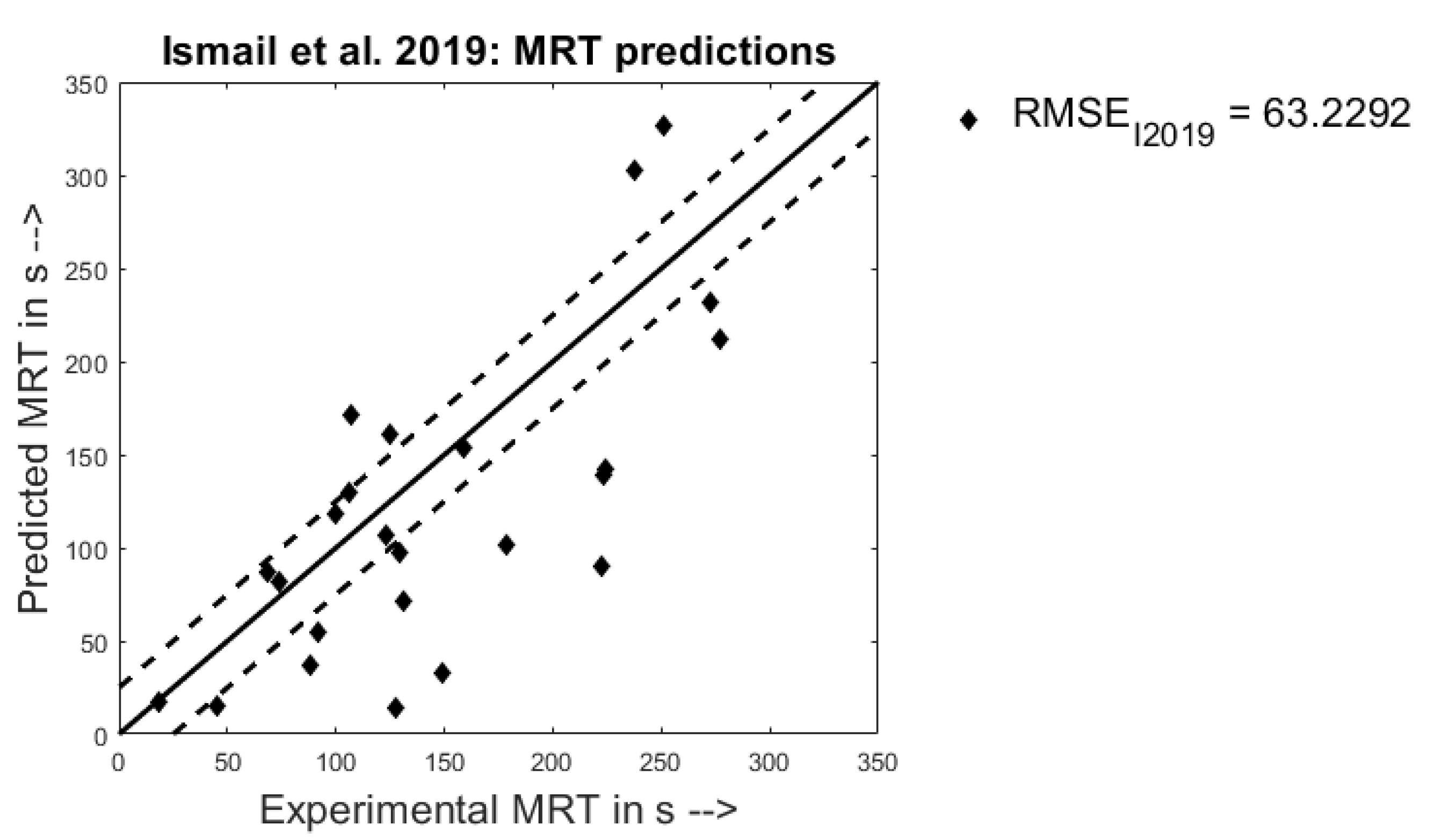
- Satisfactory parity plots, realistic narrow upper and lower bounds were set, and the model’s performance was determined based on how many predicted points fell between these limits; in addition the root mean square of errors too was evaluated as a statistical measure for goodness of fit
- (iii)
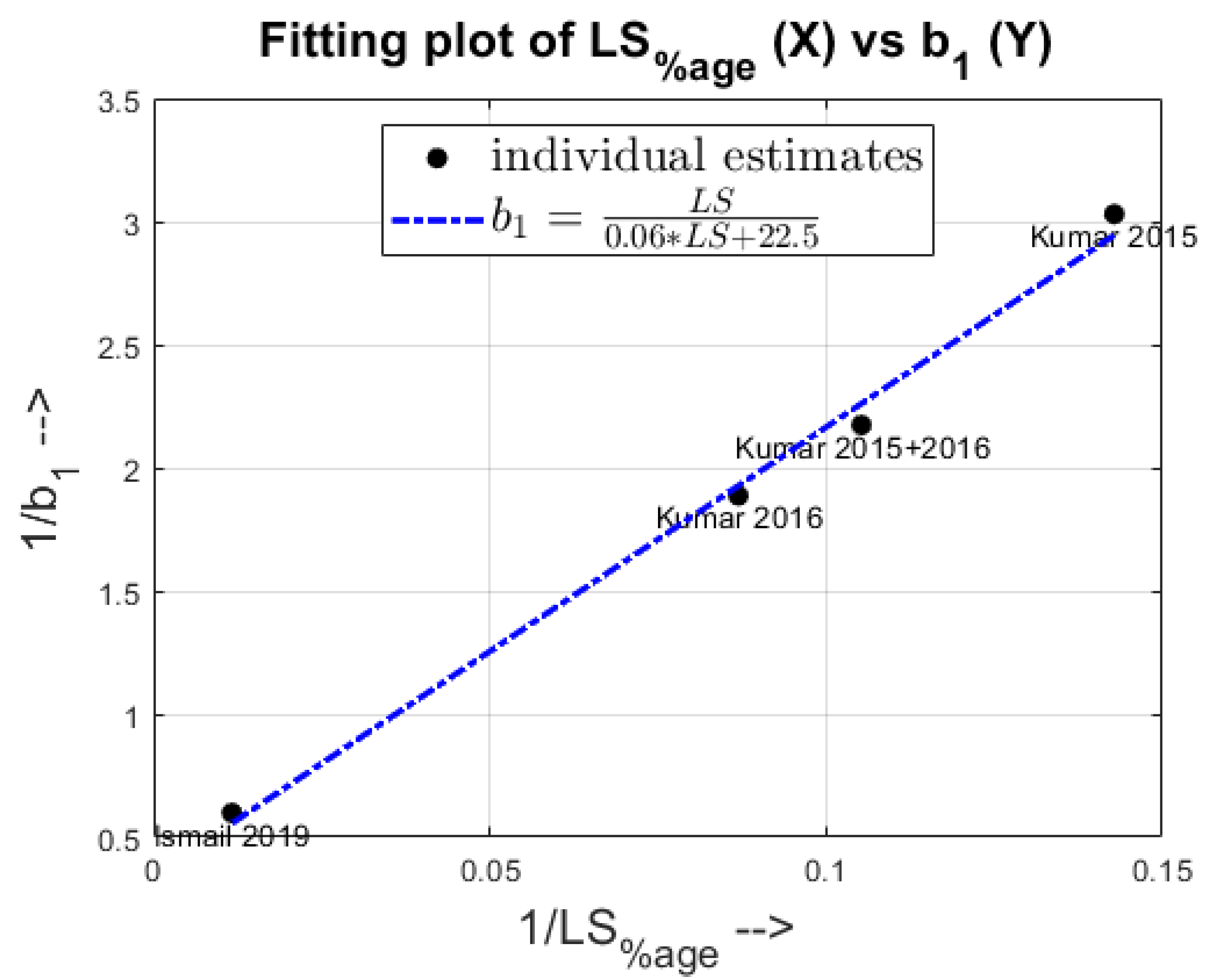
- Wherever possible, the values of the tuning parameters in the model when trained on different datasets were compared, and physical interpretation was made for their ranges
4. Results and Discussion
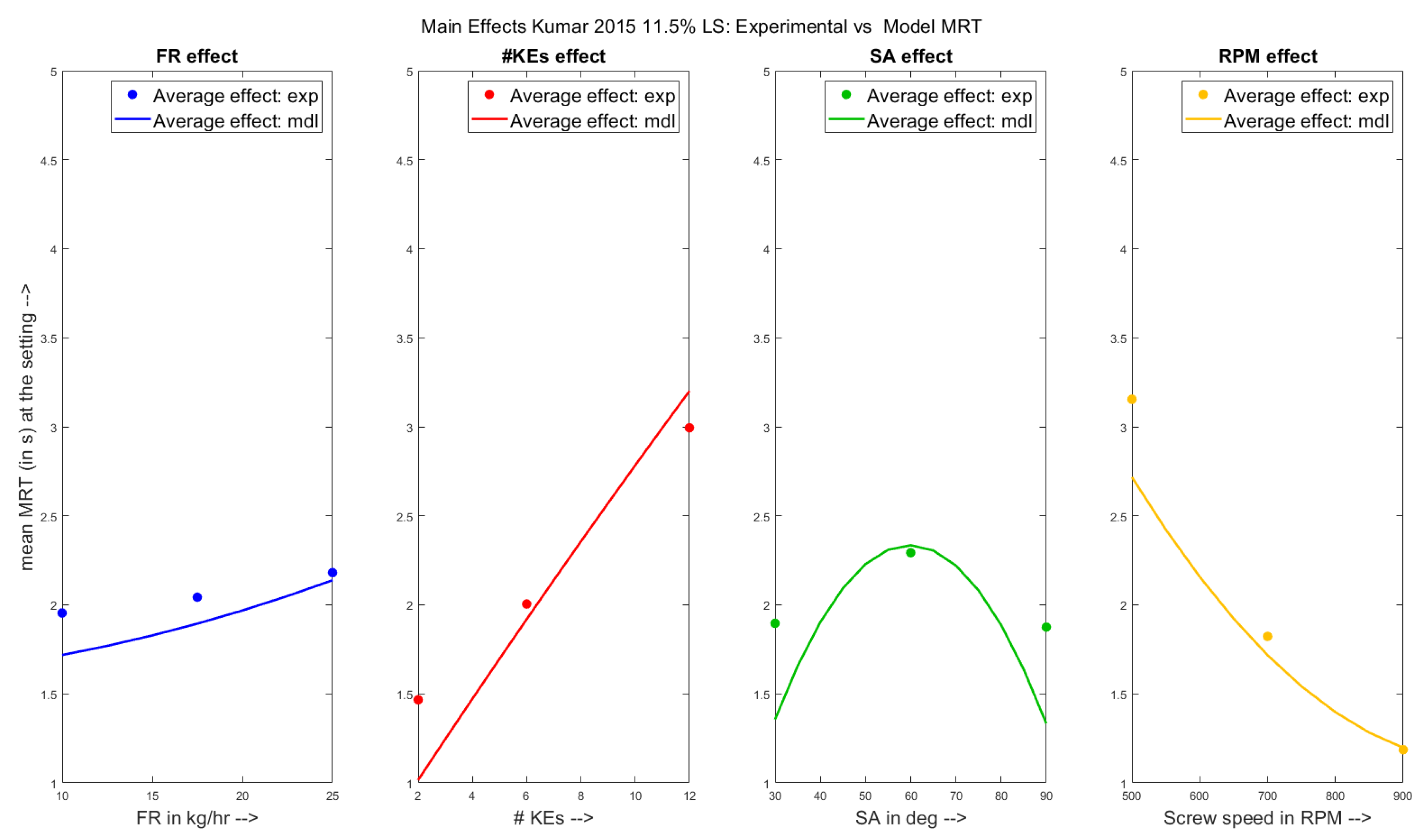
4.1. Qualitative Analysis- Main Effects Plots
4.2. Quantitative Analysis- Parity Plots
4.3. Quantitative Analysis- Comparing Model Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iveson, S.M.; Litster, J.D. Hapgood, K.; Ennis, B.J. Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technol. 2001, 117, 3–39. [Google Scholar] [CrossRef]
- Morkhade, D.M. Comparative impact of different binder addition methods, binders and diluents on resulting granule and tablet attributes via high shear wet granulation. Powder Technol. 2017, 320, 114–124. [Google Scholar] [CrossRef]
- Nie, H.; Xu, W.; Taylor, L.S.; Marsac, P.J.; Byrn, S.R. Crystalline solid dispersion-a strategy to slowdown salt disproportionation in solid state formulations during storage and wet granulation. Int. J. Pharm. 2017, 517, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, R.; Ohta, T.; Shiraki, K.; Higashi, K.; Moribe, K. Effects of wet-granulation process parameters on the dissolution and physical stability of a solid dispersion. Int. J. Pharm. 2017, 524, 304–311. [Google Scholar] [CrossRef]
- Oka, S.; Smrčka, D.; Kataria, A.; Emady, H.; Muzzio, F.; Štěpánek, F.; Ramachandran, R. Analysis of the origins of content non-uniformity in high-shear wet granulation. Int. J. Pharm. 2017, 528, 578–585. [Google Scholar] [CrossRef]
- Chaturbedi, A.; Bandi, C.K.; Reddy, D.; Pandey, P.; Narang, A.; Bindra, D.; Tao, L.; Zhao, J.; Li, J.; Hussain, M.; et al. Compartment based population balance model development of a high shear wet granulation process via dry and wet binder addition. Chem. Eng. Res. Des. 2017, 123, 187–200. [Google Scholar] [CrossRef]
- Deng, J.; Staufenbiel, S.; Hao, S.; Wang, B.; Dashevskiy, A.; Bodmeier, R. Development of a discriminative biphasic in vitro dissolution test and correlation with in vivo pharmacokinetic studies for differently formulated racecadotril granules. J. Control. Release 2017, 255, 202–209. [Google Scholar] [CrossRef]
- Chaudhury, A.; Tamrakar, A.; Schongut, M.; Smrcka, D.; Stepanek, F.; Ramachandran, R. Multidimensional population balance model development and validation of a reactive detergent granulation process. Ind. Eng. Chem. Res. 2015, 54, 842–857. [Google Scholar] [CrossRef]
- Chaudhury, A.; Kapadia, A.; Prakash, A.V.; Barrasso, D.; Ramachandran, R. An extended cell-average technique for a multi-dimensional population balance of granulation describing aggregation and breakage. Adv. Powder Technol. 2013, 24, 962–971. [Google Scholar] [CrossRef]
- Chaudhury, A.; Ramachandran, R. Integrated population balance model development and validation of a granulation process. Part. Sci. Technol. 2013, 31, 407–418. [Google Scholar] [CrossRef]
- Sen, M.; Ramachandran, R. A multi-dimensional population balance model approach to continuous powder mixing processes. Adv. Powder Technol. 2013, 24, 51–59. [Google Scholar] [CrossRef]
- El Hagrasy, A.; Hennenkamp, J.; Burke, M.; Cartwright, J.; Litster, J. Twin screw wet granulation: Influence of formulation parameters on granule properties and growth behavior. Powder Technol. 2013, 238, 108–115. [Google Scholar] [CrossRef]
- Shirazian, S.; Darwish, S.; Kuhs, M.; Croker, D.M.; Walker, G.M. Regime-separated approach for population balance modelling of continuous wet granulation of pharmaceutical formulations. Powder Technol. 2018, 325, 420–428. [Google Scholar] [CrossRef]
- Ismail, H.Y.; Singh, M.; Darwish, S.; Kuhs, M.; Shirazian, S.; Croker, D.M.; Khraisheh, M.; Albadarin, A.B.; Walker, G.M. Developing ann-kriging hybrid model based on process parameters for prediction of mean residence time distribution in twin-screw wet granulation. Powder Technol. 2019, 343, 568–577. [Google Scholar] [CrossRef]
- Poulesquen, A.; Vergnes, B. A study of residence time distribution in co-rotating twin-screw extruders. Part I: Theoretical modeling. Polym. Eng. Sci. 2003, 43, 1841–18483. [Google Scholar] [CrossRef]
- Poulesquen, A.; Vergnes, B.; Cassagnau, P.; Michel, A.; Carneiro, O.S.; Covas, J.A. A study of residence time distribution in co-rotating twin-screw extruders. Part II: Experimental validation. Polym. Eng. Sci. 2003, 43, 1849–1862. [Google Scholar] [CrossRef]
- Yeh, A.-I.; Jaw, Y.-M. Predicting residence time distributions in a single screw extruder from operating conditions. J. Food Eng. 1999, 39, 81–89. [Google Scholar] [CrossRef]
- Kumar, A.; Ganjyal, G.M.; Jones, D.D.; Hanna, M.A. Modeling residence time distribution in a twin-screw extruder as a series of ideal steady-state flow reactors. J. Food Eng. 2008, 84, 441–448. [Google Scholar] [CrossRef]
- Holland, J.F.; Martin, J.F.; Granata, T.; Bouchard, V.; Quigley, M.; Brown, L. Effects of wetland depth and flow rate on residence time distribution characteristics. Ecol. Eng. 2004, 23, 189–203. [Google Scholar] [CrossRef]
- Kumar, A.; Vercruysse, J.; Toiviainen, M.; Panouillot, P.-E.; Juuti, M.; Vanhoorne, V.; Vervaet, C.; Remon, J.P.; Gernaey, K.V.; De Beer, T.; et al. Mixing and transport during pharmaceutical twin-screw wet granulation: Experimental analysis via chemical imaging. Eur. J. Pharm. Biopharm. 2014, 87, 279–289. [Google Scholar] [CrossRef]
- Kumar, A.; Vercruysse, J.; Vanhoorne, V.; Toiviainen, M.; Panouillot, P.-E.; Juuti, M.; Vervaet, C.; Remon, J.P.; Gernaey, K.V.; De Beer, T.; et al. Conceptual framework for model-based analysis of residence time distribution in twin-screw granulation. Eur. J. Pharm. Sci. 2015, 71, 5–34. [Google Scholar] [CrossRef]
- Klinkenberg, A.; Krajenbrink, H.; Lauwerier, H. Diffusion in a fluid moving at uniform velocity in a tube. Ind. Eng. Chem. 1953, 45, 1202–1208. [Google Scholar] [CrossRef]
- Levenspiel, O.; Smith, W. Notes on the diffusion-type model for the longitudinal mixing of fluids in flow. Chem. Eng. Sci. 1957, 6, 227–235. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 5th ed.; Pearson International Edition: London, UK, 2006. [Google Scholar]
- Lee, K.T.; Ingram, A.; Rowson, N.A. Twin screw wet granulation: The study of a continuous twin screw granulator using positron emission particle tracking (pept) technique. Eur. J. Pharm. Biopharm. 2012, 81, 666–673. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Alakarjula, M.; Vanhoorne, V.; Toiviainen, M. De Leersnyder, F.; Vercruysse, J.; Juuti, M.; Ketolainen, J.; Vervaet, C.; Remon, J.P.; et al. Linking granulation performance with residence time and granulation liquid distributions in twin-screw granulation: An experimental investigation. Eur. J. Pharm. Sci. 2016, 90, 25–37. [Google Scholar] [CrossRef] [PubMed]
- Lute, S.V.; Dhenge, R.M.; Salman, A.D. Twin screw granulation: An investigation of the effect of barrel fill level. Pharmaceutics 2018, 10, 67. [Google Scholar] [CrossRef]
- Dhenge, R.M.; Cartwright, J.J.; Doughty, D.G.; Hounslow, M.J.; Salman, A.D. Twin screw wet granulation: Effect of powder feed rate. Adv. Powder Technol. 2011, 22, 162–166. [Google Scholar] [CrossRef]
- Vercruysse, J.; Díaz, D.C.; Peeters, E.; Fonteyne, M.; Delaet, U.; Van Assche, I.; De Beer, T.; Remon, J.P.; Vervaet, C. Continuous twin screw granulation: Influence of process variables on granule and tablet quality. Eur. J. Pharm. Biopharm. 2012, 82, 205–211. [Google Scholar] [CrossRef]
- Dhenge, R.M.; Fyles, R.S.; Cartwright, J.J.; Doughty, D.G.; Hounslow, M.J.; Salman, A.D. Twin screw wet granulation: Granule properties. Chem. Eng. J. 2010, 164, 322–329. [Google Scholar] [CrossRef]
- Vercruysse, J.; Toiviainen, M.; Fonteyne, M.; Helkimo, N.; Ketolainen, J.; Juuti, M.; Delaet, U.; Van Assche, I.; Remon, J.P.; Vervaet, C.; et al. Visualization and understanding of the granulation liquid mixing and distribution during continuous twin screw granulation using nir chemical imaging. Eur. J. Pharm. Biopharm. 2014, 86, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Gorringe, L.; Kee, G.; Saleh, M.; Fa, N.; Elkes, R. Use of the channel fill level in defining a design space for twin screw wet granulation. Int. J. Pharm. 2017, 519, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.; Zhang, L.; Govender, N.; Wu, C.-Y. Dem analysis of residence time distribution during twin screw granulation. Powder Technol. 2021, 377, 924–938. [Google Scholar] [CrossRef]
- Kresta, S.M. Turbulent mixing fundamentals. Pharm. Blending Mix. 2015, 27–41. [Google Scholar] [CrossRef]
- Vanarase, A.U.; Muzzio, F.J. Effect of operating conditions and design parameters in a continuous powder mixer. Powder Technol. 2011, 208, 26–36. [Google Scholar] [CrossRef]
- Vanarase, A.U.; Osorio, J.G.; Muzzio, F.J. Effects of powder flow properties and shear environment on the performance of continuous mixing of pharmaceutical powders. Powder Technol. 2013, 246, 63–72. [Google Scholar] [CrossRef]
- Gao, Y.; Vanarase, A.; Muzzio, F.; Ierapetritou, M. Characterizing continuous powder mixing using residence time distribution. Chem. Eng. Sci. 2011, 66, 417–4251. [Google Scholar] [CrossRef]
- Ravi, R. Flow characteristics of reactors—Flow modeling. In Coulson and Richardson’s Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2017; pp. 103–160. [Google Scholar]
- Chen, S.; Fan, L.T.; Watson, C. Mixing of solid particles in motionless mixer-axial-dispersed plug-flow model. Ind. Eng. Chem. Process. Des. Dev. 1973, 12, 42–47. [Google Scholar] [CrossRef]
- Cartwright, J.J.; Robertson, J.; D’Haene, D.; Burke, M.D.; Hennenkamp, J.R. Twin screw wet granulation: Loss in weight feeding of a poorly flowing active pharmaceutical ingredient. Powder Technol. 2013, 238, 116–121. [Google Scholar] [CrossRef]
- Lee, K.T. Continuous Granulation of Pharmaceutical Powder Using a Twin Screw Granulator. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2013. [Google Scholar]
- Gentzler, M.; Michaels, J.N.; Tardos, G.I. Quantification of segregation potential for polydisperse, cohesive, multi-component powders and prediction of tablet die-filling performance—A methodology for practical testing, re-formulation and process design. Powder Technol. 2015, 285, 96–102. [Google Scholar] [CrossRef]
- Liss, E.D.; Conway, S.L.; Zega, J.A.; Glasser, B.J. Segregation of powders during gravity flow through vertical pipes. Pharm. Technol. 2004, 28, 78–97. [Google Scholar]
- Shmueli, G.; Patel, N.R.; Bruce, P.C. Data Mining for Business Intelligence: Concepts, Techniques, and Applications in Microsoft Office Excel with XLMiner; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
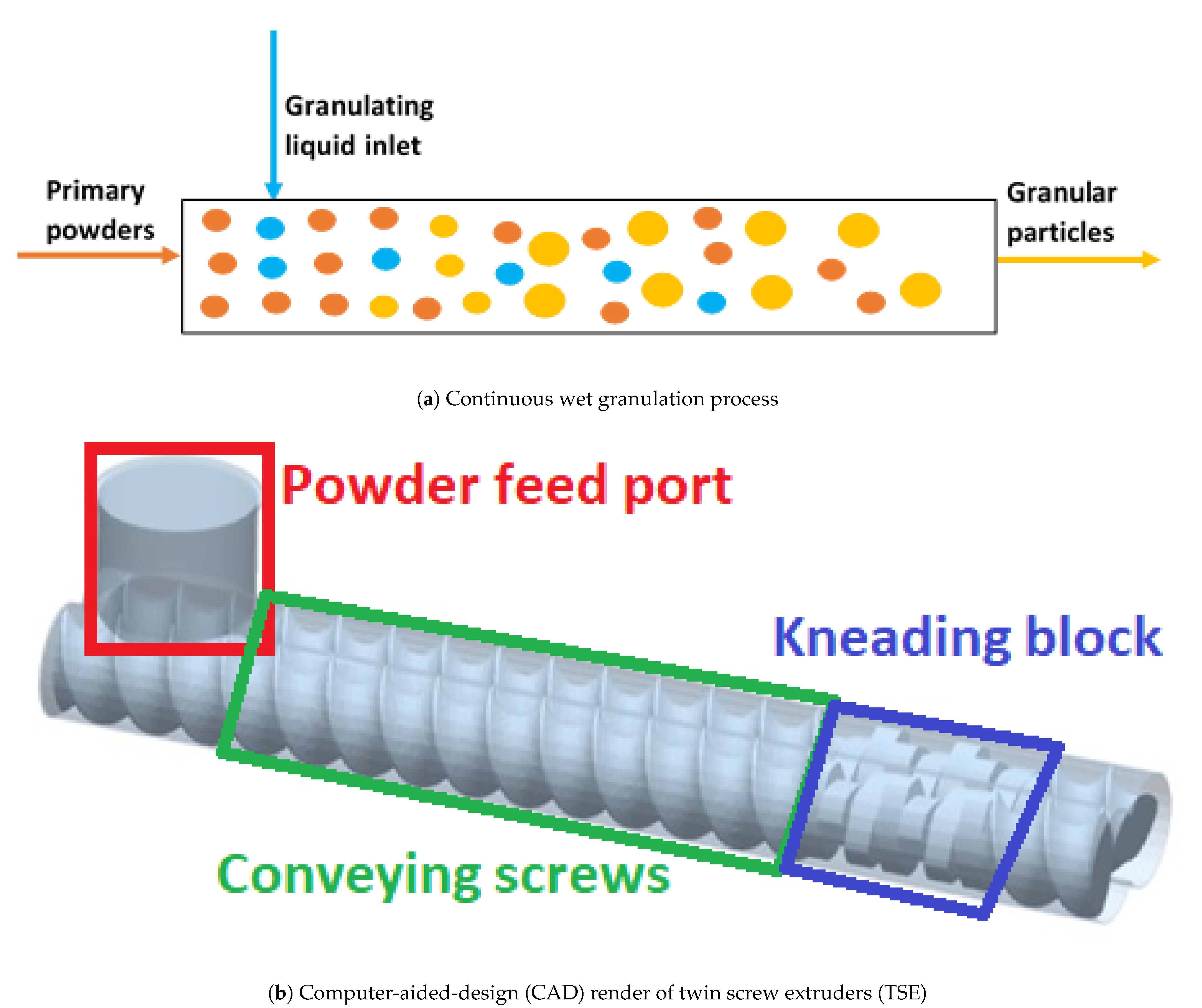
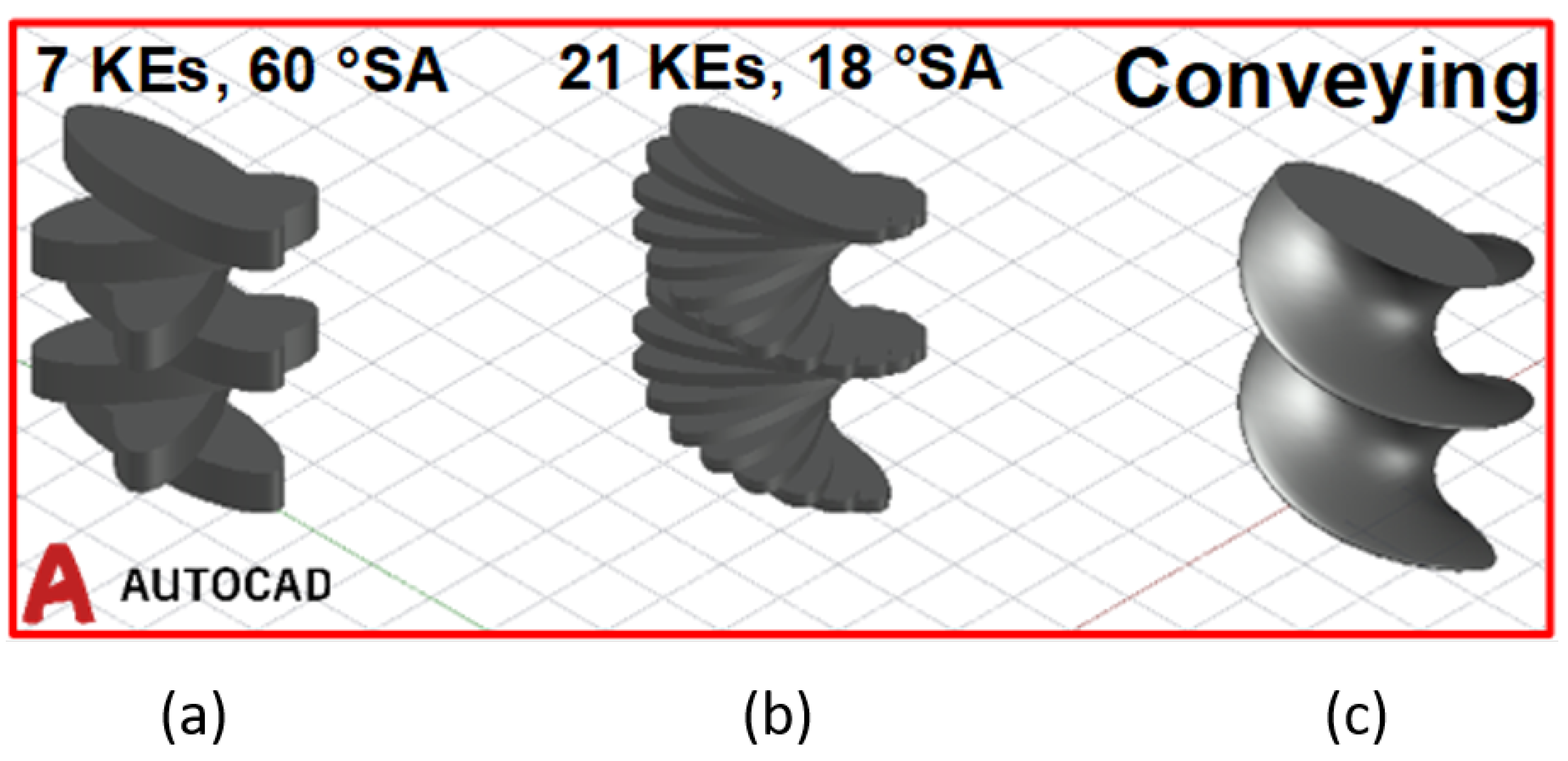
| Data Source | Equipment Name | Process Material | Varied Parameters | Number of Points |
|---|---|---|---|---|
| Kumar et al. 2015 [21] | ConsiGma-25 | -Lactose MH | FR, RPM, NK & SA | 66 |
| Kumar et al. 2016 [26] | ConsiGma-25 | -Lactose MH | FR, RPM, LS, NK & SA | 51 |
| Ismail et al. 2019 [14] | Three-Tec | Avicel PH-101 | FR, RPM, LS & NK | 24 |
| Total: 141 |
| Parameter | Kumar et al. 2015 | Kumar et al. 2015 + 2016 | Kumar et al. 2016 | Ismail et al. 2019 |
|---|---|---|---|---|
| 0.33 | 0.46 | 0.53 | 1.67 | |
| 0.99 | 1.24 | 0.33 | 0.96 | |
| 0.65 | 1.09 | 0.24 | 1.32 | |
| 1.33 | 1.15 | 1.08 | 0.63 | |
| 5.35 | 2.29 | 1.16 | - | |
| 1.99 | 2.24 | 1.33 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muddu, S.V.; Kotamarthy, L.; Ramachandran, R. A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation. Pharmaceutics 2021, 13, 393. https://doi.org/10.3390/pharmaceutics13030393
Muddu SV, Kotamarthy L, Ramachandran R. A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation. Pharmaceutics. 2021; 13(3):393. https://doi.org/10.3390/pharmaceutics13030393
Chicago/Turabian StyleMuddu, Shashank Venkat, Lalith Kotamarthy, and Rohit Ramachandran. 2021. "A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation" Pharmaceutics 13, no. 3: 393. https://doi.org/10.3390/pharmaceutics13030393
APA StyleMuddu, S. V., Kotamarthy, L., & Ramachandran, R. (2021). A Semi-Mechanistic Prediction of Residence Time Metrics in Twin Screw Granulation. Pharmaceutics, 13(3), 393. https://doi.org/10.3390/pharmaceutics13030393





