Modeling of High-Density Compaction of Pharmaceutical Tablets Using Multi-Contact Discrete Element Method
Abstract
1. Introduction
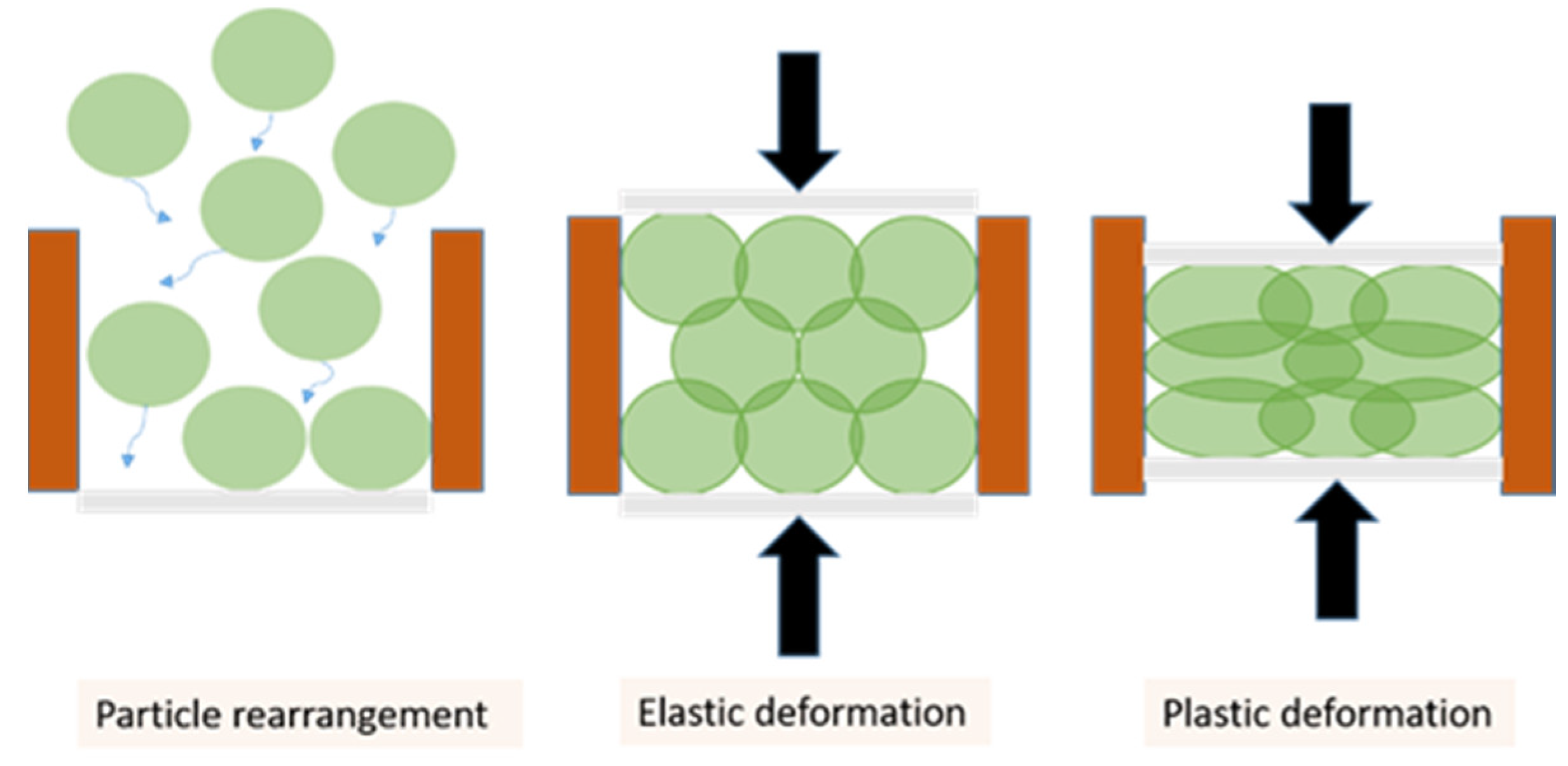
2. DEM’s Theoretical Background
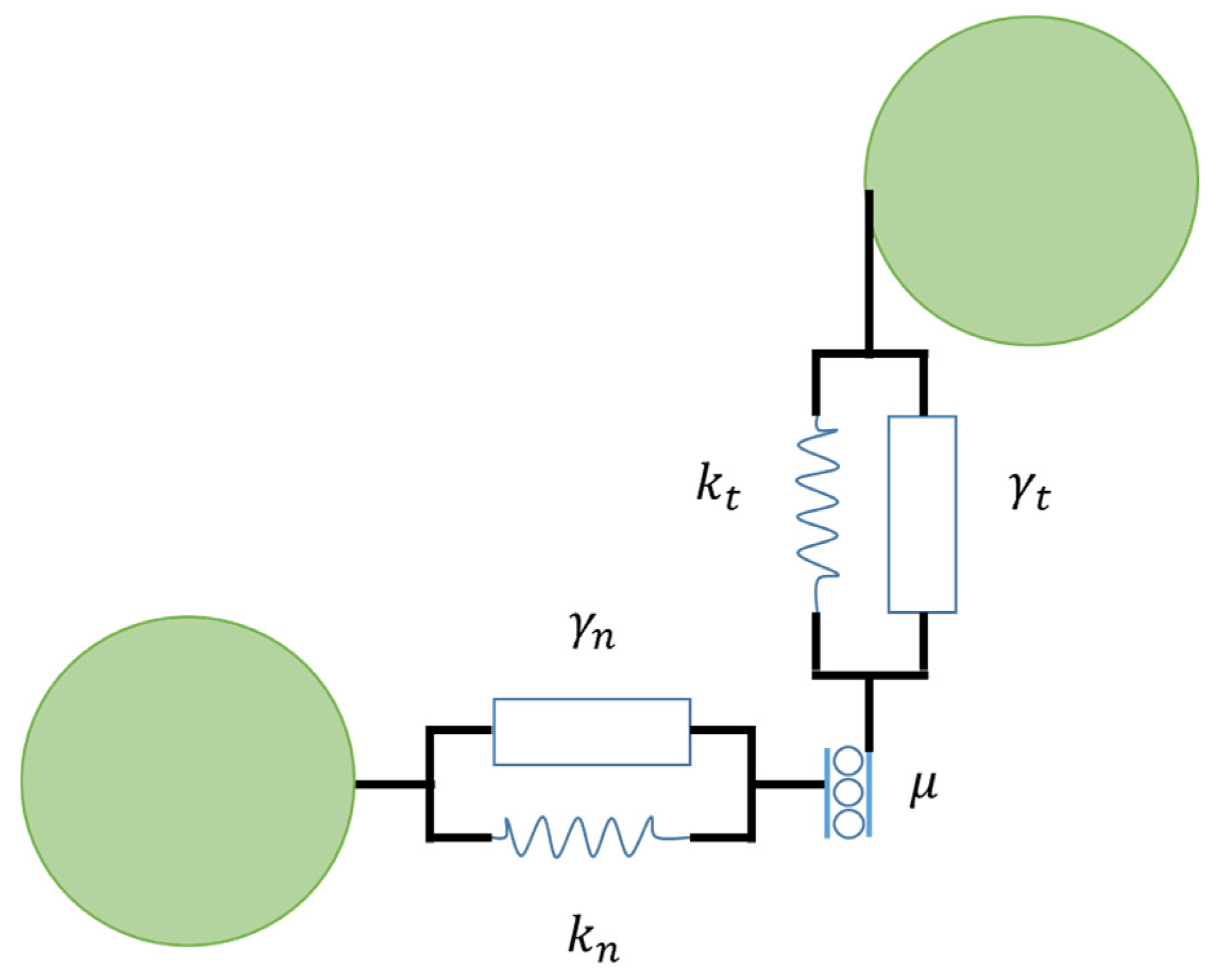
2.1. Classical Hertz–Mindlin Contact Model
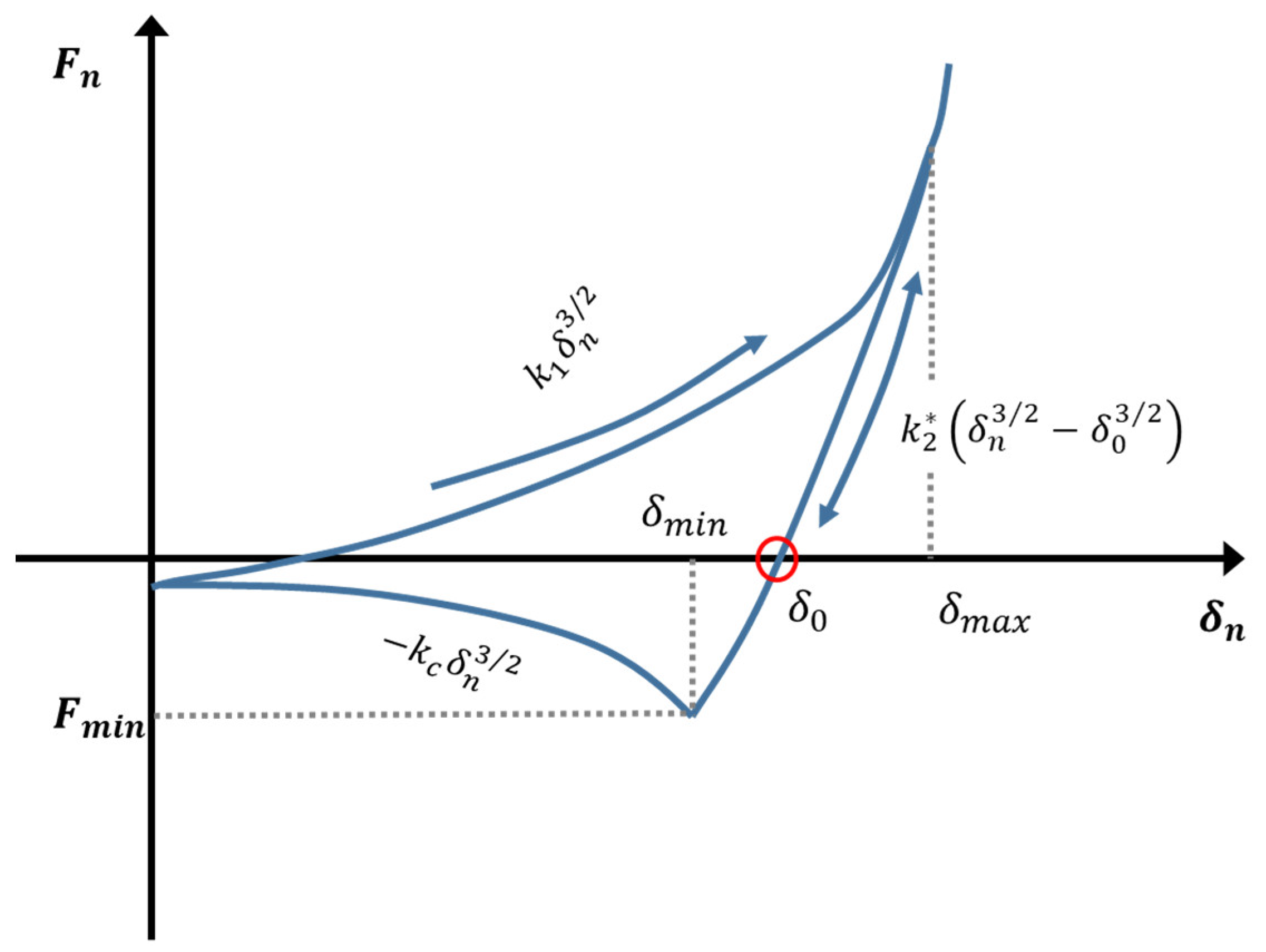
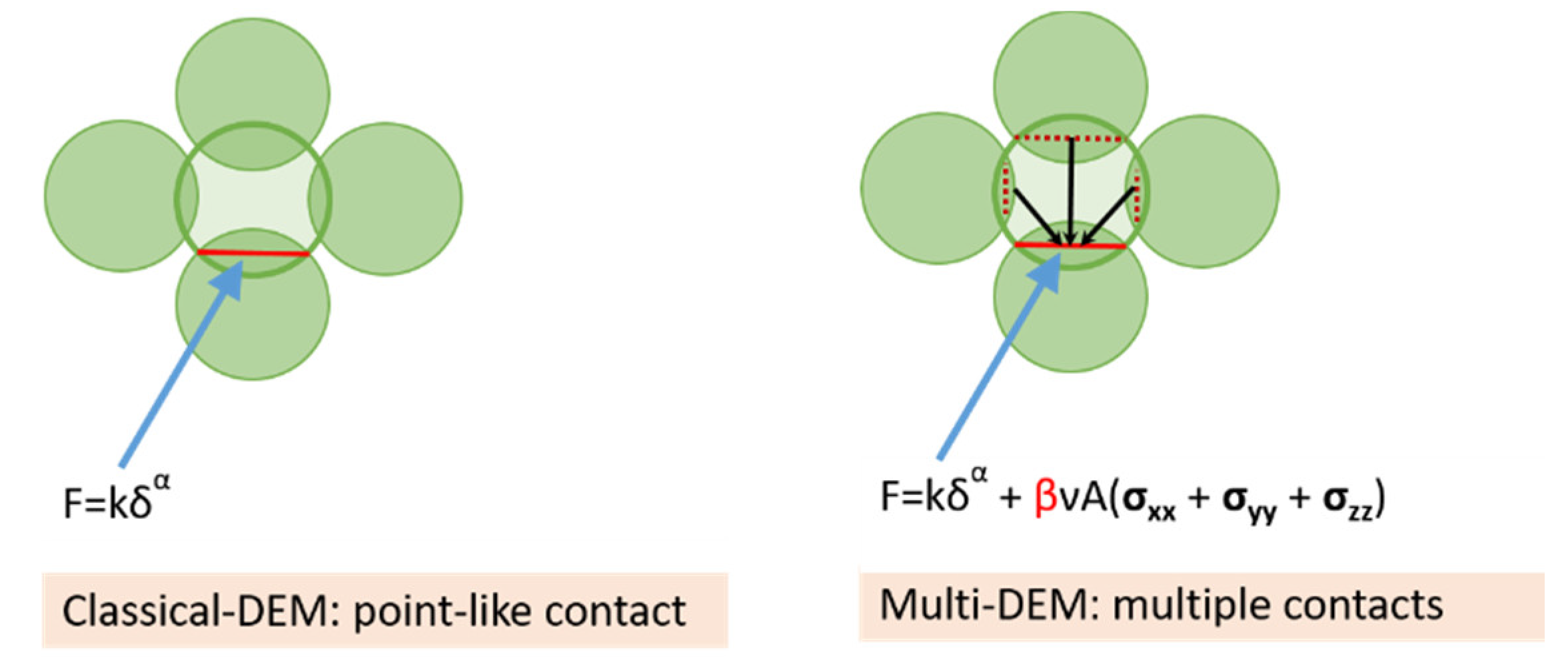
2.2. Multi-Contact Adhesive Elastic-Plastic Model
3. Materials and Methods
3.1. Materials
3.2. Experimental Methods
3.3. Numerical Methods
4. Results and Discussion
4.1. Determination of a Representative Volume Element (RVE)
4.1.1. Calibration Method for the Input Parameters of the Multi-Contact Model
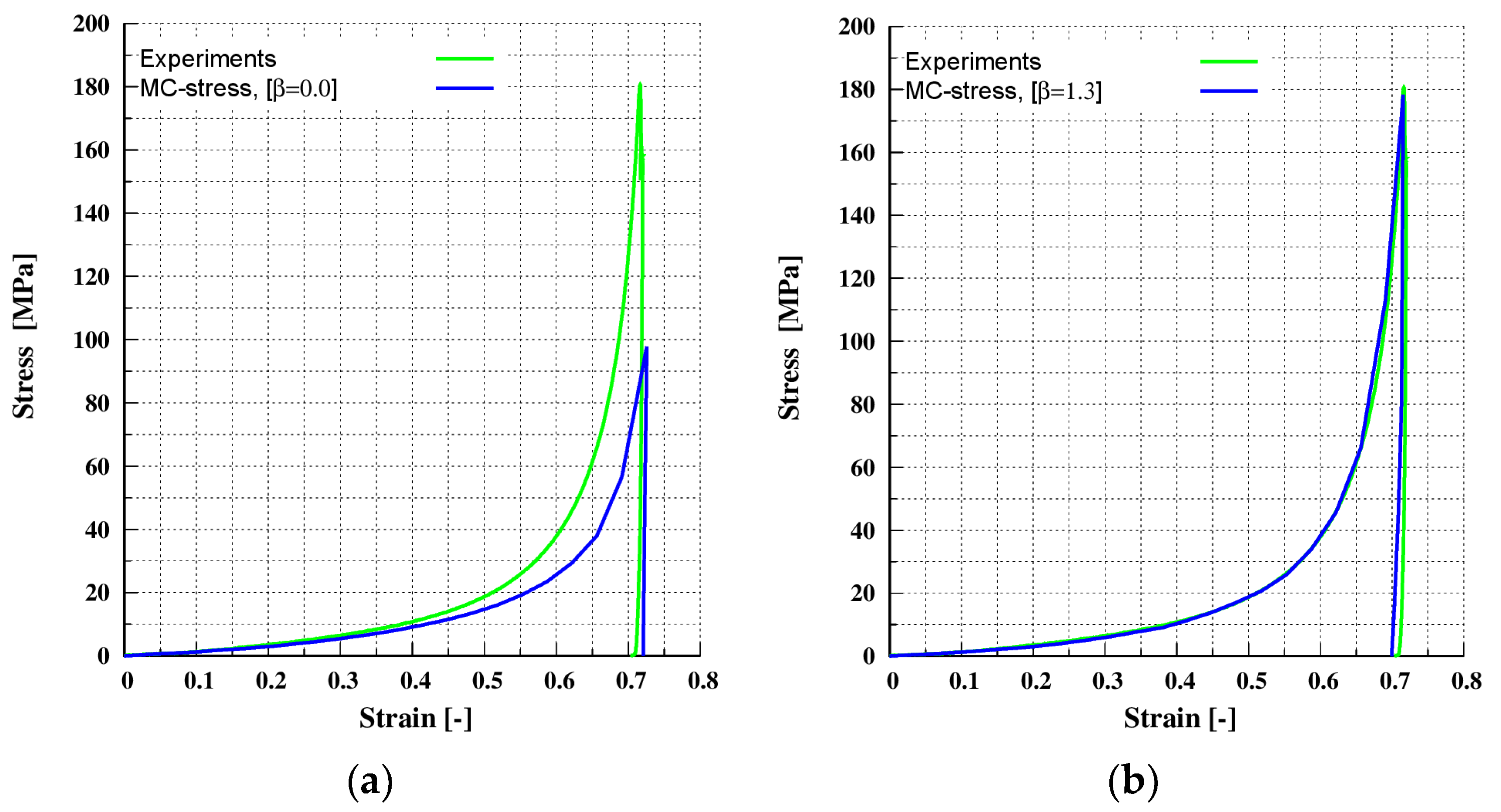
4.1.2. Verification for Uni-Axial Compaction for MCC-A
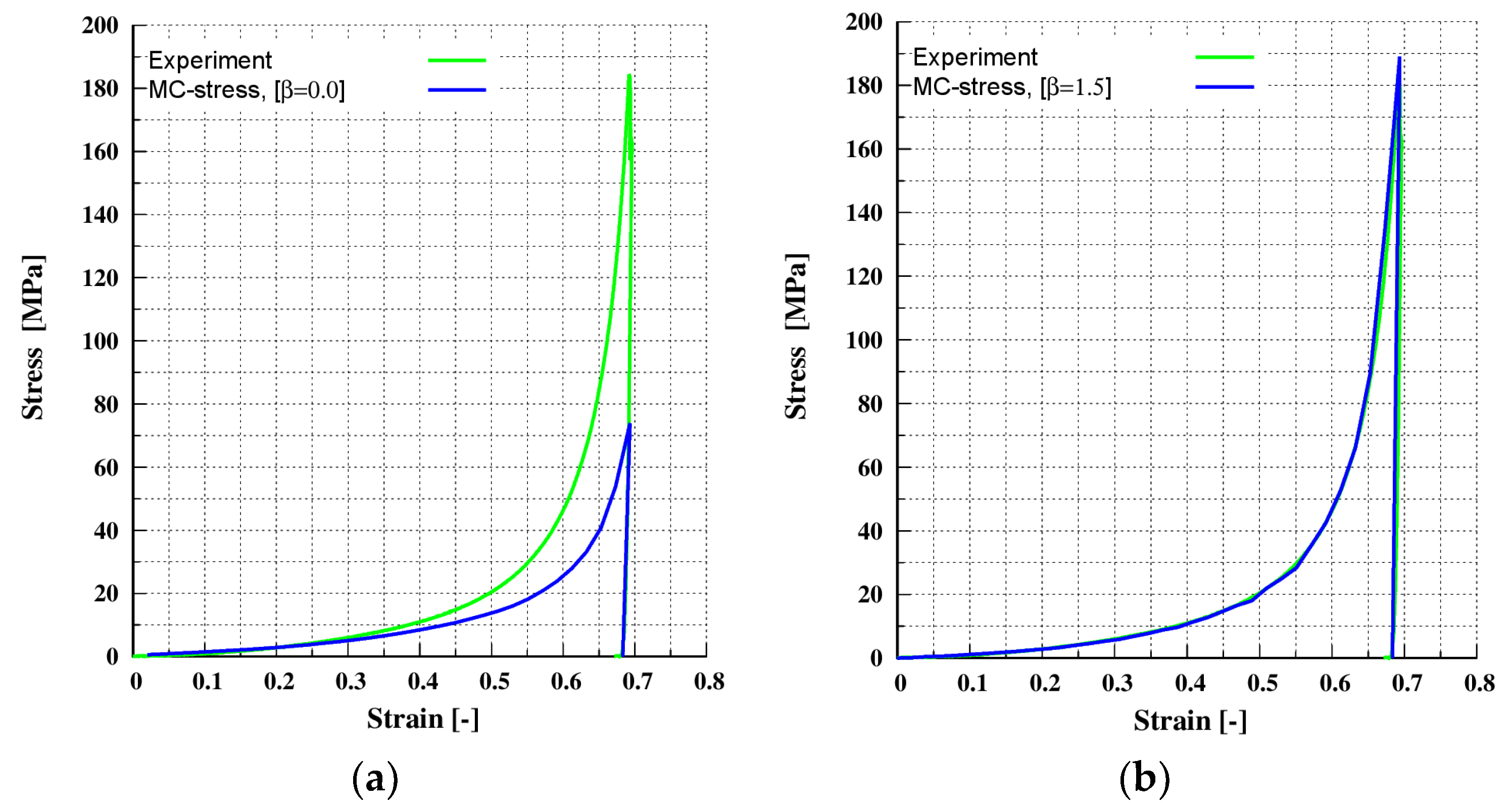
4.1.3. Verification for Uni-Axial Compaction for MCC-P
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Martin, N.L.; Schomberg, A.K.; Finke, J.H.; Abraham, T.G.; Kwade, A.; Herrmann, C. Process Modeling and Simulation of Tableting—An Agent-Based Simulation Methodology for Direct Compression. Pharmaceutics 2021, 13, 996. [Google Scholar] [CrossRef]
- Wünsch, I.; Finke, J.H.; John, E.; Juhnke, M.; Kwade, A. Mathematical Approach to Consider Solid Compressibility in the Compression of Pharmaceutical Powders. Pharmaceutics 2019, 11, 121. [Google Scholar] [CrossRef]
- Diarra, H.; Mazel, V.; Busignies, V.; Tchoreloff, P. Comparative study between Drucker-Prager/Cap and modified Cam-Clay models for the numerical simulation of die compaction of pharmaceutical powders. Powder Technol. 2017, 320, 530–539. [Google Scholar] [CrossRef]
- Ohsaki, S.; Kushida, K.; Matsuda, Y.; Nakamura, H.; Watano, S. Numerical study for tableting process in consideration of compression speed. Int. J. Pharm. 2020, 575, 118936. [Google Scholar] [CrossRef]
- Gethin, D.T.; Lewis, R.W.; Ransing, R.S. A discrete deformable element approach for the compaction of powder systems, Modelling Simul. Mater. Sci. Eng. 2003, 11, 101–114. [Google Scholar]
- Procopio, A.T.; Zavaliangos, A. Simulation of multi-axial compaction of granular media from loose to high relative densities. J. Mech. Phys. Solids 2005, 53, 1523–1551. [Google Scholar] [CrossRef]
- Demirtas, A.; Klinzing, G.R. Understanding die compaction of hollow spheres using the multi-particle finite element method (MPFEM). Powder Technol. 2021, 39, 34–45. [Google Scholar] [CrossRef]
- Stránský, J.; Jirásek, M. Open Source FEM–DEM Coupling. In Proceedings of the 18th International Conference Engineering Mechanics, Prague, Czech Republic, 18 May 2012; pp. 1237–1251. [Google Scholar]
- Frenning, G. An efficient finite/discrete element procedure for simulating compression of 3D particle assemblies. Comput. Methods Appl. Mech. Eng. 2008, 197, 4266–4272. [Google Scholar] [CrossRef]
- Luding, S. Introduction to discrete element methods. Eur. J. Environ. Civ. Eng. 2008, 12, 785–826. [Google Scholar] [CrossRef]
- Iacobellis, V.; Radhi, A.; Behdinan, K. Discrete element model for ZrB2-SiC ceramic composite sintering. Compos. Struct. 2019, 229, 111373. [Google Scholar] [CrossRef]
- Horabik, J.; Wiącek, J.; Parafiniuk, P.; Stasiak, M.; Bańda, M.; Kobyłka, R.; Molenda, M. Discrete Element Method Modelling of the Diametral Compression of Starch Agglomerates. Materials 2020, 13, 932. [Google Scholar] [CrossRef]
- Raji, A.O.; Favier, J.F. Model for the deformation in agricultural and food particulate materials under bulk compressive loading using discrete element method. I: Theory, model development and validation. J. Food Eng. 2004, 64, 359–371. [Google Scholar] [CrossRef]
- Harthong, B.; Jérier, J.-F.; Dorémus, P.; Imbault, D.; Donzé, F.-V. Modeling of high-density compaction of granular materials by the Discrete Element Method. Int. J. Solids Struct. 2009, 46, 3357–3364. [Google Scholar] [CrossRef]
- Garner, S.; Strong, J.; Zavaliangos, A. Study of the die compaction of powders to high relative densities using the discrete element method. Powder Technol. 2018, 330, 357–370. [Google Scholar] [CrossRef]
- Gao, Y.; de Simone, G.; Koorapaty, M. Calibration and verification of DEM parameters for the quantitative simulation of pharmaceutical powder compression process. Powder Technol. 2021, 378, 160–171. [Google Scholar] [CrossRef]
- Luding, S. Cohesive, frictional powders: Contact models for tension. Granul. Matter 2008, 10, 235–246. [Google Scholar] [CrossRef]
- Fischmeister, H.F.; Arzt, E. Densification of Powders by Particle Deformation. Powder Metall. 1983, 26, 82–88. [Google Scholar] [CrossRef]
- Olsson, E.; Larsson, P.-L. A numerical analysis of cold powder compaction based on micromechanical experiments. Powder Technol. 2013, 243, 71–78. [Google Scholar] [CrossRef]
- Mesarovic, S.D.; Fleck, N.A. Frictionless indentation of dissimilar elastic–plastic spheres. Int. J. Solids Struct. 2000, 37, 7071–7091. [Google Scholar] [CrossRef]
- Jonsson, H.; Gråsjö, J.; Frenning, G. Mechanical behaviour of ideal elastic-plastic particles subjected to different triaxial loading conditions. Powder Technol. 2017, 315, 347–355. [Google Scholar] [CrossRef]
- Brodu, N.; Dijksman, J.A.; Behringer, R.P. Multiple-contact discrete-element model for simulating dense granular media. Phys. Rev. E 2015, 91, 32201. [Google Scholar] [CrossRef]
- Frenning, G. Towards a mechanistic model for the interaction between plastically deforming particles under confined conditions: A numerical and analytical analysis. Mater. Lett. 2013, 92, 365–368. [Google Scholar] [CrossRef]
- Giannis, K.; Schilde, C.; Finke, J.H.; Kwade, A.; Celigueta, M.A.; Taghizadeh, K.; Luding, S. Stress based multi-contact model for discrete-element simulations. Granul. Matter 2021, 23, 1–14. [Google Scholar] [CrossRef]
- Rojek, J.; Zubelewicz, A.; Madan, N.; Nosewicz, S. The discrete element method with deformable particles. Int. J. Numer. Methods Eng. 2018, 114, 828–860. [Google Scholar] [CrossRef]
- Rojek, J.; Nosewicz, S.; Thoeni, K. 3D formulation of the deformable discrete element method. Int. J. Numer. Methods Eng. 2021, 122, 3335–3367. [Google Scholar] [CrossRef]
- Rojek, J. Contact Modeling in the Discrete Element Method. In Contact Modeling for Solids and Particles; Popp, A., Wriggers, P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 177–228. [Google Scholar]
- Thakur, S.C. Mesoscopic Discrete Element Modelling of Cohesive Powders for Bulk Handling Applications; School of Engineering the University of Edinburgh: Edinburgh, UK, 2014. [Google Scholar]
- O’Sullivan, C. Particulate Discrete Element Modelling; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Thornton, C. Granular Dynamics, Contact Mechanics and Particle System Simulations: A DEM Study, 1st ed.; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung Fester Elastischer Körper. J. Reine Angew. Math. 2009, 1882, 156–171. [Google Scholar]
- Mindlin, R.D. Compliance of Elastic Bodies in Contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic Spheres in Contact under Varying Oblique Forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Di Renzo, A.; Di Maio, F.P. An improved integral non-linear model for the contact of particles in distinct element simulations. Chem. Eng. Sci. 2005, 60, 1303–1312. [Google Scholar] [CrossRef]
- Shäfer, J.; Dippel, S.; Wolf, D.E. Force Schemes in Simulations of Granular Materials. J. Phys. I 1996, 6, 5–20. [Google Scholar] [CrossRef]
- Silbert, L.E.; Ertaş, D.; Grest, G.S.; Halsey, T.C.; Levine, D. Geometry of frictionless and frictional sphere packings. Phys. Rev. E 2002, 65, 31304. [Google Scholar] [CrossRef]
- Ai, J.; Chen, J.-F.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Persson, A.-S.; Frenning, G. An experimental evaluation of the accuracy to simulate granule bed compression using the discrete element method. Powder Technol. 2012, 219, 249–256. [Google Scholar] [CrossRef]
- Cabiscol, R.; Finke, J.H.; Kwade, A. Assessment of particle rearrangement and anisotropy in high-load tableting with a DEM-based elasto-plastic cohesive model. Granul. Matter 2019, 21, 1–23. [Google Scholar] [CrossRef]
- Cabiscol, R.; Finke, J.H.; Kwade, A. Calibration and interpretation of DEM parameters for simulations of cylindrical tablets with multi-sphere approach. Powder Technol. 2018, 327, 232–245. [Google Scholar] [CrossRef]
- Coetzee, C.J. Review: Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Simons, T.A.; Weiler, R.; Strege, S.; Bensmann, S.; Schilling, M.; Kwade, A. A Ring Shear Tester as Calibration Experiment for DEM Simulations in Agitated Mixers—A Sensitivity Study. Procedia Eng. 2015, 102, 741–748. [Google Scholar] [CrossRef]
- Paulick, M.; Morgeneyer, M.; Kwade, A. A new method for the determination of particle contact stiffness. Granul. Matter 2015, 17, 83–93. [Google Scholar] [CrossRef]
- Gitman, I.M.; Askes, H.; Sluys, L.J. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Rojek, J.; Karlis, G.F.; Malinowski, L.J.; Beer, G. Setting up virgin stress conditions in discrete element models. Comput. Geotech. 2013, 48, 228–248. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Drosopoulos, G.A.; Giannis, K.; Stavroulaki, M.E.; Stavroulakis, G.E. Metamodeling-Assisted Numerical Homogenization for Masonry and Cracked Structures. J. Eng. Mech. 2018, 144, 4018072. [Google Scholar] [CrossRef]
- Montero, F.; Medina, F. Determination of the RVE Size of Quasi-Brittle Materials Using the Discrete Element Method. In Proceedings of the II International Conference on Particle-Based Methods-Fundamentals and Applications PARTICLES 2011, Berlin, Germany, 9–12 July 2011. [Google Scholar]
- Wiącek, J.; Molenda, M.; Ooi, J.Y.; Favier, J. Experimental and numerical determination of representative elementary volume for granular plant materials. Granul. Matter 2012, 14, 449–456. [Google Scholar] [CrossRef]
- Nordström, J.; Alderborn, G.; Frenning, G. Compressibility and tablet forming ability of bimodal granule mixtures: Experiments and DEM simulations. Int. J. Pharm. 2018, 540, 120–131. [Google Scholar] [CrossRef] [PubMed]
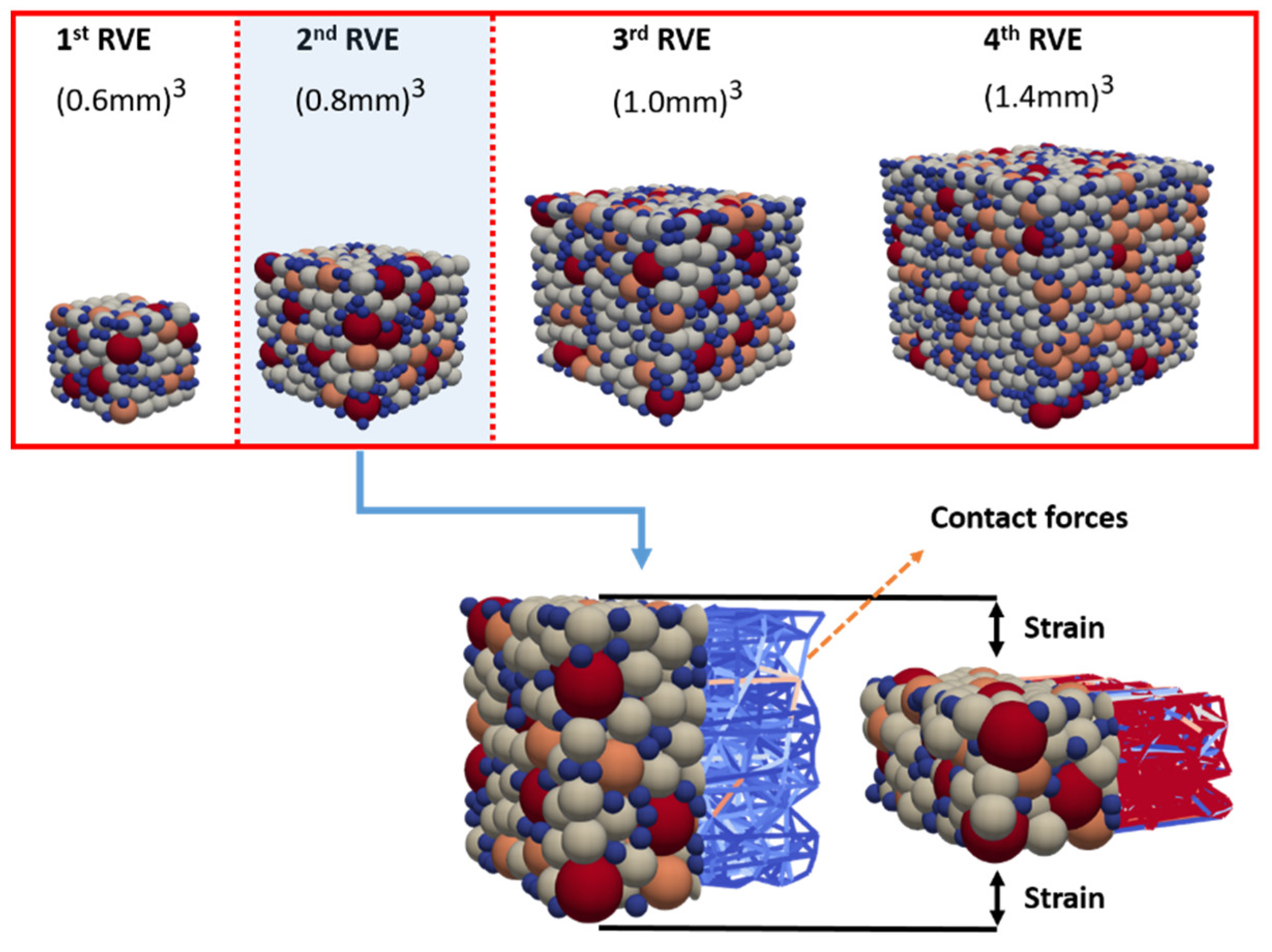


| Material | x10 (Q3) (μm) | x50 (Q3) (μm) | x90 (Q3) (μm) | Span (-) | True Density (kg m−3) |
|---|---|---|---|---|---|
| MCC-A | 82.9 | 224.6 | 379.3 | 1.32 | 1541.1 |
| MCC-P | 28.3 | 86.5 | 173.8 | 1.68 | 1533.7 |
| Property | Symbol | Units | MCC-A | MCC-P |
|---|---|---|---|---|
| Young’s modulus—particle (p) | E | Nm−2 | 2.58 × 108 | 1.34 × 109 |
| Young’s modulus—wall (w) | E | Nm−2 | 7.62 × 1010 | 7.62 × 1010 |
| Poisson’s ratio—particle | ν | - | 0.30 | 0.30 |
| Poisson’s ratio—wall | ν | - | 0.31 | 0.31 |
| Coefficient of restitution particle | COR(p-p) | - | 0.352 | 0.346 |
| Coefficient of restitutio—wall | COR(p-w) | - | 0.352 | 0.346 |
| Coefficient of sliding fric—(p-p) | μs(pp) | - | 0.561 | 0.548 |
| Coefficient of sliding f—(p-w) | μs(pw) | - | 0.707 | 0.715 |
| Coefficient of rollin—(p-p) | μr(pp) | - | 0.3 | 0.3 |
| Coefficient of rol—(p-w) | μr(pp) | - | 0.01 | 0.01 |
| Density | ρ | kg/m3 | 1541.1 | 1533.7 |
| Property | Symbol | Units | MCC-A | MCC-P |
|---|---|---|---|---|
| Unloading stiffness | k2/k1 | - | 120 | 120 |
| Adhesion stiffness ratio | Kc/k1 | - | 0.5 | 0.5 |
| Dimensionless plasticity depth | φf | - | 0.99 | 0.99 |
| Prefactor of the MC-dem | β | - | 1.3 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannis, K.; Schilde, C.; Finke, J.H.; Kwade, A. Modeling of High-Density Compaction of Pharmaceutical Tablets Using Multi-Contact Discrete Element Method. Pharmaceutics 2021, 13, 2194. https://doi.org/10.3390/pharmaceutics13122194
Giannis K, Schilde C, Finke JH, Kwade A. Modeling of High-Density Compaction of Pharmaceutical Tablets Using Multi-Contact Discrete Element Method. Pharmaceutics. 2021; 13(12):2194. https://doi.org/10.3390/pharmaceutics13122194
Chicago/Turabian StyleGiannis, Kostas, Carsten Schilde, Jan Henrik Finke, and Arno Kwade. 2021. "Modeling of High-Density Compaction of Pharmaceutical Tablets Using Multi-Contact Discrete Element Method" Pharmaceutics 13, no. 12: 2194. https://doi.org/10.3390/pharmaceutics13122194
APA StyleGiannis, K., Schilde, C., Finke, J. H., & Kwade, A. (2021). Modeling of High-Density Compaction of Pharmaceutical Tablets Using Multi-Contact Discrete Element Method. Pharmaceutics, 13(12), 2194. https://doi.org/10.3390/pharmaceutics13122194








