Modeling and Simulation of Process Technology for Nanoparticulate Drug Formulations—A Particle Technology Perspective
Abstract
1. Introduction
2. Background
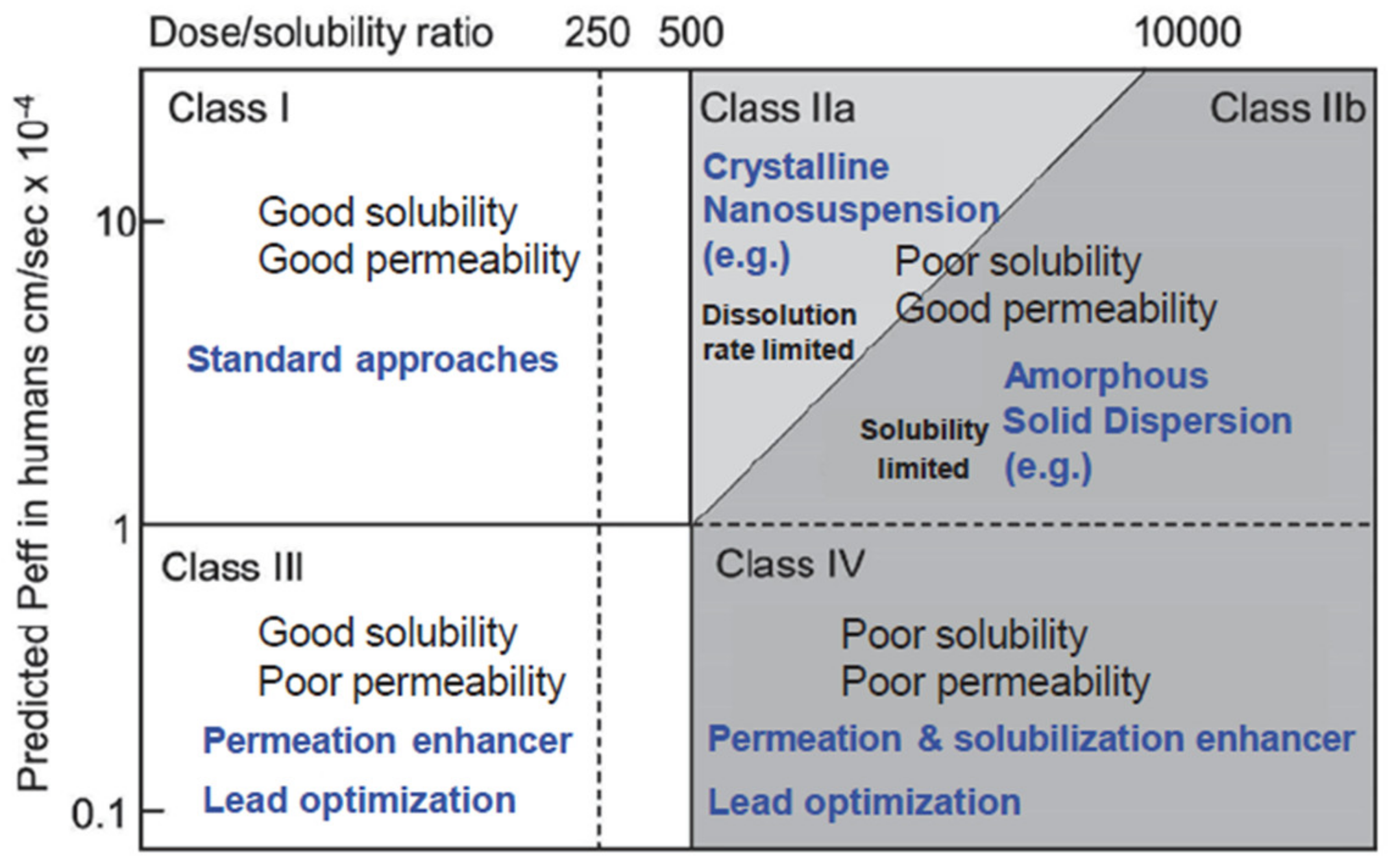
2.1. Poorly Soluble Drug Formulation Routes
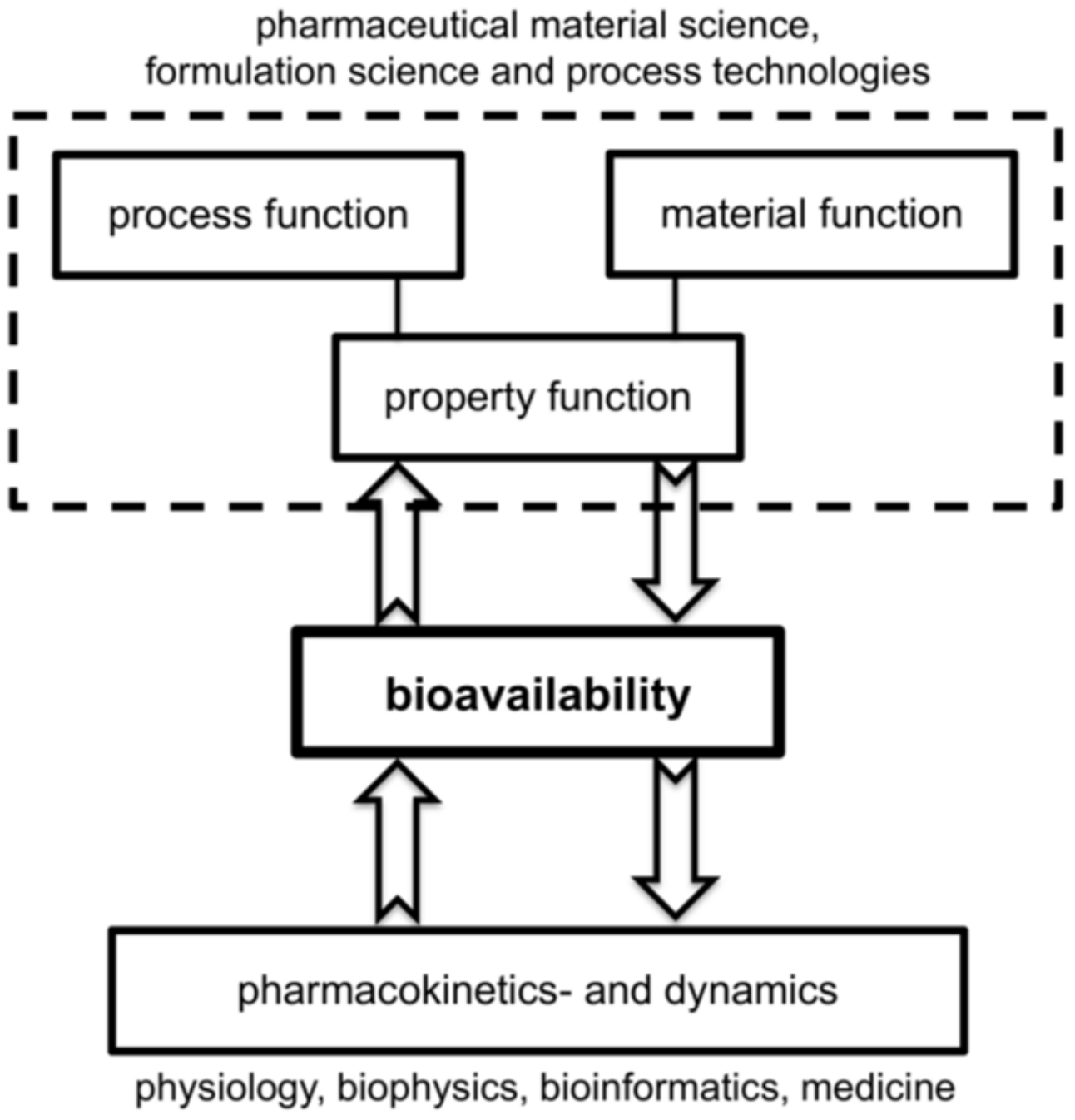
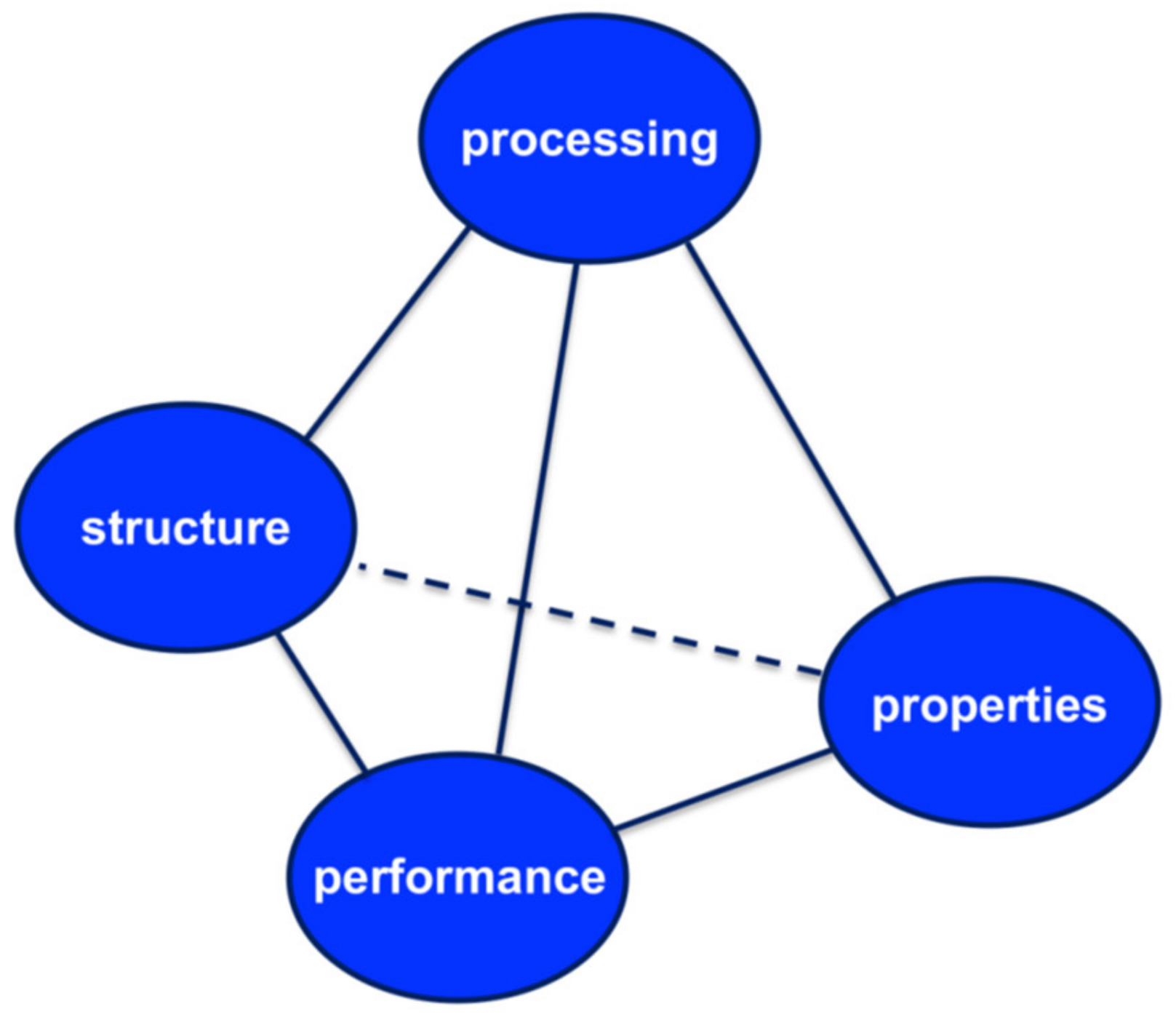
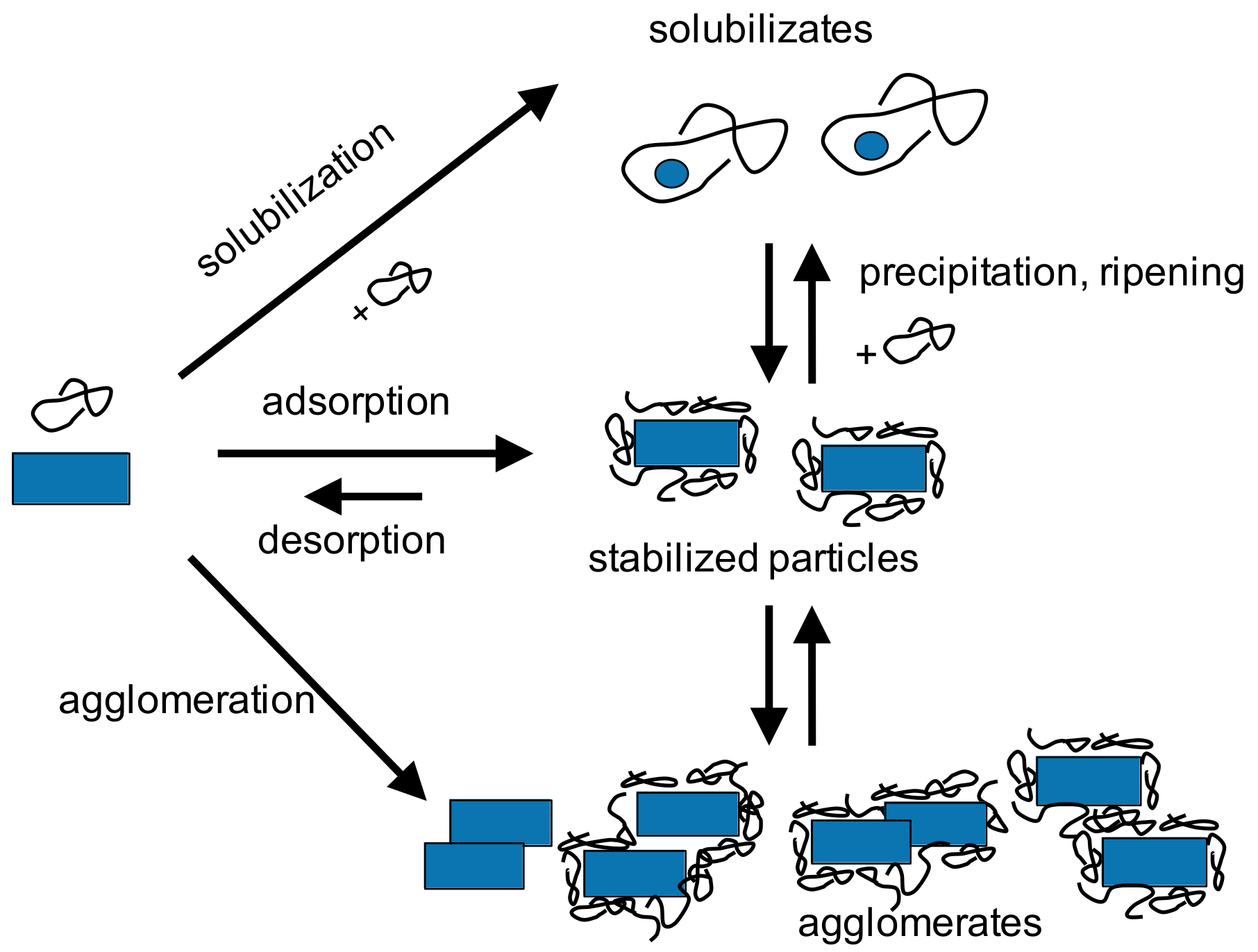
2.2. Particle Technology Applied to Drug Formulations
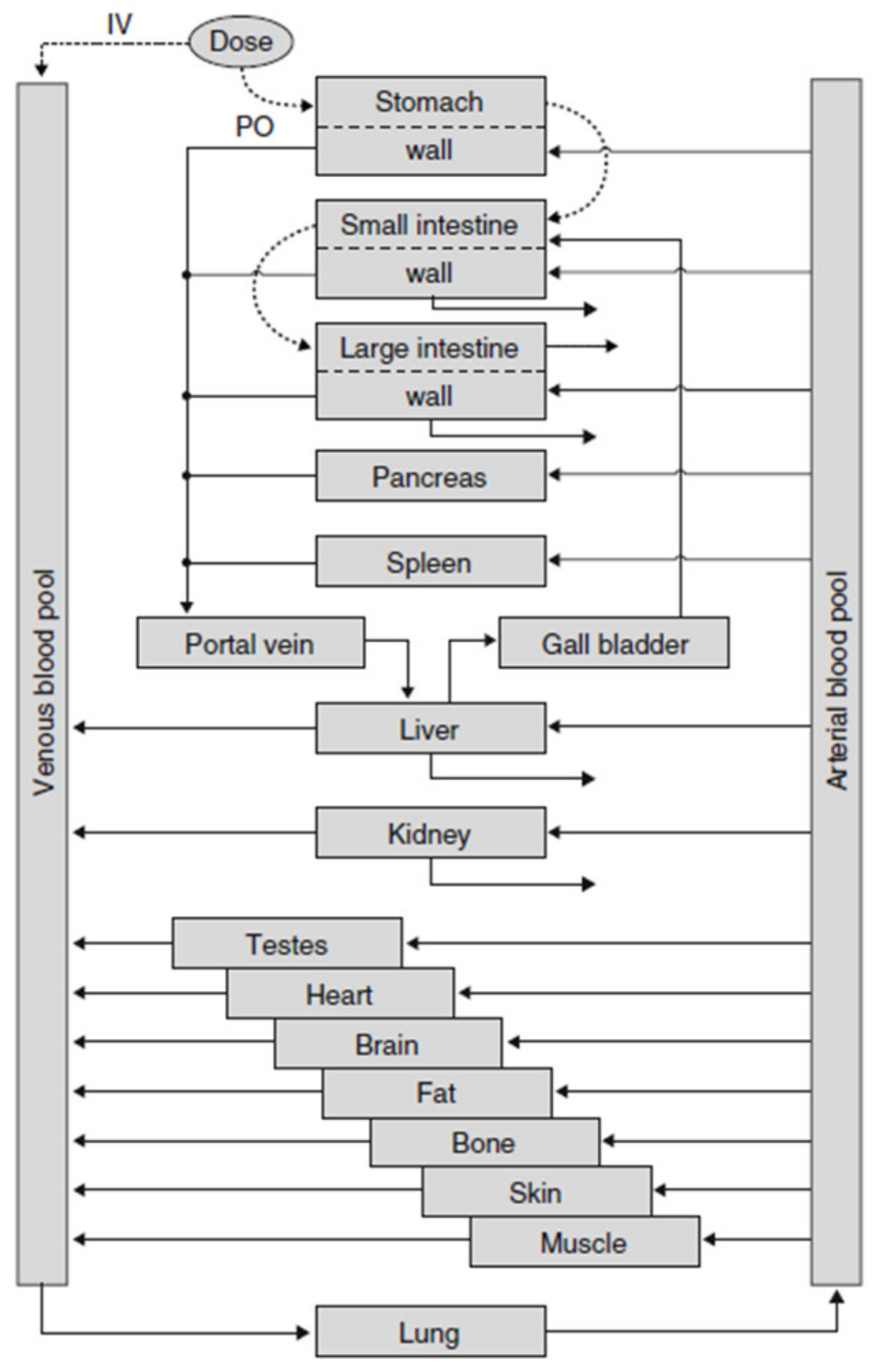
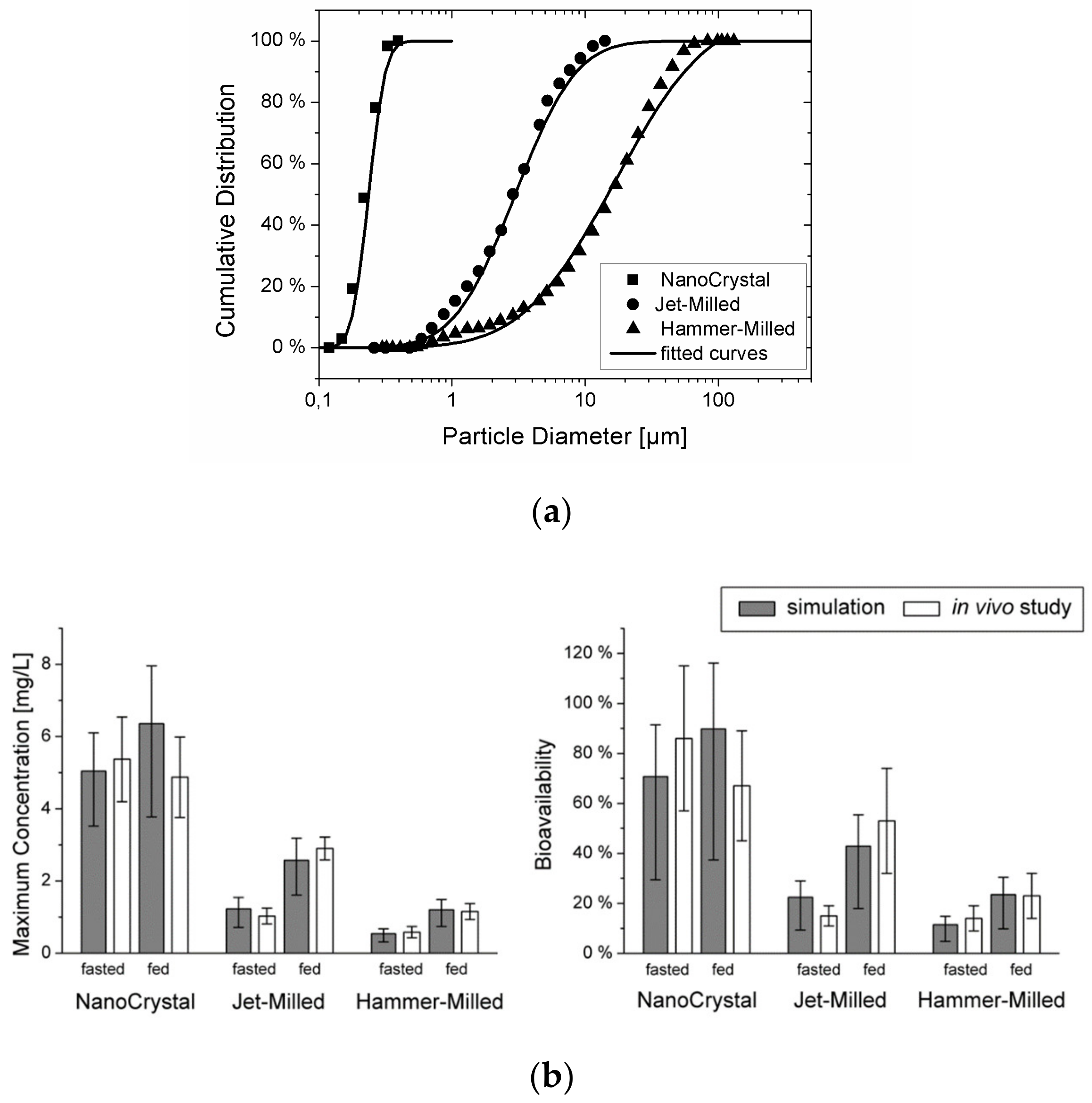
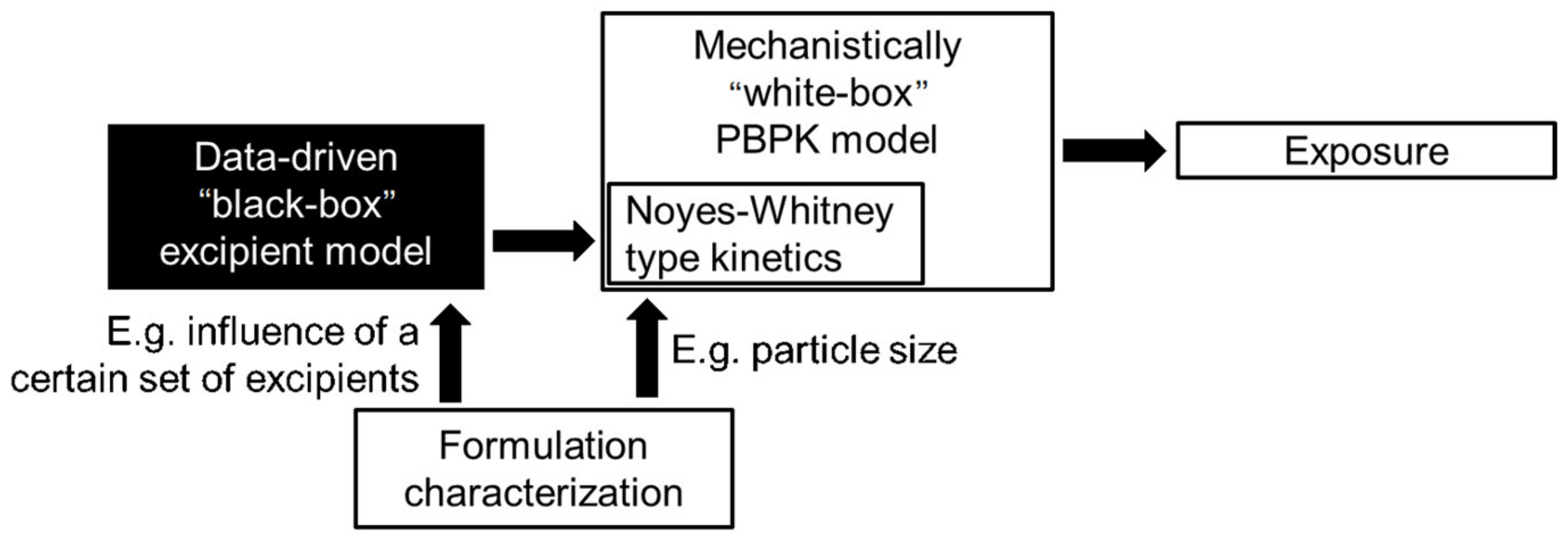
3. Modeling Particle Size-Dependent Dissolution and Absorption
4. Process Chain for Particle Formation and Formulation
4.1. Overview
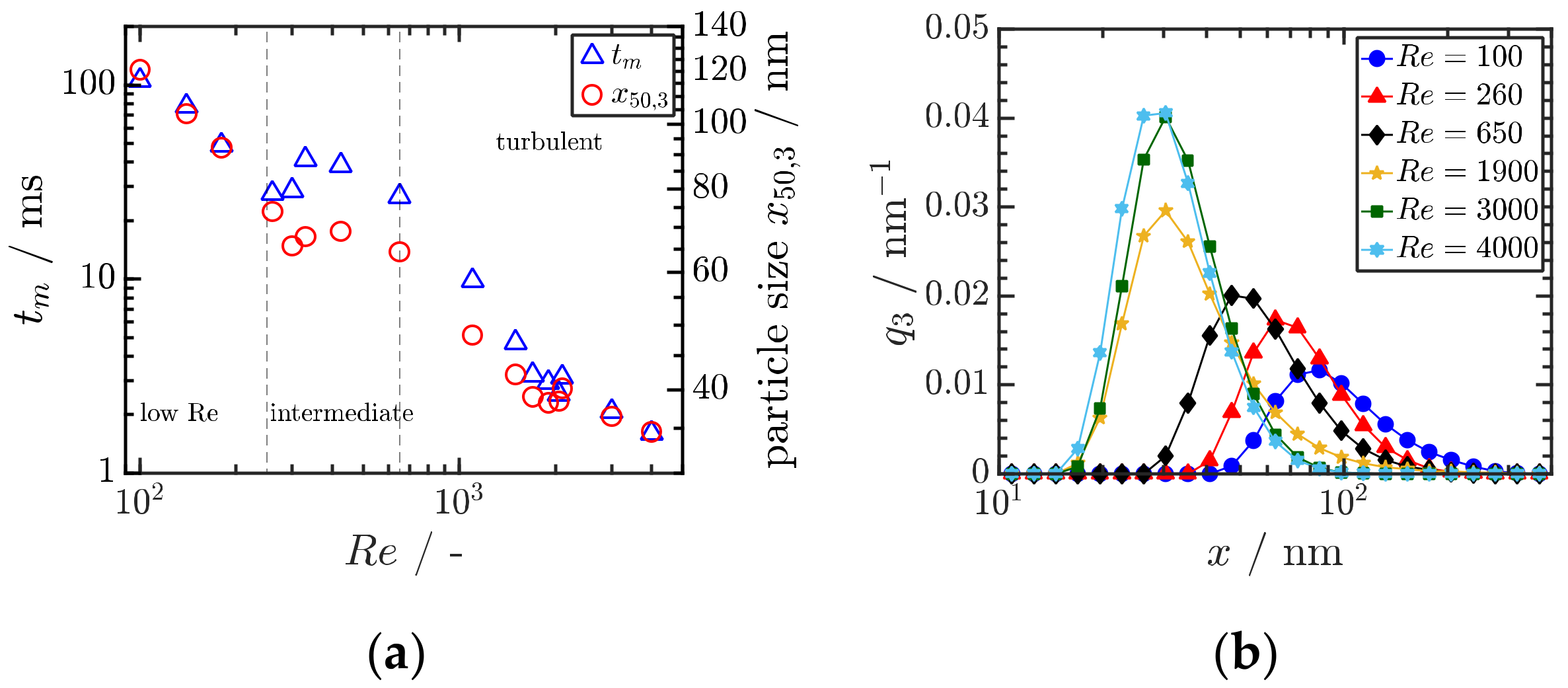
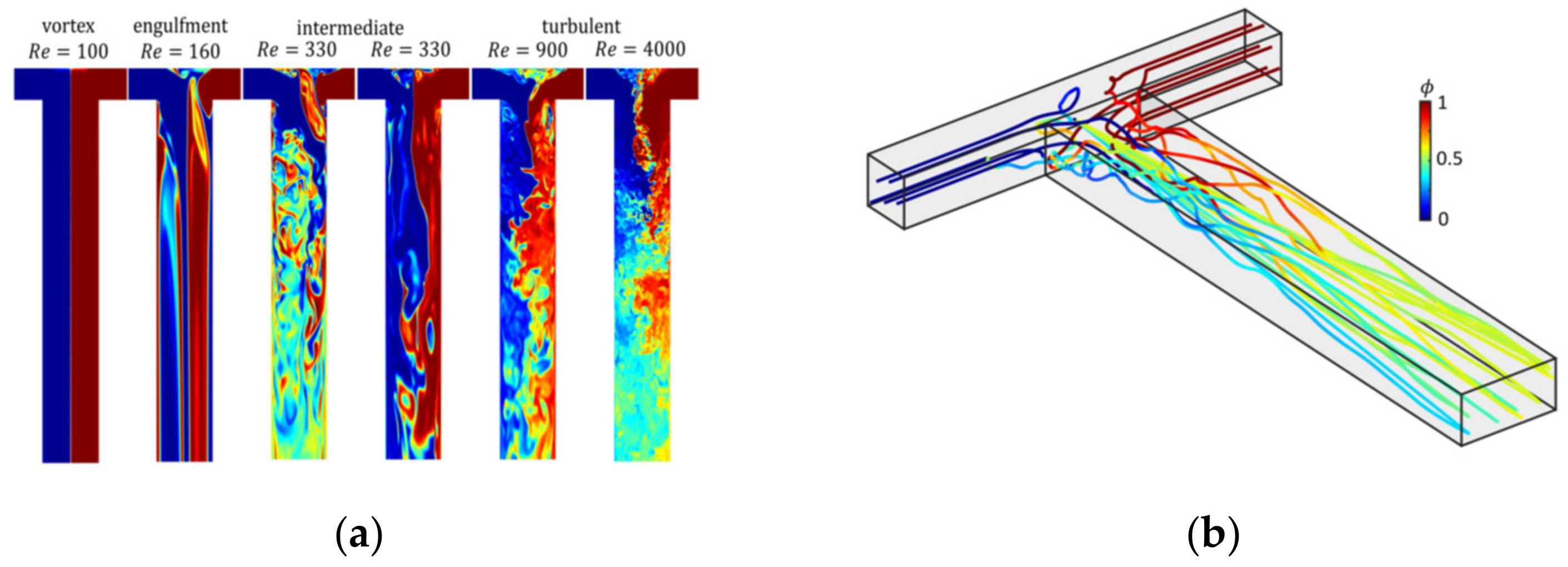
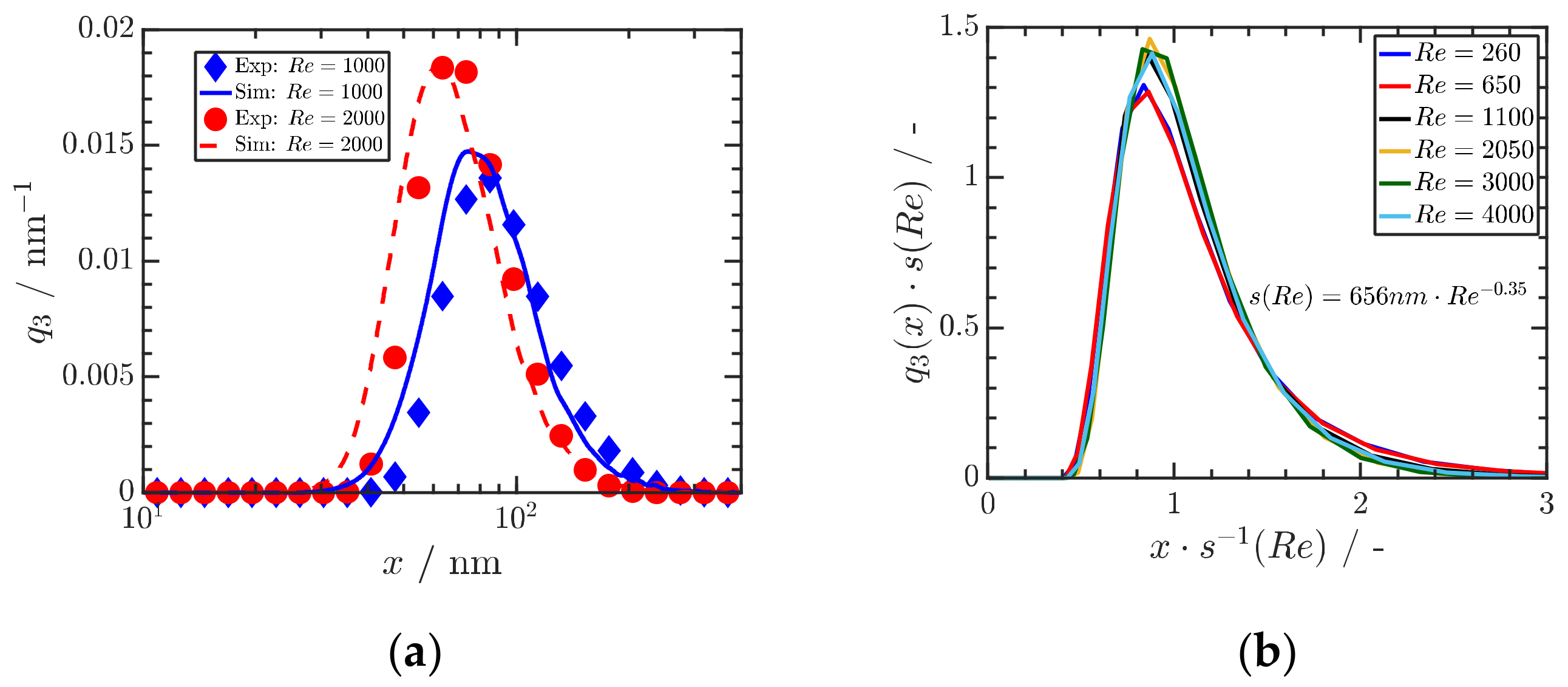
4.2. Precipitation
4.3. Stirred Media Milling
4.4. Post-Processing and Modeling of Process Chains
5. Conclusions and Unmet Needs
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cabrera-Pérez, M.Á.; Pham-The, H. Computational modeling of human oral bioavailability: What will be next? Expert Opin. Drug Discov. 2018, 13, 509–521. [Google Scholar] [CrossRef] [PubMed]
- Fahr, A.; Liu, X. Drug delivery strategies for poorly water-soluble drugs. Expert Opin. Drug Deliv. 2007, 4, 403–416. [Google Scholar] [CrossRef] [PubMed]
- Geerts, T. In Silico Predictions of ADME-Tox Properties: Drug Absorption. Comb. Chem. High Throughput Screen. 2011, 14, 339–361. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Wang, J. Structure–ADME relationship: Still a long way to go? Expert Opin. Drug Metab. Toxicol. 2008, 4, 759–770. [Google Scholar] [CrossRef] [PubMed]
- Damiati, S.A. Digital Pharmaceutical Sciences. AAPS PharmSciTech 2020, 21, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Montanari, F.; Kuhnke, L.; Ter Laak, A.; Clevert, D.-A. Modeling Physico-Chemical ADMET Endpoints with Multitask Graph Convolutional Networks. Molecules 2020, 25, 44. [Google Scholar] [CrossRef] [PubMed]
- Göller, A.H.; Kuhnke, L.; Montanari, F.; Bonin, A.; Schneckener, S.; Ter Laak, A.; Wichard, J.; Lobell, M.; Hillisch, A. Bayer’s in silico ADMET platform: A journey of machine learning over the past two decades. Drug Discov. Today 2020, 25, 1702–1709. [Google Scholar] [CrossRef]
- Segler, M.H.S.; Waller, M.P. Neural-Symbolic Machine Learning for Retrosynthesis and Reaction Prediction. Chem. A Eur. J. 2017, 23, 5966–5971. [Google Scholar] [CrossRef]
- Chaudhury, S.; Duncan, E.H.; Atre, T.; Dutta, S.; Spring, M.D.; Leitner, W.W.; Bergmann-Leitner, E.S. Combining immunoprofiling with machine learning to assess the effects of adjuvant formulation on human vaccine-induced immunity. Hum. Vaccines Immunother. 2020, 16, 400–411. [Google Scholar] [CrossRef]
- Han, R.; Xiong, H.; Ye, Z.; Yang, Y.; Huang, T.; Jing, Q.; Lu, J.; Pan, H.; Ren, F.; Ouyang, D. Predicting physical stability of solid dispersions by machine learning techniques. J. Control. Release 2019, 311–312, 16–25. [Google Scholar] [CrossRef]
- Han, R.; Yang, Y.; Li, X.; Ouyang, D. Predicting oral disintegrating tablet formulations by neural network techniques. Asian J. Pharm. Sci. 2018, 13, 336–342. [Google Scholar] [CrossRef] [PubMed]
- Singare, D.S.; Marella, S.; Gowthamrajan, K.; Kulkarni, G.T.; Vooturi, R.; Rao, P.S. Optimization of formulation and process variable of nanosuspension: An industrial perspective. Int. J. Pharm. 2010, 402, 213–220. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Ye, Z.; Liu, X.; Wei, Z.; Qiu, F.; Li, H.-F.; Zheng, Y.; Ouyang, D. Can machine learning predict drug nanocrystals? J. Control. Release 2020, 322, 274–285. [Google Scholar] [CrossRef] [PubMed]
- Di, L.; Kerns, E.H.; Carter, G.T. Drug-Like Property Concepts in Pharmaceutical Design. Curr. Pharm. Des. 2009, 15, 2184–2194. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Aller, M.R.; Guillarme, D.; Veuthey, J.-L.; Gurny, R. Strategies for formulating and delivering poorly water-soluble drugs. J. Drug Deliv. Sci. Technol. 2015, 30, 342–351. [Google Scholar] [CrossRef]
- Borchard, G. Drug Nanocrystals. In Non-Biological Complex Drugs; Crommelin, D.J.A., de Vlieger, J.S.B., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 171–189. [Google Scholar]
- Jermain, S.V.; Brough, C.; Williams, R.O. Amorphous solid dispersions and nanocrystal technologies for poorly water-soluble drug delivery—An update. Int. J. Pharm. 2018, 535, 379–392. [Google Scholar] [CrossRef] [PubMed]
- Kaptay, G. On the size and shape dependence of the solubility of nano-particles in solutions. Int. J. Pharm. 2012, 430, 253–257. [Google Scholar] [CrossRef] [PubMed]
- Chogale, M.M.; Ghodake, V.N.; Patravale, V. Performance Parameters and Characterizations of Nanocrystals: A Brief Review. Pharmaceutics 2016, 8, 26. [Google Scholar] [CrossRef]
- Van Eerdenbrugh, B.; Vermant, J.; Martens, J.A.; Froyen, L.; Van Humbeeck, J.; Mooter, G.V.D.; Augustijns, P. Solubility Increases Associated with Crystalline Drug Nanoparticles: Methodologies and Significance. Mol. Pharm. 2010, 7, 1858–1870. [Google Scholar] [CrossRef]
- Sun, W.; Mao, S.; Shi, Y.; Li, L.C.; Fang, L. Nanonization of Itraconazole by High Pressure Homogenization: Stabilizer Optimization and Effect of Particle Size on Oral Absorption. J. Pharm. Sci. 2011, 100, 3365–3373. [Google Scholar] [CrossRef]
- O’Shea, J.; Holm, R.; O’Driscoll, C.M.; Griffin, B.T. Food for thought: Formulating away the food effect—A PEARRL review. J. Pharm. Pharmacol. 2019, 71, 510–535. [Google Scholar] [CrossRef] [PubMed]
- Willmann, S.; Thelen, K.; Becker, C.; Dressman, J.B.; Lippert, J. Mechanism-based prediction of particle size-dependent dissolution and absorption: Cilostazol pharmacokinetics in dogs. Eur. J. Pharm. Biopharm. 2010, 76, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Maisel, K.; Ensign, L.; Reddy, M.; Cone, R.; Hanes, J. Effect of surface chemistry on nanoparticle interaction with gastrointestinal mucus and distribution in the gastrointestinal tract following oral and rectal administration in the mouse. J. Control. Release 2015, 197, 48–57. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.H.; Keck, C.M. Drug nanocrystals of poorly soluble drugs produced by high pressure homogenisation. Eur. J. Pharm. Biopharm. 2006, 62, 3–16. [Google Scholar] [CrossRef]
- Juhnke, M.; Berghausen, J.; Timpe, C. Accelerated Formulation Development for Nanomilled Active Pharmaceutical Ingredients Using a Screening Approach. Chem. Eng. Technol. 2010, 33, 1412–1418. [Google Scholar] [CrossRef]
- Desai, N.P.; Tao, C.; Yang, A.; Louie, L.; Zheng, T.; Yao, Z.; Soon-Shiong, P.; Magdassi, S. Protein Stabilized Pharmacologically Active Agents, Methods for the Preparation Thereof and Methods for the Use Thereof. U.S. Patent No. 5,916,596, 1999. [Google Scholar]
- Hagedorn, M.; Bögershausen, A.; Rischer, M.; Schubert, R.; Massing, U. Dual centrifugation—A new technique for nanomilling of poorly soluble drugs and formulation screening by an DoE-approach. Int. J. Pharm. 2017, 530, 79–88. [Google Scholar] [CrossRef]
- Leung, D.H.; Lamberto, D.J.; Liu, L.; Kwong, E.; Nelson, T.; Rhodes, T.; Bak, A. A new and improved method for the preparation of drug nanosuspension formulations using acoustic mixing technology. Int. J. Pharm. 2014, 473, 10–19. [Google Scholar] [CrossRef]
- Liversidge, G.G.; Cundy, K.C.; Bishop, J.F.; Czekai, D.A. Surface Modified Drug Nanoparticles. U.S. Patent No. 5,145,684, 1992. [Google Scholar]
- Bhakay, A.; Rahman, M.; Davé, R.N.; Bilgili, E. Bioavailability Enhancement of Poorly Water-Soluble Drugs via Nanocomposites: Formulation–Processing Aspects and Challenges. Pharmaceutics 2018, 10, 86. [Google Scholar] [CrossRef]
- Farjadian, F.; Ghasemi, A.; Gohari, O.; Roointan, A.; Karimi, M.; Hamblin, M.R. Nanopharmaceuticals and nanomedicines currently on the market: Challenges and opportunities. Nanomedicine 2019, 14, 93–126. [Google Scholar] [CrossRef]
- Schütte, J.K.; Becker, S.; Burmester, S.; Starosse, A.; Lenz, D.; Kröner, L.; Wappler, F.; Gerbershagen, M.U. Comparison of the therapeutic effectiveness of a dantrolene sodium solution and a novel nanocrystalline suspension of dantrolene sodium in malignant hyperthermia normal and susceptible pigs. Eur. J. Anaesthesiol. 2011, 28, 256–264. [Google Scholar] [CrossRef]
- Niwa, T.; Danjo, K. Design of self-dispersible dry nanosuspension through wet milling and spray freeze-drying for poorly water-soluble drugs. Eur. J. Pharm. Sci. 2013, 50, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Czyz, S.; Wewers, M.; Finke, J.H.; Kwade, A.; Van Eerdenbrugh, B.; Juhnke, M.; Bunjes, H. Spray drying of API nanosuspensions: Importance of drying temperature, type and content of matrix former and particle size for successful formulation and process development. Eur. J. Pharm. Biopharm. 2020, 152, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Hamad, M.L.; Bowman, K.; Smith, N.; Sheng, X.; Morris, K.R. Multi-scale pharmaceutical process understanding: From particle to powder to dosage form. Chem. Eng. Sci. 2010, 65, 5625–5638. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Gani, R. A model-based systems approach to pharmaceutical product-process design and analysis. Chem. Eng. Sci. 2010, 65, 5757–5769. [Google Scholar] [CrossRef]
- Uhlemann, J.; Costa, R.; Charpentier, J.-C. Product design and engineering—Past, present, future trends in teaching, research and practices: Academic and industry points of view. Curr. Opin. Chem. Eng. 2020, 27, 10–21. [Google Scholar] [CrossRef]
- Ticehurst, M.D.; Marziano, I. Integration of active pharmaceutical ingredient solid form selection and particle engineering into drug product design. J. Pharm. Pharmacol. 2015, 67, 782–802. [Google Scholar] [CrossRef]
- Sun, C.C. Materials Science Tetrahedron—A Useful Tool for Pharmaceutical Research and Development. J. Pharm. Sci. 2009, 98, 1671–1687. [Google Scholar] [CrossRef]
- Uhlemann, J.; Costa, R.; Charpentier, J.-C. Product Design and Engineering in Chemical Engineering: Past, Present State, and Future. Chem. Eng. Technol. 2019, 42, 2258–2274. [Google Scholar] [CrossRef]
- Willmann, S.; Lippert, J.; Sevestre, M.; Solodenko, J.; Fois, F.; Schmitt, W. PK-Sim®: A physiologically based pharmacokinetic ‘whole-body’ model. Biosilico 2003, 1, 121–124. [Google Scholar] [CrossRef]
- Johnson, K.C. Dissolution and Absorption Modeling: Model Expansion to Simulate the Effects of Precipitation, Water Absorption, Longitudinally Changing Intestinal Permeability, and Controlled Release on Drug Absorption. Drug Dev. Ind. Pharm. 2003, 29, 833–842. [Google Scholar] [CrossRef]
- Hintz, R.J.; Johnson, K.C. The effect of particle size distribution on dissolution rate and oral absorption. Int. J. Pharm. 1989, 51, 9–17. [Google Scholar] [CrossRef]
- Willmann, S.; Thelen, K.; Lippert, J. Integration of dissolution into physiologically-based pharmacokinetic models III: PK-Sim®. J. Pharm. Pharmacol. 2012, 64, 997–1007. [Google Scholar] [CrossRef] [PubMed]
- Lippert, J.; Burghaus, R.; Edginton, A.; Frechen, S.; Karlsson, M.; Kovar, A.; Lehr, T.; Milligan, P.; Nock, V.; Ramusovic, S.; et al. Open Systems Pharmacology Community—An Open Access, Open Source, Open Science Approach to Modeling and Simulation in Pharmaceutical Sciences. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 878–882. [Google Scholar] [CrossRef]
- Jinno, J.-I.; Kamada, N.; Miyake, M.; Yamada, K.; Mukai, T.; Odomi, M.; Toguchi, H.; Liversidge, G.G.; Higaki, K.; Kimura, T. Effect of particle size reduction on dissolution and oral absorption of a poorly water-soluble drug, cilostazol, in beagle dogs. J. Control. Release 2006, 111, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Dressman, J.B.; Thelen, K.; Jantratid, E. Towards Quantitative Prediction of Oral Drug Absorption. Clin. Pharmacokinet. 2008, 47, 655–667. [Google Scholar] [CrossRef]
- Konnerth, C.; Damm, C.; Schmidt, J.; Peukert, W. Mechanical activation of trans-stilbene during wet grinding. Adv. Powder Technol. 2014, 25, 1808–1816. [Google Scholar] [CrossRef]
- Schikarski, T.; Trzenschiok, H.; Avila, M.; Peukert, W. Influence of Mixing on the Precipitation of Organic Nanoparticles: A Lagrangian Perspective on Scale-up Based on Self-Similar Distributions. Chem. Eng. Technol. 2019, 42, 1635–1642. [Google Scholar] [CrossRef]
- Braig, V.; Konnerth, C.; Peukert, W.; Lee, G. Enhanced dissolution of naproxen from pure-drug, crystalline nanoparticles: A case study formulated into spray-dried granules and compressed tablets. Int. J. Pharm. 2019, 554, 54–60. [Google Scholar] [CrossRef]
- Schuldes, I.; Noll, D.M.; Schindler, T.; Zech, T.; Götz, K.; Appavou, M.-S.; Boesecke, P.; Steiniger, F.; Schulz, P.S.; Unruh, T. Internal Structure of Nanometer-Sized Droplets Prepared by Antisolvent Precipitation. Langmuir 2019, 35, 13578–13587. [Google Scholar] [CrossRef]
- Trzenschiok, H.; Distaso, M.; Peukert, W. A new approach for the stabilization of amorphous drug nanoparticles during continuous antisolvent precipitation. Chem. Eng. J. 2019, 361, 428–438. [Google Scholar] [CrossRef]
- Süß, S.; Sobisch, T.; Peukert, W.; Lerche, D.; Segets, D. Determination of Hansen parameters for particles: A standardized routine based on analytical centrifugation. Adv. Powder Technol. 2018, 29, 1550–1561. [Google Scholar] [CrossRef]
- Schikarski, T.; Trzenschiok, H.; Peukert, W.; Avila, M. Inflow boundary conditions determine T-mixer efficiency. React. Chem. Eng. 2019, 4, 559–568. [Google Scholar] [CrossRef]
- Schwarzer, H.-C.; Peukert, W. Experimental Investigation into the Influence of Mixing on Nanoparticle Precipitation. Chem. Eng. Technol. 2002, 25, 657–661. [Google Scholar] [CrossRef]
- Baldyga, J.; Bourne, J.R. Turbulent Mixing and Chemical Reactions; Wiley: Chichester, UK, 1999. [Google Scholar]
- Bockhorn, H.; Mewes, D.; Peukert, W.; Wernecke, H. Micro and Macro Mixing; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gradl, J.; Schwarzer, H.-C.; Schwertfirm, F.; Manhart, M.; Peukert, W. Precipitation of nanoparticles in a T-mixer: Coupling the particle population dynamics with hydrodynamics through direct numerical simulation. Chem. Eng. Process. Process. Intensif. 2006, 45, 908–916. [Google Scholar] [CrossRef]
- Gradl, J.; Peukert, W. Simultaneous 3D observation of different kinetic subprocesses for precipitation in a T-mixer. Chem. Eng. Sci. 2009, 64, 709–720. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Computational Models for Polydisperse Particulate and Multiphase Systems; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Schikarski, T.; Peukert, W.; Avila, M. Direct numerical simulation of water–ethanol flows in a T-mixer. Chem. Eng. J. 2017, 324, 168–181. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Haderlein, M.; Güldenpfennig, A.; Segets, D.; Peukert, W. A widely applicable tool for modeling precipitation processes. Comput. Chem. Eng. 2017, 98, 197–208. [Google Scholar] [CrossRef]
- Konnerth, C.; Flach, F.; Breitung-Faes, S.; Damm, C.; Schmidt, J.; Kwade, A.; Peukert, W. Impact of stressing conditions and polymer–surfactant interactions on product characteristics of organic nanoparticles produced by media milling. Powder Technol. 2016, 294, 71–79. [Google Scholar] [CrossRef]
- Ito, A.; Konnerth, C.; Schmidt, J.; Peukert, W. Effect of polymer species and concentration on the production of mefenamic acid nanoparticles by media milling. Eur. J. Pharm. Biopharm. 2016, 98, 98–107. [Google Scholar] [CrossRef]
- Kwade, A.; Schwedes, J. Breaking characteristics of different materials and their effect on stress intensity and stress number in stirred media mills. Powder Technol. 2002, 122, 109–121. [Google Scholar] [CrossRef]
- Toneva, P.; Wirth, K.-E.; Peukert, W. Grinding in an air classifier mill—Part II: Characterisation of the two-phase flow. Powder Technol. 2011, 211, 28–37. [Google Scholar] [CrossRef]
- Strobel, A.; Romeis, S.; Wittpahl, S.; Herre, P.; Schmidt, J.; Peukert, W. Characterization of stressing conditions in mills—A comprehensive research strategy based on well-characterized model particles. Powder Technol. 2017, 305, 652–661. [Google Scholar] [CrossRef]
- Strobel, A.; Köninger, B.; Romeis, S.; Schott, F.; Wirth, K.-E.; Peukert, W. Assessing stress conditions and impact velocities in fluidized bed opposed jet mills. Particuology 2020. [Google Scholar] [CrossRef]
- Armstrong, P.; Knieke, C.; Mačković, M.; Frank, G.; Hartmaier, A.; Göken, M.; Peukert, W. Microstructural evolution during deformation of tin dioxide nanoparticles in a comminution process. Acta Mater. 2009, 57, 3060–3071. [Google Scholar] [CrossRef]
- Meier, M.; John, E.; Wieckhusen, D.; Wirth, W.; Peukert, W. Influence of mechanical properties on impact fracture: Prediction of the milling behaviour of pharmaceutical powders by nanoindentation. Powder Technol. 2009, 188, 301–313. [Google Scholar] [CrossRef]
- Meier, M.; John, E.; Wieckhusen, D.; Wirth, W.; Peukert, W. Generally applicable breakage functions derived from single particle comminution data. Powder Technol. 2009, 194, 33–41. [Google Scholar] [CrossRef]
- Konnerth, C.; Braig, V.; Ito, A.; Schmidt, J.; Lee, G.; Peukert, W. Formation of Mefenamic Acid Nanocrystals with Improved Dissolution Characteristics. Chem. Ing. Tech. 2017, 89, 1060–1071. [Google Scholar] [CrossRef]
- Sutkar, V.S.; Deen, N.G.; Patil, A.V.; Salikov, V.; Antonyuk, S.; Heinrich, S.; Kuipers, J.A.M. CFD–DEM model for coupled heat and mass transfer in a spout fluidized bed with liquid injection. Chem. Eng. J. 2016, 288, 185–197. [Google Scholar] [CrossRef]
- El Hagrasy, A.S.; Hennenkamp, J.R.; Burke, M.D.; Cartwright, J.J.; Litster, J.D. Twin screw wet granulation: Influence of formulation parameters on granule properties and growth behavior. Powder Technol. 2013, 238, 108–115. [Google Scholar] [CrossRef]
- Heinrich, S. Dynamic Flowsheet Simulation of Solids Processes; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Schuppert, A.; Mrziglod, T. Hybrid Model Identification and Discrimination with Practical Examples from the Chemical Industry. Hybrid Model. Process Ind. 2018, 63–88. [Google Scholar] [CrossRef]
- Schneckener, S.; Grimbs, S.; Hey, J.; Menz, S.; Osmers, M.; Schaper, S.; Hillisch, A.; Göller, A.H. Prediction of Oral Bioavailability in Rats: Transferring Insights from in Vitro Correlations to (Deep) Machine Learning Models Using in Silico Model Outputs and Chemical Structure Parameters. J. Chem. Inf. Model. 2019, 59, 4893–4905. [Google Scholar] [CrossRef] [PubMed]
- Banda, A.; Manchanda, A.; Zhang, W.; Alba, G.M.; Nagapudi, K. Comparative Assessment of Miniaturized Screening Approaches for Selection of Polymers for Amorphous Drug Stabilization. J. Pharm. Sci. 2018, 107, 897–908. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uhlemann, J.; Diedam, H.; Hoheisel, W.; Schikarski, T.; Peukert, W. Modeling and Simulation of Process Technology for Nanoparticulate Drug Formulations—A Particle Technology Perspective. Pharmaceutics 2021, 13, 22. https://doi.org/10.3390/pharmaceutics13010022
Uhlemann J, Diedam H, Hoheisel W, Schikarski T, Peukert W. Modeling and Simulation of Process Technology for Nanoparticulate Drug Formulations—A Particle Technology Perspective. Pharmaceutics. 2021; 13(1):22. https://doi.org/10.3390/pharmaceutics13010022
Chicago/Turabian StyleUhlemann, Jens, Holger Diedam, Werner Hoheisel, Tobias Schikarski, and Wolfgang Peukert. 2021. "Modeling and Simulation of Process Technology for Nanoparticulate Drug Formulations—A Particle Technology Perspective" Pharmaceutics 13, no. 1: 22. https://doi.org/10.3390/pharmaceutics13010022
APA StyleUhlemann, J., Diedam, H., Hoheisel, W., Schikarski, T., & Peukert, W. (2021). Modeling and Simulation of Process Technology for Nanoparticulate Drug Formulations—A Particle Technology Perspective. Pharmaceutics, 13(1), 22. https://doi.org/10.3390/pharmaceutics13010022




