A Mathematical Approach to Consider Solid Compressibility in the Compression of Pharmaceutical Powders
Abstract
1. Introduction
2. Theory
2.1. Model of Heckel
2.2. Model of Cooper & Eaton
3. Materials
4. Methods
4.1. Powder Characterization
4.2. Determination of the Bulk Modulus
4.3. Tableting
4.4. Application of the Compression Equations
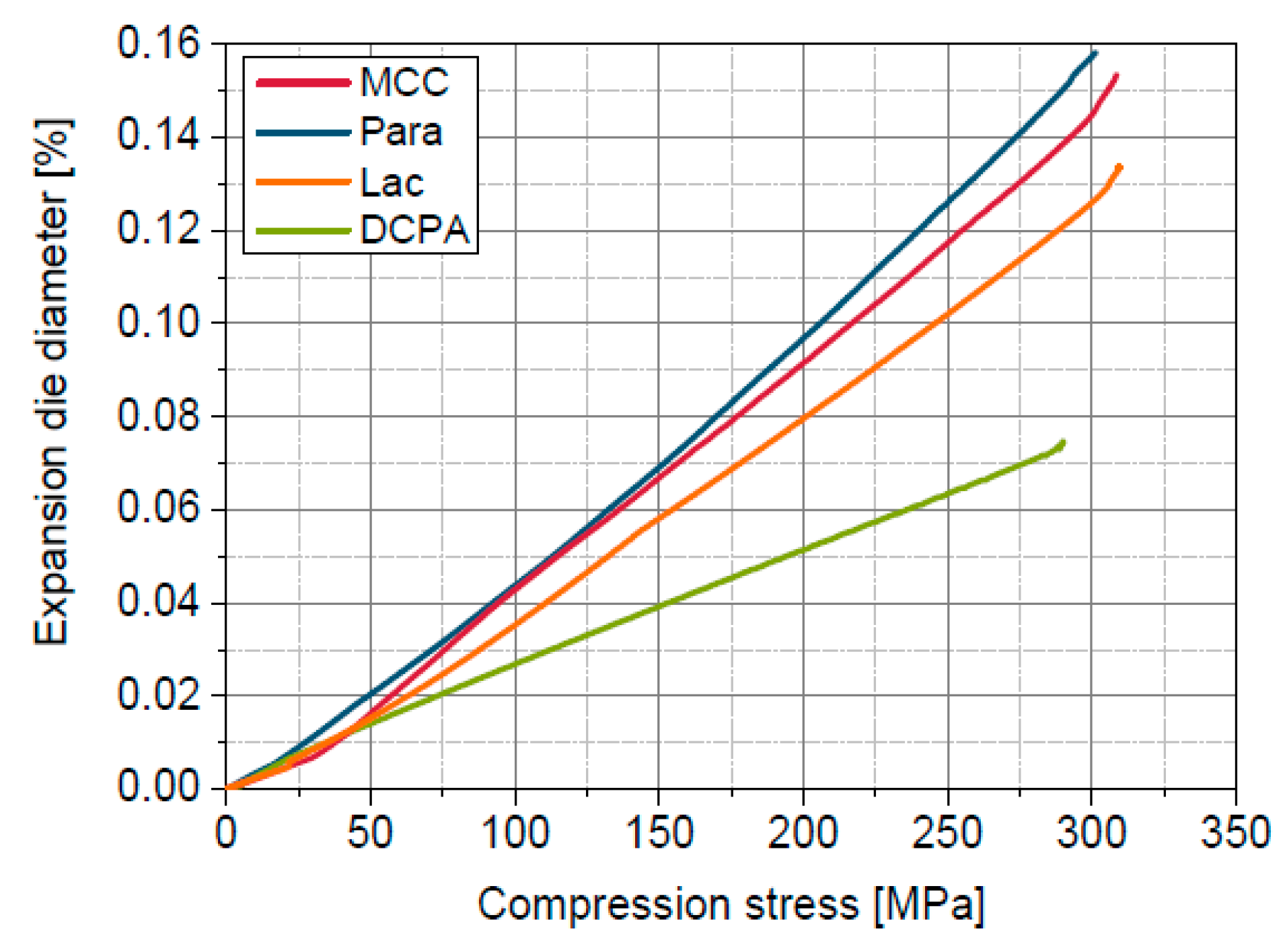
4.5. Estimation of Radial Die Expansion
5. Results and Discussion
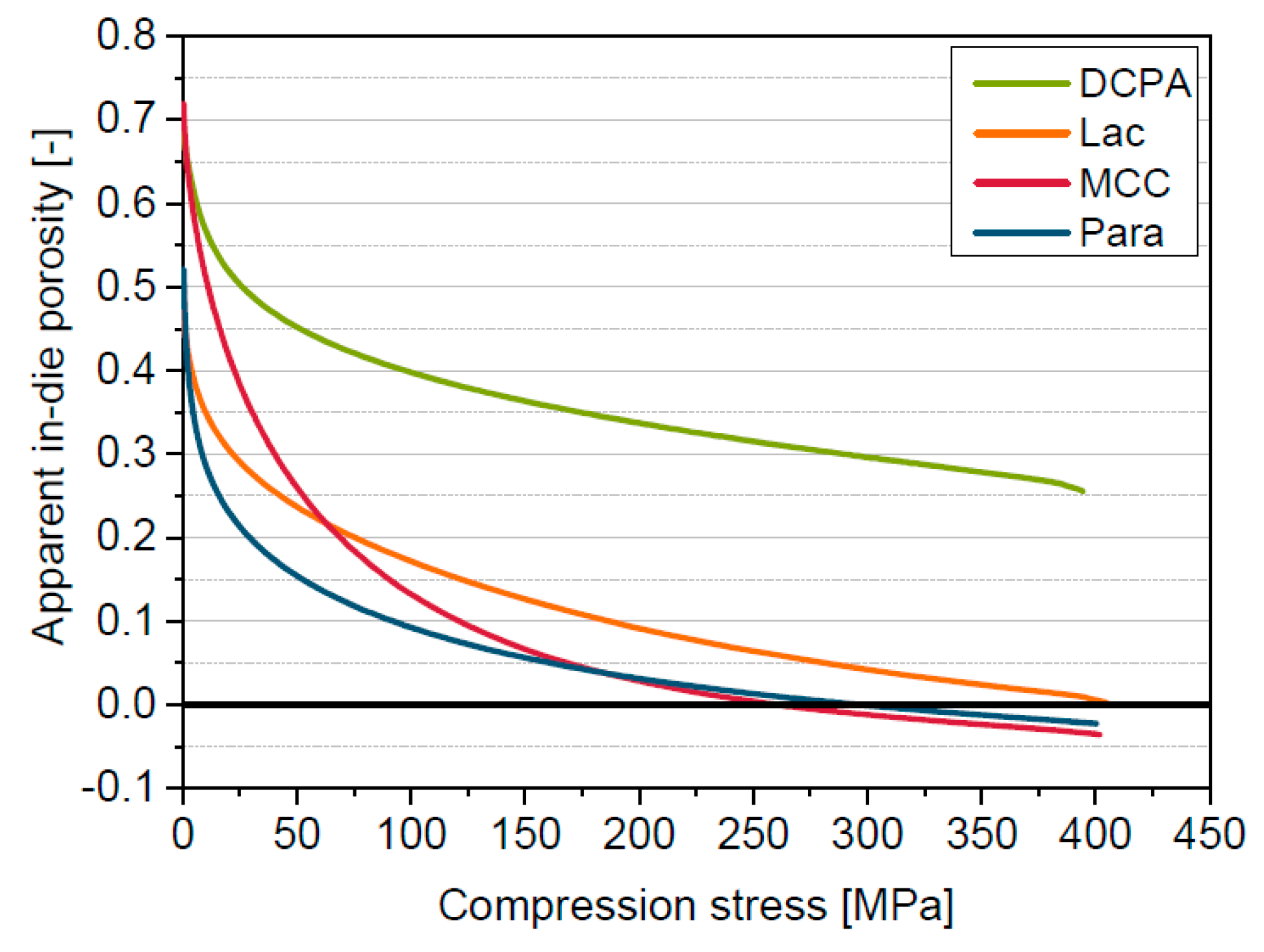
5.1. Compression Behavior of the Model Materials
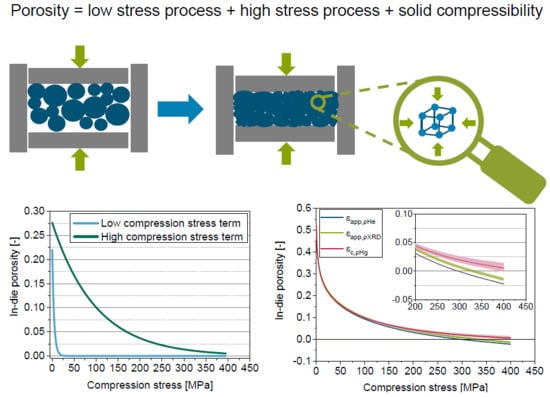
5.2. Reasons for Apparent in-Die Porosities Below Zero
5.3. Introduction of the Solid Compressibility Term
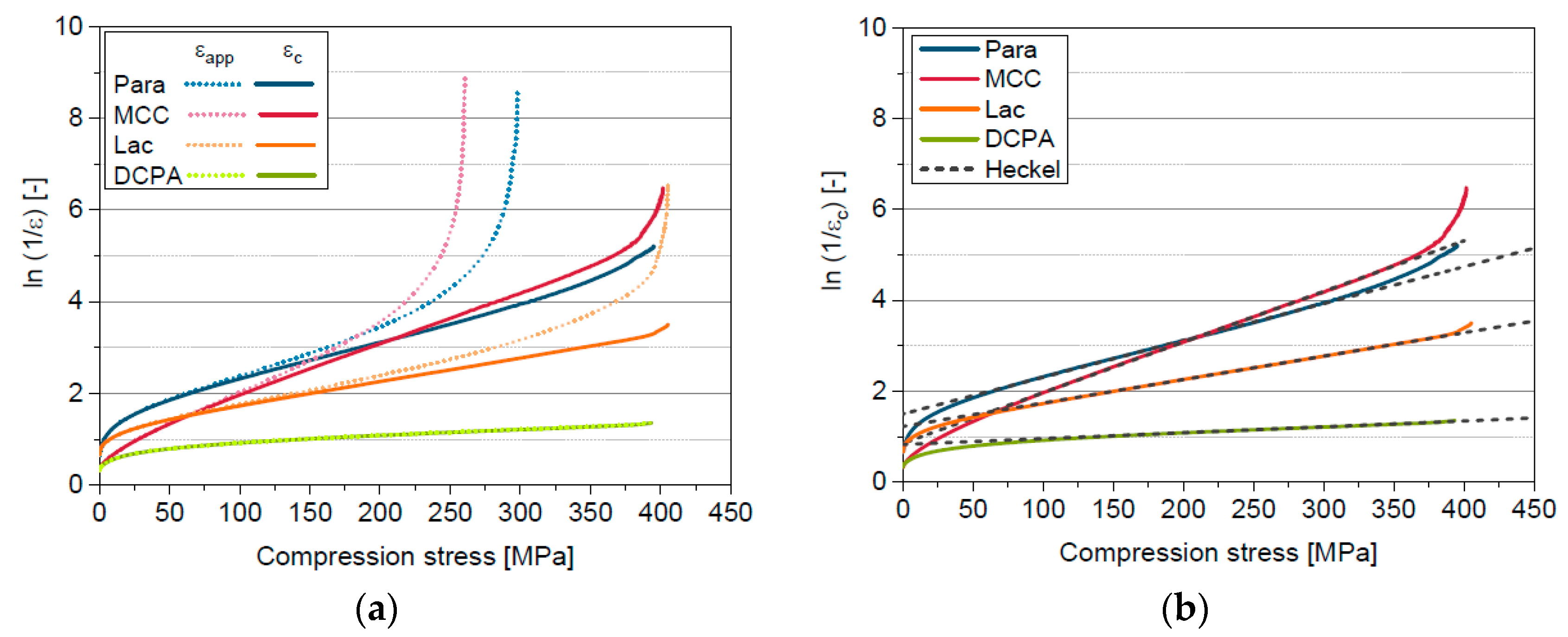
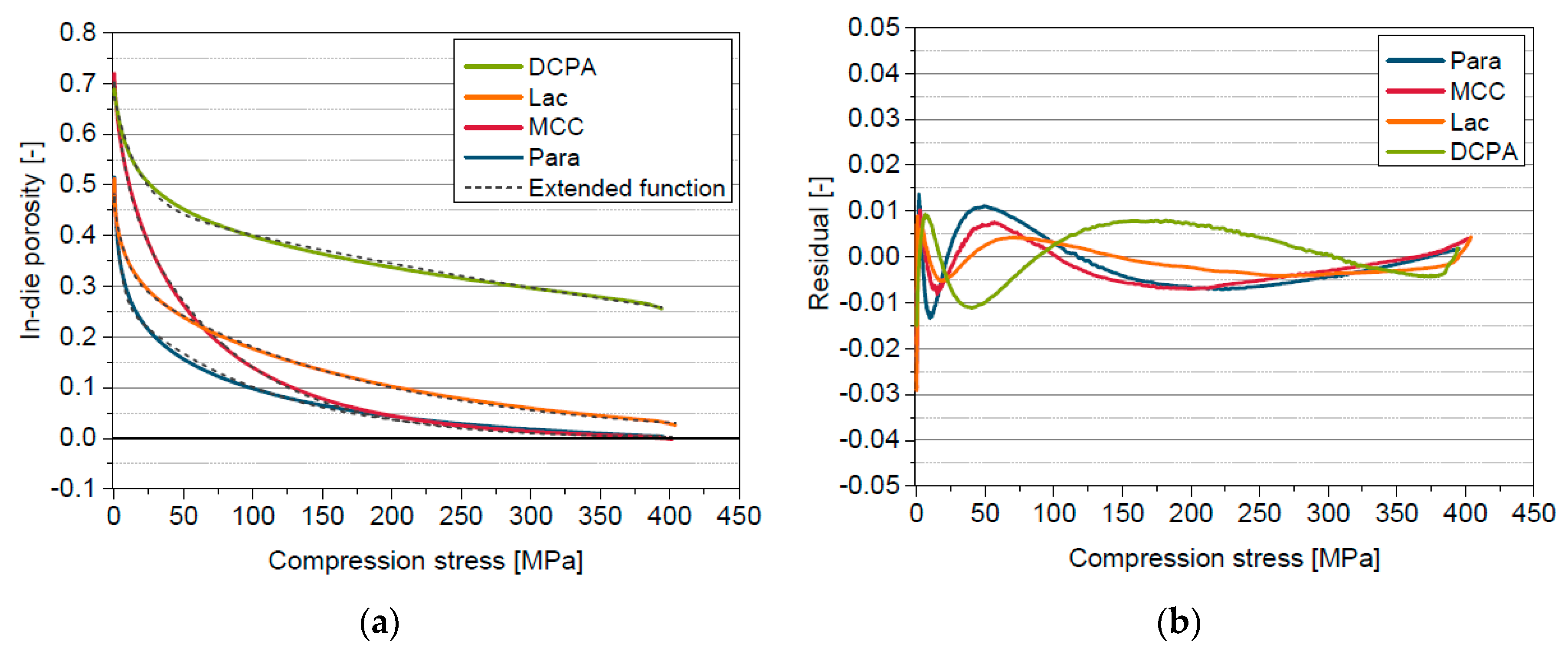
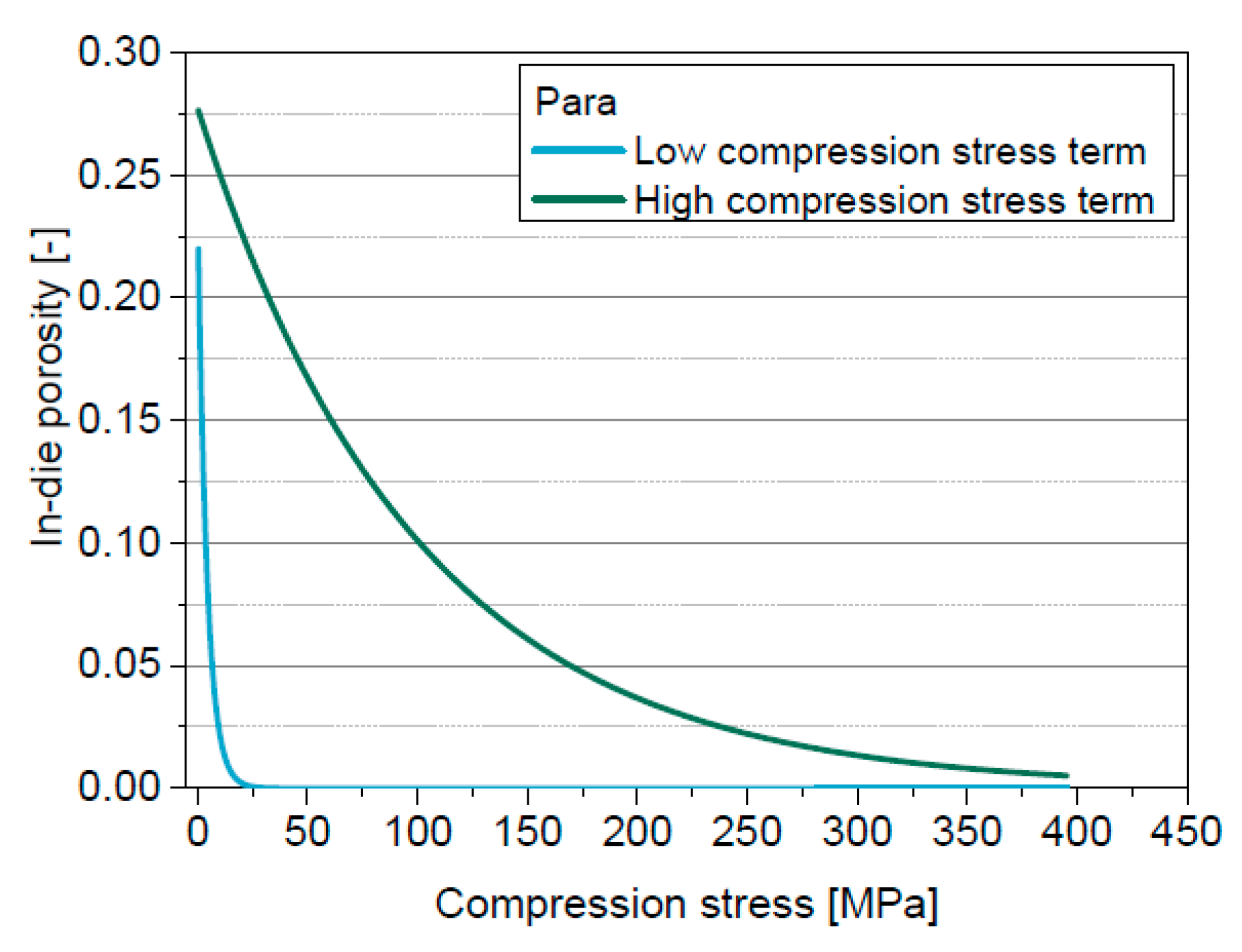
5.4. Extension of the Model of Heckel by the Solid Compressibility Term
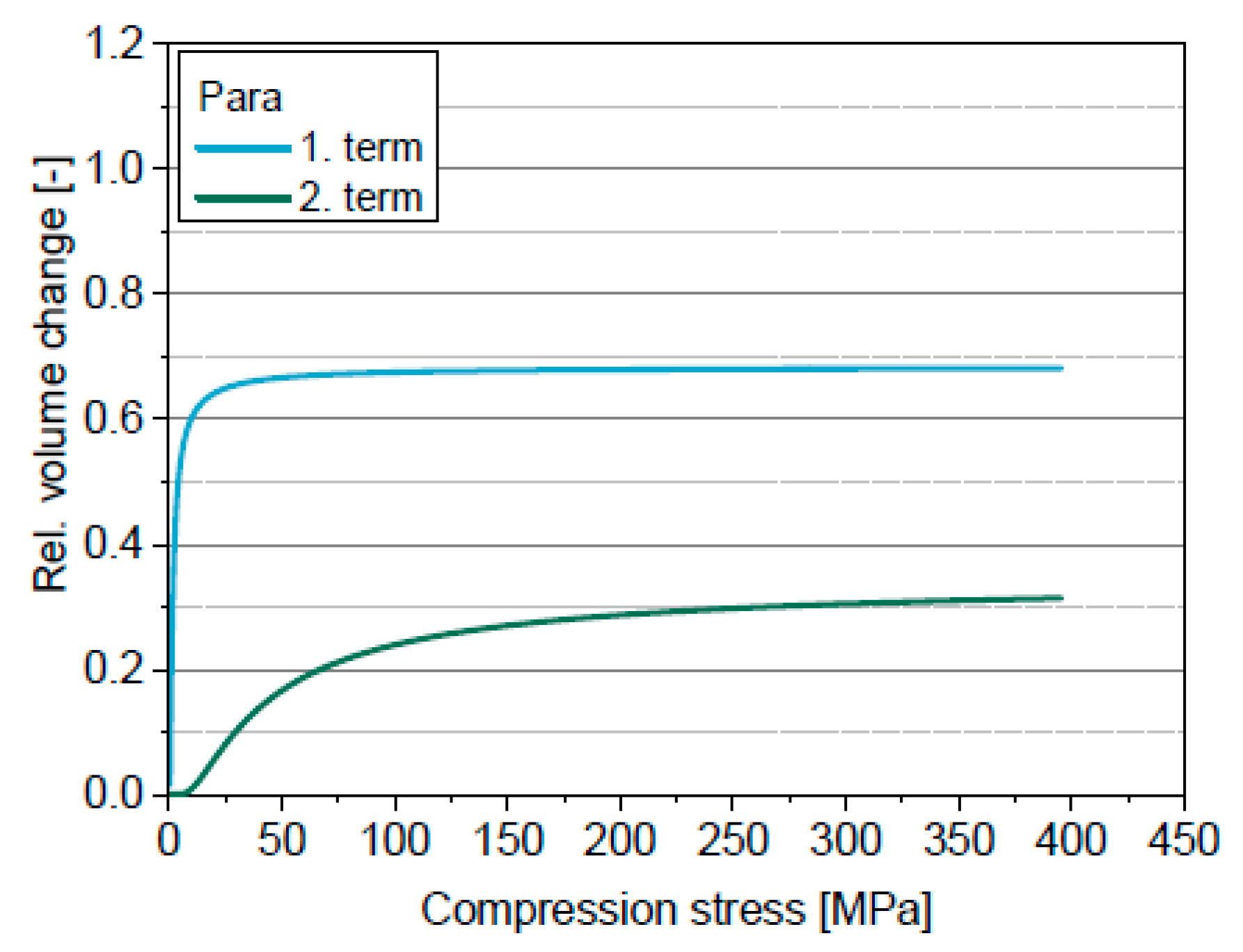
5.5. Extension of the Model of Cooper & Eaton by the Solid Compressibility Term
5.6. Extended in-die Compression Function
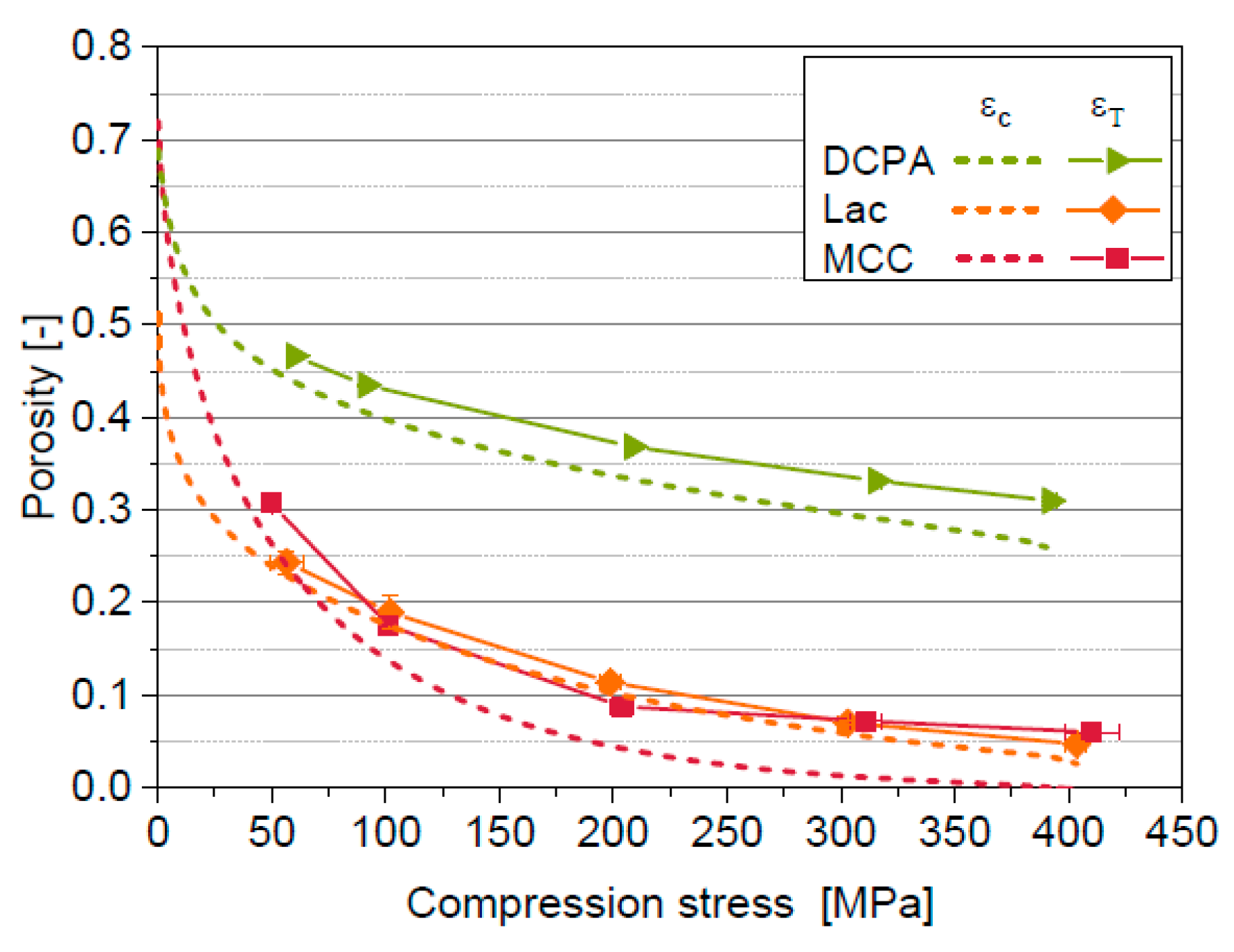
5.7. Comparison in- and out-of-die Compressibility
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Podczeck, F.; Sharma, M. The influence of particle size and shape of components of binary powder mixtures on the maximum volume reduction due to packing. Int. J. Pharm. 1996, 1, 41–47. [Google Scholar] [CrossRef]
- Tye, C.K.; Sun, C.; Amidon, G.E. Evaluation of the effects of tableting speed on the relationships between compaction pressure, tablet tensile strength, and tablet solid fraction. J. Pharm. Sci. 2005, 3, 465–472. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Kaushal, A.M.; Bansal, A.K. Effect of Particle Size and Compression Force on Compaction Behavior and Derived Mathematical Parameters of Compressibility. Pharm. Res. 2006, 1, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Kaerger, J.; Edge, S.; Price, R. Influence of particle size and shape on flowability and compactibility of binary mixtures of paracetamol and microcrystalline cellulose. Eur. J. Pharm. Sci. 2004, 2–3, 173–179. [Google Scholar] [CrossRef] [PubMed]
- David, S.T.; Augsburger, L.L. Plastic Flow during Compression of Directly Compressible Fillers and Its Effect on Tablet Strength. J. Pharm. Sci. 1977, 2, 155–159. [Google Scholar] [CrossRef]
- Hiestand, E.N.; Wells, J.E.; Peot, C.B.; Ochs, J.F. Physical Processes of Tableting. J. Pharm. Sci. 1977, 4, 510–519. [Google Scholar] [CrossRef]
- Leuenberger, H.; Rohera, B.D. Fundamentals of Powder Compression. I. The Compactibility and Compressibility of Pharmaceutical Powders. Pharm. Res. 1986, 1, 12–22. [Google Scholar] [CrossRef] [PubMed]
- USP. Tablet Compression Characterization, Second Supplement to USP 40-NF 35; The United States Pharmacopeial Convention: North Bethesda, MD, USA, 2017.
- Train, D. An investigation into the compaction of powders. J. Pharm. Pharmacol. 1956, 1, 745–761. [Google Scholar] [CrossRef]
- Wray, P.E. The Physics of Tablet Compaction Revisited. Drug Dev. Ind. Pharm. 2008, 6-7, 627–658. [Google Scholar] [CrossRef]
- Hiestand, E.N. Powders: Particle-Particle Interactions. J. Pharm. Sci. 1966, 12, 1325–1344. [Google Scholar] [CrossRef]
- Hiestand, E.N. Dispersion Forces and Plastic Deformation in Tablet Bond. J. Pharm. Sci. 1985, 7, 768–770. [Google Scholar] [CrossRef]
- Kawakita, K.; Lüdde, K.-H. Some considerations on powder compression equations. Powder Technol. 1971, 2, 61–68. [Google Scholar] [CrossRef]
- Çelik, M. Overview of Compaction Data Analysis Techniques. Drug Dev. Ind. Pharm. 2008, 6–7, 767–810. [Google Scholar] [CrossRef]
- Heckel, R.W. Density-Pressure Relationships in Powder Compaction. Trans. Metall. AIME 1961, 221, 97–101. [Google Scholar]
- Cooper, A.R.; Eaton, L.E. Compaction Behavior of Several Ceramic Powders. J Am. Ceram. Soc. 1962, 3, 97–101. [Google Scholar] [CrossRef]
- Sun, C.; Grant, D.J. Influence of Elastic Deformation of Particles on Heckel Analysis. Pharm. Dev. Technol. 2001, 2, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Katz, J.M.; Buckner, I.S. Full Out-of-Die Compressibility and Compactibility Profiles From Two Tablets. J. Pharm. Sci. 2017, 3, 843–849. [Google Scholar] [CrossRef] [PubMed]
- Sonnergaard, J. A critical evaluation of the Heckel equation. Int. J. Pharm. 1999, 1, 63–71. [Google Scholar] [CrossRef]
- Katz, J.M.; Roopwani, R.; Buckner, I.S. A Material-Sparing Method for Assessment of Powder Deformation Characteristics Using Data Collected During a Single Compression–Decompression Cycle. J. Pharm. Sci. 2013, 10, 3687–3693. [Google Scholar] [CrossRef] [PubMed]
- Pederson, S.; Kristensen, H.G. Compressibility of 18 Molecular Organic Solids to 45 kbar. J. Chem. Phys. 1971, 55, 987–992. [Google Scholar]
- Klevan, I.; Nordström, J.; Bauer-Brandl, A.; Alderborn, G. On the physical interpretation of the initial bending of a Shapiro–Konopicky–Heckel compression profile. Eur. J. Pharm. Biopharm. 2009, 2, 395–401. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Kaushal, A.M.; Bansal, A.K. Mechanistic investigation on pressure dependency of Heckel parameter. Int. J. Pharm. 2010, 1–2, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Boldyreva, E.V. High-pressure diffraction studies of molecular organic solids. A personal view. Acta Crystallogr. A Found. Crystallogr. 2008, 1, 218–231. [Google Scholar] [CrossRef] [PubMed]
- Fabbiani, F.P.A.; Allan, D.R.; David, W.I.F.; Davidson, A.J.; Lennie, A.R.; Parsons, S.; Pulham, C.R.; Warren, J.E. High-Pressure Studies of Pharmaceuticals: An Exploration of the Behavior of Piracetam. Cryst. Growth Des. 2007, 6, 1115–1124. [Google Scholar] [CrossRef]
- Vaidya, S.N.; Kennedy, G.C. Compressibility of 18 Molecular Organic Solids to 45 kbar. J. Chem. Phys. 1971, 3, 987–992. [Google Scholar] [CrossRef]
- Gane, P.A.; Kettle, J.P.; Matthews, P.G.; Ridgway, C.J. Void Space Structure of Compressible Polymer Spheres and Consolidated Calcium Carbonate Paper-Coating Formulations. Ind. Eng. Chem. Res. 1996, 5, 1753–1764. [Google Scholar] [CrossRef]
- Ridgway, C.J.; Ridgway, K.; Matthews, P.G. Modelling of the Void Space of Tablets Compacted Over a Range of Pressures. J. Pharm. Pharmacol. 1997, 4, 377–383. [Google Scholar] [CrossRef]
- Sun, C.C. Mechanism of moisture induced variations in true density and compaction properties of microcrystalline cellulose. Int. J. Pharm. 2008, 1–2, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Gabaude, C.M.; Guillot, M.; Gautier, J.; Saudemon, P.; Chulia, D. Effects of true density, compacted mass, compression speed, and punch deformation on the mean yield pressure. J. Pharm. Sci. 1999, 7, 725–730. [Google Scholar] [CrossRef] [PubMed]
- Sun, C. True Density of Microcrystalline Cellulose. J. Pharm. Sci. 2005, 10, 2132–2134. [Google Scholar] [CrossRef] [PubMed]
- Heckel, R.W. A Normalized Density-Pressure Curve for Powder Compaction. Trans. Metall. AIME 1962, 224, 1073–1074. [Google Scholar]
- Hersey, J.A.; Rees, T.E. Proceeding of the Second Particle Size Analysis Conference; Society for Analytical Chemistry, University of Bradford: Bradford, UK, 1970. [Google Scholar]
- Beitz, W.; Grote, K.-H. Dubbel Taschenbuch für den Maschinenbau; Springer: Berlin, Germany, 1997. [Google Scholar]
- Perry, J.; Aboudi, J. Elasto-Plastic Stresses in Thick Walled Cylinders. Trans. ASME 2003, 248–252. [Google Scholar] [CrossRef]
- Sun, C. A Novel Method for Deriving True Density of Pharmaceutical Solids Including Hydrates and Water-Containing Powders. J. Pharm. Sci. 2004, 3, 646–653. [Google Scholar] [CrossRef] [PubMed]
- Viana, M. About pycnometric density measurements. Talanta 2002, 3, 583–593. [Google Scholar] [CrossRef]
- Mazel, V.; Busignies, V.; Diarra, H.; Tchoreloff, P. Measurements of Elastic Moduli of Pharmaceutical Compacts: A New Methodology Using Double Compaction on a Compaction Simulator. J. Pharm. Sci. 2012, 6, 2220–2228. [Google Scholar] [CrossRef] [PubMed]
- Mazel, V.; Busignies, V.; Diarra, H.; Tchoreloff, P. On the Links Between Elastic Constants and Effective Elastic Behavior of Pharmaceutical Compacts: Importance of Poisson’s Ratio and Use of Bulk Modulus. J. Pharm. Sci. 2013, 11, 4009–4014. [Google Scholar] [CrossRef] [PubMed]
- Bassam, F.; York, P.; Rowe, R.C.; Roberts, R.J. Young’s modulus of powders used as pharmaceutical excipients. Int. J. Pharm. 1990, 1, 55–60. [Google Scholar] [CrossRef]
- Higuchi, T.; Shimamoto, T.; Eriksen, S.P.; Yashiki, T. Physics of Tablet Compression XIV. Lateral Die Wall Pressure During and After Compression. J. Pharm. Sci. 1965, 1, 111–118. [Google Scholar] [CrossRef]
- Windheuser, J.J.; Misra, J.; Eriksen, S.P.; Higuchi, T. Physics of Tablet Compression XIII. J. Pharm. Sci. 1963, 8, 767–772. [Google Scholar] [CrossRef]
- Abdel-Hamid, S.; Betz, G. Study of radial die-wall pressure changes during pharmaceutical powder compaction. Drug Dev. Ind. Pharm. 2010, 4, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Brewin, P.R. Modelling of Powder Die Compaction; Springer: London, UK, 2008. [Google Scholar]
- Abdel-Hamid, S. Instrumentation of Tableting Machines: High Speed Compaction Investigation through Simulation and Radial Die-Wall Pressure Monitoring. Ph.D. Thesis, University of Basel, Basel, Switzerland, 2011. [Google Scholar]
- Murnaghan, F.D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 1944, 9, 244–247. [Google Scholar] [CrossRef]
- Zhang, Y.; Law, Y.; Chakrabarti, S. Physical properties and compact analysis of commonly used direct compression binders. AAPS PharmSciTech 2003, 4, 489–499. [Google Scholar] [CrossRef] [PubMed]
- Haware, R.V.; Tho, I.; Bauer-Brandl, A. Application of multivariate methods to compression behavior evaluation of directly compressible materials. Eur. J. Pharm. Biopharm. 2009, 1, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Sonnergaard, J. Investigation of a new mathematical model for compression of pharmaceutical powders. Eur. J. Pharm. Sci. 2001, 2, 149–157. [Google Scholar] [CrossRef]



| Material | x10 [µm] | x50 [µm] | x90 [µm] | ρs [g/cm3] |
|---|---|---|---|---|
| MCC | 36 | 125 | 261 | 1.5537 ± 0.0080 |
| Para | 4 | 25 | 72 | 1.2863 ± 0.0001 |
| Lac | 12 | 147 | 342 | 1.5524 ± 0.0077 |
| DCPA | 77 | 190 | 302 | 2.7718 ± 0.0097 |
| Material | Bulk Modulus K [GPa] | Min. Apparent in-die porosity εapp,He,min [-] | Min. in-die porosity εc,Hg,min [-] |
|---|---|---|---|
| MCC | 10.22 ± 1.02 | −0.035 | 0.006 |
| Para | 14.93 ± 3.67 | −0.023 | 0.005 |
| Lac | 27.07 ± 7.13 | 0.001 | 0.016 |
| DCPA | - | 0.256 | - |
| Material | Stress Ratio [-] | Die Expansion Coefficient [GPa] | Difference of Porosity at 400 MPa [-] |
|---|---|---|---|
| MCC | 0.47–0.81 | 207 ± 4 | 3.7 × 10−6 |
| Para | 0.50–0.85 | 196 ± 3 | 4.2 × 10−6 |
| Lac | 0.45–0.71 | 237 ± 4 | 2.9 × 10−6 |
| DCPA | 0.21–0.43 | 382 ± 5 | 1.1 × 10−6 |
| Material | Bulk Modulus K [GPa] | CHeckel [GPa] | CCooper &Eaton [GPa] | CExtended function [GPa] |
|---|---|---|---|---|
| MCC | 10.22 ± 1.02 | 11.51 ± 0.17 | 11.87 ± 0.12 | 11.74 ± 0.30 |
| Para | 14.93 ± 3.67 | 15.22 ± 0.07 | 18.41 ± 0.74 | 15.97 ± 1.00 |
| Lac | 27.07 ± 7.13 | 14.09 ± 0.03 | - | 14.80 ± 1.46 |
| DCPA | - | 150.02 ± 17.24 | - | 277.06 ± 10.02 |
| Material | Py [MPa] | Fit Range | With Solid Compressibility Term | Py,T [MPa] | ||
|---|---|---|---|---|---|---|
| Py,c [MPa] | Fit Range | R2 [-] Entire Curve | ||||
| MCC | 72.6 ± 1.0 | 10–50% σmax | 89.3 ± 1.2 | 40–90% σmax | 0.9860 | 543.5 |
| Para | 93.5 ± 1.2 | 6–56% σmax | 121.2 ± 2.7 | 30–80% σmax | 0.9739 | - |
| Lac | 145.6 ± 0.5 | 25–75% σmax | 194.5 ± 0.6 | 40–90% σmax | 0.9935 | 233.1 |
| DCPA | 765.4 ± 1.5 | 38–88% σmax | 771.2 ± 2.5 | 40–90% σmax | 0.9313 | 1062.6 |
| Material | V*app | With Solid Compressibility Term V*c | |||||||
|---|---|---|---|---|---|---|---|---|---|
| a1 [-] | k1 [MPa] | a2 [-] | k2 [MPa] | a1c [-] | k1c [MPa] | a2c [-] | k2c [MPa] | R2 [-] | |
| MCC | 0.58 ± 0.01 | 1.46 ± 0.16 | 0.45 ± 0.01 | 20.2 ± 1.0 | 0.57 ± 0.01 | 1.43 ± 0.20 | 0.45 ± 0.01 | 18.7 ± 0.9 | 0.9998 |
| Para | 0.70 ± 0.003 | 1.40 ± 0.10 | 0.35 ± 0.003 | 43.7 ± 2.4 | 0.69 ± 0.003 | 1.37 ± 0.10 | 0.34 ± 0.003 | 38 ± 2.0 | 0.9993 |
| Lac | 0.52 ± 0.002 | 0.84 ± 0.00 | 0.54 ± 0.002 | 53.6 ± 0.4 | 0.9963 | ||||
| DCPA | 0.45 ± 0.01 | 0.96 ± 0.10 | 0.42 ± 0.009 | 29.2 ± 1.9 | 0.9926 | ||||
| Material | εl [-] | σl [MPa] | εh [-] | σh [MPa] | C [GPa] | R2 [-] |
|---|---|---|---|---|---|---|
| MCC | 0.20 ± 0.00 | 8.5 ± 0.6 | 0.51 ± 0.01 | 79.0 ± 1.9 | 11.74 ± 0.30 | 0.9998 |
| Para | 0.24 ± 0.00 | 4.3 ± 0.1 | 0.28 ± 0.00 | 99.2 ± 3.2 | 15.97 ± 1.00 | 0.9993 |
| Lac | 0.14 ± 0.01 | 9.4 ± 0.5 | 0.32 ± 0.00 | 177.3 ± 5.6 | 14.80 ± 1.46 | 0.9997 |
| DCPA | 0.21 ± 0.00 | 16.8 ± 0.2 | 0.47 ± 0.00 | 668.6 ± 3.5 | 277.06 ± 10.20 | 0.9993 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wünsch, I.; Finke, J.H.; John, E.; Juhnke, M.; Kwade, A. A Mathematical Approach to Consider Solid Compressibility in the Compression of Pharmaceutical Powders. Pharmaceutics 2019, 11, 121. https://doi.org/10.3390/pharmaceutics11030121
Wünsch I, Finke JH, John E, Juhnke M, Kwade A. A Mathematical Approach to Consider Solid Compressibility in the Compression of Pharmaceutical Powders. Pharmaceutics. 2019; 11(3):121. https://doi.org/10.3390/pharmaceutics11030121
Chicago/Turabian StyleWünsch, Isabell, Jan Henrik Finke, Edgar John, Michael Juhnke, and Arno Kwade. 2019. "A Mathematical Approach to Consider Solid Compressibility in the Compression of Pharmaceutical Powders" Pharmaceutics 11, no. 3: 121. https://doi.org/10.3390/pharmaceutics11030121
APA StyleWünsch, I., Finke, J. H., John, E., Juhnke, M., & Kwade, A. (2019). A Mathematical Approach to Consider Solid Compressibility in the Compression of Pharmaceutical Powders. Pharmaceutics, 11(3), 121. https://doi.org/10.3390/pharmaceutics11030121