Characterization of Mechanical Property Distributions on Tablet Surfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Powder Characterization
2.3. Tableting
2.4. Tablet Characterization
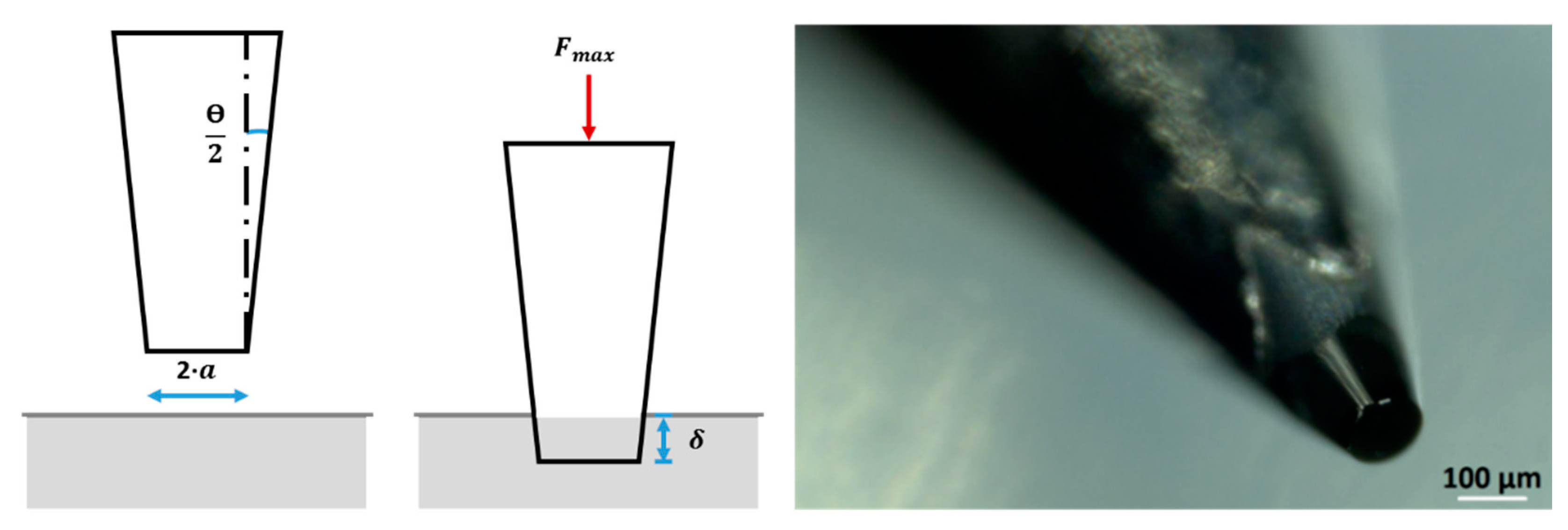
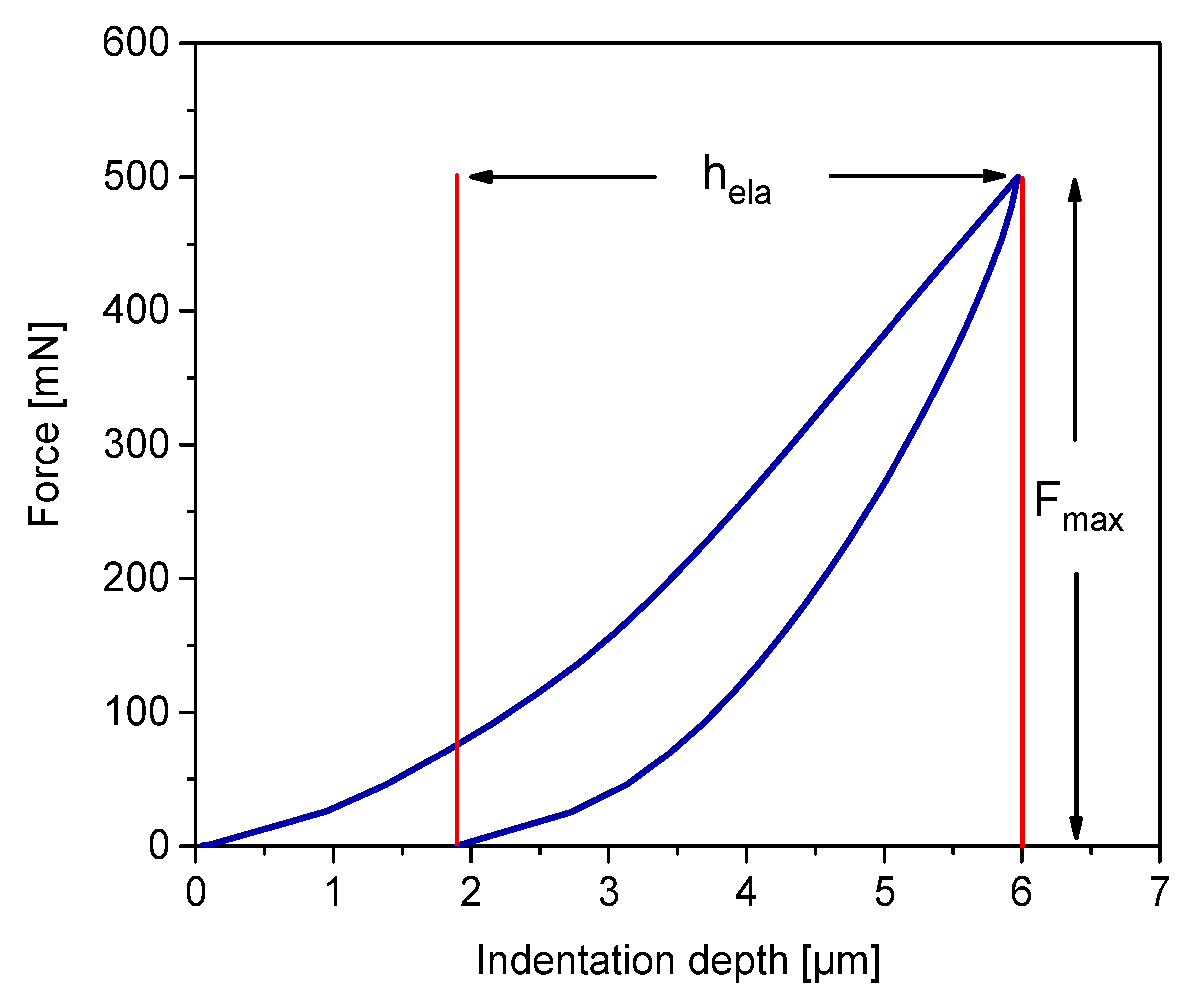
2.5. Microindentation
3. Results and Discussion
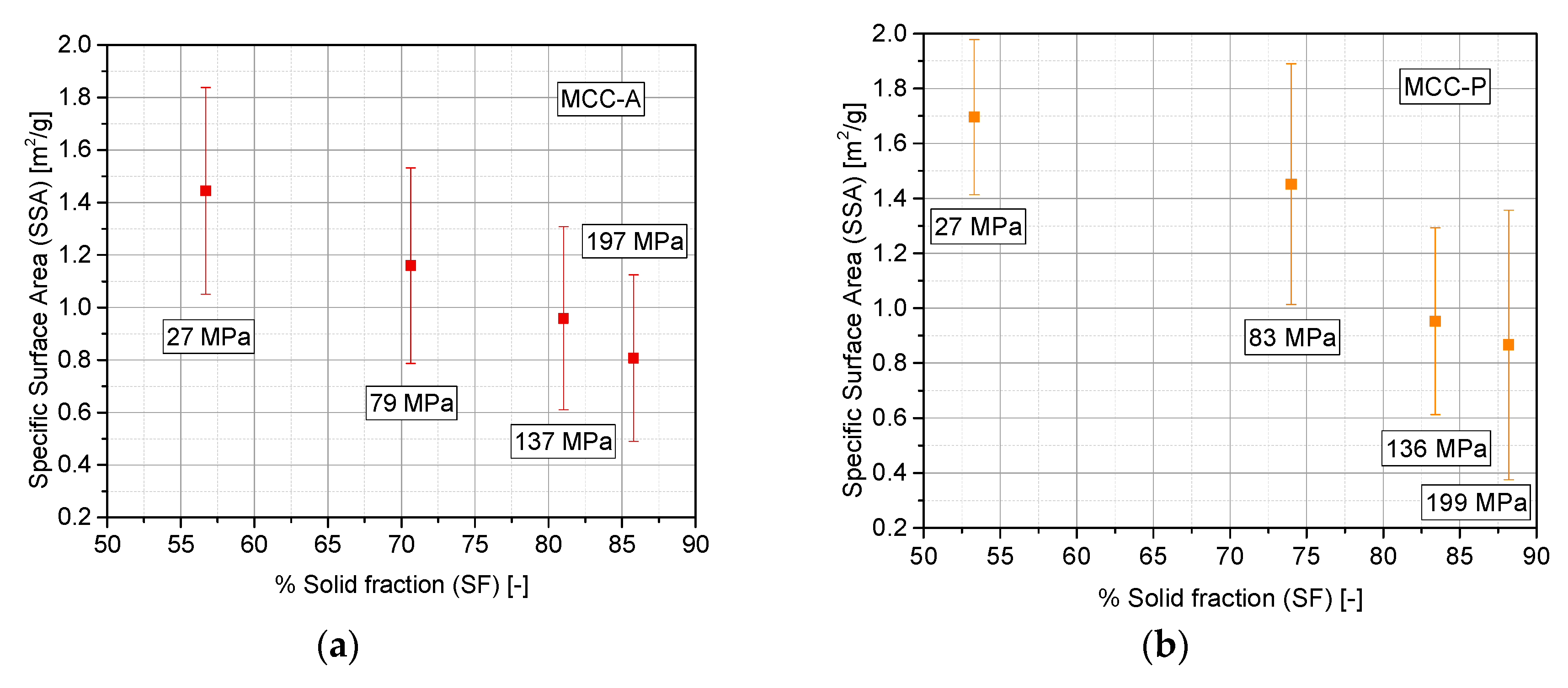
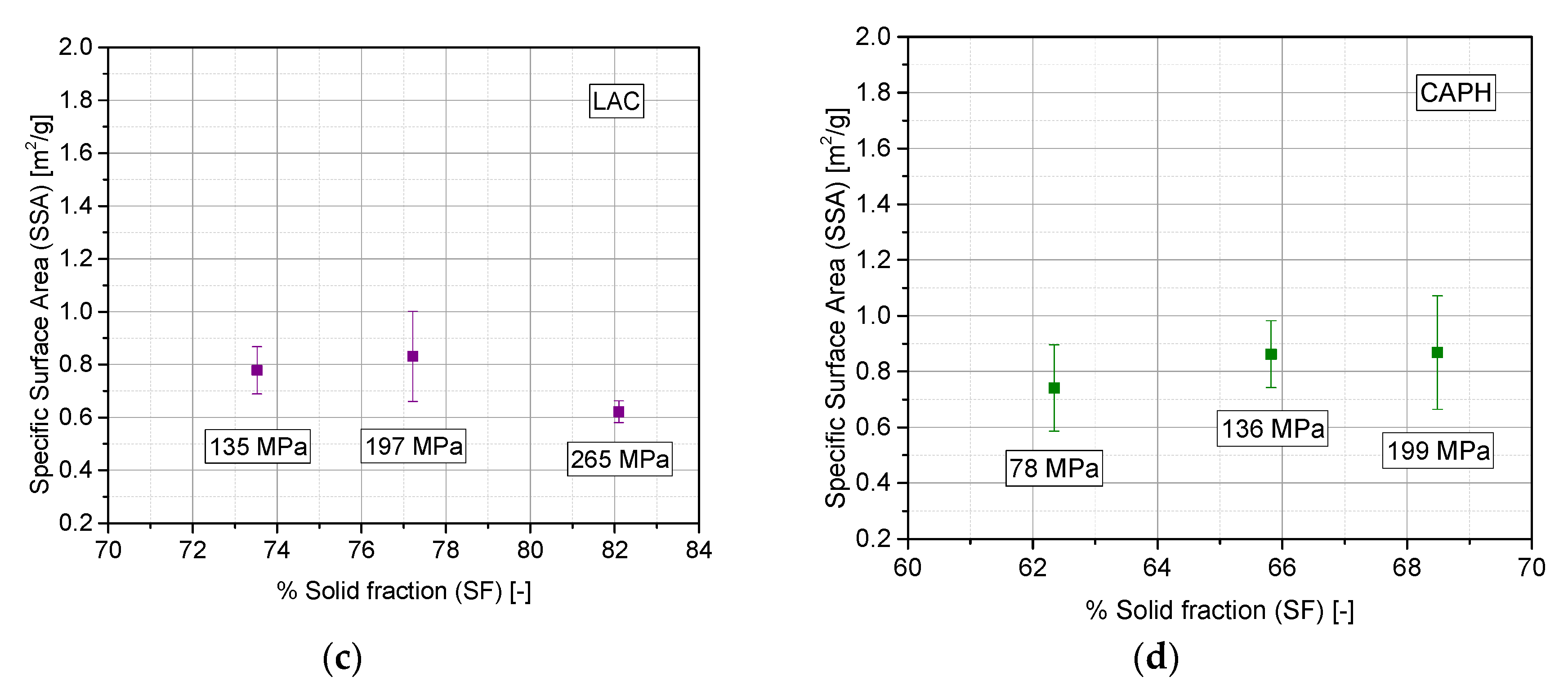
3.1. Powder Characterization
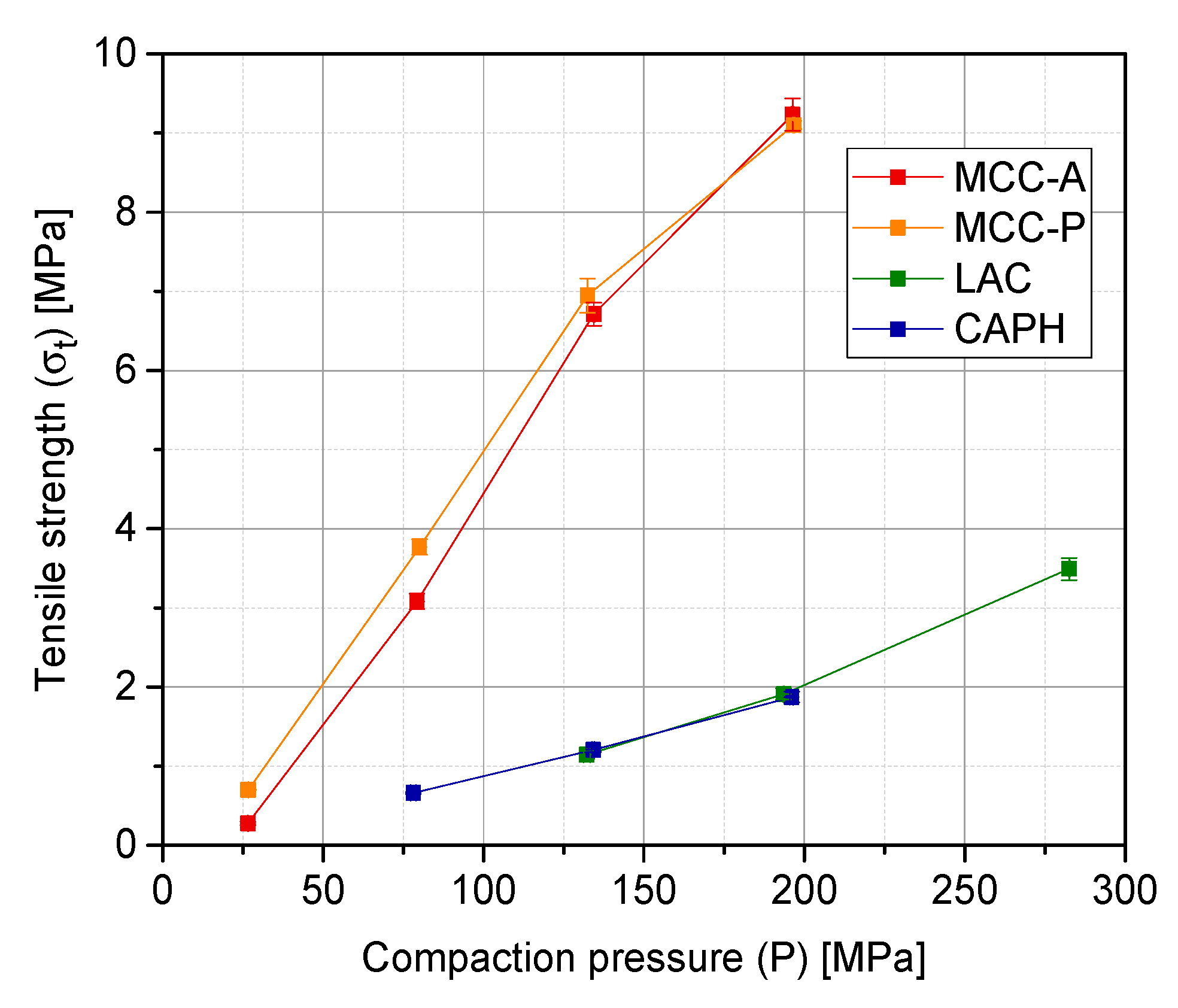
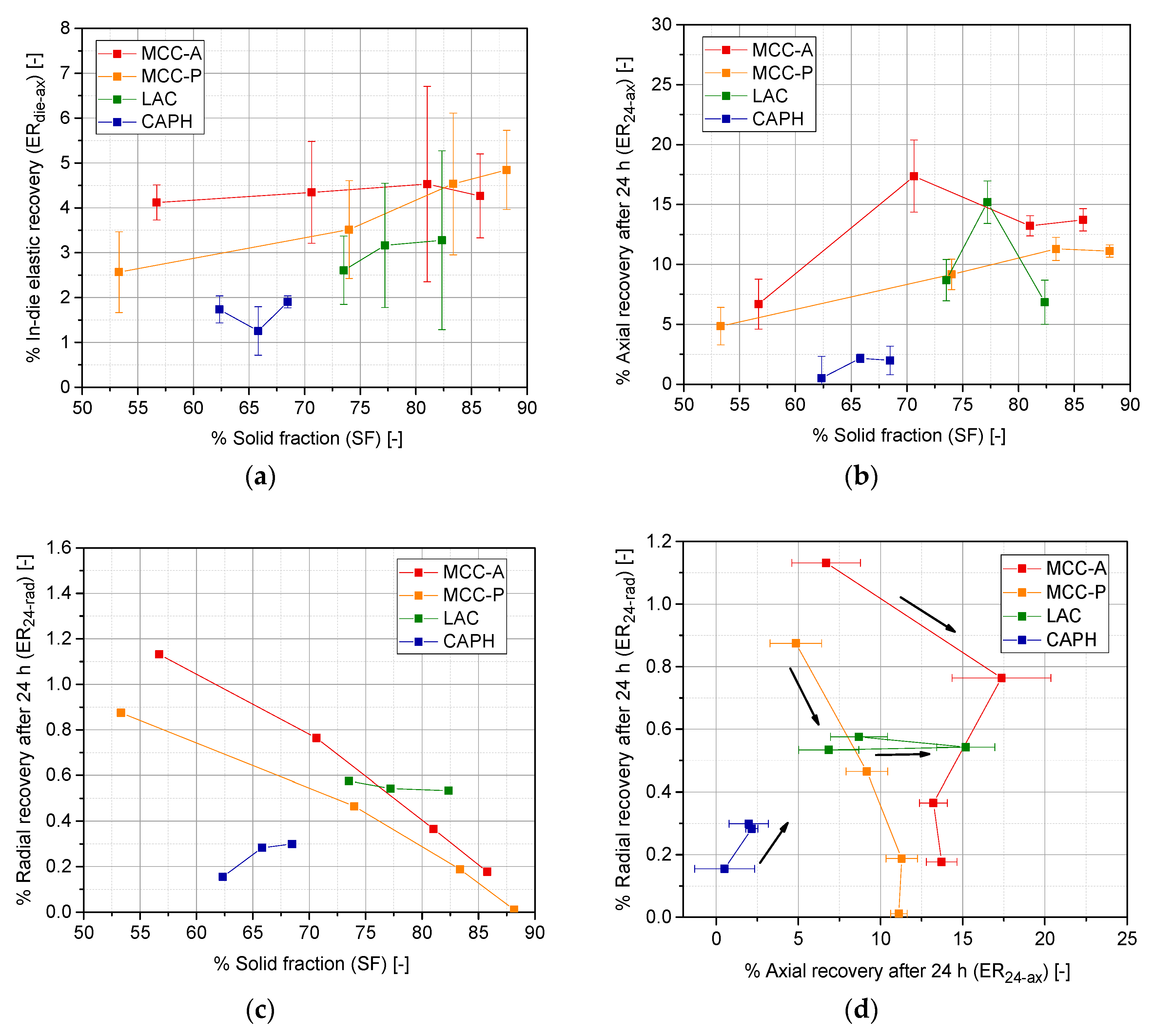
3.2. Tablet Quality Parameters: Tensile Strength, In-Die Elastic Recovery and 24 h Elastic Recovery
3.3. Evaluation of Densification Mechanism
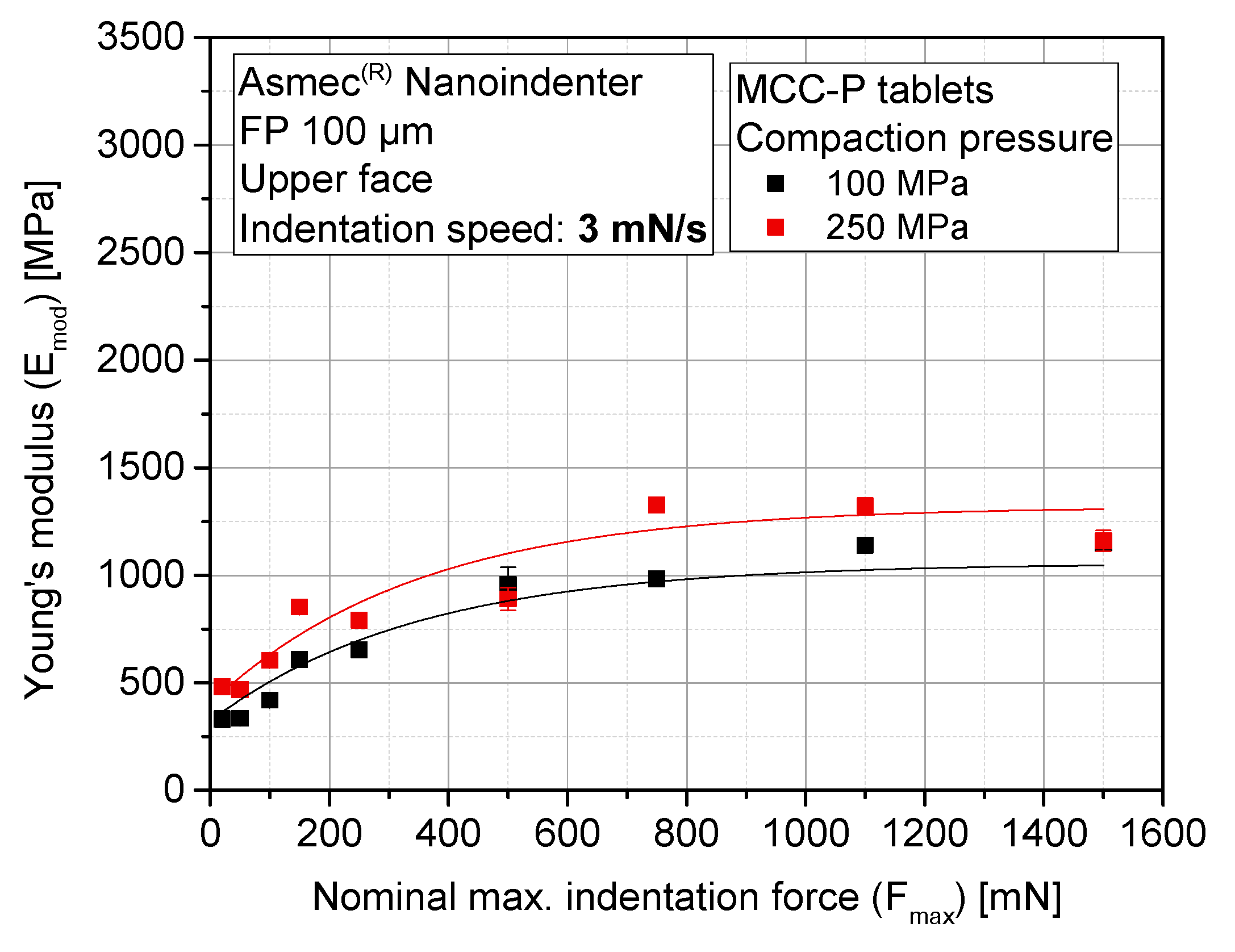
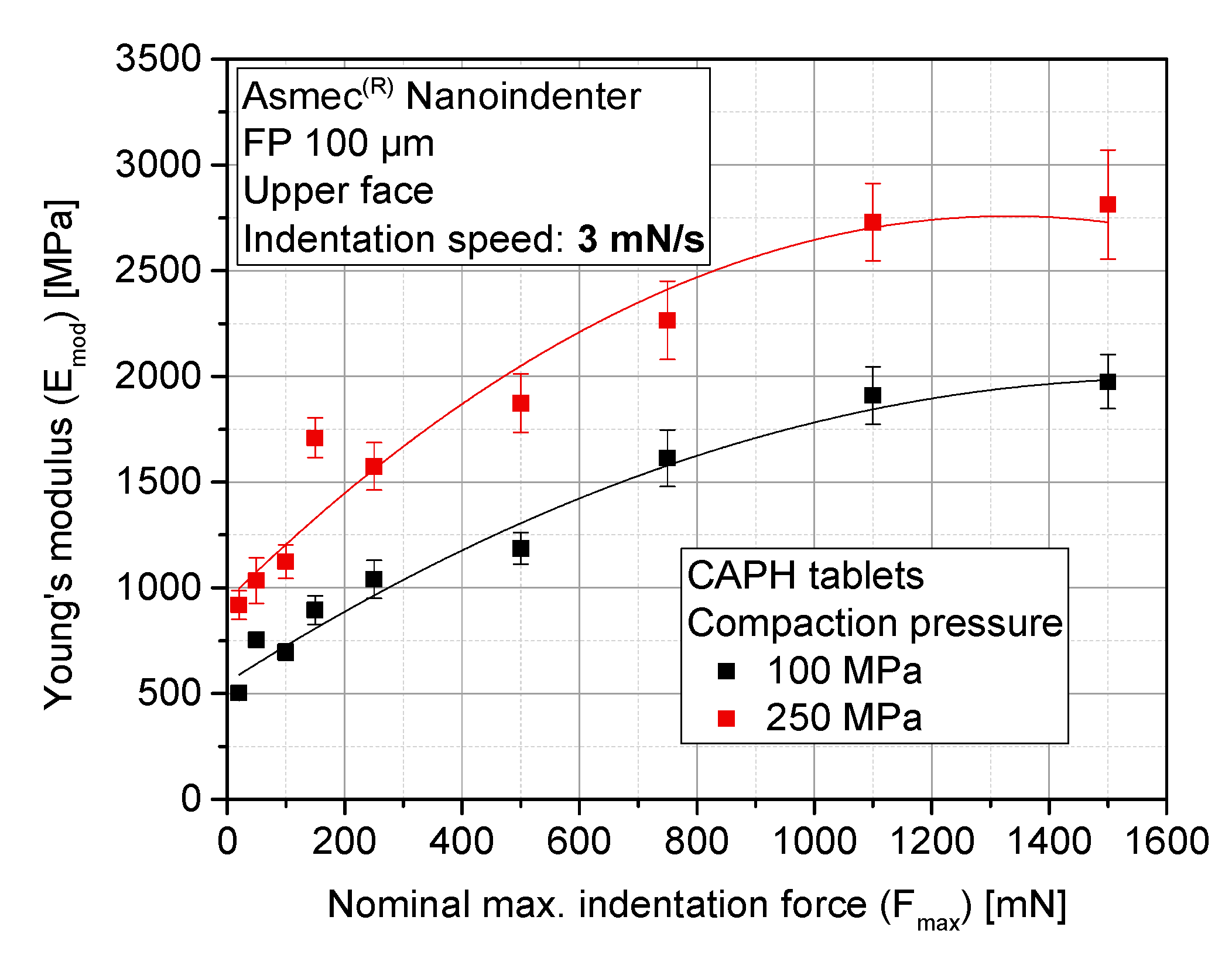
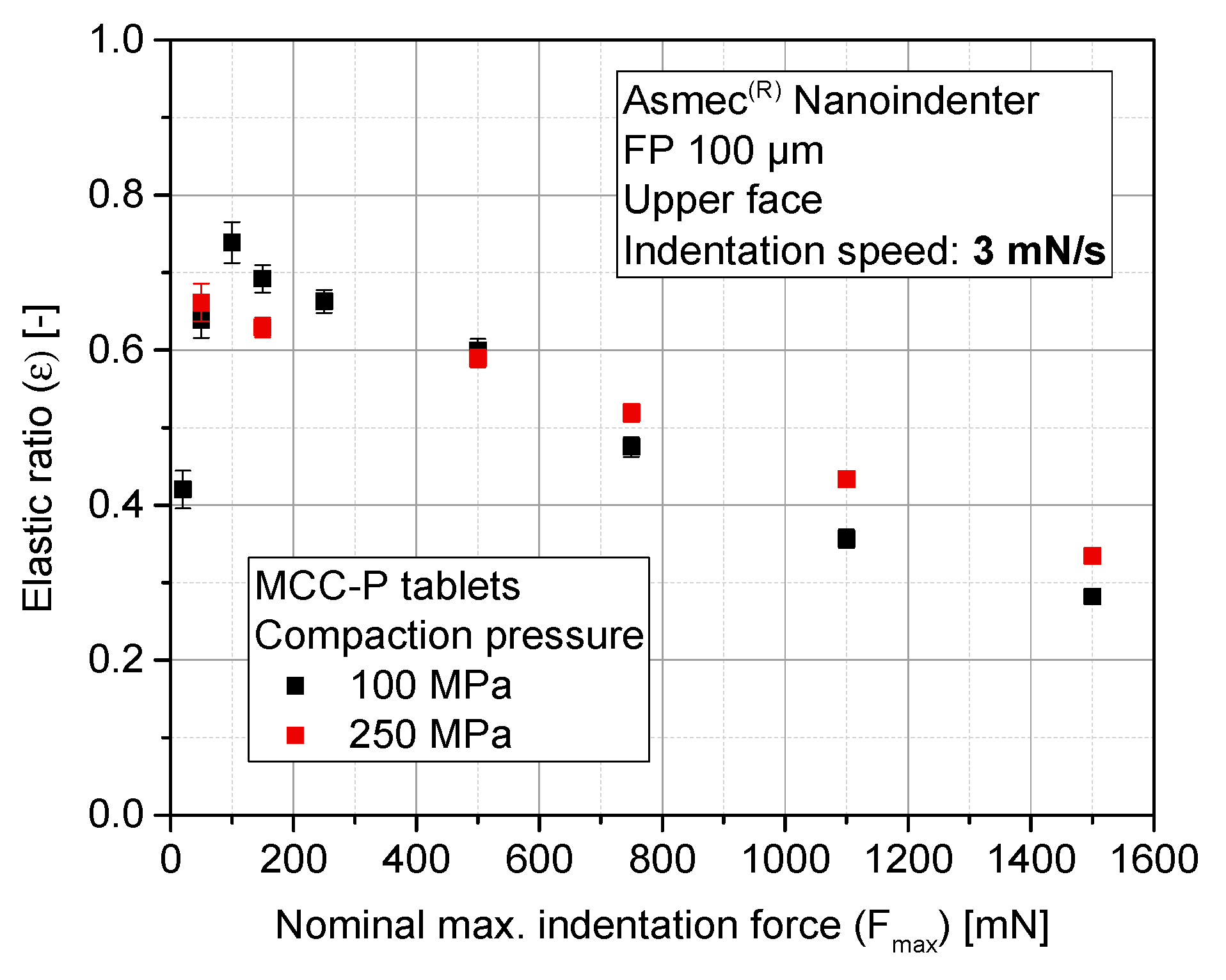
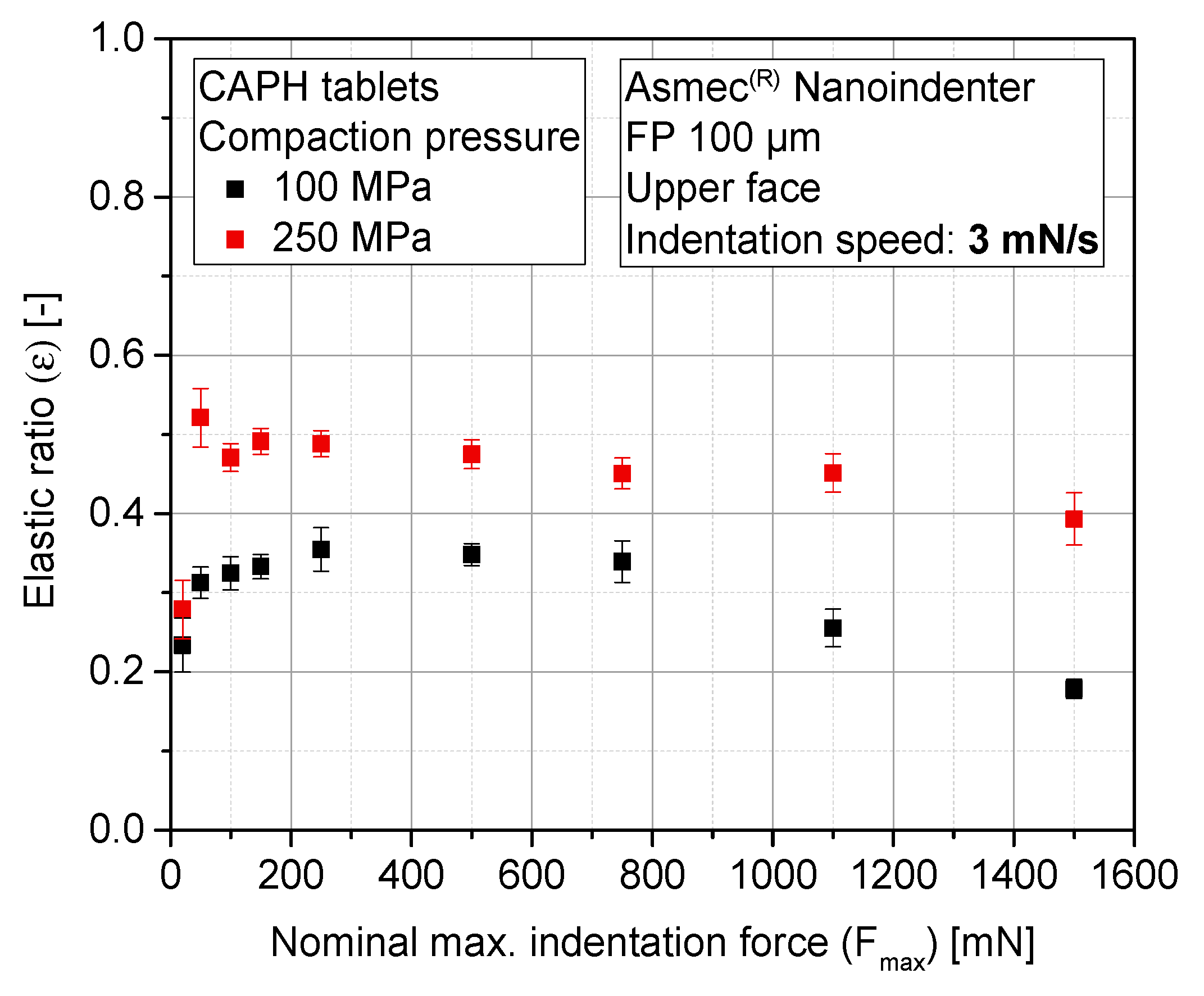
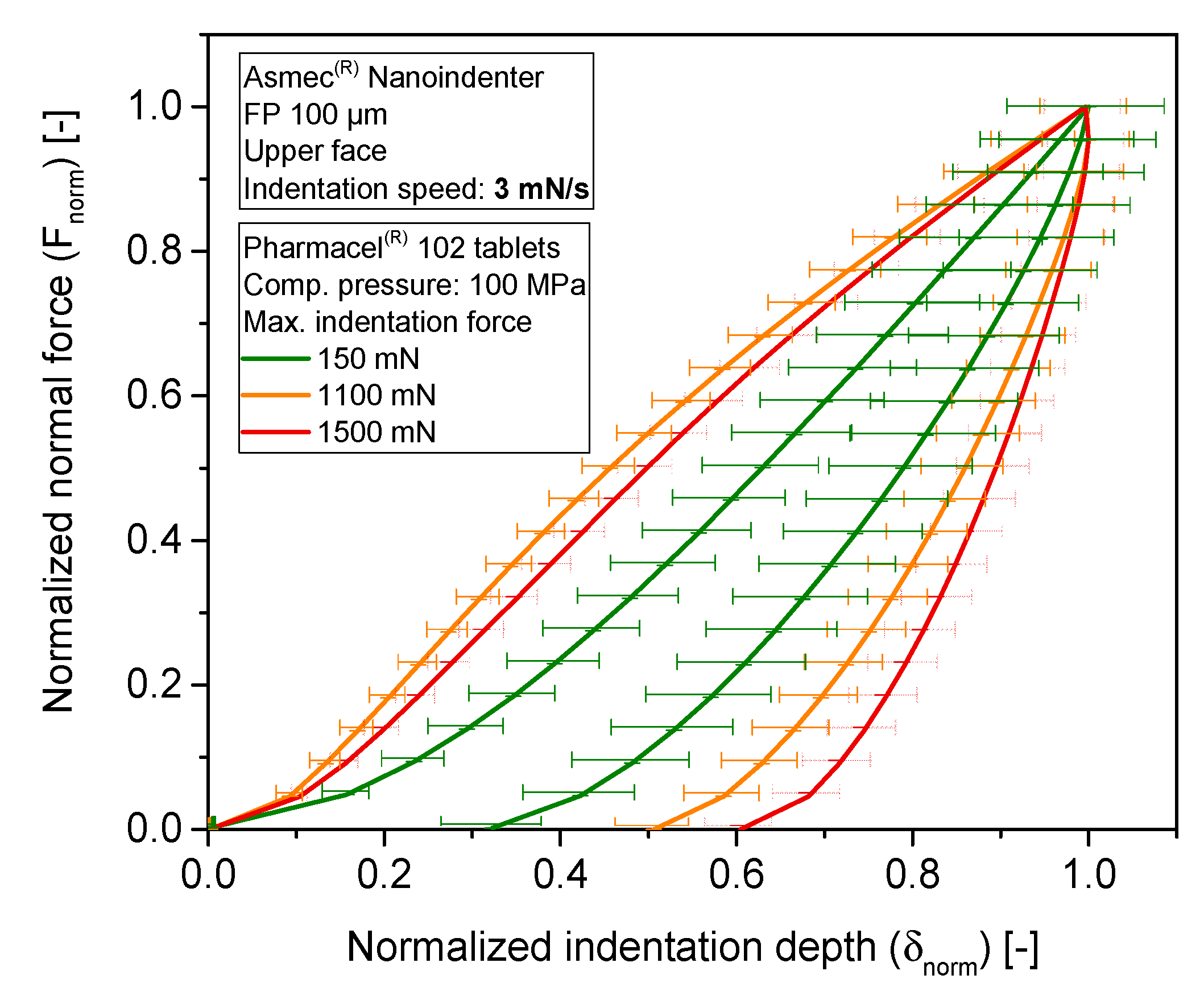
3.4. Sensitivity Analysis of Maximum Indentation Force and Structural Inhomogeneity
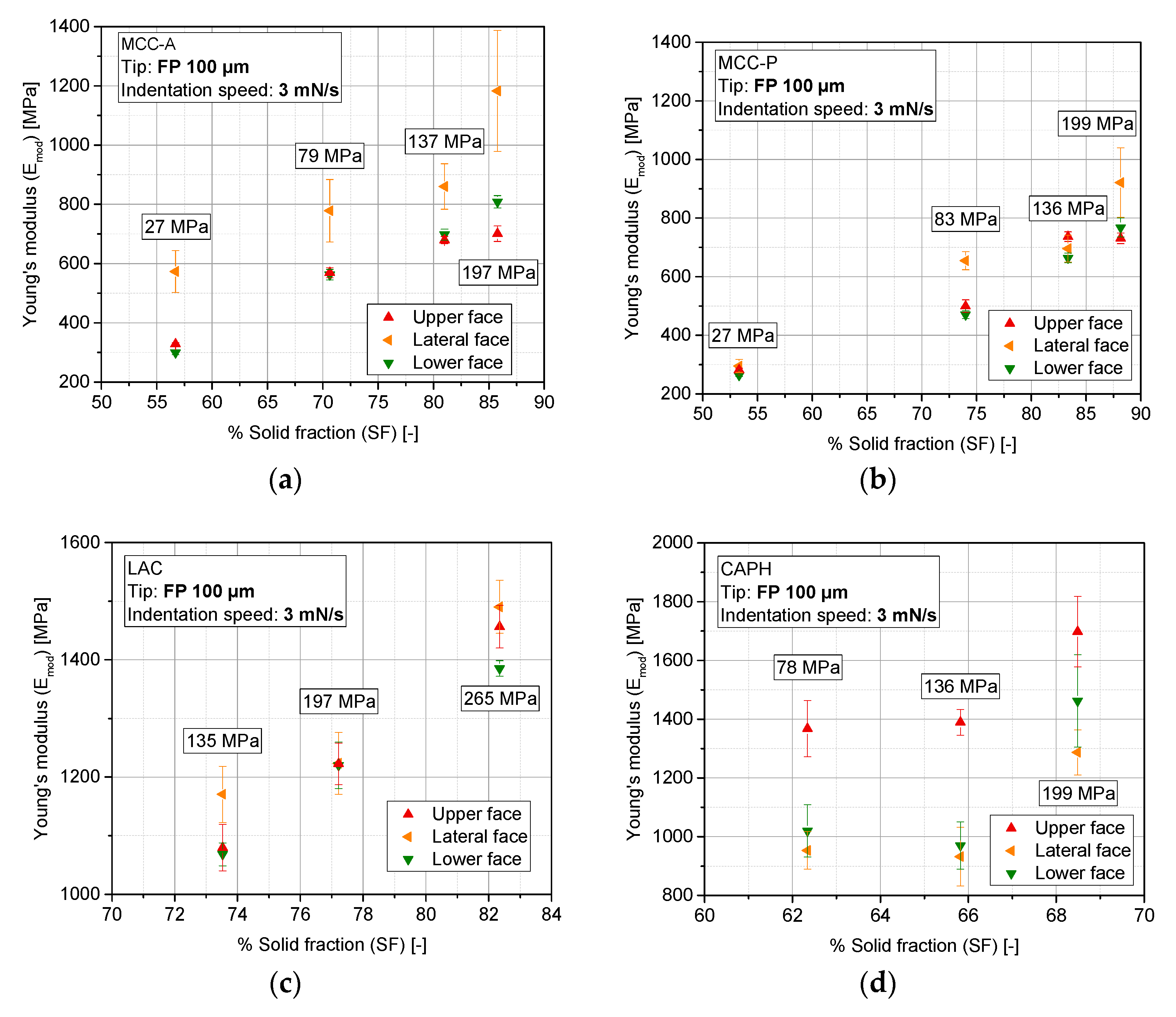
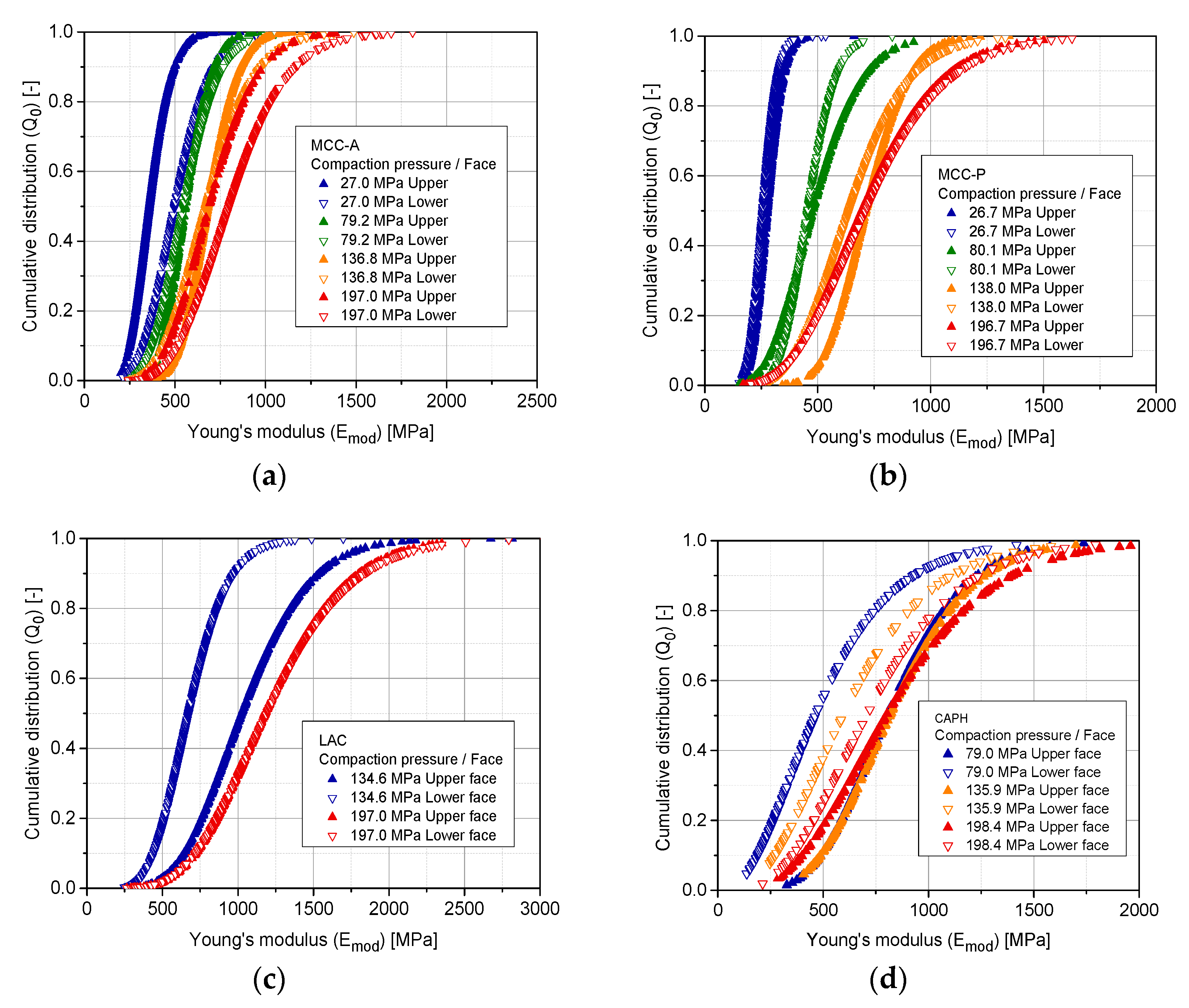
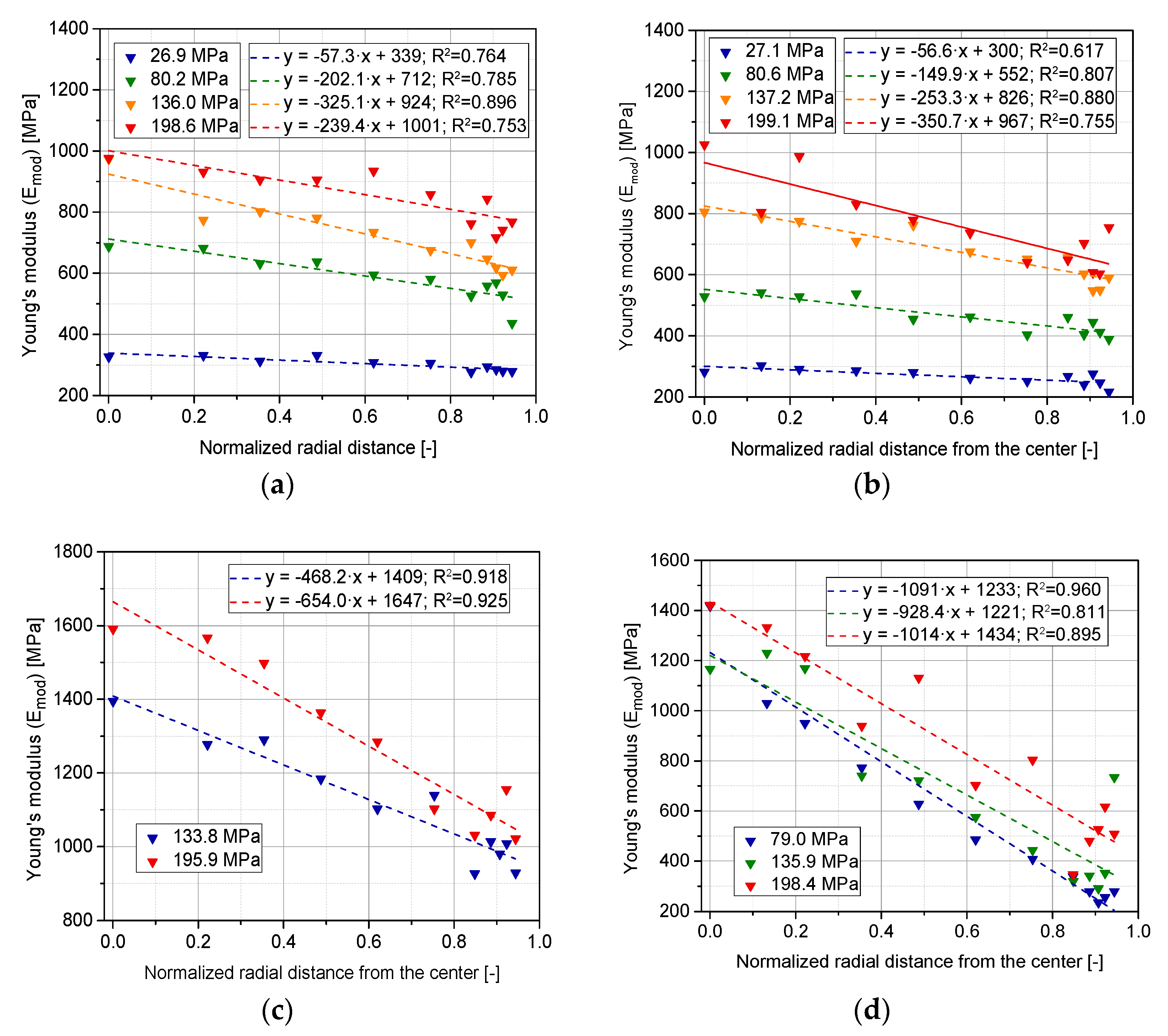
3.5. Evolution of Stiffness with Compaction Pressure at Different Locations of the Tablet (Upper, Lower, and Lateral Faces)
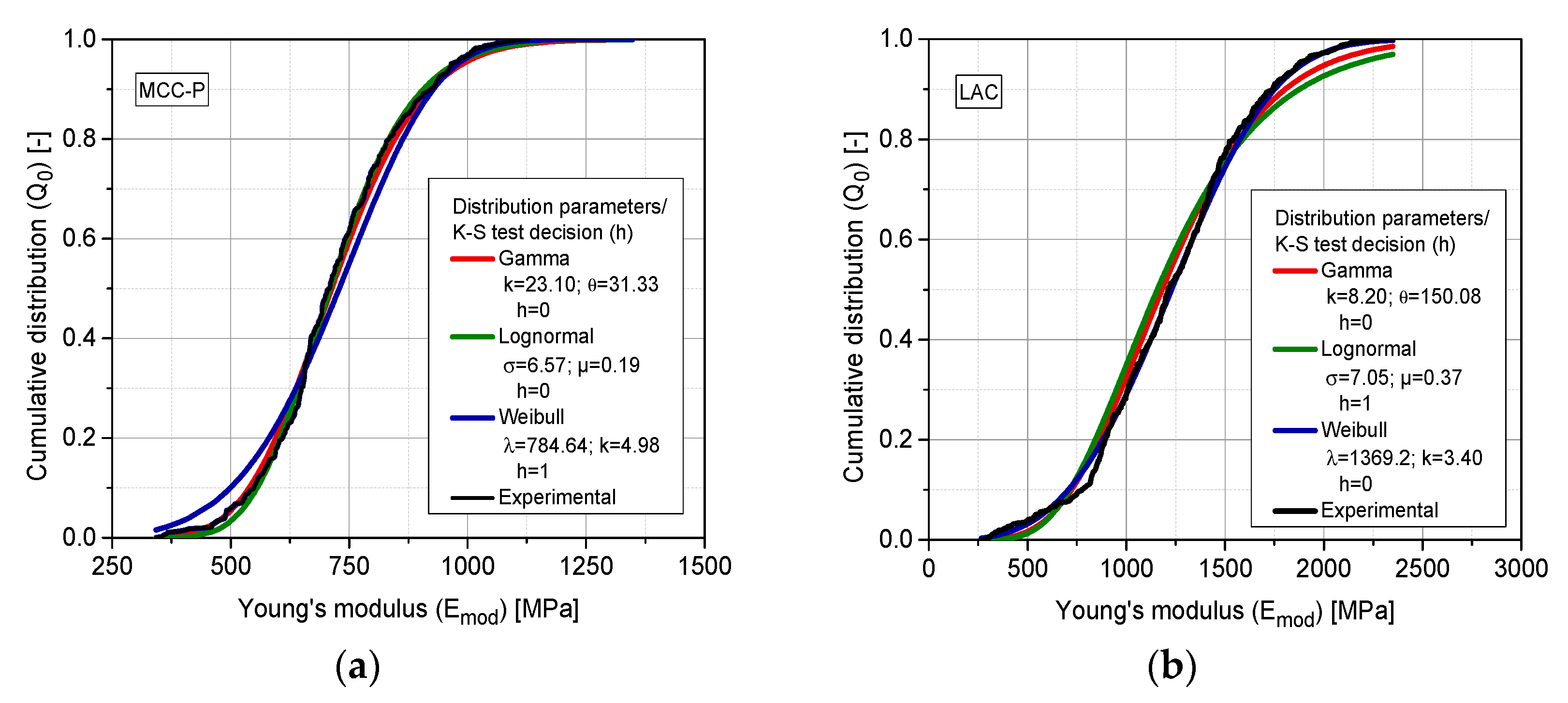
3.6. Cumulative Property Analysis
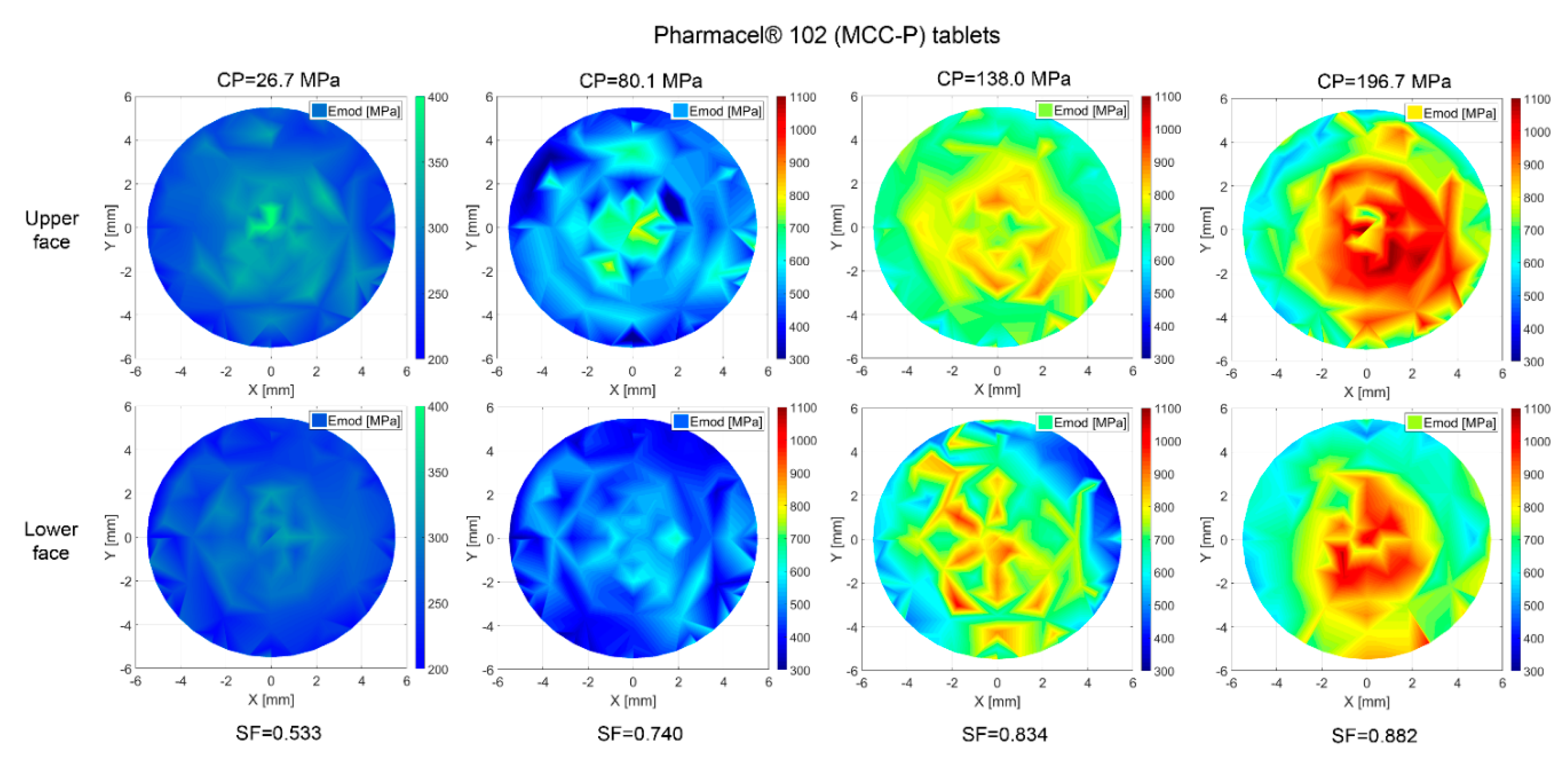
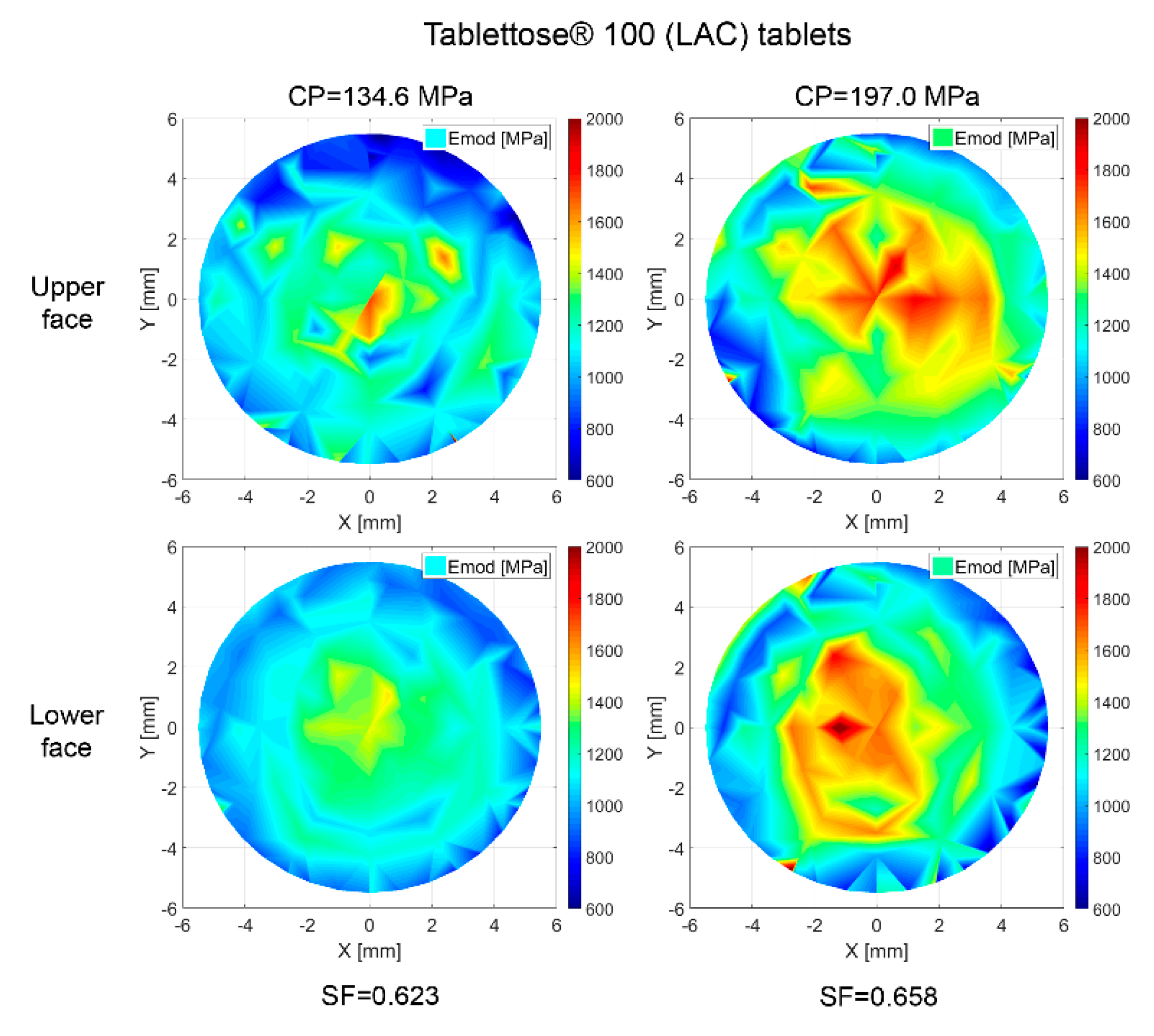
3.7. Property Distribution over Tablet Faces
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akseli, I.; Mani, G.N.; Cetinkaya, C. Non-destructive acoustic defect detection in drug tablets. Int. J. Pharm. 2008, 360, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Sinka, I.; Burch, S.; Tweed, J.; Cunningham, J. Measurement of density variations in tablets using X-ray computed tomography. Int. J. Pharm. 2004, 271, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Markl, D.; Bawuah, P.; Ridgway, C.; van den Ban, S.; Goodwin, D.J.; Ketolainen, J.; Gane, P.; Peiponen, K.E.; Zeitler, J.A. Fast and non-destructive pore structure analysis using terahertz time-domain spectroscopy. Int. J. Pharm. 2018, 537, 102–110. [Google Scholar] [CrossRef] [PubMed]
- Mullarney, M.P.; Hancock, B.C. Mechanical property anisotropy of pharmaceutical excipient compacts. Int. J. Pharm. 2006, 314, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Narayan, P.; Hancock, B.C. The relationship between the particle properties, mechanical behavior, and surface roughness of some pharmaceutical excipient compacts. Mater. Sci. Eng. A 2003, 355, 24–36. [Google Scholar] [CrossRef]
- Nyström, C.; Alex, W.; Malmqvist, K. A new approach to tensile strength measurement of tablets. Acta Pharm. Suec. 1977, 14, 317. [Google Scholar] [PubMed]
- Yap, S.F.; Adams, M.J.; Seville, J.P.; Zhang, Z. Single and bulk compression of pharmaceutical excipients: Evaluation of mechanical properties. Powder Technol. 2008, 185, 1–10. [Google Scholar] [CrossRef]
- Nyström, C.; Malmqvist, K.; Mazur, J.; Alex, W.; Hölzer, A. Measurement of axial and radial tensile strength of tablets and their relation to capping. Acta Pharm. Suec. 1978, 15, 226–232. [Google Scholar] [PubMed]
- Galen, S.; Zavaliangos, A. Strength anisotropy in cold compacted ductile and brittle powders. Acta Mater. 2005, 53, 4801–4815. [Google Scholar] [CrossRef]
- Ittershagen, T.; Kwade, A. Measurement of anisotropic consolidation behavior. Part. Sci. Technol. 2011, 29, 79–88. [Google Scholar] [CrossRef]
- Lannutti, J.J. Characterization and control of compact microstructure. MRS Bull. 1997, 22, 38–44. [Google Scholar] [CrossRef]
- Lee, J. Drug nano-and microparticles processed into solid dosage forms: Physical properties. J. Pharm. Sci. 2003, 92, 2057–2068. [Google Scholar] [CrossRef] [PubMed]
- Çelik, M.; Aulton, M.E. The Viscoelastic Deformation of Some Tableting Materials as Assessed by Indentation Rheology. Drug Dev. Ind. Pharm. 1996, 22, 67–75. [Google Scholar] [CrossRef]
- Jamrógiewicz, M. Application of the near-infrared spectroscopy in the pharmaceutical technology. J. Pharm. Biomed. Anal. 2012, 66, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Liew, C.V.; Karande, A.D.; Heng, P.W.S. In-line quantification of drug and excipients in cohesive powder blends by near infrared spectroscopy. Int. J. Pharm. 2010, 386, 138–148. [Google Scholar] [CrossRef] [PubMed]
- Akseli, I.; Cetinkaya, C. Air-coupled non-contact mechanical property determination of drug tablets. Int. J. Pharm. 2008, 359, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Van Landingham, M.R. Review of instrumented indentation. J. Res. Natl. Inst. Stand. Technol. 2003, 108, 249. [Google Scholar] [CrossRef] [PubMed]
- Ridgway, K.; Aulton, M.; Rosser, P. The surface hardness of tablets. J. Pharm. Pharmacol. 1970, 22, 70S–78S. [Google Scholar] [CrossRef]
- Wenzel, U.; Podczeck, F. Measurement of hardness of tablets. Acta Pharm. Technol.-Int. J. Drug Forumlation Biopharm. 1988, 34, 208–212. [Google Scholar]
- Leuenberger, H. The compressibility and compactibility of powder systems. Int. J. Pharm. 1982, 12, 41–55. [Google Scholar] [CrossRef]
- Jetzer, W.; Leuenberger, H.; Sucker, H. The compressibility and compactibility of pharmaceutical powders. Pharm. Technol. 1983, 7, 36–39. [Google Scholar]
- Riccardi, B.; Montanari, R. Indentation of metals by a flat-ended cylindrical punch. Mater. Sci. Eng. A 2004, 381, 281–291. [Google Scholar] [CrossRef]
- Murthy, T.G.; Saldana, C.; Hudspeth, M.; M’Saoubi, R. Deformation field heterogeneity in punch indentation. Proc. R. Soc. A 2014, 470, 20130807. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Blanchard, J.P. An elastic-plastic indentation model and its solutions. J. Mater. Res. 1996, 11, 2358–2367. [Google Scholar] [CrossRef]
- Fell, J.T.; Newton, J.M. Determination of tablet strength by the diametral-compression test. J. Pharma. Sci. 1970, 59, 688–691. [Google Scholar] [CrossRef]
- Heckel, R. Density-pressure relationships in powder compaction. Trans. Metall. Soc. AIME 1961, 221, 671–675. [Google Scholar]
- Katz, J.M.; Buckner, I.S. Characterization of strain rate sensitivity in pharmaceutical materials using indentation creep analysis. Int. J. Pharm. 2013, 442, 13–19. [Google Scholar] [CrossRef] [PubMed]
- York, P. A consideration of experimental variables in the analysis of powder compaction behaviour. J. Pharm. Pharmacol. 1979, 31, 244–246. [Google Scholar] [CrossRef] [PubMed]
- Çelik, M.; Marshall, K. Use of a compaction simulator system in tabletting research. Drug Dev. Ind. Pharm. 1989, 15, 759–800. [Google Scholar] [CrossRef]
- Führer, C.; Karehill, P.-G.; Ragnarsson, G.; Müller, F.; Leuenberger, H.; Leu, R.; Bonny, J.-D.; Davies, P.N.; Newton, J.M.; Armstrong, N.A. Pharmaceutical Powder Compaction Technology; Marcel Dekker: New York, NY, USA, 1996. [Google Scholar]
- Engqvist, H.; Wiklund, U. Mapping of mechanical properties of WC–Co using nanoindentation. Tribol. Lett. 2000, 8, 147–152. [Google Scholar] [CrossRef]
- Roberts, R.J.; Rowe, R.C.; York, P. The Poisson’s ratio of microcrystalline cellulose. Int. J. Pharm. 1994, 105, 177–180. [Google Scholar] [CrossRef]
- Ning, Z.; Boerefijn, R.; Ghadiri, M.; Thornton, C. Distinct element simulation of impact breakage of lactose agglomerates. Adv. Powder Technol. 1997, 8, 15–37. [Google Scholar] [CrossRef]
- Nichols, G.; Byard, S.; Bloxham, M.J.; Botterill, J.; Dawson, N.J.; Dennis, A.; Diart, V.; North, N.C.; Sherwood, J.D. A review of the terms agglomerate and aggregate with a recommendation for nomenclature used in powder and particle characterization. J. Pharm. Sci. 2002, 91, 2103–2109. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wen, H.; Desai, D. Lubrication in tablet formulations. Eur. J. Pharm. Biopharma. 2010, 75, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Bonacucina, G.; Cespi, M.; Misici-Falzi, M.; Palmieri, G.F. Mechanical characterization of pharmaceutical solids: A comparison between rheological tests performed under static and dynamic porosity conditions. Eur. J. Pharm. Biopharm. 2007, 67, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Picker, K.M. Time dependence of elastic recovery for characterization of tableting materials. Pharm. Dev. Technol. 2001, 6, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Harthong, B.; Jérier, J.F.; Dorémus, P.; Imbault, D.; Donzé, F.V. Modeling of high-density compaction of granular materials by the Discrete Element Method. Int. J. Solids Struct. 2009, 46, 3357–3364. [Google Scholar] [CrossRef]
- Cahyadi, C.; Tan, B.X.; Chan, L.W.; Heng, P.W.S. A Study on In-Line Tablet Coating—The Influence of Compaction and Coating on Tablet Dimensional Changes. AAPS PharmSciTech 2012, 13, 785–792. [Google Scholar] [CrossRef] [PubMed]
- Cabiscol, R.; Finke, J.H.; Kwade, A. Calibration and interpretation of DEM parameters for simulations of cylindrical tablets with multi-sphere approach. Powder Technol. 2018, 327, 232–245. [Google Scholar] [CrossRef]
- Hardman, J.; Lilley, B. Mechanisms of compaction of powdered materials. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1973, 333, 183–199. [Google Scholar] [CrossRef]
- Masteau, J.-C.; Thomas, G. Modelling to understand porosity and specific surface area changes during tabletting. Powder Technol. 1999, 101, 240–248. [Google Scholar] [CrossRef]
- Busignies, V.; Leclerc, B.; Truchon, S.; Tchoreloff, P. Changes in the specific surface area of tablets composed of pharmaceutical materials with various deformation behaviors. Drug Dev. Ind. Pharm. 2011, 37, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Freitag, F.; Runge, J.; Kleinebudde, P. Coprocessing of Powdered Cellulose and Magnesium Carbonate: Direct Tableting Versus Tableting After Roll Compaction/Dry Granulation. Pharm. Dev. Technol. 2005, 10, 353–362. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, N.A.; Haines-Nutt, R.F. Elastic recovery and surface area changes in compacted powder systems. Powder Technol. 1974, 9, 287–290. [Google Scholar] [CrossRef]
- Lee, J. Structural heterogeneity of pharmaceutical compacts probed by micro-indentation. J. Mater. Sci. Mater. Med. 2008, 19, 1981–1990. [Google Scholar] [CrossRef] [PubMed]
- Ellison, C.D.; Ennis, B.J.; Hamad, M.L.; Lyon, R.C. Measuring the distribution of density and tabletting force in pharmaceutical tablets by chemical imaging. J. Pharm. Biomed. Anal. 2008, 48, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Edge, S.; Steele, D.F.; Chen, A.; Tobyn, M.J.; Staniforth, J.N. The mechanical properties of compacts of microcrystalline cellulose and silicified microcrystalline cellulose. Int. J. Pharm. 2000, 200, 67–72. [Google Scholar] [CrossRef]
- Procopio, A.T.; Zavaliangos, A. Simulation of multi-axial compaction of granular media from loose to high relative densities. J. Mech. Phys. Solids 2005, 53, 1523–1551. [Google Scholar] [CrossRef]
- Strege, S.; Weuster, A.; Zetzener, H.; Brendel, L.; Kwade, A.; Wolf, D. Approach to structural anisotropy in compacted cohesive powder. Granul. Matter 2014, 16, 401–409. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Sulla determinazione empirica di una legge di distribuzione. Inst. Ital. Attuari Giorn. 1933, 4, 83–91. [Google Scholar]
- Smirnov, N.V.E. Sur la Distribution de W2. CR Acad. Sci. Paris 1936, 202, 449. [Google Scholar]
- MATLABTM, Documentation Delaunay Triangulation. Available online: https://de.mathworks.com/help/matlab/ref/delaunay.html (accessed on 3 January 2018).
- May, R.K.; Su, K.; Han, L.; Zhong, S.; Elliott, J.A.; Gladden, L.F.; Evans, M.; Shen, Y.; Zeitler, J.A. Hardness and Density Distributions of Pharmaceutical Tablets Measured by Terahertz Pulsed Imaging. J. Pharm. Sci. 2013, 102, 2179–2186. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Elliott, J.; Bentham, A.; Mills, A.; Amidon, G.; Hancock, B. A modified Drucker-Prager Cap model for die compaction simulation of pharmaceutical powders. Int. J. Solids Struct. 2008, 45, 3088–3106. [Google Scholar] [CrossRef]
- Eiliazadeh, B.; Pitt, K.; Briscoe, B. Effects of punch geometry on powder movement during pharmaceutical tabletting processes. Int. J. Solids Struct. 2004, 41, 5967–5977. [Google Scholar] [CrossRef]
- Zavaliangos, A. A Numerical Study of the Development of Tensile Principal Stresses During Die Compaction. Part. Sci. Technol. 2003, 21, 105–115. [Google Scholar] [CrossRef]
- Olsson, H.; Nyström, C. Assessing tablet bond types from structural features that affect tablet tensile strength. Pharm. Res. 2001, 18, 203–210. [Google Scholar] [CrossRef] [PubMed]


| Material | x10 (Q3) (µm) | x50 (Q3) (µm) | x90 (Q3) (µm) | Span (-) | Measuring Technique | True Density (kg·m−3) | Measuring Technique |
|---|---|---|---|---|---|---|---|
| MCC-A | 82.9 | 224.6 | 379.3 | 1.32 | Dynamic particle image analysis | 1541.1 | Helium pycnometry |
| MCC-P | 28.3 | 86.5 | 173.8 | 1.68 | 1533.7 | ||
| CAPH | 131.6 | 210.5 | 298.4 | 0.79 | 1763.3 | ||
| LAC | 34.3 | 107.8 | 302.0 | 2.48 | Laser diffraction | 2766.0 |
| Material | Compaction Pressure (MPa) | Face | Gamma Factor (-) | Gamma Factor (-) |
|---|---|---|---|---|
| MCC-A | 27.0 | Upper | 11.20 | 29.29 |
| Lower | 13.10 | 42.95 | ||
| 79.2 | Upper | 24.15 | 23.41 | |
| Lower | 24.15 | 23.41 | ||
| 136.8 | Upper | 27.27 | 25.36 | |
| Lower | 10.77 | 64.40 | ||
| 197.0 | Upper | 11.40 | 62.24 | |
| Lower | 10.32 | 79.97 | ||
| MCC-P | 26.7 | Upper | 24.75 | 11.34 |
| Lower | 25.98 | 10.02 | ||
| 80.1 | Upper | 8.43 | 59.07 | |
| Lower | 22.17 | 20.86 | ||
| 138.0 | Upper | 23.10 | 31.33 | |
| Lower | 9.78 | 67.52 | ||
| 196.7 | Upper | 6.90 | 105.84 | |
| Lower | 6.90 | 108.56 | ||
| LAC | 134.6 | Upper | 8.98 | 118.56 |
| Lower | 10.77 | 64.40 | ||
| 197.0 | Upper | 8.20 | 150.08 | |
| Lower | 7.81 | 159.26 | ||
| CAPH | 79.0 | Upper | 8.09 | 103.87 |
| Lower | 2.95 | 176.51 | ||
| 135.9 | Upper | 7.61 | 112.02 | |
| Lower | 3.70 | 176.57 | ||
| 198.4 | Upper | 4.59 | 187.66 | |
| Lower | 4.56 | 167.26 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabiscol, R.; Finke, J.H.; Zetzener, H.; Kwade, A. Characterization of Mechanical Property Distributions on Tablet Surfaces. Pharmaceutics 2018, 10, 184. https://doi.org/10.3390/pharmaceutics10040184
Cabiscol R, Finke JH, Zetzener H, Kwade A. Characterization of Mechanical Property Distributions on Tablet Surfaces. Pharmaceutics. 2018; 10(4):184. https://doi.org/10.3390/pharmaceutics10040184
Chicago/Turabian StyleCabiscol, Ramon, Jan Henrik Finke, Harald Zetzener, and Arno Kwade. 2018. "Characterization of Mechanical Property Distributions on Tablet Surfaces" Pharmaceutics 10, no. 4: 184. https://doi.org/10.3390/pharmaceutics10040184
APA StyleCabiscol, R., Finke, J. H., Zetzener, H., & Kwade, A. (2018). Characterization of Mechanical Property Distributions on Tablet Surfaces. Pharmaceutics, 10(4), 184. https://doi.org/10.3390/pharmaceutics10040184








