Simple Mathematical Models Do Not Accurately Predict Early SIV Dynamics
Abstract
:1. Introduction
2. Results
2.1. Extended Standard Mathematical Model for HIV/SIV Dynamics
2.1.1. Mathematical Model

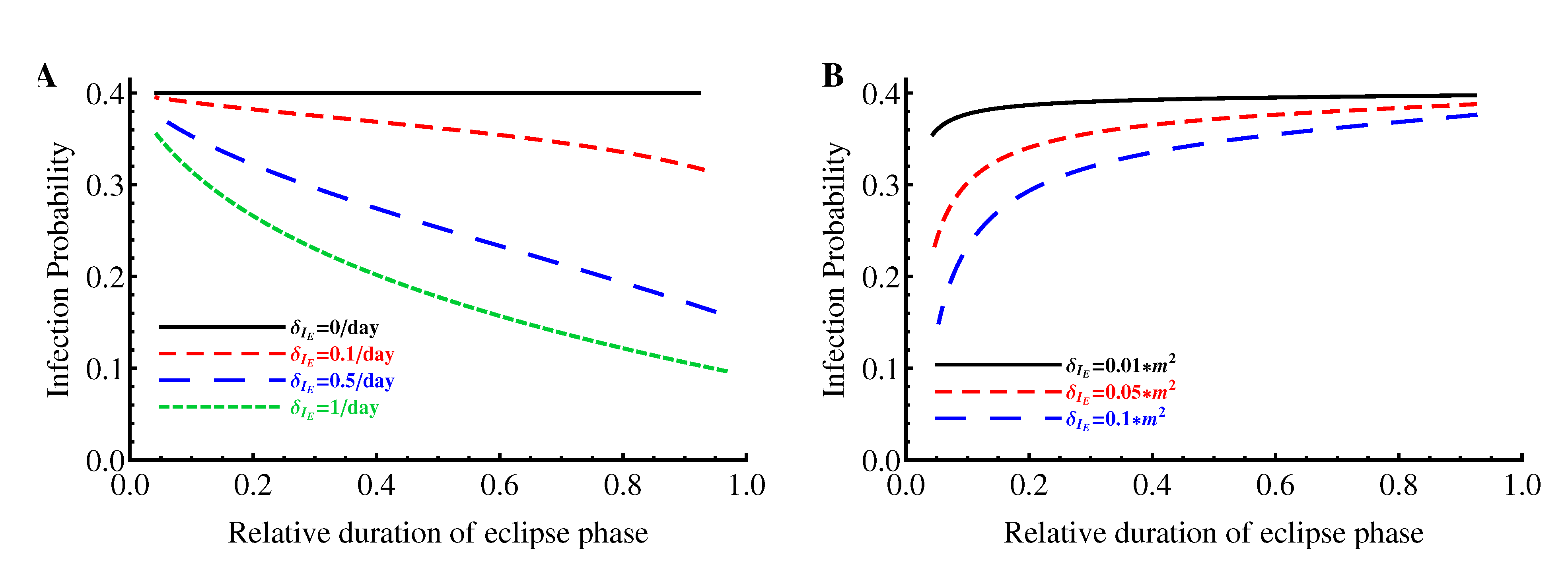
2.1.2. Relative Duration of the Eclipse Phase
2.1.3. Asymptotic Behavior of the Model
2.1.4. Probability of Extinction
2.1.5. Parameter Estimations
| Parameter, Units | Virus Production Mode | Parameter Description | References | |||
|---|---|---|---|---|---|---|
| Continuous | Intermediate | Burst | ||||
| δIE, day−1 | 0.5 | 0.5 | 0.5 | death rate of cells in the eclipse phase | unknown | |
| m, day−1 | 5.0 | 1.5 | 0.7 | eclipse phase transition rate | [54,55] | |
| δI, day−1 | 0.583 | 1.313 | 5.06 | death rate of virus-producing cells | unknown | |
| min(m + δIE, δI) | 0.583 | 1.313 | 1.2 | virus decay rate during HAART | [51,52,53,54,58] | |
| c, day−1 | 20 | 20 | 20 | virion clearance rate | [49,50] | |
| N | 10 | 10 | 10 | infectious virion burst size | unknown | |
| βT, day−1 | 20 | 20 | 20 | rate of infection | unknown | |
| Tm | 0.10 | 0.40 | 0.81 | relative duration of the eclipse phase | unknown | |
| ro, day−1 | 1.443 | 1.445 | 1.433 | observed net viral growth rate | [16,39] | |
2.2. Simulating Virus Dynamics
2.2.1. In Deterministic Simulations, the Mode of Virus Production by Infected Cells Does Not Strongly Impact the Time to Virus Detection
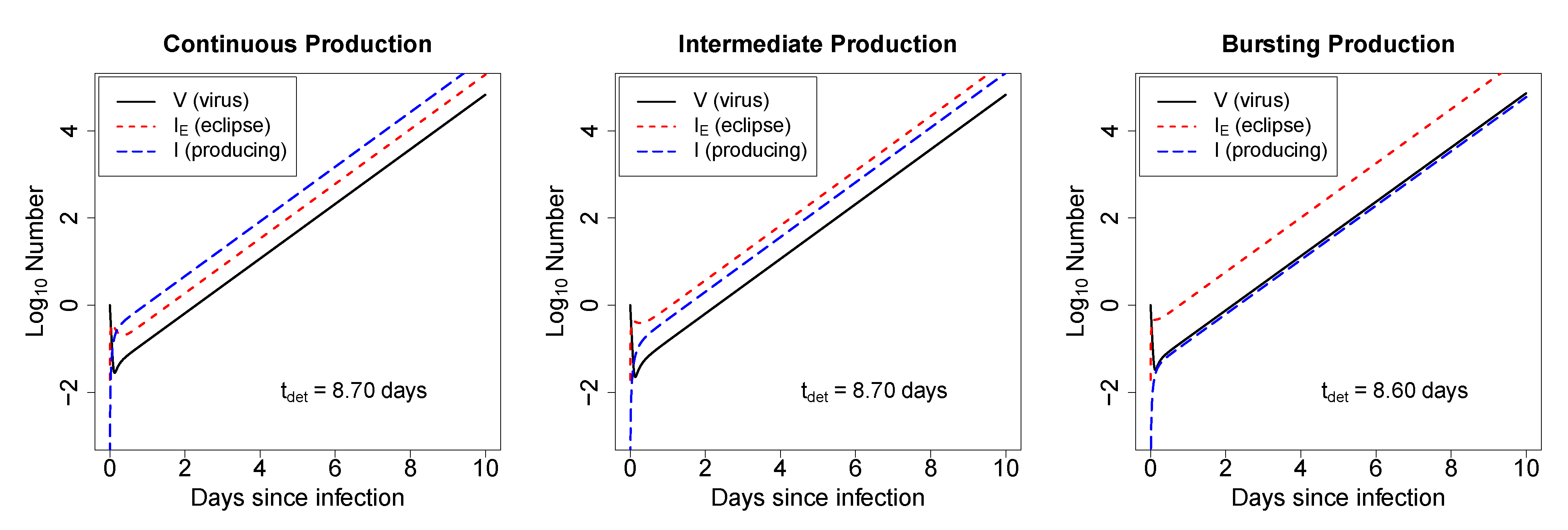
2.2.2. In Stochastic Simulations, the Initial Viral Dose Impacts the Time to Virus Detection but the Mode of Virus Production Does Not
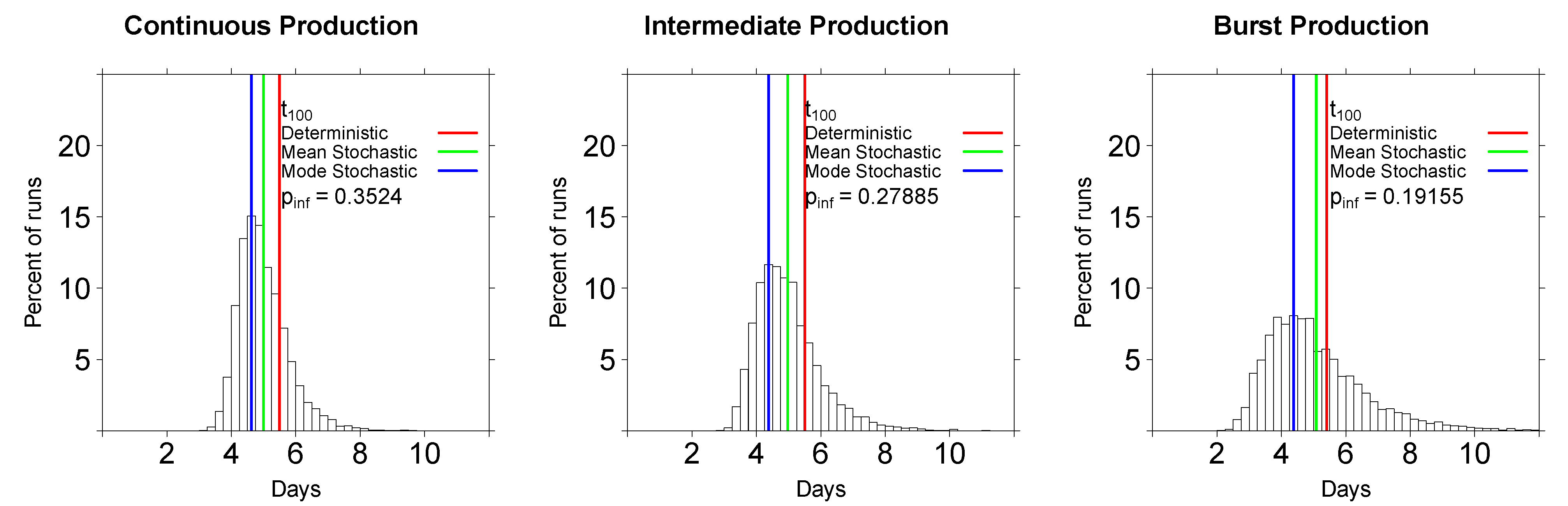
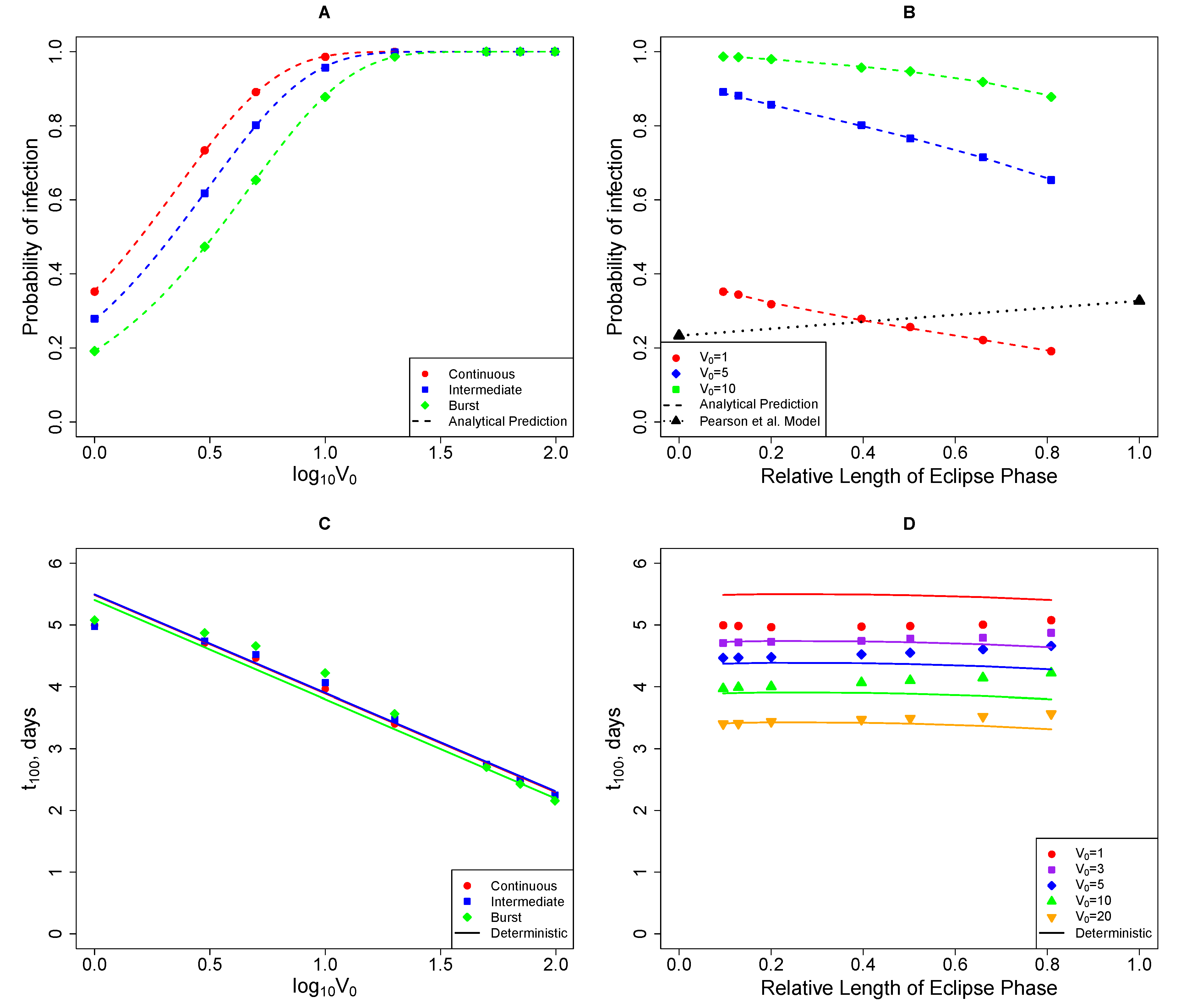
2.3. Comparing Model Predictions with Experimental Data
2.3.1. The Model Does Not Accurately Predict the Change in the Virus Detection Time with Increasing Viral Dose
2.3.2. The Model Does Not Accurately Predict the Change in the Probability of Established Infection with Increasing Viral Dose
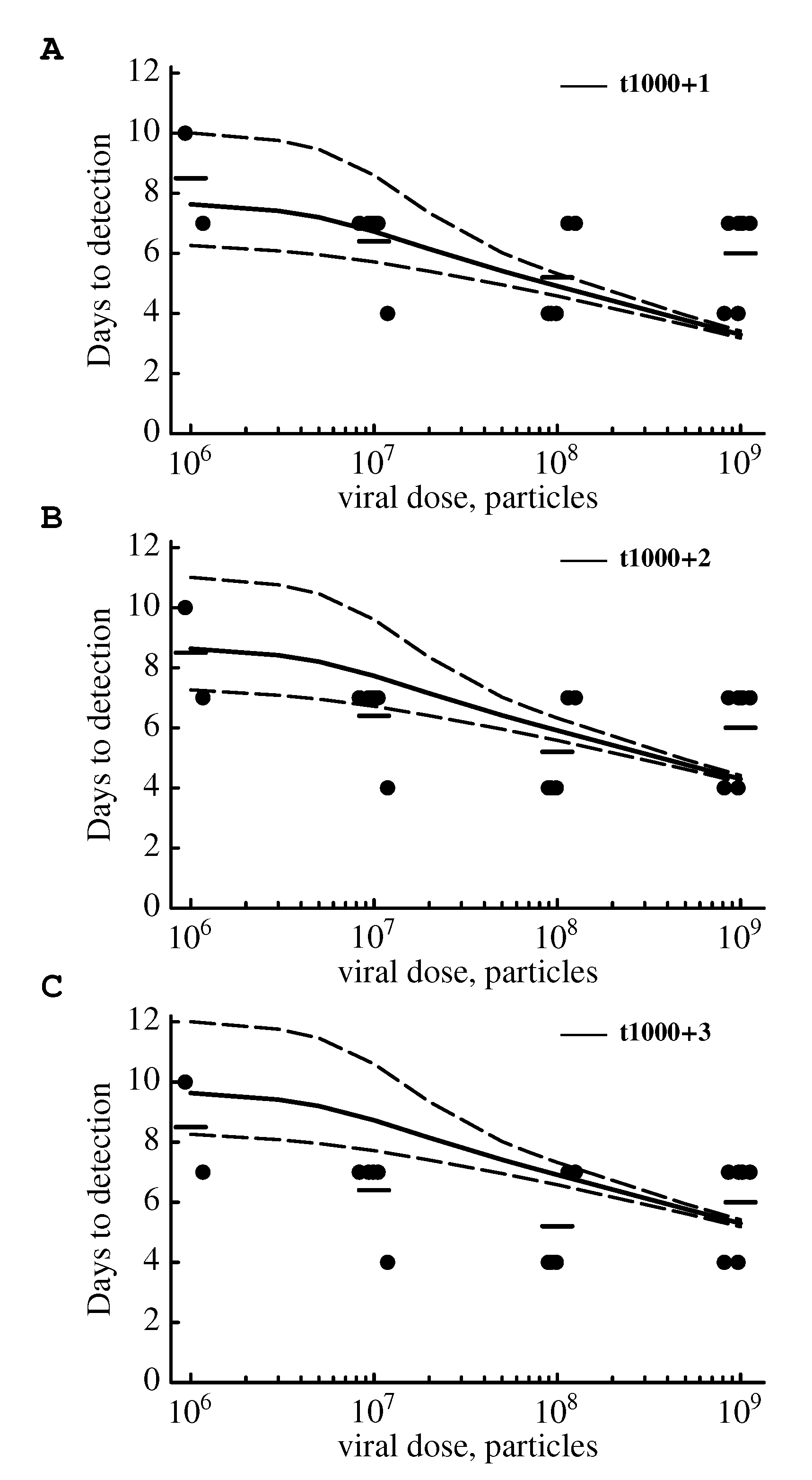
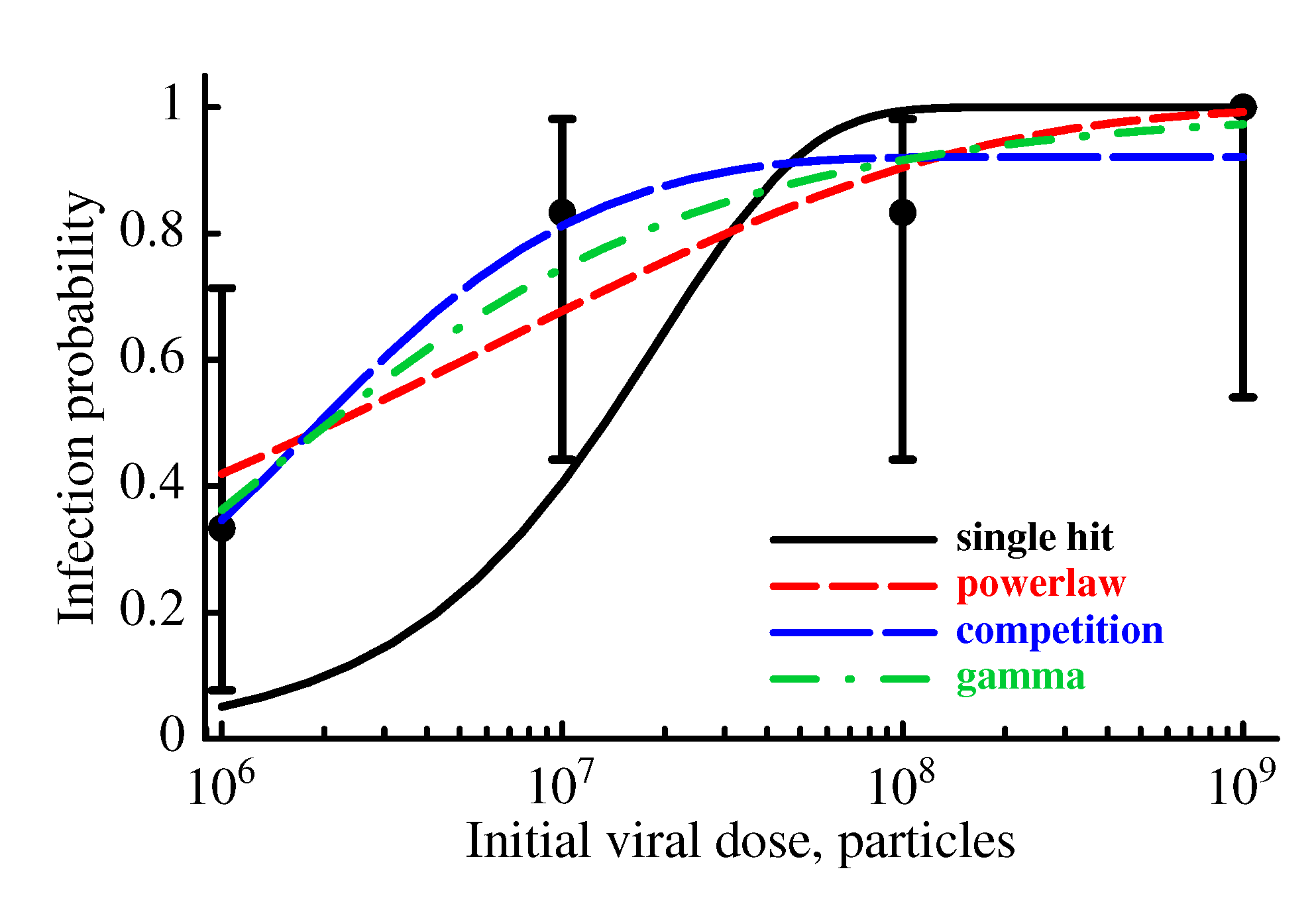
3. Discussion
4. Materials and Methods
4.1. Implementing Stochastic Simulations
4.2. Statistical Tests
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- McMichael, A.J.; Borrow, P.; Tomaras, G.D.; Goonetilleke, N.; Haynes, B.F. The immune response during acute HIV-1 infection: Clues for vaccine development. Nat. Rev. Immunol. 2010, 10, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Gardner, M.B.; Miller, C.J. Simian immunodeficiency virus rapidly penetrates the cervicovaginal mucosa after intravaginal inoculation and infects intraepithelial dendritic cells. J. Virol. 2000, 74, 6087–6095. [Google Scholar] [CrossRef] [PubMed]
- Gasper-Smith, N.; Crossman, D.M.; Whitesides, J.F.; Mensali, N.; Ottinger, J.S.; Plonk, S.G.; Moody, M.A.; Ferrari, G.; Weinhold, K.J.; Miller, S.E.; et al. Induction of plasma (TRAIL), TNFR-2, Fas ligand, and plasma microparticles after human immunodeficiency virus type 1 (HIV-1) transmission: Implications for HIV-1 vaccine design. J. Virol. 2008, 82, 7700–7710. [Google Scholar] [CrossRef] [PubMed]
- Gay, C.; Dibben, O.; Anderson, J.A.; Stacey, A.; Mayo, A.J.; Norris, P.J.; Kuruc, J.D.; Salazar-Gonzalez, J.F.; Li, H.; Keele, B. F.; et al. Cross-sectional detection of acute HIV infection: Timing of transmission, inflammation and antiretroviral therapy. PLOS ONE 2011, 6, e19617. [Google Scholar] [CrossRef] [PubMed]
- Haase, A.T. Targeting early infection to prevent HIV-1 mucosal transmission. Nature 2010, 464, 217–223. [Google Scholar] [CrossRef]
- Paiardini, M.; Pandrea, I.; Apetrei, C.; Silvestri, G. Lessons learned from the natural hosts of HIV-related viruses. Annu. Rev. Med. 2009, 60, 485–495. [Google Scholar] [CrossRef] [PubMed]
- Sodora, D.L.; Allan, J.S.; Apetrei, C.; Brenchley, J.M.; Douek, D.C.; Else, J.G.; Estes, J.D.; Hahn, B.H.; Hirsch, V.M.; Kaur, A.; et al. Toward an AIDS vaccine: Lessons from natural simian immunodeficiency virus infections of African nonhuman primate hosts. Nat. Med. 2009, 15, 861–865. [Google Scholar] [CrossRef] [PubMed]
- Rompay, K.K.A.V. The use of nonhuman primate models of HIV infection for the evaluation of antiviral strategies. AIDS Res. Hum. Retrovir. 2012, 28, 16–35. [Google Scholar] [CrossRef] [PubMed]
- Apetrei, C.; Pandrea, I.; Mellors, J.W. Nonhuman primate models for HIV cure research. PLOS Pathog. 2012, 8, e1002892. [Google Scholar]
- Reynolds, M.; Rakasz, E.; Skinner, P.; White, C.; Abel, K.; Ma, Z.; Compton, L.; Napoe, G.; Wilson, N.; Miller, C.J.; et al. CD8+ T-lymphocyte response to major immunodominant epitopes after vaginal exposure to simian immunodeficiency virus: too late and too little. J. Virol. 2005, 79, 9228–9235. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Skinner, P.J.; Ha, S.J.; Duan, L.; Mattila, T.L.; Hage, A.; White, C.; Barber, D.L.; O’Mara, L.; Southern, P. J.; et al. Visualizing antigen-specific and infected cells in situ predicts outcomes in early viral infection. Science 2009, 323, 1726–1729. [Google Scholar] [CrossRef] [PubMed]
- Haase, A.T. Early events in sexual transmission of HIV and SIV and opportunities for interventions. Annu. Rev. Med. 2011, 62, 127–139. [Google Scholar] [CrossRef] [PubMed]
- McDermott, A.; Mitchen, J.; Piaskowski, S.; de Souza, I.; Yant, L.; Stephany, J.; Furlott, J.; Watkins, D. Repeated low-dose mucosal simian immunodeficiency virus SIVmac239 challenge results in the same viral and immunological kinetics as high-dose challenge: A model for the evaluation of vaccine efficacy in nonhuman primates. J. Virol. 2004, 78, 3140–3144. [Google Scholar] [CrossRef] [PubMed]
- Fenizia, C.; Keele, B.F.; Nichols, D.; Cornara, S.; Binello, N.; Vaccari, M.; Pegu, P.; Robert-Guroff, M.; Ma, Z.-M.; Miller, C. J.; et al. TRIM5α Does Not Affect Simian Immunodeficiency Virus SIVmac251 Replication in Vaccinated or Unvaccinated Indian Rhesus Macaques following Intrarectal Challenge Exposure. J. Virol. 2011, 85, 12399–12409. [Google Scholar] [CrossRef] [PubMed]
- Keele, B.F.; Li, H.; Learn, G.H.; Hraber, P.; Giorgi, E.E.; Grayson, T.; Sun, C.; Chen, Y.; Yeh, W.W.; Letvin, N. L.; et al. Low-dose rectal inoculation of rhesus macaques by SIVsmE660 or SIVmac251 recapitulates human mucosal infection by HIV-1. J. Exp. Med. 2009, 206, 1117–1134. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Keele, B.F.; Li, H.; Keating, S.; Norris, P.J.; Carville, A.; Mansfield, K.G.; Tomaras, G.D.; Haynes, B.F.; Kolodkin-Gal, D.; et al. Low-dose mucosal simian immunodeficiency virus infection restricts early replication kinetics and transmitted virus variants in rhesus monkeys. J. Virol. 2010, 84, 10406–10412. [Google Scholar] [CrossRef] [PubMed]
- Barouch, D.H.; Liu, J.; Li, H.; Maxfield, L.F.; Abbink, P.; Lynch, D.M.; Iampietro, M.J.; SanMiguel, A.; Seaman, M.S.; Ferrari, G.; et al. Vaccine protection against acquisition of neutralization-resistant SIV challenges in rhesus monkeys. Nature 2012, 482, 89–93. [Google Scholar] [CrossRef] [PubMed]
- Hansen, S.G.; Ford, J.C.; Lewis, M.S.; Ventura, A.B.; Hughes, C.M.; Coyne-Johnson, L.; Whizin, N.; Oswald, K.; Shoemaker, R.; Swanson, T.; et al. Profound early control of highly pathogenic SIV by an effector memory T-cell vaccine. Nature 2011, 473, 523–527. [Google Scholar] [CrossRef] [PubMed]
- Demberg, T.; Robert-Guroff, M. Controlling the HIV/AIDS epidemic: Current status and global challenges. Front. Immunol. 2012, 3, e250. [Google Scholar] [CrossRef]
- Picker, L.J.; Hansen, S.G.; Lifson, J.D. New paradigms for HIV/AIDS vaccine development. Annu. Rev. Med. 2012, 63, 95–111. [Google Scholar] [CrossRef] [PubMed]
- Stafford, M.A.; Corey, L.; Cao, Y.; Daar, E.S.; Ho, D.D.; Perelson, A.S. Modeling Plasma Virus Concentration during Primary HIV Infection. J. Theor. Biol. 2000, 203, 285–301. [Google Scholar] [CrossRef] [PubMed]
- Pearson, J.E.; Krapivsky, P.; Perelson, A.S. Stochastic theory of early viral infection: Continuous versus burst production of virions. PLOS Comput. Biol. 2011, 7, e1001058. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Allen, L.J.S. Stochastic models for virus and immune system dynamics. Math. Biosci. 2011, 234, 84–94. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.M.; Konrad, B.P.; Coombs, D. Stochastic analysis of pre- and post-exposure prophylaxis against HIV infection. SIAM J. Appl. Math. 2013, 73, 904–928. [Google Scholar] [CrossRef]
- Perelson, A.; Kirschner, D.; de Boer, R. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef] [PubMed]
- Ho, D.; Neumann, A.; Perelson, A.; Chen, W.; Leonard, J.; Markowitz, M. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature 1995, 373, 123–126. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S. Modelling viral and immune system dynamics. Nat. Rev. Immunol. 2002, 2, 28–36. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.; Neumann, A.; Markowitz, M.; Leonard, J.; Ho, D. HIV-1 dynamics in vivo: Virion clearance rate, infected cell lifespan, and viral generation time. Science 1996, 271, 1582–1586. [Google Scholar] [CrossRef] [PubMed]
- De Boer, R.J. Which of our modeling predictions are robust? PLOS Comput. Biol. 2012, 8, e1002593. [Google Scholar] [CrossRef] [PubMed]
- De Boer, R. Understanding the failure of CD8+ T-cell vaccination against simian/human immunodeficiency virus. J. Virol. 2007, 81, 2838–2848. [Google Scholar] [CrossRef] [PubMed]
- Beauchemin, C.A.A.; Handel, A. A review of mathematical models of influenza A infections within a host or cell culture: Lessons learned and challenges ahead. BMC Public Health 2011, 11 (Suppl 1), eS7. [Google Scholar] [CrossRef] [PubMed]
- Louzoun, Y.; Ganusov, V.V. Evolution of viral life-cycle in response to cytotoxic T lymphocyte-mediated immunity. J. Theor. Biol. 2012, 310C, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A.; Garcia, M.; Petrovas, C.; Yamamoto, T.; Koup, R.A.; Nabel, G.J. HIV-1 causes CD4 cell death through DNA-dependent protein kinase during viral integration. Nature 2013, 498, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Doitsh, G.; Galloway, N.L.K.; Geng, X.; Yang, Z.; Monroe, K.M.; Zepeda, O.; Hunt, P.W.; Hatano, H.; Sowinski, S.; Munoz-Arias, I.; et al. Cell death by pyroptosis drives CD4 T-cell depletion in HIV-1 infection. Nature 2014, 505, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Goto, T.; Harada, S.; Yamamoto, N.; Nakai, M. Entry of human immunodeficiency virus (HIV) into MT-2, human T cell leukemia virus carrier cell line. Arch. Virol. 1988, 102, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Platt, E.J.; Kozak, S.L.; Durnin, J.P.; Hope, T.J.; Kabat, D. Rapid dissociation of HIV-1 from cultured cells severely limits infectivity assays, causes the inactivation ascribed to entry inhibitors, and masks the inherently high level of infectivity of virions. J. Virol. 2010, 84, 3106–3110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Q.; Wietgrefe, S.W.; Li, Q.; Shore, M.D.; Duan, L.; Reilly, C.; Lifson, J.D.; Haase, A.T. Roles of substrate availability and infection of resting and activated CD4+ T cells in transmission and acute simian immunodeficiency virus infection. Proc. Natl. Acad. Sci. USA 2004, 101, 5640–5645. [Google Scholar] [CrossRef] [PubMed]
- Haase, A. Perils at mucosal front lines for HIV and SIV and their hosts. Nat. Rev. Immunol. 2005, 5, 783–792. [Google Scholar] [CrossRef] [PubMed]
- Davenport, M.; Ribeiro, R.; Perelson, A. Kinetics of virus-specific CD8+ T cells and the control of human immunodeficiency virus infection. J. Virol. 2004, 78, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, A.L. The dependence of viral parameter estimates on the assumed viral life cycle: Limitations of studies of viral load data. Proc. R. Soc. Lond. B Biol. Sci. 2001, 268, 847–854. [Google Scholar] [CrossRef]
- Ribeiro, R.M.; Qin, L.; Chavez, L.L.; Li, D.; Self, S.G.; Perelson, A.S. Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection. J. Virol. 2010, 84, 6096–6102. [Google Scholar] [CrossRef] [PubMed]
- Whitney, J.B.; Hill, A.L.; Sanisetty, S.; Penaloza-MacMaster, P.; Liu, J.; Shetty, M.; Parenteau, L.; Cabral, C.; Shields, J.; Shields, J.; et al. Rapid seeding of the viral reservoir prior to SIV viraemia in rhesus monkeys. Nature 2014, 512, 74–77. [Google Scholar] [PubMed]
- Furumoto, W.A.; Mickey, R. A mathematical model for the infectivity-dilution curve of tobacco mosaic virus: Experimental tests. Virology 1967, 32, 224–233. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.E., Jr. Some classes of hit theory models. Math. Biosci. 1975, 23, 219–235. [Google Scholar] [CrossRef]
- Haas, C.N. Estimation of risk due to low doses of microorganisms: A comparison of alternative methodologies. Am. J. Epidemiol. 1983, 118, 573–582. [Google Scholar] [PubMed]
- Teunis, P.F.; Nagelkerke, N.J.; Haas, C.N. Dose response models for infectious gastroenteritis. Risk Anal. 1999, 19, 1251–1260. [Google Scholar] [PubMed]
- Salazar-Gonzalez, J.F.; Salazar, M.G.; Keele, B.F.; Learn, G.H.; Giorgi, E.E.; Li, H.; Decker, J.M.; Wang, S.; Baalwa, J.; Kraus, M.H.; et al. Genetic identity, biological phenotype, and evolutionary pathways of transmitted/founder viruses in acute and early HIV-1 infection. J. Exp. Med. 2009, 206, 1273–1289. [Google Scholar] [CrossRef]
- Regoes, R.; Hottinger, J.; Sygnarski, L.; Ebert, D. The infection rate of Daphnia magna by Pasteuria ramosa conforms with the mass-action principle. Epidemiol. Infect. 2003, 131, 957–966. [Google Scholar] [CrossRef]
- Zhang, L.; Dailey, P.J.; He, T.; Gettie, A.; Bonhoeffer, S.; Perelson, A.S.; Ho, D.D. Rapid clearance of simian immunodeficiency virus particles from plasma of rhesus macaques. J. Virol. 1999, 73, 855–860. [Google Scholar] [PubMed]
- De Boer, R.J.; Ribeiro, R.M.; Perelson, A.S. Current estimates for HIV-1 production imply rapid viral clearance in lymphoid tissues. PLoS Comput. Biol. 2010, 6, e1000906. [Google Scholar] [CrossRef] [PubMed]
- Brandin, E.; Thorstensson, R.; Bonhoeffer, S.; Albert, J. Rapid viral decay in simian immunodeficiency virus-infected macaques receiving quadruple antiretroviral therapy. J. Virol. 2006, 80, 9861–9864. [Google Scholar] [CrossRef] [PubMed]
- Wong, J.K.; Strain, M.C.; Porrata, R.; Reay, E.; Sankaran-Walters, S.; Ignacio, C.C.; Russell, T.; Pillai, S.K.; Looney, D.J.; Dandekar, S. In vivo CD8+ T-cell suppression of siv viremia is not mediated by CTL clearance of productively infected cells. PLOS Pathog. 2010, 6, e1000748. [Google Scholar] [CrossRef] [PubMed]
- Klatt, N.R.; Shudo, E.; Ortiz, A.M.; Engram, J.C.; Paiardini, M.; Lawson, B.; Miller, M.D.; Else, J.; Pandrea, I.; Estes, J.D.; et al. CD8+ lymphocytes control viral replication in SIVmac239-infected rhesus macaques without decreasing the lifespan of productively infected cells. PLOS Pathog. 2010, 6, e1000747. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.M.; Kelleher, A.D.; Cooper, D.A. Timing of the components of the HIV life cycle in productively infected CD4+ T cells in a population of HIV-infected individuals. J. Virol. 2011, 85, 10798–10805. [Google Scholar] [CrossRef] [PubMed]
- Dixit, N.; Markowitz, M.; Ho, D.; Perelson, A. Estimates of intracellular delay and average drug efficacy from viral load data of HIV-infected individuals under antiretroviral therapy. Antivir. Ther. 2004, 9, 237–246. [Google Scholar] [PubMed]
- Althaus, C.L.; Vos, A.S.D.; Boer, R.J.D. Reassessing the human immunodeficiency virus type 1 life cycle through age-structured modeling: Life span of infected cells, viral generation time, and basic reproductive number, R0. J. Virol. 2009, 83, 7659–7667. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.Y.; DiMascio, M.; Perelson, A.S.; Ho, D.D.; Zhang, L. Determination of virus burst size in vivo using a single-cycle SIV in rhesus macaques. Proc. Natl. Acad. Sci. USA 2007, 104, 19079–19084. [Google Scholar] [CrossRef] [PubMed]
- Markowitz, M.; Louie, M.; Hurley, A.; Sun, E.; di Mascio, M.; Perelson, A.S.; Ho, D.D. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J. Virol. 2003, 77, 5037–5038. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D. Exact stochastic simulation of coupled chemical-reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Miller, C.; Li, Q.; Abel, K.; Kim, E.; Ma, Z.; Wietgrefe, S.; La Franco-Scheuch, L.; Compton, L.; Duan, L.; Shore, M.; et al. 2005 propagation and dissemination of infection after vaginal transmission of simian immunodeciency virus. J. Virol. 2005, 79, 9217–9227. [Google Scholar] [CrossRef] [PubMed]
- Brown, L.; Cai, T.; DasGupta, A.; Agresti, A.; Coull, B.; Casella, G.; Corcoran, C.; Mehta, C.; Ghosh, M.; Santner, T.J.; et al. Interval estimation for a binomial proportion. Stat. Sci. 2001, 16, 101–133. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer-Verlag: New York, NY, USA, 2002. [Google Scholar]
- Muller, V.; Maree, A.F.; de Boer, R.J. Small variations in multiple parameters account for wide variations in HIV-1 set-points: A novel modelling approach. Proc. R. Soc. Lond. B Biol. Sci. 2001, 268, 235–242. [Google Scholar] [CrossRef]
- Sergeev, R.A.; Batorsky, R.E.; Rouzine, I.M. Model with two types of CTL regulation and experiments on CTL dynamics. J. Theor. Biol. 2010, 263, 369–384. [Google Scholar] [CrossRef] [PubMed]
- Althaus, C.L.; Boer, R.J.D. Implications of CTL-mediated killing of HIV-infected cells during the non-productive stage of infection. PLOS ONE 2011, 6, e16468. [Google Scholar] [CrossRef] [PubMed]
- Tan, W.Y.; Wu, H. Stochastic modeling of the dynamics of CD4+ T-cell infection by HIV and some Monte Carlo studies. Math. Biosci. 1998, 147, 173–205. [Google Scholar] [CrossRef] [PubMed]
- Kamina, A.; Makuch, R.W.; Zhao, H. A stochastic modeling of early HIV-1 population dynamics. Math. Biosci. 2001, 170, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, J.M.; Wahl, L.M. Monte Carlo estimates of natural variation in HIV infection. J. Theor. Biol. 2005, 236, 137–153. [Google Scholar]
- Lee, H.Y.; Giorgi, E.E.; Keele, B.F.; Gaschen, B.; Athreya, G.S.; Salazar-Gonzalez, J.F.; Pham, K.T.; Goepfert, P.A.; Kilby, J.M.; Saag, M. S.; et al. Modeling sequence evolution in acute HIV-1 infection. J. Theor. Biol. 2009, 261, 341–360. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, R.M.; Bonhoeffer, S. Production of resistant HIV mutants during antiretroviral therapy. Proc. Natl. Acad. Sci. USA 2000, 97, 7681–7686. [Google Scholar] [CrossRef] [PubMed]
- Horton, R.E.; Ball, T.B.; Wachichi, C.; Jaoko, W.; Rutherford, W.J.; Mckinnon, L.; Kaul, R.; Rebbapragada, A.; Kimani, J.; Plummer, F.A. Cervical HIV-specific IgA in a population of commercial sex workers correlates with repeated exposure but not resistance to HIV. AIDS Res. Hum. Retrovir. 2009, 25, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Restrepo, C.; Rallon, N.I.; del Romero, J.; Rodriguez, C.; Hernando, V.; Lopez, M.; Peris, A.; Lozano, S.; Sempere-Ortells, J.M.; Soriano, V.; et al. Low-level exposure to HIV induces virus-specific T cell responses and immune activation in exposed HIV-seronegative individuals. J. Immunol. 2010, 185, 982–989. [Google Scholar] [CrossRef] [PubMed]
- Snyder, W.S.; Cook, M.J.; Nasset, E.; Karhusen, L.R.; Parry Howells, G.; Tipton, I.H. Report of the Task Group on Reference Man; Pergamon Press: Paris, France, 1975. [Google Scholar]
- Mohammadi, P.; Desfarges, S.; Bartha, I.; Joos, B.; Zangger, N.; MuÃs´oz, M.; GÃijnthard, H.F.; Beerenwinkel, N.; Telenti, A.; Ciuffi, A.; et al. 24 h in the life of HIV-1 in a T cell line. PLOS Pathog. 2013, 9, e1003161. [Google Scholar] [CrossRef] [PubMed]
- Petravic, J.; Ellenberg, P.; Chan, M.-L.; Paukovics, G.; Smyth, R.P.; Mak, J.; Davenport, M.P. Intracellular dynamics of HIV infection. J. Virol. 2014, 88, 1113–1124. [Google Scholar] [CrossRef]
- Bachar, M.; Dorfmayr, A. HIV treatment models with time delay. C. R. Biol. 2004, 327, 983–994. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.W.; Perelson, A.S. Mathematical analysis of delay differential equation models of HIV-1 infection. Math. Biosci. 2002, 179, 73–94. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.W.; Murray, J.D.; Perelson, A.S. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Harris, T.E. The Theory of Branching Processes; Springer: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Kampen, N.G.V. Stochastic Processes in Physics and Chemistry; Van Kampen, N.G., Ed.; Elsevier North-Holland: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Veazey, R.; DeMaria, M.; Chalifoux, L.; Shvetz, D.; Pauley, D.; Knight, H.; Rosenzweig, M.; Johnson, R.; Desrosiers, R.; Lackner, A.A. Gastrointestinal tract as a major site of CD4+ T cell depletion and viral replication in SIV infection. Science 1998, 280, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Mattapallil, J.; Douek, D.; Hill, B.; Nishimura, Y.; Martin, M.; Roederer, M. Massive infection and loss of memory CD4+ T cells in multiple tissues during acute SIV infection. Nature 2005, 434, 1093–1097. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Duan, L.; Estes, J.; Ma, Z.; Rourke, T.; Wang, Y.; Reilly, C.; Carlis, J.; Miller, C.; Haase, A.T. Peak SIV replication in resting memory CD4+ T cells depletes gut lamina propria CD4+ T cells. Nature 2005, 434, 1148–1152. [Google Scholar] [PubMed]
- Murooka, T.T.; Deruaz, M.; Marangoni, F.; Vrbanac, V.D.; Seung, E.; von Andrian, U.H.; Tager, A.M.; Luster, A.D.; Mempel, T.R. HIV-infected T cells are migratory vehicles for viral dissemination. Nature 2012, 490, 283–287. [Google Scholar] [CrossRef]
- Lay, M.D.H.; Petravic, J.; Gordon, S.N.; Engram, J.; Silvestri, G.; Davenport, M.P. Is the gut the major source of virus in early simian immunodeficiency virus infection? J. Virol. 2009, 83, 7517–7523. [Google Scholar] [CrossRef] [PubMed]
- Ciuffi, A.; Bleiber, G.; Munoz, M.; Martinez, R.; Loeuillet, C.; Rehr, M.; Fischer, M.; Gunthard, H.F.; Oxenius, A.; Meylan, P.; et al. Entry and transcription as key determinants of differences in CD4 T-cell permissiveness to human immunodeficiency virus type 1 infection. J. Virol. 2004, 78, 10747–10754. [Google Scholar] [CrossRef] [PubMed]
- Pawitan, Y. In All Likelihood: Statistical Modelling and Inference Using Likelihood; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Conway, J.M.; Coombs, D. A stochastic model of latently infected cell reactivation and viral blip generation in treated HIV patients. PLOS Comput. Biol. 2011, 7, e1002033. [Google Scholar] [CrossRef] [PubMed]
- Karlin, S.; Taylor, H.M. A First Course in Stochastic Processes; Academic Press: San Diego, CA, USA, 1975. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noecker, C.; Schaefer, K.; Zaccheo, K.; Yang, Y.; Day, J.; Ganusov, V.V. Simple Mathematical Models Do Not Accurately Predict Early SIV Dynamics. Viruses 2015, 7, 1189-1217. https://doi.org/10.3390/v7031189
Noecker C, Schaefer K, Zaccheo K, Yang Y, Day J, Ganusov VV. Simple Mathematical Models Do Not Accurately Predict Early SIV Dynamics. Viruses. 2015; 7(3):1189-1217. https://doi.org/10.3390/v7031189
Chicago/Turabian StyleNoecker, Cecilia, Krista Schaefer, Kelly Zaccheo, Yiding Yang, Judy Day, and Vitaly V. Ganusov. 2015. "Simple Mathematical Models Do Not Accurately Predict Early SIV Dynamics" Viruses 7, no. 3: 1189-1217. https://doi.org/10.3390/v7031189
APA StyleNoecker, C., Schaefer, K., Zaccheo, K., Yang, Y., Day, J., & Ganusov, V. V. (2015). Simple Mathematical Models Do Not Accurately Predict Early SIV Dynamics. Viruses, 7(3), 1189-1217. https://doi.org/10.3390/v7031189







