Synergizing Attribute-Guided Latent Space Exploration (AGLSE) with Classical Molecular Simulations to Design Potent Pep-Magnet Peptide Inhibitors to Abrogate SARS-CoV-2 Host Cell Entry
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Selection and Comparative Analysis
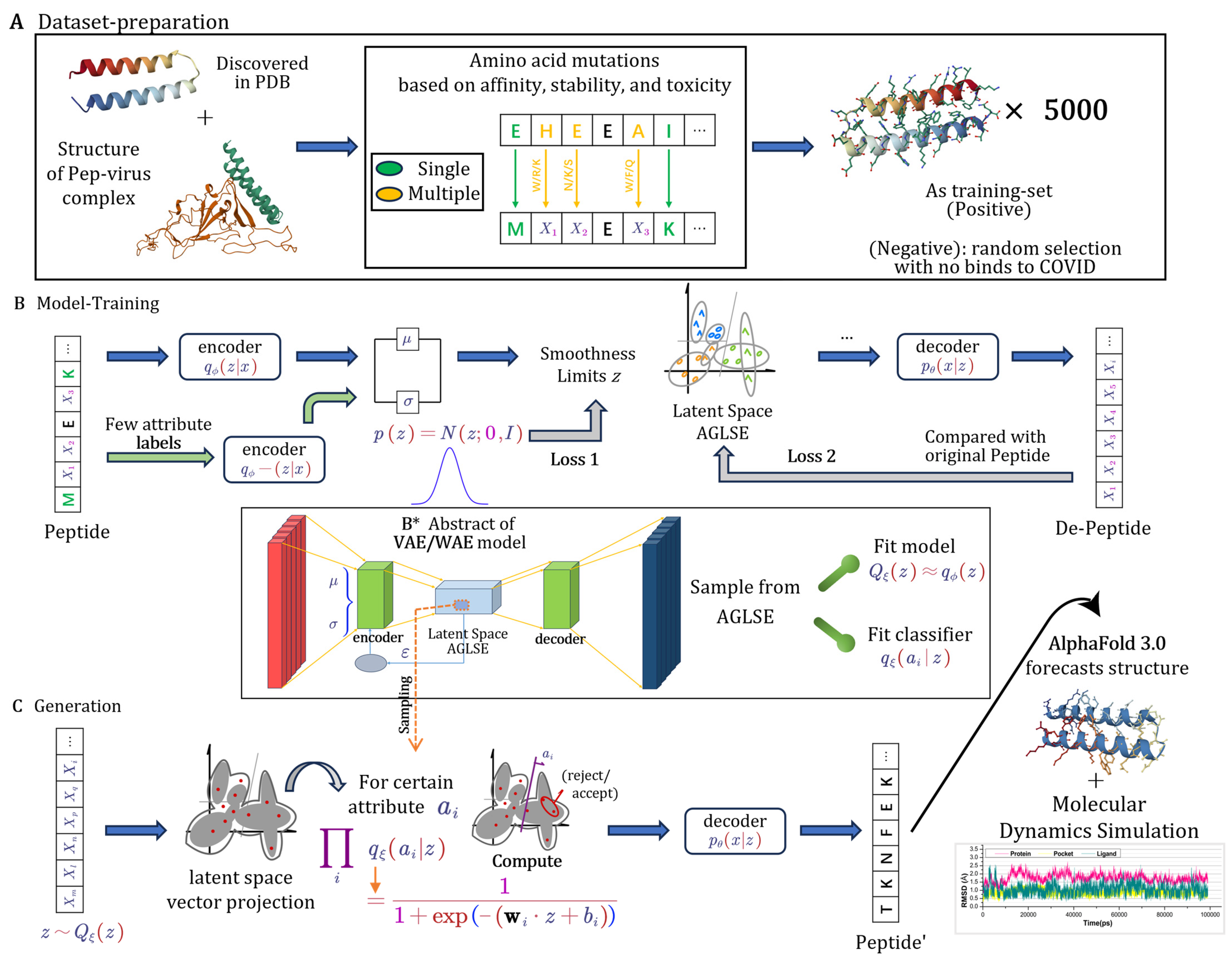
2.1.1. Dataset Generation from Structural Insights
2.1.2. Core Components and Regularization of Model
2.1.3. Attribute-Guided Latent Space Exploration (AGLSE)
2.1.4. Training and Optimization
2.1.5. Peptide Generation
2.1.6. Structure Preparation
2.1.7. Molecular Docking
2.1.8. Molecular Dynamics Simulation
2.1.9. Dynamic Cross-Correlation Map (DCCM)
2.1.10. Principal Components Analysis PCA
2.1.11. Binding Free Energy Calculation (BFE)
3. Results
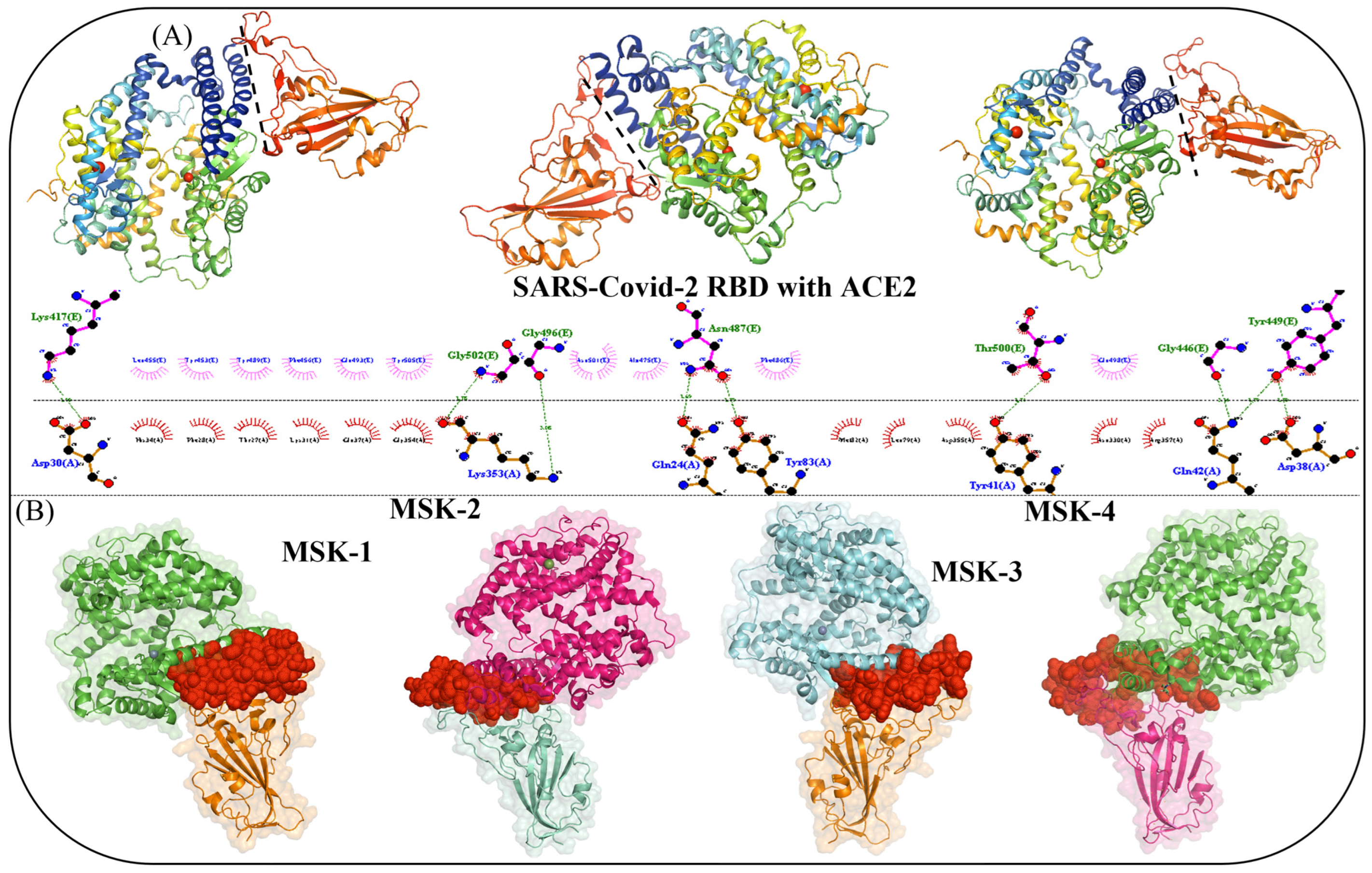
3.1. Interface Analysis and Mechanism of Viral Interaction
3.1.1. Peptide Toxicity and Allergenicity
3.1.2. Physiochemical Properties of Predicted Antiviral Peptides
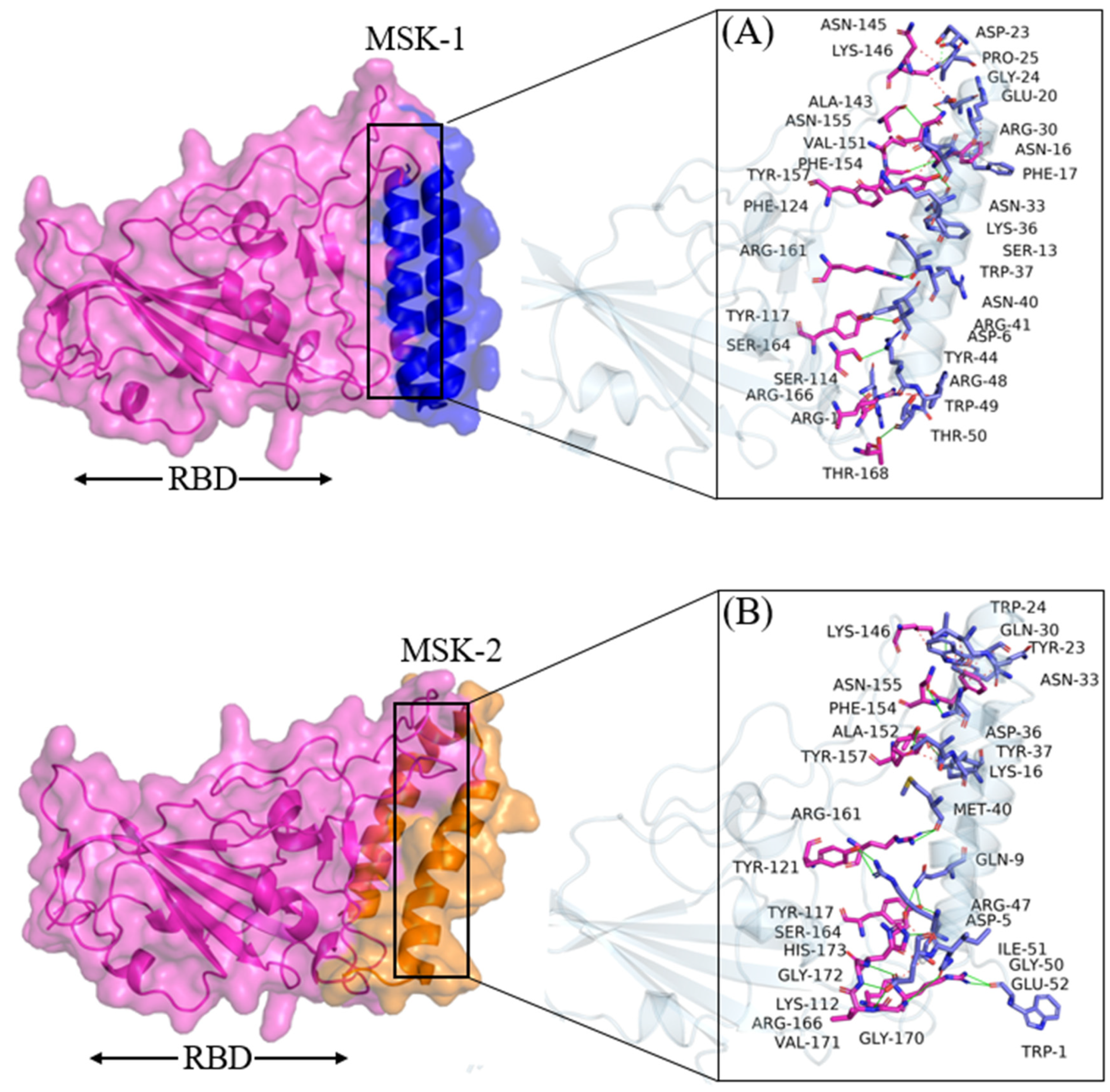
3.1.3. Molecular Docking Analysis of MSK-1 and MSK-2
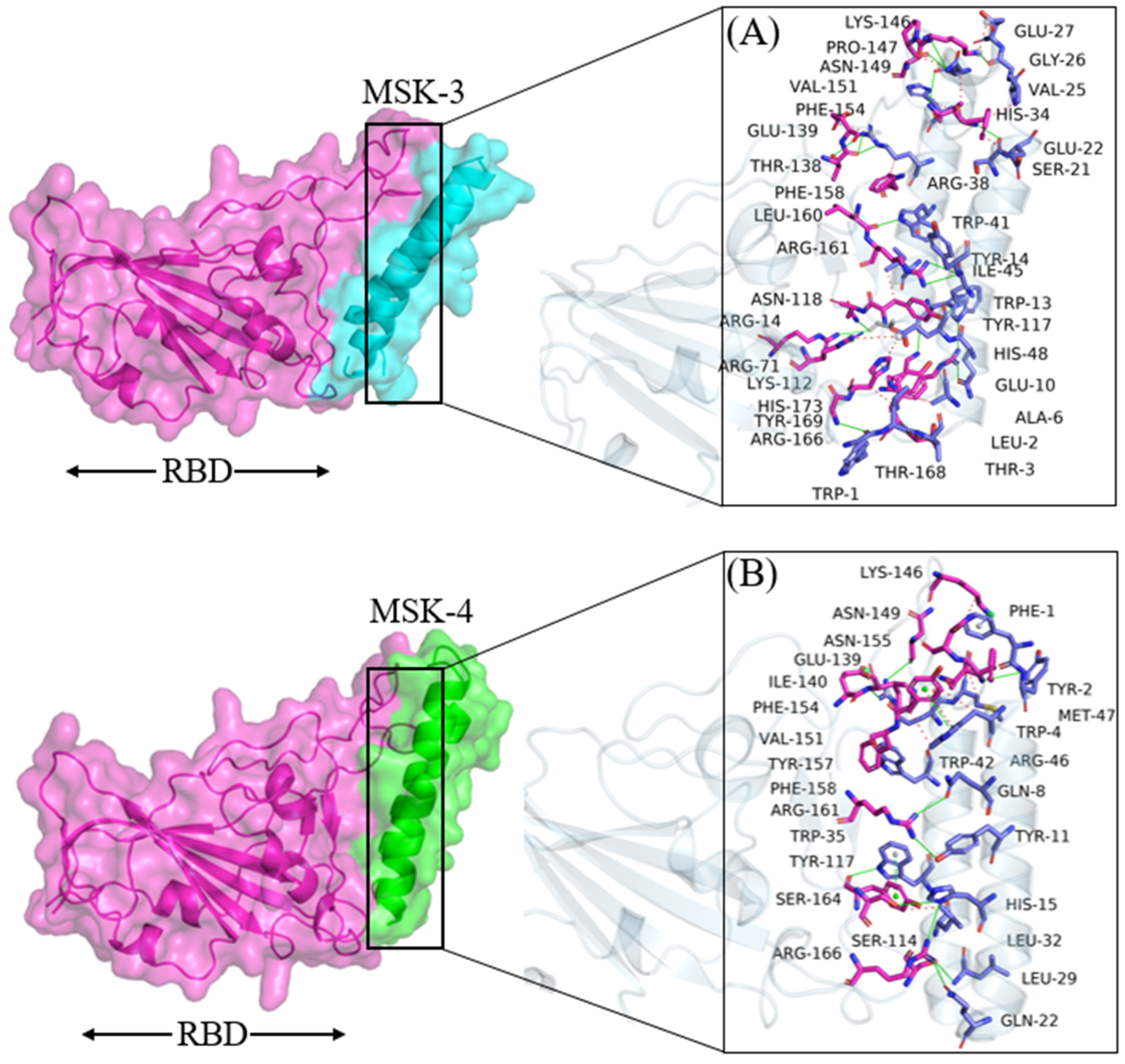
3.1.4. Docking Analysis of MSK-3 and MSK-4
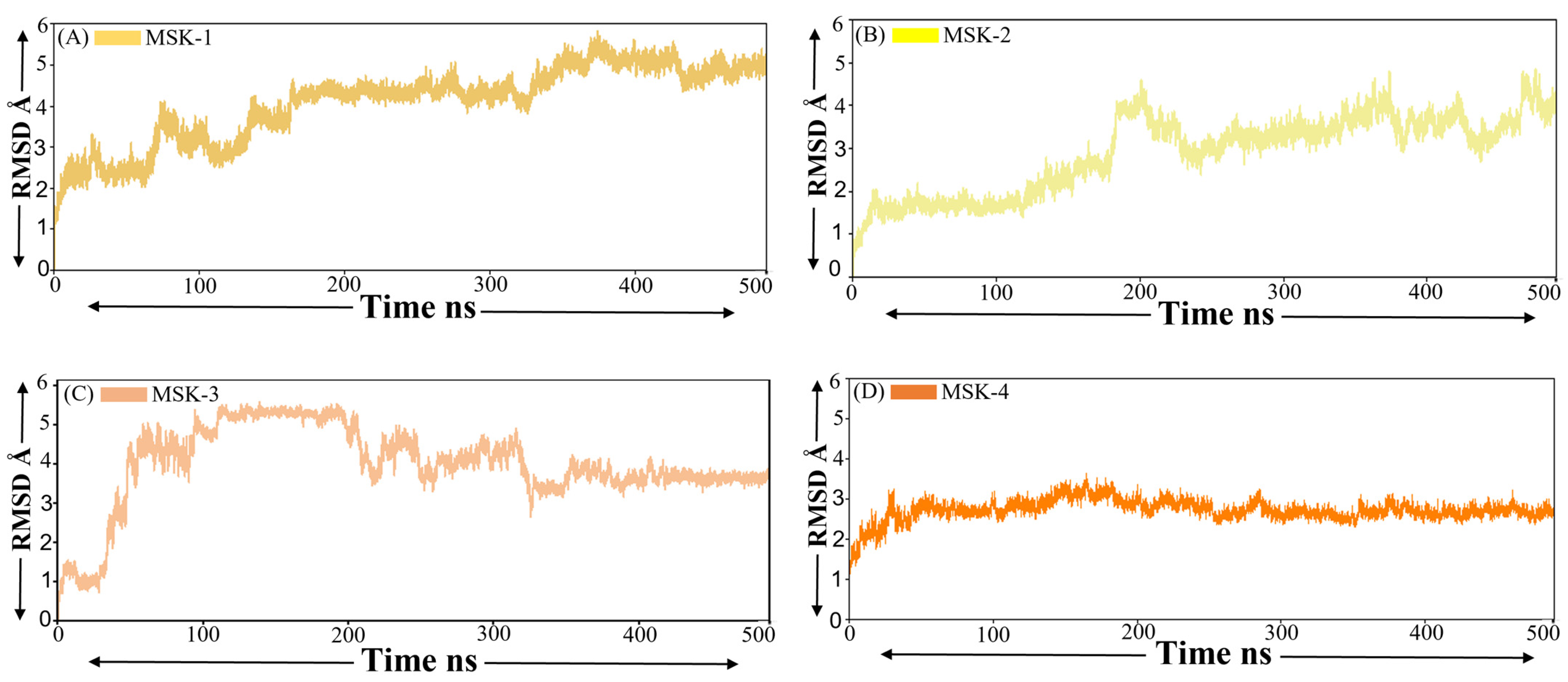
3.1.5. Root Mean Square Deviation (RMSD)
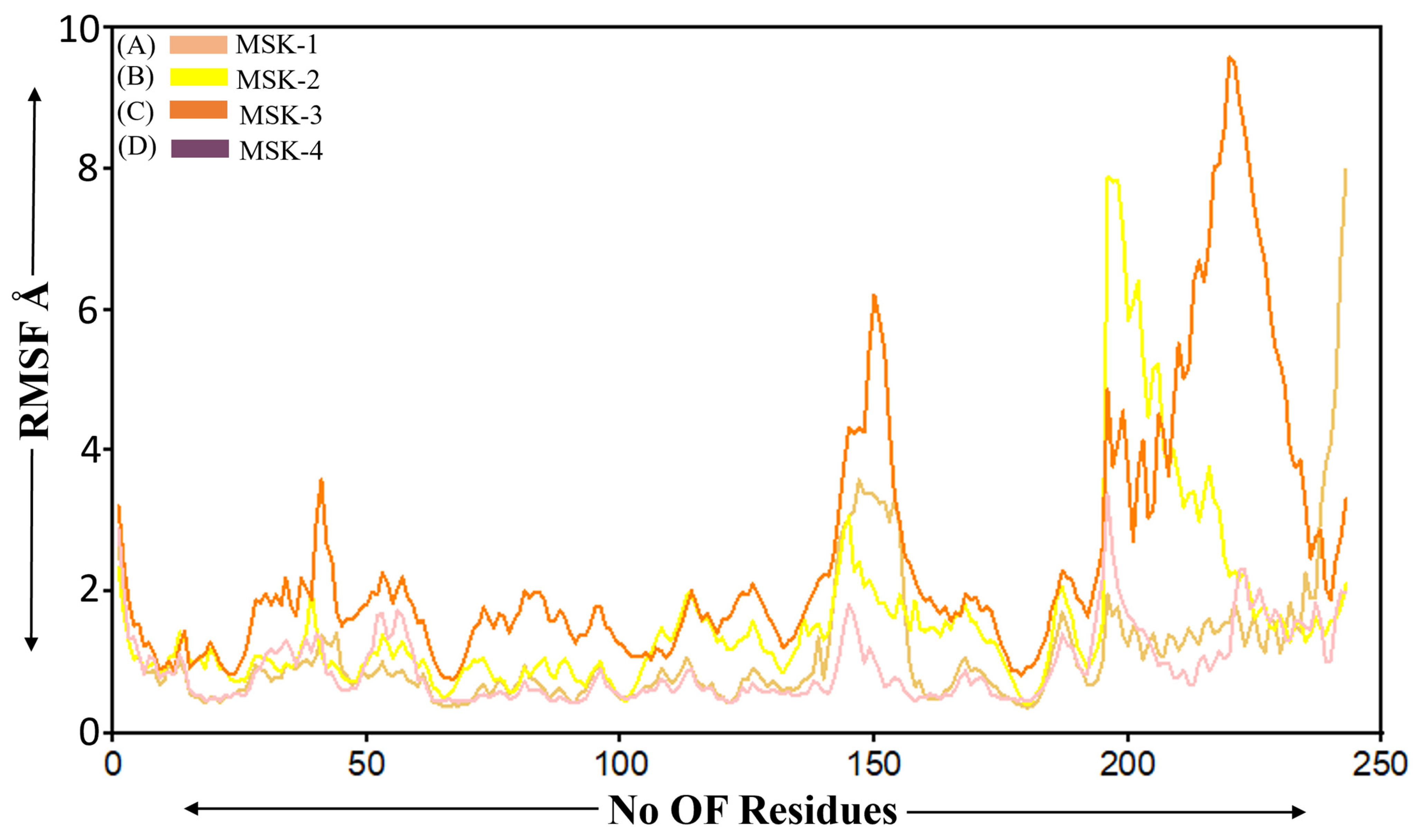
3.1.6. Root Mean Square Fluctuation
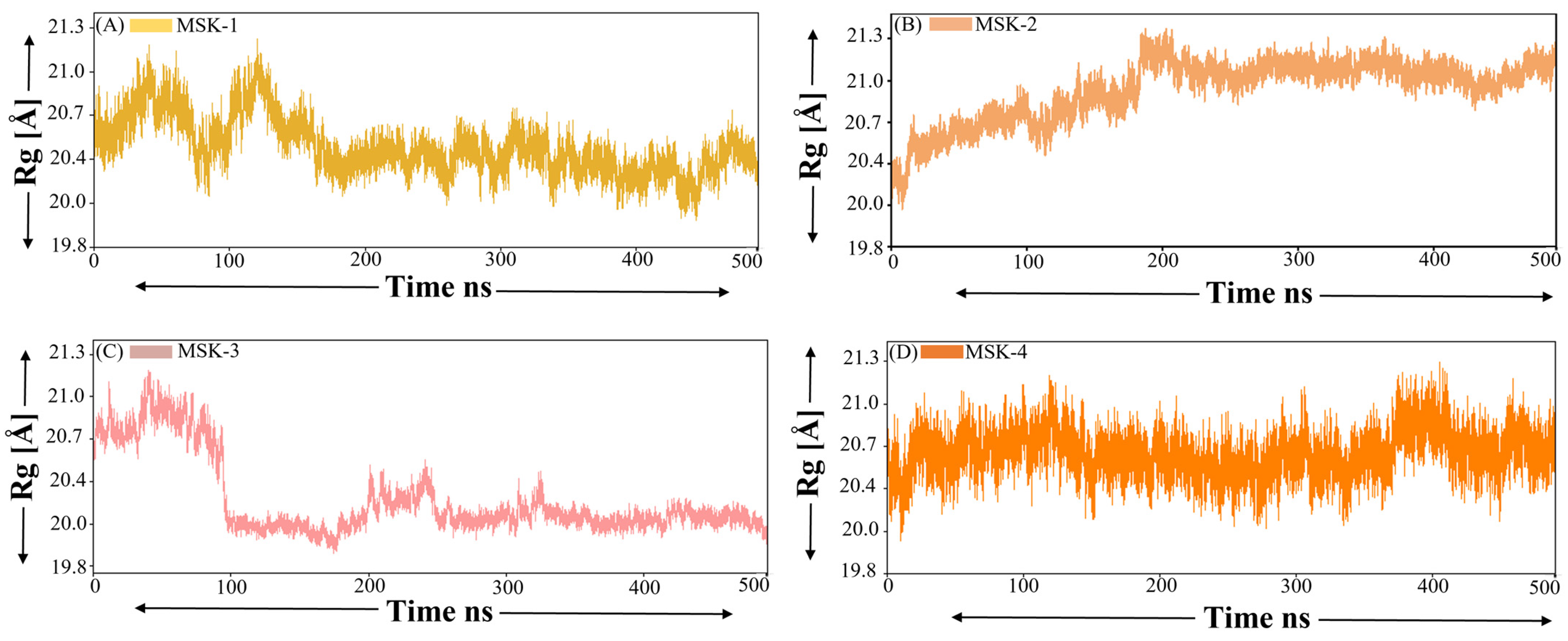
3.1.7. Radius of Gyration (ROG)
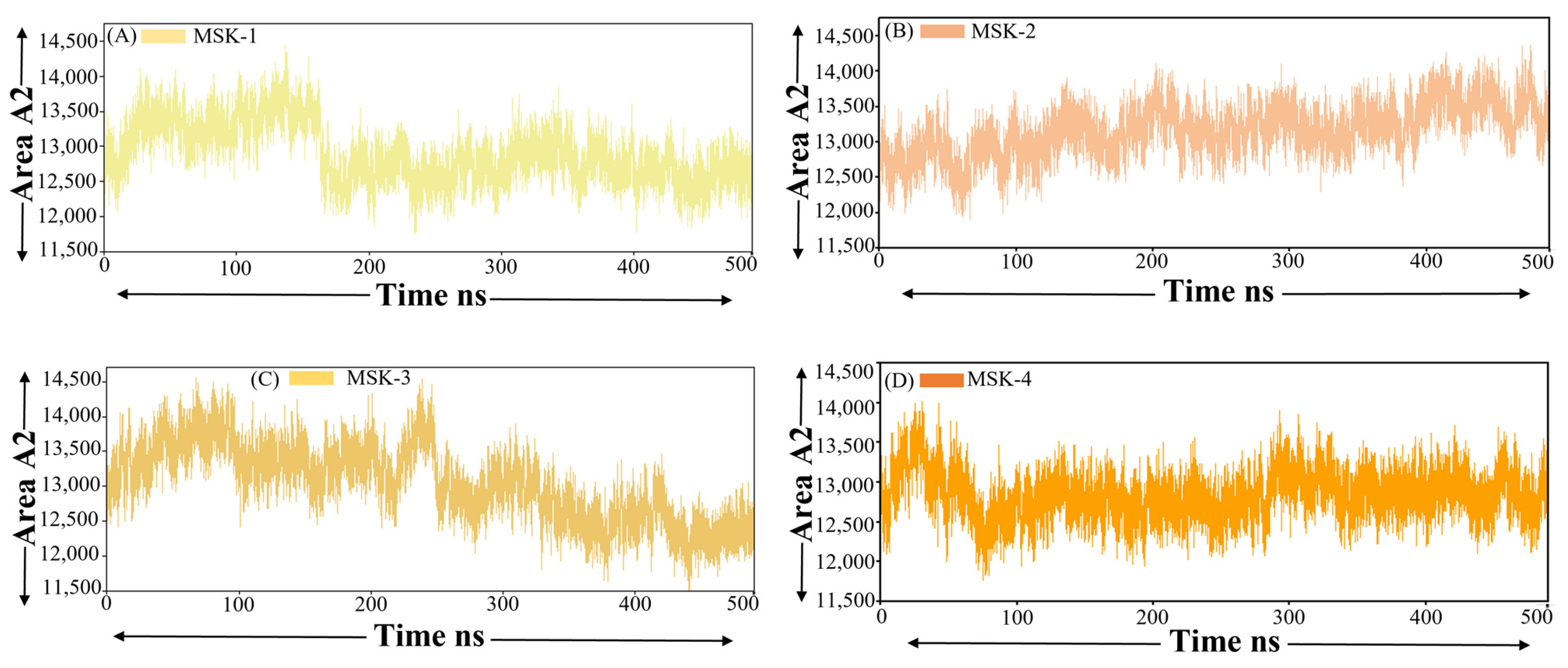
3.1.8. Solvent-Accessible Surface Area
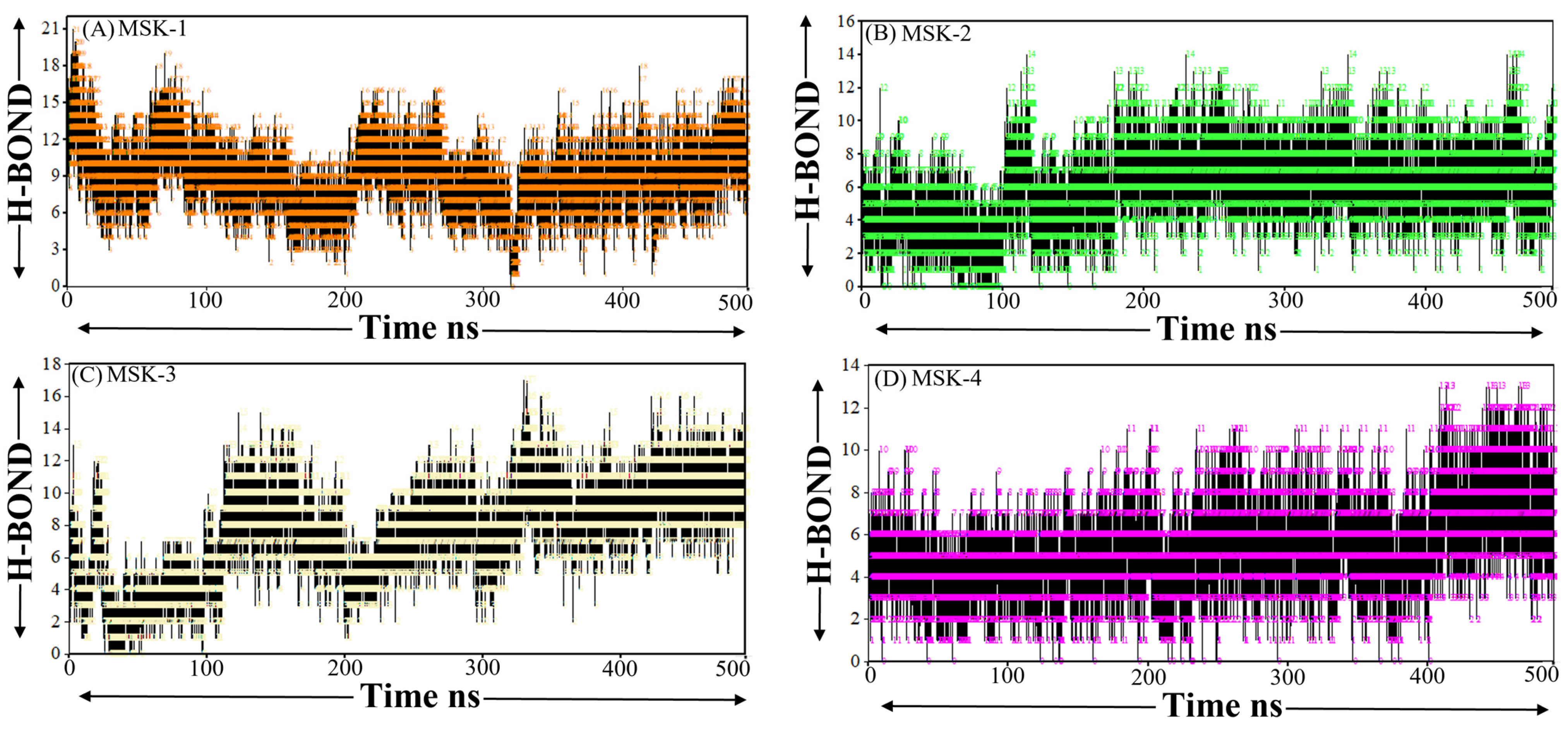
3.1.9. Hydrogen Bond Analysis
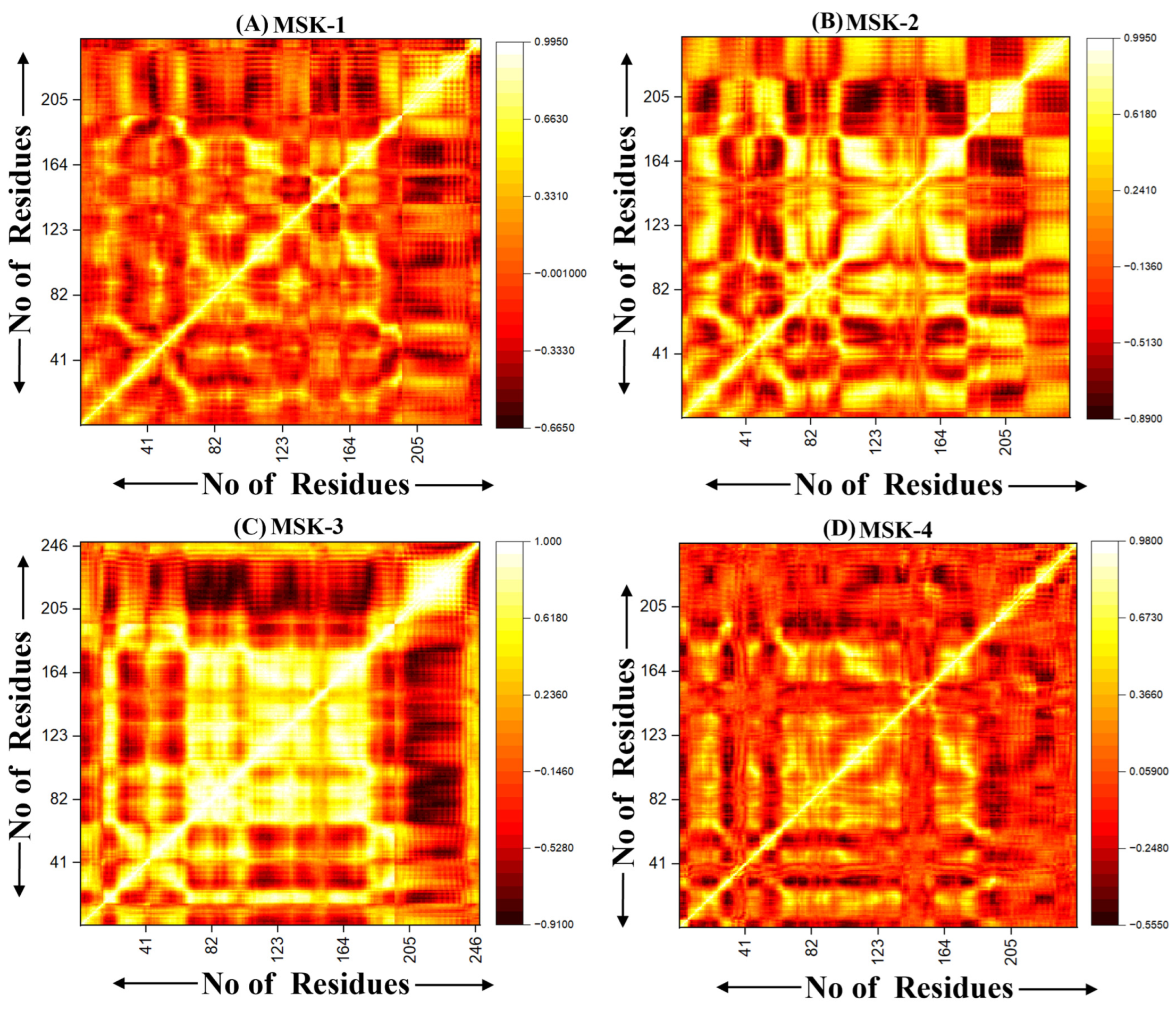
3.1.10. Dynamic Cross-Correlation Analysis (DCCM)
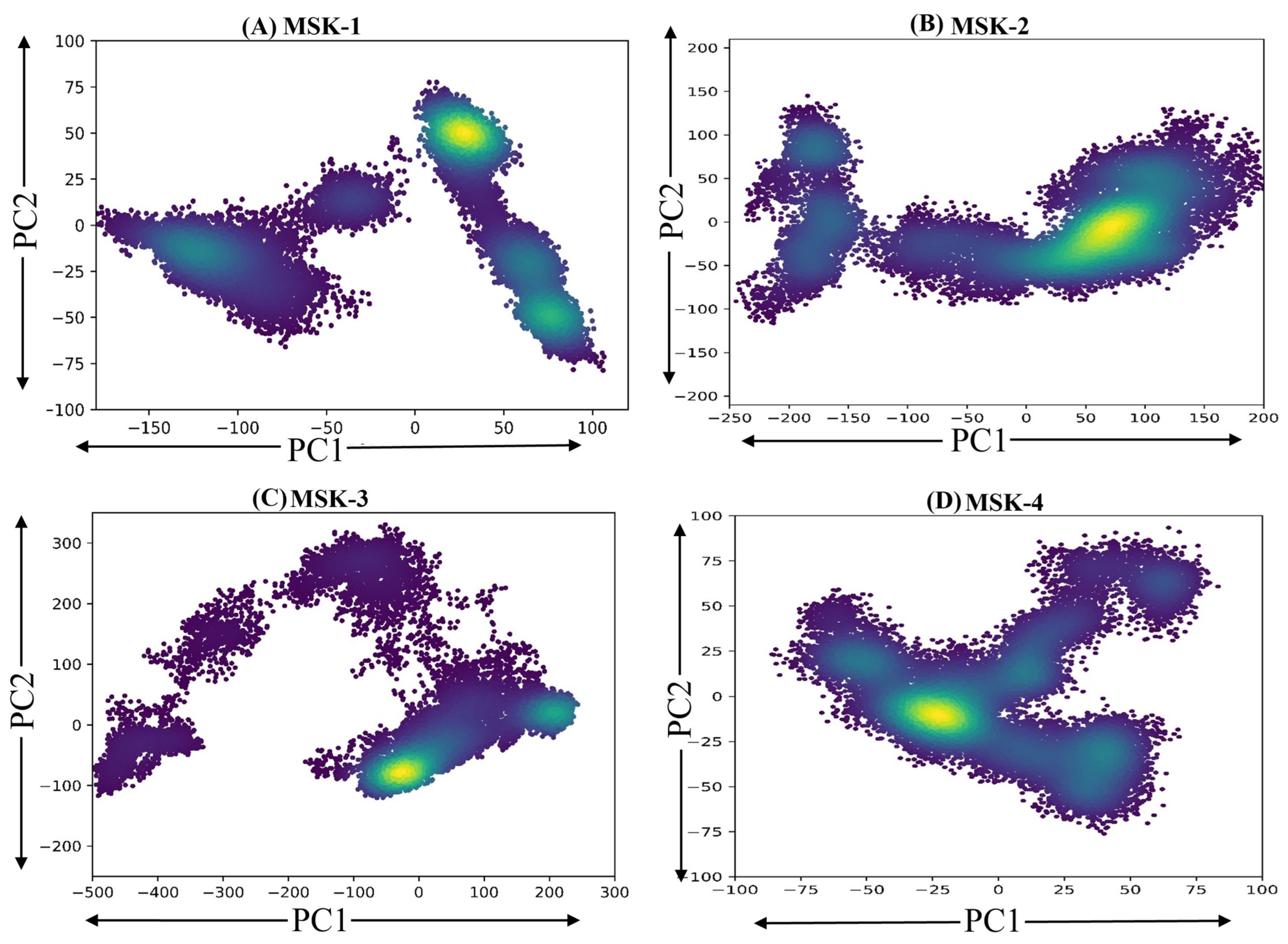
3.1.11. Principal Components Analysis
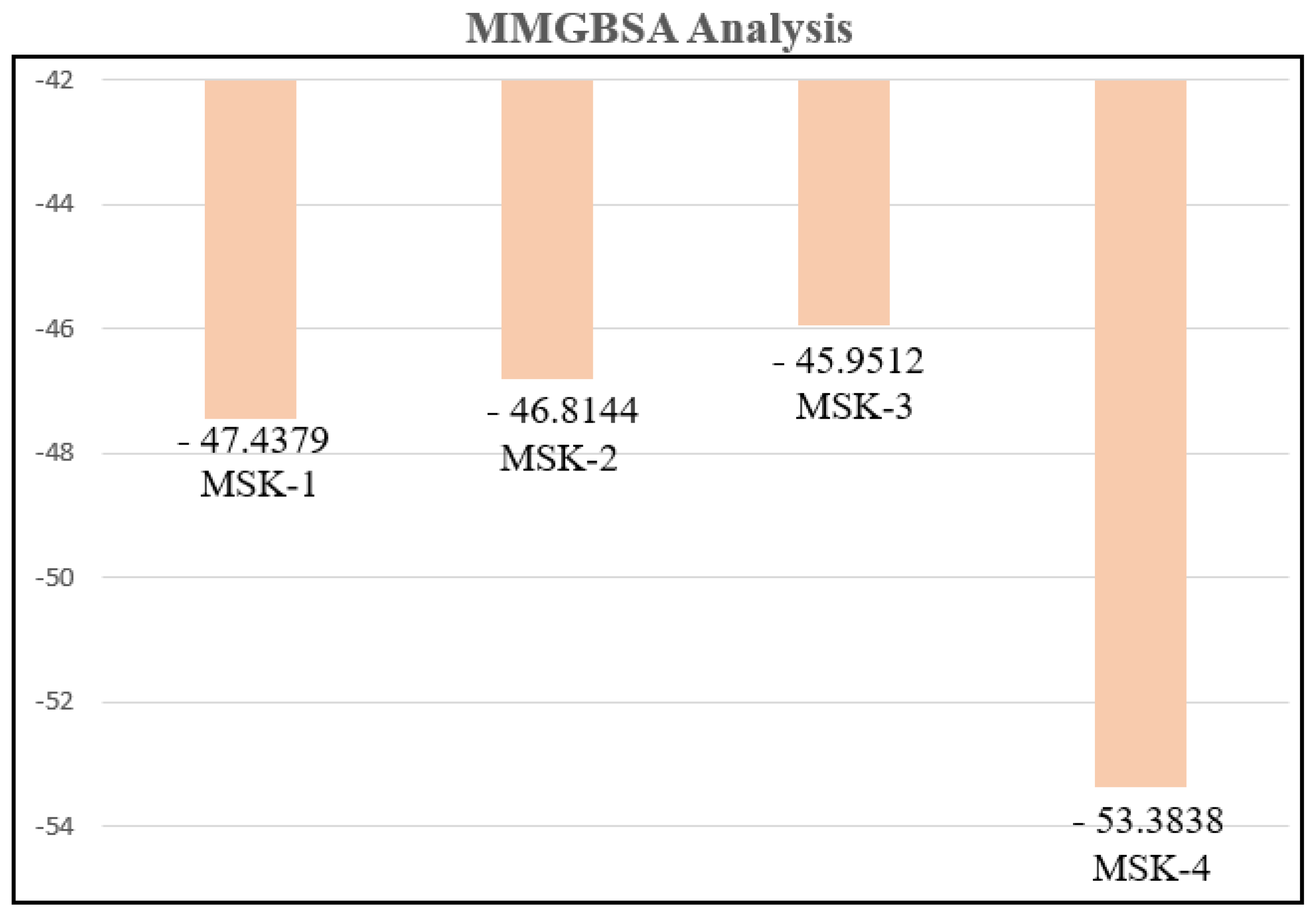
3.1.12. MMGBSA Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ullah, S.; Rahman, W.; Ullah, F.; Ullah, A.; Jehan, R.; Iqbal, M.N.; Irfan, M. A molecular dynamics simulations analysis of repurposing drugs for COVID-19 using bioinformatics methods. J. Biomol. Struct. Dyn. 2024, 42, 9561–9570. [Google Scholar] [CrossRef] [PubMed]
- Samad, A.; Ajmal, A.; Mahmood, A.; Khurshid, B.; Li, P.; Jan, S.M.; Rehman, A.U.; He, P.; Abdalla, A.N.; Umair, M.; et al. Identification of novel inhibitors for SARS-CoV-2 as therapeutic options using machine learning-based virtual screening, molecular docking and MD simulation. Front. Mol. Biosci. 2023, 10, 1060076. [Google Scholar] [CrossRef]
- Jarvis, L.M. THE NEW DRUGS of 2019 the 48 medicines represent another highly productive year for the pharmaceutical industry, with cancer and rare-disease drugs again dominating the list. Chem. Eng. News 2020, 98, 30–36. [Google Scholar]
- Sun, N.; Su, Z.; Zheng, X. Research progress of mosquito-borne virus mRNA vaccines. Mol. Ther. Methods Clin. Dev. 2025, 33, 101398. [Google Scholar] [CrossRef]
- Lee, Y.-C.J.; Shirkey, J.D.; Park, J.; Bisht, K.; Cowan, A.J. An overview of antiviral peptides and rational biodesign considerations. BioDes. Res. 2022, 2022, 9898241. [Google Scholar] [CrossRef] [PubMed]
- Abd El-Aziz, T.M.; Stockand, J.D. Recent progress and challenges in drug development against COVID-19 coronavirus (SARS-CoV-2)-an update on the status. Infect. Genet. Evol. 2020, 83, 104327. [Google Scholar] [CrossRef]
- Rana, R.; Kant, R.; Huirem, R.S.; Bohra, D.; Ganguly, N.K. Omicron variant: Current insights and future directions. Microbiol. Res. 2022, 265, 127204. [Google Scholar] [CrossRef]
- Monroe, M.K.; Wang, H.; Anderson, C.F.; Jia, H.; Flexner, C.; Cui, H. Leveraging the therapeutic, biological, and self-assembling potential of peptides for the treatment of viral infections. J. Control. Release 2022, 348, 1028–1049. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Nguyen, H.M.; Wagner, K.M.; Stewart, R.; Singh, V.; Thapa, P.; Ton, A.T.; Kondo, R.P.; Ghetti, A.; Pennington, M.W. Computational design of peptides to target NaV1. 7 channel with high potency and selectivity for the treatment of pain. Biophys. J. 2023, 122, 309a. [Google Scholar] [CrossRef]
- Han, Y.; Král, P. Computational design of ACE2-based peptide inhibitors of SARS-CoV-2. ACS Nano 2020, 14, 5143–5147. [Google Scholar] [CrossRef]
- Walkinshaw, M.D. Protein targets for structure-based drug design. Med. Res. Rev. 1992, 12, 317–372. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Lin, H.; Bai, R.; Duan, H. Deep learning for advancing peptide drug development: Tools and methods in structure prediction and design. Eur. J. Med. Chem. 2024, 268, 116262. [Google Scholar] [CrossRef]
- Sutskever, I. Sequence to Sequence Learning with Neural Networks. arXiv 2014, arXiv:1409.3215. [Google Scholar]
- Yang, L.; Yang, G.; Bing, Z.; Tian, Y.; Huang, L.; Niu, Y.; Yang, L. Accelerating the discovery of anticancer peptides targeting lung and breast cancers with the Wasserstein autoencoder model and PSO algorithm. Brief. Bioinform. 2022, 23, bbac320. [Google Scholar] [CrossRef]
- Van Damme, E.; Abeywickrema, P.; Yin, Y.; Xie, J.; Jacobs, S.; Mann, M.K.; Doijen, J.; Miller, R.; Piassek, M.; Marsili, S.; et al. A small-molecule SARS-CoV-2 inhibitor targeting the membrane protein. Nature 2025, 640, 506–513. [Google Scholar] [CrossRef]
- Nakamura, S.; Tanimura, Y.; Nomura, R.; Suzuki, H.; Nishikawa, K.; Kamegawa, A.; Numoto, N.; Tanaka, A.; Kawabata, S.; Sakaguchi, S.; et al. Structure-guided engineering of a mutation-tolerant inhibitor peptide against variable SARS-CoV-2 spikes. Proc. Natl. Acad. Sci. USA 2025, 122, e2413465122. [Google Scholar] [CrossRef]
- Tolstikhin, I.; Bousquet, O.; Gelly, S.; Schoelkopf, B. Wasserstein auto-encoders. arXiv 2017, arXiv:1711.01558. [Google Scholar]
- Chen, Y.; Liu, J.; Peng, L.; Wu, Y.; Xu, Y.; Zhang, Z. Auto-encoding variational bayes. Camb. Explor. Arts Sci. 2024, 2, 1–8. [Google Scholar] [CrossRef]
- Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef]
- Takale, D.G.; Mahalle, P.N.; Sule, B. Generative AI Models: A Comparative Analysis. J. Comput. Sci. Eng. Softw. Test. 2024, 10, 32–38. [Google Scholar]
- Szymczak, P.; Możejko, M.; Grzegorzek, T.; Jurczak, R.; Bauer, M.; Neubauer, D.; Sikora, K.; Michalski, M.; Sroka, J.; Setny, P. Discovering highly potent antimicrobial peptides with deep generative model HydrAMP. Nat. Commun. 2023, 14, 1453. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Sercu, T.; Wadhawan, K.; Padhi, I.; Gehrmann, S.; Cipcigan, F.; Chenthamarakshan, V.; Strobelt, H.; Dos Santos, C.; Chen, P.-Y. Accelerated antimicrobial discovery via deep generative models and molecular dynamics simulations. Nat. Biomed. Eng. 2021, 5, 613–623. [Google Scholar] [CrossRef] [PubMed]
- Bengesi, S.; El-Sayed, H.; Sarker, M.K.; Houkpati, Y.; Irungu, J.; Oladunni, T. Advancements in Generative AI: A Comprehensive Review of GANs, GPT, Autoencoders, Diffusion Model, and Transformers. IEEE Access 2024, 12, 69812–69837. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Y.; Iketani, S.; Nair, M.S.; Li, Z.; Mohri, H.; Wang, M.; Yu, J.; Bowen, A.D.; Chang, J.Y. Antibody evasion by SARS-CoV-2 Omicron subvariants BA. 2.12. 1, BA. 4 and BA. 5. Nature 2022, 608, 603–608. [Google Scholar] [CrossRef]
- Mueller, B.K.; Subramaniam, S.; Senes, A. A frequent, GxxxG-mediated, transmembrane association motif is optimized for the formation of interhelical Cα–H hydrogen bonds. Proc. Natl. Acad. Sci. USA 2014, 111, E888–E895. [Google Scholar] [CrossRef]
- Shin, J.-E.; Riesselman, A.J.; Kollasch, A.W.; McMahon, C.; Simon, E.; Sander, C.; Manglik, A.; Kruse, A.C.; Marks, D.S. Protein design and variant prediction using autoregressive generative models. Nat. Commun. 2021, 12, 2403. [Google Scholar] [CrossRef]
- Popova, M.; Isayev, O.; Tropsha, A. Deep reinforcement learning for de novo drug design. Sci. Adv. 2018, 4, eaap7885. [Google Scholar] [CrossRef]
- Ingraham, J.; Garg, V.; Barzilay, R.; Jaakkola, T. Generative models for graph-based protein design. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8 December 2019; Volume 32. [Google Scholar]
- Zhou, Z.; Kearnes, S.; Li, L.; Zare, R.N.; Riley, P. Optimization of molecules via deep reinforcement learning. Sci. Rep. 2019, 9, 10752. [Google Scholar] [CrossRef] [PubMed]
- Paszke, A. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Torres, M.D.; Sothiselvam, S.; Lu, T.K.; de la Fuente-Nunez, C. Peptide design principles for antimicrobial applications. J. Mol. Biol. 2019, 431, 3547–3567. [Google Scholar] [CrossRef]
- Abramson, J.; Adler, J.; Dunger, J.; Evans, R.; Green, T.; Pritzel, A.; Ronneberger, O.; Willmore, L.; Ballard, A.J.; Bambrick, J. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 2024, 630, 493–500. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liao, H.; Meng, Y.; Li, W.; Han, P.; Liu, K.; Wang, Q.; Li, D.; Zhang, Y.; Wang, L.; et al. Structural basis of human ACE2 higher binding affinity to currently circulating Omicron SARS-CoV-2 sub-variants BA.2 and BA.1.1. Cell 2022, 185, 2952–2960.e2910. [Google Scholar] [CrossRef] [PubMed]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Dominguez, C.; Boelens, R.; Bonvin, A.M. HADDOCK: A protein—protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 2003, 125, 1731–1737. [Google Scholar] [CrossRef] [PubMed]
- Dhingra, N.; Bhardwaj, R.; Bhardwaj, U.; Kapoor, K. Design of hACE2-based small peptide inhibitors against spike protein of SARS-CoV-2: A computational approach. Struct. Chem. 2023, 34, 1843–1856. [Google Scholar] [CrossRef]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III.; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E. Amber 2021; University of California: San Francisco, CA, USA, 2021. [Google Scholar]
- Ullah, S.; Rahman, W.; Ullah, F.; Ullah, A.; Ahmad, G.; Ijaz, M.; Ullah, H.; Sharafmal, D. The HABD: Home of All Biological Databases Empowering Biological Research with Cutting-Edge Database Systems. Curr. Protoc. 2024, 4, e1063. [Google Scholar] [CrossRef]
- Ullah, S.; Ullah, F.; Rahman, W.; Ullah, A.; Haider, S.; Yueguang, C. Elucidating the inhibitory mechanism of Zika virus NS2B-NS3 protease with dipeptide inhibitors: Insights from molecular docking and molecular dynamics simulations. PLoS ONE 2024, 19, e0307902. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., 3rd; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Fukuyoshi, S.; Kometani, M.; Watanabe, Y.; Hiratsuka, M.; Yamaotsu, N.; Hirono, S.; Manabe, N.; Takahashi, O.; Oda, A. Molecular Dynamics Simulations to Investigate the Influences of Amino Acid Mutations on Protein Three-Dimensional Structures of Cytochrome P450 2D6.1, 2, 10, 14A, 51, and 62. PLoS ONE 2016, 11, e0152946. [Google Scholar] [CrossRef]
- Nangraj, A.S.; Khan, A.; Umbreen, S.; Sahar, S.; Arshad, M.; Younas, S.; Ahmad, S.; Ali, S.; Ali, S.S.; Ali, L. Insights into mutations induced conformational changes and rearrangement of Fe2+ Ion in pncA gene of mycobacterium tuberculosis to decipher the mechanism of resistance to pyrazinamide. Front. Mol. Biosci. 2021, 8, 633365. [Google Scholar] [CrossRef]
- Samad, A.; Khurshid, B.; Mahmood, A.; Rehman, A.U.; Khalid, A.; Abdalla, A.N.; Algarni, A.S.; Wadood, A. Identification of novel peptide inhibitors for oncogenic KRAS G12D as therapeutic options using mutagenesis-based remodeling and MD simulations. J. Biomol. Struct. Dyn. 2023, 41, 13425–13437. [Google Scholar] [CrossRef] [PubMed]
- Flores-Canales, J.C.; Kurnikova, M. Targeting electrostatic interactions in accelerated molecular dynamics with application to protein partial unfolding. J. Chem. Theory Comput. 2015, 11, 2550–2559. [Google Scholar] [CrossRef]
- Elber, R.; Ruymgaart, A.P.; Hess, B. SHAKE parallelization. Eur. Phys. J. Spec. Top. 2011, 200, 211–223. [Google Scholar] [CrossRef]
- DeLano, W.L. Pymol: An open-source molecular graphics tool. CCP4 Newsl. Protein Crystallogr. 2002, 40, 82–92. [Google Scholar]
- Ullah, S.; Zheng, Z.; Rahman, W.; Ullah, F.; Ullah, A.; Iqbal, M.; Iqbal, N.; Gao, T. A computational approach to fighting type 1 diabetes by targeting 2C Coxsackie B virus protein with flavonoids. PLoS ONE 2023, 18, e0290576. [Google Scholar] [CrossRef]
- Kumar, S.U.; Sankar, S.; Kumar, D.T.; Younes, S.; Younes, N.; Siva, R.; Doss, C.G.P.; Zayed, H. Molecular dynamics, residue network analysis, and cross-correlation matrix to characterize the deleterious missense mutations in GALE causing galactosemia III. Cell Biochem. Biophys. 2021, 79, 201–219. [Google Scholar] [CrossRef]
- Kumari, M.; Singh, R.; Subbarao, N. Exploring the interaction mechanism between potential inhibitor and multi-target Mur enzymes of mycobacterium tuberculosis using molecular docking, molecular dynamics simulation, principal component analysis, free energy landscape, dynamic cross-correlation matrices, vector movements, and binding free energy calculation. J. Biomol. Struct. Dyn. 2022, 40, 13497–13526. [Google Scholar] [PubMed]
- Huggins, D.J.; Biggin, P.C.; Dämgen, M.A.; Essex, J.W.; Harris, S.A.; Henchman, R.H.; Khalid, S.; Kuzmanic, A.; Laughton, C.A.; Michel, J. Biomolecular simulations: From dynamics and mechanisms to computational assays of biological activity. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 9, e1393. [Google Scholar] [CrossRef]
- Giuliani, A. The application of principal component analysis to drug discovery and biomedical data. Drug Discov. Today 2017, 22, 1069–1076. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Stanzione, F.; Giangreco, I.; Cole, J.C. Use of molecular docking computational tools in drug discovery. Prog. Med. Chem. 2021, 60, 273–343. [Google Scholar] [PubMed]
- Roe, D.R.; Cheatham, T.E., 3rd. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Limongelli, V. Ligand binding free energy and kinetics calculation in 2020. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1455. [Google Scholar] [CrossRef]
- Amadei, A.; Linssen, A.B.; Berendsen, H.J. Essential dynamics of proteins. Proteins Struct. Funct. Bioinform. 1993, 17, 412–425. [Google Scholar] [CrossRef]
- Laskowski, R.A.; Swindells, M.B. LigPlot+: Multiple Ligand–Protein Interaction Diagrams for Drug Discovery; ACS Publications: Washington, DC, USA, 2011. [Google Scholar]
- Dimitrov, I.; Bangov, I.; Flower, D.R.; Doytchinova, I. AllerTOP v. 2—A server for in silico prediction of allergens. J. Mol. Model. 2014, 20, 2278. [Google Scholar] [CrossRef]
- Rathore, A.S.; Choudhury, S.; Arora, A.; Tijare, P.; Raghava, G.P. ToxinPred 3.0: An improved method for predicting the toxicity of peptides. Comput. Biol. Med. 2024, 179, 108926. [Google Scholar] [CrossRef]
- Han, S.; Zhao, G.; Wei, Z.; Chen, Y.; Zhao, J.; He, Y.; He, Y.J.; Gao, J.; Chen, S.; Du, C.; et al. An angiotensin-converting enzyme-2-derived heptapeptide GK-7 for SARS-CoV-2 spike blockade. Peptides 2021, 145, 170638. [Google Scholar] [CrossRef]
- Pei, P.; Qin, H.; Chen, J.; Wang, F.; He, C.; He, S.; Hong, B.; Liu, K.; Qiao, R.; Fan, H.; et al. Computational design of ultrashort peptide inhibitors of the receptor-binding domain of the SARS-CoV-2 S protein. Brief. Bioinform. 2021, 22, bbab243. [Google Scholar] [CrossRef]
- Garg, V.K.; Avashthi, H.; Tiwari, A.; Jain, P.A.; Ramkete, P.W.; Kayastha, A.M.; Singh, V.K. MFPPI–multi FASTA ProtParam interface. Bioinformation 2016, 12, 74. [Google Scholar] [CrossRef]
- Zazeri, G.; Povinelli, A.P.R.; Le Duff, C.S.; Tang, B.; Cornelio, M.L.; Jones, A.M. Synthesis and Spectroscopic Analysis of Piperine- and Piperlongumine-Inspired Natural Product Scaffolds and Their Molecular Docking with IL-1β and NF-κB Proteins. Molecules 2020, 25, 2841. [Google Scholar] [CrossRef]
- Zazeri, G.; Povinelli, A.P.R.; Pavan, N.M.; Jones, A.M.; Ximenes, V.F. Solvent-Induced Lag Phase during the Formation of Lysozyme Amyloid Fibrils Triggered by Sodium Dodecyl Sulfate: Biophysical Experimental and In Silico Study of Solvent Effects. Molecules 2023, 28, 6891. [Google Scholar] [CrossRef]
- Salo-Ahen, O.M.; Alanko, I.; Bhadane, R.; Bonvin, A.M.; Honorato, R.V.; Hossain, S.; Juffer, A.H.; Kabedev, A.; Lahtela-Kakkonen, M.; Larsen, A.S. Molecular dynamics simulations in drug discovery and pharmaceutical development. Processes 2020, 9, 71. [Google Scholar] [CrossRef]
- Shukla, R.; Tripathi, T. Molecular dynamics simulation of protein and protein–ligand complexes. In Computer-Aided Drug Design; Springer Nature: Cham, Switzerland, 2020; pp. 133–161. [Google Scholar]
- Pal, P.; Chakraborty, S.; Jana, B. Number of hydrogen bonds per unit solvent accessible surface area: A descriptor of functional states of proteins. J. Phys. Chem. B 2022, 126, 10822–10833. [Google Scholar] [CrossRef]
- Wei, G.; Xi, W.; Nussinov, R.; Ma, B. Protein ensembles: How does nature harness thermodynamic fluctuations for life? The diverse functional roles of conformational ensembles in the cell. Chem. Rev. 2016, 116, 6516–6551. [Google Scholar] [CrossRef]
- Liu, Z. Principal Component Analysis and Normal Mode Analysis of Elastic Network Models and Their Applications to Myosin Motor Proteins; Wayne State University: Detroit, MI, USA, 2022. [Google Scholar]
- Deganutti, G.; Liang, Y.-L.; Zhang, X.; Khoshouei, M.; Clydesdale, L.; Belousoff, M.J.; Venugopal, H.; Truong, T.T.; Glukhova, A.; Keller, A.N. Dynamics of GLP-1R peptide agonist engagement are correlated with kinetics of G protein activation. Nat. Commun. 2022, 13, 92. [Google Scholar] [CrossRef]
- Ostermeir, K.; Zacharias, M. Rapid alchemical free energy calculation employing a generalized born implicit solvent model. J. Phys. Chem. B 2015, 119, 968–975. [Google Scholar] [CrossRef]
- Wang, E.; Sun, H.; Wang, J.; Wang, Z.; Liu, H.; Zhang, J.Z.; Hou, T. End-point binding free energy calculation with MM/PBSA and MM/GBSA: Strategies and applications in drug design. Chem. Rev. 2019, 119, 9478–9508. [Google Scholar] [CrossRef]
- Varghese, J.J.; Mushrif, S.H. Origins of complex solvent effects on chemical reactivity and computational tools to investigate them: A review. React. Chem. Eng. 2019, 4, 165–206. [Google Scholar] [CrossRef]
- Ullah, S.; Ullah, F.; Rahman, W.; Karras, D.; Ullah, A.; Gulzar, M.; Ijaz, M.; Gao, T.; Lab, S.K.; Pakhtunkhwa, K. The Cancer Research Database (CRDB): Integrated Platform to Gain Statistical Insight Into the Correlation Between Cancer and COVID-19. JMIR Cancer 2022, 8, e35020. [Google Scholar] [CrossRef]
- Khandia, R.; Singhal, S.; Alqahtani, T.; Kamal, M.A.; Nahed, A.; Nainu, F.; Desingu, P.A.; Dhama, K. Emergence of SARS-CoV-2 Omicron (B.1.1.529) variant, salient features, high global health concerns and strategies to counter it amid ongoing COVID-19 pandemic. Environ. Res. 2022, 209, 112816. [Google Scholar] [CrossRef]
- Jung, C.; Kmiec, D.; Koepke, L.; Zech, F.; Jacob, T.; Sparrer, K.M.; Kirchhoff, F. Omicron: What makes the latest SARS-CoV-2 variant of concern so concerning? J. Virol. 2022, 96, e02077-21. [Google Scholar] [CrossRef] [PubMed]
- Mengist, H.M.; Kombe Kombe, A.J.; Mekonnen, D.; Abebaw, A.; Getachew, M.; Jin, T. Mutations of SARS-CoV-2 spike protein: Implications on immune evasion and vaccine-induced immunity. Semin. Immunol. 2021, 55, 101533. [Google Scholar] [CrossRef] [PubMed]
- Ullah, S.; Rahman, W.; Ullah, F.; Ullah, A.; Jehan, R.; Iqbal, M.; Ali, I.; Tianshun, G. Identification of lead compound screened from the natural products atlas to treat renal inflammasomes using molecular docking and dynamics simulation. J. Biomol. Struct. Dyn. 2023, 42, 4851–4861. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Zhu, K.L.; Jiang, X.L.; Wang, X.J.; Zhan, B.D.; Gao, H.X.; Geng, X.Y.; Duan, L.J.; Dai, E.H.; Ma, M.J. Omicron subvariants escape antibodies elicited by vaccination and BA.2.2 infection. Lancet. Infect. Dis. 2022, 22, 1116–1117. [Google Scholar] [CrossRef]
- Titus, R.; Mandal, M.; Dutta, G. Electrochemical biosensor designs used for detecting SARS-CoV-2 virus: A review. Next Gener. Smart Nano-Bio-Devices 2022, 147, 187–209. [Google Scholar]
- Kennedy, D.A.; Read, A.F. Why the evolution of vaccine resistance is less of a concern than the evolution of drug resistance. Proc. Natl. Acad. Sci. USA 2018, 115, 12878–12886. [Google Scholar] [CrossRef]
| Name | Peptide Seq | Toxicity | Solubility | Allergenicity |
|---|---|---|---|---|
| MSK-1 | FYNWLDKQHRYIFHHIFVHIRQDN SAVSLASLVKQTTNKFTWEARMD | Non-toxic | Goodwater solubility | Non-allergen |
| MSK-2 | RPKQLDKQHNRASYWNFYHERQ DGPPNSYRLANLVKWTKNRQTYE ETRWT | Non-toxic | Goodwater solubility | Non-allergen |
| MSK-3 MSK-4 | WLTLDARRQEEYWYRKQKAETS EYWVGEELQKENHADYRKMWN EAIYRHSGIEL WLTLDARRQEEYWYRKQKETSE YWVGEELQKENHADYRKMWNE AIYRHSG | Non-toxic Non-toxic | Goodwater solubility Goodwater solubility | Non-allergen Non-allergen |
| MSK-5 | STIEE----SSLAS | Non-toxic | Goodwater solubility | Allergen |
| GKGDFRI [60] | Non-toxic | Goodwater solubility | Allergen | |
| QAKTFLD [61] | Non-toxic | Goodwater solubility | Allergen |
| Peptide | Length | Pep Mass Dalton | Charge | Pi | Hydrophobicity (Wimley–White Whole-Residue) | Hydropathy Value | Boman Index (kcal/mol) |
|---|---|---|---|---|---|---|---|
| MSK-1 | 47 | 5793.57 | +3 | 9.40 | 3.38 | −0.55 | 2.16 kcal/mol |
| MSK-2 | 50 | 6308.95 | +5.5 | 9.99 | 12.57 | −1.87 | 3.97 kcal/mol |
| MSK-3 | 54 | 6835.55 | −1.5 | 5.62 | 17.69 | −1.42 | 3.2 kcal/mol |
| MSK-4 | 50 | 6409.03 | −0.5 | 6.11 | 16.37 | −1.67 | 3.55 kcal/mol |
| Parameter | MSK-1 | MSK-2 | MSK-3 | MSK-4 |
|---|---|---|---|---|
| HADDOCK score | −106.4 ± 4.3 | −126.2 ± 5.6 | −125.7 ± 4.3 | −127.8 ± 4.3 |
| Cluster size | 17 | 29 | 28 | 26 |
| RMSD | 10.0 ± 0.4 | 11.6 ± 0.0 | 0.4 ± 0.2 | 0.8 ± 0.2 |
| VdW energy | −74.5 ± 8.7 | −88.1 ± 3.5 | −74.7 ± 4.9 | −77.6 ± 3.6 |
| Electrostatic energy | −176.2 ± 9.6 | −197.9 ± 30.2 | −277.3 ± 10.9 | −283.3 ± 11.9 |
| Desolvation energy | −42.4 ± 3.7 | −42.1 ± 2.5 | −23.2 ± 2.6 | −42.2 ± 2.9 |
| Restraint’s violation of energy | 457.6 ± 37.1 | 436.0 ± 25.3 | 467.2 ± 66.6 | 447.2 ± 65.6 |
| Buried Surface Area | 2111.3 ± 99.9 | 2569.3 ± 79.7 | 2260.1 ± 155.1 | 2150.1 ± 148.1 |
| Z-score | −2.3 | −1.8 | −2.0 | −2.4 |
| Peptides | Hydrogen Bond Interaction Residues | Other Interactions | Salt Bridge Interaction | π-Cation Interaction Residues |
|---|---|---|---|---|
| MSK-1 | Tyr117,Arg166,Glu139,Asn149, Gly153,Arg161,ALA143, Thr168 | Asn145, Lys146, Val151, Phe154, Tyr157, Tyr157, Phe124, Ser164, Ser114, | Arg46, | Phe154, Tyr114 |
| MSK-2 | Tyr1117,Ala143,Ala152, Phe154,Asn155,Arg161, Ser164, Arg166, Thr168 | Lys146, Tyr157, Tyr121, His173, Gly172, Lys112, Val171 | Asp23, | N/A |
| MSK-3 | Lys112, Tyr117, Tyr121, Lys146, Ala152, Asn155, Tyr157, arg161, Ser162, Arg166, Glu172, His173 | Pro147, Asn149, Val151, Phe154, Glu139, Thr138, Phe158, Leu160, Asn118, Arg114, Tyr169, Arg71 | Asp45 | Tyr117 |
| MSK-4 | Lys112, Glu139, Lys146, Pro147, Cyc148, Asn149, Phe154, Leu160, Arg161, Glu172, His173 | Asn155, Ile140, Val151, Tyr157, Phe158, Trp35, Tyr117, Ser164, Arg166, Ser114 | Glu27, Arg38, Glu10 | N/A |
| No. | Peptides | VDWAALS | EGB | EEL | ESURF | ΔTotal |
|---|---|---|---|---|---|---|
| 2 | MSK-1 | −72.1669 | −45.7232 | 95.7396 | −9.2874 | −47.4379 |
| 3 | MSK-2 | −62.0268 | −86.7830 | 110.4271 | −8.4317 | −46.8144 |
| 4 | MSK-3 | −74.8832 | 383.2921 | −344.3527 | −10.0074 | −45.9512 |
| 5 | MSK-4 | −59.7891 | 327.9998 | −294.1442 | −9.4503 | −53.3838 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, F.; Xiao, A.; Ullah, S.; Yang, N.; Lei, M.; Chen, L.; Wang, S. Synergizing Attribute-Guided Latent Space Exploration (AGLSE) with Classical Molecular Simulations to Design Potent Pep-Magnet Peptide Inhibitors to Abrogate SARS-CoV-2 Host Cell Entry. Viruses 2025, 17, 828. https://doi.org/10.3390/v17060828
Ullah F, Xiao A, Ullah S, Yang N, Lei M, Chen L, Wang S. Synergizing Attribute-Guided Latent Space Exploration (AGLSE) with Classical Molecular Simulations to Design Potent Pep-Magnet Peptide Inhibitors to Abrogate SARS-CoV-2 Host Cell Entry. Viruses. 2025; 17(6):828. https://doi.org/10.3390/v17060828
Chicago/Turabian StyleUllah, Farhan, Aobo Xiao, Shahid Ullah, Na Yang, Min Lei, Liang Chen, and Sheng Wang. 2025. "Synergizing Attribute-Guided Latent Space Exploration (AGLSE) with Classical Molecular Simulations to Design Potent Pep-Magnet Peptide Inhibitors to Abrogate SARS-CoV-2 Host Cell Entry" Viruses 17, no. 6: 828. https://doi.org/10.3390/v17060828
APA StyleUllah, F., Xiao, A., Ullah, S., Yang, N., Lei, M., Chen, L., & Wang, S. (2025). Synergizing Attribute-Guided Latent Space Exploration (AGLSE) with Classical Molecular Simulations to Design Potent Pep-Magnet Peptide Inhibitors to Abrogate SARS-CoV-2 Host Cell Entry. Viruses, 17(6), 828. https://doi.org/10.3390/v17060828







