Effects of Mosquito Biology on Modeled Chikungunya Virus Invasion Potential in Florida
Abstract
1. Introduction
2. Materials and Methods
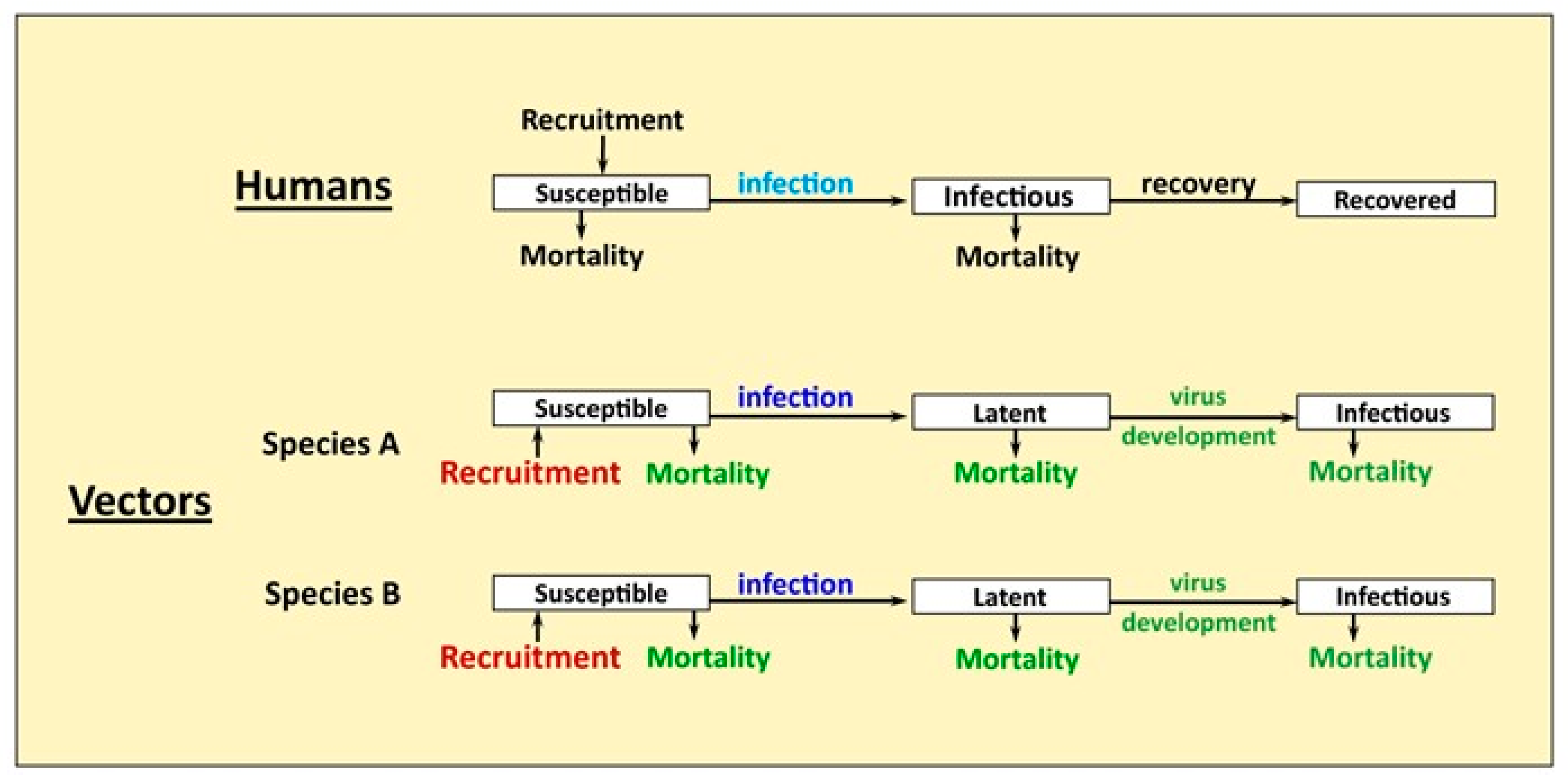
2.1. Model Structure
2.1.1. Temperature Cycle
2.1.2. Human Population
2.1.3. Mosquito Population Dynamics and Seasonality
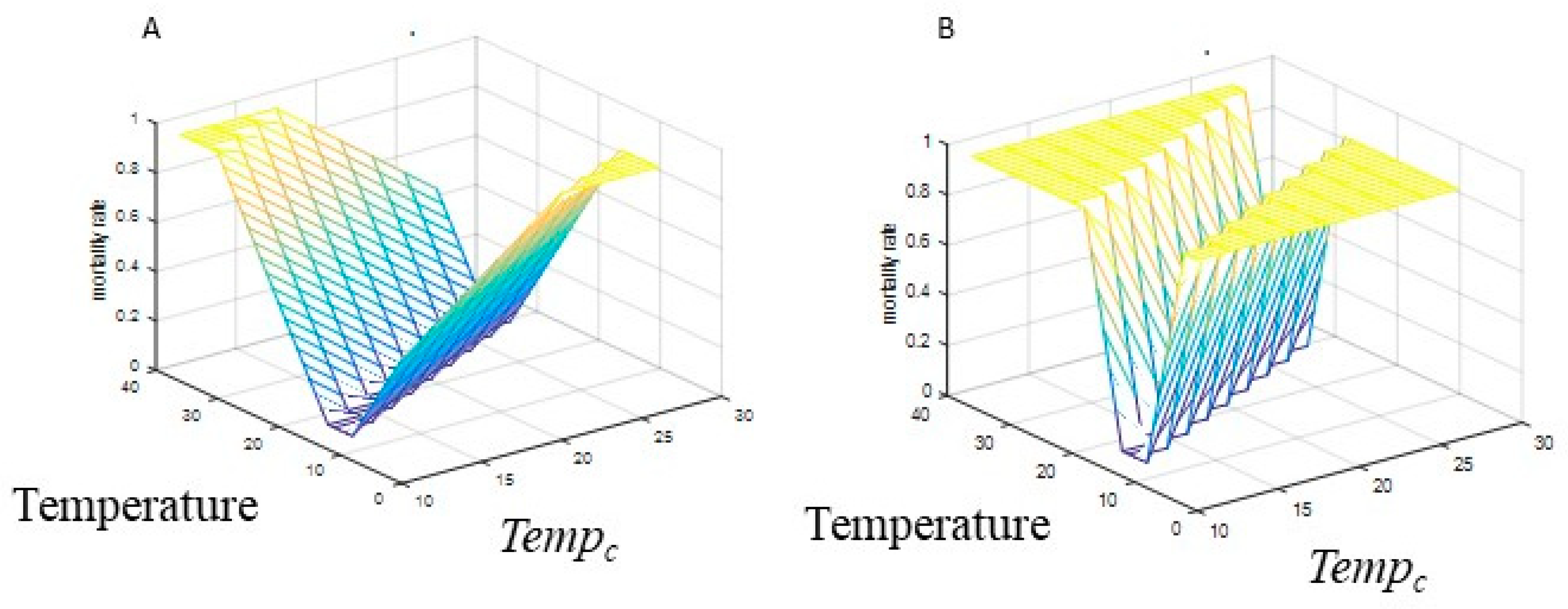
2.1.4. Mosquito Mortality
2.1.5. Virus Development in Mosquitoes and Vector Competence
2.1.6. Model Equations
2.2. Parameter Values and Sensitivity Analysis
2.2.1. Mosquito Population Dynamics and Seasonality
2.2.2. Mosquito Mortality
2.2.3. Biting Rate
2.2.4. Vector Competence and Virus Development in Mosquitoes
2.2.5. Outcome Variables
2.2.6. Analysis
3. Results
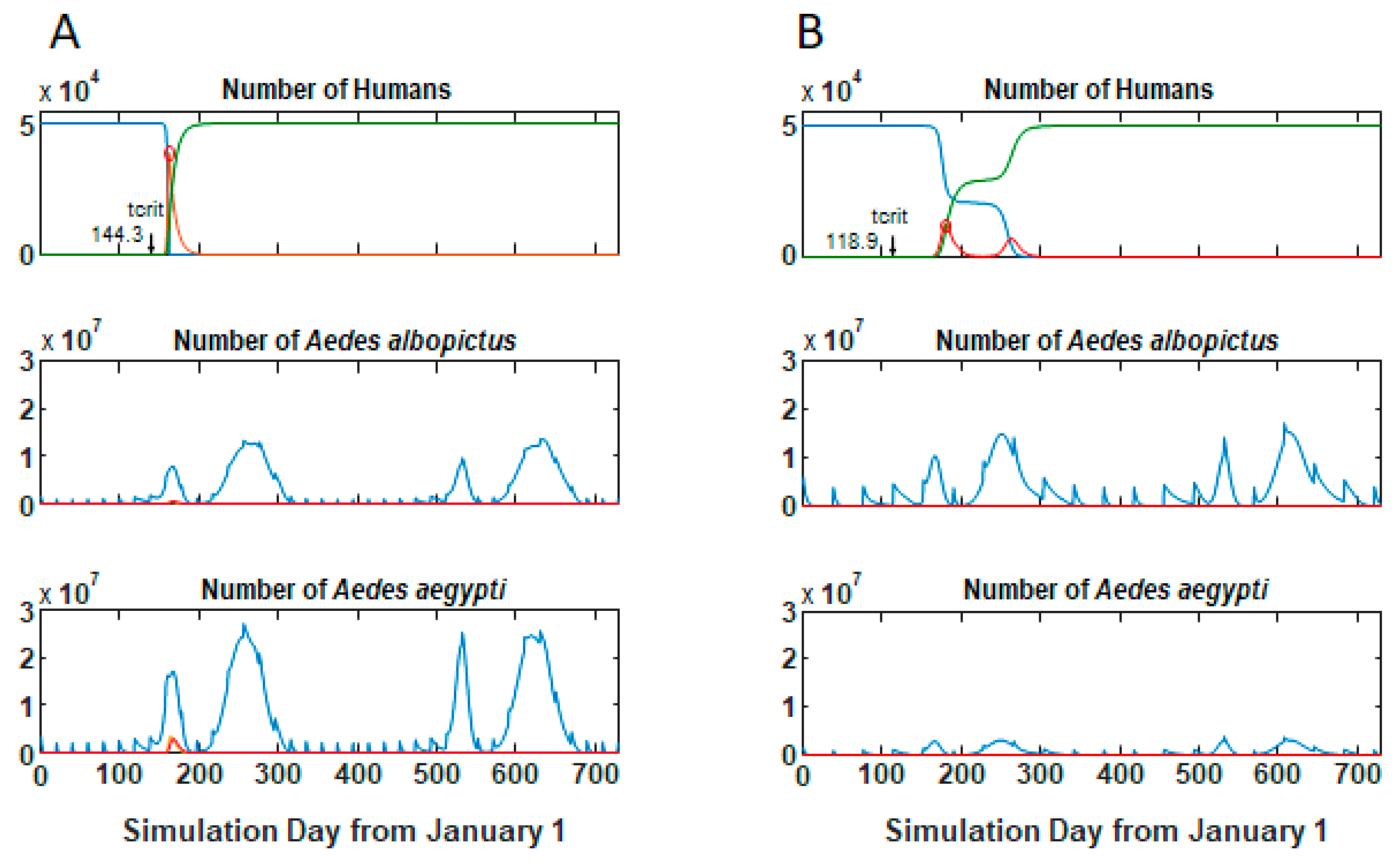
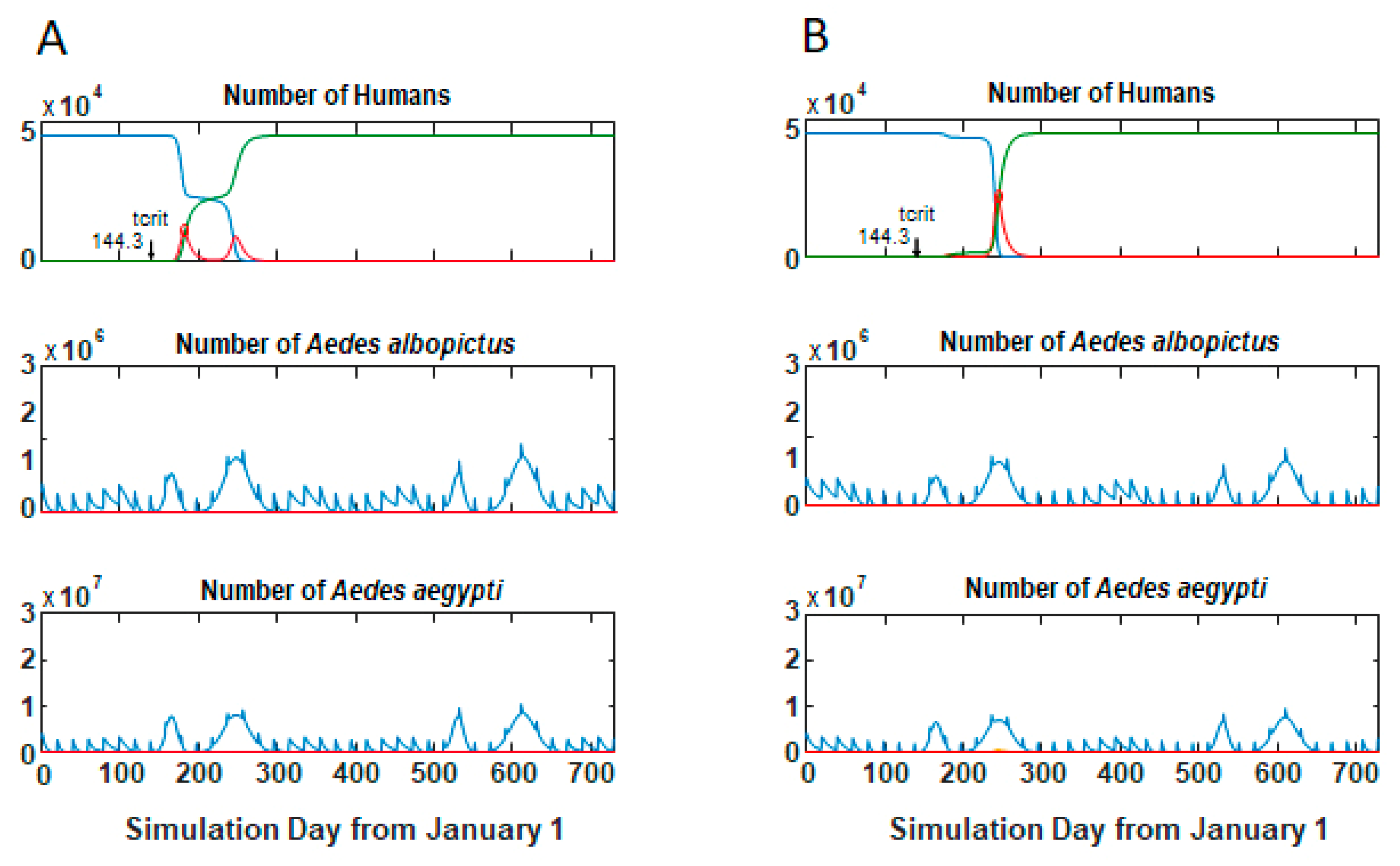
3.1. Epidemic Behavior
3.2. Size and Lag Time of Epidemics
3.3. Comparisons of Parameter Sets Across Tempc
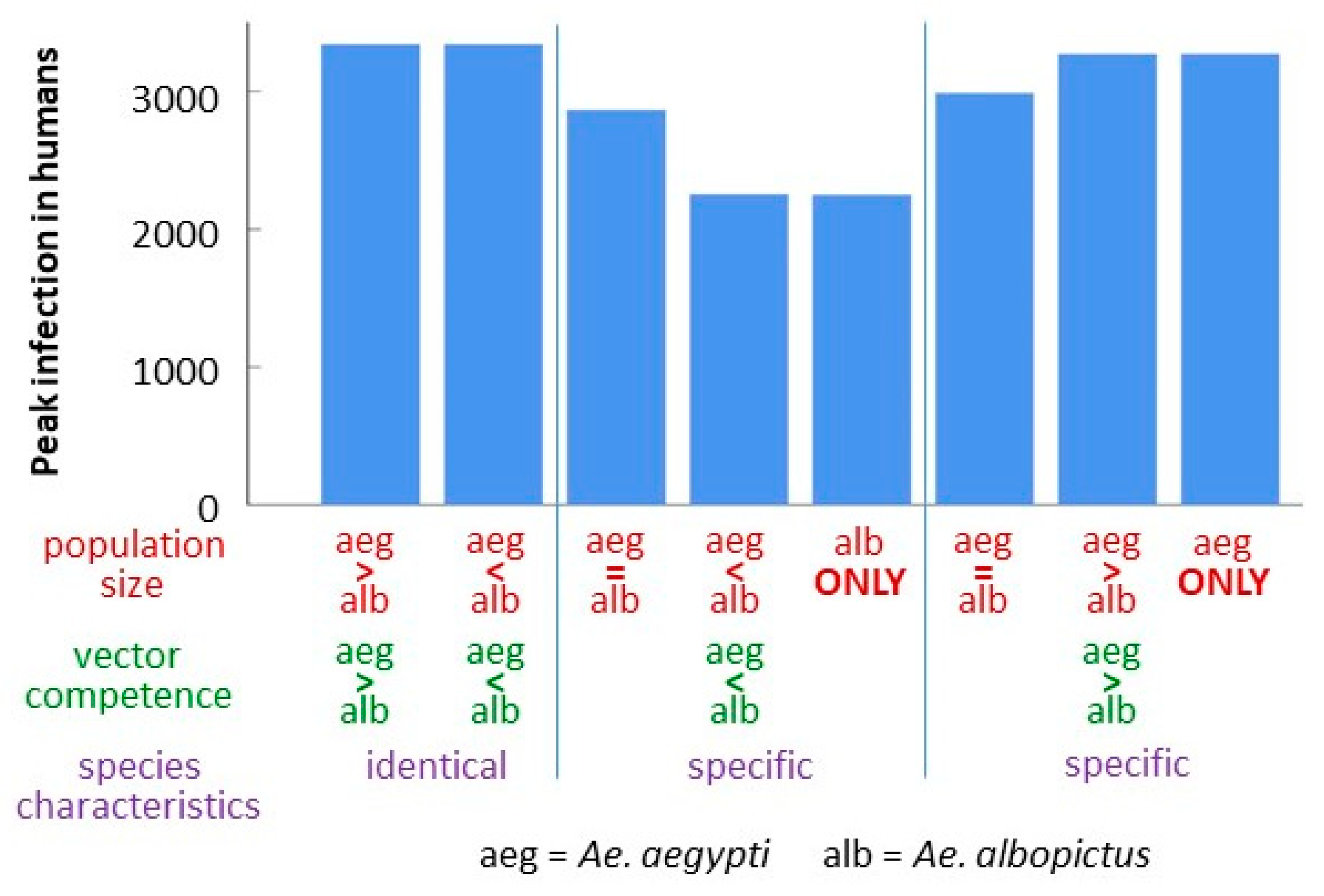
3.4. Comparison of Strain-Species Combinations
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zeller, H.; Van Bortel, W.; Sudre, B. Chikungunya: Its history in Africa and Asia and its spread to new regions in 2013–2014. J. Infec. Dis. 2016, 214, S436–S440. [Google Scholar] [CrossRef]
- Morrison, T.E. Reemergence of Chikungunya virus. J. Virol. 2014, 88, 11644–11647. [Google Scholar] [CrossRef]
- Langsjoen, R.M.; Haller, S.L.; Roy, C.J.; Vinet-Oliphant, H.; Bergren, N.A.; Erasmus, J.H.; Livengood, J.A.; Powell, T.D.; Weaver, S.C.; Rossi, S.L. Chikungunya virus strains show lineage-specific variations in virulence and cross-protective ability in murine and nonhuman primate models. mBio 2018, 9. [Google Scholar] [CrossRef]
- Tsetsarkin, K.A.; Vanlandingham, D.L.; McGee, C.E.; Higgs, S. A single mutation in Chikungunya virus affects vector specificity and epidemic potential. PLoS Pathog. 2007, 3, 1895–1906. [Google Scholar] [CrossRef] [PubMed]
- ECDC. Chikungunya Worldwide Overview. Available online: https://www.ecdc.europa.eu/en/chikungunya-monthly (accessed on 6 May 2020).
- BMOS. Monitoramento dos Casos de Arboviroses Urbanas Transmitidas Pelo Aedes (Dengue, Chikungunya e Zika), Semanas Epidemiológicas 1 a 22. 2020. Available online: https://www.saude.gov.br/boletins-epidemiologicos (accessed on 23 June 2020). (In Portuguese)
- Souza, T.M.L.; Vieira, Y.R.; Delatorre, E.; Barbosa-Lima, G.; Luiz, R.L.F.; Vizzoni, A.; Jain, K.; Miranda, M.M.; Bhuva, N.; Gogarten, J.F.; et al. Emergence of the East-Central-South-African genotype of Chikungunya virus in Brazil and the city of Rio de Janeiro may have occurred years before surveillance detection. Sci. Rep. 2019, 9, 2760. [Google Scholar] [CrossRef] [PubMed]
- Trout, A.; Baracco, G.; Rodriguez, M.; Barber, J.; Leal, A.; Radke, E.; Weis, K.; Stanek, D.; Stark, L.; Blackmore, C.; et al. Locally acquired dengue-Key West, Florida, 2009-2010. J. Amer. Med. Assoc. 2010, 303, 2465–2468. [Google Scholar]
- FLDOH. Dengue Fever. Available online: http://www.floridahealth.gov/diseases-and-conditions/dengue/ (accessed on 6 May 2020).
- Messenger, A.M. Serological evidence of ongoing transmission of Dengue virus in permanent residents of Key West, Florida. Vector. Borne. Zoon. Dis. 2014, 14, 783–787. [Google Scholar] [CrossRef]
- Rey, J.R. Dengue in Florida (USA). Insects 2014, 5, 991–1000. [Google Scholar] [CrossRef]
- FLDOH. Chikungunya Fever (CHIK). Available online: http://www.floridahealth.gov/diseases-and-conditions/chikungunya/index.html/ (accessed on 6 May 2020).
- Kendrick, K.D.; Stanek, C.; Blackmore, C. Transmission of Chikungunya virus in the Continental United States–Florida, 2014. MMWR 2014, 63, 1137. [Google Scholar]
- Hennessey, M.; Fischer, M.; Staples, J.E. Zika virus spreads to new areas—region of the Americas, May 2015–January 2016. Am. J. Transplant. 2016, 16, 1031–1034. [Google Scholar] [CrossRef]
- Likos, A.; Griffin, I.; Bingham, A.M.; Stanek, D.; Fischer, M.; White, S.; Hamilton, J.; Eisenstein, L.; Atrubin, D.; Mulay, P.; et al. Local mosquito-borne transmission of Zika virus—Miami-Dade and Broward Counties, Florida, June-August 2016. MMWR 2016, 65, 1032–1038. [Google Scholar] [CrossRef] [PubMed]
- Focks, D.A.; Daniels, E.; Haile, D.G.; Keesling, J.E. A simulation model of the epidemiology of urban Dengue fever: Literature analysis, model development, preliminary validation, and samples of simulation results. Am. J. Trop. Med. Hyg. 1995, 53, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Lord, C.C.; Day, J.F. Simulation studies of St. Louis encephalitis in South Florida. Vector. Borne. Zoon. Dis. 2001, 1, 299–316. [Google Scholar] [CrossRef] [PubMed]
- Lord, C.C.; Day, J.F. Simulation studies of St. Louis encephalitis and West Nile viruses: The impact of bird mortality. Vector. Borne. Zoon. Dis. 2001, 1, 317–330. [Google Scholar] [CrossRef]
- Lord, C.C. The effect of multiple vectors on arbovirus transmission. Israel J. Ecol. Evol. 2010, 55, 371–392. [Google Scholar] [CrossRef]
- Manore, C.A.; Hickmann, K.S.; Xu, S.; Wearing, H.J.; Hyman, J.M. Comparing Dengue and Chikungunya emergence and endemic transmission in A. aegypti and A. albopictus. J. Theor. Biol. 2014, 356, 174–191. [Google Scholar] [CrossRef]
- Andraud, M.; Hens, N.; Marais, C.; Beutels, P. Dynamic epidemiological models for Dengue transmission: A systematic review of structural approaches. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Wonham, M.J.; Lewis, M.A.; Rencławowicz, J.; Van Den Driessche, P. Transmission assumptions generate conflicting predictions in host–vector disease models: A case study in West Nile virus. Ecol. Lett. 2006, 9, 706–725. [Google Scholar] [CrossRef]
- Reiner, R.C.; Perkins, T.A.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.C.; Bisanzio, D.; et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J. Roy. Soc. Inter. 2013, 10, 20120921. [Google Scholar] [CrossRef]
- Smith, D.L.; Perkins, T.A.; Reiner, R.C., Jr.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.C.; et al. Recasting the theory of mosquito-borne pathogen transmission dynamics and control. Trans. Roy. Soc. Trop. Med. Hyg. 2014, 108, 185–197. [Google Scholar] [CrossRef]
- Mordecai, E.A.; Cohen, J.M.; Evans, M.V.; Gudapati, P.; Johnson, L.R.; Lippi, C.A.; Miazgowicz, K.; Murdock, C.C.; Rohr, J.R.; Ryan, S.J.; et al. Detecting the impact of temperature on transmission of Zika, Dengue, and Chikungunya using mechanistic models. PLoS Negl. Trop. Dis. 2017, 11. [Google Scholar] [CrossRef] [PubMed]
- Bellan, S.E. The importance of age dependent mortality and the extrinsic incubation period in models of mosquito-borne disease transmission and control. PLoS ONE 2010, 5. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.M.; Macoris, M.L.G.; Galvani, K.C.; Andrighetti, M.T.M.; Wanderley, D.M.V. Assessing the effects of temperature on the population of Aedes aegypti, the vector of Dengue. Epidemiol. Infect. 2009, 137, 1188–1202. [Google Scholar] [CrossRef] [PubMed]
- O’Meara, G.F.; Gettman, A.D.; Evans, L.F., Jr.; Curtis, G.A. The spread of Aedes albopictus in Florida. Am. Entomol. 1993, 39, 163–173. [Google Scholar] [CrossRef]
- O’Meara, G.F.; Evans, L.F.; Gettman, A.D.; Cuda, J.P. Spread of Aedes albopictus and decline of Aedes aegypti (Diptera: Culicidae) in Florida. J. Med. Entomol. 1995, 32, 554–562. [Google Scholar] [CrossRef]
- Reiskind, M.H.; Lounibos, L.P. Spatial and temporal patterns of abundance of Aedes aegypti L. (Stegomyia aegypti) and Aedes albopictus (Skuse) [Stegomyia albopictus (Skuse)] in southern Florida. Med. Vet. Entomol. 2013, 27, 421–429. [Google Scholar] [CrossRef]
- Lounibos, L.P.; Bargielowski, I.E.; Carrasquilla, M.C.; Nishimura, N. Coexistence of Aedes aegypti and Aedes albopictus (Diptera: Culicidae) in peninsular Florida two decades after competitive displacements. J. Med. Entomol. 2016, 53, 1385–1390. [Google Scholar] [CrossRef]
- Parker, C.; Ramirez, D.; Thomas, C.; Rutledge, C.C. Baseline susceptibility status of Florida populations of Aedes aegypti (Diptera: Culicidae) and Aedes albopictus. J. Med. Entomol. 2020. [Google Scholar] [CrossRef]
- Scott, T.W.; Chow, E.; Strickman, D.; Kittayapong, P.; Wirtz, R.A.; Lorenz, L.H.; Edman, J.D. Blood-feeding patterns of Aedes aegypti (Diptera: Culicidae) collected in a rural Thai village. J. Med. Entomol. 1993, 30, 922–927. [Google Scholar] [CrossRef]
- Scott, T.W.; Amerasinghe, P.H.; Morrison, A.C.; Lorenz, L.H.; Clark, G.G.; Strickman, D.; Kittayapong, P.; Edman, J.D. Longitudinal studies of Aedes aegypti (Diptera: Culicidae) in Thailand and Puerto Rico: Blood feeding frequency. J. Med. Entomol. 2000, 37, 89–101. [Google Scholar] [CrossRef]
- Richards, S.L.; Ponnusamy, L.; Unnasch, T.R.; Hassan, H.K.; Apperson, C.S. Host-feeding patterns of Aedes albopictus (Diptera: Culicidae) in relation to availability of human and domestic animals in suburban landscapes of central North Carolina. J. Med. Entomol. 2006, 43, 543–551. [Google Scholar] [CrossRef]
- Lounibos, L.P.; Kramer, L.D. Invasiveness of Aedes aegypti and Aedes albopictus and vectorial capacity for Chikungunya virus. J. Infect. Dis. 2016, 214, S453–S458. [Google Scholar] [CrossRef] [PubMed]
- Stenn, T.; Peck, K.J.; Rocha Pereira, G.; Burkett-Cadena, N.D. Vertebrate hosts of Aedes aegypti, Aedes albopictus, and Culex quinquefasciatus (Diptera: Culicidae) as potential vectors of Zika virus in Florida. J. Med. Entomol. 2019, 56, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Gasque, P.; Bandjee, M.C.J.; Reyes, M.M.; Viasus, D. Chikungunya pathogenesis: From the clinics to the bench. J. Infect. Dis. 2016, 214, S446–S448. [Google Scholar] [CrossRef] [PubMed]
- Staples, J.E.; Breiman, R.F.; Powers, A.M. Chikungunya fever: An epidemiological review of a re-emerging infectious disease. Clin. Infect. Dis. 2009, 49, 942–948. [Google Scholar] [CrossRef]
- Pardigon, N. The biology of Chikungunya: A brief review of what we still do not know. Pathol. Biol. 2009, 57, 127–132. [Google Scholar] [CrossRef] [PubMed]
- Powers, A.M. How Chikungunya virus virology affects its epidemiology and transmission: Implications for influencing public health. J. Infect. Dis. 2016, 214, S449–S452. [Google Scholar] [CrossRef]
- Riswari, S.F.; Ma’roef, C.N.; Djauhari, H.; Kosasih, H.; Perkasa, A.; Yudhaputri, F.A.; Artika, I.M.; Williams, M.; van der Ven, A.; Myint, K.S.; et al. Study of viremic profile in febrile specimens of Chikungunya in Bandung, Indonesia. J. Clin. Virol. 2016, 74, 61–65. [Google Scholar] [CrossRef]
- Xiao, F.-Z.; Zhang, Y.; Deng, Y.-Q.; He, S.; Xie, H.-G.; Zhou, X.-N.; Yan, Y.-S. The effect of temperature on the extrinsic incubation period and infection rate of dengue virus serotype 2 infection in Aedes albopictus. Arch. Virol. 2014, 159, 3053–3057. [Google Scholar] [CrossRef]
- Chan, M.; Johansson, M.A. The incubation periods of Dengue viruses. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Reisen, W.K.; Fang, Y.; Lothrop, H.D.; Martinez, V.M.; Wilson, J.; O’Connor, P.; Carney, R.; Cahoon-Young, B.; Shafii, M.; Brault, A.C. Overwintering of West Nile virus in Southern California. J. Med. Entomol. 2006, 43, 344–355. [Google Scholar] [CrossRef] [PubMed]
- Vega-Rúa, A.; Zouache, K.; Girod, R.; Failloux, A.-B.; Lourenco-De-Oliveira, R. High vector competence of Aedes aegypti and Aedes albopictus from ten American countries as a crucial factor of the spread of Chikungunya. J. Virol. 2014, 90. [Google Scholar] [CrossRef] [PubMed]
- Zouache, K.; Fontaine, A.; Vega-Rua, A.; Mousson, L.; Thiberge, J.-M.; Lourenco-De-Oliveira, R.; Caro, V.; Lambrechts, L.; Failloux, A.-B. Three-way interactions between mosquito population, viral strain and temperature underlying chikungunya virus transmission potential. Proc. Roy. Soc. B 2014, 281, 20141078. [Google Scholar] [CrossRef] [PubMed]
- Dubrulle, M.; Mousson, L.; Moutailler, S.; Vazeille, M.; Failloux, A.-B. Chikungunya virus and Aedes mosquitoes: Saliva is infectious as soon as two days after oral infection. PLoS ONE 2009, 4. [Google Scholar] [CrossRef]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example. Int. Stat. Rev. 1994, 62, 229–243. [Google Scholar] [CrossRef]
- Lounibos, L.; Escher, R.; Lourenço-de-Oliveira, R. Asymmetric evolution of photoperiodic diapause in temperate and tropical invasive populations of Aedes albopictus (Diptera: Culicidae). Annals. Entomol. Soc. Am. 2003, 96, 512–518. [Google Scholar] [CrossRef]
- Juliano, S.A.; O’Meara, G.F.; Morrill, J.R.; Cutwa, M.M. Desiccation and thermal tolerance of eggs and the coexistence of competing mosquitoes. Oecologia 2002, 130, 458–469. [Google Scholar] [CrossRef]
- Brady, O.J.; Johansson, M.A.; Guerra, C.A.; Bhatt, S.; Golding, N.; Pigott, D.M.; Delatte, H.; Grech, M.G.; Leisnham, P.T.; Maciel-de-Freitas, R.; et al. Modelling adult Aedes aegypti and Aedes albopictus survival at different temperatures in laboratory and field settings. Parasites Vectors 2013, 6. [Google Scholar] [CrossRef]
- Scott, T.W.; Morrison, A.C.; Lorenz, L.H.; Clark, G.G.; Strickman, D.; Kittayapong, P.; Zhou, H.; Edman, J.D. Longitudinal studies of Aedes aegypti (Diptera: Culicidae) in Thailand and Puerto Rico: Population dynamics. J. Med. Entomol. 2000, 37, 77–88. [Google Scholar] [CrossRef]
- Ponlawat, A.; Harrington, L.C. Blood feeding patterns of Aedes aegypti and Aedes albopictus in Thailand. J. Med. Entomol. 2005, 42, 844–849. [Google Scholar] [CrossRef]
- Vega-Rua, A.; Lourenco-de-Oliveira, R.; Mousson, L.; Vazeille, M.; Fuchs, S.; Yebakima, A.; Gustave, J.; Girod, R.; Dusfour, I.; Leparc-Goffart, I.; et al. Chikungunya virus transmission potential by local Aedes mosquitoes in the Americas and Europe. PLoS Negl. Trop. Dis. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Alto, B.W.; Wiggins, K.; Eastmond, B.; Velez, D.; Lounibos, L.P.; Lord, C.C. Transmission risk of two Chikungunya lineages by invasive mosquito vectors from Florida and the Dominican Republic. PLoS Negl. Trop. Dis. 2017, 11. [Google Scholar] [CrossRef] [PubMed]
- Weaver, S.C.; Reisen, W.K. Present and future arboviruses threats. Antiviral Res. 2010, 85, 328–345. [Google Scholar] [CrossRef] [PubMed]
- Edman, J.D.; Taylor, D.J. Culex nigripalpus: Seasonal shift in the bird-mammal feeding ratio in a mosquito vector of human encephalitis. Science 1968, 161, 67–68. [Google Scholar] [CrossRef]
- Takken, W.; Verhulst, N.O. Host preferences of blood-feeding mosquitoes. Ann. Rev. Entomol. 2013, 58, 433–453. [Google Scholar] [CrossRef]
- Burkett-Cadena, N.D.; Bingham, A.M.; Porterfield, C.; Unnasch, T.R. Innate preference or opportunism: Mosquitoes feeding on birds of prey at the Southeastern Raptor Center. J. Vector. Ecol. 2014, 39, 21–31. [Google Scholar] [CrossRef]
- Farjana, T.; Tuno, N. Multiple blood feeding and host-seeking behavior in Aedes aegypti and Aedes albopictus (Diptera: Culicidae). J. Med. Entomol. 2013, 50, 838–846. [Google Scholar] [CrossRef]
- McMeniman, C.J.; Lane, R.V.; Cass, B.N.; Fong, A.W.C.; Sidhu, M.; Wang, Y.F.; O’Neill, S.L. Stable introduction of a life-shortening Wolbachia infection into the mosquito Aedes aegypti. Science 2009, 323, 141–144. [Google Scholar] [CrossRef]
- Dong, Y.; Morton, J.C.; Ramirez, J.L.; Souza-Neto, J.A.; Dimopoulos, G. The entomopathogenic fungus Beauveria bassiana activate toll and JAK-STAT pathway-controlled effector genes and anti-dengue activity in Aedes aegypti. Insect. BioChem. Mol. Bio. 2012, 42, 126–132. [Google Scholar] [CrossRef]
- Champer, J.; Buchman, A.; Akbari, O.S. Cheating evolution: Engineering gene drives to manipulate the fate of wild populations. Nat. Rev. Genetics. 2016, 17, 146–159. [Google Scholar] [CrossRef]
- Moreno-Madriñán, M.; Turell, M. History of mosquito borne diseases in the United States and implications for new pathogens. Emerg. Infect. Dis. 2018, 24, 821. [Google Scholar] [CrossRef] [PubMed]

| Descriptions | Symbol | Distribution a | Range | Center |
|---|---|---|---|---|
| State variables | ||||
| Susceptible humans | Hs | |||
| Infectious humans | Hin | |||
| Recovered humans | Hr | |||
| Susceptible mosquitoes, species j | Sj | |||
| Latent mosquitoes, species j | Lj | |||
| Infectious mosquitoes, species j | Yj | |||
| Parameters | ||||
| Mean of temperature curve | Tmean | Uni | 18–27 | |
| Day virus is introduced | tcrit | Uni | 5–360 | |
| Human recovery rate | rH | Fixed | 0.125 | |
| Total (initial) number of humans | Htot | Fixed | 50,000 | |
| Both mosquito species | ||||
| Interval between pulses (both species) | iv | Uni | 10–50 | |
| Mean day peak one (from January 1) | q1 | Fixed | 165 | |
| Spread peak one | σ1 | Fixed | 7 | |
| Mean day peak two (from January 1) | q2 | Fixed | 245 | |
| Spread peak two | σ2 | Fixed | 15 | |
| Width of optimal survival range | W | Fixed | 2 | |
| Central point of optimal survival temperature range | Tempc | Set values | [10,16,22] | |
| Aedes albopictus | ||||
| Transmission mosquito to human host | balb | Tri | 0.1–0.7 | 0.4 |
| Transmission human host to mosquito | βalb | Tri | 0.1–0.7 | 0.4 |
| Days between blood feeding on humans | αalb | Tri | 2–20 | 5 |
| Proportion of population in peak one | pδ1,alb | Fixed | 0.2 | |
| Proportion of population in pulses all year | pbase,alb | Fixed | 0.15 | |
| Temperature—mortality slope | µsl,alb | Uni | 0.05–0.15 | |
| Virus development at 22.5 °C | γ22,alb | Fixed | 0.25 | |
| Temperature—virus development slope | γsl,alb | Tri | 0.004–0.02 | 0.015 |
| Maximum recruitment | ρmax,alb | Tri | 100–20,000 | 5000 |
| Total recruitment through year | Rtot,alb | Calculated | ||
| Aedes aegypti | ||||
| Transmission mosquito to human host | baeg | Tri | 0.1–0.7 | 0.4 |
| Transmission human host to mosquito | βaeg | Tri | 0.1–0.7 | 0.4 |
| Days between blood feeding on humans | αaeg | Tri | 1–5 | 3 |
| Proportion of population in peak one | pδ1,aeg | Fixed | 0.25 | |
| Proportion of population in pulses all year | pbase,aeg | Fixed | 0.13 | |
| Minimum mortality (at Tempc ± W) | µmin,aeg | Fixed | 0.1 | |
| Slope of temperature—mortality line | µsl,aeg | Uni | 0.05–0.15 | |
| Virus development at 22.5 °C | γ22,aeg | Fixed | 0.25 | |
| Temperature—virus development slope | γsl,aeg | Tri | 0.004–0.02 | 0.015 |
| Maximum recruitment | ρmax,aeg | Tri | 100–20,000 | 5000 |
| Total recruitment through year | Rtot,aeg | Calculated | ||
| Central Temperature, Tempc (°C) | |||
|---|---|---|---|
| Outcome Variable | 10 | 16 | 22 |
| # Epidemics (out of 250 parameter sets) | 75 | 135 | 178 |
| Average MaxHi (for epidemic runs) | 13,579 | 17,174 | 26,443 |
| MaxHi range | 2.02–34,916 | 2.02–38,804 | 3.71–41,621 |
| Average (range) lag (time from introduction to MaxHi, epidemic runs) | 63.9 (9.7–286.8) | 68 (9.1–373) | 37.7 (8.85–139.2) |
| Logistic regression on epidemics, adjusted R2 | 0.1 | 0.14 | 0.12 |
| Regression model for MaxHi (epidemic runs only), adjusted R2 | 0.5 | 0.34 | 0.1 |
| Regression model for lag (epidemic runs only), adjusted R2 | 0.2 | 0.3 | 0.2 |
| Central Temperature, Tempc (°C) | ||
|---|---|---|
| 10 | 16 | 22 |
| Annual mean temperature (Tmean) (−) | Annual mean temperature (Tmean) (−) | Annual mean temperature (Tmean) |
| Day of introduction (tcrit) | ||
| Ae. albopictus recruitment per host (ρmax,alb) | Ae. albopictus recruitment per host (ρmax,alb) (−) | |
| Ae. aegypti recruitment per host (ρmax,aeg) | Ae. aegypti recruitment per host (ρmax,aeg) | |
| Transmission: humans to Ae. aegypti (βaeg) | Transmission: humans to Ae. aegypti (βaeg) | |
| Transmission: Ae. aegypti to humans (baeg) | ||
| Ae. aegypti biting frequency (αaeg) (−) | Ae. aegypti biting frequency (αaeg) (−) | |
| Ae. aegypti mortality–temperature slope (µsl,aeg) (−) | Ae. aegypti mortality–temperature slope (µsl,aeg) (−) | |
| Central Temperature, Tempc (°C) | ||
|---|---|---|
| 10 | 16 | 22 |
| Annual mean temperature (Tmean) (-) | ||
| Day of introduction (tcrit) (-) | ||
| Transmission: humans to Ae. albopictus (βalb) | ||
| Ae. albopictus biting frequency (αalb) (-) | Ae. albopictus biting frequency (αalb) (-) | |
| Ae. aegypti recruitment per host (ρmax,aeg) | Ae. aegypti recruitment per host (ρmax,aeg) | |
| Transmission: humans to Ae. aegypti (βaeg) | Transmission: humans to Ae. aegypti (βaeg) | Transmission: humans to Ae. aegypti (βaeg) |
| Transmission: Ae. aegypti to humans (baeg) | Transmission: Ae. aegypti to humans (baeg) | |
| Ae. aegypti biting frequency (αaeg) (-) | Ae. aegypti biting frequency (αaeg) (-) | Ae. aegypti biting frequency (αaeg) (-) |
| Central Temperature, Tempc (°C) | ||
|---|---|---|
| 10 | 16 | 22 |
| Annual mean temperature (Tmean) (-) | Annual mean temperature (Tmean) | |
| Transmission: Ae. albopictus to humans (balb) (-) | ||
| Transmission: humans to Ae. albopictus (βalb) | ||
| Ae. albopictus biting frequency (αalb) | ||
| Ae. albopictus mortality—temperature slope (µsl,alb) (-) | ||
| Ae. albopictus temperature—virus development slope (γsl,alb) | ||
| Ae. albopictus recruitment per host (ρmax,alb)(-) | Ae. albopictus recruitment per host (ρmax,alb)(-) | |
| Ae. aegypti recruitment per host (ρmax,alb)(-) | Ae. aegypti recruitment per host (ρmax,aeg)(-) | |
| Transmission: humans to Ae. aegypti (βaeg) | Transmission: humans to Ae. aegypti (βaeg)(-) | |
| Ae. aegypti biting frequency (αaeg) | Ae. aegypti biting frequency (αaeg) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lord, C.C.; Lounibos, L.P.; Pohedra, J.J.; Alto, B.W. Effects of Mosquito Biology on Modeled Chikungunya Virus Invasion Potential in Florida. Viruses 2020, 12, 830. https://doi.org/10.3390/v12080830
Lord CC, Lounibos LP, Pohedra JJ, Alto BW. Effects of Mosquito Biology on Modeled Chikungunya Virus Invasion Potential in Florida. Viruses. 2020; 12(8):830. https://doi.org/10.3390/v12080830
Chicago/Turabian StyleLord, Cynthia C., L. Philip Lounibos, Joseph J. Pohedra, and Barry W. Alto. 2020. "Effects of Mosquito Biology on Modeled Chikungunya Virus Invasion Potential in Florida" Viruses 12, no. 8: 830. https://doi.org/10.3390/v12080830
APA StyleLord, C. C., Lounibos, L. P., Pohedra, J. J., & Alto, B. W. (2020). Effects of Mosquito Biology on Modeled Chikungunya Virus Invasion Potential in Florida. Viruses, 12(8), 830. https://doi.org/10.3390/v12080830





