Causes and Consequences of Spatial Within-Host Viral Spread
Abstract
1. Introduction
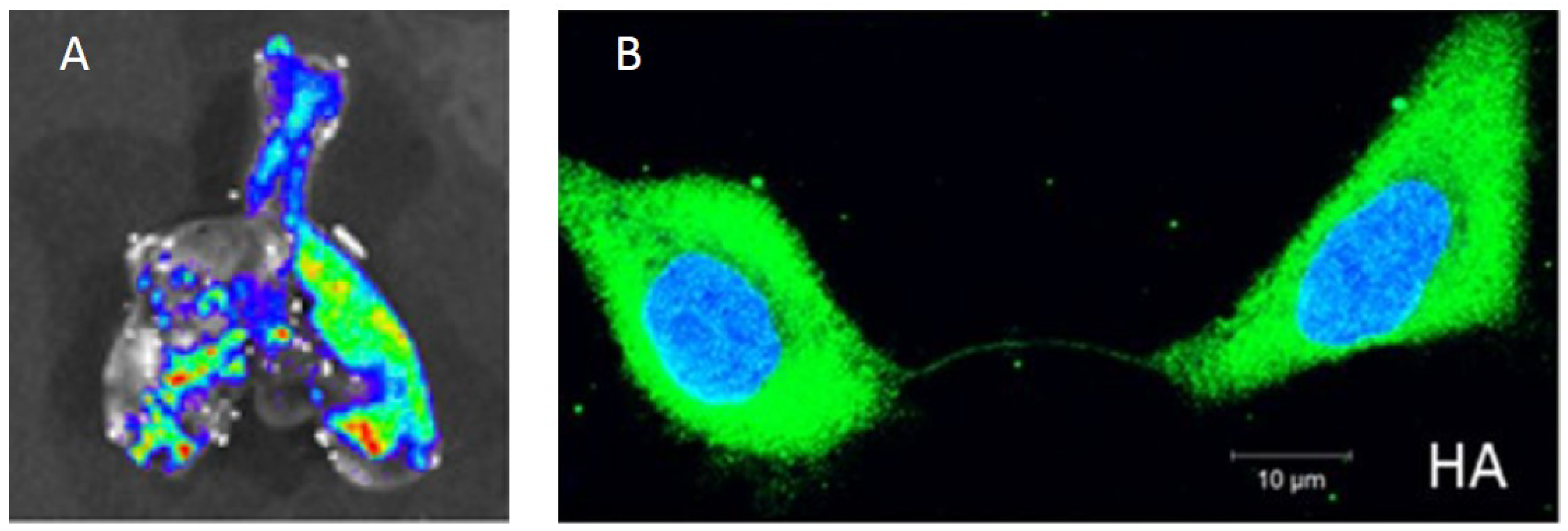
2. Experimental Studies Indicate That Within-Host IAV Spread Is a Strongly Spatially Structured Process
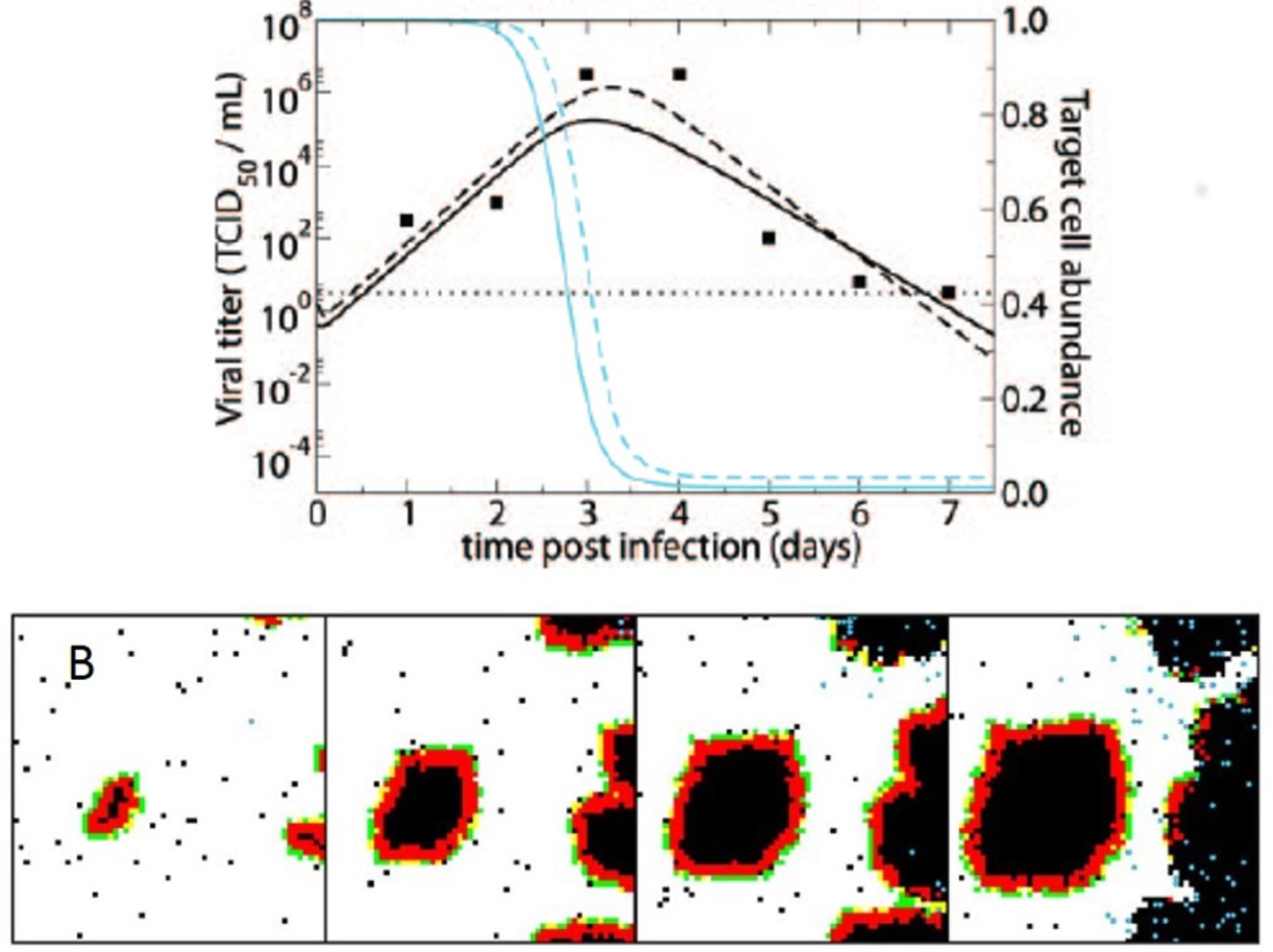
3. Computational Models of Spatial Within-Host Influenza Virus Spread
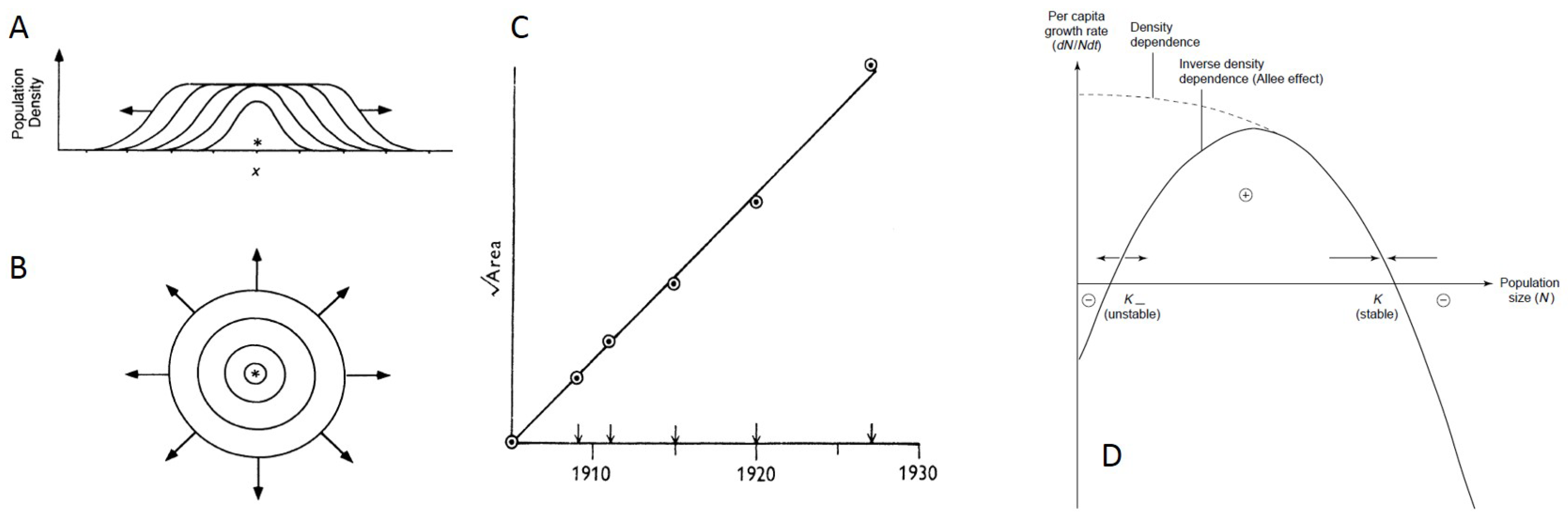
4. Ecological Factors Driving Patterns of Spatial Spread
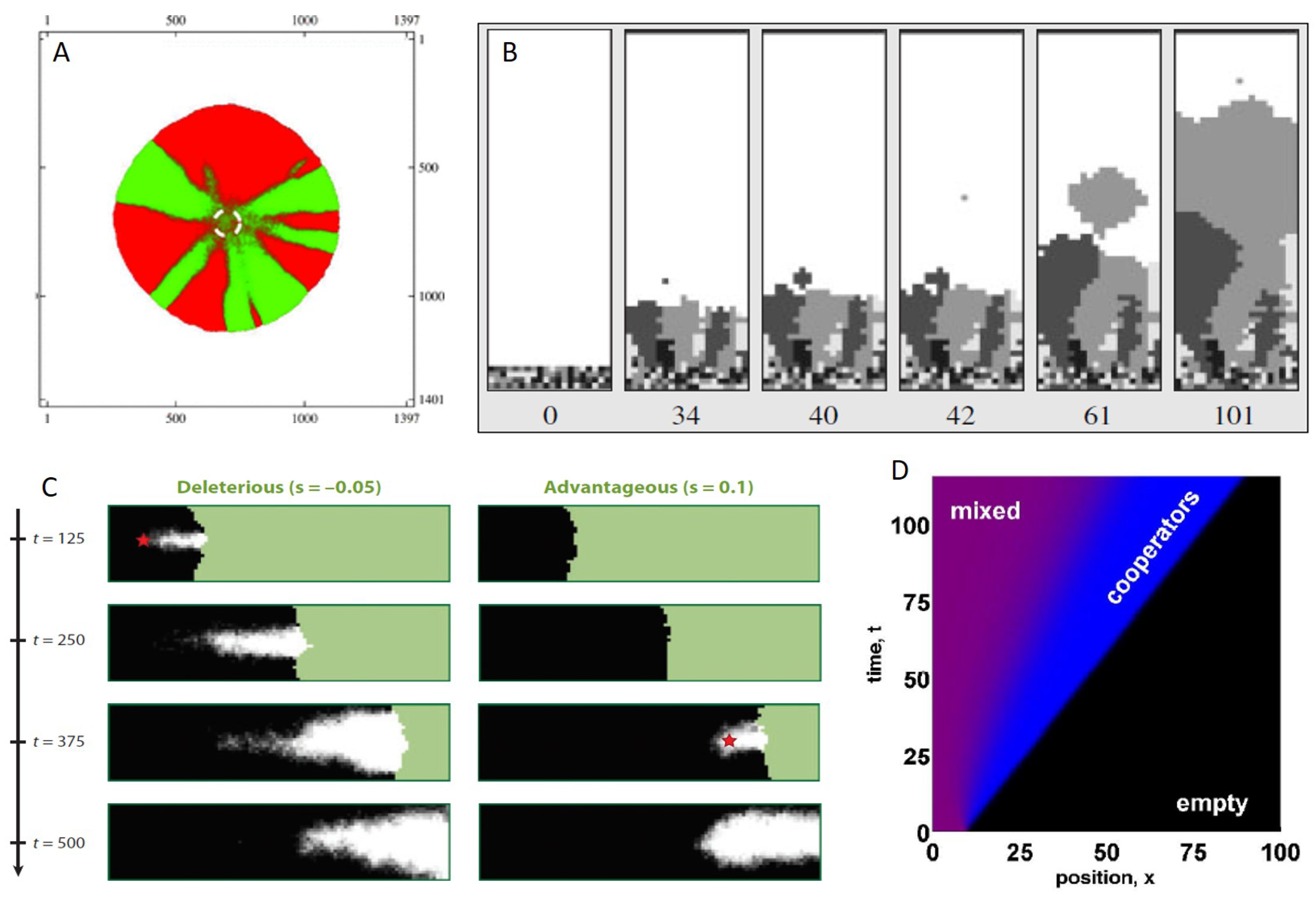
5. The Consequences of Spatial Spread on Population Evolution
6. Discussion
Acknowledgments
Conflicts of Interest
References
- Furuse, Y.; Oshitani, H. Global Transmission Dynamics of Measles in the Measles Elimination Era. Viruses 2017, 9, 82. [Google Scholar] [CrossRef] [PubMed]
- Salje, H.; Lessler, J.; Berry, I.M.; Melendrez, M.C.; Endy, T.; Kalayanarooj, S.; A-Nuegoonpipat, A.; Chanama, S.; Sangkijporn, S.; Klungthong, C.; et al. Dengue diversity across spatial and temporal scales: Local structure and the effect of host population size. Science 2017, 355, 1302–1306. [Google Scholar] [CrossRef] [PubMed]
- Viboud, C.; Bjornstad, O.N.; Smith, D.L.; Simonsen, L.; Miller, M.A.; Grenfell, B.T. Synchrony, Waves, and Spatial Hierarchies in the Spread of Influenza. Science 2006, 312, 447–451. [Google Scholar] [CrossRef] [PubMed]
- Bozick, B.A.; Real, L.A. The Role of Human Transportation Networks in Mediating the Genetic Structure of Seasonal Influenza in the United States. PLoS Pathog. 2015, 11, e1004898. [Google Scholar] [CrossRef] [PubMed]
- Charu, V.; Zeger, S.; Gog, J.; Bjørnstad, O.N.; Kissler, S.; Simonsen, L.; Grenfell, B.T.; Viboud, C. Human mobility and the spatial transmission of influenza in the United States. PLoS Comput. Biol. 2017, 13, e1005382. [Google Scholar] [CrossRef] [PubMed]
- Bajardi, P.; Poletto, C.; Ramasco, J.J.; Tizzoni, M.; Colizza, V.; Vespignani, A. Human Mobility Networks, Travel Restrictions, and the Global Spread of 2009 H1N1 Pandemic. PLoS ONE 2011, 6, e16591. [Google Scholar] [CrossRef] [PubMed]
- Stoddard, S.T.; Forshey, B.M.; Morrison, A.C.; Paz-Soldan, V.A.; Vazquez-Prokopec, G.M.; Astete, H.; Reiner, R.C.; Vilcarromero, S.; Elder, J.P.; Halsey, E.S.; et al. House-to-house human movement drives dengue virus transmission. Proc. Natl. Acad. Sci. USA 2012, 110, 994–999. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.G.; Perkins, T.A.; Cummings, D.A.T.; Zakar, R.; Hay, S.I.; Smith, D.L.; Reiner, R.C. Big city, small world: density, contact rates, and transmission of dengue across Pakistan. J. R. Soc. Interface 2015, 12, 20150468. [Google Scholar] [CrossRef] [PubMed]
- Messina, J.P.; Kraemer, M.U.; Brady, O.J.; Pigott, D.M.; Shearer, F.M.; Weiss, D.J.; Golding, N.; Ruktanonchai, C.W.; Gething, P.W.; Cohn, E.; et al. Mapping global environmental suitability for Zika virus. eLife 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Renzette, N.; Pokalyuk, C.; Gibson, L.; Bhattacharjee, B.; Schleiss, M.R.; Hamprecht, K.; Yamamoto, A.Y.; Mussi-Pinhata, M.M.; Britt, W.J.; Jensen, J.D.; et al. Limits and patterns of cytomegalovirus genomic diversity in humans. Proc. Natl. Acad. Sci. USA 2015, 112, E4120–E4128. [Google Scholar] [CrossRef] [PubMed]
- Renzette, N.; Gibson, L.; Bhattacharjee, B.; Fisher, D.; Schleiss, M.R.; Jensen, J.D.; Kowalik, T.F. Rapid Intrahost Evolution of Human Cytomegalovirus Is Shaped by Demography and Positive Selection. PLoS Genet. 2013, 9, e1003735. [Google Scholar] [CrossRef] [PubMed]
- Ball, J.K.; Holmes, E.C.; Whitwell, H.; Desselberger, U. Genomic variation of human immunodeficiency virus type 1 (HIV-1): Molecular analyses of HIV-1 in sequential blood samples and various organs obtained at autopsy. J. Gener. Virol. 1994, 75, 867–879. [Google Scholar] [CrossRef] [PubMed]
- Korber, B.; Kunstman, K.J.; Patterson, B.K.; Furtado, M.; McEvilly, M.M.; Levy, R.; Wolinsky, S.M. Genetic differences between blood-and brain-derived viral sequences from human immunodeficiency virus type 1-infected patients: evidence of conserved elements in the V3 region of the envelope protein of brain-derived sequences. J. Virol. 1994, 68, 7467–7481. [Google Scholar] [PubMed]
- Law, K.M.; Komarova, N.L.; Yewdall, A.W.; Lee, R.K.; Herrera, O.L.; Wodarz, D.; Chen, B.K. In vivo HIV-1 cell-to-cell transmission promotes multicopy micro-compartmentalized infection. Cell Rep. 2016, 15, 2771–2783. [Google Scholar] [CrossRef] [PubMed]
- van den Brand, J.M.A.; Stittelaar, K.J.; van Amerongen, G.; Reperant, L.; de Waal, L.; Osterhaus, A.D.M.E.; Kuiken, T. Comparison of Temporal and Spatial Dynamics of Seasonal H3N2, Pandemic H1N1 and Highly Pathogenic Avian Influenza H5N1 Virus Infections in Ferrets. PLoS ONE 2012, 7, e42343. [Google Scholar] [CrossRef] [PubMed]
- Graw, F.; Balagopal, A.; Kandathil, A.J.; Ray, S.C.; Thomas, D.L.; Ribeiro, R.M.; Perelson, A.S. Inferring Viral Dynamics in Chronically HCV Infected Patients from the Spatial Distribution of Infected Hepatocytes. PLoS Comput. Biol. 2014, 10, e1003934. [Google Scholar] [CrossRef] [PubMed]
- Wieland, S.; Makowska, Z.; Campana, B.; Calabrese, D.; Dill, M.T.; Chung, J.; Chisari, F.V.; Heim, M.H. Simultaneous detection of hepatitis C virus and interferon stimulated gene expression in infected human liver. Hepatology 2014, 59, 2121–2130. [Google Scholar] [CrossRef] [PubMed]
- Sanjuán, R. Collective Infectious Units in Viruses. Trends Microbiol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Balsitis, S.J.; Coloma, J.; Castro, G.; Alava, A.; Flores, D.; McKerrow, J.H.; Beatty, P.R.; Harris, E. Tropism of dengue virus in mice and humans defined by viral nonstructural protein 3-specific immunostaining. Am. J. Trop. Med. Hyg. 2009, 80, 416–424. [Google Scholar] [CrossRef] [PubMed]
- Matrosovich, M.N.; Matrosovich, T.Y.; Gray, T.; Roberts, N.A.; Klenk, H.D. Human and avian influenza viruses target different cell types in cultures of human airway epithelium. Proc. Natl. Acad. Sci. USA 2004, 101, 4620–4624. [Google Scholar] [CrossRef] [PubMed]
- Kumberger, P.; Frey, F.; Schwarz, U.S.; Graw, F. Multiscale modeling of virus replication and spread. FEBS Lett. 2016, 590, 1972–1986. [Google Scholar] [CrossRef] [PubMed]
- Culshaw, R.V.; Ruan, S.; Webb, G. A mathematical model of cell-to-cell spread of HIV-1 that includes a time delay. J. Math. Biol. 2003, 46, 425–444. [Google Scholar] [CrossRef] [PubMed]
- Beauchemin, C.; Samuel, J.; Tuszynski, J. A simple cellular automaton model for influenza A viral infections. J. Theor. Biol. 2005, 232, 223–234. [Google Scholar] [CrossRef] [PubMed]
- Komarova, N.L.; Levy, D.N.; Wodarz, D. Synaptic transmission and the susceptibility of HIV infection to anti-viral drugs. Sci. Rep. 2013, 3, 2103. [Google Scholar] [CrossRef] [PubMed]
- Graw, F.; Martin, D.N.; Perelson, A.S.; Uprichard, S.L.; Dahari, H. Quantification of HCV cell-to-cell spread using a stochastic modeling approach. J. Virol. 2015, 89, 6551–6561. [Google Scholar] [CrossRef] [PubMed]
- Funk, G.A.; Jansen, V.A.; Bonhoeffer, S.; Killingback, T. Spatial models of virus-immune dynamics. J. Theor. Biol. 2005, 233, 221–236. [Google Scholar] [CrossRef] [PubMed]
- Miyashita, S.; Ishibashi, K.; Kishino, H.; Ishikawa, M. Viruses roll the dice: the stochastic behavior of viral genome molecules accelerates viral adaptation at the cell and tissue levels. PLoS Biol. 2015, 13, e1002094. [Google Scholar] [CrossRef] [PubMed]
- Shurin, J.B. Top-Down and Bottom-Up Regulation of Communities; Oxford University Press: Oxford, UK, 2012. [Google Scholar] [CrossRef]
- Guarner, J.; Shieh, W.J.; Dawson, J.; Subbarao, K.; Shaw, M.; Ferebee, T.; Morken, T.; Nolte, K.B.; Freifeld, A.; Cox, N.; et al. Immunohistochemical and In Situ Hybridization Studies of Influenza A Virus Infection in Human Lungs. Am. J. Clin. Pathol. 2000, 114, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Walsh, J.J.; Dietlein, L.F.; Low, F.N.; Burch, G.E.; Mogabgab, W.J. Bronchotracheal response in human influenza: type A, Asian strain, as studied by light and electron microscopic examination of bronchoscopic biopsies. Arch. Intern. Med. 1961, 108, 376–388. [Google Scholar] [CrossRef] [PubMed]
- Manicassamy, B.; Manicassamy, S.; Belicha-Villanueva, A.; Pisanelli, G.; Pulendran, B.; Garcia-Sastre, A. Analysis of in vivo dynamics of influenza virus infection in mice using a GFP reporter virus. Proc. Natl. Acad. Sci. USA 2010, 107, 11531–11536. [Google Scholar] [CrossRef] [PubMed]
- Fukuyama, S.; Katsura, H.; Zhao, D.; Ozawa, M.; Ando, T.; Shoemaker, J.E.; Ishikawa, I.; Yamada, S.; Neumann, G.; Watanabe, S.; et al. Multi-spectral fluorescent reporter influenza viruses (Color-flu) as powerful tools for in vivo studies. Nat. Commun. 2015, 6, 6600. [Google Scholar] [CrossRef] [PubMed]
- Marshall, N.; Priyamvada, L.; Ende, Z.; Steel, J.; Lowen, A.C. Influenza virus reassortment occurs with high frequency in the absence of segment mismatch. PLoS Pathog. 2013, 9, e1003421. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Kim, J.H.; Ranjan, P.; Metcalfe, M.G.; Cao, W.; Mishina, M.; Gangappa, S.; Guo, Z.; Boyden, E.S.; Zaki, S.; et al. Influenza virus exploits tunneling nanotubes for cell-to-cell spread. Sci. Rep. 2017, 7, 40360. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Dong, Z.; Li, F.; Meng, W.; Feng, L.; Niu, X.; Li, C.; Luo, Q.; Li, Z.; Sun, C.; et al. Visualizing influenza virus infection in living mice. Nat. Commun. 2013, 4, 2369. [Google Scholar] [CrossRef] [PubMed]
- Heaton, N.S.; Leyva-Grado, V.H.; Tan, G.S.; Eggink, D.; Hai, R.; Palese, P. In Vivo Bioluminescent Imaging of Influenza A Virus Infection and Characterization of Novel Cross-Protective Monoclonal Antibodies. J. Virol. 2013, 87, 8272–8281. [Google Scholar] [CrossRef] [PubMed]
- Tran, V.; Moser, L.A.; Poole, D.S.; Mehle, A. Highly Sensitive Real-Time In Vivo Imaging of an Influenza Reporter Virus Reveals Dynamics of Replication and Spread. J. Virol. 2013, 87, 13321–13329. [Google Scholar] [CrossRef] [PubMed]
- Czakó, R.; Vogel, L.; Lamirande, E.W.; Bock, K.W.; Moore, I.N.; Ellebedy, A.H.; Ahmed, R.; Mehle, A.; Subbarao, K. In Vivo Imaging of Influenza Virus Infection in Immunized Mice. mBio 2017, 8, e00714-17. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, E.A.; Meliopoulos, V.A.; Savage, C.; Livingston, B.; Mehle, A.; Schultz-Cherry, S. Visualizing real-time influenza virus infection, transmission and protection in ferrets. Nat. Commun. 2015, 6, 6378. [Google Scholar] [CrossRef] [PubMed]
- Cobey, S.; Hensley, S.E. Immune history and influenza virus susceptibility. Curr. Opin. Virol. 2017, 22, 105–111. [Google Scholar] [CrossRef] [PubMed]
- de Graaf, M.; Fouchier, R.A. Role of receptor binding specificity in influenza A virus transmission and pathogenesis. EMBO J. 2014, 33, 823–841. [Google Scholar] [CrossRef] [PubMed]
- Rimmelzwaan, G.F.; Nieuwkoop, N.J.; de Mutsert, G.; Boon, A.C.; Kuiken, T.; Fouchier, R.A.; Osterhaus, A.D. Attachment of infectious influenza A viruses of various subtypes to live mammalian and avian cells as measured by flow cytometry. Virus Res. 2007, 129, 175–181. [Google Scholar] [CrossRef] [PubMed]
- Ibricevic, A.; Pekosz, A.; Walter, M.J.; Newby, C.; Battaile, J.T.; Brown, E.G.; Holtzman, M.J.; Brody, S.L. Influenza virus receptor specificity and cell tropism in mouse and human airway epithelial cells. J. Virol. 2006, 80, 7469–7480. [Google Scholar] [CrossRef] [PubMed]
- van Riel, D.; den Bakker, M.A.; Leijten, L.M.; Chutinimitkul, S.; Munster, V.J.; de Wit, E.; Rimmelzwaan, G.F.; Fouchier, R.A.; Osterhaus, A.D.; Kuiken, T. Seasonal and pandemic human influenza viruses attach better to human upper respiratory tract epithelium than avian influenza viruses. Am. J. Pathol. 2010, 176, 1614–1618. [Google Scholar] [CrossRef] [PubMed]
- Shinya, K.; Ebina, M.; Yamada, S.; Ono, M.; Kasai, N.; Kawaoka, Y. Avian flu: Influenza virus receptors in the human airway. Nature 2006, 440, 435–436. [Google Scholar] [CrossRef] [PubMed]
- Lakdawala, S.S.; Jayaraman, A.; Halpin, R.A.; Lamirande, E.W.; Shih, A.R.; Stockwell, T.B.; Lin, X.; Simenauer, A.; Hanson, C.T.; Vogel, L.; et al. The soft palate is an important site of adaptation for transmissible influenza viruses. Nature 2015, 526, 122–125. [Google Scholar] [CrossRef] [PubMed]
- Palese, P.; Tobita, K.; Ueda, M.; Compans, R.W. Characterization of temperature sensitive influenza virus mutants defective in neuraminidase. Virology 1974, 61, 397–410. [Google Scholar] [CrossRef]
- Liu, C.; Eichelberger, M.C.; Compans, R.W.; Air, G.M. Influenza type A virus neuraminidase does not play a role in viral entry, replication, assembly, or budding. J. Virol. 1995, 69, 1099–1106. [Google Scholar] [PubMed]
- Job, E.R.; Bottazzi, B.; Short, K.R.; Deng, Y.M.; Mantovani, A.; Brooks, A.G.; Reading, P.C. A single amino acid substitution in the hemagglutinin of H3N2 subtype influenza A viruses is associated with resistance to the long pentraxin PTX3 and enhanced virulence in mice. J. Immunol. 2014, 192, 271–281. [Google Scholar] [CrossRef] [PubMed]
- Ehre, C.; Worthington, E.N.; Liesman, R.M.; Grubb, B.R.; Barbier, D.; O’Neal, W.K.; Sallenave, J.M.; Pickles, R.J.; Boucher, R.C. Overexpressing mouse model demonstrates the protective role of Muc5ac in the lungs. Proc. Natl. Acad. Sci. USA 2012, 109, 16528–16533. [Google Scholar] [CrossRef] [PubMed]
- Gulati, S.; Lasanajak, Y.; Smith, D.F.; Cummings, R.D.; Air, G.M. Glycan array analysis of influenza H1N1 binding and release. Cancer Biomark. 2014, 14, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Böttcher, E.; Matrosovich, T.; Beyerle, M.; Klenk, H.D.; Garten, W.; Matrosovich, M. Proteolytic activation of influenza viruses by serine proteases TMPRSS2 and HAT from human airway epithelium. J. Virol. 2006, 80, 9896–9898. [Google Scholar] [CrossRef] [PubMed]
- Yasuoka, S.; Ohnishi, T.; Kawano, S.; Tsuchihashi, S.; Ogawara, M.; Masuda, K.I.; Yamaoka, K.; Takahashi, M.; Sano, T. Purification, characterization, and localization of a novel trypsin-like protease found in the human airway. Am. J. Respir. Cell Mol. Biol. 1997, 16, 300–308. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, M.; Sano, T.; Yamaoka, K.; Kamimura, T.; Umemoto, N.; Nishitani, H.; Yasuoka, S. Localization of human airway trypsin-like protease in the airway: An immunohistochemical study. Histochem. Cell Biol. 2001, 115, 181–187. [Google Scholar] [PubMed]
- Ganesan, S.; Comstock, A.T.; Sajjan, U.S. Barrier function of airway tract epithelium. Tissue Barriers 2013, 1, e24997. [Google Scholar] [CrossRef] [PubMed]
- Roberts, K.L.; Manicassamy, B.; Lamb, R.A. Influenza A Virus Uses Intercellular Connections to Spread to Neighboring Cells. J. Virol. 2014, 89, 1537–1549. [Google Scholar] [CrossRef] [PubMed]
- Jonsson, C.B.; Camp, J.V.; Wu, A.; Zheng, H.; Kraenzle, J.L.; Biller, A.E.; Vanover, C.D.; Chu, Y.K.; Ng, C.K.; Proctor, M.; et al. Molecular imaging reveals a progressive pulmonary inflammation in lower airways in ferrets infected with 2009 H1N1 pandemic influenza virus. PLoS ONE 2012, 7, e40094. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.M.; Perelson, A.S. Influenza A virus infection kinetics: quantitative data and models: Modeling influenza kinetics. Wiley Interdiscip. Rev. Syst. Biol. Med. 2011, 3, 429–445. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.M. Host-pathogen kinetics during influenza infection and coinfection: Insights from predictive modeling. Immunol. Rev. 2018, 285, 97–112. [Google Scholar] [CrossRef] [PubMed]
- Baccam, P.; Beauchemin, C.; Macken, C.A.; Hayden, F.G.; Perelson, A.S. Kinetics of Influenza A Virus Infection in Humans. J. Virol. 2006, 80, 7590–7599. [Google Scholar] [CrossRef] [PubMed]
- Carrat, F.; Vergu, E.; Ferguson, N.M.; Lemaitre, M.; Cauchemez, S.; Leach, S.; Valleron, A.J. Time lines of infection and disease in human influenza: a review of volunteer challenge studies. Am. J. Epidemiol. 2008, 167, 775–785. [Google Scholar] [CrossRef] [PubMed]
- Saenz, R.A.; Quinlivan, M.; Elton, D.; MacRae, S.; Blunden, A.S.; Mumford, J.A.; Daly, J.M.; Digard, P.; Cullinane, A.; Grenfell, B.T.; et al. Dynamics of influenza virus infection and pathology. J. Virol. 2010, 84, 3974–3983. [Google Scholar] [CrossRef] [PubMed]
- Pawelek, K.A.; Huynh, G.T.; Quinlivan, M.; Cullinane, A.; Rong, L.; Perelson, A.S. Modeling Within-Host Dynamics of Influenza Virus Infection Including Immune Responses. PLoS Comput. Biol. 2012, 8, e1002588. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.P.; Moquin, D.J.; Bernhauerova, V.; Smith, A.M. Influenza Virus Infection Model With Density Dependence Supports Biphasic Viral Decay. Front. Microbiol. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.; Moore, J.; Manicassamy, B.; Garcia-Sastre, A.; Handel, A.; Antia, R. Mathematical analysis of a mouse experiment suggests little role for resource depletion in controlling influenza infection within host. arXiv, 2017; arXiv:1705.02565. [Google Scholar]
- Bocharov, G.; Romanyukha, A. Mathematical model of antiviral immune response III. Influenza A virus infection. J. Theor. Biol. 1994, 167, 323–360. [Google Scholar] [CrossRef] [PubMed]
- Beauchemin, C. Probing the effects of the well-mixed assumption on viral infection dynamics. J. Theor. Biol. 2006, 242, 464–477. [Google Scholar] [CrossRef] [PubMed]
- Bauer, A.L.; Beauchemin, C.A.; Perelson, A.S. Agent-based modeling of host–pathogen systems: The successes and challenges. Inf. Sci. 2009, 179, 1379–1389. [Google Scholar] [CrossRef]
- Strain, M.; Richman, D.; Wong, J.; Levine, H. Spatiotemporal dynamics of HIV propagation. J. Theor. Biol. 2002, 218, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Beauchemin, C.A.; Handel, A. A review of mathematical models of influenza A infections within a host or cell culture: lessons learned and challenges ahead. BMC Public Health 2011, 11, S7. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, H.; Levin, D.; Forrest, S.; Beauchemin, C.A.A.; Tipper, J.; Knight, J.; Donart, N.; Layton, R.C.; Pyles, J.; Gao, P.; et al. Higher Level of Replication Efficiency of 2009 (H1N1) Pandemic Influenza Virus than Those of Seasonal and Avian Strains: Kinetics from Epithelial Cell Culture and Computational Modeling. J. Virol. 2011, 85, 1125–1135. [Google Scholar] [CrossRef] [PubMed]
- Levin, D.; Forrest, S.; Banerjee, S.; Clay, C.; Cannon, J.; Moses, M.; Koster, F. A spatial model of the efficiency of T cell search in the influenza-infected lung. J. Theor. Biol. 2016, 398, 52–63. [Google Scholar] [CrossRef] [PubMed]
- Reperant, L.A.; Kuiken, T.; Grenfell, B.T.; Osterhaus, A.D.M.E.; Dobson, A.P. Linking Influenza Virus Tissue Tropism to Population-Level Reproductive Fitness. PLoS ONE 2012, 7, e43115. [Google Scholar] [CrossRef] [PubMed]
- Koelle, K.; Farrell, A.; Brooke, C.; Ke, R. Within-host infectious disease models accommodating cellular coinfection, with an application to influenza. bioRxiv 2018. [Google Scholar] [CrossRef]
- Xue, K.S.; Moncla, L.H.; Bedford, T.; Bloom, J.D. Within-Host Evolution of Human Influenza Virus. Trends Microbiol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Lion, S.; Gandon, S. Spatial evolutionary epidemiology of spreading epidemics. Proc. R. Soc. B Biol. Sci. 2016, 283, 20161170. [Google Scholar] [CrossRef] [PubMed]
- Habets, M.G.; Czaran, T.; Hoekstra, R.F.; de Visser, J.A.G. Spatial structure inhibits the rate of invasion of beneficial mutations in asexual populations. Proc. R. Soc. Lond. B Biol. Sci. 2007, 274, 2139–2143. [Google Scholar] [CrossRef] [PubMed]
- Holmes, E.E.; Lewis, M.A.; Banks, J.E.; Veit, R.R. Partial Differential Equations in Ecology: Spatial Interactions and Population Dynamics. Ecology 1994, 75, 17–29. [Google Scholar] [CrossRef]
- Skellam, J.G. Random dispersal in theoretical populations. Biometrika 1951, 38, 196–218. [Google Scholar] [CrossRef] [PubMed]
- Courchamp, F.; Clutton-Brock, T.; Grenfell, B. Inverse density dependence and the Allee effect. Trends Ecol. Evol. 1999, 14, 405–410. [Google Scholar] [CrossRef]
- Aronson, D.G.; Weinberger, H.F. Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. In Partial Differential Equations and Related Topics; Springer: Berlin/Heidelberg, Germany, 1975; pp. 5–49. [Google Scholar]
- Fife, P.C.; McLeod, J.B. The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Ration. Mech. Anal. 1977, 65, 335–361. [Google Scholar] [CrossRef]
- Lewis, M.; Kareiva, P. Allee Dynamics and the Spread of Invading Organisms. Theor. Popul. Biol. 1993, 43, 141–158. [Google Scholar] [CrossRef]
- Hastings, A. Models of Spatial Spread: Is the Theory Complete? Ecology 1996, 77, 1675–1679. [Google Scholar] [CrossRef]
- Hastings, A.; Cuddington, K.; Davies, K.F.; Dugaw, C.J.; Elmendorf, S.; Freestone, A.; Harrison, S.; Holland, M.; Lambrinos, J.; Malvadkar, U.; et al. The spatial spread of invasions: new developments in theory and evidence:Spatial spread of invasions. Ecol. Lett. 2004, 8, 91–101. [Google Scholar] [CrossRef]
- Van den Bosch, F.; Hengeveld, R.; Metz, J.A.J. Analysing the Velocity of Animal Range Expansion. J. Biogeogr. 1992, 19, 135. [Google Scholar] [CrossRef]
- Brooke, C.B. Biological activities of ’noninfectious’ influenza A virus particles. Future Virol. 2014, 9, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Brooke, C.B.; Ince, W.L.; Wrammert, J.; Ahmed, R.; Wilson, P.C.; Bennink, J.R.; Yewdell, J.W. Most influenza a virions fail to express at least one essential viral protein. J. Virol. 2013. [Google Scholar] [CrossRef] [PubMed]
- Shigesada, N.; Kawasaki, K.; Takeda, Y. Modeling stratified diffusion in biological invasions. Am. Nat. 1995, 146, 229–251. [Google Scholar] [CrossRef]
- Kot, M.; Lewis, M.A.; van den Driessche, P. Dispersal Data and the Spread of Invading Organisms. Ecology 1996, 77, 2027–2042. [Google Scholar] [CrossRef]
- Le Corre, V.; Machon, N.; Petit, R.J.; Kremer, A. Colonization with long-distance seed dispersal and genetic structure of maternally inherited genes in forest trees: A simulation study. Genet. Res. 1997, 69, 117–125. [Google Scholar] [CrossRef]
- Hart, D.R.; Gardner, R.H. A spatial model for the spread of invading organisms subject to competition. J. Math. Biol. 1997, 35, 935–948. [Google Scholar] [CrossRef]
- Keeling, M.J.; Woolhouse, M.E.; Shaw, D.J.; Matthews, L.; Chase-Topping, M.; Haydon, D.T.; Cornell, S.J.; Kappey, J.; Wilesmith, J.; Grenfell, B.T. Dynamics of the 2001 UK Foot and Mouth Epidemic: Stochastic dispersal in a heterogeneous landscape. Sci. New Ser. 2001, 294, 813–817. [Google Scholar] [CrossRef] [PubMed]
- Sharov, A.A.; Liebhold, A.M. Model of Slowing the Spread of Gypsy Moth (Lepidoptera: Lymantriidae) with a Barrier Zone. Ecol. Appl. 1998, 8, 1170. [Google Scholar] [CrossRef]
- Childs, J.E.; Curns, A.T.; Dey, M.E.; Real, L.A.; Rupprecht, C.E.; Krebs, J.W. Rabies Epizootics Among Raccoons Vary Along a North–South Gradient in the Eastern United States. Vector-Borne Zoonotic Dis. 2001, 1, 253–267. [Google Scholar] [CrossRef] [PubMed]
- Matrosovich, M.; Tuzikov, A.; Bovin, N.; Gambaryan, A.; Klimov, A.; Castrucci, M.R.; Donatelli, I.; Kawaoka, Y. Early alterations of the receptor-binding properties of H1, H2, and H3 avian influenza virus hemagglutinins after their introduction into mammals. J. Virol. 2000, 74, 8502–8512. [Google Scholar] [CrossRef] [PubMed]
- van Riel, D.; Munster, V.J.; de Wit, E.; Rimmelzwaan, G.F.; Fouchier, R.A.; Osterhaus, A.D.; Kuiken, T. Human and avian influenza viruses target different cells in the lower respiratory tract of humans and other mammals. Am. J. Pathol. 2007, 171, 1215–1223. [Google Scholar] [CrossRef] [PubMed]
- Okubo, A.; Maini, P.K.; Williamson, M.H.; Murray, J.D. On the Spatial Spread of the Grey Squirrel in Britain. Proc. R. Soc. Biol. Sci. 1989, 238, 113–125. [Google Scholar] [CrossRef]
- Austerlitz, F.; Jung-Muller, B.; Godelle, B.; Gouyon, P.H. Evolution of Coalescence Times, Genetic Diversity and Structure during Colonization. Theor. Popul. Biol. 1997, 51, 148–164. [Google Scholar] [CrossRef]
- Excoffier, L.; Foll, M.; Petit, R.J. Genetic Consequences of Range Expansions. Ann. Rev. Ecol. Evol. Syst. 2009, 40, 481–501. [Google Scholar] [CrossRef]
- Hallatschek, O.; Nelson, D.R. Gene surfing in expanding populations. Theor. Popul. Biol. 2008, 73, 158–170. [Google Scholar] [CrossRef] [PubMed]
- Roques, L.; Garnier, J.; Hamel, F.; Klein, E.K. Allee effect promotes diversity in traveling waves of colonization. Proc. Natl. Acad. Sci. USA 2012, 109, 8828–8833. [Google Scholar] [CrossRef] [PubMed]
- Excoffier, L.; Ray, N. Surfing during population expansions promotes genetic revolutions and structuration. Trends Ecol. Evol. 2008, 23, 347–351. [Google Scholar] [CrossRef] [PubMed]
- McCrone, J.T.; Woods, R.J.; Martin, E.T.; Malosh, R.E.; Monto, A.S.; Lauring, A.S. Stochastic processes constrain the within and between host evolution of influenza virus. eLife 2018, 7. [Google Scholar] [CrossRef] [PubMed]
- Bialozyt, R.; Ziegenhagen, B.; Petit, R.J. Contrasting effects of long distance seed dispersal on genetic diversity during range expansion. J. Evol. Biol. 2006, 19, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, K.; Nichols, R.; Hewitt, G. Spatial patterns of genetic variation generated by different forms of dispersal during range expansion. Heredity 1996, 77, 282–291. [Google Scholar] [CrossRef]
- Austerlitz, F.; Mariette, S.; Machon, N.; Gouyon, P.H.; Godelle, B. Effects of Colonization Processes on Genetic Diversity: Differences Between Annual Plants and Tree Species. Genetics 2000, 154, 1309–1321. [Google Scholar] [PubMed]
- Dou, D.; Hernández-Neuta, I.; Wang, H.; Östbye, H.; Qian, X.; Thiele, S.; Resa-Infante, P.; Kouassi, N.M.; Sender, V.; Hentrich, K.; et al. Analysis of IAV Replication and Co-infection Dynamics by a Versatile RNA Viral Genome Labeling Method. Cell Rep. 2017, 20, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Hallatschek, O.; Nelson, D.R. Life at the front of an expanding population. Evol. Int. J. Organ. Evol. 2010, 64, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Korolev, K.S. The Fate of Cooperation during Range Expansions. PLoS Comput. Biol. 2013, 9, e1002994. [Google Scholar] [CrossRef] [PubMed]
- Wegmann, D.; Currat, M.; Excoffier, L. Molecular Diversity After a Range Expansion in Heterogeneous Environments. Genetics 2006, 174, 2009–2020. [Google Scholar] [CrossRef] [PubMed]
- Varble, A.; Albrecht, R.A.; Backes, S.; Crumiller, M.; Bouvier, N.M.; Sachs, D.; García-Sastre, A.; tenOever, B.R. Influenza A virus transmission bottlenecks are defined by infection route and recipient host. Cell Host Microbe 2014, 16, 691–700. [Google Scholar] [CrossRef] [PubMed]
- Klopfstein, S. The Fate of Mutations Surfing on the Wave of a Range Expansion. Mol. Biol. Evol. 2005, 23, 482–490. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, C.A.; Lillie, A.S.; Cavalli-Sforza, L.L. Mutations arising in the wave front of an expanding population. Proc. Natl. Acad. Sci. USA 2004, 101, 975–979. [Google Scholar] [CrossRef] [PubMed]
- Travis, J.M.J.; Munkemuller, T.; Burton, O.J.; Best, A.; Dytham, C.; Johst, K. Deleterious Mutations Can Surf to High Densities on the Wave Front of an Expanding Population. Mol. Biol. Evol. 2007, 24, 2334–2343. [Google Scholar] [CrossRef] [PubMed]
- Peischl, S.; Kirkpatrick, M.; Excoffier, L. Expansion load and the evolutionary dynamics of a species range. Am. Nat. 2015, 185, E81–E93. [Google Scholar] [CrossRef] [PubMed]
- Peischl, S.; Dupanloup, I.; Kirkpatrick, M.; Excoffier, L. On the accumulation of deleterious mutations during range expansions. Mol. Ecol. 2013, 22, 5972–5982. [Google Scholar] [CrossRef] [PubMed]
- Visher, E.; Whitefield, S.E.; McCrone, J.T.; Fitzsimmons, W.; Lauring, A.S. The Mutational Robustness of Influenza A Virus. PLoS Pathog. 2016, 12, e1005856. [Google Scholar] [CrossRef] [PubMed]
- Pybus, O.G.; Rambaut, A.; Belshaw, R.; Freckleton, R.P.; Drummond, A.J.; Holmes, E.C. Phylogenetic evidence for deleterious mutation load in RNA viruses and its contribution to viral evolution. Mol. Biol. Evol. 2007, 24, 845–852. [Google Scholar] [CrossRef] [PubMed]
- Koelle, K.; Rasmussen, D.A. The effects of a deleterious mutation load on patterns of influenza A/H3N2’s antigenic evolution in humans. eLife 2015, 4. [Google Scholar] [CrossRef] [PubMed]
- Fitch, W.M.; Bush, R.M.; Bender, C.A.; Cox, N.J. Long term trends in the evolution of H(3) HA1 human influenza type A. Proc. Natl. Acad. Sci. USA 1997, 94, 7712–7718. [Google Scholar] [CrossRef] [PubMed]
- Bolker, B.M.; Nanda, A.; Shah, D. Transient virulence of emerging pathogens. J. R. Soc. Interface 2010, 7, 811–822. [Google Scholar] [CrossRef] [PubMed]
- Travis, J.M.J.; Dytham, C. Dispersal evolution during invasions. Evol. Ecol. Res. 2002, 4, 1119–1129. [Google Scholar]
- Díaz-Muñoz, S.L.; Sanjuán, R.; West, S. Sociovirology: Conflict, Cooperation, and Communication among Viruses. Cell Host Microbe 2017, 22, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Robbins, A.; Borden, M.; Windmiller, B.; Niezgoda, M.; Marcus, L.; O’Brien, S.; Kreindel, S.; McGuill, M.; DeMaria, J.A.; Rupprecht, C.; et al. Prevention of the spread of rabies to wildlife by oral vaccination of raccoons in Massachusetts. J. Am. Vet. Med. Assoc. 1998, 213, 1407–1412. [Google Scholar] [PubMed]
- Hickman, H.D.; Reynoso, G.V.; Ngudiankama, B.F.; Rubin, E.J.; Magadán, J.G.; Cush, S.S.; Gibbs, J.; Molon, B.; Bronte, V.; Bennink, J.R.; et al. Anatomically restricted synergistic antiviral activities of innate and adaptive immune cells in the skin. Cell Host Microbe 2013, 13, 155–168. [Google Scholar] [CrossRef] [PubMed]
- Cush, S.S.; Reynoso, G.V.; Kamenyeva, O.; Bennink, J.R.; Yewdell, J.W.; Hickman, H.D. Locally produced IL-10 limits cutaneous vaccinia virus spread. PLoS Pathog. 2016, 12, e1005493. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.S. Defective interfering viruses. Ann. Rev. Microbiol. 1973, 27, 101–118. [Google Scholar] [CrossRef] [PubMed]
- Dimmock, N.J.; Dove, B.K.; Scott, P.D.; Meng, B.; Taylor, I.; Cheung, L.; Hallis, B.; Marriott, A.C.; Carroll, M.W.; Easton, A.J. Cloned Defective Interfering Influenza Virus Protects Ferrets from Pandemic 2009 Influenza A Virus and Allows Protective Immunity to Be Established. PLoS ONE 2012, 7, e49394. [Google Scholar] [CrossRef] [PubMed]
- Handel, A.; Liao, L.E.; Beauchemin, C.A. Progress and trends in mathematical modelling of influenza A virus infections. Curr. Opin. Syst. Biol. 2018, 12, 30–36. [Google Scholar] [CrossRef]
- Frensing, T.; Heldt, F.S.; Pflugmacher, A.; Behrendt, I.; Jordan, I.; Flockerzi, D.; Genzel, Y.; Reichl, U. Continuous influenza virus production in cell culture shows a periodic accumulation of defective interfering particles. PLoS ONE 2013, 8, e72288. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.E.; Iwami, S.; Beauchemin, C.A. (In) validating experimentally derived knowledge about influenza A defective interfering particles. J. R. Soc. Interface 2016, 13, 20160412. [Google Scholar] [CrossRef] [PubMed]
- Laske, T.; Heldt, F.S.; Hoffmann, H.; Frensing, T.; Reichl, U. Modeling the intracellular replication of influenza A virus in the presence of defective interfering RNAs. Virus Res. 2016, 213, 90–99. [Google Scholar] [CrossRef] [PubMed]
- Farrell, A.; Brooke, C.; Koelle, K.; Ke, R. Modeling the use of defective interfering particles as a treatment of natural influenza A infections. 2018; in press. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallagher, M.E.; Brooke, C.B.; Ke, R.; Koelle, K. Causes and Consequences of Spatial Within-Host Viral Spread. Viruses 2018, 10, 627. https://doi.org/10.3390/v10110627
Gallagher ME, Brooke CB, Ke R, Koelle K. Causes and Consequences of Spatial Within-Host Viral Spread. Viruses. 2018; 10(11):627. https://doi.org/10.3390/v10110627
Chicago/Turabian StyleGallagher, Molly E., Christopher B. Brooke, Ruian Ke, and Katia Koelle. 2018. "Causes and Consequences of Spatial Within-Host Viral Spread" Viruses 10, no. 11: 627. https://doi.org/10.3390/v10110627
APA StyleGallagher, M. E., Brooke, C. B., Ke, R., & Koelle, K. (2018). Causes and Consequences of Spatial Within-Host Viral Spread. Viruses, 10(11), 627. https://doi.org/10.3390/v10110627




