Assessing the Spatial and Spatio-Temporal Distribution of Forest Species via Bayesian Hierarchical Modeling
Abstract
1. Introduction
2. Materials and Methods
2.1. Abies alba Mill.
2.2. Castanea sativa Mill.
2.3. Pinus pinaster Ait.
2.4. Quercus robur L.
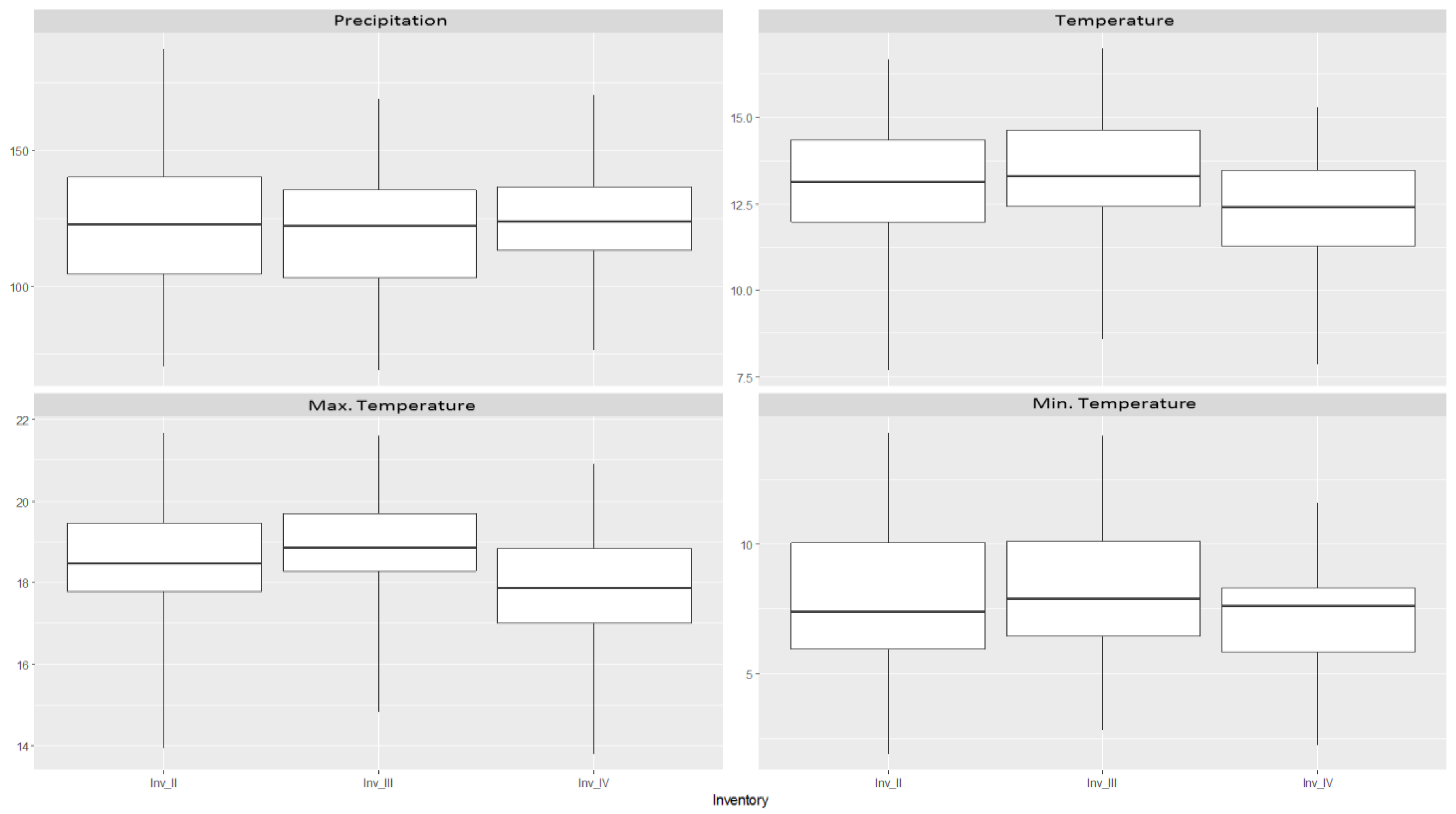
2.5. Environmental Variables
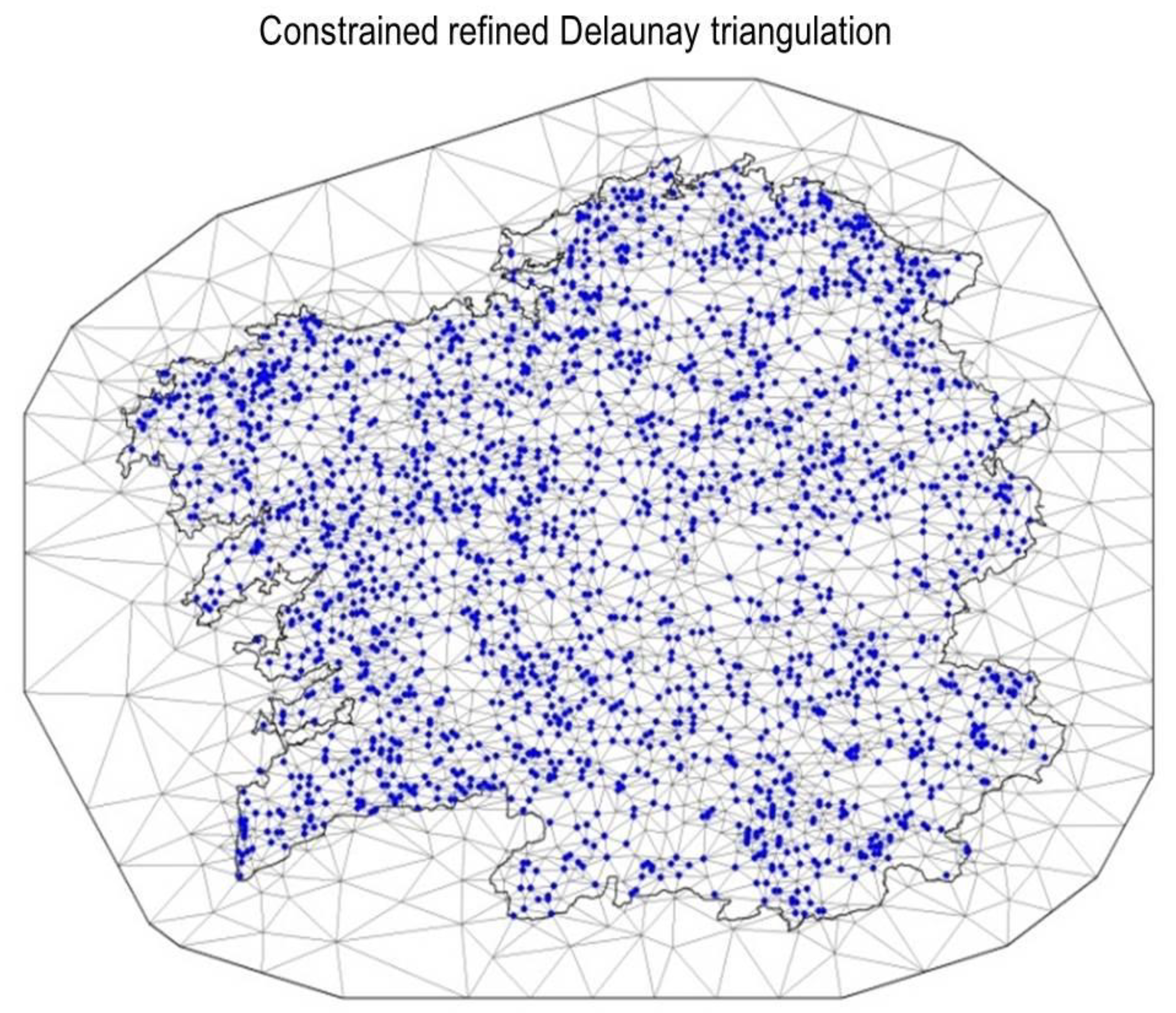
2.6. Spatial Model
2.7. Spatio-Temporal Model
2.8. Implementation
3. Results
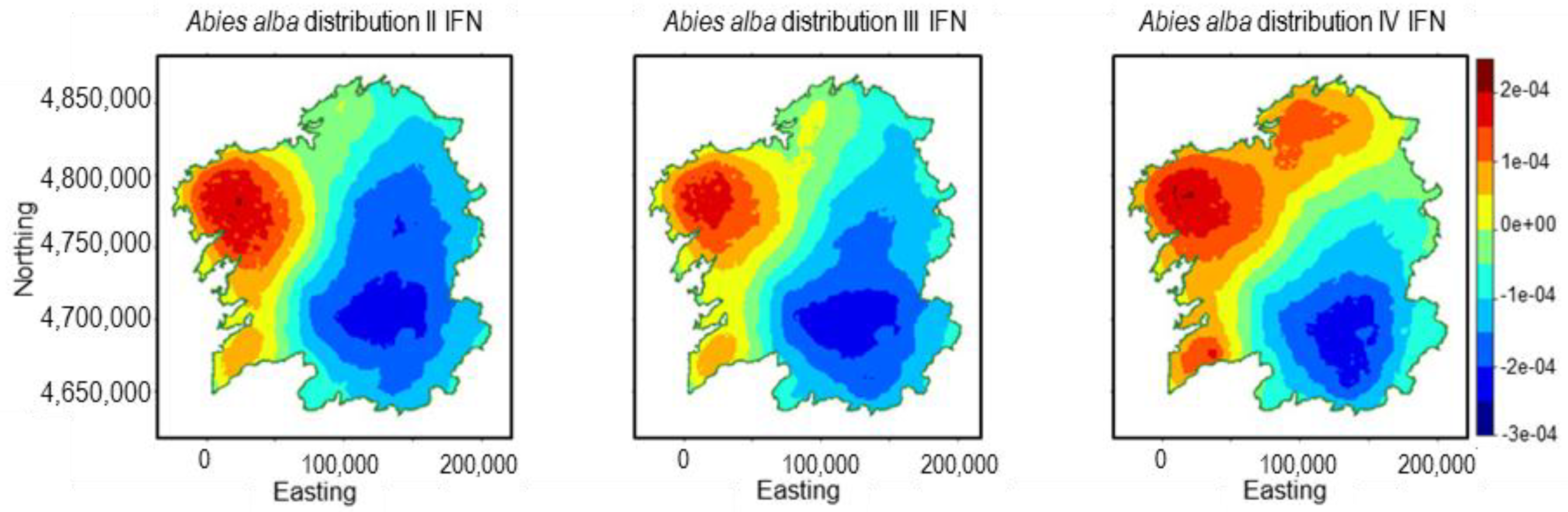
3.1. Abies alba
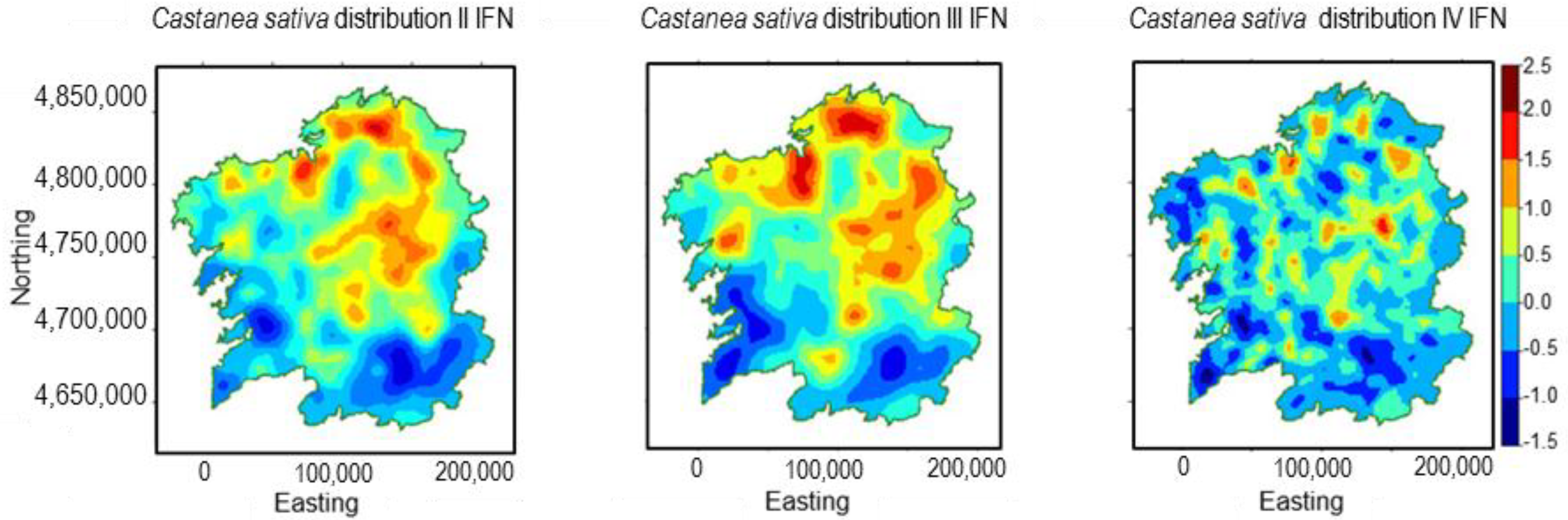
3.2. Castanea sativa
3.3. Pinus pinaster
3.4. Quercus robur
3.5. Summary
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Boisvenue, C.; Running, S.W. Impacts of climate change on natural forest productivity–evidence since the middle of the 20th century. Glob. Chang. Biol. 2006, 12, 862–882. [Google Scholar] [CrossRef]
- Davis, M.B.; Shaw, R.G. Range shifts and adaptive responses to Quaternary climate change. Science 2001, 292, 673–679. [Google Scholar] [CrossRef] [PubMed]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Adams, H.D.; Macalady, A.K.; Breshears, D.D.; Allen, C.D.; Stephenson, N.L.; Saleska, S.R.; Huxman, T.E.; McDowell, N.G. Climate-induced tree mortality: Earth system consequences. Eos 2010, 91, 153–154. [Google Scholar] [CrossRef]
- Schröter, D.; Cramer, W.; Leemans, R.; Prentice, I.C.; Araújo, M.B.; Arnell, N.W.; Bondeau, A.; Bugmann, H.; Carter, T.R.; Gracia, C.A.; et al. Ecosystem service supply and vulnerability to global change in Europe. Science 2005, 310, 1333–1337. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Spathelf, P.; van der Maaten, E.; van der Maaten-Theunissen, M.; Campioli, M.; Dobrowolska, D. Climate change impacts in European forests: The expert views of local observers. Ann. For. Sci. 2014, 71, 131–137. [Google Scholar] [CrossRef]
- de Rivera, O.R.; Blangiardo, M.; López-Quílez, A.; Martín-Sanz, I. Species distribution modelling through Bayesian hierarchical approach. Theor. Ecol. 2018. [Google Scholar] [CrossRef]
- Lindner, M.; Fitzgerald, J.B.; Zimmermann, N.E.; Reyer, C.; Delzon, S.; Maaten, E.; Schelhaas, M.J.; Lasch, P.; Eggers, J.; Maaten-Theunissen, M.; et al. Climate change and European forests: What do we know, what are the uncertainties, and what are the implications for forest management? J. Environ. Manag. 2014, 146, 69–83. [Google Scholar] [CrossRef] [PubMed]
- Hanewinkel, M.; Cullmann, D.A.; Schelhaas, M.J.; Nabuurs, G.J.; Zimmermann, N.E. Climate change may cause severe loss in the economic value of European forest land. Nat. Clim. Chang. 2013, 3, 203–207. [Google Scholar] [CrossRef]
- Maaten, E.; Hamann, A.; Maaten-Theunissen, M.; Bergsma, A.; Hengeveld, G.; Lammeren, R.; Mohren, F.; Nabuurs, G.J.; Terhürne, R.; Sterck, F. Species distribution models predict temporal but not spatial variation in forest growth. Ecol. Evol. 2017, 7, 2585–2594. [Google Scholar] [CrossRef] [PubMed]
- Elith, J.; Leathwick, J.R. Species distribution models: Ecological explanation and prediction across space and time. Ann. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar] [CrossRef]
- O’Neill, G.A.; Hamann, A.; Wang, T. Accounting for population variation improves estimates of the impact of climate change on species’ growth and distribution. J. Appl. Ecol. 2008, 45, 1040–1049. [Google Scholar] [CrossRef]
- Gray, L.K.; Hamann, A. Strategies for reforestation under uncertain future climates: Guidelines for Alberta, Canada. PLoS ONE 2011, 6, e22977. [Google Scholar] [CrossRef] [PubMed]
- Gray, L.K.; Hamann, A. Tracking suitable habitat for tree populations under climate change in western North America. Clim. Chang. 2013, 117, 289–303. [Google Scholar] [CrossRef]
- Hamann, A.; Aitken, S.N. Conservation planning under climate change: Accounting for adaptive potential and migration capacity in species distribution models. Divers. Distrib. 2013, 19, 268–280. [Google Scholar] [CrossRef]
- Schelhaas, M.J.; Nabuurs, G.J.; Hengeveld, G.; Reyer, C.; Hanewinkel, M.; Zimmermann, N.E.; Cullmann, D. Alternative forest management strategies to account for climate change-induced productivity and species suitability changes in Europe. Reg. Environ. Chang. 2015, 15, 1581–1594. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Elith, J.; Species Distribution Modelling with R. The R Foundation for Statistical Computing. Available online: http://cran.r-project.org/ web/packages/dismo/vignettes/sdm.pdf (accessed on 5 May 2018).
- Simpson, D.; Lindgren, F.; Rue, H. Fast approximate inference with INLA: The past, the present and the future. arXiv, 2011; arXiv:1105.2982. [Google Scholar]
- Chakraborty, A.; Gelfand, A.E.; Wilson, A.M.; Latimer, A.M.; Silander, J.A., Jr. Modeling large scale species abundance with latent spatial processes. Ann. Appl. Stat. 2010, 4, 1403–1429. [Google Scholar] [CrossRef]
- Pressey, R.L.; Cabeza, M.; Watts, M.E.; Cowling, R.M.; Wilson, K.A. Conservation planning in a changing world. Trends Ecol. Evol. 2007, 22, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Midgley, G.F.; Thuiller, W. Potential vulnerability of Namaqualand plant diversity to anthropogenic climate change. J. Arid Environ. 2007, 70, 615–628. [Google Scholar] [CrossRef]
- Loarie, S.R.; Carter, B.E.; Hayhoe, K.; McMahon, S.; Moe, R.; Knight, C.A.; Ackerly, D.D. Climate change and the future of California’s endemic flora. PLoS ONE 2008, 3, e2502. [Google Scholar] [CrossRef] [PubMed]
- Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Graham, C.H. The ability of climate envelope models to predict the effect of climate change on species distributions. Glob. Chang. Biol. 2006, 12, 2272–2281. [Google Scholar] [CrossRef]
- Wisz, M.S.; Hijmans, R.J.; Li, J.; Peterson, A.T.; Graham, C.H.; Guisan, A. Effects of sample size on the performance of species distribution models. Divers. Distrib. 2008, 14, 763–773. [Google Scholar] [CrossRef]
- Rivera, Ó.R.; López-Quílez, A. Development and Comparison of Species Distribution Models for Forest Inventories. ISPRS Int. J. Geo-Inf. 2017, 6, 176. [Google Scholar] [CrossRef]
- Guisan, A.; Edwards, T.C.; Hastie, T. Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Model. 2002, 157, 89–100. [Google Scholar] [CrossRef]
- Busby, J. BIOCLIM—A bioclimate analysis and prediction system. Plant Prot. Q. (Aust.) 1991, 6, 64–68. [Google Scholar]
- Leathwick, J.R.; Rowe, D.; Richardson, J.; Elith, J.; Hastie, T. Using multivariate adaptive regression splines to predict the distributions of New Zealand’s freshwater diadromous fish. Freshw. Biol. 2005, 50, 2034–2052. [Google Scholar] [CrossRef]
- Munoz, F.; Pennino, M.G.; Conesa, D.; López-Quílez, A.; Bellido, J.M. Estimation and prediction of the spatial occurrence of fish species using Bayesian latent Gaussian models. Stoch. Environ. Res. Risk Assess. 2013, 27, 1171–1180. [Google Scholar] [CrossRef]
- Underwood, A.J. Techniques of analysis of variance in experimental marine biology and ecology. Oceanography and marine biology: An annual review. Ann. Rev. Oceanogr. Mar. Biol. 1981, 19, 513–605. [Google Scholar]
- Hurlbert, S.H. Pseudoreplication and the design of ecological field experiments. Ecol. Monogr. 1984, 54, 187–211. [Google Scholar] [CrossRef]
- Royle, J.A.; Kéry, M.; Gautier, R.; Schmid, H. Hierarchical spatial models of abundance and occurrence from imperfect survey data. Ecol. Monogr. 2007, 77, 465–481. [Google Scholar] [CrossRef]
- Cressie, N.; Calder, C.A.; Clark, J.S.; Hoef, J.M.V.; Wikle, C.K. Accounting for uncertainty in ecological analysis: The strengths and limitations of hierarchical statistical modeling. Ecol. Appl. 2009, 19, 553–570. [Google Scholar] [CrossRef] [PubMed]
- Gelfand, A.E.; Diggle, P.J.; Fuentes, M.; Guttorp, P. (Eds.) Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Svenning, J.C.; Normand, S.; Kageyama, M. Glacial refugia of temperate trees in Europe: Insights from species distribution modelling. J. Ecol. 2008, 96, 1117–1127. [Google Scholar] [CrossRef]
- López Sáez, J.A.; López García, P.; López Merino, L. La transición Mesolítico-Neolítico en el Valle Medio del Ebro y en el Prepirineo aragonés desde una perspectiva paleoambiental: Dinámica de la antropización y origen de la agricultura. Rev. Iberoam. Hist. 2006, 1, 4–11. [Google Scholar]
- López Sáez, J.A.; López García, P.; López Merino, L. El impacto humano en la Cordillera Cantábrica: Estudios palinológicos durante el Holoceno medio. Zona Arqueol. 2006, 7, 122–131. [Google Scholar]
- López Sáez, J.A.; Galop, D.; Iriarte Chiapusso, M.J.; López Merino, L. Paleoambiente y antropización en los Pirineos de Navarra durante el Holoceno medio (VI–IV milenios cal. BC): Una perspectiva palinológica. Veleia 2008, 24–25, 645–653. [Google Scholar]
- Carrión, J.S.; Fuentes, N.; González-Sampériz, P.; Quirante, L.S.; Finlayson, J.C.; Fernández, S.; Andrade, A. Holocene environmental change in a montane region of southern Europe with a long history of human settlement. Quat. Sci. Rev. 2007, 26, 1455–1475. [Google Scholar] [CrossRef]
- Matejicek, L.; Vavrova, E.; Cudlin, P. Spatio-temporal modelling of ground vegetation development in mountain spruce forests. Ecol. Model. 2011, 222, 2584–2592. [Google Scholar] [CrossRef]
- Gratzer, G.; Canham, C.; Dieckmann, U.; Fischer, A.; Iwasa, Y.; Law, R.; Lexer, M.J.; Sandmann, H.; Spies, T.A.; Splechtna, B.E.; et al. Spatio-temporal development of forests–current trends in field methods and models. Oikos 2004, 107, 3–15. [Google Scholar] [CrossRef]
- O’Rourke, S.; Kelly, G.E. Spatio-temporal modelling of forest growth spanning 50 years—The effects of different thinning strategies. Procedia Environ. Sci. 2015, 26, 101–104. [Google Scholar] [CrossRef]
- Diggle, P.J. Statistical Analysis of Spatial Point Patterns; Arnold: London, UK, 2003. [Google Scholar]
- Stoyan, D.; Penttinen, A. Recent applications of point process methods in forestry statistics. Stat. Sci. 2000, 15, 61–78. [Google Scholar]
- Illian, J.; Penttinen, A.; Stoyan, H.; Stoyan, D. Statistical Analysis and Modelling of Spatial Point Patterns; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 70. [Google Scholar]
- Grabarnik, P.; Särkkä, A. Modelling the spatial structure of forest stands by multivariate point processes with hierarchical interactions. Ecol. Model. 2009, 220, 1232–1240. [Google Scholar] [CrossRef]
- Cosandey-Godin, A.; Krainski, E.T.; Worm, B.; Flemming, J.M. Applying Bayesian spatiotemporal models to fisheries bycatch in the Canadian Arctic. Can. J. Fish. Aquat. Sci. 2014, 72, 186–197. [Google Scholar] [CrossRef]
- Wade, P.R. Bayesian methods in conservation biology. Conserv. Biol. 2000, 14, 1308–1316. [Google Scholar] [CrossRef]
- Wintle, B.A.; McCarthy, M.A.; Volinsky, C.T.; Kavanagh, R.P. The use of Bayesian model averaging to better represent uncertainty in ecological models. Conserv. Biol. 2003, 17, 1579–1590. [Google Scholar] [CrossRef]
- Illian, J.B.; Martino, S.; Sørbye, S.H.; Gallego-Fernández, J.B.; Zunzunegui, M.; Esquivias, M.P.; Travis, J.M. Fitting complex ecological point process models with integrated nested Laplace approximation. Methods Ecol. Evol. 2013, 4, 305–315. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S. Approximate Bayesian inference for hierarchical Gaussian Markov random field models. J. Stat. Plan. Inference 2007, 137, 3177–3192. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach. J. R. Stat. Soc. Ser. B 2011, 73, 423–498. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Beguin, J.; Martino, S.; Rue, H.; Cumming, S.G. Hierarchical analysis of spatially autocorrelated ecological data using integrated nested Laplace approximation. Methods Ecol. Evol. 2012, 3, 921–929. [Google Scholar] [CrossRef]
- Dutra Silva, L.; Brito de Azevedo, E.; Bento Elias, R.; Silva, L. Species Distribution Modeling: Comparison of Fixed and Mixed Effects Models Using INLA. ISPRS Int. J. Geo-Inf. 2017, 6, 391. [Google Scholar] [CrossRef]
- San-Miguel-Ayanz, J.; Rigo, D.D.; Caudullo, G.; Houston Durrant, T.; Mauri, A. European Atlas of Forest Tree Species; European Commission, Joint Research Centre: Brussels, Belgium, 2016. [Google Scholar]
- Herrera, S.; Gutiérrez, J.M.; Ancell, R.; Pons, M.R.; Frías, M.D.; Fernández, J. Development and analysis of a 50-year high-resolution daily gridded precipitation dataset over Spain (Spain02). Int. J. Climatol. 2012, 32, 74–85. [Google Scholar] [CrossRef]
- Herrera, S.; Fernández, J.; Gutiérrez, J.M. Update of the Spain02 gridded observational dataset for EURO-CORDEX evaluation: Assessing the effect of the interpolation methodology. Int. J. Climatol. 2016, 36, 900–908. [Google Scholar] [CrossRef]
- Gastón, A.; Soriano, C.; Gómez-Miguel, V. Lithologic data improve plant species distribution models based on coarse-grained occurrence data. For. Syst. 2009, 18, 42–49. [Google Scholar]
- Van Liedekerke, M.; Jones, A.; Panagos, P. ESDBv2 Raster Library—A Set of Rasters Derived from the European Soil Database Distribution v2.0; European Commission and the European Soil Bureau Network, CDROM, EUR, 19945; European Commission: Brussels, Belgium, 2006. [Google Scholar]
- Gelfand, A.E.; Silander, J.A.; Wu, S.; Latimer, A.; Lewis, P.O.; Rebelo, A.G.; Holder, M. Explaining species distribution patterns through hierarchical modeling. Bayesian Anal. 2006, 1, 41–92. [Google Scholar] [CrossRef]
- Blangiardo, M.; Cameletti, M. Spatial and Spatio-Temporal Bayesian Models with R-INLA; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Geisser, S.; Eddy, W.F. A predictive approach to model selection. J. Am. Stat. Assoc. 1979, 74, 153–160. [Google Scholar] [CrossRef]
- Vehtari, A.; Lampinen, J. Bayesian model assessment and comparison using cross-validation predictive densities. Neural Comput. 2002, 14, 2439–2468. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Shalizi, C.R. Philosophy and the practice of Bayesian statistics. Br. J. Math. Stat. Psychol. 2013, 66, 8–38. [Google Scholar] [CrossRef] [PubMed]
- Spiegelhalter, D.; Best, N.G.; Carlin, B.P.; Van der Linde, A. Bayesian measures of model complexity and fit. Qual. Control Appl. Stat. 2003, 48, 431–432. [Google Scholar] [CrossRef]
- Van Der Linde, A. DIC in variable selection. Stat. Neerl. 2005, 59, 45–56. [Google Scholar] [CrossRef]
- Watanabe, S. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]
- Li, L.; Qiu, S.; Zhang, B.; Feng, C.X. Approximating cross-validatory predictive evaluation in Bayesian latent variable models with integrated IS and WAIC. Stat. Comput. 2016, 26, 881–897. [Google Scholar] [CrossRef]
- Pettit, L.I. The conditional predictive ordinate for the normal distribution. J. R. Stat. Soc. Ser. B 1990, 52, 175–184. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Roos, M.; Held, L. Sensitivity analysis in Bayesian generalized linear mixed models for binary data. Bayesian Anal. 2011, 6, 259–278. [Google Scholar] [CrossRef]
- Golding, N.; Purse, B.V. Fast and flexible Bayesian species distribution modelling using Gaussian processes. Methods Ecol. Evol. 2016, 7, 598–608. [Google Scholar] [CrossRef]
- Warton, D.I.; Blanchet, F.G.; O’Hara, R.B.; Ovaskainen, O.; Taskinen, S.; Walker, S.C.; Hui, F.K. So Many Variables: Joint Modeling in Community Ecology. Trends Ecol. Evol. 2015, 30, 766–779. [Google Scholar] [CrossRef] [PubMed]
- Redding, D.W.; Cunningham, A.A.; Woods, J.; Jones, K.E. Spatial and seasonal predictive models of Rift Valley Fever disease. Philos. Trans. R. Soc. Lond. B 2016, 372, 20160165. [Google Scholar] [CrossRef] [PubMed]
- Renner, I.W.; Warton, D.I. Equivalence of MAXENT and Poisson Point Process Models for Species Distribution Modeling in Ecology. Biometrics 2013, 69, 274–281. [Google Scholar] [CrossRef] [PubMed]

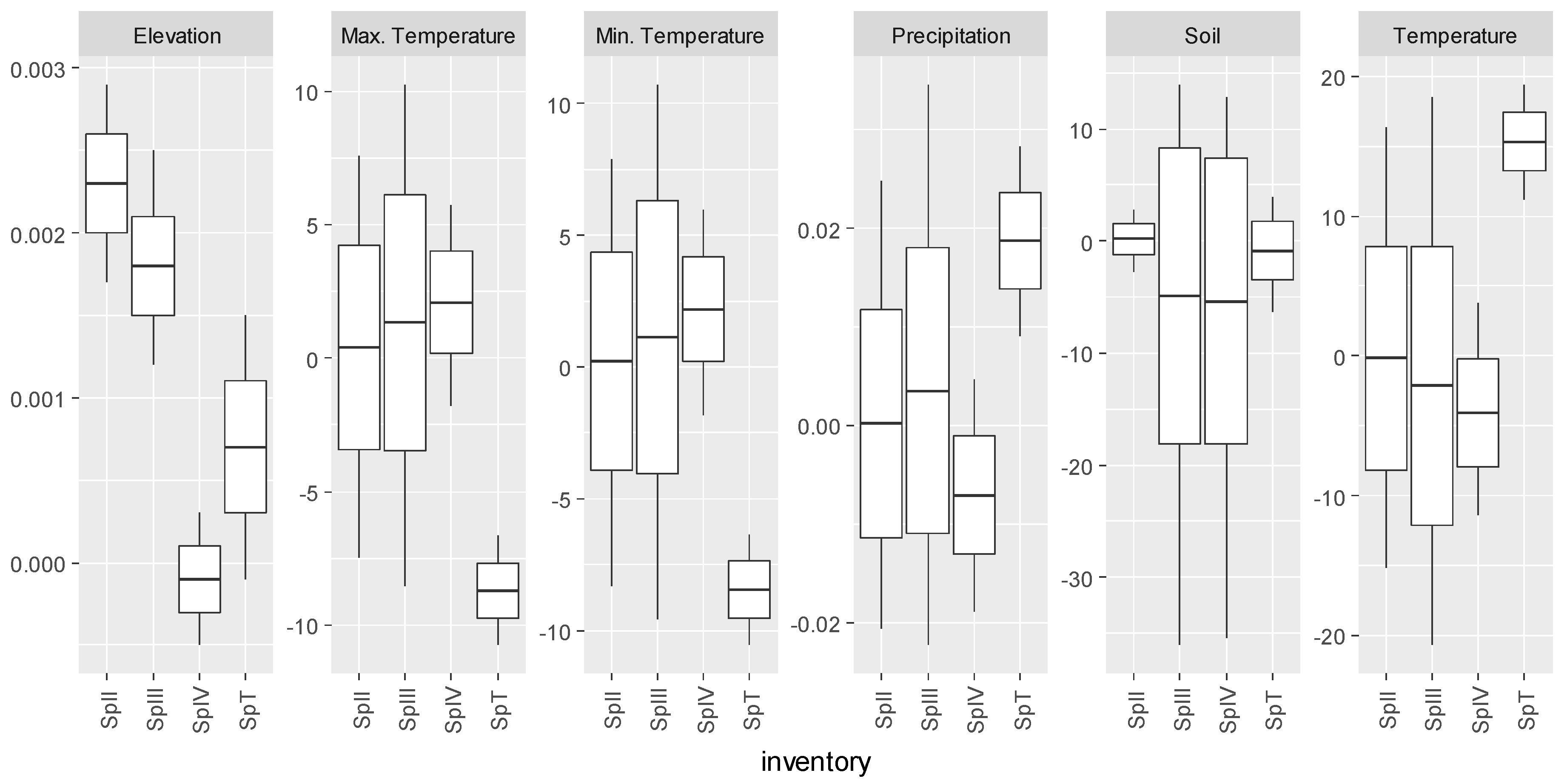
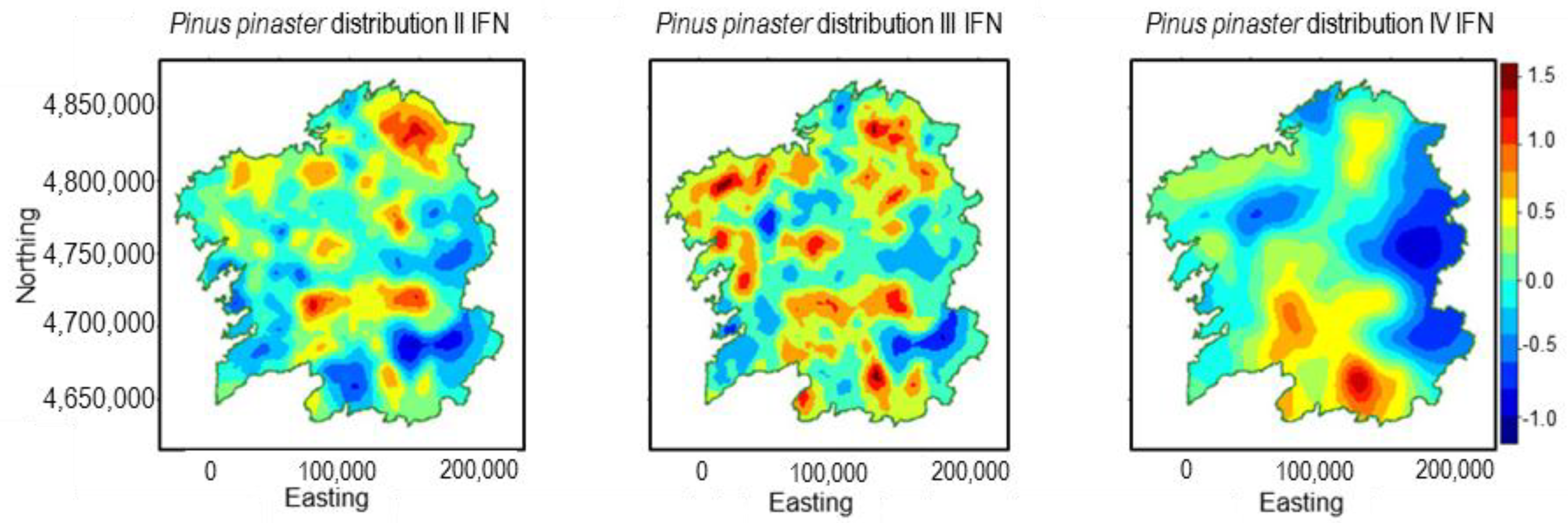
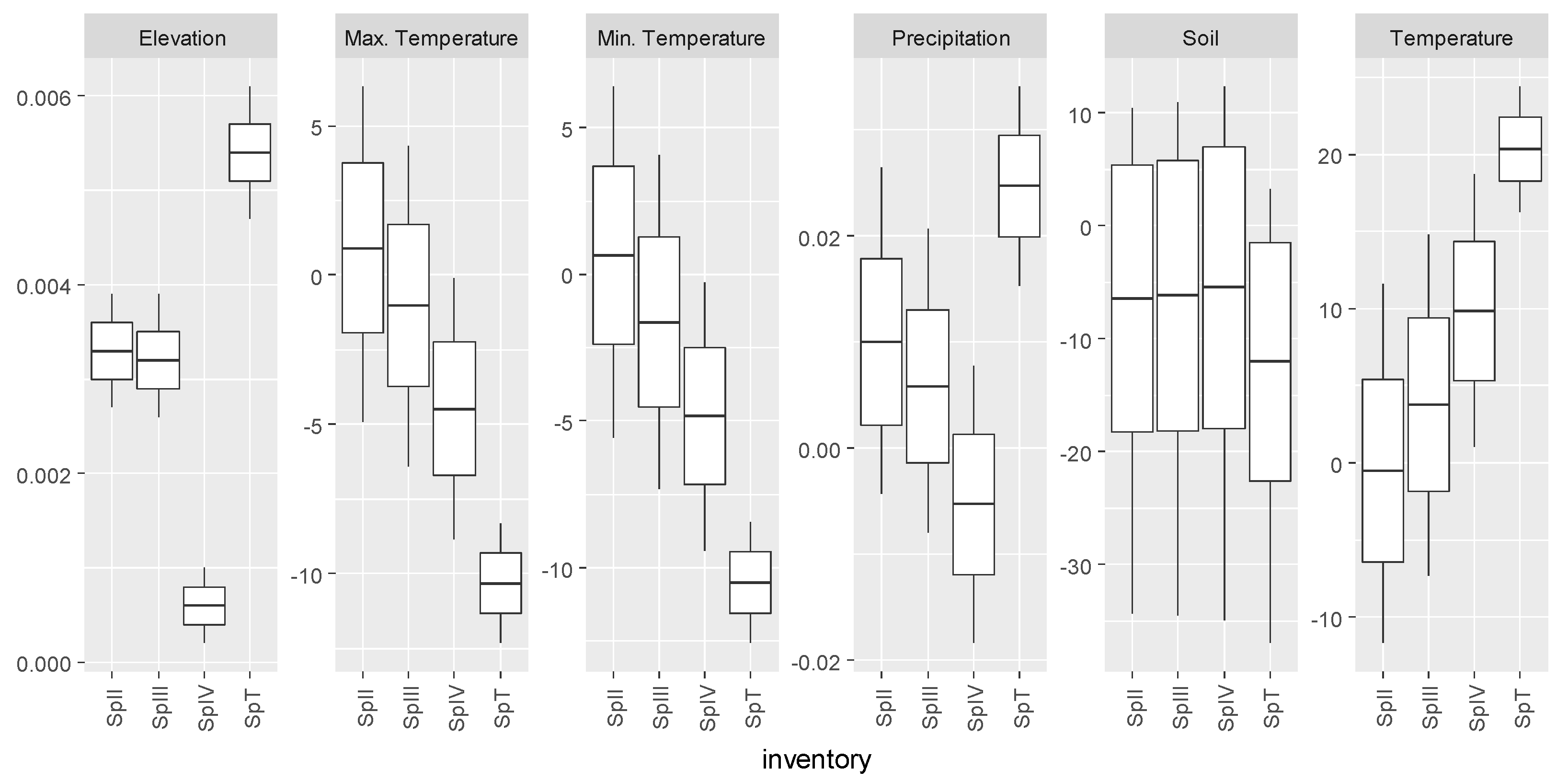

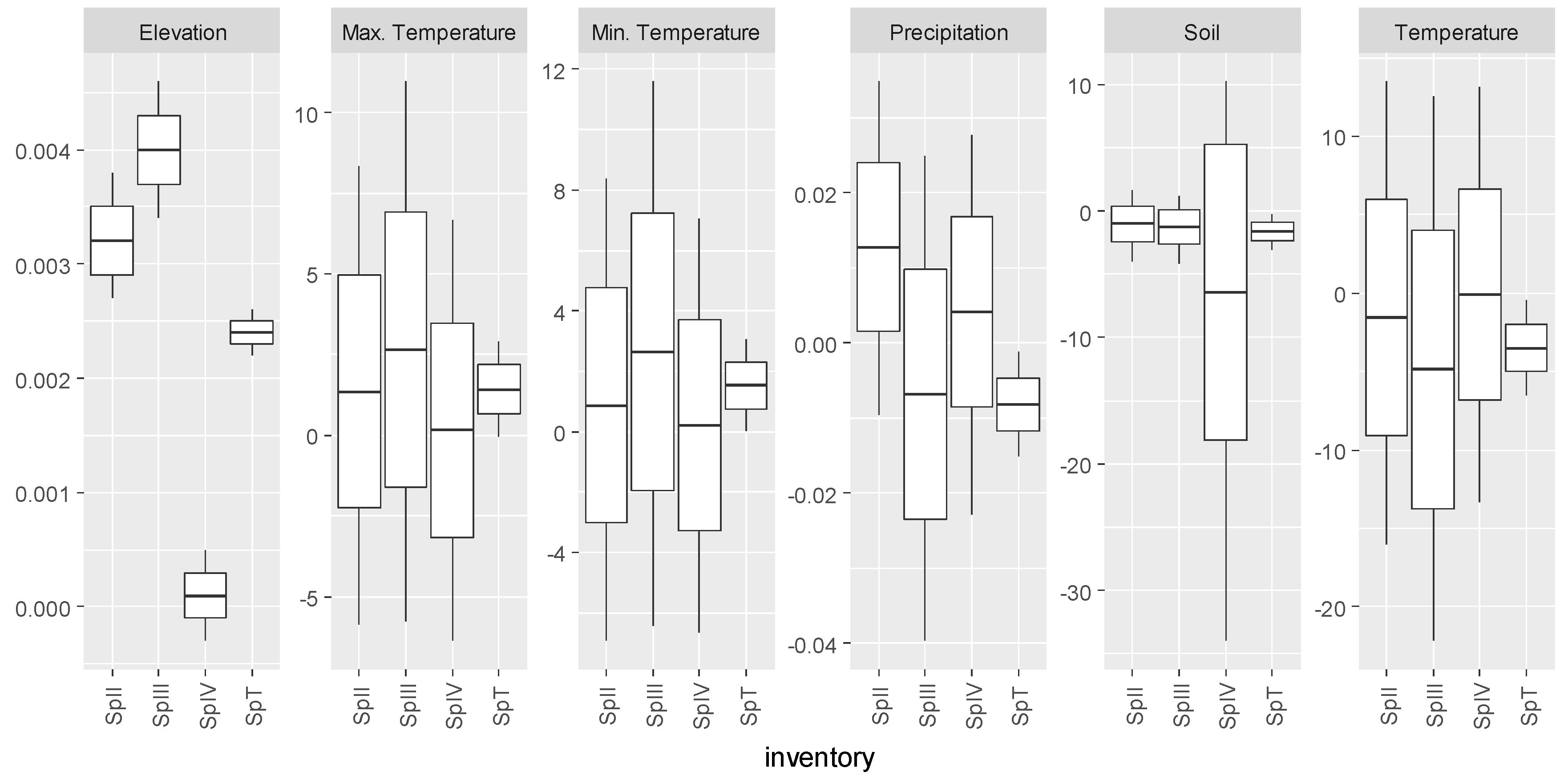
| Inventory | Abies alba Mill. | Castanea sativa Mill. | Pinus pinaster Ait. | Quercus robur L. |
|---|---|---|---|---|
| II (1980s) | 1% | 26% | 51% | 51% |
| III (1990s) | 2% | 15% | 38% | 40% |
| IV (2000s) | 1% | 35% | 46% | 59% |
| Abies alba | Castanea sativa | Pinus pinaster | Quercus robur | |||||
|---|---|---|---|---|---|---|---|---|
| Spatial | Spatio-Temporal | Spatial | Spatio-Temporal | Spatial | Spatio-Temporal | Spatial | Spatio-Temporal | |
| Elevation | − | − | Rn | Rn | + | + | + | + |
| Soil | Rn | Rn | Rn | Rn | Rn | Rn | Rn | − |
| Precipitation | − | − | Rn | Rn | Rn | + | Rn | − |
| Temperature | − | − | Rn | Rn | Rn | + | Rn | − |
| Max. Temperature | − | − | Rn | − | Rn | − | Rn | Rn |
| Min. Temperature | − | − | Rn | − | Rn | − | Rn | − |
| Abies alba | Castanea sativa | Pinus pinaster | Quercus robur | |||||
|---|---|---|---|---|---|---|---|---|
| Spatial | Spatio-Temporal | Spatial | Spatio-Temporal | Spatial | Spatio-Temporal | Spatial | Spatio-Temporal | |
| WAIC | 15.54 | 12.73 | 5.435 | 10.629 | 4.621 | 3.385 | 9.676 | 1.837 |
| LCPO | 1.531 | 1.251 | 2.327 | 2.986 | 3.725 | 2.327 | 2.382 | 1.965 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez de Rivera, Ó.; López-Quílez, A.; Blangiardo, M. Assessing the Spatial and Spatio-Temporal Distribution of Forest Species via Bayesian Hierarchical Modeling. Forests 2018, 9, 573. https://doi.org/10.3390/f9090573
Rodríguez de Rivera Ó, López-Quílez A, Blangiardo M. Assessing the Spatial and Spatio-Temporal Distribution of Forest Species via Bayesian Hierarchical Modeling. Forests. 2018; 9(9):573. https://doi.org/10.3390/f9090573
Chicago/Turabian StyleRodríguez de Rivera, Óscar, Antonio López-Quílez, and Marta Blangiardo. 2018. "Assessing the Spatial and Spatio-Temporal Distribution of Forest Species via Bayesian Hierarchical Modeling" Forests 9, no. 9: 573. https://doi.org/10.3390/f9090573
APA StyleRodríguez de Rivera, Ó., López-Quílez, A., & Blangiardo, M. (2018). Assessing the Spatial and Spatio-Temporal Distribution of Forest Species via Bayesian Hierarchical Modeling. Forests, 9(9), 573. https://doi.org/10.3390/f9090573







