Developing Allometric Equations for Estimating Shrub Biomass in a Boreal Fen
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Aboveground Biomass Sampling
2.3. Allometrics
2.3.1. Local Equations
2.3.2. Published Equations
3. Results
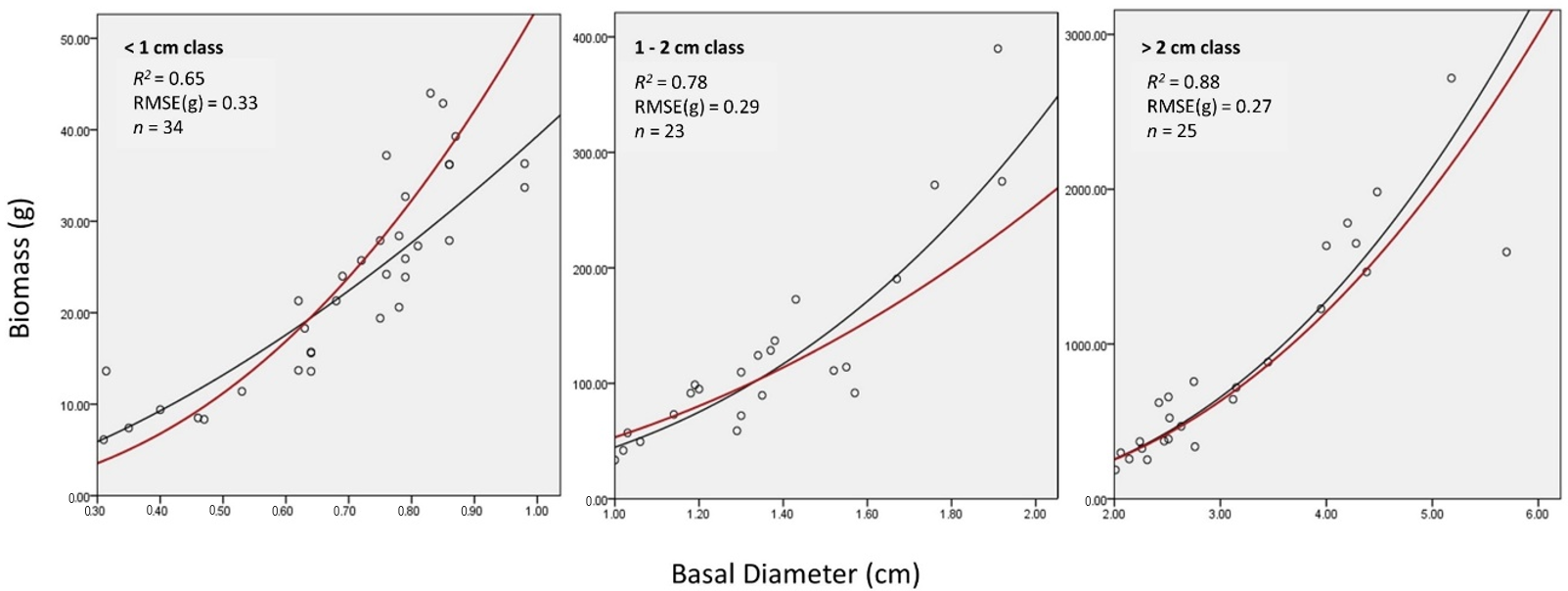
3.1. Local Equations
3.2. Published Equations
4. Discussion
4.1. The Value of Phylogenetic Equations
4.2. Equation Portability
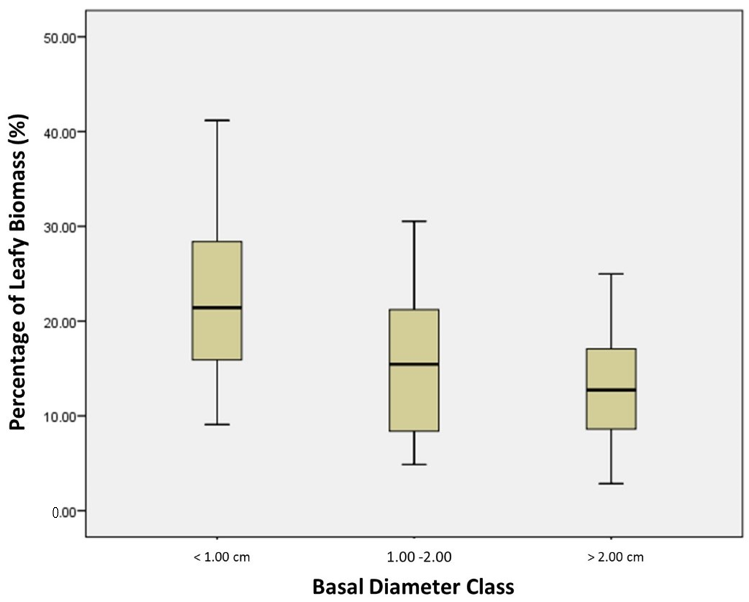
4.3. The Variability in Size Classes
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Brown, S. Measuring carbon in forests: Current status and future challenges. Environ. Pollut. 2002, 116, 363–372. [Google Scholar] [CrossRef]
- Nwaishi, F.; Petrone, R.M.; Price, J.S.; Andersen, R. Towards developing a functional-based approach for constructed peatlands evaluation in the Alberta oil sands region, Canada. Wetlands 2015, 35, 211–225. [Google Scholar] [CrossRef]
- Tarnocai, C. The impact of climate change on Canadian peatlands. Can. Water Resour. J. 2009, 34, 453–466. [Google Scholar] [CrossRef]
- Yu, Z.; Loisel, J.; Brosseau, D.P.; Beilman, D.W.; Hunt, S.J. Global peatland dynamics since the Last Glacial Maximum. Geophys. Res. Lett. 2010, 37, 13. [Google Scholar] [CrossRef]
- Le Quere, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Pongratz, J.; Manning, A.C.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; Jackson, R.B.; et al. Global carbon budget 2017. Earth Syst. Sci. Data 2018, 10, 405–448. [Google Scholar] [CrossRef]
- Paul, K.I.; Roxburgh, S.H.; Chave, J.; England, J.R.; Zerihun, A.; Specht, A.; Lewis, T.; Bennett, L.T.; Baker, T.G.; Adams, M.A.; et al. Testing the generality of above-ground biomass allometry across plant functional types at the continent scale. Glob. Chang. Biol. 2016, 22, 2106–2124. [Google Scholar] [CrossRef] [PubMed]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The biomass mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.S.; Trettin, C.C.; Li, H.; Sun, G. An integrated model of soil, hydrology, and vegetation for carbon dynamics in wetland ecosystems. Glob. Biogeochem. Cycles 2002, 16, 1061. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface lidar remote sensing of basal area and biomass in deciduous forests of eastern Maryland, U.S.A. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Kankare, V.; Raty, M.; Yu, X.W.; Holopainen, M.; Vastaranta, M.; Kantola, T.; Hyyppa, J.; Hyyppa, H.; Alho, P.; Viitala, R. Single tree biomass modelling using airborne laser scanning. Isprs J. Photogramm. Remote Sens. 2013, 85, 66–73. [Google Scholar] [CrossRef]
- Hyde, P.; Dubayah, R.; Walker, W.; Blair, J.B.; Hofton, M.; Hunsaker, C. Mapping forest structure for wildlife habitat analysis using multi-sensor (LiDAR, SAR/InSAR, ETM+, Quickbird) synergy. Remote Sens. Environ. 2006, 102, 63–73. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Stasko, T.H.; Conrado, R.J.; Wankerl, A.; Labatut, R.; Tasseff, R.; Mannion, J.T.; Gao, H.O.; Sanborn, S.D.; Knott, G. Mapping woody-biomass supply costs using forest inventory and competing industry data. Biomass Bioenergy 2011, 35, 263–271. [Google Scholar] [CrossRef]
- Verwijst, T.; Telenius, B. Biomass estimation procedures in short rotation forestry. For. Ecol. Manag. 1999, 121, 137–146. [Google Scholar] [CrossRef]
- Seidel, D.; Fleck, S.; Leuschner, C.; Hammett, T. Review of ground-based methods to measure the distribution of biomass in forest canopies. Ann. For. Sci. 2011, 68, 225–244. [Google Scholar] [CrossRef] [Green Version]
- TerMikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef] [Green Version]
- Whitehouse, H.E.; Bayley, S.E. Vegetation patterns and biodiversity of peatland plant communities surrounding mid-boreal wetland ponds in Alberta, Canada. Can. J. Bot. 2005, 83, 621–637. [Google Scholar] [CrossRef]
- Campbell, C.; Vitt, D.H.; Halsey, L.A.; Campbell, I.D.; Thormann, M.N.; Bayley, S.E. Net Primary Production and Standing Biomass in Northern Continental Wetlands; Information Report-Northern Forestry Centre, Canadian Forest Service: Edmonton, AB, Canada, 2000.
- Connolly, B.J.; Grigal, D.F. Biomass estimation equations for wetland tall shrubs. Minn. For. Res. Notes 1983, 284, 4. [Google Scholar]
- Mosseler, A.; Major, J.E.; Larocque, G.R. Allometric relationships from coppice structure of seven North American willow (salix) species. Biomass Bioenergy 2016, 88, 97–105. [Google Scholar] [CrossRef]
- Muukkonen, P. Generalized allometric volume and biomass equations for some tree species in Europe. Eur. J. For. Res. 2007, 126, 157–166. [Google Scholar] [CrossRef]
- Law, B.E.; Van Tuyl, S.; Cescatti, A.; Baldocchi, D.D. Estimation of leaf area index in open-canopy ponderosa pine forests at different successional stages and management regimes in Oregon. Agric. For. Meteorol. 2001, 108, 1–14. [Google Scholar] [CrossRef]
- Buech, R.R.; Rugg, D.J. Biomass relations of shrub components and their generality. For. Ecol. Manag. 1989, 26, 257–264. [Google Scholar] [CrossRef]
- Mandal, G.; Joshi, S.P. Estimation of above-ground biomass and carbon stock of an invasive woody shrub in the subtropical deciduous forests of Doon Valley, Western Himalaya, India. J. For. Res. 2015, 26, 291–305. [Google Scholar] [CrossRef]
- Rojo, V.; Arzamendia, Y.; Perez, C.; Baldo, J.; Vila, B. Double sampling methods in biomass estimates of andean shrubs and tussocks. Rangel. Ecol. Manag. 2017, 70, 718–722. [Google Scholar] [CrossRef]
- Huff, S.; Ritchie, M.; Temesgen, H. Allometric equations for estimating aboveground biomass for common shrubs in northeastern california. For. Ecol. Manag. 2017, 398, 48–63. [Google Scholar] [CrossRef]
- Berner, L.T.; Alexander, H.D.; Loranty, M.M.; Ganzlin, P.; Mack, M.C.; Davydov, S.P.; Goetz, S.J. Biomass allometry for alder, dwarf birch, and willow in boreal forest and tundra ecosystems of far northeastern Siberia and north-central Alaska. For. Ecol. Manag. 2015, 337, 110–118. [Google Scholar] [CrossRef]
- Paul, K.I.; Roxburgh, S.H.; England, J.R.; Ritson, P.; Hobbs, T.; Brooksbank, K.; Raison, R.J.; Larmour, J.S.; Murphy, S.; Norris, J.; et al. Development and testing of allometric equations for estimating above-ground biomass of mixed-species environmental plantings. For. Ecol. Manag. 2013, 310, 483–494. [Google Scholar] [CrossRef]
- Roxburgh, S.H.; Paul, K.I.; Clifford, D.; England, J.R.; Raison, R.J. Guidelines for constructing allometric models for the prediction of woody biomass: How many individuals to harvest? Ecosphere 2015, 6, 38. [Google Scholar] [CrossRef]
- Sun, H.; Wang, X.P.; Fan, Y.W.; Liu, C.; Wu, P.; Li, Q.Y.; Yin, W.L. Effects of biophysical constraints, climate and phylogeny on forest shrub allometries along an altitudinal gradient in northeast china. Sci. Rep. 2017, 7, 43769. [Google Scholar] [CrossRef] [PubMed]
- Brand, G.J.; Smith, W.B. Evaluating allometric shrub biomass equations fit to generated data. Can. J. Bot. 1985, 63, 64–67. [Google Scholar] [CrossRef]
- Natural Regions Committee. Natural Regions and Subregions of Alberta; Government of Alberta: Edmonton, AB, Canada, 2006.
- Bond-Lamberty, B.; Wang, C.; Gower, S.T. Aboveground and belowground biomass and sapwood area allometric equations for six boreal tree species of northern Manitoba. Can. J. For. Res. Rev. 2002, 32, 1441–1450. [Google Scholar] [CrossRef]
- Roussopoulos, P.J.; Loomis, R.M. Weights and Dimensional Properties of Shrubs and Small Trees of the Great Lakes Conifer Forest; USDA Forest Service: St. Paul, MN, USA, 1979; NC-178.
- Zar, J.H. Biostatistical Analysis, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999; pp. 324–359. [Google Scholar]
- Forrester, D.I.; Tachauer, I.H.H.; Annighoefer, P.; Barbeito, I.; Pretzsch, H.; Ruiz-Peinado, R.; Stark, H.; Vacchiano, G.; Zlatanov, T.; Chakraborty, T.; et al. Generalized biomass and leaf area allometric equations for European tree species incorporating stand structure, tree age and climate. For. Ecol. Manag. 2017, 396, 160–175. [Google Scholar] [CrossRef]
- Shaiek, O.; Loustau, D.; Trichet, P.; Meredieu, C.; Bachtobji, B.; Garchi, S.; Aouni, M.H.E. Generalized biomass equations for the main aboveground biomass components of maritime pine across contrasting environments. Ann. For. Sci. 2011, 68, 443. [Google Scholar] [CrossRef]
- Levia, D.F., Jr. A generalized allometric equation to predict foliar dry weight on the basis of trunk diameter for eastern white pine (Pinus strobus L). For. Ecol. Manag. 2008, 255, 1789–1792. [Google Scholar] [CrossRef]
- Porté, A.; Bosc, A.; Champion, I.; Loustau, D. Estimating the foliage area of maritime pine (Pinus pinaster Ait.) branches and crowns with application to modelling the foliage area distribution in the crown. Ann. For. Sci. 2000, 57, 73–86. [Google Scholar] [CrossRef]
- Wutzler, T.; Wirth, C.; Schumacher, J. Generic biomass functions for Common beech (Fagus sylvatica) in Central Europe: Predictions and components of uncertainty. Can. J. For. Res. 2008, 38, 1661–1675. [Google Scholar] [CrossRef]

| Shrubs Harvested | Stems Harvested | Average Height (m) | Average Number of Stems per Shrub | Basal Diameter Range (cm) | Stem Length Range (cm) | Dried Stem Biomass Range (g) | |
|---|---|---|---|---|---|---|---|
| Site 1 | |||||||
| Alnus spp. | 8 | 21 | 3.09 | 8 | 0.64–5.70 | 89–389 | 16–1598 |
| Salix spp. | 16 | 37 | 1.46 | 26 | 0.31–2.76 | 60–209 | 7–386 |
| Betula pumila | 13 | 25 | 1.59 | 18 | 0.31–1.37 | 39–250 | 6–129 |
| Site 2 | |||||||
| Alnus spp. | 6 | 6 | 4.89 | 1 | 3.12–5.18 | 381–545 | 643–2718 |
| Salix spp. | 12 | 12 | 3.45 | 1 | 1.16–2.75 | 242–450 | 78–1635 |
| n | a | B | R2 | RMSE (g) | MAPE | CV-RMSE (g) | a Test-t-Value (p) | b Test-t-Value (p) | |
|---|---|---|---|---|---|---|---|---|---|
| Phylogenetic Equations | |||||||||
| Alnus | 27 | 44.06 | 2.395 | 0.983 | 0.209 | 2.9% | 0.194 | 1.83 (0.07) | 1.83 (0.07) |
| Salix | 49 | 55.85 | 2.325 | 0.943 | 0.344 | 6.2% | 0.325 | 0.94 (0.35) | 1.56 (0.12) |
| Betula | 25 | 49.52 | 2.027 | 0.907 | 0.254 | 7.2% | 0.260 | 0.19 (0.85) | 0.77 (0.44) |
| Alnus & Salix | 76 | 52.88 | 2.291 | 0.961 | 0.314 | 5.4% | 0.293 | 0.44 (0.66) | 0.56 (0.57) |
| General Equation | |||||||||
| General | 82 | 53.37 | 2.251 | 0.967 | 0.291 | 5.9% | 0.287 | N/A | N/A |
| D Range (cm) | a | b | R2 | RMSE (g) | b Test-t-Value (p) | |
|---|---|---|---|---|---|---|
| Conolly & Grigal [20] | ||||||
| Alnus rugosa | 0.25–3 | 33.722 | 2.712 | 0.880 | 0.558 | 4.56 (<0.01) * |
| Salix spp. | 0.25–3 | 60.153 | 2.202 | 0.962 | 0.315 | 0.72 (0.48) |
| Betula pumila | 0.25–2.25 | 59.777 | 2.579 | 0.930 | 0.426 | 3.92 (<0.01) * |
| Berner et al. [28] | ||||||
| Alnus spp. pooled | 0.18–9.52 | 19.40 | 2.78 | 0.608 | 1.006 | 3.18 (<0.01) * |
| Salix spp. pooled | 0.01–6.30 | 21.80 | 2.64 | 0.687 | 0.899 | 2.64 (<0.01) * |
| Betula spp. pooled | 0.09–2.53 | 28.97 | 2.88 | 0.810 | 0.701 | 5.28 (<0.01) * |
| Brand & Smith [32] | ||||||
| Salix spp. | 0.25–3.81 | 44.86 | 2.539 | 0.947 | 0.372 | 3.81 (<0.01) * |
| Alnus | Betula | Salix | Alnus-Salix | |
|---|---|---|---|---|
| Alnus | - | - | - | - |
| Betula | 2.45 (0.02) * | - | - | - |
| Salix | 0.67 (0.50) | 1.86 (0.07) | - | - |
| Alnus-Salix | 1.25 (0.22) | 1.80 (0.08) | 0.34 (0.73) | - |
| <1 cm Class | 1–2 cm Class | >2 cm Class | |
|---|---|---|---|
| MAPE | 8.2% | 5.3% | 2.0% |
| t-value | 4.58 (<0.01) * | 2.00 (0.05) * | 0.36 (0.72) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, A.; McDermid, G.J.; Rahman, M.M.; Strack, M.; Saraswati, S.; Xu, B. Developing Allometric Equations for Estimating Shrub Biomass in a Boreal Fen. Forests 2018, 9, 569. https://doi.org/10.3390/f9090569
He A, McDermid GJ, Rahman MM, Strack M, Saraswati S, Xu B. Developing Allometric Equations for Estimating Shrub Biomass in a Boreal Fen. Forests. 2018; 9(9):569. https://doi.org/10.3390/f9090569
Chicago/Turabian StyleHe, Annie, Gregory J. McDermid, Mir Mustafizur Rahman, Maria Strack, Saraswati Saraswati, and Bin Xu. 2018. "Developing Allometric Equations for Estimating Shrub Biomass in a Boreal Fen" Forests 9, no. 9: 569. https://doi.org/10.3390/f9090569
APA StyleHe, A., McDermid, G. J., Rahman, M. M., Strack, M., Saraswati, S., & Xu, B. (2018). Developing Allometric Equations for Estimating Shrub Biomass in a Boreal Fen. Forests, 9(9), 569. https://doi.org/10.3390/f9090569






