1. Introduction
A large number of companies are thinking to switch to lean and agile manufacturing systems [
1]. Supply chain managers strongly rely on their ability to reduce costs and waste, increase customer service, and provide a competitive advantage. Lean and agile manufacturing systems are multi-dimensional approaches that contain a variety of management practices. Resources efficiency and high performance are key stones of lean manufacturing, while the capabilities of addressing customer requirements are on the side of agile manufacturing [
2].
Lean manufacturing can be described as developing a value stream to eliminate all waste including time, and ensure a level schedule [
3]. A manufacturing process working away from variation and uncertainty can be defined as a level schedule, which ensures high capacity utilization, thus leading to lower manufacturing costs. Consequently, lean manufacturing is a system mainly that is focused on increasing the efficiency of operations. Contrarily, [
4] agile manufacturing is a system that is capable of operating profitably in a competitive environment, where customer demands continuously and unpredictably change. Agility reacts quickly and effectively to changing customer needs in a volatile marketplace; it is able to handle variety and introduce new products. The ability to introduce highly customized products is a key component of agile systems, which is addressed with capabilities to change between products without significant investment. However, such flexibility increases manufacturing and transportation costs [
5]. Thus, a lean manufacturing approach is predominant in production systems that are focused on products that satisfy basic needs, where the products demand is stable with large life cycles. Contrarily, an agile manufacturing approach is predominant in production systems that advocate innovative products that satisfy sophisticated needs, where the products demand is almost unpredictable with short life cycles [
6].
The adoption of emergent manufacturing systems principles should be subject to accurate economic analyses. However, there is no substantive economic evidence at the bottom of the economic forest company level to support their implementation. Hence, we reviewed the related literature to suggest a framework to address manufacturing system evaluation.
This type of systems evaluations have been performed using discrete event simulation (DES) models, measuring their advantages in different industries when adopting lean, agile, and hybrid principles, but only at the shop floor level of the factory [
1]. On the other hand, mixed-integer linear programming (MIP) models have been used to elucidate the ability of agile principles in order to improve the economic performance for supply chain network design. Strategic and tactical decisions such as opening facilities and their capacities, and selecting transportation modes were considered [
7]. Although the previous research is novel, it does not address the short-term aggregate planning problem where the ability of the manufacturing system must be measured.
Lean, agile, and hybrid manufacturing are philosophies that are easy to understand; however, their complexity appears during implementation. Goldsby et al. [
1] modeled a supply chain (SC) for lean, agile, and hybrid manufacturing to evaluate their benefits and tradeoffs. A DES model was used to simulate the SC. The results showed costs, lead times, and inventory tradeoff between manufacturing environments. However, there was no mention of how product demand patterns should be assessed in order to better represent the manufacturing philosophies. Another attempt to quantify lean manufacturing benefits was made by Al-Aomar et al. [
8]. The manufacturing system was modeled with DES, and a tabu search approach (TS) was used to find the model parameters that optimized the lean measures (e.g., work in process (WIP) and lead times (LT)). As lean measures with one objective could be contradictory, a multi-objective cost function to rank solutions at each TS step was applied. Although this approach considered the effect of lean techniques on profits, it is not clear how this method balanced lean measures, as the author claimed.
Despite efforts to measure the benefits of manufacturing systems with models, most research has been conducted for only one facility, regardless of the effect on the SC, and without considering demand changes [
9]. Until now, researchers have been applying DES, value stream mapping (VSM), experimental design, and TS to find the setting that optimizes the balance between manufacturing measures. These approaches have been successful when modeling floor variables, given their stochastic nature. Unfortunately, these efforts fail to explicitly measure the impact of the manufacturing principles on economic performance. On the other hand, MIP have been used to optimize short-term production planning [
10], where policies to manage inventory, production capacity, customer service, and lead times can be easily tested. Thus, the mid and short-term production planning problem represents a suitable scenario for testing lean, agile, and hybrid manufacturing environments.
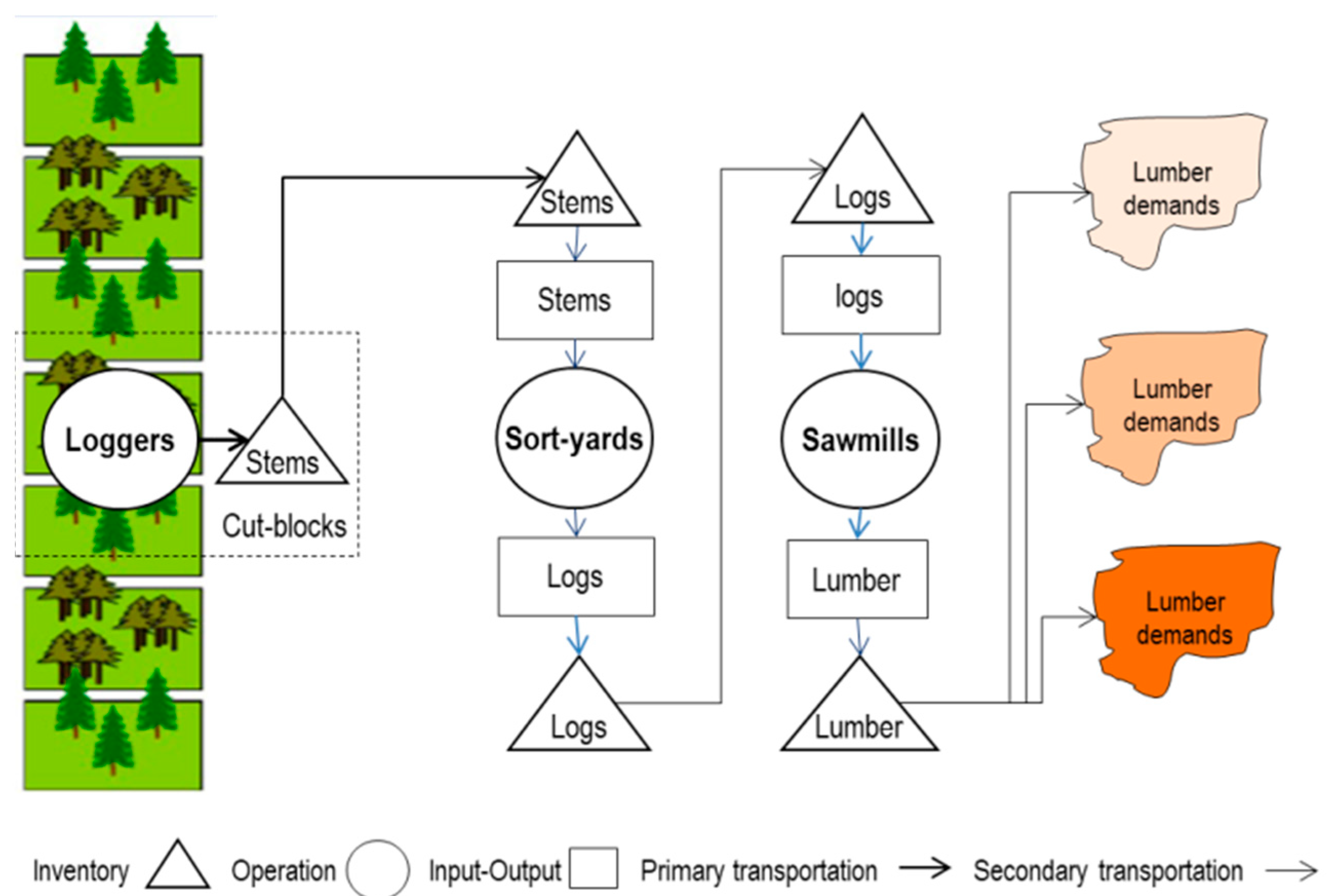
The SC uses raw materials, which are resources with limited capacities to produce products that satisfy customer demand, optimizing the tradeoff between setup and inventory holding costs [
11]. The problem has been solved with MIP formulations. Furthermore, Billington et al. [
12] suggest that the problem begins when material requirement planning (MRP) systems assume no constraints for facilities; hence, any amount of production is presumed to be possible in each facility. However, lead times (setup and production time) can increase due to bottleneck operations, triggering unpredictable lead times. This problem has been called a capacity-constrained production scheduling problem.
Depending on the manufacturing system, different modeling approaches can be applied. A tradeoff analysis between setup and holding inventory costs should be conducted [
10]. Multiple products and capacity constraints increase the complexity of the problem. The MIP formulations usually focus on minimizing the setup and holding inventory costs, which are subject to material balance constraints, plus capacity and market constraints. However, in practice, the number of binary and continuous variables (i.e., production quantities by product and setup cost) makes the problem intractable with exact algorithms.
MRP calculates the requirements for all items, including raw materials, parts, components, and subassemblies. MRP determination is based on master planning scheduling, capacity requirement planning, and lot-sizing determinations. Lot-sizing decisions may be made based on previous requirements, and always consider materials, machines, and labor constraints. If there are capacity constraints, this problem could become a single or multiple-level capacitated lot-sizing problem [
13].
In this context, the well-defined and rich literature on lean tools and methods is contradicted by a few documented quantitative implementations [
14] in which the value of lean manufacturing using DES and VSM was tested. A pull strategy to reduce WIP and LT in relation to a push strategy (i.e., large WIP and LT) was assessed, but there are no details on how the pull future state was developed.
Although there is evidence that lean manufacturing techniques (i.e., Just In Time (JIT), total preventive maintenance (TPM), and cellular manufacturing) improve performance in discrete manufacturing, evidence on continuous production is scarce. Aldulmalek et al. [
15] performed an analysis of a continuous manufacturing process based on DES, VSM, and historical data. They introduced buffers and scheduling around the bottleneck work station. Later, a DES was run and set up with two levels of TPM, two setup times, and push and hybrid pull manufacturing. Their results showed that pull hybrid manufacturing and TPM trigger significant lead-time reductions, as well as strong reductions in WIP.
Consequently, we sorted a hierarchically and translated lean, agile, and hybrid principles into planning drivers. As a matter of fact, the literature on manufacturing systems is extensive, yet few quantitative implementations can be found, and almost no publications are available for forest industry applications. Meanwhile, not all of the drivers that were mentioned in the literature can be translated and used in a mathematical formulation. We summarized the key drivers based on a large but not extensive literature review, as shown in
Table 1 (detailed information can be found at Hallgren et al. [
2,
3,
6,
16,
17,
18,
19,
20,
21]. Translation of the drivers was applied later on the model formulation of each manufacturing environment (ME).
The current manufacturing system of the British Columbia forest industry lacks a differentiation of manufacturing systems by product demand, assuming that a high rate of utilization and increasing throughput are good enough to keep the competitiveness [
22]. This industry does not recognize the ability of an agile system to capture higher value when producing highly customized lumber products. However, due to the changeable lumber market conditions, it is necessary to test emerging manufacturing systems to explore the benefits for this industry.
The objective of this research was to determine the impact on profits due to the decision of changing the manufacturing system. We first translated manufacturing system soft drivers into hard mathematical constraints. Second, we formulated three MIP optimization models that represent lean, agile, and hybrid manufacturing systems to solve the forest-to-lumber planning problem. Third, these models were applied under different lumber demand scenarios to represent the variability faced by the forest industry [
1,
6]. A Coastal British Columbia integrated forest company was chosen as the case study. The aim of this study was to explore the relationships between lean–agile–hybrid drivers and decision outcomes, highlighting their benefits and tradeoffs. To our knowledge, this is the first initiative in which lean, agile, and hybrid manufacturing systems have been evaluated and compared based on soft drivers translated into hard constraints to be modeled with mathematical programming. This study first provides descriptions of the essential drivers of the manufacturing systems, previous research, and a detailed case study. Then, a methodology to model the manufacturing principles is explained, followed by the results of the assessment of the performance of the manufacturing environment. The final sections contain discussion and conclusions, where highlights and conclusions on selecting manufacturing principles are explained.
3. Results
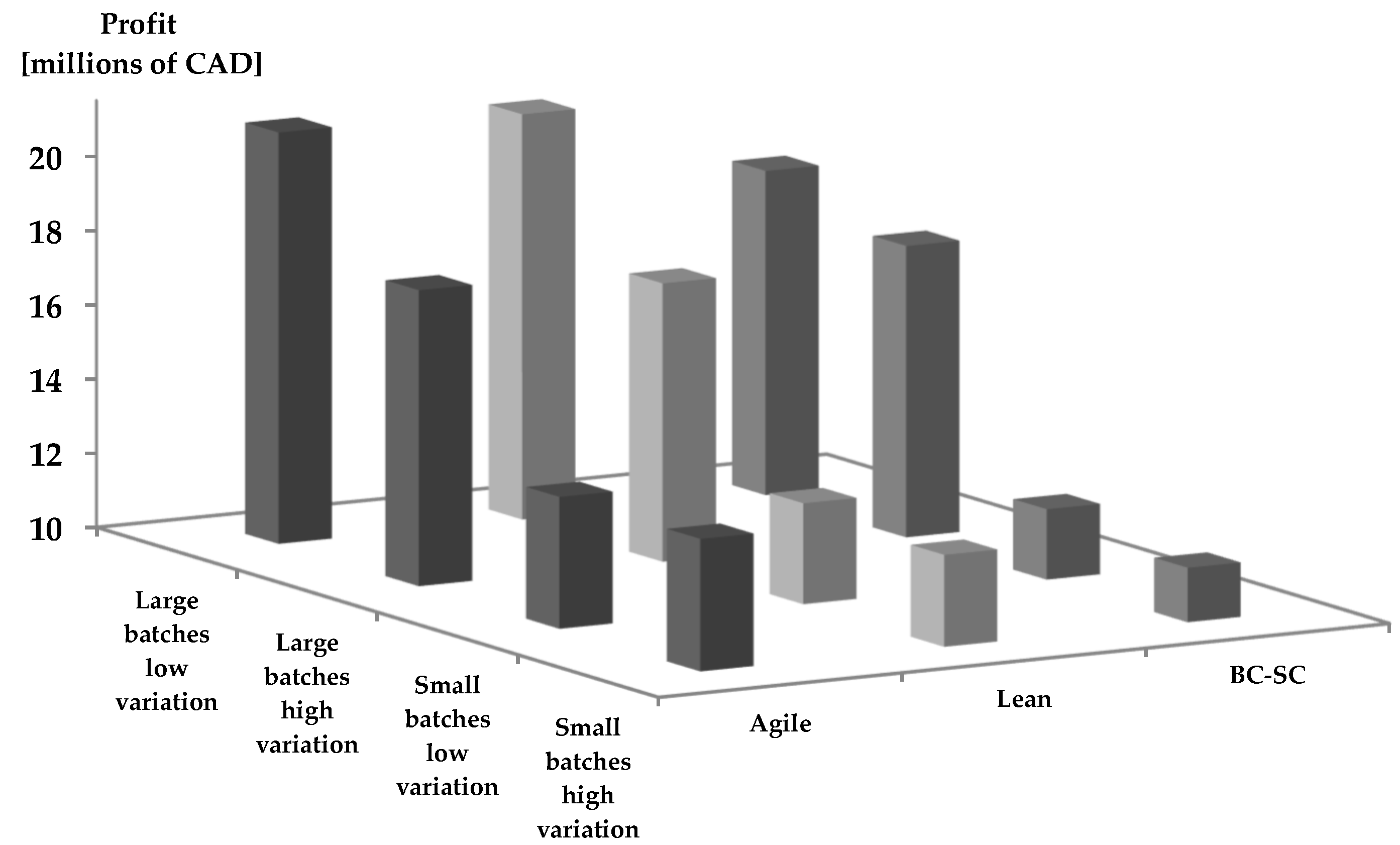
For the sake of simplicity, the averages of the optimization models’ economic outcomes were aggregated by: manufacturing environment, batch sizes, and demand variation inside the batch. Incomes for the lumber demand scenarios were similar; however, operation costs guided by manufacturing drivers determined different profit and performances (see
Table A8, and
Figure 2). A descriptive results analysis per ME and LDS follows.
Results for MEs
On average, the agile approach was the most profitable approach, followed by lean (3.9% below agile) and BC-SC (6.4% below agile). Regardless of the variation, for large batches, agile was still the most profitable, followed by lean (1.6% below agile) and BC-SC (6.3% below agile). For large batches with low variation, the agile and lean approaches obtained almost equal profits, followed by BC-SC (11.1% below agile and lean). For high variation, agile and lean profits were almost equal, followed closely by BC-SC (2.6% below lean and agile). Regardless of the variation, the differences were larger for small batches than for large batches, where the agile approach remained the most profitable, followed by the lean (7.1% below) and BC-SC (13.8% below) approaches. For small batches with low variation, agile still produced the highest profits, followed by the lean (6.1% below) approach and then the BC-SC (12.1% below) approach. For high variation, the differences were larger, with agile being the most profitable, followed by lean (8.0% below) and then BC-SC (15.5% below).
The agile approach led to lower harvest levels, followed by the lean and BC-SC approaches. The timber volume supplied to the sawmill followed the same trend. As a consequence, procurement and manufacturing costs followed the same order, and because the lumber demand data were the same in each LDS, incomes were similar for the agile, lean, and BC-SC approaches, although the BC-SC and lean approaches had higher costs. Over and under-capacity costs were not significant due to the low allowable capacity deviation between periods.
In our formulations, overproduction was paid for with lower prices, while underproduction was penalized by charging a cost for the underproduction, which was determined by multiplying the volume of underproduction by a fraction of the lumber price. This mechanism was efficient at controlling production, and brought flexibility that was translated to a customer service emphasis in all of the approaches. The agile approach had the smallest magnitude of lumber over and underproduction, with the exception of large batches with low variation. Lumber production was mostly below lumber demand. The lean approach produced large volumes over and under the demand for most of the small and large batches. The BC-SC approach produced large over-demand volumes for most of the small and large batches, with the exception of large batches with low variation.
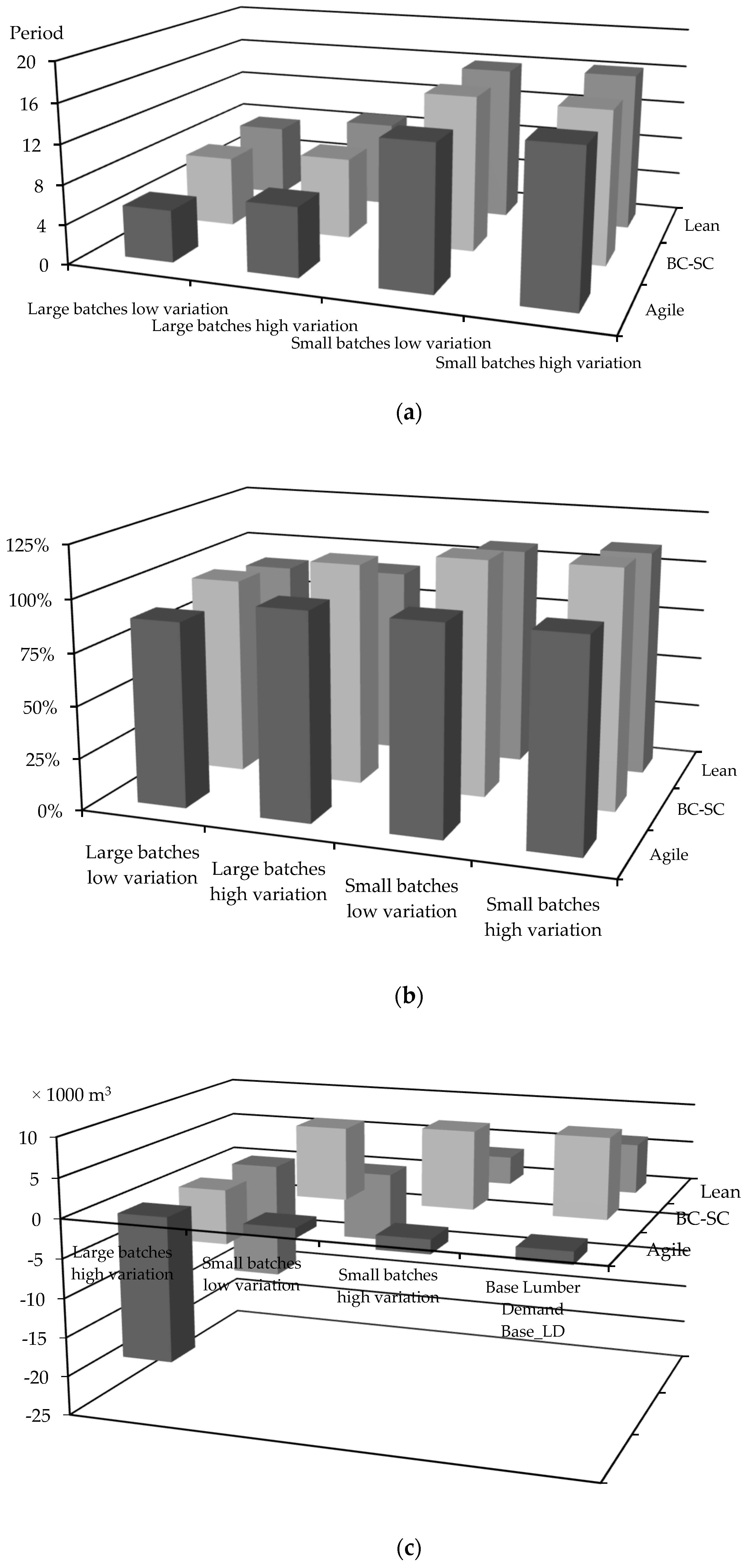
In terms of order fulfillment, the agile approach led to production levels being as close as possible to demand, with 89%, 99%, 99%, and 98% of demand met by production for large batches with low and high variation and small batches with low and high variation, respectively. For the lean approach, order fulfillment was less stable, with 91% and 92% of demand met by production for large batches with low and high variation, respectively, and 107% and 111% of demand met by production for small batches with low and high variation, respectively. The BC-SC approach produced over the demand most of the time, with 96% and 108% of demand met by production for large batches with low and high variation, respectively, and 114% and 115% of demand met by production for small batches with low and high variation, respectively. Consequently, BC-SC was the worst at controlling lumber production. The flow time indicates the degree of responsiveness; thus, on average, the agile approach showed 10.4 periods; the BC-SC approach showed 11.7 periods, and the lean approach showed 12.2 periods of flow time. These results agree with Narasimhan et al. [
26], who found higher delivery speeds and reliability for the agile approach compared with the lean approach (
Figure 3,
Table A8 and
Table A9 in the
Appendix B).
4. Discussion
The industrial relevance of lean, agile, and hybrid manufacturing systems is clear, but there is a need to unpack these ambiguous terms, if integration of these conflicting paradigms is to be logically developed to meet specific business needs [
27]. An analysis and discussion of tradeoffs based on variation, inventory, and capacity follows.
Our results can be compared with Goldsby et al. [
1] with respect to the economic performance of MEs, although they used DES and we used MIP to model the SC. Nevertheless, both analyses determined the operational costs. The lowest costs were produced by the agile approach, followed by the lean approach (5% over) and the BC-SC approach (14% over). However, Goldsby et al. [
1] showed only a small difference between the lean and agile costs (e.g., only 2%) and a hybrid with 15% higher costs. Although the differences in percentages between our costs were larger, both results are close in terms of magnitudes and trends. Furthermore, we found that the operational costs agree with the results of [Narasimhan et al. [
26], in which lean costs were the lowest, closely followed by agile costs. Goldsby et al. [
1] analyzed the concept of the “order-to-ship time” as a customer service parameter. Also, Qrunfleh et al. [
28] explored the ability of lean and agile systems to increase responsiveness and waste elimination. They found that an agile SC strategy contributes significantly to building SC responsiveness. Contrarily, no significant relationship between a lean SC strategy and SC chain responsiveness was found. However, a lean SC strategy has a significant relationship with waste elimination. In our study, we did not explicitly model delivery time, although order fulfillment or over/under production attempts to capture this. They stated that lean exhibits three times lower order-to-ship times than the hybrid (i.e., BC-SC) approach and eight times slower order-to-ship times compared to the agile approach, without mentioning backorder numbers. We considered customer service parameters as order fulfillments, as did Babazadeh et al. [
7]. Nevertheless, our results show that the lean approach produced double the number of backorders of agile, which agrees with the results of Narasimhan et al. [
26] and Enriquez et al. [
29], which showed higher delivery speeds and delivery reliability for the agile approach over the lean approach. These experimental results are in great tuning with manager perceptions, which strongly believes that lean SC strategy is mostly focused on waste elimination rather that responsiveness improvement; this is the capital emphasis of agile SC strategy [
28].
The lean supply paradigms perform better with a low variation of products enabling flow, and reducing the need for buffer or protective inventory and capacity. However, with the growth in products innovation and demand uncertainty, supply chains need to strategically locate inventory and capacity to enable the flow of production [
27]. However, our results indicate that lean accumulates more inventories than agile. Also, Goldsby et al. [
1] found more inventory in agile than in hybrid, but we found the opposite. The differences in inventory can be related to our over and under-demand lumber production constraints, which cannot be stated in a DES model as explicitly as in an MIP model. There are also ship-to-order and order fulfillment conceptual differences between the studies. However, our results for the order fulfillment, overproduction, and underproduction of lumber and inventory are in agreement with the results of Hallgren et al. [
2], which showed that the lean approach had a significant impact on cost efficiency, while the agile approach did not. However, the agile approach had a higher delivery performance (e.g., order fulfillment).
In an effort to measure the impacts of demand variation and batch size, we tested the impact of lumber demand scenarios on MEs. Unfortunately, we found a few quantitative and theoretical research to compare with, so we can only benchmark our results with them. Our results show that the agile approach has the highest profit, closely followed by the lean and BC-SC approaches. Goldsby et al. [
1] showed that the agile and lean approaches were equally cost-efficient, while the hybrid approach was by far the most expensive (the most cost-efficient ME was assumed to be the one with highest profits). Enriquez et al. [
29] found that the agile system is more attractive when one of the demands is low and there is a high variation of demands, which is equivalent to small batches with high variation in our study. Our results showed that the agile and lean approaches continued to have higher profits than the BC-SC approach for large batches without considering the effect of demand variation. When lumber demand showed low variation, no change was observed between the agile and lean profits, while the profits of BC-SC decreased by half. These profits are comparable to those identified by Christopher et al. [
6]. While the lean approach was expected to have higher profitability than the agile approach for this type of lumber demand, instead it showed the same costs as the agile approach. However, when lumber demand shows high variation, differences in profits were tiny, with the agile and BC-SC approach were leading profits, followed closely by the lean approach. These profits are in agreement with those of Christopher et al. [
6]. The BC-SC approach had the highest profits for product demands characterized by high variation and high volumes.
For small batches, the agile approach had higher profits than the lean and BC-SC approaches, but with larger profit differences. Our results for high variation again agreed with those of Christopher et al. [
6], who stated that “agile profitably responds to high variety and low volumes”. However, for low variation, my results did not show that the BC-SC approach had a higher profit as Christopher et al. [
6] suggested, probably because we did not explicitly work with mixed portfolios of demands, where the hybrid approach is supposed to perform better.
In compliance with the economic penalties used for over and under-demand and capacity usage deviations, the agile approach always showed lower costs than the lean approach, which was able to use more capacity and deviate farther from demand, while compromising costs. The BC-SC approach showed the highest costs because log demand was a forecasted average per period and was not exactly the required log demand. As a consequence, order fulfillment (%) and lumber production deviations were higher than they were in the lean and agile approaches, where timber was pulled directly from sawmills every period.
The models determined the expected result patterns with an objective function as a central driver plus constraints as second order drivers. Although Al-Aomar et al. [
8] claimed that lean objectives are in conflict and a multi-objective formulation is required, we showed that ME attributes, such as customer service, chase and level manufacturing strategies, can be modeled with MIP, as Babazadeh et al. [
7] did when modeling the design of an agile SC. Alternatively, if agile, lean, and hybrid approaches are required to be measured in the short term, their stochastic shop floor techniques could be modeled with DES and VSM, and multi-objective techniques.
Lumber production outsourcing, interchanges of lumber between sawmills, over/under capacity usage, and over/under demand features increase the ability of our formulations to represent MEs. Although over/underproduction capacity usage penalties did not play a large role in costs, because their related constraints were too tight, these constraints actively helped to model chase and level manufacturing strategies. However, over/under demand lumber production constraints played a large role in relaxing and controlling order fulfillment and in controlling lumber production, which is another central feature of MEs [
16].
For SC practitioners, the results of this research highlight the benefits that forest firms can capitalize if they consider the introduction of lean, agile, and hybrid SC strategies. However, SC managers should be aware of the nature of the lumber products demand before choosing any of them. Another aspect that should be kept in mind is that the type of SC can capitalize the benefits of the lean agile appraoch, and hybrid (leagile) manufacturing [
30]. The ability of these managerial tools to improve SC performance has been identified. Business units containing corporate headquarters, sales and services groups, inventory and management groups, and production units are the SCs with higher advantages. Furthermore, there are other SC concepts that were not included in this research as postponement or supplier partnerships [
28], which could add extra criteria for SC strategy selection.
5. Conclusions
Our research shows that MEs for the case studies can be modeled with a reasonable level of detail with MIP, and that these formulations react to the lumber demand scenarios, as stated in our objectives. Indeed, our results highlight how manufacturing drivers and demand attributes influence the economic performance of lean, hybrid, and agile approaches for the forest-to-lumber SC.
When suggesting that ME should be adopted for the particular case of integrated BC coastal forest-to-lumber SCs, the attributes of demand should be considered. When lumber demand is stable with low variation and large volumes, agile or lean principles should be adopted. However, when lumber demand is unstable with high variation and large volumes, hybrid or agile principles should be maintained. When lumber demand is unstable with high variation and small volumes, an agile approach clearly provides higher profits than any other ME. For the same conditions of lumber demand, but with low variation, the agile approach is recommended; however, further analysis is required, because a hybrid (i.e., BC-SC) approach is in theory supposed to be the most appropriate under these circumstances.
There is an opportunity to increase profits by 11.1% by adopting an agile approach when lumber demand is stable with low variation and large volumes. However, the opportunity for increased profits is zero under the same demand attributes, but with high variation. Contrarily, there is an opportunity to increase profits by 12.1% by adopting agile or lean approaches when lumber demand is stable with low variation and small volumes, and there is an opportunity to increase profits by 15.5% when lumber demand is unstable with high variation and small volumes. However, these profit increments are subject to over/under capacity and demand penalties, the lumber demand scenarios, and the exploratory nature of this work. These results are specific to our case studies and the over/under demand and production penalties we used.