Spatial Variation in Canopy Structure across Forest Landscapes
Abstract
1. Introduction
2. Materials and Methods
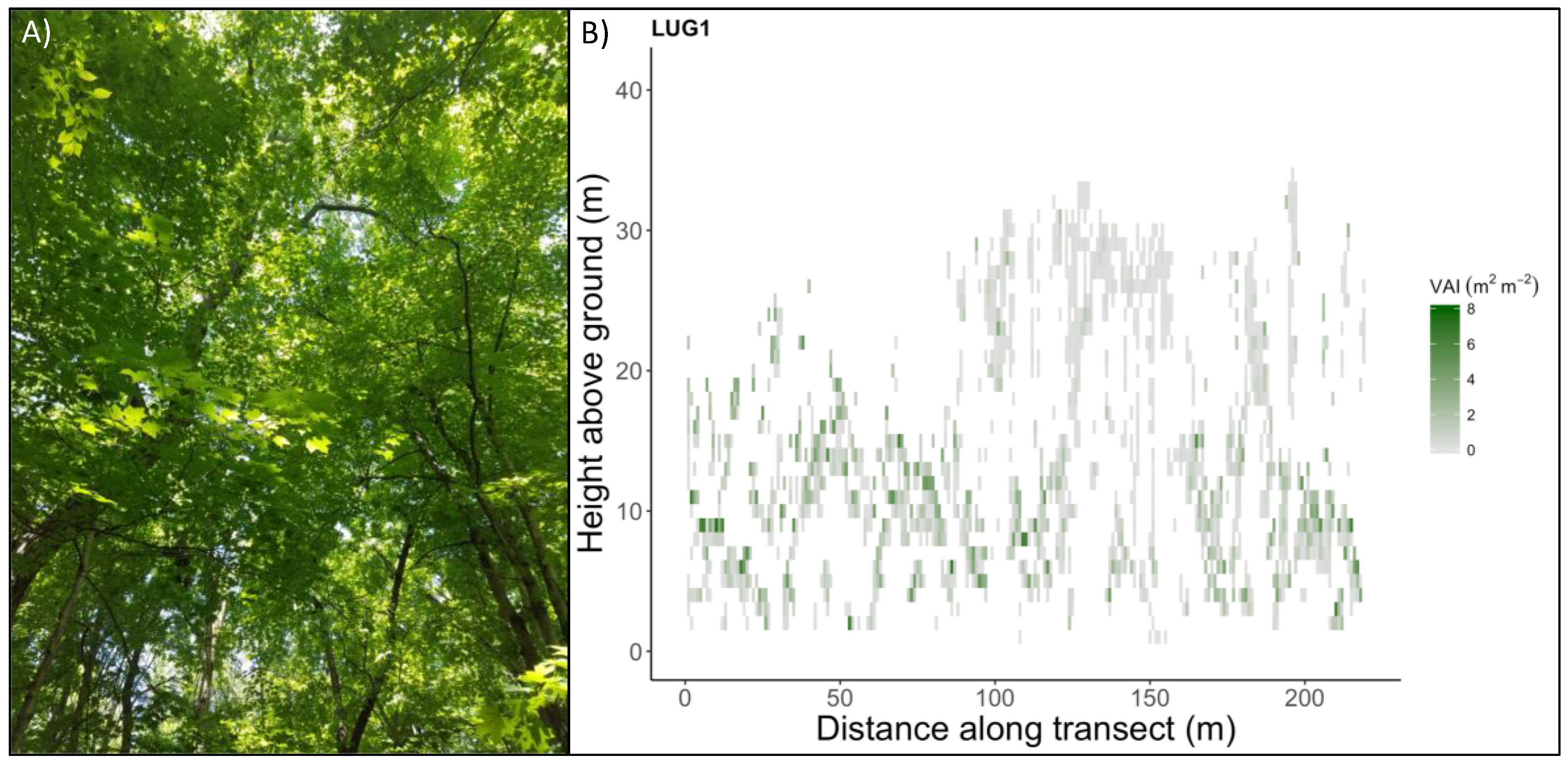
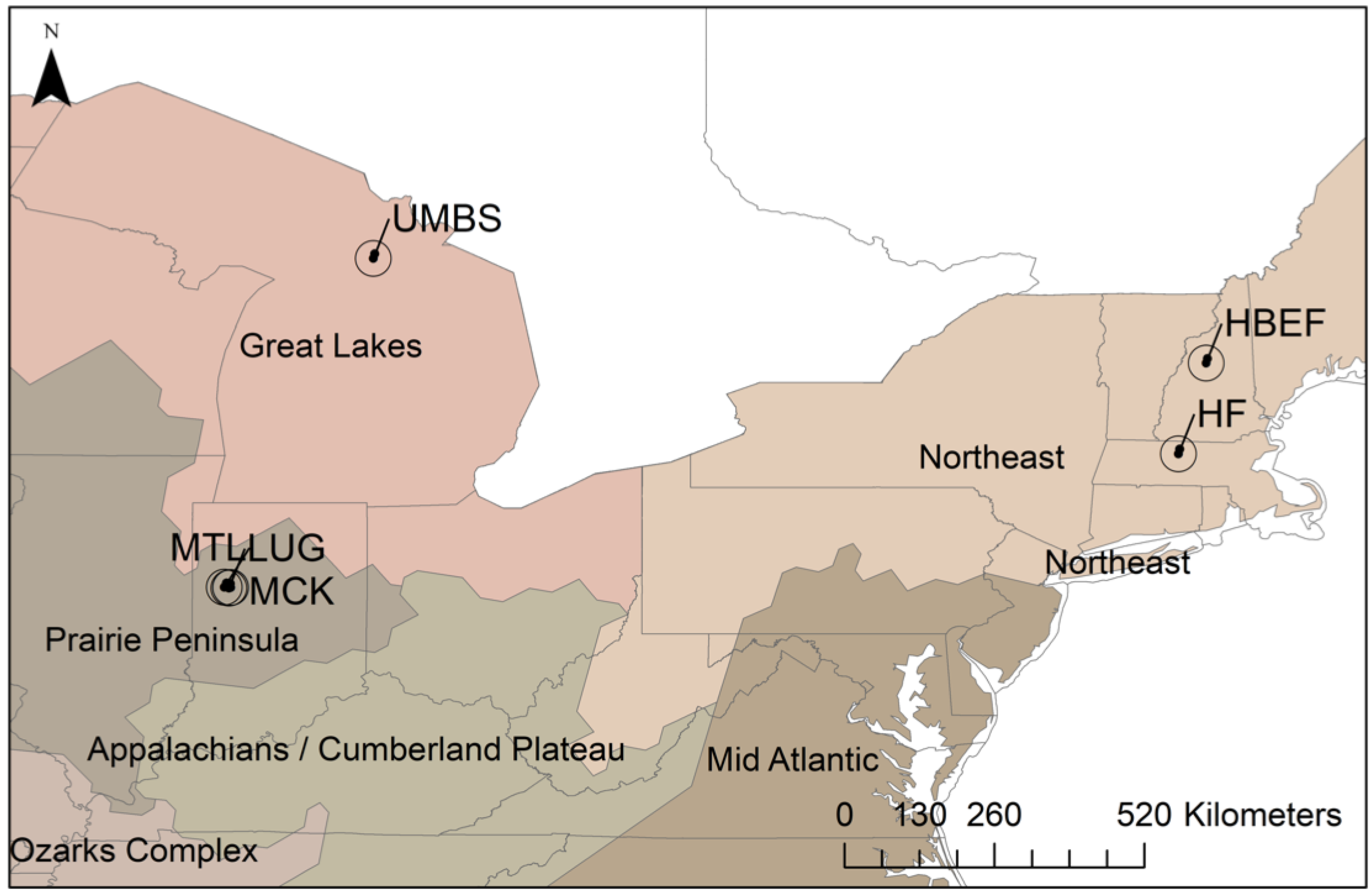
2.1. Portable Canopy LiDAR and Forest Landscapes
2.2. Canopy Structural Complexity
2.3. Statistical Analyses
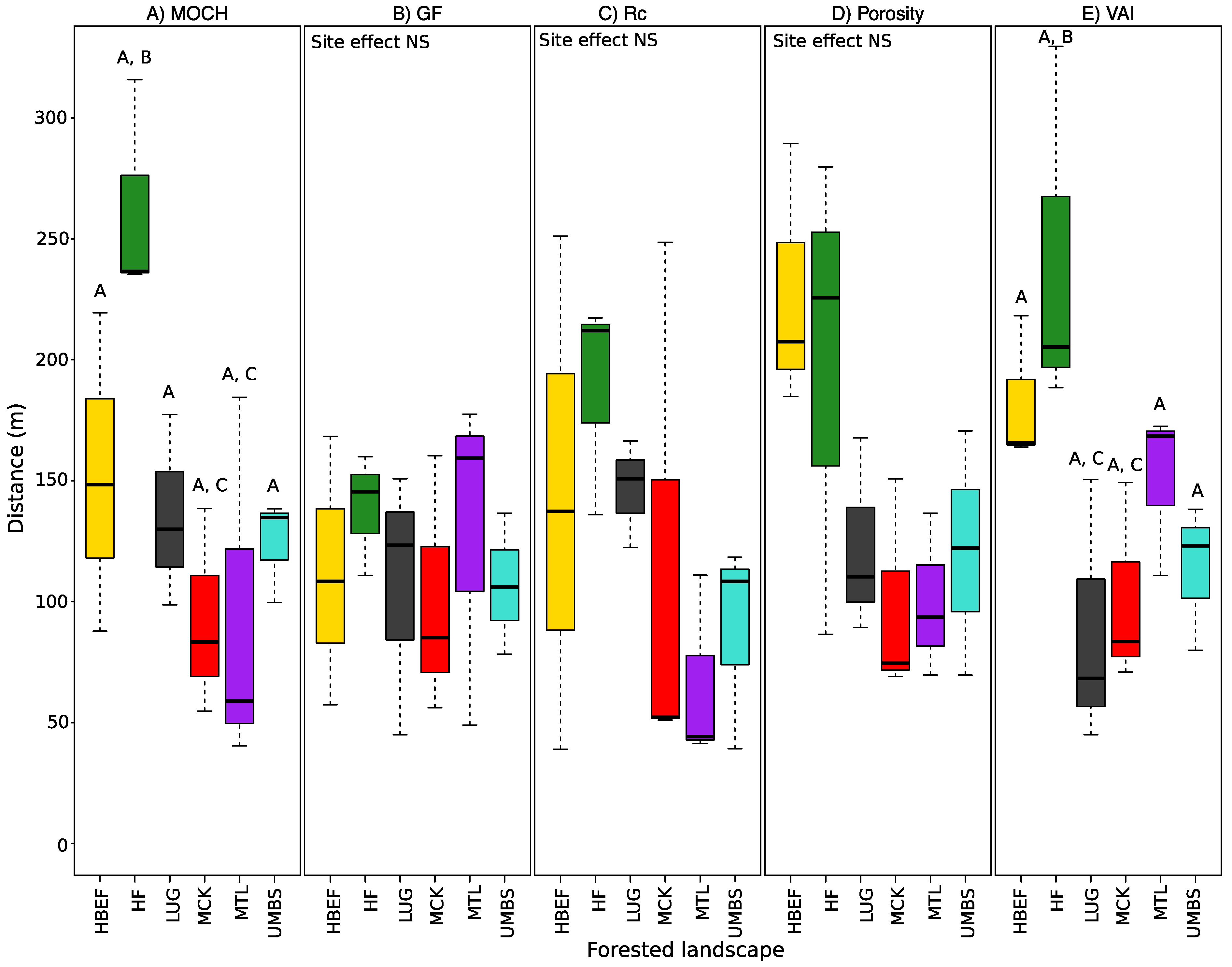
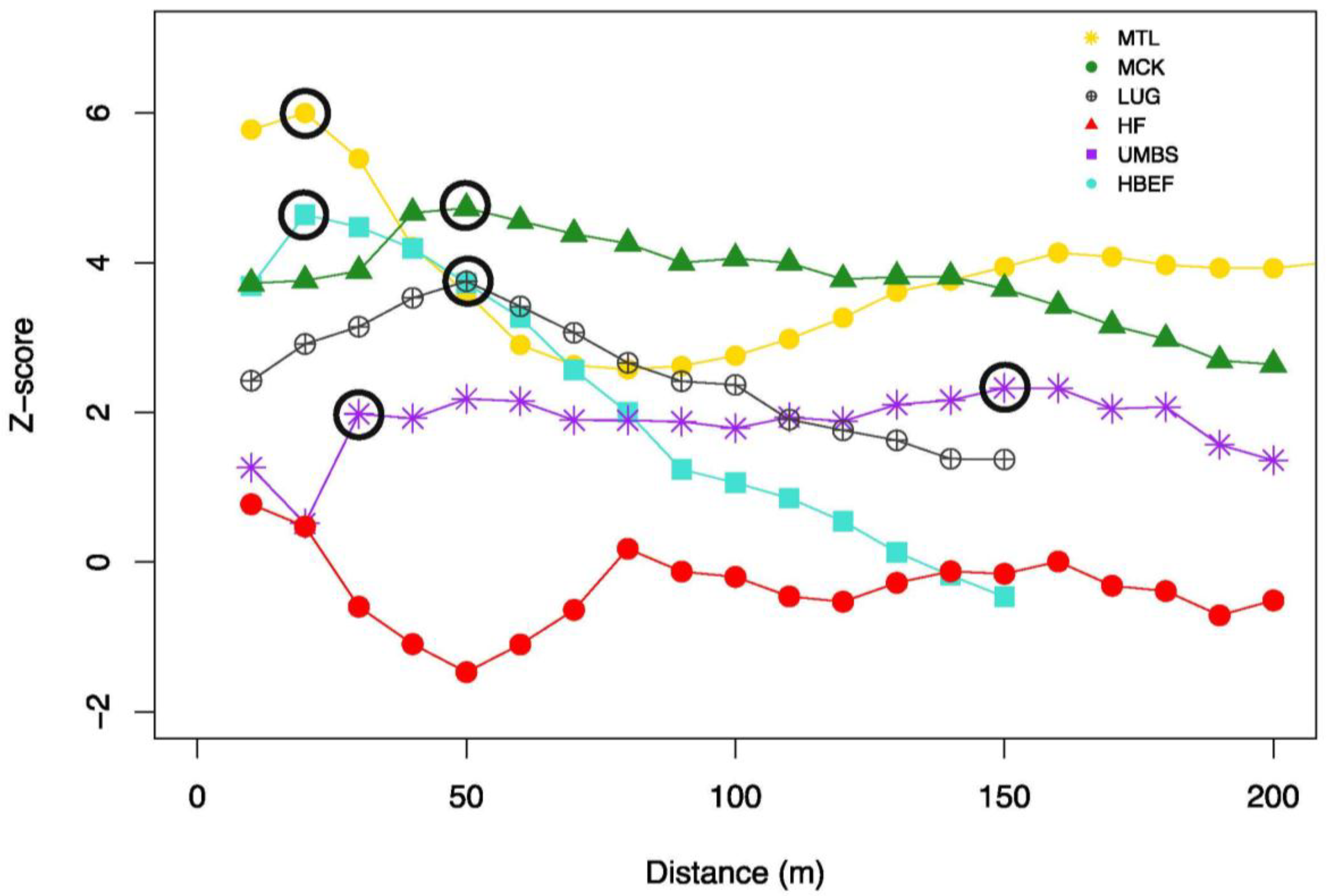
3. Results
3.1. Transect Lengths at Which CS Metrics Stabilize
3.2. Scales of Canopy Structure Autocorrelation
4. Discussion
4.1. Spatial Variation and Autocorrelation of Canopy Structure
4.2. Relevance to Canopy Structural Scaling and Modelling Efforts
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Atkins, J.W.; Fahey, R.T.; Hardiman, B.S.; Gough, C.M. Forest Canopy Structural Complexity and light absorption relationships at the subcontinental scale. J. Geophys. Res. Biogeosci. 2018, 123, 1387–1405. [Google Scholar] [CrossRef]
- Hardiman, B.S.; Bohrer, G.; Gough, C.M.; Vogel, C.S.; Curtis, P.S. The role of canopy structural complexity in wood net primary production of a maturing northern deciduous forest. Ecology 2011, 92, 1818–1827. [Google Scholar] [CrossRef] [PubMed]
- Hardiman, B.S.; Gough, C.M.; Halperin, A.; Hofmeister, K.L.; Nave, L.E.; Bohrer, G.; Curtis, P.S. Maintaining high rates of carbon storage in old forests: A mechanism linking canopy structure to forest function. For. Ecol. Manag. 2013, 298, 111–119. [Google Scholar] [CrossRef]
- Maurer, K.D.; Hardiman, B.S.; Vogel, C.S.; Bohrer, G. Canopy-structure effects on surface roughness parameters: Observations in a great lakes mixed-deciduous forest. Agric. For. Meteorol. 2013, 177, 24–34. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Friedl, M.A. Modeling the effects of three-dimensional vegetation structure on surface radiation and energy balance in boreal forests. J. Geophys. Res. 2003, 108, 8615. [Google Scholar] [CrossRef]
- Ellsworth, D.S.; Reich, P.B. Canopy structure and vertical patterns of photosynthesis and related leaf traits in a deciduous forest. Oecologia 1993, 96, 169–178. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Friedl, M.A. Determination of roughness lengths for heat and momentum over boreal forests. Bound.-Layer Meteorol. 2003, 107, 581–603. [Google Scholar] [CrossRef]
- Aber, J.D.; Pastor, J.; Melillo, J.M. Changes in forest canopy structure along a site quality gradient in southern Wisconsin, USA. Am. Midl. Nat. 1982, 108, 256–265. [Google Scholar] [CrossRef]
- Parker, G.G.; Russ, M.E. The canopy surface and stand development: Assessing forest canopy structure and complexity with near-surface altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- Hutchison, B.A.; Matt, D.R.; Mcmillen, R.T.; Gross, L.J.; Tajchman, S.J.; Norman, J.M. The architecture of a deciduous forest canopy in eastern Tennessee, USA. J. Ecol. 1986, 74, 635–646. [Google Scholar] [CrossRef]
- Nadkarni, N.M.; McIntosh, A.C.S.; Cushing, J.B. A framework to categorize forest structure concepts. For. Ecol. Manag. 2008, 256, 872–882. [Google Scholar] [CrossRef]
- Kane, V.R.; Bakker, J.D.; McGaughey, R.J.; Lutz, J.A.; Gersonde, R.F.; Franklin, J.F. Examining conifer canopy structural complexity across forest ages and elevations with LiDAR data. Can. J. For. Res. Can. Res. 2010, 40, 774–787. [Google Scholar] [CrossRef]
- Ishii, H.T.; Tanabe, S.; Hiura, T. Exploring the relationships among canopy structure, stand productivity, and biodiversity of temperature forest ecosystems. For. Sci. 2004, 50, 342–355. [Google Scholar]
- Lefsky, M.A.; Hudak, A.T.; Cohen, W.B.; Acker, S.A. Geographic variability in lidar predictions of forest stand structure in the Pacific Northwest. Remote Sens. Environ. 2005, 95, 532–548. [Google Scholar] [CrossRef]
- Paynter, I.; Saenz, E.; Genest, D.; Peri, F.; Erb, A.; Li, Z.; Wiggin, K.; Muir, J.; Raumonen, P.; Schaaf, E.S.; et al. Observing ecosystems with lightweight, rapid-scanning terrestrial lidar scanners. Remote Sens. Ecol. Conserv. 2016, 2, 174–189. [Google Scholar] [CrossRef]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial laser scanning for plot-scale forest measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- Kükenbrink, D.; Schneider, F.D.; Leiterer, R.; Schaepman, M.E.; Morsdorf, F. Quantification of hidden canopy volume of airborne laser scanning data using a voxel traversal algorithm. Remote Sens. Environ. 2017, 194, 424–436. [Google Scholar] [CrossRef]
- Thorpe, A.S.; Barnett, D.T.; Elmendorf, S.C.; Hinckley, E.L.S.; Hoekman, D.; Jones, K.D.; Levan, K.E.; Meier, C.L.; Stanish, L.F.; Thibault, K.M. Introduction to the sampling designs of the national ecological observatory network terrestrial observation system. Ecosphere 2016, 7, 1–11. [Google Scholar] [CrossRef]
- Atkins, J.; Bohrer, G.; Fahey, R.; Hardiman, B.; Morin, T.; Stovall, A.; Zimmerman, N.; Gough, C. Quantifying forest and canopy structural complexity metrics from terrestrial LiDAR data using the forestr R package. Methods Ecol. Evol. 2018, in press. [Google Scholar] [CrossRef]
- Niinemets, Ü. Photosynthesis and resource distribution through plant canopies. Plant Cell Environ. 2007, 30, 1052–1071. [Google Scholar] [CrossRef] [PubMed]
- Mori, A.; Niinemets, Ü. Plant responses to heterogeneous environments: Scaling from shoot modules and whole-plant functions to ecosystem processes. Ecol. Res. 2010, 25, 691–692. [Google Scholar] [CrossRef]
- Niinemets, Ü. A review of light interception in plant stands from leaf to canopy in different plant functional types and in species with varying shade tolerance. Ecol. Res. 2010, 25, 671–693. [Google Scholar] [CrossRef]
- Ishii, H.; Asano, S. The role of crown architecture, leaf phenology and photosynthetic activity in promoting complementary use of light among coexisting species in temperate forests. Ecol. Res. 2009, 25, 715–722. [Google Scholar] [CrossRef]
- Pretzsch, H.; Forrester, D.I.; Rötzer, T. Representation of species mixing in forest growth models: A review and perspective. Ecol. Model. 2015, 313, 276–292. [Google Scholar] [CrossRef]
- Curtis, P.S.; Gough, C.M. Forest aging, disturbance and the carbon cycle. New Phytol. 2018, in press. [Google Scholar] [CrossRef] [PubMed]
- Franklin, J. Disturbances and structural development of natural forest ecosystems with silvicultural implications, using Douglas-fir forests as an example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Fotis, A.T.; Morin, T.H.; Fahey, R.T.; Hardiman, B.S.; Bohrer, G.; Curtis, P.S. Forest structure in space and time: Biotic and abiotic determinants of canopy complexity and their effects on net primary productivity. Agric. For. Meteorol. 2018, 250–251, 181–191. [Google Scholar] [CrossRef]
- Sagara, B.T.; Fahey, R.T.; Vogel, C.S.; Fotis, A.T.; Curtis, P.S.; Gough, C.M. Moderate disturbance has similar effects on production regardless of site quality and composition. Forests 2018, 9, 70. [Google Scholar] [CrossRef]
- Tanaka, H.; Nakashizuka, T. Fifteen years of canopy dynamics analyzed by aerial photographs in a temperate deciduous forest, Japan. Ecology 1997, 78, 612–620. [Google Scholar] [CrossRef]
- Hardiman, B.S.; Bohrer, G.; Gough, C.M.; Curtis, P.S. Canopy structural changes following widespread mortality of canopy dominant trees. Forests 2013, 4, 537–552. [Google Scholar] [CrossRef]
- Pederson, N.; Dyer, J.M.; Mcewan, R.W.; Hessl, A.E.; Mock, C.J.; Orwig, D.A.; Rieder, H.E.; Cook, B.I. The legacy of episodic climatic events in shaping temperate, broadleaf forests. Ecol. Monogr. 2014, 84, 599–620. [Google Scholar] [CrossRef]
- Fahey, R.T.; Alveshere, B.C.; Burton, J.I.; D’Amato, A.W.; Dickinson, Y.L.; Keeton, W.S.; Kern, C.C.; Larson, A.J.; Palik, B.J.; Puettmann, K.J.; et al. Shifting conceptions of complexity in forest management and silviculture. For. Ecol. Manag. 2018, 421, 59–71. [Google Scholar] [CrossRef]
- Hiroaki, T.; Van Pelt, R.; Parker, G.; Nadkarni, N. Age-related development of canopy structure and its ecological functions. In Forest Canopies; Lowman, M., Rinker, H., Eds.; Elsevier Academic Press: Amsterdam, The Netherlands, 2004; pp. 102–117. [Google Scholar]
- Fahey, R.T.; Fotis, A.T.; Woods, K.D. Quantifying canopy complexity and effects on productivity and resilience in late-successional hemlock-hardwood forests. Ecol. Appl. 2015, 25, 834–847. [Google Scholar] [CrossRef] [PubMed]
- McMahon, S.M.; Parker, G.G.; Miller, D.R. Evidence for a recent increase in forest growth. Proc. Natl. Acad. Sci. USA 2010, 107, 3611–3615. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, R.A.; Chazdon, R.L. Forest structure, canopy architecture, and light transmittance in tropical wet forests. Ecology 2001, 82, 2707–2718. [Google Scholar] [CrossRef]
- McMahon, S.M.; Bebber, D.P.; Butt, N.; Crockatt, M.; Kirby, K.; Parker, G.G.; Riutta, T.; Slade, E.M. Ground based LiDAR demonstrates the legacy of management history to canopy structure and composition across a fragmented temperate woodland. For. Ecol. Manag. 2015, 335, 255–260. [Google Scholar] [CrossRef]
- Nave, L.E.; Sparks, J.P.; Le Moine, J.; Hardiman, B.S.; Nadelhoffer, K.J.; Tallant, J.M.; Vogel, C.S.; Strahm, B.D.; Curtis, P.S. Changes in soil nitrogen cycling in a northern temperate forest ecosystem during succession. Biogeochemistry 2014, 3, 471–488. [Google Scholar] [CrossRef]
- Morton, D.C.; Nagol, J.; Carabajal, C.C.; Rosette, J.; Palace, M.; Cook, B.D.; Vermote, E.F.; Harding, D.J.; North, P.R.J. Amazon forests maintain consistent canopy structure and greenness during the dry season. Nature 2014, 506, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragao, L.E.O.C.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent effects of a severe drought on Amazonian forest canopy. Proc. Natl. Acad. Sci. USA 2013, 110, 565–570. [Google Scholar] [CrossRef] [PubMed]
- Wirth, R.; Weber, B.; Ryel, R.J. Spatial and temporal variability of canopy structure in a tropical moist forest. Acta Oecol. 2001, 22, 235–244. [Google Scholar] [CrossRef]
- Parker, G.G.; Harding, D.J.; Berger, M.L. A portable LIDAR system for rapid determination of forest canopy structure. J. Appl. Ecol. 2004, 41, 755–767. [Google Scholar] [CrossRef]
- Schmid, H.P.; Su, H.B.; Vogel, C.S.; Curtis, P.S. Ecosystem-atmosphere exchange of carbon dioxide over a mixed hardwood forest in northern lower Michigan. J. Geophys. Res. 2003, 108, 19. [Google Scholar] [CrossRef]
- Kane, V.R.; Gersonde, R.F.; Lutz, J.A.; McGaughey, R.J.; Bakker, J.D.; Franklin, J.F. Patch dynamics and the development of structural and spatial heterogeneity in Pacific Northwest forests. Can. J. For. Res. 2011, 41, 2276–2291. [Google Scholar] [CrossRef]
- Miller, T.F.; Mladenoff, D.J.; Clayton, M.K. Old-growth northern hardwood forests: Spatial autocorrelation and pattern of understory vegetation. Ecol. Monogr. 2002, 72, 487–503. [Google Scholar] [CrossRef]
- Runkle, J.R. Gap regeneration in some old-growth forests of the Eastern-United-States. Ecology 1981, 62, 1041–1051. [Google Scholar] [CrossRef]
- Runkle, J.R.; Yetter, T.C. Treefalls revisited: Gap dynamics in the southern appalachians. Ecology 1987, 68, 417–424. [Google Scholar] [CrossRef]
- Hibbs, D.E. Gap Dynamics in A Hemlock Hardwood Forest. Can. J. For. Res. Can. Rech. For. 1982, 12, 522–527. [Google Scholar] [CrossRef]
- Orwig, D.A.; Cobb, R.C.; D’Amato, A.W.; Kizlinski, M.L.; Foster, D.R. Multi-year ecosystem response to hemlock woolly adelgid infestation in southern New England forests. Can. J. For. Res. Can. Rech. For. 2008, 38, 834–843. [Google Scholar] [CrossRef]
- Orwig, D.A.; Barker Plotkin, A.A.; Davidson, E.A.; Lux, H.; Savage, K.E.; Ellison, A.M. Foundation species loss affects vegetation structure more than ecosystem function in a northeastern USA forest. Peer J. 2013, 1, e41. [Google Scholar] [CrossRef] [PubMed]
- Pickell, P.D.; Coops, N.C.; Gergel, S.E.; Andison, D.W.; Marshall, P.L. Evolution of Canada’s boreal forest spatial patterns as seen from space. PLoS ONE 2016, 11, e0157736. [Google Scholar] [CrossRef] [PubMed]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastellu-Etchegorry, J.P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating imaging spectrometer data: 3D forest modeling based on LiDAR and in situ data. Remote Sens. Environ. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Moran, C.J.; Rowell, E.M.; Seielstad, C.A. A data-driven framework to identify and compare forest structure classes using LiDAR. Remote Sens. Environ. 2018, 211, 154–166. [Google Scholar] [CrossRef]
- Ehbrecht, M.; Schall, P.; Ammer, C.; Seidel, D. Quantifying stand structural complexity and its relationship with forest management, tree species diversity and microclimate. Agric. For. Meteorol. 2017, 242, 1–9. [Google Scholar] [CrossRef]
- LaRue, E.; Atkins, J.; Dahlin, K.; Fahey, R.; Fei, S.; Gough, C.; Hardiman, B. Linking Landsat to terrestrial LiDAR: Vegetation metrics of forest greenness are correlated with canopy structural complexity. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 420–427. [Google Scholar] [CrossRef]
- Mahadevan, P.; Wofsy, S.C.; Matross, D.M.; Xiao, X.; Dunn, A.L.; Lin, J.C.; Gerbig, C.; Munger, J.W.; Chow, V.Y.; Gottlieb, E.W. A satellite-based biosphere parameterization for net ecosystem CO2 exchange: Vegetation photosynthesis and respiration model (VPRM). Glob. Biogeochem. Cycles 2008, 22. [Google Scholar] [CrossRef]
- Medvigy, D.; Wofsy, S.C.; Munger, J.W.; Hollinger, D.Y.; Moorcroft, P.R. Mechanistic scaling of ecosystem function and dynamics in space and time: Ecosystem demography model version 2. J. Geophys. Res. 2009, 114, 1–21. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Fisk, J.P.; Holm, J.A.; Bailey, V.; Bohrer, G.; Gough, C.M. Moderate forest disturbance as a stringent test for gap and big-leaf models. Biogeosciences 2015, 12, 513–526. [Google Scholar] [CrossRef]
| Driver | Literature Source |
|---|---|
| Crown morphology/architecture | [21,22,23,24,25] |
| Disturbance | [26,27,28,29,30,31,32] |
| Demographics (community composition, diversity, succession) | [10,28,33,34,35,36,37,38] |
| Edaphic factors (topography, soil moisture, nutrient status, etc.) | [9,39,40,41,42,43] |
| Site | MOCH | GF | RC | Porosity | VAI | Mean |
|---|---|---|---|---|---|---|
| UMBS | --- | --- | 20 | 20 | --- | 20 |
| HEBF | 30 | 50 | 20 | 40 | 150 | 58 |
| HF | 30 | 30 | 50 | 110 | 50 | 54 |
| LUG | 40 | --- | 50 | 20 | --- (70) | 37 |
| MCK | 20 | --- | --- (80) | 30/100 | 30/140 | 64 |
| MTL | 20/120 | --- | 30/150 | 180 | 70 | 95 |
| Mean | 43 | 40 | 53 | 71 | 88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hardiman, B.S.; LaRue, E.A.; Atkins, J.W.; Fahey, R.T.; Wagner, F.W.; Gough, C.M. Spatial Variation in Canopy Structure across Forest Landscapes. Forests 2018, 9, 474. https://doi.org/10.3390/f9080474
Hardiman BS, LaRue EA, Atkins JW, Fahey RT, Wagner FW, Gough CM. Spatial Variation in Canopy Structure across Forest Landscapes. Forests. 2018; 9(8):474. https://doi.org/10.3390/f9080474
Chicago/Turabian StyleHardiman, Brady S., Elizabeth A. LaRue, Jeff W. Atkins, Robert T. Fahey, Franklin W. Wagner, and Christopher M. Gough. 2018. "Spatial Variation in Canopy Structure across Forest Landscapes" Forests 9, no. 8: 474. https://doi.org/10.3390/f9080474
APA StyleHardiman, B. S., LaRue, E. A., Atkins, J. W., Fahey, R. T., Wagner, F. W., & Gough, C. M. (2018). Spatial Variation in Canopy Structure across Forest Landscapes. Forests, 9(8), 474. https://doi.org/10.3390/f9080474






