State of the Art on the Use of Trees as Supports and Anchors in Forest Operations

Abstract

Tree stability assessment is fundamental to preserve the safety of both people and goods. This topic attributes high relevance to cable-supported harvesting where trees and stumps are used as supporting and anchoring elements. In this case, the applied external loads are characterized by higher magnitude and dynamic amplification effects than the typical forces acting on trees (e.g., those derived from meteorological events). Consequently, due to the higher forces involved on cable-supported harvesting on relatively young trees used as supports and anchors, the risk of uprooting and stem failures is real. Numerous studies have been conducted on tree stability and the impact of the external loads has been positively linked to the consequent tree failures, in terms of root-plate overturning and stem breakages, or parasite-mediated wood decay involving the root system, thus giving a better understanding of how different trees species deal with such occurrences. This review aims to synthetize and examine the main aspects covered by research works available in literature that, directly or indirectly, might be helpful in clarifying the behavior of standing trees or tree stumps used as supports and anchors in cable-supported forest operations. Lastly, areas that lack research in this particular topic as well as consequent operating suggestions are highlighted in the conclusions.

1. Introduction

Forest operations in mountainous areas are complex due mainly to the geo-physical conditions and in some case also in terms of accessibility. As a consequence, specific harvesting technologies have been developed in order to facilitate wood mobilization in such difficult conditions [1]. Among all these, cable-based systems (or “cable-supported harvesting systems”) requiring the use of live trees as anchors and/or supports are the most common in steep and very steep terrain.

The cable-logging (or cable-yarder) systems and the more recent winch-assist (or cable-assist) systems are nowadays the two main cable-supported harvesting systems. The cable logging systems consist of extraction methods based on one or more suspended cables for the full- or semi-suspended transportation of logs [2], while the winch-assist systems consist of ground-based machines which take advantage of a constant-pull capstan winch (integrated in the same machine or mounted on and powered by a second machine) to prevent the loss of traction from moving up and down along the slope [3,4]. In both systems, live-trees and stumps can be used as anchors, while only in the case of cable logging systems live-trees can be also used as supports or tail spars.

Focusing on cable logging systems, they may significantly differ according to the technology of the machines and site-dependent criteria such as topographic characteristics, silvicultural prescriptions and forest management requirements [5,6]. As a consequence, such dependency has led to the development of different approaches, each one covering the necessary aspects to design a cable logging system: the employed yarding method, the design of the cable path, the type of pulling carriage and the anchoring of the whole structure to the ground. All the aforementioned characteristics are conceived to obtain the most sustainable cable logging operations in terms of technical feasibility, economic efficiency, environmental soundness and institutional feasibility [1]. This approach is also promoted in numerous practice manuals and safety regulations worldwide [2,5,7,8,9,10,11,12]. However, in specific, the design of supporting and anchoring systems, which requires the utmost importance for the safety of the working site, is still based on simplified assumptions and on the experience gained by the designer [5].

The second procedure, winch-assist systems, has been developing in the field of forest operations due to several introduced advantages among which are the mechanization of working procedures. This concept is typically associated with an increase in productivity and in safety when a ground-based harvesting machine is used in very steep terrain. The latter can be explained by the reduction of manual works, normally considered highly hazardous operations [13,14,15]. While anchor-based machines do not require the use of natural anchors (they are substituted by bulldozers, excavators or specially designed machines), ground machines like harvesters and forwarders equipped with integrated winches involve the use of live-trees or stumps and may still induce failure in the anchorages as warned by [3,16].

This review will focus on the behavior of standing trees or tree stumps used as supports and anchors to keep skylines, mainlines, haul-back lines or guylines sufficiently tensioned and to create cable-bracing systems for the vertical supports (e.g., mobile towers, headspars, tailspars, intermediate supports, etc.). Additionally, even if a number of research works concentrate on forces generated in cable logging systems, several outcomes could be also applied in the evaluation of the safety of anchors used in harvesting with winch-assist solutions. However, the different distresses on the anchorages generated by the two alternative cable-supported harvesting systems should be take into consideration. Again, in the case of a cable logging-system, it is worth noting that the term anchor is referred hereafter to all the trees used as supports that allow the cable to maintain its initially designed shape and/or working tension (and the corresponding allowed deflection under the logging operations).

2. Safety of Anchorages in Cable-Supported Forest Operations

Figure 1 shows a schematic representation of the technical aspects that ought to be investigated in order to assess the safety of a cable-supported harvesting system during its design and gives a rough suggestion about the level of knowledge of each aspect derived from the available literature. This chain-like scheme also helps to clear out the order in which the safety of a cable-supported forest operation ought to be assessed. Usually, the more “reliable” variables in the design process are the characteristics of the skyline i.e., line geometry, ropes mechanical properties, carriage weight and hauling weight. Occasional information is available in literature concerning the actual variation of tension in the ropes of a cable-logging system. However, a rather significant difference between design and actual tension values recorded on the cable during the loading cycles has been found [17] in a cable-logging system. Furthermore, even less information is available on the behavior of trees used as anchors, and the quote “the only way to estimate an anchor’s capacity is by experience usually gained the hard way” [5] may sometimes be considered still actual, also because below-ground root rots are difficult to assess. This, highlights the need for research to be done on the anchors in the field of cable-logging systems which, according to a recent literature review on cable logging [18], still lack of detailed investigation.

The lower the amount of supports and anchors employed in a cable logging system, the more important should be the safety margins to be assumed in the definition of the load-bearing capacity of those elements. For example, a single-span cable anchored to a mobile tower on one end and to a tree stump to the other, may require only five anchors: four at the yarding site to contrast the out-of-plane deflection of the mobile tower (guyline anchors) and one at the end of the line (tail anchor). Nevertheless, the failure of whatever anchor could sometimes lead to a cascading effect concluding with the collapse of the main tower and consequently the whole yarding system [19,20]. For this reason manuals suggest using multiple guylines and anchors to stabilize a single support [9,10,11,12]. In the case of a multi-span configuration, Figure 2, the introduction of intermediate supports realized with existing trees (spar trees) adds supplementary variables to the problem, represented by the application of an external force applied at a significant height from the stem base [21,22].

With regard to the recent spread of winch-assist solutions, advancements in the technology employed by such machines is expanding the operating range of ground-based systems onto steeper slopes [3]. Tension-limiting features are being included in new winch-assisted forest machines, thus reducing and limiting the tension forces [4]. However there is little detailed information about these systems. In the case of large cable-winch forwarder, the operator can adjust the tensile force to different settings ranging from 0 to 90 kN [16]. Other potential alternatives suggest the use of skidders as mobile anchors [23], which relieve excessive cable tension by allowing a certain sliding movement of the anchor. In fact, when the anchor capacity is overdone, the mobile anchor can slide forward discharging cable tensions [3,23]. Those provisions might increase the safety level with respect to cable failure but still do not give the worker any advice on the state of the anchor. Therefore, it is important to shed some light on this particular aspect and better understand the reliability of anchorages. However, the use of heavy forest machines as mobile anchors provides a higher flexibility in terms of anchor position and because of that, these machines can be used on an ad hoc basis for multiple steep terrain machines [3].

Anyway, the choice of the natural anchoring solution (or rigging solution) is dependent strongly on the availability of existing natural elements. As a recognized rule in current practice, the employment of more economical methods is always preferred, i.e., the choice of using existing standing trees or stumps available in the working site [5] rather that providing artificial and usually more work-demanding solutions like pegs driven into the terrain or anchors buried in the ground [9]. Independently from their position with respect to the working line, it is desired to anchor the cable close to the root of the tree [2], in order to reduce as much as possible the equivalent bending moment (BM) applied to the base-resisting structure (i.e., the root system). If nearby obstacles (like the presence of rocks or recesses) force to set the cable end at a significant height, to ease logging and yarding operations, additional second order-effects must be taken into account in the analysis of the anchor stability (i.e., the amount of allowed deflection [8]), and therefore provisions like multiple anchors in series are to be provided [5]. In this context, some safety manuals exclude the use of single anchors for rigging guylines [11] even for a large, deeply rooted stump [5]. However, in these circumstances the force distribution on the various anchors should be carefully evaluated [24].

3. Dynamic Nature of the Force Applied by the Cable

The design of cable layouts is a combination of typical structural engineering challenges, intrinsically related to the cable system, coupled with always changing site-specific conditions, which express the natural variability of the forest environment. Calculation of the economically efficient load path or the maximum payload for a given cable geometry are the two general types of problems to be encountered [25]. Traditional designs of these systems have been based on the strong assumption of linear distribution of forces where only geometrical effects are considered in the calculation model [26]. Thanks to improvements of computer technologies, additional non-linearities (e.g., change in shape of the model during loading phases) have been investigated and more refined models proposed [27,28,29,30,31]. More recent attempts to predict skyline tensions adopting more refined problems have been analytically derived by Dupire et al. [32]. However, assuming a static behavior without considering the dynamic nature of the real cable systems remains a strong simplification, which does not always collide with safety provisions.

Dynamic tension fluctuations due to the cyclic nature of the yarding operations, have been analytically derived by Womack and Laursen [33], while experimental measurements conducted in a noteworthy work by Pyles et al. [17] extrapolated the details on the oscillations of the tensile forces acting on the main cables. The main outcomes confirmed a highly variable magnitude of loads. They also compared the different dynamic behaviors (damping, natural frequencies) of the skyline with respect to mainlines and guylines [17], which is also a direct result of the different properties (e.g., cable lay, nominal diameter, steel grade) and geometries of the ropes that characterize each line. A filtering ability of the supporting structure emerged and could significantly reduce the effective loads on tailspars, towers and anchors. This suggest that the dynamic behavior of a cable-logging system could be assimilated to a real structural system for which a dynamic characterization of every component may possibly clear out the most significant parameters affecting the final behavior (e.g., dynamic behavior of the tower and spars); however, no research works are available to support such a statement.

Actually, interest in the dynamic behavior of the tensile force in the employed cables is again growing. Recently, dynamic fluctuations of cables have been experimentally measured on both cable logging and winch-assist systems [4,16,34,35,36]. With reference to the first typology, each working phase (i.e., outhaul, hooking, lateral skidding, inhauling and unloading) produces solicitations into the skyline with different dynamic characteristics. For example, lateral skidding usually delivers high peak impulsive loads, while the inhauling phase provides a fluctuating input to the system [35]. The observed common outcome is that the safety levels accounted for in cable tension design are regularly not respected [35]. Again, design often refers to the minimum breaking strength of the clean cable without taking into account reduction due to fatigue loading [37,38] for which only the endurance limit is normally checked (50% of the minimum breaking load). More precisely, additional attention should be given to the actual cyclic amplitude in relation to the mean tension level to which the cable is subjected and also to the actual number of working cycles that the cable is capable of [37].

The dynamic behavior of the load in winch-assist systems is quite different. In particular, peak breakout loads are observed during loading procedures as well as during the unloaded travelling phase while, in general, dynamic fluctuations are rather reduced. In a tension-monitoring work conducted by Mologni et al. [16], a sequence of spikes of force in the cables between the loading and driving on the trail was observed and ought to be caused by the non-perfect synchronization between the machine movements and the winch.

These considerations enhance the concept that increasing the knowledge on both the applied force and the actual reactions originating from the system should be the very first fundamental step in the evaluation of the safety level on the load-bearing capacity of the anchoring system.

4. Response of the Tree Used as Support and Anchor to Static/Dynamic Actions

As discussed in the previous section, the understanding the static and dynamic characteristics of the actions conveyed from the cables to the tree is a compulsory step in stability analysis. The aims of comprehensive research concerning tree response to external forces are closely linked to damages caused by meteorological phenomena such as windthrow and snowfall [39,40,41,42] or rockfall and debris-flow hazards [43,44,45]. Only a few works deal with static or dynamic punctual forces applied to the tree stem like the ones involved in cable-logging harvesting, e.g., [46,47]. It is worth noting that dynamic actions applied among the tree crowns are normally transposed into equivalent static forces applied on occasion to the center of gravity or center of crown mass [40]. Recent research works and reviews are available regarding tree dynamics [48,49,50] and the relative tree anchorage mechanical behavior [51].

5. Mechanical Behavior of the Tree from Experimental Tests

Research activities related to tree stability frequently involve tree-pulling tests. Such experimentations consist of applying horizontal forces to the tree stem until the complete collapse either of the stem or the root plate system is induced. The common aim is to associate dendrometric characteristics of the collapsed tree to the observed mechanical response. Consequently, data acquired from such tests form the statistical basis for the realization and calibration of analytical and numerical models that are used to provide a reliable guess of the tree mechanical behavior in response to externally applied loads.

Most of the available works on tree stability are related to conifers (in particular on conifer tree species with shallow roots, or plate-like roots, such as Norvegian spruce), although more recent works are focusing also on deciduous trees as well as tropical species [52,53,54], the latter especially in the context of urban trees, where root and trunk decay are mainly responsible for tree failures [55,56].

5.1. Tree-Pulling Test Setup and Data Acquisition Technology

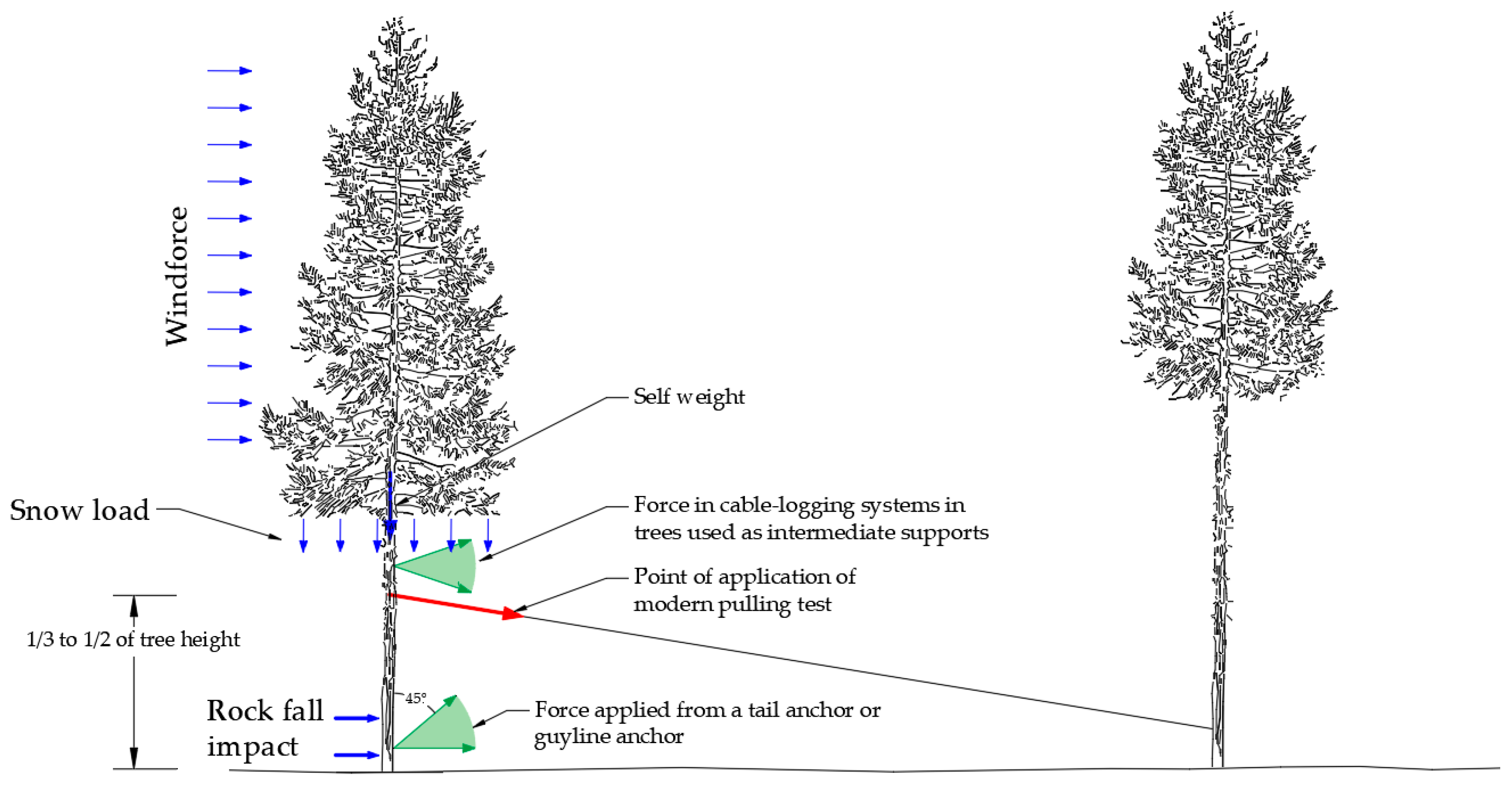
Generally, pulling tests of trees require placing a rope at a sufficient height to induce uprooting failure while avoiding fragile failure of the stem. Pulling tests, commonly known as winching tests, for academic research purposes are a practice mainly started in 1960 [57,58] and have been evolving gradually thanks to the continuous improvement of available instrumentations. Up until 1980, winching tests were conducted by applying an almost horizontal force at one-third of the tree height in order to properly simulate windthrow conditions [58]. Wood [59] calculated that a pulling height equal to 80% of tree height should give a uniform stress along the tree stem. However in modern tree pulling the force is normally applied between one-third and one-half of the tree height (see Figure 3), and therefore stem failure normally occurs on the lower portion of the stem [60]. Modern tests setup use a pulling cable fixed to a round-sling placed possibly at half tree height on the pull-tree [39] and apply the force with a sufficiently low angle with respect to the horizontal. Details of pulling tests and data acquisition methodology are clarified in [39,61,62].

Active discussion is being undertaken on defining actual differences between the force applied to the tree in static pulling tests and the actual wind-induced forces [63]; however this is of less concern regarding the simulation of realistic applied forces typical of cable-supported forest operations. In these cases, the height of the applied force is correlated to the intended use of the anchor (green arrows in Figure 3). In detail, for tail anchors or guyline anchors the cable is attached at the lowest point possible to exploit the higher diameter in proximity to the trunk collar. By contrast, intermediate spar trees have the cable necessarily anchored to a suitable height in order to ease the passage of carriage and hauled logs. Most of manuals [5,9] suggest placing guyline cables at an angle of maximum ±45° with respect to the horizontal line depending on the uphill/downhill conditions. This circumstance produces additional tensile or shear components to the tree with respect to a pure horizontal loading condition. Hence, different mechanisms could be enabled by those components especially in the root-soil system. In fact, it is not to exclude that the vertical component of the applied force becomes higher than the tree’s weight enabling an uplift component other than the overturning moment.

One last under-investigated aspect concerning the force applied to the tree comprises the evaluation of tree stability in relation to cyclic loading, for which very few experimental works are yet available. Nearly all the studies recalled in the following paragraphs use equivalent static experimental tests while dynamic swaying tests are used only for the dynamic characterization of the tree and rarely refer to the allowable resistance. O’Sullivan and Ritchie [64] found that trees with mean diameter at breast height (DBH) equal to 30 cm cyclically loaded up with a rate close to their natural frequency suffered from progressive failure. However, failure due to accumulated damage is possibly more correlated to the dynamic input of forces in cable systems than for wind-induced loading, and therefore this topic should be more deeply analyzed in the future.

Sensor type, precision and the main features used in winching tests depend upon the aim of the physical phenomenon to be investigated, and therefore two distinct situations can be observed. Tests where mainly static loads are applied present typical experimental condition in which the precision of measurements can be more easily obtained. This is the case of winching tests where load cells, displacement transducers, strain gauges, tilt sensors (i.e., clinometers) [47,62] and, more recently, video-based acquisition techniques [65,66,67] are typically employed. However, such tests may involve a sudden brittle failure, typical of root breakage [68] or stem breakage of the tree used as support or anchor, thus requiring particular care in the design of such tests in order to avoid damages to the measuring instruments. This is due to the magnitude of loads that can be reached when pulling high DBH trees or tree stumps [47,69].

By contrast, in tests involving dynamic loading conditions (e.g., swaying tests), it is preferred to use accelerometers [70], specifically designed strain gauges [71], precision instruments [72] or displacement transducers [61,63] able to monitor tree characteristics also in the long-term. Digital clinometers have been used also to derive displacement of trees [73] by using classic trigonometry once the geometry of the tree has been carefully quantified. James et al. [52,74] made a successful attempt to use a low-cost accelerometer as a tilt sensor and used it on both winching tests and continuous monitoring.

5.2. Test on Stumps

There is a relative lack of work in literature dealing with static or dynamic tests of tree stumps. This is mainly due to the high loads involved (for high DBH trees), which is a consequence of the absence of leverage effects typically exploited in tree-pulling tests. In fact, Coutts [75] completed 14 tests on trees sawn at 1.8 m of height from soil in order to remove the effects of stem and crown overhanging effect that eventually occur for higher displacements. Toupin et.al. [24] studied the load transmission between multiple stump-anchoring solutions. An important outcome was that less than 50% of the load is transferred to the second stump. Biller and Baumgras [76] again tested only small DBH stumps while Pyles and Stoupa [77] tested a total of 42 stumps of second-growth Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) and western hemlock with the direct purpose of studying the stumps’ load carrying capacity for cable-logging systems. They developed a load-slip hyperbolic function to predict the load for a given stump displacement based on the DBH. Consistent research works were carried out in New Zealand on the load-bearing capacity of tree stumps. Smith and Mcmahon [78] tested 118 stumps of Radiata pine (Pinus radiata) on cohesive and granular terrain. The pulling setup was able to reach loads of 1000 kN, thus uprooting stumps with DBH up to 72 cm. In this work, they demonstrated that granular soil produces lower mean uprooting strength than cohesive soil and, as a consequence, simplified predictive equations (or DBH vs. strength trends) should not be used as the sole basis to predict the stump load-bearing capacity and to use them in forest operations. Finally, they evidenced three types of failure for tree stumps subjected to pulling loads: uprooting failure, slabbing failure and shearing failure. Parker [47] and Higman et al. [79] developed a pulling exercise to evaluate the load-carrying capacity of 9 first-cut stumps in the context of temporary forest road design for which stumps are used as a supporting structure for road reinforcement. Lastly, with the aim of stump harvesting, other works performed tests on stumps to determine the force necessary to eradicate them. Berg et al. [80] measured the torque necessary to twist them and remove trees stumps from the ground whereas Lindroos et al. [81] evaluated experimentally the force to vertically uproot them, finding that it requires a force five times less than that needed to laterally uproot it for the same DBH. However, the difference in the applied loading conditions (in terms of direction and magnitude) between stump harvesting tests and cable-supported forest operations tests makes these two works less relevant in this particular context.

5.3. Test on Trees

The structural characterization of complete standing trees has been explored much more than that of stumps due to the multiple aspects that are involved in this circumstance: urban green, windthrow effects in forests, rockfall and snow avalanche hazards, etc. Most of these works have been performed to evaluate the reliability of mechanistic models that predict the effects of wind forces. Several recent reviews and data collection works are available on this topic [39,48]. However, part of these studies, relative to the mechanics of the root-soil system and the flexural behavior of the stem might also be correlated to the analyses of anchoring systems of ropes in cable-supported forest operations. In detail, if stem failure due to concentrated tension (or compression) shear stresses is temporarily disregarded, the load-bearing capacity of a standing tree when subjected to mainly horizontal forces can be expressed by the maximum resistive BM of the root-soil plate, which should be independent from the nature of the applied load, proving the usefulness of the several works available in literature regarding this topic. For this reason, we think that part of the data obtained by winching tests for windthrow effects analysis (e.g., the root-plate stiffness and the maximum overturning reaction demonstrated by the tree) could be a starting point in the analysis of the stability of supports or anchors for cable-supported harvesting operations.

Fraser [57] and Fraser and Gardiner [58] performed the first winching tests and analyses on the stability of coniferous trees in the United Kingdom. Later, Coutts [75,82] studied in detail the root architecture in response to tree stability of superficially root-plated Sitka spruce (Picea sitchensis (Bong.) Carr.) in UK soils. He developed the first mechanical model confirming that the angle of the stem is produced by a combination of stem bending and displacement of the root-soil plate. Papesch et al. [83] analyzed the results of 63 pulling tests in New Zealand founding that Radiata pine had lower stem deflection than Sitka spruce measured by Coutts [75], thus confirming that the contribution of crown overhanging to the applied BM is correlated to the stem bending stiffness. Moore [60] collected data from the winching tests of 164 Radiata pine in New Zealand and Moore and Gardiner [41] tried comparing wind-firmness between Radiata pine and Douglas fir. Nicoll et al. [61] and Peltola et al. [63] tested and compared the anchorage strength of Norway spruce (Picea abies), Scots pine (Pinus sylvestris) and Douglas fir. All these analyses as well as the resulting mechanical models (presented in Section 6) may have important reflections on the use of standing trees as intermediate support on a multi-span configuration. Knowing the displacement capacity at a certain height could reduce the errors in computing the actual tensile force during rigging operations, consequently leading to a better design of the guylines [21].

It must be emphasized that the tendency of workers is to anchor cables around trees with the highest DBH in the harvesting area, as strength should be directly proportional to the DBH squared [26]. Small DBH trees are employed in multiple-anchor configurations in order to distribute forces [2,5]. However, the aforementioned works involving static pulling tests analyzed the behavior of trees characterized by small DBH, with exception of [60,83] for Radiata pine. The size of a tree (i.e., height and volume of stem) influences the magnitude of the forces and the modes of failure [52] but there is a lack of information regarding pulling tests of trees with relatively high DBH. Lundström et al. [66,69] studied the tree stability of mature trees in Switzerland by pulling tests on Norway spruce, Silver fir and Scots pine in Switzerland with mean DBH = 44 cm, 34 m of height and mean age of 81 years. The trees were pulled in the axis of the prevailing winds and the expected maximum anchorage moment. They focused on the definition of the rotational stiffness of the soil-tree apparatus as well as the definition of the stem deflection curves.

5.4. Primary Site-Specific Variables Analyzed: Slope, Wind Direction and Soil Type

Regions characterized by slopes with high gradients are strongly related to the use of cable-based harvesting solutions [84]. It is also a consolidated fact that slopes, and the correlated resulting difference of mean wind speeds between upslope and downslope directions, directly affect the root system development. Nicoll et al. [85] winched 36 relatively young Sitka spruce trees with mean height of 22.3 m and DBH of 23.4 cm. They did not find significant differences between trees on horizontal and sloping terrain (30°), although they confirmed the difference in terms of total applied BM between pulling uphill and downhill. Nicoll et al. measured higher critical turning moment when trees were overturned upslope than downslope, which might be the result of an increased root growth on the downhill side or a relatively greater structural root development on the upslope and a corresponding increase in rigidity of the root-soil plate [85]. Therefore, it is to be expected that the slope degree plays an essential role in the evaluation of tree stability and safety of the anchorages. However, there have been few works in literature that focus on this particular aspect or that try to compare the mechanical behavior of a tree or stump between a sloped and a non-sloped terrain. Jonsonn et al. [86] tested 23 Norway spruce on an average slope of 32° to 34° to define the rotational stiffness at the base of the tree but they did not compare values with trees on horizontal terrain.

Concerning geomorphological characteristics, Nicoll et al. [39] observed that forests with higher average wind speeds could provide better load-bearing capacity for the same species of conifers. In this context, it was stated by Coutts [75] that the major contribution to tree uprooting are given by the windward roots thus the primary direction of wind directly affects the robustness of the anchorage. In this context, there is also evidence that roots are able to optimize their shape to resist applied loads by concentrating material in regions of greater stress and adapt to the weakness of the soil matrix [87,88]. Regarding the soil type, results of test on stumps performed by Smith and Macmahon [78] showed that the bigger the anchorage, the higher is the difference in terms of load-bearing capacity between a granular and a cohesive soil. Such a difference was confirmed in the whole investigated DBH range between 30 and 70 cm. An experimental comparison performed by Moore [60] on Radiata pine trees confirmed that the failure mode is closely linked to soil type. Non-cohesive soils induced uprooting failure whereas cohesive soils led on most of the cases of stem failure. Additionally, these results suggested that an architecture of sound, not infected roots is rather more important than root size in the overall mechanical performance of the anchor [60]. An additional factor may be the tendency for conifer roots on peaty soils to develop eccentric “I-beam” cross-sectional shapes [88]. This behavior is important in tree stability because a healthy root with such a shape can have 300% of the flexural stiffness of a circular root with the same cross sectional area. Nicoll et al. [39] collected data from 2000 pulled trees in UK. The majority of tests involved Sitka spruce trees, with the important outcome that they demonstrated worse anchoring capabilities in granular mineral soil and with shallow roots than on peaty (cohesive) soil. Such trends have been generalized to plate-like root species from previous numerical simulations conducted by Dupuy et al. [89]. Peltola et al. [61] pulled 95 trees between Scots pine and Norway spruce in Eastern Finland and found that frozen soil always led to stem breakage. This fact could have particular relevance for winch-assisted ground machines, where such equipment are often used in colder seasons in order to reduce soil compaction issues due to their heavy weight [84].

6. Mechanical Models for the Load-Bearing Capacity of an Anchorage

Most of the aforementioned experimental works aimed to obtain valuable information for the prediction of tree failures. In this context, statistical models and (i.e., mostly linear regression models) have been developed to relate the tree or tree stump load-bearing capacity, usually expressed as the maximum (or peak) bending moment (BM), to some significant dendrometric characteristics. Alternatively, more refined analytical formulations have been trying to analyze failure mechanism of both stem and root-plate, see Figure 4, to fully predict the mechanical response of the anchorage (e.g., load vs. displacement curves and moment vs. rotation curves). Nevertheless, all these models have been continuously calibrated and refined throughout the experimental tests as those previously reported.

Figure 4 shows a schematic representation of the loads, reactions and contribution to the tree deflection of the root-plate and stem rotational stiffness. Moreover, it helps to clarify the differences and analogies on the mechanical behavior during a traditional pulling test (Figure 4a) and in the anchor of a cable-logging system (Figure 4b). In particular, the lower the leverage involved, the higher the force magnitude to be applied in order to reach the same level bending moment reaction at the base. However, this higher shear load translates into an accumulation of stresses in the stem that may shift failure from a typical root-plate failure to a stem failure. Again, it must be emphasized that these mechanisms can be considered valid only for shallowly-rooted trees and may not be easily extended to other root systems (e.g., taproot systems).

6.1. Dendrometric Variables

Most of the studies on tree stability correlate the anchor load bearing capacity with several dendrometric characteristics of the tree [60,83,90]. Stem breakage has been commonly associated to the exceedance of stress that may overpass the Modulus of Rupture (MOR) of the tree stem for green timber [56,91,92]. However, Moore [60] experimented with lower values than the theoretical formulation provided by Petty and Worrell analytical proposals [91] suggesting that empirical approaches rather than analytical equations should be used in the field of wind damage risk assessment. It is worth noting that, in the case of anchors, formulation including the possible shear or slabbing failure [78] of the stem should be included, due to the higher shear load involved (see Figure 4b). The maximum BM has been positively correlated with diameter at breast height (DBH), stem volume approximation (i.e., DBH² × tree height), and stem mass. Regressions are available also on indirect measurements such as DBH³ or the slenderness ratio (DBH/H) and belowground characteristics like root-plate size and root angular distribution [60,69,93]. For example, Cremer et al. [94] found that for Australian Pinus radiata a slenderness ratio less than 60 was associated with tree stability, while trees exceeding a value of 100 were subjected to tree instability, which is a similar approach used in structural engineering regulations for buckling analysis. Peltola et al. [61] found that Norway spruce had lower strength than Scots pine, due to the lower MOR and shallower rooting. However, regressions in the Finnish study are based on critical turning moment against tree height × DBH² (stem volume) rather than stem mass × root depth or stem mass × soil type used by Nicoll et al. [39]. Moore [60] found dependency on DBH and stem weight. He also demonstrated that BM was associated to root plate diameter and depth. The strongest correlation was obtained between maximum BM and stem volume.

6.2. Root-plate Overturning Behavior and Stem Base Stiffness

Similarly to the approach applied in the study of concrete structures, for which moment-curvature laws are used to characterize the non-linear response of a beam cross-section, moment vs. rotation (M(θ)) curves can be derived to express the mechanical behavior of the section of a tree trunk. Such behavior should be independent of the height of the applied force (see Figure 4). Coutts [82] identified four main components that are responsible for the root anchorage of shallowly rooted Sitka spruce: (1) tensile strength of windward roots; (2) weight of the root-soil plate; (3) resistance of leeward roots to bending at the hinge region; (4) resistance to failure of the soil underneath the root-soil plate. Uprooting failure is described as a rotation on the hinge line near the edge of the root-plate about which the entire tree and root-plate system rotates as the tree uproots and falls over. Blackwell et al. [95] refined the mechanical model proposed by Coutts [82] for Sitka spruce trees with shallow roots by including above- and below ground characteristics. Achim et al. [93] proposed a model that reduced the components of tree stability to the contribution of the windward roots and the weight of the root-soil plate and meanwhile added the horizontal spread of the root plate. Nicoll and Ray [88] confirmed that shallowly rooted trees have little anchorage from downward roots, and stability depends largely on the rigidity of the soil-root plate. For this reason, the contribution to tree overturning is a combination between an externally applied load to the crown (first-order effect), and a contribution of the tree mass overhanging from an original equilibrium condition (second-order effect). In Sitka spruce, pulling tests performed by Coutts [75] and Dupuy [89] noted the behavior of the observed moment curve is almost ideally plastic at a quasi-constant peak moment. Rather different results occurred in that performed on a different study for larch and Norway spruce [66,96] where, after reaching a peak value, the curve shows a subsequent immediate drop [66].

Brudi and Wassenaer [62] reported an elastic limit in terms of rotation of 0.25° and that irreversible failures usually occur above 2°. Jonsonn et al. [86] applied a static force to rotate stem base up to 2.5° and set the limit to calculate the root plate stiffness (secant stiffness) at 0.5°. They observed that neglecting forces excerpted by the overhanging stem and tree crown produced an underestimation of stiffness of 14%. Regarding the rotation at stem base corresponding to the peak BM, Lundström et al. [69] obtained values between between 2° and 15°, for trees with mean DBH of 46 cm, mean height of 33 m, and age of 90 years. They also obtained a log-linear correlation between the rotation θ at the maximum BM (calculated including tree overhanging). The stiffer and larger the tree, the higher the rotational stiffness and consequently, the smaller the rotation at the peak BM. Based on experimental tests they extrapolated empirical M(θ) curves starting from a normalized M(θ) law and varying the DBH. With respect to these M(θ) relations, the smaller the tree, the bigger the contribution of gravity to overturning. This is due to the stem flexibility that enables second-order effects.

6.3. Strength and Stiffness of the Stem

If multi-span cable systems are employed (e.g., on convex slopes or slopes with subsequent variations of degree), the use of intermediate supports (spar trees) is needed. In these cases, the load is applied at a certain height from the trunk base, and therefore, stem flexibility has to be taken into account in stability analysis, even more when trees are limbed and bent at the base to realize a clear passage for the logs. Although the evaluation of the anchor strength is required to avoid stem breakage or root-plate overturning, the determination of the allowable displacements of the rigging point (with or without additional guylines) could be helpful when bypass sheaves are employed.

Early studies adopted classic beam theory to evaluate the allowable bending and compression stress of the tree stems assuming them as straight, cylindrical slender columns [22]. Flexural behavior was analyzed [97] and elastic equations were analytically derived [98]. On these conditions, Lyons and Pyles [99,100] evaluated failure due to bending for a rigid spar tree including the second order effects due to stem deflection and varying the tree slenderness. Neild and Wood [101] proposed a non-destructive method for distinguishing root flexibility from stem flexibility in living trees and this was successfully applied to Sitka spruce but remained valid for all species. Input properties are Young’s modulus and root-anchorage stiffness. Stem flexibility directly affects the maximum overturning moment because the overhanging mass, subjected to an increasing eccentricity with respect to the root-plate center, lead to a reduction of the external force to be applied at the tree. A detailed review of the mechanistic modelling approaches on the bases of tree-pulling tests and wind tunnel experiments is available in [63] while Achim and Nicoll [93] provided a mechanistic model to predict anchorage strength of shallow-rooted trees which account for both stem and root-plate stiffness.

6.4. Numerical Models

As discussed in section three, computers have been used to solve analytical problems, but computer-aided solutions are also very helpful to develop parametric analyses that may partially substitute the effort of carrying out intense and expensive experimental tests. Normally, such numerical models are characterized by important simplifications in the definition of the material properties (e.g., isotropic behavior of wood, absence of imperfections, etc.) and boundary conditions (e.g., the root constraint level, the application of loads). In this context, a structural-like approach was chosen by Pyles and Lyons [100] to evaluate stem failure of backspars rigidly anchored to the ground. Saravi and Lyons [102] developed an inverse approach, in which the allowable skyline strap tension has been assumed as the tension that produces the maximum normal stress on a transverse cross section of the tree being equal to an assumed allowable stress. These finite element models involved simple isotropic bi-dimensional (2D) beam elements or orthotropic three-dimensional (3D) brick elements.

More refined and detailed 2D and 3D numerical models mostly concentrated in the analysis of the interaction between root-system and soil [89,103,104] and did not included stem modelling. A rather simplified beam model that accounted for both stem deflection and root rotation was developed by Jonsonn et al. [86] to perform parametric analyses and evaluate the moment-curvature laws of Norway spruce trees. The model was calibrated by means of pulling tests and helped to obtain a series of M(θ) relations. Lastly, in a work presented in Moore and Maguire [105] three existing trees were reproduced with a refined beam model to investigate tree dynamics. Stem, main branches and crown mass were successfully reproduced to analyze swaying capabilities of the branches and their impact on the dynamic behavior of the tree.

7. Conclusions

Most of the significant aspects concerning the mechanical behavior of trees subjected to external loading conditions have been analyzed in detail by several research works. However, in order to transfer all the available knowledge in tree stability to the behavior of trees or stumps used as supports in forest operations with cable-supported systems, some emerging differences are to be highlighted demonstrating that several aspects still ought to be investigated in the future.

The majority of the examined literature works deal with tree stability in relation to external forces caused by meteorological phenomena. However, in the context of cable-supported forest operations, such forces are characterized by greater magnitude, and their dynamic components show high amplitude cycles in a relatively short period (compared to the life of a tree). Moreover, the different inclination of cables may produce additional shear-tensile components on the anchor with respect to assumptions normally applied for wind forces or rockfall impact (i.e., of mainly horizontal loads).

In the available experimental test data, another emerging problem is that the literature hardly refers to mature trees (i.e., conspicuous DBH or stem volume), which is a typical condition in harvesting, as they involve more difficult and expensive test setups and economical efforts. Additionally, as cable-supported systems are mostly used on sloped terrain, there is a lack of tree-stability experimentations with this particular but important condition. Efforts should be made to study the behavior of trees as anchors on sloped terrains or to try deriving possible correlations with the existing knowledge on non-sloped terrain. Moreover, the nature of the cyclic force is scarcely taken into account in most of the works. It could be expected that cyclic loading conditions might produce an accumulation of damage in the anchors, which could reduce the actual load-bearing capacity with respect to static conditions. Lastly, the protocols of tree-pulling tests are often different between similar works, e.g., in terms of pulling height and load inclination. The variability of results obtained even with similar testing conditions reflects this potential issue.

Nevertheless, the aforementioned literature, mainly developed on an experimental basis, constitutes a solid basis from which to start developing the mechanical models that aim to express the mechanical behavior of trees used as anchors. In particular, works done to evaluate the moment-curvature laws might be useful to realizing a stress-test procedure to obtain an initial helpful characterization of the anchoring strength as already suggested in literature research should focus on trying to correlate the behavior on anchorages in highly sloped terrains.

An eventual solution could be the development of a unified testing procedure to evaluate the safety of a tree used as support or anchor by following a few clear steps: (a) assess of presence of root rots and wood decays through a preliminary investigation; (b) evaluate the tensile force to be applied to the anchor, from available static models, applying a reduction coefficient according to the presence and intensity of root and trunk decay; (c) apply a dynamic amplification factor to fit with the actual behavior of the cables involved; (d) do an initial stress test, by monitoring stem deflection and root stiffness with proper instrumentation, and assess the level of safety; (e) eventually keep the tree monitored during forest operations to detect possible accumulation of damage due to fatigue.

Lastly, the use of numerical simulations has been already positively applied to the dynamic characterization of trees as intermediate supports, where loads are applied at a significant height, by evaluating their damping capabilities and their influence in the dynamic behavior of the complete multi-span cable-logging systems. These static and dynamic analyses, performed only on single components (trees, cables), might be extended to study the behavior of a complete cable-supported system, taking into account the modern computational capabilities available nowadays.