1. Introduction
Fires affect terrestrial ecosystems and have profound consequences on global climate, air quality and vegetation [
1,
2]. Fire regimes are determined by climate variability, vegetation and direct human influence. Seasonal weather is the most variable factor and has the greatest effect on regional burned area [
3,
4]. Climate change lengthens fire seasons, with an associated trend towards increasing extent, frequency and severity of fires, as well as the global occurrence of extreme (mega) fire events [
5] in many regions of the Earth (e.g., in the Mediterranean [
6] and boreal [
7] regions). At the same time, human activity is the primary source of ignition in global forest, savanna and agricultural regions. Indonesia is one of the countries that has experienced particularly large-scale peatland and forest fire disasters [
8]. According to the World Bank [
9], 2.6 million hectares of Indonesian land burned between June and October 2015, costing Indonesia USD 16.1 billion.
Most fires in Indonesia are induced by human activity [
9]. Forest and land clearing for plantations and agriculture have been cited by various researchers as the major causes of these fires [
10]. Indonesia contains 47% of the global area of tropical peatland, located mostly in peat swamp forest [
11]. Large peatland areas have been converted to agriculture, initially under the Indonesian Government’s transmigration program, and later for commercial oil palm and paper pulp tree plantations, especially in Sumatra and Kalimantan [
12,
13]. Draining and conversion of peatland, driven largely by palm oil production, contributes to the intensity of haze from fire [
9]. Peatlands account for about one-third of the area burned, but are responsible for the vast majority of the haze and CO
emissions from the fires [
9].
Fires have a large disruptive impact in Indonesia, affecting millions of hectares of land, producing severe smoke haze pollution. There are multiple negative effects of wildfires in Indonesia on climate change [
14], health [
15], the economy [
8,
9] and biodiversity (
http://fires.globalforestwatch.org/about/). Indonesia’s biomass burning emissions are comparable to the annual fossil fuel CO
emissions of countries such as Japan and India [
16,
17].
The overall fire situation in Indonesia is described in various papers [
18,
19]. In this study, we apply a mechanistic wildfire model to estimate burned area in Indonesia. Fire models are developed for hazard assessment, as well as forest and fuel management planning, including prescribed burning and suppression efforts. The paper led by Herawati [
20] reviewed available fire models (e.g., the Risco de Queimada/fire risk model (RisQue), Coupled Atmosphere-Wildland Fire-Environment (CAWFE) and FireFamilyPlus), which could be potentially used in Indonesia. However, we have not come across a mechanistic model that specifically focuses on modeling burned areas in the forest and peatland of Indonesia in the literature. This motivated us to apply the Wildfire Climate Impacts and Adaptation Model (FLAM) to modeling burned areas in Indonesia, as described in this paper.
There have been studies from different territories where historical climate data in combination with Moderate Resolution Imaging Spectroradiometer (MODIS) satellite data were used in fire mapping [
21,
22]. However, they did not deal with explicit modeling of burned areas. At the same time, area burned is the most commonly-used indicator when fire trends are being examined [
23], and the assessment of burned area is an important step in estimating the cost of fire [
9], as well as the air quality impacts [
24]. Previously in studies led by Khabarov [
25] and Krasovskii [
26], FLAM (formerly known as the Standalone Fire Model (SFM)) was applied to modeling burned areas in Europe. In this study, we enhance the model by estimating several wildfire process parameters to better fit regional conditions in Indonesia. For the purposes of this paper, we separate peat fires from wildfires.
Methodologically, our paper contributes to the development of the original algorithm by Arora and Boer [
27]. In a recent study, Arora and Melton [
28] linked fire extinguishing probability with population density. We demonstrate that this simplified approach can be improved by an explicit calibration of suppression efficiency.
In this paper, we test the following hypotheses: (1) the observed burned area in Indonesia reported by the Global Fire Emission Dataset (GFED) [
29] (which is based on satellite observations) can be modeled independently by FLAM; (2) the approach integrating the Canadian Fire Weather Index (FWI) [
30,
31,
32] into a mechanistic fire model provides good accuracy in assessment of burned area; (3) the spatial suppression efficiency calibrated using observed burned area improves the original fire algorithm for area burned by wildfires and peat fires.
2. Materials and Methods
FLAM is used to reproduce historical and to project future burned area, as well as to assess climate change impacts and adaptation options (
http://www.iiasa.ac.at/flam). FLAM is able to capture impacts of climate, human activity and fuel availability on burned areas. It uses a process-based fire parametrization algorithm that was developed to link a fire model with the Dynamic Global Vegetation Models (DGVMs) in the literature [
27,
28,
33,
34,
35,
36]. FLAM is a standalone fire model based on the Arora and Boer [
27] algorithm, being decoupled from DGVM. This allows for faster running times and application of the calibration approach, described below. The key features implemented in FLAM include fuel moisture computation based on the Fine Fuel Moisture Code (FFMC) of the Canadian FWI [
30] and a procedure to calibrate regional fire suppression efficiency as proposed in previous studies [
25,
26].
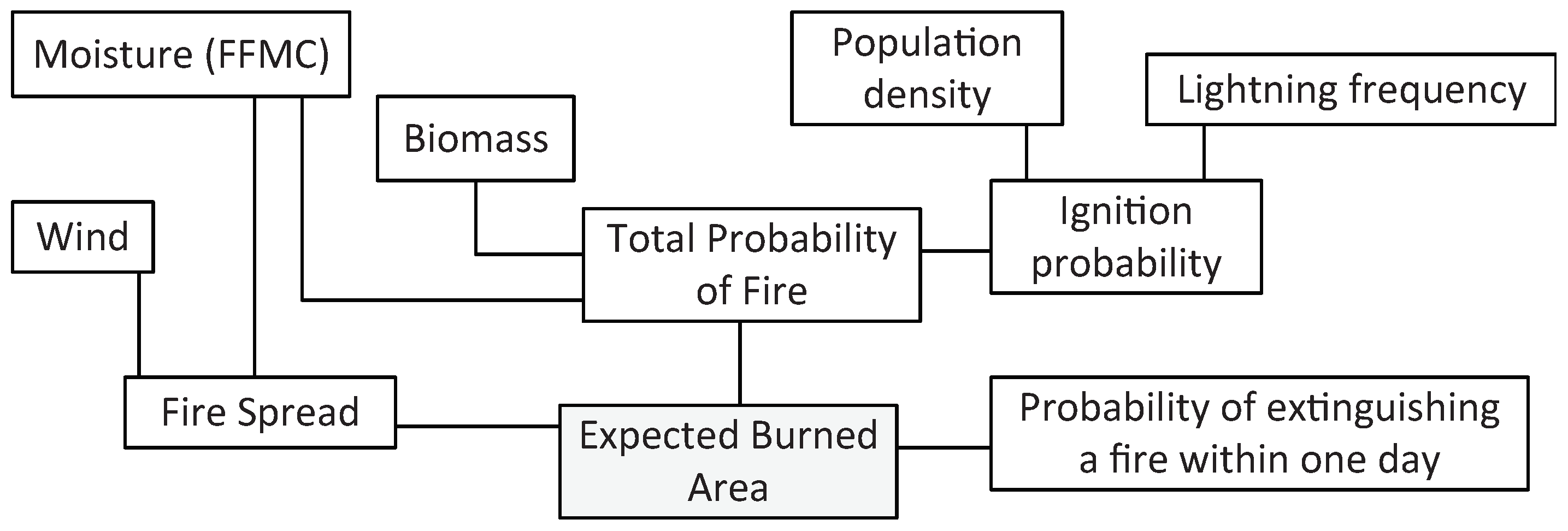
The FLAM flowchart is depicted in
Figure 1. The model operates with a daily time-step at 0.25-arc degree spatial resolution. All inputs were re-sampled to fit the model resolution, using the resample and aggregate functions of the raster package [
37] in the R software; we used the country shape of Indonesia from the wrld_simpl dataset available in R.
To model daily fire occurrences, FLAM computes three conditional probabilities of fire:
probability of ignition depending on natural and human sources
probability of ignition subject to fuel availability
probability of ignition depending on weather
2.1. Ignition Probability
There are two causes of ignition: (i) natural and (ii) human activity. Natural ignition is represented in the model by lightning frequency. Our approach to modeling human ignition and suppression consists of two steps. Firstly, we use a standard procedure, where population density is transformed into probability functions of human ignition and simultaneously suppression [
35], i.e., “unsuppressed ignition”. Secondly, we apply a calibration procedure that identifies pixels with higher or lower suppression efficiency [
26], i.e., probability of extinguishing a fire within one day, based on observed burned areas. In the case when the calibrated probability in a pixel equals one, the fire is suppressed “immediately”. Thus, observations help us to additionally identify the human activity impact independently from population density.
In this study, population density was taken from the dynamic maps of the Gridded Population of the World, v4 [
38]. We used maps for the years 2000, 2005, 2010 and 2015, inside the modeling interval 2000–2016. Original data were averaged using the mean function excluding empty data cells. The corresponding human ignition probability (
) is implemented in FLAM using the equation that relates fire occurrence to population density
:
where a threshold value (
) was set to 300 inhabitants/km
[
35]. The suppression probability (
) depends on the population density in the following manner. More likely, fire suppression is provided in densely-populated areas, where typically high property values are at risk and more resources and infrastructures are available for suppression [
35,
36]. The probability function is parameterized as follows [
39]:
Equation (
2) assumes that fire suppression increases for low values of
, and then declines, reflecting the fact that in more densely-populated areas, 90% of the fires are almost immediately suppressed [
35].
Lightning represents a natural ignition source in the model. Here, we use monthly climatology averaged from 1995–2014 at 0.5-degree resolution from LIS/OTD Gridded Lightning Climatology Data Collection Version 2.3.2015 [
40]. According to a recent study [
41], excluding the inter-annual variability of monthly lightning forcing has only a minor affect on simulated burned area. The LIS/OTD 0.5 Degree High Resolution Monthly Climatology (HRMC) contains gridded data of total lightning flash rates obtained from two lightning detection sensors: the spaceborne Optical Transient Detector (OTD) on Orbview-1 and the Lightning Imaging Sensor (LIS) onboard the Tropical Rainfall Measuring Mission (TRMM) satellite. The long LIS (equatorward of about 38 degree) record makes the merged climatology most robust in the tropics and subtropics. Data were resampled to 0.25-arc degree resolution.
The algorithm used in FLAM is based on the assumption that cloud-to-ground lightning frequency (
[flashes/km
/month]) varies from a specified lower value of essentially no lightning (
flashes/km
/month) to an upper value close to the maximum observed (
flashes/km
/month) [
27]. Therefore, the lightning frequency can be transformed to a value from 0–1 according to the equation:
The probability of lightning ignition (
) is modeled using the function:
Using Equations (
1)–(
3), the daily probability of unsuppressed ignition is calculated as follows:
2.2. Fuel Availability and Weather
In this study, we used the tropical biomass map of [
42], providing the Aboveground Biomass (AGB) density of vegetation in units of Mg/ha with the cell size of 0.008 arc degrees, corresponding to around one kilometer. The value for each pixel of the map was converted to gC/m
by multiplying the original values by 50 [
43] and aggregated using the R’s mean function under the exclusion of no available data cells.
To model fuel available for burning, we need information about litter and Coarse Woody Debris (CWD). We used the data from the Global Forest Resources Assessment 2015 (FRA 2015) of the Food and Agriculture Organization of the United Nations to obtain the shares of these components in the above-ground biomass (AGB). As these values were not available for Indonesia, we used the values reported for neighboring tropical countries. The dead wood information was available for Philippines, where the ratio of dead wood to AGB was
. The litter fraction in AGB was also not available for Indonesia; therefore, an average of the neighboring countries (Laos, Malaysia, Myanmar, Philippines) was calculated, resulting in a litter-to-biomass ratio of
. Biomass available for burning (
B), which is the sum of litter and CWD, was transformed to the ignition probability conditional on fuel availability (
) according to the equation:
where
and
are constants set to 200 gC × m
and 1000 gC × m
, respectively [
36].
Climate is one of the main drivers of fire dynamics in FLAM. Climate change effects on wildfire risk are discussed in many studies [
17,
25,
44,
45]. A well-established Fire Weather Index (FWI), initially developed for Canada by Van Wagner and Pickett [
30], is used to assess fire danger in many regions of the world, outside of Canada. The applications of FWI include European countries [
46], as well as Indonesia and Malaysia [
47]. Daily Fine Fuel Moisture Code (FFMC) values from the Global Fire WEather Database (GWFED) [
48] were used as FLAM inputs in the period 2000–2016. GFWED is comprised of eight different sets of FWI calculations, all using temperature, relative humidity, wind speed and snow depth estimates from the NASA Modern Era Retrospective Analysis for Research and Applications Version 2 (MERRA-2) [
49]. We used the version based on the observation-corrected precipitations [
50]. The data are available from 1981 globally at a resolution of
arc degrees. We used the data till 2016 for our modeling, as there was no complete data for 2017 in the dataset. The FFMC values were resampled to 0.25-arc degree resolution and converted to moisture content values, used in FLAM. Here, we applied the transformation derived from the FWI equation [
30]:
where
is the FFMC value and
m is the fuel moisture content (ratio between 0 and 1). The daily probability (
) of ignition is calculated as:
where
is the moisture of extinction (ratio between 0 and 1) [
33,
35,
51]. Note that
corresponds to
.
Based on Equations (
4)–(
6), the total daily probability of fire is calculated by multiplication:
2.3. Fire Spread Rate and Expected Burned Area
Fire spread rate is limited by the moisture content and wind speed. The daily wind speed data were taken from the MERRA-2 dataset and resampled to 0.25-arc degree resolution. Fire spread rate in (km/h) in the downwind direction is calculated using the equation [
35]:
where
w is wind speed (km/h) and
km/h is the maximum spread rate. Here, function
g describes the dependence on the wind speed:
while function
h, the dependence on moisture content:
The total area burned is calculated as follows:
where
is the length to breath ratio of an ellipse approximating burned area:
Assuming that a particular fire is put out on a given day with probability
q, the expected area burned within one day can be calculated as follows:
where
is the probability of extinguishing a fire in one day and
P is the total probability of fire (Equation (
7)).
2.4. Calibration Procedure Implemented in FLAM
In FLAM as in the original fire algorithm [
27], the efficiency of fire suppression is defined as the probability
q of extinguishing a fire within one given day (see
Figure 1). Potential area burned within one day (Equation (
9)) and the cumulative burned area over any time period of
N days for a grid pixel are calculated as follows:
where coefficient
reflects the availability of fuel, ignition sources and weather conditions, but is not a function of
q [
27,
35],
is probability (
7) for a particular day
j and
is calculated for the same day
j using Equation (
8). In our calibration procedure, we find a value of the variable
such that
, where
is the observed cumulative burned area in a grid cell over a given time period [
25,
26]. Based on a non-calibrated model run with an arbitrary value of
(
) delivering accumulated burned area
for a time period for a given grid cell, the calibrated value
is defined by the following equation:
here:
Substituting the value
(
10) into Equation (
11), we get that parameter
equals
, and therefore, the calibrated value of suppression efficiency
does not depend on the arbitrary selected value
. Nevertheless, model runs with a determinate (place-holding) value for
(e.g., 0.5) are necessary to obtain the value of
. We apply this calibration procedure at the pixel level, forcing the model to fit the total accumulated burned area (as reported in GFED datasets) over the calibration period, which is long enough relative to the model’s operating daily time step. Let us note that calibrated values are sometimes considerably lower than the
threshold, discussed by Arora and Melton [
28], corresponding to the average duration of fire in the absence of human influence as 1 day. The expected fire duration is calculated according to the equation [
28]:
Below, we will show that in peatland, the values of
could be below 0.2, meaning that in these areas, average fire duration,
, could be much longer than 1 day, i.e., up to 173 days depending on the location (see the modeling results in
Section 3.2).
The calibrated values of
are then used in FLAM for calculating daily burned areas, i.e., (
9) is modified as:
Below, we describe three special cases arising during the calibration procedure.
2.4.1. Case I: Probability of Suppression Equals One
In the case when the accumulated burned area in a grid cell modeled by FLAM during the calibration period is above zero and, at the same time, the accumulated burned area reported in GFED in the same grid cell is zero, the value of parameter
. This means that although in this pixel, the total probability of fire (Equation (
7)) is positive and results in modeled burned area, the calibration procedure identified that in this pixel, fire is not possible, i.e., the fire was never observed during the calibration period. In terms of modeling, this means that the fire is suppressed immediately after ignition. This fact could have different interpretations: firstly, this could be a correcting factor to the probability of human ignition discussed in
Section 2.1; secondly, this could also be a proxy of a change in land cover, zeroing the probability conditional on biomass, which in turn is also a result of human activity, decreasing fire occurrence [
52].
2.4.2. Case II: No Burned Area in Both GFED and FLAM
In the case when in a grid cell, both GFED and FLAM report zero burned area, the calibration procedure is not able to set a value of for this grid cell. To avoid indifference in choosing , we keep the value of in those pixels in order to validate FLAM in the validation period. Note that this case is rare for Indonesia.
2.4.3. Case III: Not Feasible for Calibration
During the calibration procedure, there could be pixels where GFED reports burned area, while FLAM does not. In this case, the calibration procedure is not feasible mathematically. We identify those pixels during the calibration procedure, explain the reasons for their occurrence and exclude them from analysis as described in
Section 3.2.
2.5. GFED Data Used in the Study
By applying historical climate data, we compare FLAM results with observed burned areas from the most recent Global Fire Emission Database GFEDv4 [
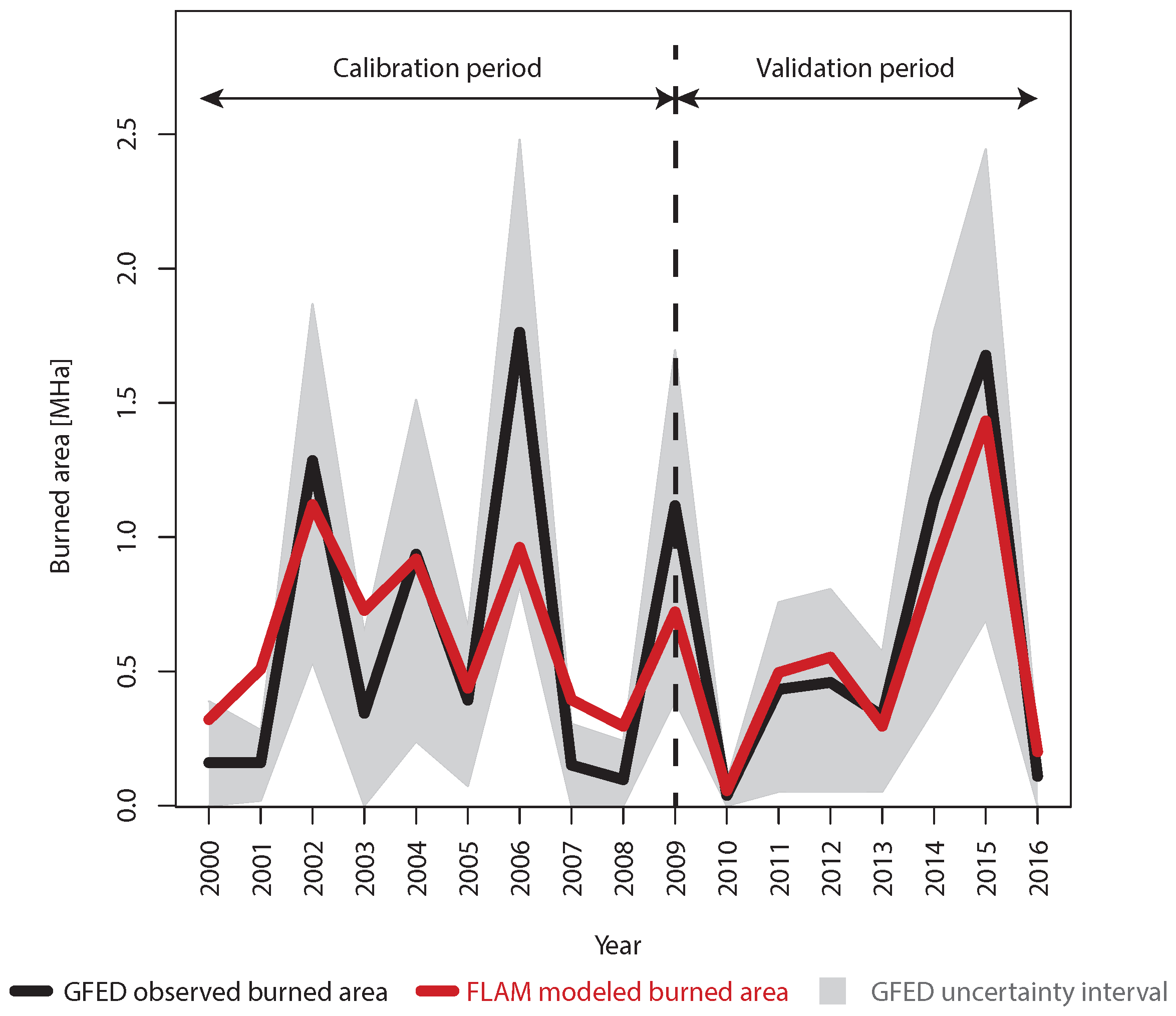
29] for the period 2000–2016. The starting year 2000 is chosen due to the MODIS era starting in GFED in 2000, and the end year is determined by the availability of GFED data. In the study, the time period is divided into two intervals: the period 2000–2009 is used for FLAM calibration, while the period 2010–2016 is used for FLAM validation. In the calibration period, we use GFED data accumulated from 2000–2009. It is important to note that calibration and validation are two independent processes: for the period 2010–2016, FLAM is not calibrated against data or information from GFED; rather, GFED is used only for validation purposes, i.e., the comparison of burned area and location with the output of FLAM.
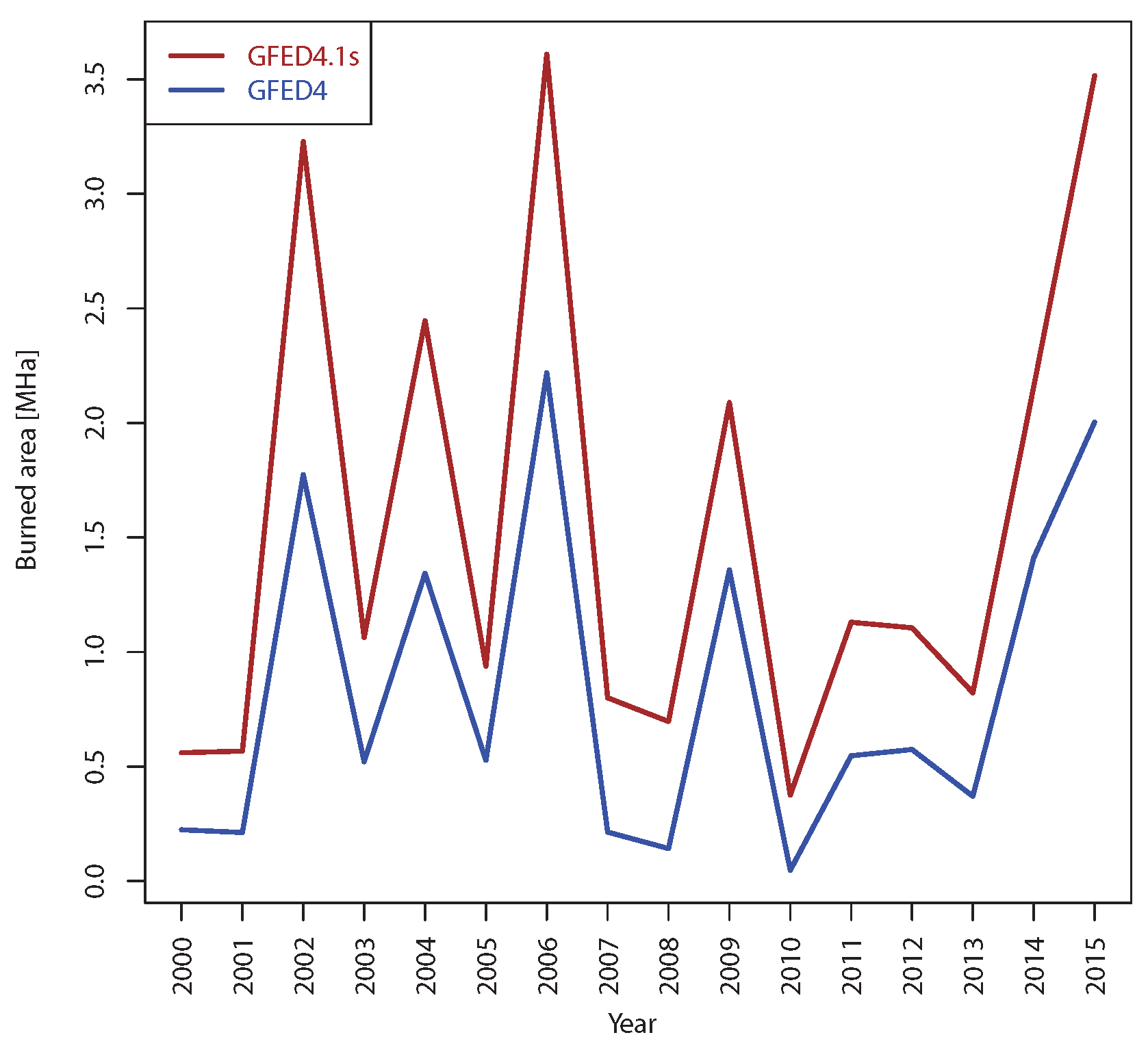
Currently, two versions of GFED are available: the one that includes small fires and another one that does not include them [
53]; these are compared for Indonesia in
Figure A1. One can see that small fires considerably increased the reported burned area, while the shape of the inter-annual variability stayed similar to the version without small fires. In this study, we use the version without small fires for the following reasons. Firstly, it includes the year 2016 (Version 4.1s is till 2015). Secondly, it contains information from the University of Maryland (UMD) land cover classification scheme applied to burned area and provides ratios of area burned in each of those classes, as well as the ratios of area burned in peatland. Note that GFED4.1s contains a split only for emissions. In our study, we model wildfires, and therefore, we choose burned area in the following 10 classes (out of 18): evergreen needleleaf forest, evergreen broadleaf forest, deciduous needleleaf forest, deciduous broadleaf forest, mixed forests, closed shrublands, open shrubland, woody savannas, savannas, grasslands [
54]. Additionally, we use information on uncertainty intervals provided in GFED4, referred to as GFED in this paper.
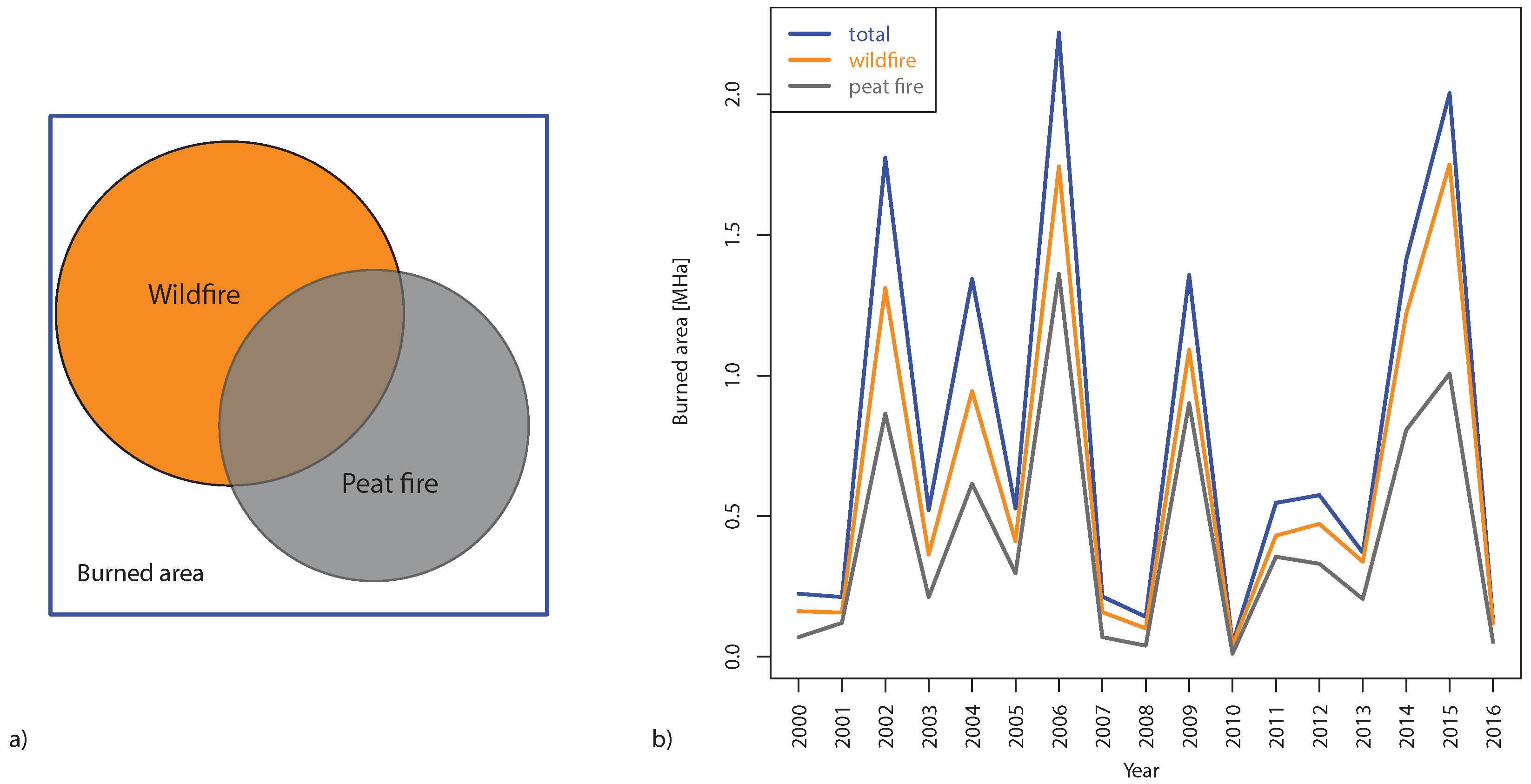
A schematic illustration of how burned area is presented in GFED is shown in
Figure 2a. Each grid cell contains information about total burned area. Additionally, we use the information of the fraction of area of wildfire (10 UMD land classes as mentioned above) and the fraction of area allocated to peat fire. Those fractions are independent, meaning that area burned by wildfire and peat fire can intersect in some areas, as indicated in the figure.
Figure 2b shows actual data extracted for Indonesia from GFED separately for the total area burned, in wildland and peatland. The sum of areas burned in peatland and wildland is higher than the total burned area.
In our modeling, we use a similar approach. FLAM is calibrated separately for wildfire and peat fire, i.e., there are different suppression efficiencies. This approach allows us to distinguish between smoldering fires in peatland and flaming fires in forest.
2.6. Peatland Ratio Map
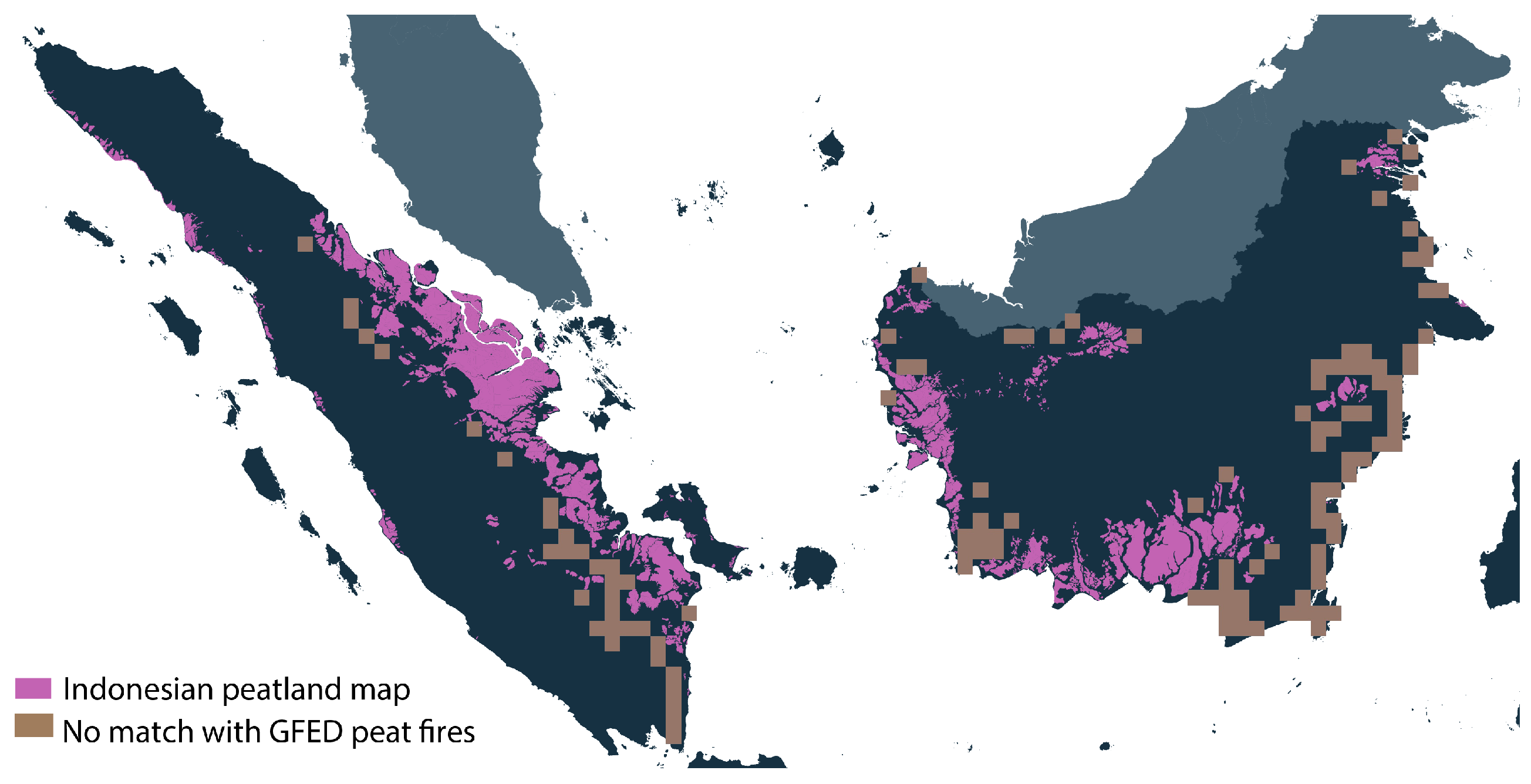
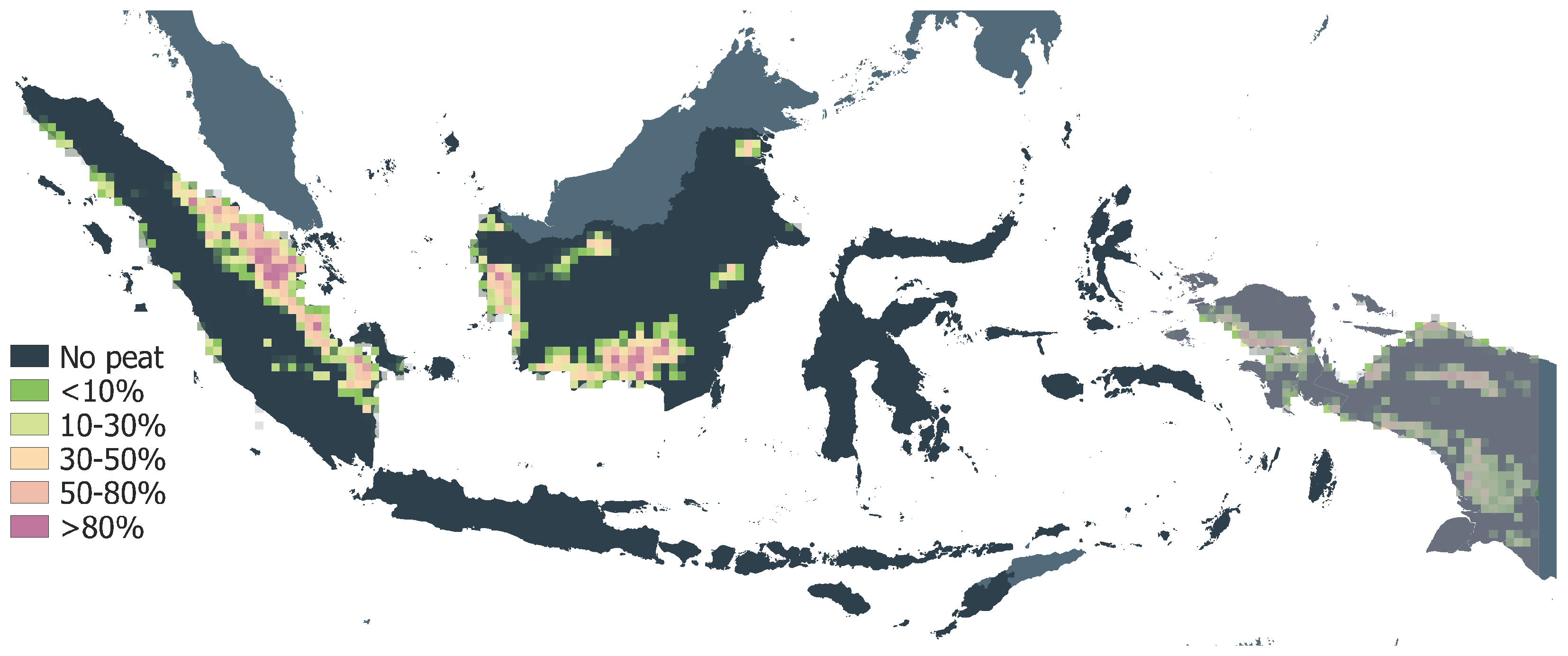
To calculate the fraction of area burned in peatland, we use a map produced by the Indonesian Ministry of Agriculture [
55]. This map provides information on total share of peat in a grid cell in addition to burned peat within total burned area available in GFED. Original map indicated values of 1 for peat and 0 for no peat in each pixel at 30-m resolution. Based on these data, we calculated the ratio of peatland in each pixel at the 0.25-arc degree resolution as shown in
Figure 3. The GFED dataset contains information on peat fires for Kalimantan and Sumatra. Therefore, in our analysis, we use the peatland map only for these islands. Nevertheless, we show the entire map with Papua greyed out.
4. Discussion
In this study, we applied FLAM to the assessment of burned areas in Indonesia. The model was calibrated in the 10-year period (2000–2009) and validated over the seven-year period (2010–2016) using GFED observed burned area. In order to check how results would change with respect to different calibration/validation periods, we considered an alternative split of the historical period into two intervals: seven years for calibration (2000–2006) and 10 years for validation (2007–2016). The corresponding modeling results are given in
Table A1. The results show that because of a shorter calibration period, the values of the Pearson’s
r are lower compared to those in
Table 1. Nevertheless, the correlation with GFED is still very good in the extended validation period (2007–2016): 0.914 for peat fire and 0.956 for wildfire. The corresponding MAE values are 87.65 and 154.9 thousands ha (38% and 36% with respect to average annual burned area). This increase in MAE compared to that of the 10-year calibration period is due to the fact that years 2007–2009, where FLAM is challenged in reproducing burned areas, are now included in the validation period. Experiments with shorter calibration periods provide a decrease in Pearson’s
r in validation periods as the model requires sufficient number of years with “peaks” (2002, 2004, 2006) for calibration. In our view, the 10-year calibration period is sufficient for calibrating FLAM.
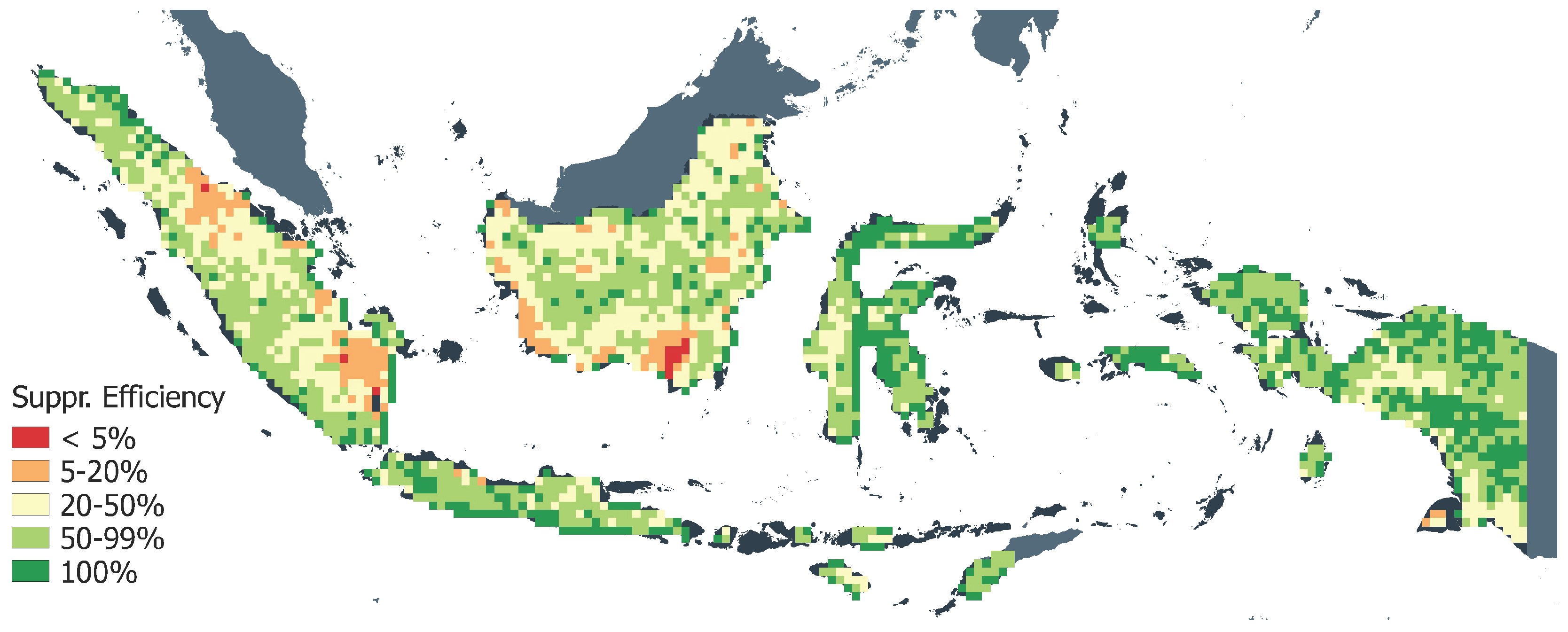
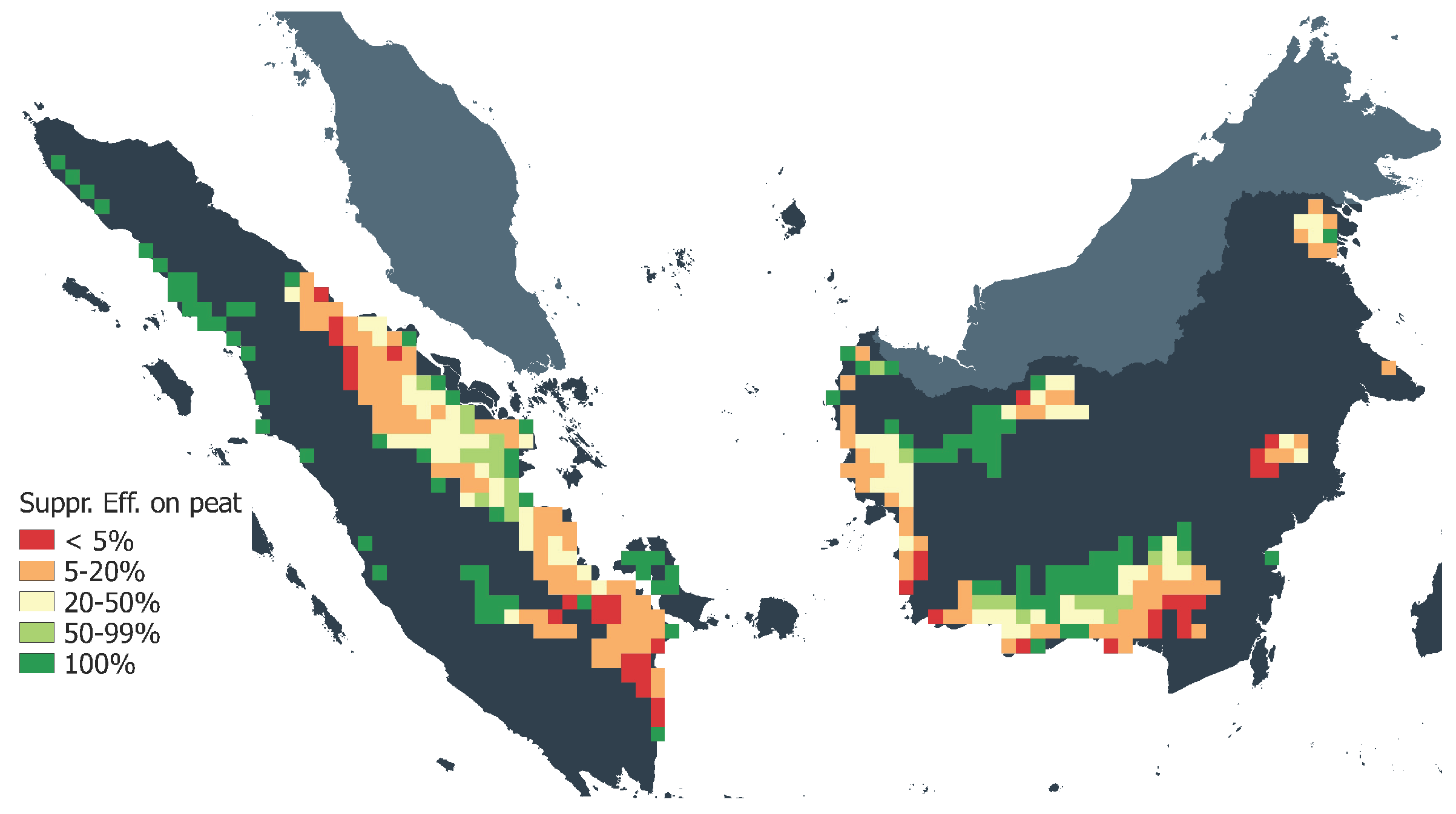
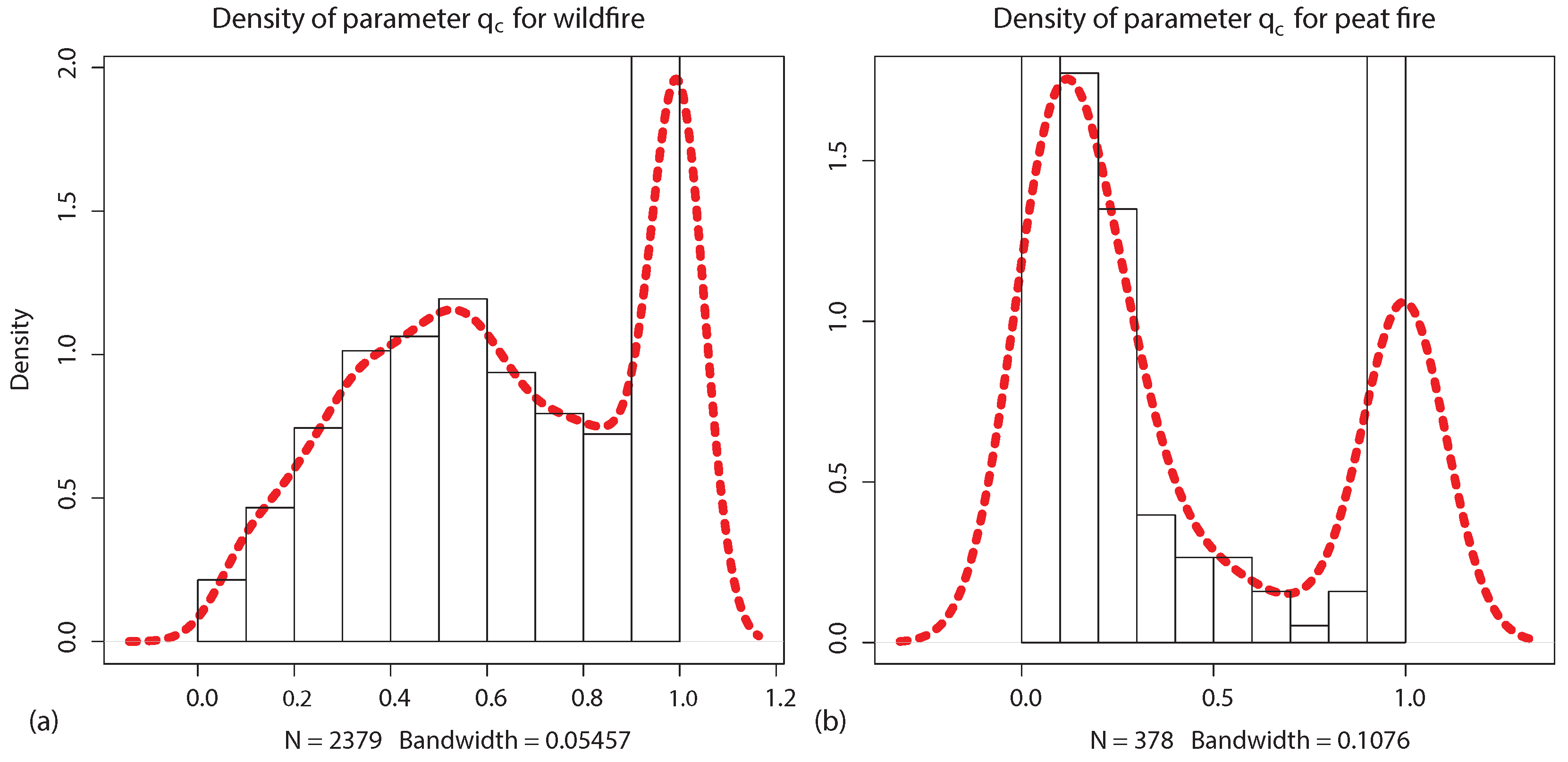
Calibration of the spatial suppression efficiency performed in this study provides an important development in the methodology of the application of the original Arora and Boer [
27] algorithm. Our findings show that the distribution of suppression efficiency has a bimodal density function. A recent publication [
28] applying the same core algorithm by Arora and Boer [
27] for fire modeling states that in the absence of any human influence, the probability of extinguishing a fire within one day equals 0.5 and corresponds to an average fire duration of one day; the extinguishing probability increases with population density. We show that this global value is unrealistic for tropical forests using the example of Indonesia. The results of model calibration using historical GFED data [
29] show that in Indonesia, 95% of area burned by wildfire is located in pixels where the extinguishing probability is below 0.5. It could be as low as 0.0057 in the peatland of the Borneo swamp forest, where the Mega Rice project [
59] took place, corresponding to an average fire duration of 173 days. This reflects the actual situation in Southeast Asia, where once established, peat fires may burn for months and are very difficult to extinguish [
57]. We show that the application of the algorithm without calibration considerably underestimated burned area, particularly in peatland. Our conclusion is that the approach proposed by Arora and Melton [
28] may help to fit a decreasing trend in global burned area, but at the price of considerably underestimating regional burned area, e.g., in Indonesia, which produces a great deal of global CO
emissions. Underestimation of burned area by the original fire algorithm with
could also be the reason why the majority of global fire models underestimate the global burned area, as reported in the study led by Andela [
52].
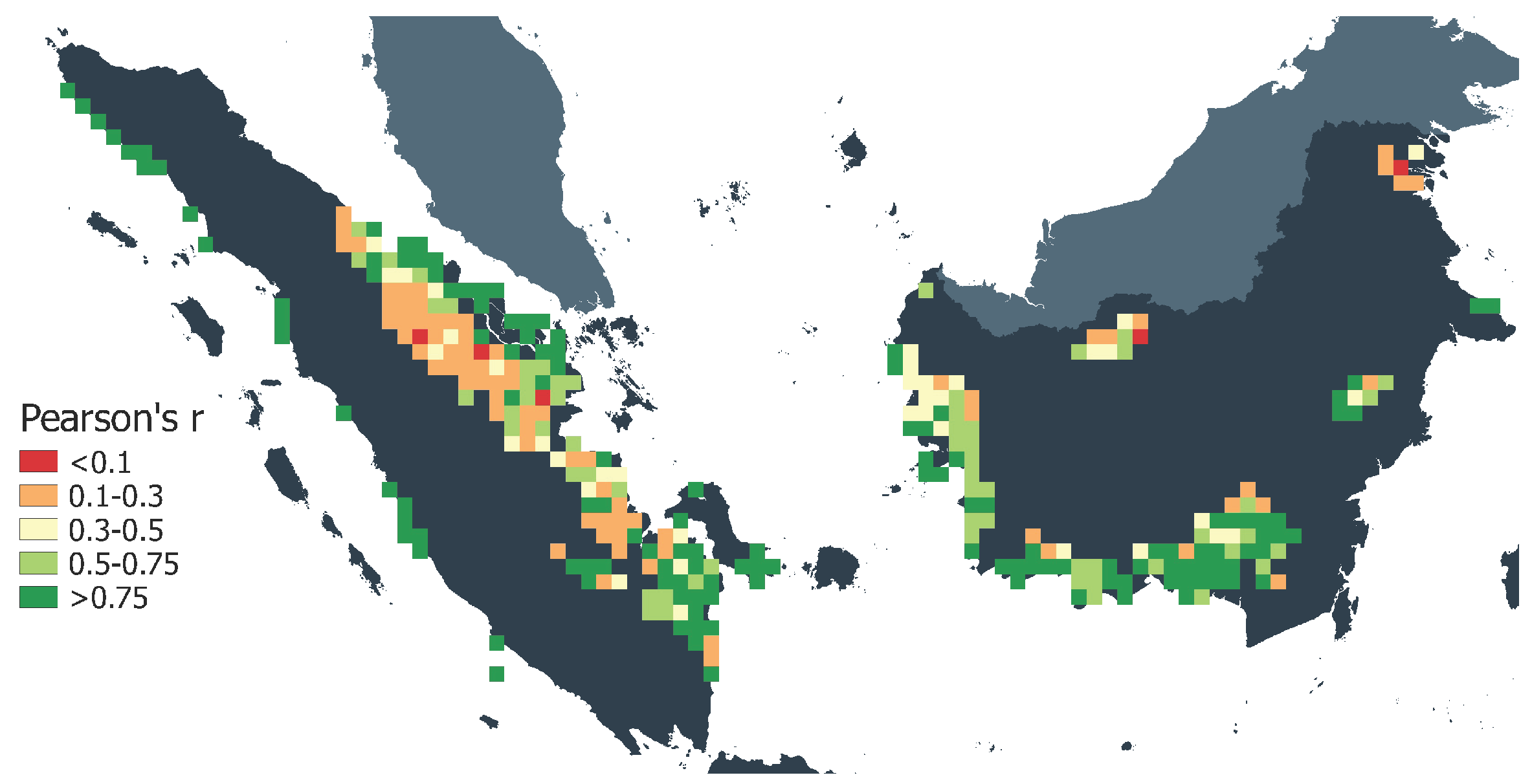
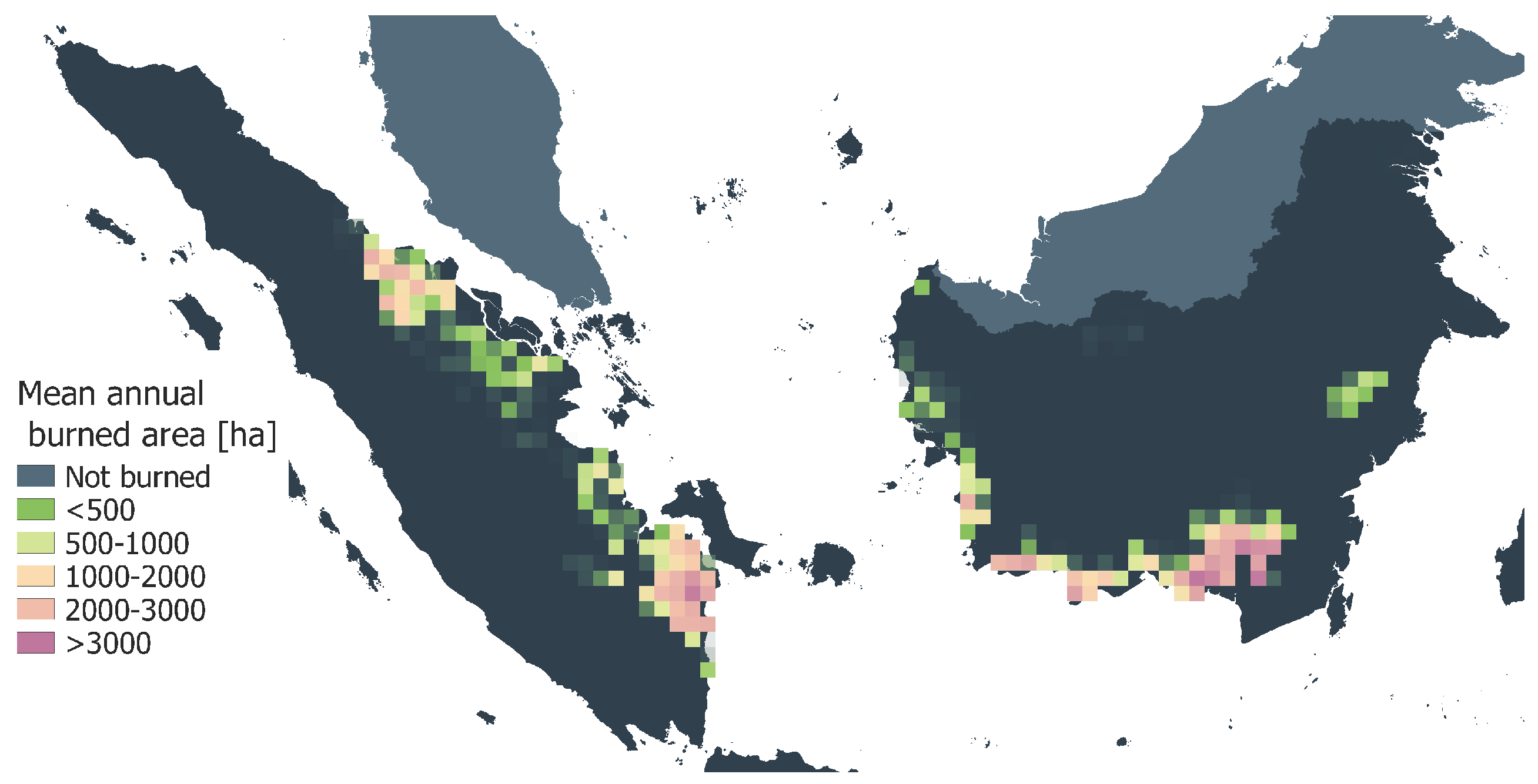
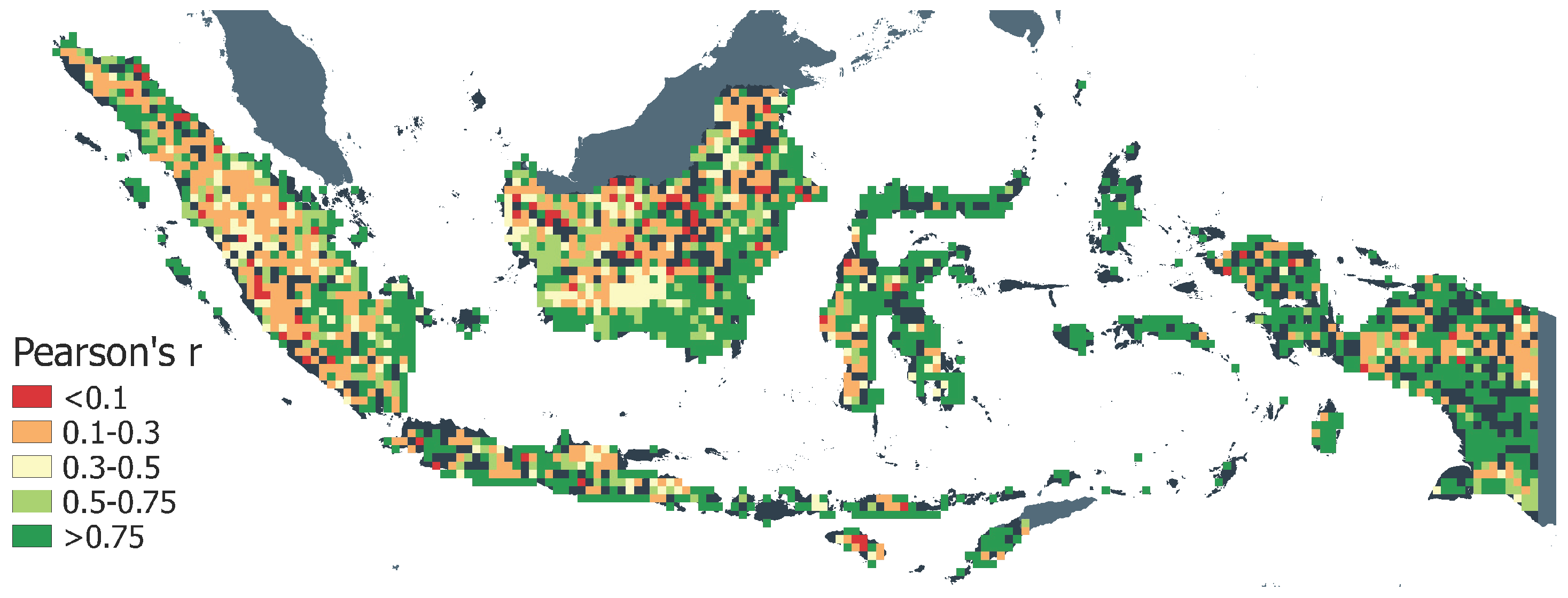
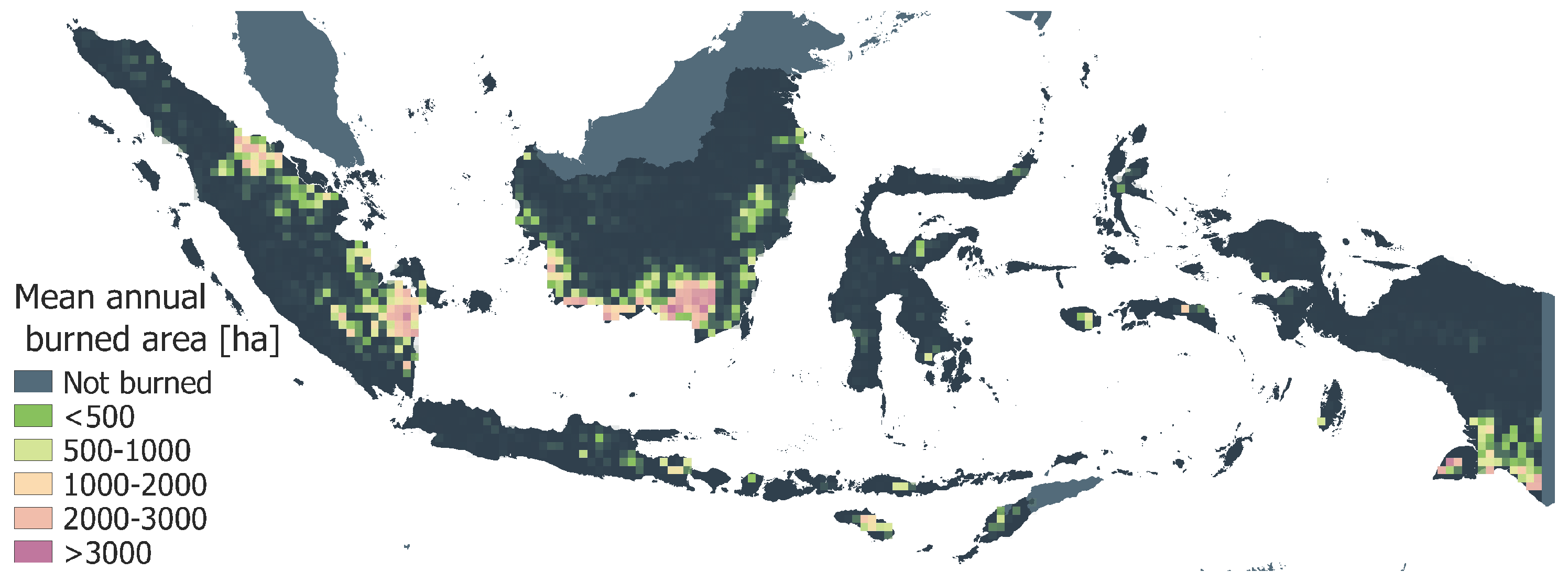
Validation results on a pixel scale show that in pixels where around 70% of area is burned, the correlation coefficients are above 0.6 and in those where around 30% of area is burned, above 0.9, both for peat and wildfire. We show figures for the spatial distribution of correlation coefficients and compare them with the maps of mean annual burned area. The comparison of maps shows that high correlation is often achieved in the pixels with a large burned area, mostly located in the peatland of Sumatra and Kalimantan. At the same time, lower correlation coefficients are often in the pixels with small burned area. Capturing pixels with small fires could be a potential direction for spatial improvement of FLAM modeling, where the GFED version with small fires can be used [
53].
We would like to emphasize that the simplified approach used for modeling peat fires produced good results. It is also interesting to mention that areas with large wildfires and peat fires often coincide. Our analysis of the spatial variability of the suppression efficiency for wildfires and peat fires can potentially allow one to find the areas where smoldering and flaming fires are tightly related [
58]. However, further analysis has to be carried out in this direction.
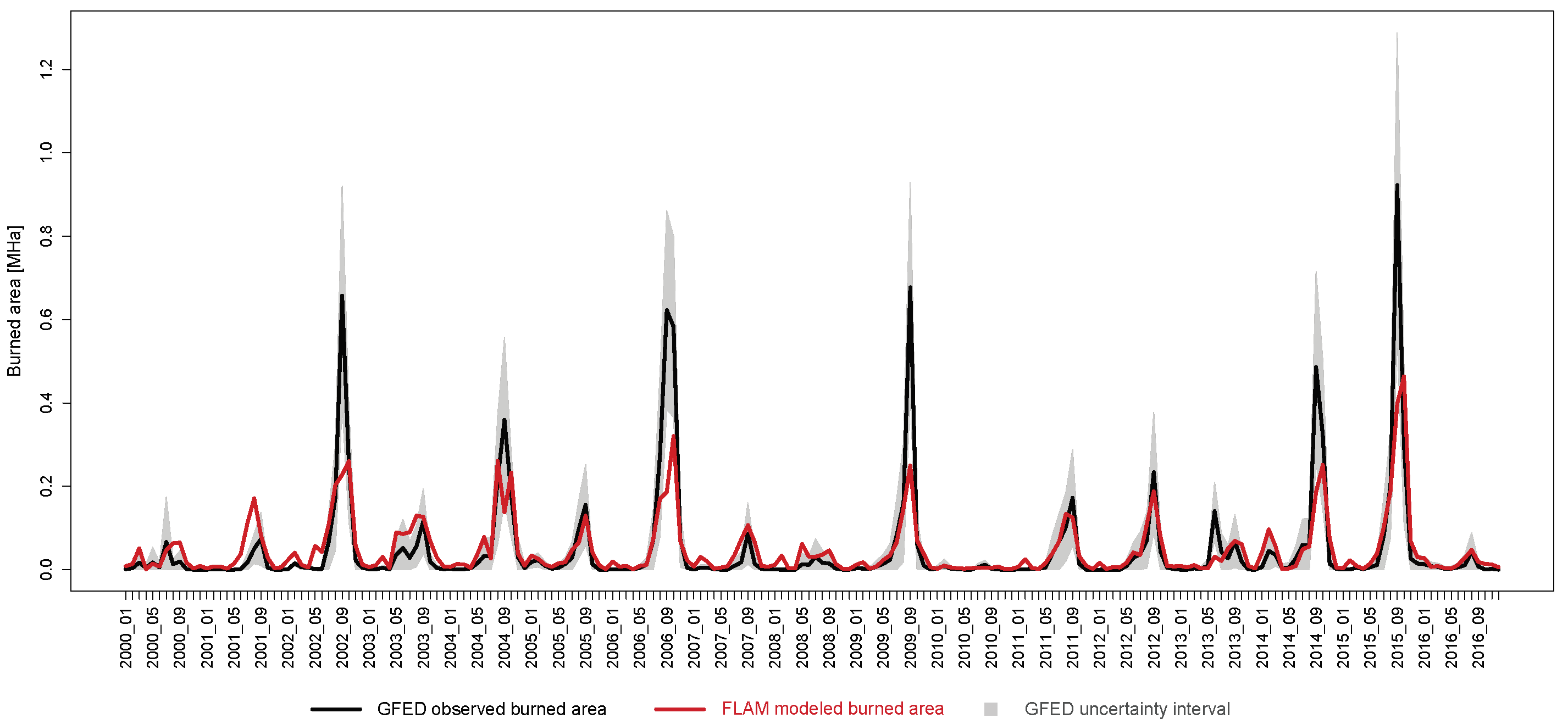
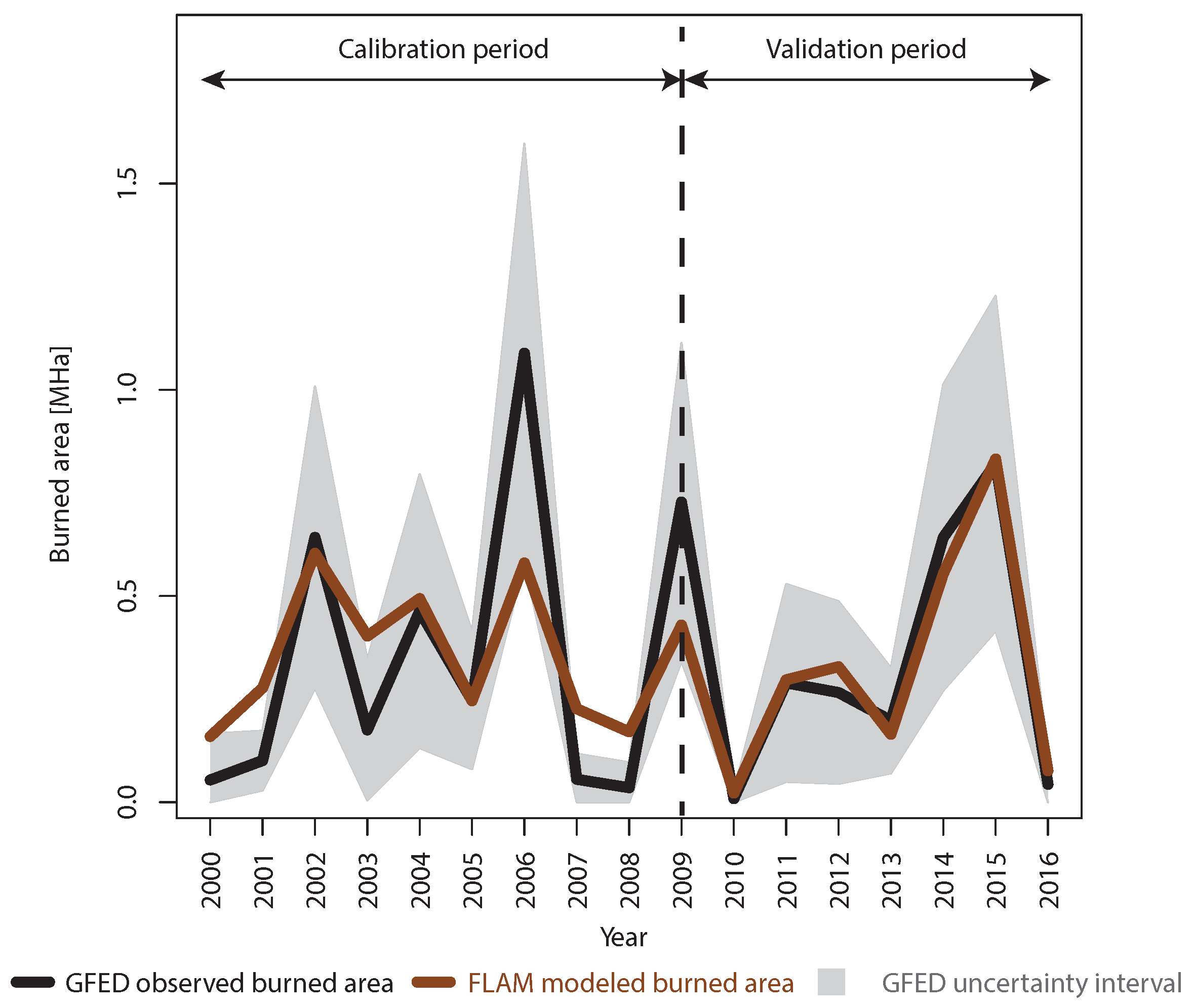
FLAM was able to correctly estimate extreme burned area in 2015, which caused a lot of damage in Indonesia [
9]. While the calibration procedure uses only accumulated burned area from GFED, the good inter-annual variability is due to adequate representation of daily weather dynamics in FLAM. An interesting observation is that FLAM was not able to capture 2006 in the calibration period. This could indicate an uncertainty in the GFED dataset, bias in climate data or an increase of ignition potential, e.g., due to human activity. Finally, we explored the fire dynamics at a finer temporal scale and showed a comparison of monthly dynamics between GFED and FLAM areas burned by wildfires in
Figure A4. Preliminary analysis based on the figure shows that FLAM is not always capturing the highest burned area in September. Potentially, seasonal calibration of the suppression efficiency could lead to the improvement of FLAM monthly estimates, and consequently better spatial and temporal results. A promising direction for future research would be the assessment of greenhouse gases emissions based on burned areas modeled by FLAM.
Current peat fires and wildfires can affect future fires in two main areas. On the non-anthropogenic side, current fires will highly affect soil moisture and the water content of biomass. This will increase the likelihood of fire occurrence within a relatively short period until adequate rainfall compensates the loss of soil moisture and water content. From the anthropogenic perspective, physical alteration of the environment such as canal drainage in peat areas or land clearance for crop production can have an effect. If no restoration activities are carried out, peat fire is likely to reoccur.
5. Conclusions
In this study, we applied FLAM to estimate burned area in Indonesia and validated these results independently of the model calibration for the first time. For burned areas aggregated over Indonesia, we obtained Pearson’s correlation coefficient separately for wildfires and peat fires, which turns out to be equal to 0.988 in both cases. Spatial correlation analysis showed that in pixels where around 70% of area is burned, the correlation coefficients are above 0.6, and in those, where 30% of area is burned, above 0.9. We showed that FLAM is capable of capturing not only flaming, but also smoldering peat fires, which are crucially important for Indonesia.
The suggested approach for the spatial calibration of the probability of extinguishing a fire improves the results of the original Arora and Boer fire algorithm. We showed that the calibrated parameter has a bimodal distribution over Indonesia; in areas where the probability is found to be close to one, the fire occurrence could be diminished due to human activity; at the same time, in areas where this parameter is found to be close to zero, human activity, on the contrary, leads to extensive fire, for example due to slash and burn agriculture or peatland drainage. Very low suppression levels are found in the peatland of Kalimantan and Sumatra, where fire can burn for very long periods of time despite extensive rains, weather changes and fire-fighting attempts.
The results presented in this paper are a prerequisite for estimating future burned area under projected climate change and for modeling adaptation options. Modeling burned area in Indonesia and an assessment of corresponding impacts, e.g., CO
emissions, can be potentially used for climate/economic damage assessments. This could also help to adequately represent the risks of wildland fires in REDD+ programs [
60,
61]. Modeling fire ignition and suppression can also help the implementation of fire prevention policies and provide important information for building adequate and cost-efficient fire response infrastructure.