Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level
Abstract
1. Introduction
2. Materials and Methods
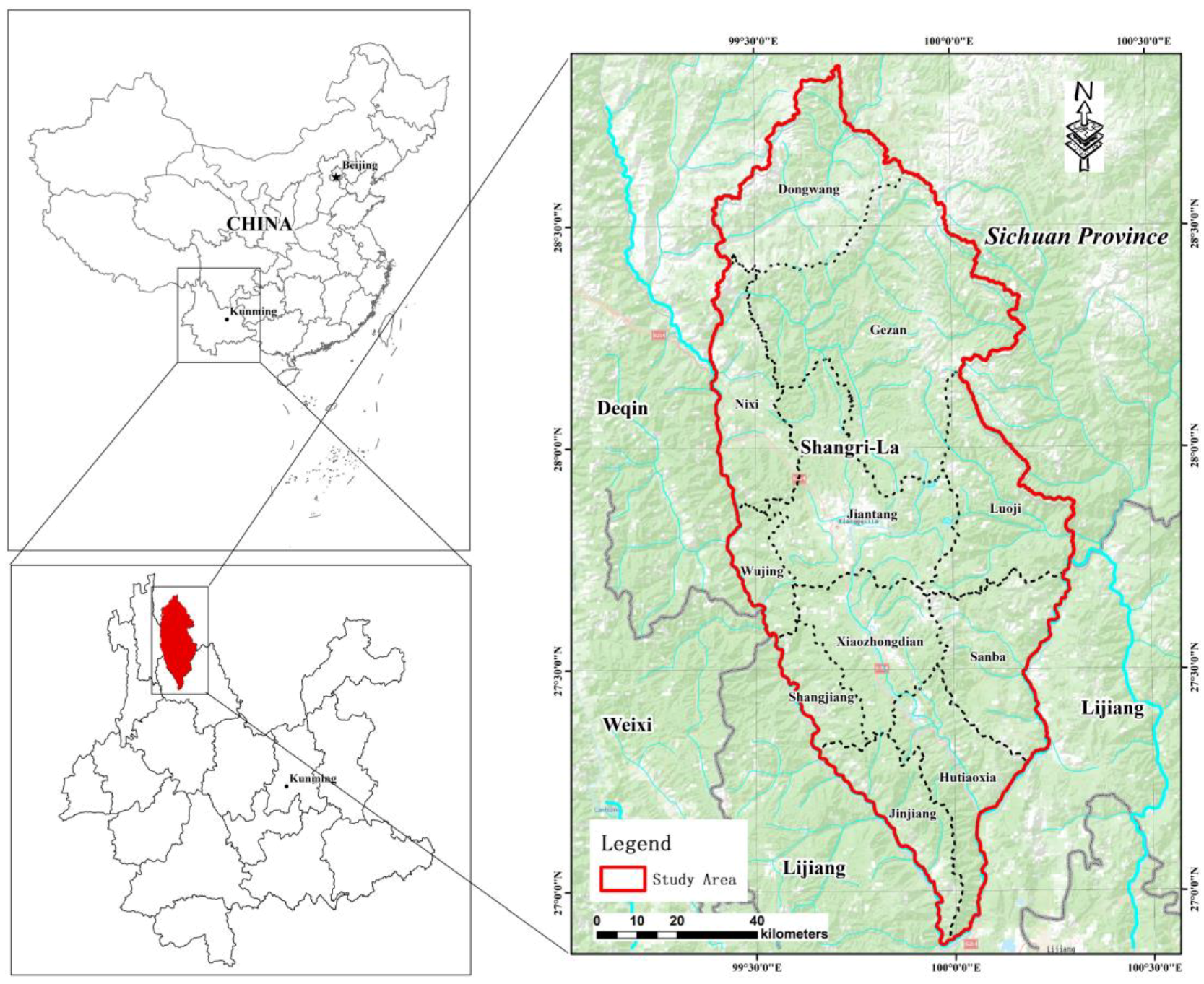
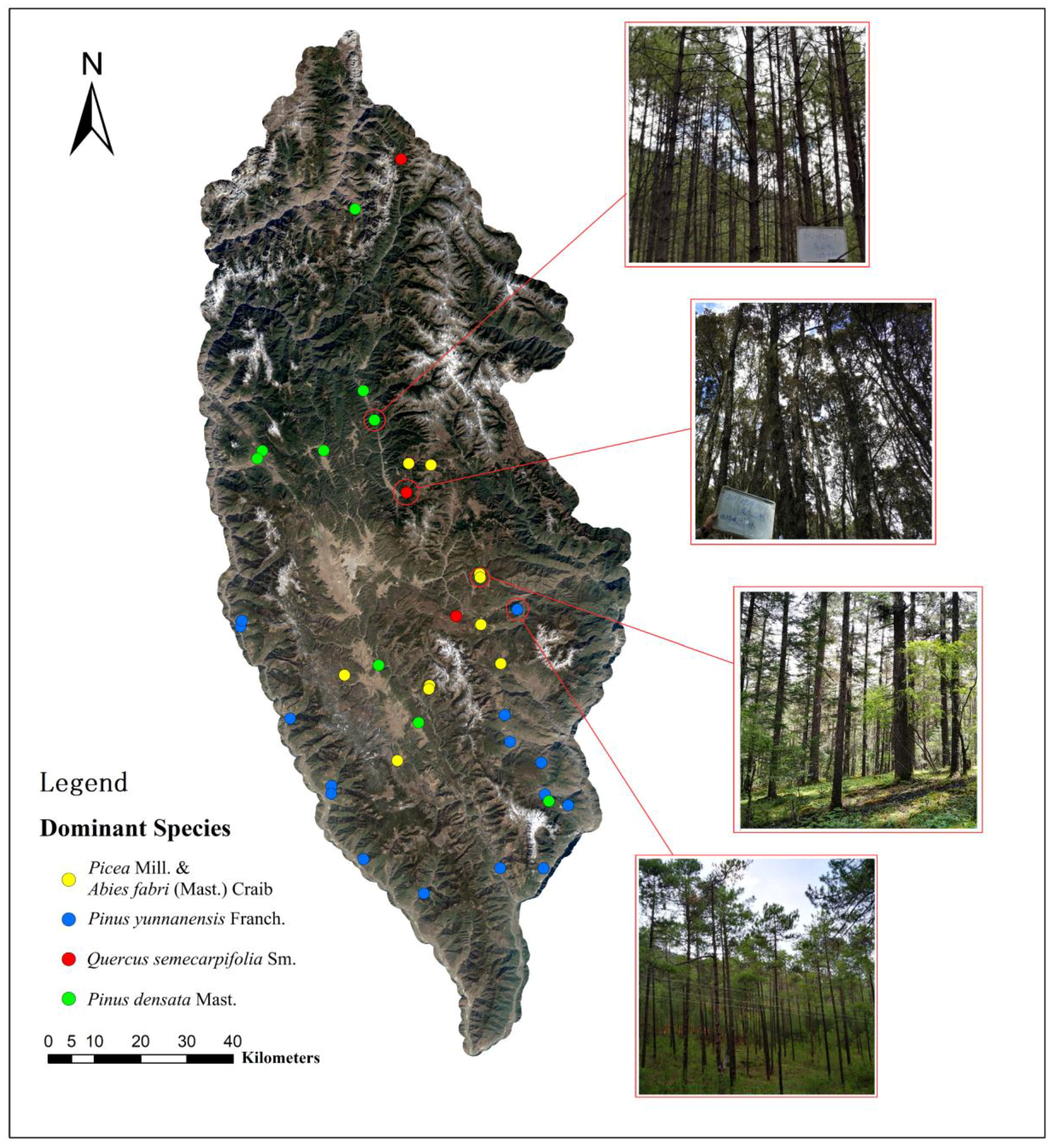
2.1. Study Area and Sample Plots
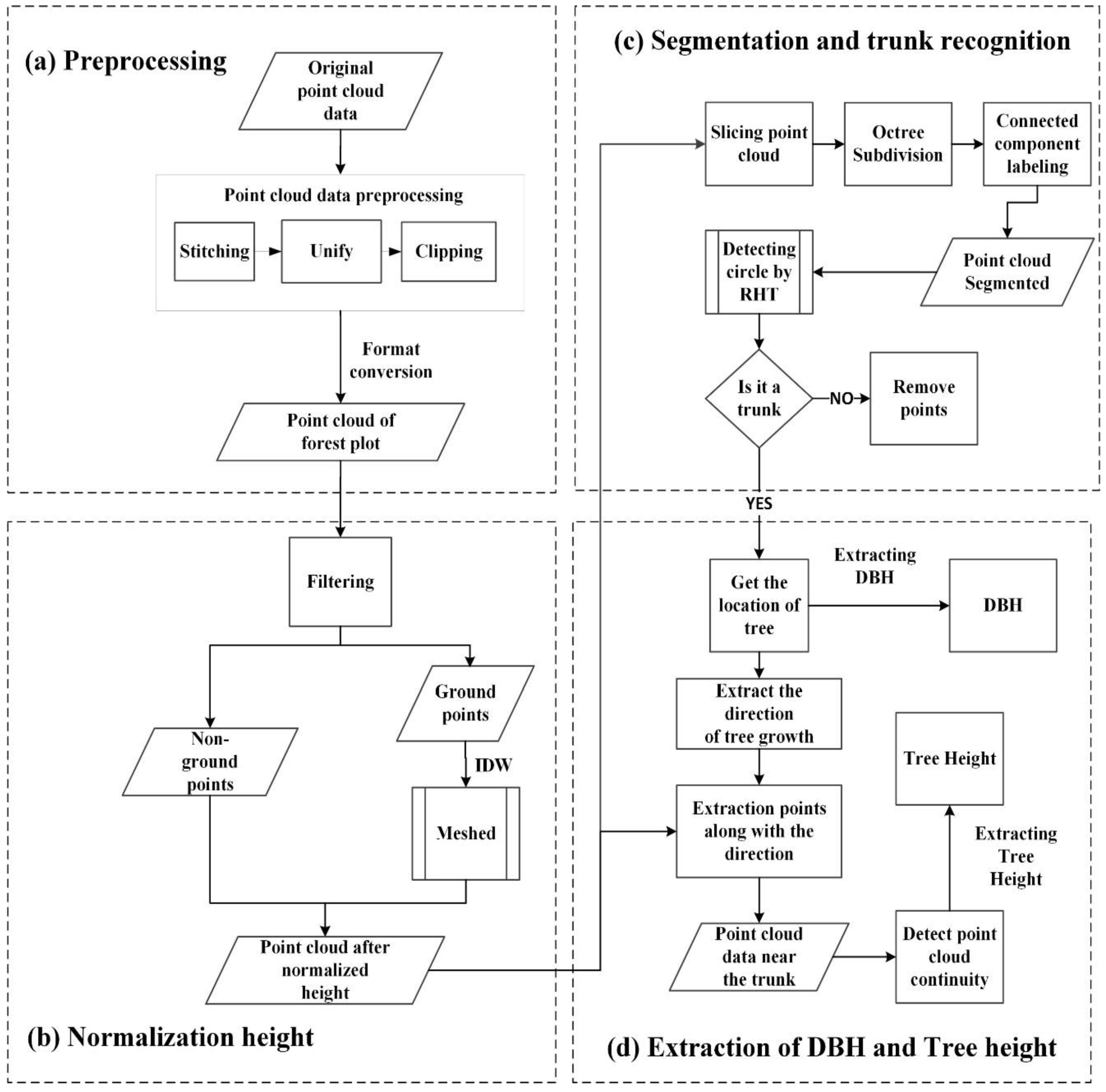
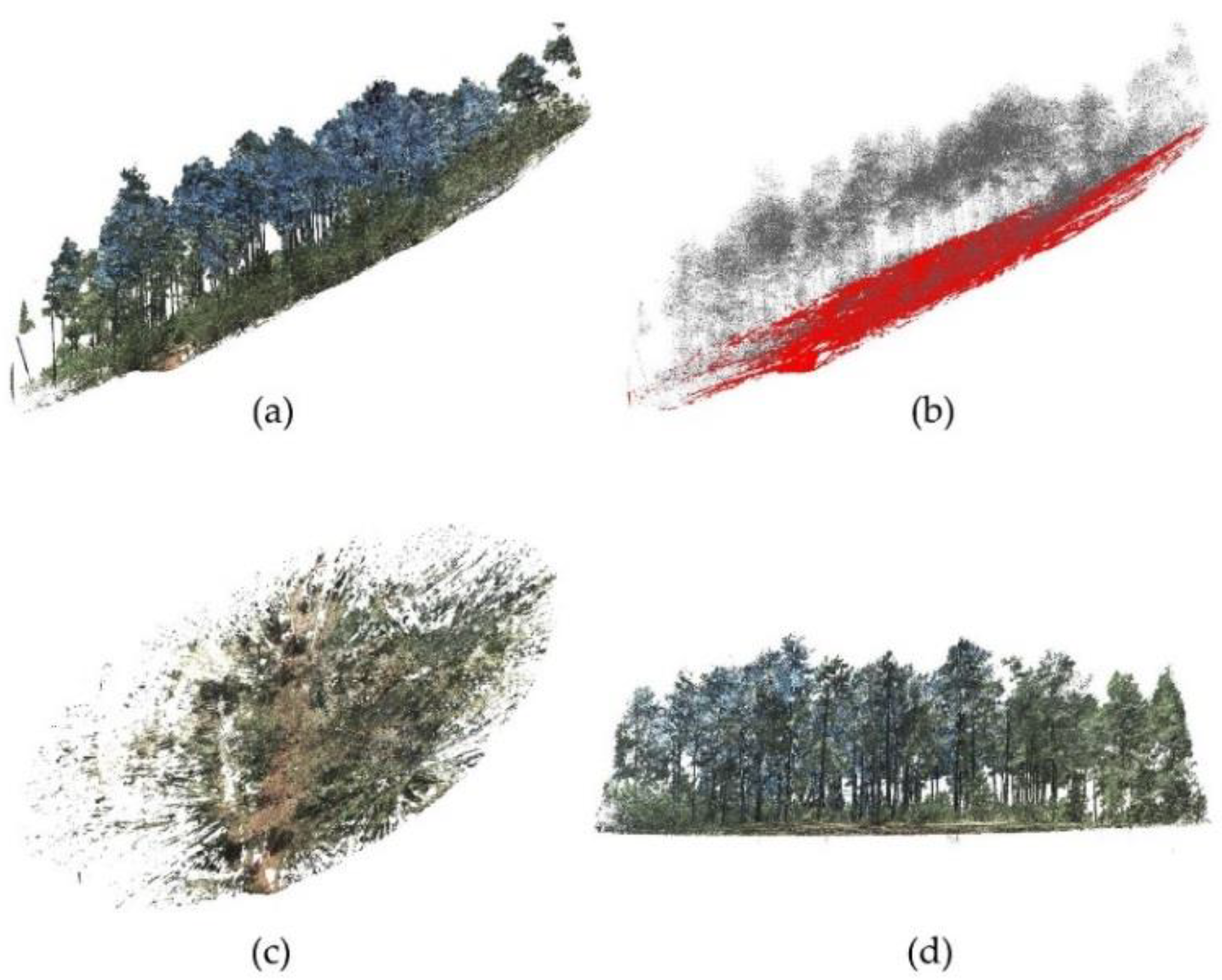
2.2. Data Acquisition and Processing
2.2.1. Normalization of Point Cloud Height
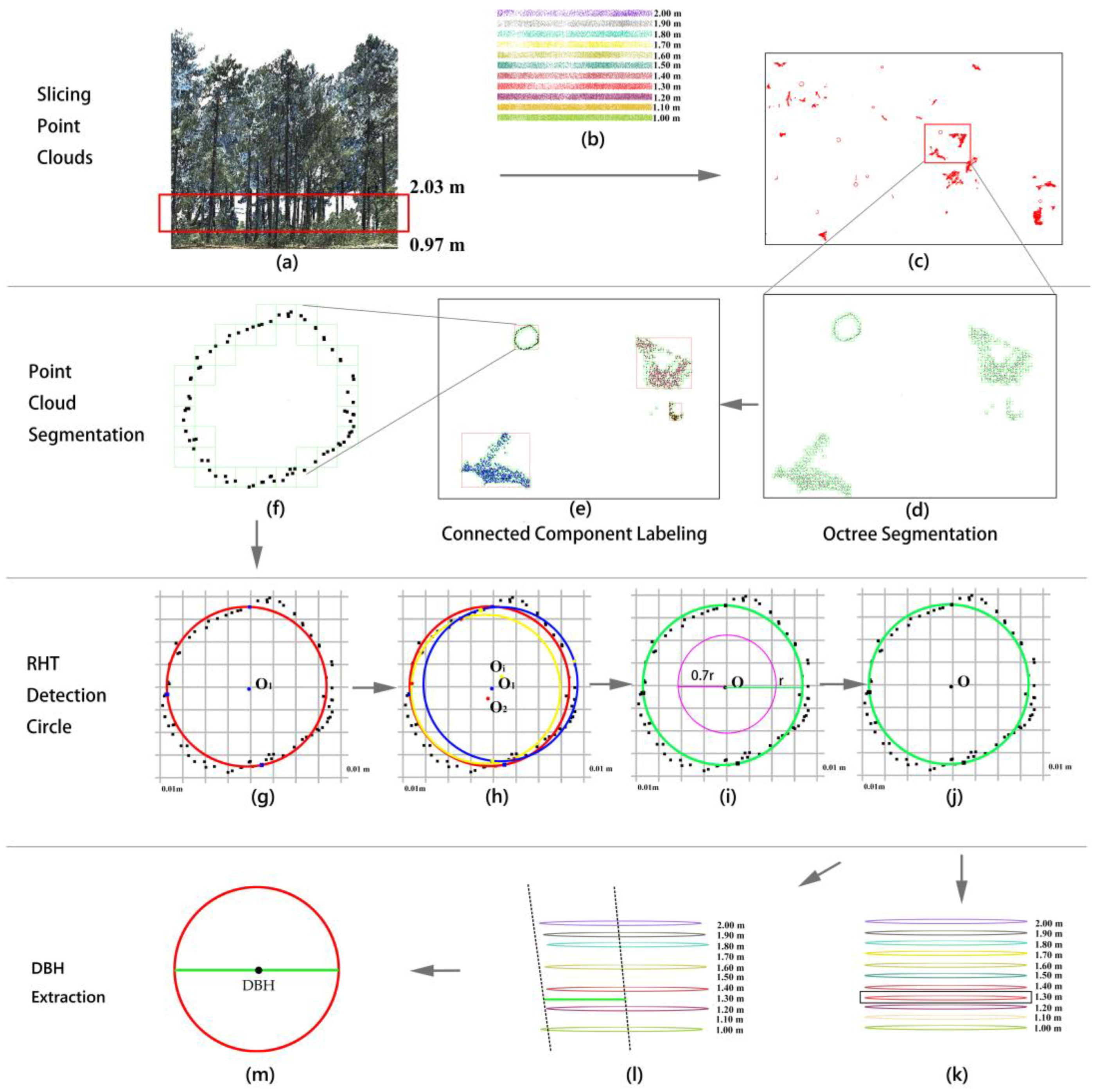
2.2.2. Slicing Point Clouds
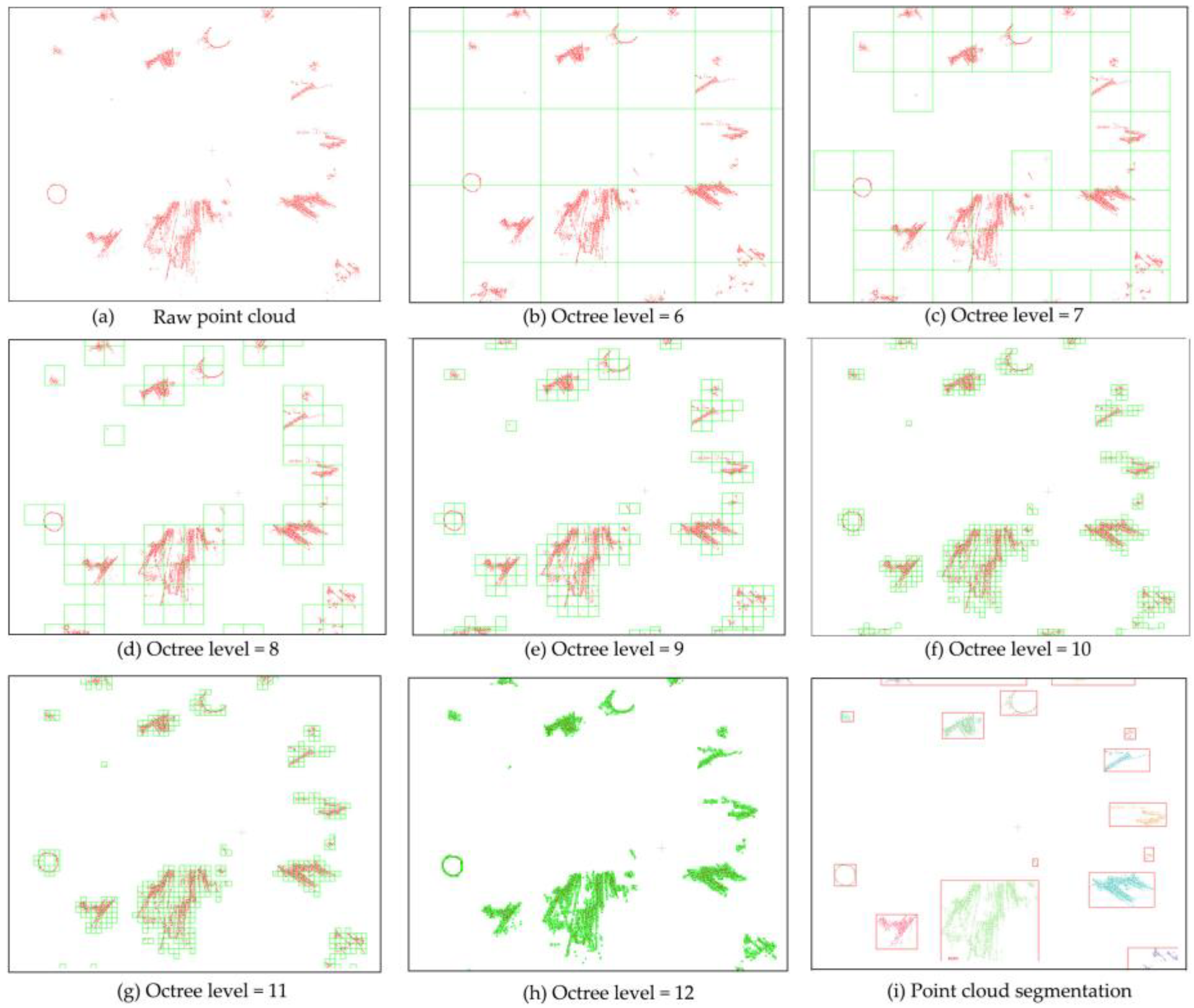
2.2.3. Octree Segmentation and Connected Component Labeling
2.2.4. Random Hough Transform and DBH Extraction
- (1)
- First, the point set P is projected onto the X–Y plane in the direction of Z-axis to form a 2-D point cloud set P′ (Figure 6f). Defining the Hough space M (m, n, r) is carried out, where m is the number of grids with 0.01 m intervals for point cloud set P’ in the direction of X-axis, n is the number of grids with 0.01 m intervals for P′ in the direction of Y-axis, and r is the radius stored in millimeters (Figure 6g, the gray grid under points). Three points p1(x1, y1), p2(x2, y2), p3(x3, y3) that are non-collinear and where the distance between any two points is greater than 0.02 m are selected from the point cloud set P’ randomly. The condition of three non-collinear points p1(x1, y1), p2(x2, y2), p3(x3, y3) can be expressed as:The distance conditions between the points are:Then, these 3 points can form a circle C1, with the center point O1 (a1, b1) (Figure 6g) and the radius r1 of the circle can be obtained. According to our field survey results, if r1 > 0.7 or r1 < 0.03 (trees with DBH larger than 1.40 m or less than 0.06 m are not extracted), a new set of three points should be selected for calculating the radius ri until ri satisfies 0.03 ri 0.7. The corresponding Hough parameter space is voted in as M(ai,bi,ri) = M(ai,bi,ri) + 1.
- (2)
- This method is repeatedly performed on the remaining point clouds until the elements in P′ are depleted, so that the final M is obtained. If the difference between the radii of two concentric circles in M is less than 0.01 m, the circles are considered to be the same circle, the average radius of all concentric circles is used as the final radius, and the final voting result is the sum of all circles that meet the conditions. Formula (3) expresses the voting result in M:where, ε is the threshold value of a circle detected for sliced point cloud of trees. Many tests in the study show that the accuracy of DBH extraction is high when ε = 0.80. The next condition needing to be tested is the relative position between any point (xi,yi) in point cloud P’ and the circle Ci (ai,bi,ri) satisfying the voting result in M:Equation (4) indicates that there are points inside the identified trunk, which are inconsistent with the actual results and should be excluded from the circle that satisfies the voting result.
- (3)
- Using this method, all layers of point clouds are extracted, and the trunk position and the trunk section radius of each layer of trees are obtained. If the position of tree trunk is detected in four or more layers, it is assumed that there is a tree at this position, and the single-wood position is the center of the trunk closest to the ground. If a trunk can be accurately identified at a height of 1.30 m, DBH of the tree is diameter of the circle identified (Figure 6k). If the trunk cannot be identified, the linear regression method is used to fit the trunk radius and trunk height to obtain DBH (Figure 6i).
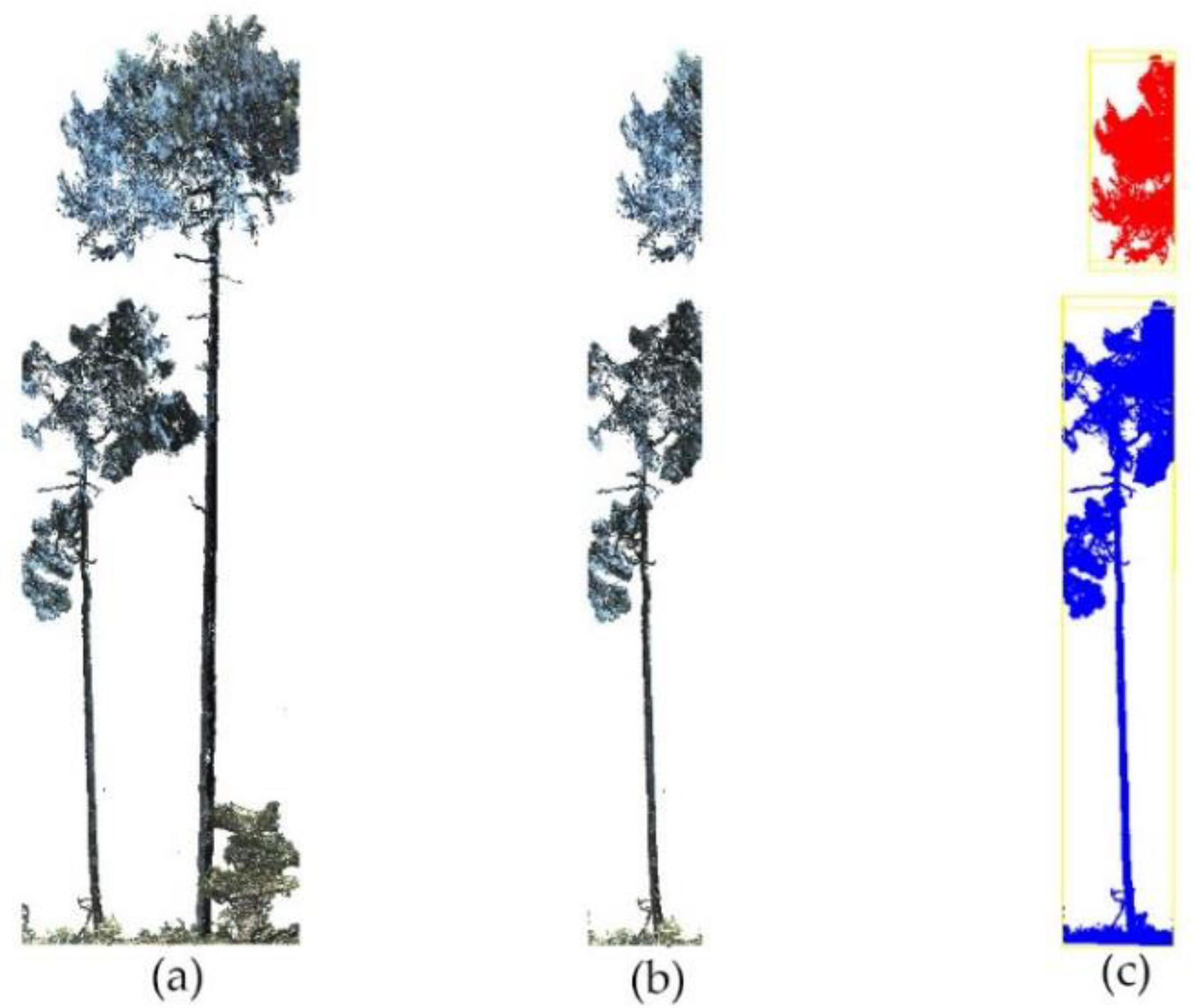
2.2.5. Tree Height Extraction
3. Results and Discussion
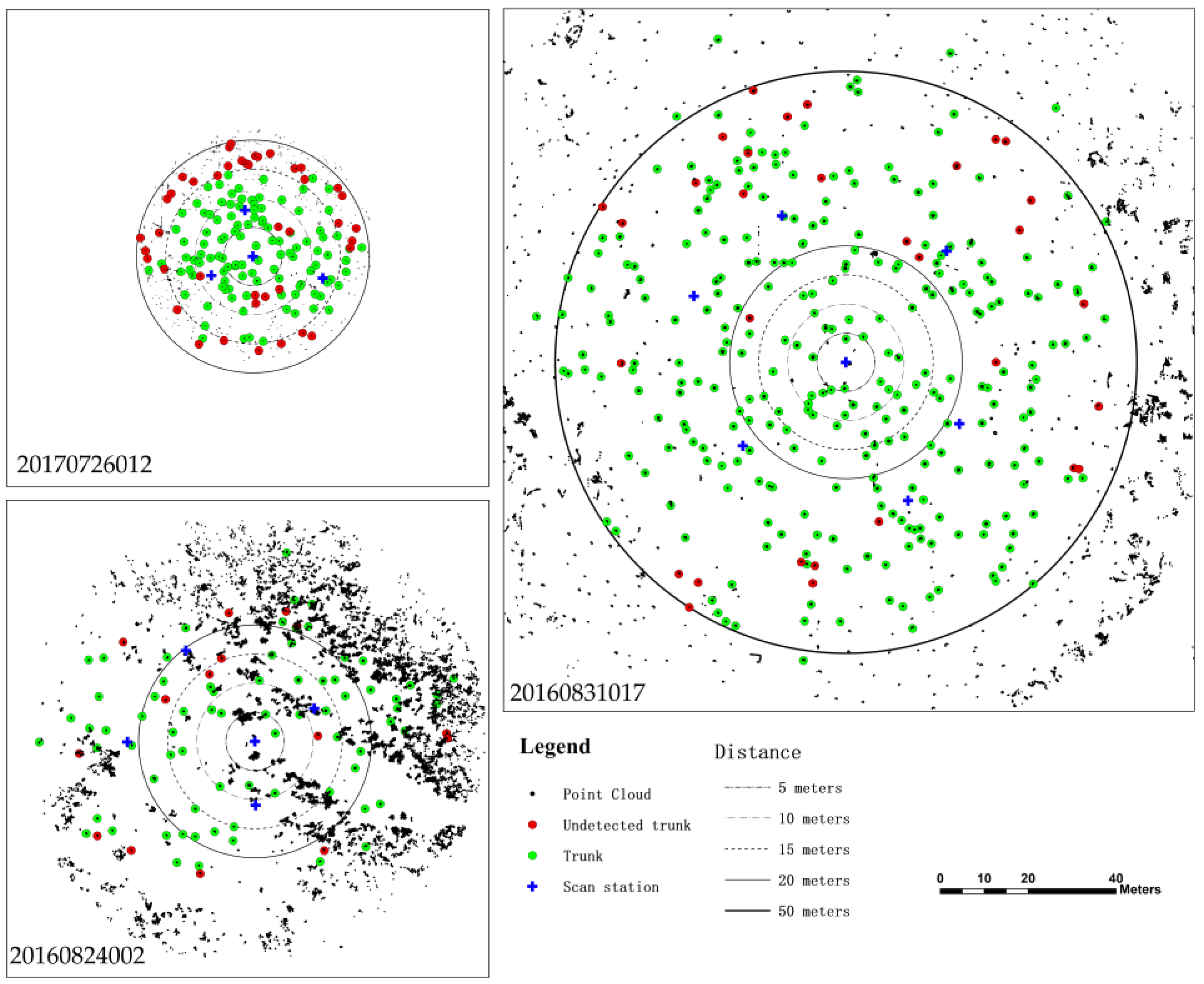
3.1. Analysis of the Influence of Forest Density on Scanning Range and Accuracy
- (1)
- The scanning range of high-density young forest sample plots is seriously affected by the mutual obstruction between trees. Trees can be identified more accurately (99/106) within a range of 15 m centered on the central station, but there are a small number of missing trees (7 trees) due to mutual shelter between trees within the forest sample plot (5 m–10 m). The identification accuracy of trees near the edge of the young sample plot (distance from the center of the sample plot > 15 m) is low, and there are a large number of missed trees (35). The DBH and extraction accuracy of tree height of the entire sample plot is relatively high (mean RMSE of DBH is 1.03 cm, and mean RMSE of the tree height is 0.51 m). The maximum error is also located near the edge of the sample plot.
- (2)
- The scanning range of the medium–density plot is mainly affected by the topography and low bushes under the forest canopy. In areas with low tree density and relatively flat terrain, a larger range of scanning areas can be obtained and the accuracy of tree identification and height/DBH extraction are higher as well. For the sample plot of NO. 20160831017, within the range of 20 m from the center of the sample plot, 64 out of 66 trees are identified, with an RMSE of 1.28 cm for DBH, and an RMSE of 0.57 m for tree height. When the distance from the tree to the center of the sample plot exceeds 20 m, the tree recognition accuracy decreases slightly. The tree height and DBH extraction accuracy also slightly decreases with the increase of the distance from the tree to the center of the sample plot.
- (3)
- Low–density mature forests have a relatively complete vertical structure of individual trees. The growth space under the forest canopy is sufficient for the growth of low shrubs. It can be seen from the point clouds (Plot 20160824002) that a large number of shrub points are included in the point cloud near the ground. Meanwhile, the effective range of sample plots obtained by multi–station scanning is limited due to terrain influences. It can be seen from Table 4 that extraction results obtained within the range of 20 m is better than those beyond the range: The tree detection rate is high (36/40), with an RMSE of 1.24 cm for DBH, and an RMSE of 0.46 m for tree height. When the distance from the tree to the TLS scanner is more than 20 m, the accuracy of tree detection is slightly reduced (40/51) due to the longer distance and the influence of shrubs around the station.
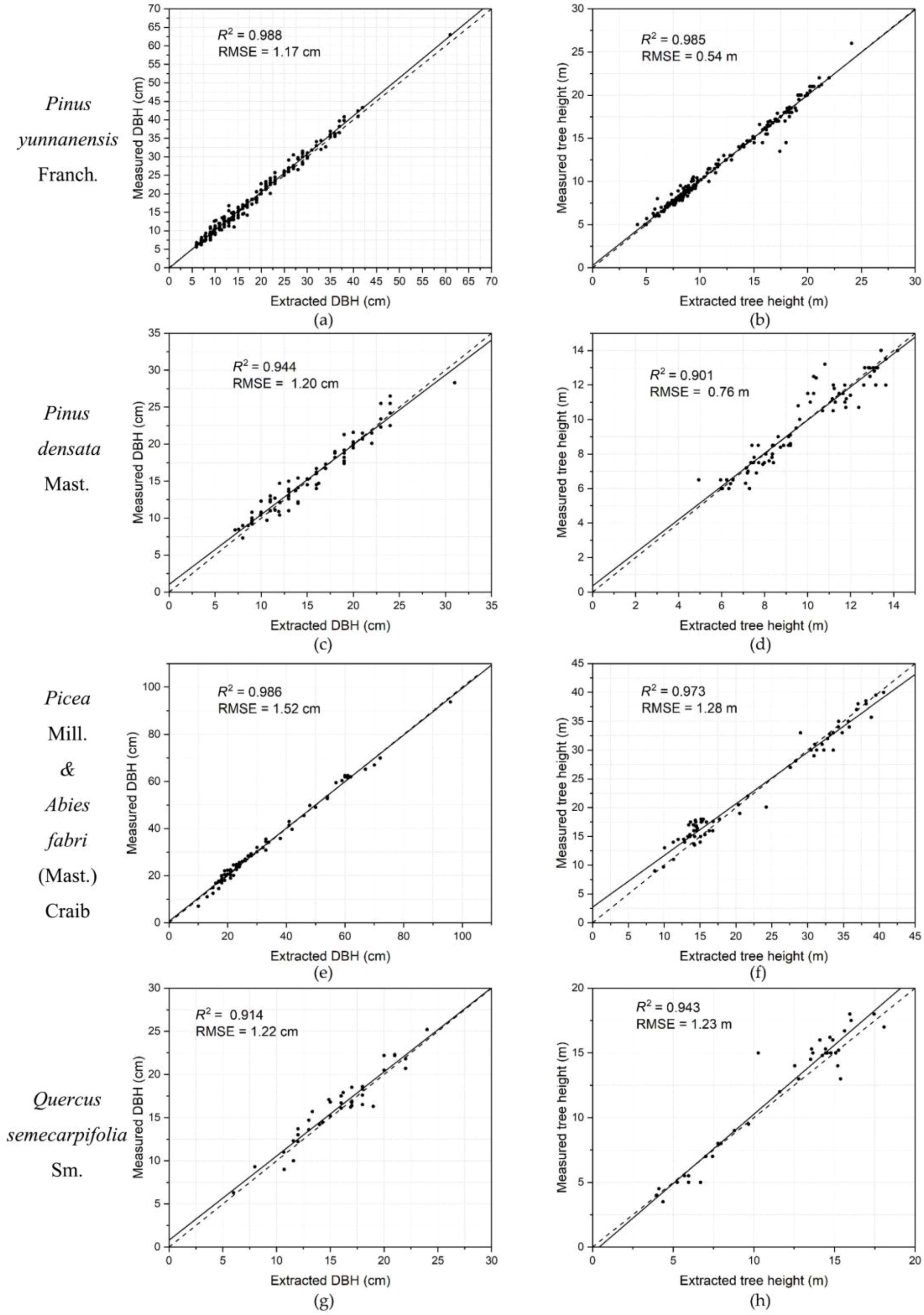
3.2. Analysis of the Influence of Forest Types on the Accuracy of Results
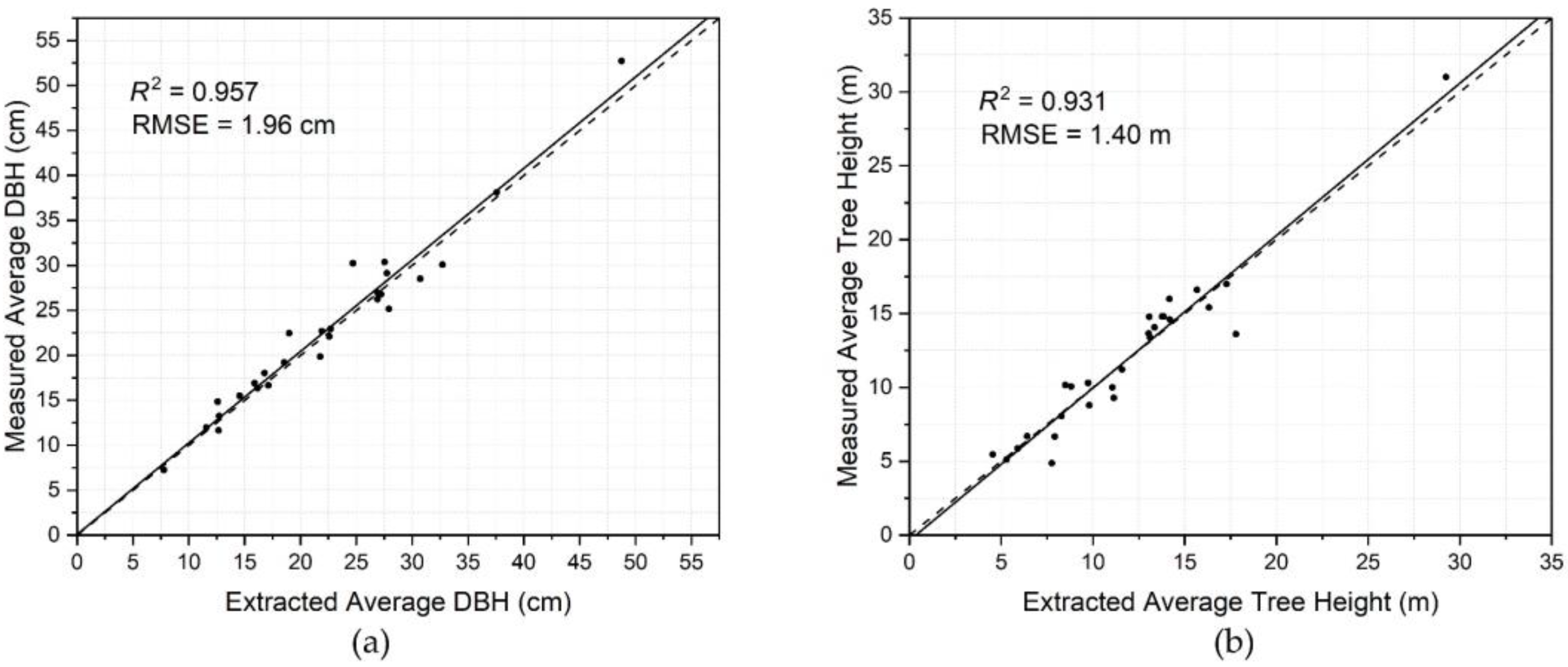
3.3. Accuracy Analysis of Results in Forest Sample Plots
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, D.; Li, B.; Yang, A. Estimation of tree height and biomass based on long time series data of landsat. Eng. Surv. Mapp. 2017, 1–5. [Google Scholar] [CrossRef]
- Lu, D. Aboveground biomass estimation using landsat TM data in the Brazilian amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Liu, X.; Dan, Z.; Xing, Y. Study on Crown Diameter Extraction and Tree Height Inversion Based on High-resolution Images of UAV. Cent. South For. Invent. Plan. 2017, 36, 39–43. [Google Scholar] [CrossRef]
- Dong, L. New Development of Forest Canopy Height Remote Sensing. Remote Sens. Technol. Appl. 2016, 31, 833–845. [Google Scholar] [CrossRef]
- Ozdemir, I.; Karnieli, A. Predicting forest structural parameters using the image texture derived from worldview-2 multispectral imagery in a dryland forest, Israel. Int. J. Appl. Earth Obs. Geoinform. 2011, 13, 701–710. [Google Scholar] [CrossRef]
- Gibbs, H.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making redd a reality. Environ. Res. Lett. 2007, 2, 045023. [Google Scholar] [CrossRef]
- Chopping, M.; Nolin, A.; Moisen, G.G.; Martonchik, J.V.; Bull, M. Forest canopy height from the multiangle imaging spectroradiometer (MISR) assessed with high resolution discrete return lidar. Remote Sens. Environ. 2009, 113, 2172–2185. [Google Scholar] [CrossRef]
- Rauste, Y. Multi-temporal jers sar data in boreal forest biomass mapping. Remote Sens. Environ. 2005, 97, 263–275. [Google Scholar] [CrossRef]
- Wang, Y. Estimation of Forest Volume Based on Multi-Source Remote Sensing Data; Beijing Forestry University: Beijing, China, 2015. [Google Scholar]
- Watanabe, M.; Motohka, T.; Thapa, R.B.; Shimada, M. Correlation between L-band SAR Polarimetric Parameters and LiDAR Metrics over a Forested Area. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1574–1577. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Gobakken, T.; Næsset, E.; Weydahl, D.J. Estimating spruce and pine biomass with interferometric X-band SAR. Remote Sens. Environ. 2010, 114, 2353–2360. [Google Scholar] [CrossRef]
- Magnard, C.; Morsdorf, F.; Small, D.; Stilla, U.; Schaepman, M.E.; Meier, E. Single tree identification using airborne multibaseline sar interferometry data. Remote Sens. Environ. 2016, 186, 567–580. [Google Scholar] [CrossRef]
- Wu, Y.; Hong, W.; Wang, Y. The Current Status and Implications of Polarimetric SAR Interferometry. J. Electron. Inf. Technol. 2007, 29, 1258–1262. [Google Scholar]
- Khati, U.; Kumar, S.; Agrawal, S.; Singh, J. Forest height estimation using space-borne polinsar dataset over tropical forests of India. ESA POLinSAR 2015, 4. [Google Scholar] [CrossRef]
- Luo, H.; Chen, E.; Li, Z.; Cao, C. Forest above ground biomass estimation methodology based on polarization coherence tomography. J. Remote Sens. 2011, 15, 1138–1155. [Google Scholar] [CrossRef]
- Schaedel, M.S.; Larson, A.J.; Affleck, D.L.; Belote, R.T.; Goodburn, J.M.; Wright, D.K.; Sutherland, E.K. Long-term precommercial thinning effects on larix occidentalis (western larch) tree and stand characteristics. Can. J. For. Res. 2017, 47, 861–874. [Google Scholar] [CrossRef]
- Huang, K.; Pang, Y.; Shu, Q.; Fu, T. Aboveground forest biomass estimation using ICESat GLAS in Yunnan, China. J. Remote Sens. 2013, 17, 169–183. [Google Scholar] [CrossRef]
- Man, Q.; Dong, P.; Guo, H.; Liu, G.; Shi, R. Light detection and ranging and hyperspectral data for estimation of forest biomass: A review. J. Appl. Remote Sens. 2014, 8, 081598. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, L. ICESat-GLAS Full Waveform-based Study on Forest Canopy Height Retrieval in Sloped Area—A Case Study of Forests in Changbai Mountains, Jilin. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 696–700. [Google Scholar]
- Nie, S.; Wang, C.; Zeng, H.; Xi, X.; Xia, S. A revised terrain correction method for forest canopy height estimation using icesat/glas data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 183–190. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Q.; Pang, Y. Review on forest parameters inversion using LiDAR. J. Remote Sens. 2016, 20, 1138–1150. [Google Scholar] [CrossRef]
- Liu, L.; Pang, Y.; Li, Z. Individual Tree DBH and Height Estimation Using Terrestrial Laser Scanning (TLS) in A Subtropical Forest. Sci. Silvae Sin. 2016, 52, 26–37. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Nuttens, T.; De Wulf, A.; Bral, L.; De Wit, B.; Carlier, L.; De Ryck, M.; Stal, C.; Constales, D.; De Backer, H. High Resolution Terrestrial Laser Scanning for Tunnel Deformation Measurements. In Proceedings of the 2010 FIG Congress, Sydney, Australia, 11–16 April 2010. [Google Scholar]
- Fröhlich, C.; Mettenleiter, M. Terrestrial laser scanning—New perspectives in 3d surveying. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Telling, J.; Lyda, A.; Hartzell, P.; Glennie, C. Review of earth science research using terrestrial laser scanning. Earth Sci. Rev. 2017, 169, 35–68. [Google Scholar] [CrossRef]
- Buckley, S.J.; Howell, J.; Enge, H.; Kurz, T. Terrestrial laser scanning in geology: Data acquisition, processing and accuracy considerations. J. Geol. Soc. 2008, 165, 625–638. [Google Scholar] [CrossRef]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Prokop, A.; Panholzer, H. Assessing the capability of terrestrial laser scanning for monitoring slow moving landslides. Nat. Hazards Earth Syst. Sci. 2009, 9, 1921–1928. [Google Scholar] [CrossRef]
- Olsen, M.J.; Cheung, K.F.; Yamazaki, Y.; Butcher, S.; Garlock, M.; Yim, S.; McGarity, S.; Robertson, I.; Burgos, L.; Young, Y.L. Damage assessment of the 2010 chile earthquake and tsunami using terrestrial laser scanning. Earthq. Spectra 2012, 28, S179–S197. [Google Scholar] [CrossRef]
- Rosser, N.; Petley, D.; Lim, M.; Dunning, S.; Allison, R. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol. 2005, 38, 363–375. [Google Scholar] [CrossRef]
- Vos, S.; Lindenbergh, R.; de Vries, S.; Aagaard, T.; Deigaard, R.; Fuhrman, D. Coastscan: Continuous monitoring of coastal change using terrestrial laser scanning. In Proceedings of the Coastal Dynamics 2017, Helsingør, Denmark, 12–16 June 2017; Volume 233, pp. 1518–1528. [Google Scholar]
- Kuhn, D.; Prüfer, S. Coastal cliff monitoring and analysis of mass wasting processes with the application of terrestrial laser scanning: A case study of Rügen, Germany. Geomorphology 2014, 213, 153–165. [Google Scholar] [CrossRef]
- Anderson, K.E.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K.; Derryberry, D.R. Methodological considerations of terrestrial laser scanning for vegetation monitoring in the sagebrush steppe. Environ. Monit. Assess. 2017, 189, 578. [Google Scholar] [CrossRef] [PubMed]
- Pirotti, F.; Guarnieri, A.; Vettore, A. Ground filtering and vegetation mapping using multi-return terrestrial laser scanning. ISPRS J. Photogram. Remote Sens. 2013, 76, 56–63. [Google Scholar] [CrossRef]
- Vaaja, M.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Hyyppä, H.; Alho, P. Mapping topography changes and elevation accuracies using a mobile laser scanner. Remote Sens. 2011, 3, 587–600. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.-W. Terrestrial laser scanning as an effective tool to retrieve tree level height, crown width, and stem diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef]
- Moskal, L.M.; Zheng, G. Retrieving forest inventory variables with terrestrial laser scanning (TLS) in urban heterogeneous forest. Remote Sens. 2011, 4, 1–20. [Google Scholar] [CrossRef]
- Thies, M.; Spiecker, H. Evaluation and future prospects of terrestrial laser scanning for standardized forest inventories. Forest 2004, 2, 1. [Google Scholar]
- Li, D.; Pang, Y.; Yue, C.; Zhao, D.; Xue, G. Extraction of individual tree DBH and height based on terrestrial laser scanner data. J. Beijing For. Univ. 2012, 34, 79–86. [Google Scholar] [CrossRef]
- Bienert, A.; Scheller, S.; Keane, E.; Mullooly, G.; Mohan, F. Application of terrestrial laser scanners for the determination of forest inventory parameters. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Dresden, Germany, 25–27 September 2006; Volume 36. [Google Scholar]
- Brolly, G.; Király, G. Algorithms for stem mapping by means of terrestrial laser scanning. Acta Silvatica et Lignaria Hungarica 2009, 5, 119–130. [Google Scholar]
- Shang, R.; Xi, X.; Wang, C.; Wang, X.; Luo, S. Retrieval of individual tree parameters using terrestrial laser scanning data. Sci. Surv. Mapp. 2015, 40, 78–81. [Google Scholar] [CrossRef]
- Janowski, A. The circle object detection with the use of msplit estimation. E3S Web Conf. 2018, 26, 00014. [Google Scholar] [CrossRef]
- Janowski, A.; Bobkowska, K.; Szulwic, J. 3D modelling of cylindrical-shaped objects from lidar data-an assessment based on theoretical modelling and experimental data. Metrol. Meas. Syst. 2018, 25. [Google Scholar] [CrossRef]
- Bobkowska, K.; Szulwic, J.; Tysiąc, P. Bus bays inventory using a terrestrial laser scanning system. MATEC Web Conf. 2017, 122, 04001. [Google Scholar] [CrossRef]
- Cao, T.; Xiao, A.; Wu, L.; Mao, L. Automatic fracture detection based on terrestrial laser scanning data: A new method and case study. Comput. Geosci. 2017, 106, 209–216. [Google Scholar] [CrossRef]
- Wezyk, P.; Koziol, K.; Glista, M.; Pierzchalski, M. Terrestrial laser scanning versus traditional forest inventory first results from the polish forests. Tanpakushitsu Kakusan Koso Protein Nucleic Acid Enzyme 2007, 44, 325–337. [Google Scholar]
- Čerňava, J.; Tuček, J.; Koreň, M.; Mokroš, M. Estimation of diameter at breast height from mobile laser scanning data collected under a heavy forest canopy. J. For. Sci. 2017, 63, 433–441. [Google Scholar]
- Wezyk, P.; Koziol, K.; Glista, M.; Pierzchalski, M. Terrestrial Laser Scanning Versus Traditional Forest Inventory: First Results from the Polish Forests. In Proceedings of the ISPRS Workshop on Laser Scanning, Espoo, Finland, 12–14 September 2007; pp. 12–14. [Google Scholar]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the ransac algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne lidar data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Serra, J.; Vincent, L. An overview of morphological filtering. Circ. Syst. Signal Process. 1992, 11, 47–108. [Google Scholar] [CrossRef]
- Dillencourt, M.B.; Samet, H.; Tamminen, M. A general approach to connected-component labeling for arbitrary image representations. J. ACM 1992, 39, 253–280. [Google Scholar] [CrossRef]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogram. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Király, G.; Brolly, G. Tree height estimation methods for terrestrial laser scanning in a forest reserve. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2007, 36, 211–215. [Google Scholar]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogram. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]

| Indicators | Descriptions |
|---|---|
| Range Accuracy | 1.2 mm + 10 ppm |
| 3D position Accuracy | 3 mm @ 50 m 6 mm @ 100 m |
| Wavelength | 1550nm (invisible); 658 nm (visible) |
| Scan Rate | Up to 1,000,000 points per second |
| Field-of-View | 360° (Horizontal); 290° (Vertical) |
| Range and Reflectivity | Minimum range: 0.4 m Maximum range at reflectivity: 120 m (8%), 180 m (18%), 270 m (34%) |
| Range Noise | 0.4 mm RMS at 10 m 0.5 mm RMS at 50 m |
| Dominant Forest Species | Age of Stand | Number of Sample Plots | Number of Stations | Average Altitude (Unit: m) | Average Slope (Unit: Degree) |
|---|---|---|---|---|---|
| Quercus semecarpifolia Sm. | Young | 1 | 5 | 3892 | 11.0 |
| Middle | 2 | 10 | 3673 | 15.0 | |
| Mature | 1 | 4 | 3723 | 30.0 | |
| Pinus densata Mast. | Young | 3 | 17 | 3225 | 16.0 |
| Middle | 4 | 20 | 3210 | 16.4 | |
| Mature | 2 | 9 | 3128 | 23.5 | |
| Pinus yunnanensis Franch. | Young | 3 | 14 | 2538 | 19.3 |
| Middle | 5 | 25 | 2692 | 15.3 | |
| Mature | 8 | 43 | 2316 | 13.9 | |
| Picea Mill. & Abies fabri (Mast.) Craib | Young | 2 | 10 | 3453 | 23.3 |
| Middle | 4 | 20 | 3604 | 13.0 | |
| Mature | 4 | 19 | 3680 | 15.6 |
| Thickness (cm) | RMSE 1 | Number of Trees Detected Correctly | Number of Trees Undetected | Error Detection 2 |
|---|---|---|---|---|
| 1.00 | 2.92 | 53 | 27 | 22 |
| 2.00 | 3.04 | 63 | 17 | 20 |
| 3.00 | 2.58 | 75 | 5 | 29 |
| 4.00 | 2.99 | 74 | 6 | 14 |
| 5.00 | 2.57 | 74 | 6 | 8 |
| 6.00 | 2.33 | 75 | 5 | 5 |
| 7.00 | 2.53 | 75 | 5 | 7 |
| 8.00 | 2.62 | 78 | 2 | 17 |
| 9.00 | 2.65 | 78 | 2 | 15 |
| 10.00 | 2.74 | 76 | 4 | 12 |
| Plot # | Stand Age | Mean DBH | Mean T.H.1 | <5 m | 5 m–10 m | ||||||
| RMSE | Trees Num. | ER Trees2 | RMSE | Trees Num. | ER Trees | ||||||
| DBH | T.H. | DBH | T.H. | ||||||||
| 20170726012 | Young | 11.30 | 8.2 | 0.91 | 0.41 | 13 | 0 | 1.09 | 0.44 | 43 | 7 |
| 20160831017 | Middle-age | 24.70 | 15.2 | 1.27 | 0.54 | 2 | 0 | 1.20 | 0.89 | 18 | 0 |
| 20160824002 | Mature | 28.40 | 18.0 | 0.68 | 0.59 | 2 | 0 | 1.64 | 0.46 | 6 | 0 |
| 10 m–15 m | 15–20 m | >20 m | |||||||||
| RMSE | Trees Num | ER Trees | RMSE | Trees Num. | ER Trees | RMSE | Trees Num. | ER Trees | |||
| DBH | T.H. | DBH | T.H. | DBH | T.H. | ||||||
| 0.81 | 0.57 | 43 | 0 | 1.30 | 0.60 | 12 | 35 | – | – | □ | – |
| 1.28 | 0.56 | 18 | 1 | 1.36 | 0.30 | 26 | 1 | 1.33 | 0.78 | 218 | 30 |
| 1.64 | 0.52 | 10 | 2 | 1.00 | 0.17 | 18 | 2 | 1.43 | 0.84 | 40 | 11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. https://doi.org/10.3390/f9070398
Liu G, Wang J, Dong P, Chen Y, Liu Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests. 2018; 9(7):398. https://doi.org/10.3390/f9070398
Chicago/Turabian StyleLiu, Guangjie, Jinliang Wang, Pinliang Dong, Yun Chen, and Zhiyuan Liu. 2018. "Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level" Forests 9, no. 7: 398. https://doi.org/10.3390/f9070398
APA StyleLiu, G., Wang, J., Dong, P., Chen, Y., & Liu, Z. (2018). Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests, 9(7), 398. https://doi.org/10.3390/f9070398







