Quantifying Impacts of Forest Recovery on Water Yield in Two Large Watersheds in the Cold Region of Northeast China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Watersheds
2.2. Data
2.2.1. Forest Cover Data
2.2.2. Hydrometeorological Data
2.3. Data Analysis Methods
2.3.1. Trend Analysis on Hydrological and Climatic Series
2.3.2. Time Series Correlation Analysis
2.3.3. Separation of the Impacts of Climatic Variability and Forest Recovery on Annual Streamflow
Modified Double Mass Curve Method
Sensitivity-Based Method
Time Trend Analysis Method
3. Results
3.1. Trends of Annual and Seasonal Hydrometeorological Variables
3.2. Cross-Correlations between Forest Cover and Hydrological Variables
3.3. Separating the Relative Contributions of Forest Recovery and Climate Variability to the Changes in Annual Streamflow
4. Discussion
4.1. The Effects of Forest Recovery on Water Yield
4.2. The Effects of Forest Type and Topography on the Response Intensity of Water Yield to Forest Recovery
4.3. The Relative Contributions of Forest Recovery and Climate Variability to Water Yield Variations
4.4. Implications and Uncertainty
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Piao, S.; Li, L.Z.X.; Chen, A.; Wang, X.; Ciais, P.; Huang, L.; Lian, X.; Peng, S.; Zeng, Z. Divergent hydrological response to large-scale afforestation and vegetation greening in China. Sci. Adv. 2018, 4, eaar4182. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yang, D.; Yang, Y.; Piao, S.; Yang, H.; Lei, H.; Fu, B. Excessive afforestation and soil drying on China’s loess plateau. J. Geophys. Res. Biogeosci. 2018, 123, 923–935. [Google Scholar] [CrossRef]
- Qiu, J. China drought highlights future climate threats. Nature 2010, 465, 142–143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Liu, N.; Harper, R.; Li, Q.; Liu, K.; Wei, X.; Ning, D.; Hou, Y.; Liu, S. A global review on hydrological responses to forest change across multiple spatial scales: Importance of scale, climate, forest type and hydrological regime. J. Hydrol. 2017, 546, 44–59. [Google Scholar] [CrossRef]
- Li, Q.; Wei, X.; Zhang, M.; Liu, W.; Fan, H.; Zhou, G.; Giles-Hansen, K.; Liu, S.; Wang, Y. Forest cover change and water yield in large forested watersheds: A global synthetic assessment. Ecohydrology 2017, 10, e1838. [Google Scholar] [CrossRef]
- Kiely, G.; Nadezhdina, N.; Zappa, M. The response of the water fluxes of the boreal forest region at the volga’s source area to climatic and land-use changes. Phys. Chem. Earth 2002, 27, 675–690. [Google Scholar]
- Wattenbach, M.; Zebisch, M.; Hattermann, F.; Gottschalk, P.; Goemann, H.; Kreins, P.; Badeck, F.; Lasch, P.; Suckow, F.; Wechsung, F. Hydrological impact assessment of afforestation and change in tree-species composition—A regional case study for the federal state of Brandenburg (Germany). J. Hydrol. 2007, 346, 1–17. [Google Scholar] [CrossRef]
- Duan, L.L.; Man, X.L.; Kurylyk, B.L.; Cai, T.J.; Li, Q. Distinguishing streamflow trends caused by changes in climate, forest cover, and permafrost in a large watershed in northeastern China. Hydrol. Process. 2017, 31, 1938–1951. [Google Scholar] [CrossRef]
- Wei, X.H.; Zhang, M.F. Quantifying streamflow change caused by forest disturbance at a large spatial scale: A single watershed study. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Li, Q.; Wei, X.; Zhang, M.; Liu, W.; Giles-Hansen, K.; Wang, Y. The cumulative effects of forest disturbance and climate variability on streamflow components in a large forest-dominated watershed. J. Hydrol. 2017, 557, 448–459. [Google Scholar] [CrossRef]
- Wei, X.; Li, Q.; Zhang, M.; Giles-Hansen, K.; Liu, W.; Fan, H.; Wang, Y.; Zhou, G.; Piao, S.; Liu, S. Vegetation cover—Another dominant factor in determining global water resources in forested regions. Glob. Chang. Biol. 2017, 24, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wei, X. The effects of cumulative forest disturbance on streamflow in a large watershed in the central interior of British Columbia, Canada. Hydrol. Earth Syst. Sci. 2012, 16, 2021–2034. [Google Scholar] [CrossRef]
- Zhao, F.F.; Zhang, L.; Xu, Z.X.; Scott, D.F. Evaluation of methods for estimating the effects of vegetation change and climate variability on streamflow. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; Mcvicar, T.R.; Yang, D. An analytical solution for the impact of vegetation changes on hydrological partitioning within the budyko framework. Water Resour. Res. 2018, 54, 519–537. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; Dijk, A.I.J.M.V.; Guerschman, J.P.; Mulligan, M.; Bruijnzeel, L.A.; Mcvicar, T.R. Detecting changes in streamflow after partial woodland clearing in two large catchments in the seasonal tropics. J. Hydrol. 2012, 416, 60–71. [Google Scholar] [CrossRef]
- Beck, H.E.; Bruijnzeel, L.A.; Dijk, A.I.J.M.V.; Mcvicar, T.R. The impact of forest regeneration on streamflow in 12 meso-scale humid tropical catchments. Hydrol. Earth Syst. Sci. 2013, 17, 2613–2635. [Google Scholar] [CrossRef]
- Wei, X.H.; Liu, W.F.; Zhou, P.C. Quantifying the relative contributions of forest change and climatic variability to hydrology in large watersheds: A critical review of research methods. Water 2013, 5, 728–746. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Chang, Y.; Weisberg, P.J.; He, H.S. Spatial patterns and drivers of fire occurrence and its future trend under climate change in a boreal forest of northeast china. Glob. Chang. Biol. 2012, 18, 2041–2056. [Google Scholar] [CrossRef]
- Chen, X. Modeling the effects of global climatic change at the ecotone of boreal larch forest and temperate forest in northeast china. Clim. Change 2002, 55, 77–97. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Xu, X.; Kuang, W.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; Yu, D.; Wu, S. Spatial patterns and driving forces of land use change in china during the early 21st century. J. Geog. Sci. 2010, 20, 483–494. [Google Scholar] [CrossRef]
- Brown, J.; Ferrians Jr, O.; Heginbottom, J.; Melnikov, E. Circum-Arctic Map of Permafrost and Ground-Ice Conditions, Version 2; NSIDC: National Snow and Ice Data Center: Boulder, CO, USA, 2002. [Google Scholar]
- Serreze, M.; Walsh, J.; Chapin Iii, F.; Osterkamp, T.; Dyurgerov, M.; Romanovsky, V.; Oechel, W.; Morison, J.; Zhang, T.; Barry, R. Observational evidence of recent change in the northern high-latitude environment. Clim. Change 2000, 46, 159–207. [Google Scholar] [CrossRef]
- Group, M.I.E.W.; Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar]
- Woo, M.K.; Kane, D.L.; Carey, S.K.; Yang, D.Q. Progress in permafrost hydrology in the new millennium. Permafr. Periglac. Process. 2008, 19, 237–254. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic impacts of thawing permafrost-a review. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Duan, L.; Man, X.; Kurylyk, B.L.; Cai, T. Increasing winter baseflow in response to permafrost thaw and precipitation regime shifts in northeastern China. Water 2017, 9, 25. [Google Scholar] [CrossRef]
- Yao, Y.; Cai, T.; Ju, C.; He, C. Effect of reforestation on annual water yield in a large watershed in northeast China. J. For. Res. 2015, 26, 697–702. [Google Scholar] [CrossRef]
- Pettitt, A. A non-parametric approach to the change-point problem. Applied Statistics 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend analysis in reference evapotranspiration using mann-kendall and spearman’s rho tests in arid regions of Iran. Water Resour. Manag. 2012, 26, 211–224. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975; p. 202. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water-quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M. Time series analysis: Forecasting and control. In Holden-Day Series in Time Series Analysis; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Jassby, A.D.; Powell, T.M. Detecting changes in ecological time-series. Ecology 1990, 71, 2044–2052. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Wei, X.H.; Chen, X.Z.; Zhou, P.; Liu, X.D.; Xiao, Y.; Sun, G.; Scott, D.F.; Zhou, S.Y.D.; Han, L.S.; et al. Global pattern for the effect of climate and land cover on water yield. Nat. Commun. 2015, 6, 5918. [Google Scholar] [CrossRef] [PubMed]
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential evaporation functions compared on us watersheds: Possible implications for global-scale water balance and terrestrial ecosystem modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar] [CrossRef]
- Pyzoha, J.E.; Callahan, T.J.; Sun, G.; Trettin, C.C.; Miwa, M. A conceptual hydrologic model for a forested Carolina bay depressional wetland on the coastal plain of south Carolina, USA. Hydrol. Process. 2008, 22, 2689–2698. [Google Scholar] [CrossRef]
- Sun, G.; Zuo, C.; Liu, S.; Liu, M.; Mcnulty, S.G.; Vose, J.M. Watershed evapotranspiration increased due to changes in vegetation composition and structure under a subtropical climate1. J. Am. Water Resour. Assoc. 2008, 44, 1164–1175. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. A simple framework for examining the interannual variability of land surface moisture fluxes. J. Clim. 1999, 12, 1911–1917. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A. Macroscale water fluxes—2. Water and energy supply control of their interannual variability. Water Resour. Res. 2002, 38, 1–9. [Google Scholar] [CrossRef]
- Li, L.J.; Zhang, L.; Wang, H.; Wang, J.; Yang, J.W.; Jiang, D.J.; Li, J.Y.; Qin, D.Y. Assessing the impact of climate variability and human activities on streamflow from the wuding river basin in China. Hydrol. Process. 2007, 21, 3485–3491. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical methods in water resources; US Geological Survey: Reston, VA, USA, 2002; Volume 323.
- Liu, W.; Wei, X.; Liu, S.; Liu, Y.; Fan, H.; Zhang, M.; Yin, J.; Zhan, M. How do climate and forest changes affect long-term streamflow dynamics? A case study in the upper reach of Poyang river basin. Ecohydrology 2015, 8, 46–57. [Google Scholar] [CrossRef]
- Tuteja, N.K.; Vaze, J.; Teng, J.; Mutendeudzi, M. Partitioning the effects of pine plantations and climate variability on runoff from a large catchment in southeastern Australia. Water Res. Res. 2007, 43, 199–212. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Wei, X.H.; Luo, Y.; Zhang, M.F.; Li, Y.L.; Qiao, Y.N.; Liu, H.G.; Wang, C.L. Forest recovery and river discharge at the regional scale of Guangdong province, China. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Gafur, A.; Jensen, J.R.; Borggaard, O.K.; Petersen, L. Runoff and losses of soil and nutrients from small watersheds under shifting cultivation (Jhum) in the Chittagong hill tracts of Bangladesh. J. Hydrol. 2003, 274, 30–46. [Google Scholar] [CrossRef]
- Scott, D.; Smith, R. Preliminary empirical models to predict reductions in total and low flows resulting from afforestation. Water SA. 1997, 23, 135–140. [Google Scholar]
- Bruijnzeel, L.A. Hydrology of moist tropical forests and effects of conversion: A state of knowledge review. J. Hydrol. 1990, 129, 397–399. [Google Scholar]
- Farley, K.A.; Jobbágy, E.G.; Jackson, R.B. Effects of afforestation on water yield: A global synthesis with implications for policy. Glob. Chang. Biol. 2005, 11, 1565–1576. [Google Scholar] [CrossRef]
- Lan, C.; Lettenmaier, D.P.; Alberti, M.; Richey, J.E. Effects of a century of land cover and climate change on the hydrology of the puget sound basin. Hydrolog. Process. 2009, 23, 907–933. [Google Scholar]
- Buttle, J.M.; Metcalfe, R.A. Boreal forest disturbance and streamflow response, northeastern Ontario. Can. J. Fish. Aquat. Sci. 2000, 57, 5–18. [Google Scholar] [CrossRef]
- Mu, T. The estimation of transpiration of main tree species and water consumption of larch in Da Hinggan Moutains. Inn. Mong. For. Sci. Technol. 1980, 2, 3. [Google Scholar]
- Komatsu, H.; Tanaka, N.; Kume, T. Do coniferous forests evaporate more water than broad-leaved forests in Japan? J. Hydrol. 2007, 336, 361–375. [Google Scholar] [CrossRef]
- Vertessy, R.; Zhang, L.; Dawes, W.R. Plantations, river flows and river salinity. Aust. For. 2003, 66, 55–61. [Google Scholar] [CrossRef]
- Bosch, J.M.; Hewlett, J. A review of catchment experiments to determine the effect of vegetation changes on water yield and evapotranspiration. J. Hydrol. 1982, 55, 3–23. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Karlsen, R.H.; Grabs, T.; Bishop, K.; Buffam, I.; Laudon, H.; Seibert, J. Landscape controls on spatiotemporal discharge variability in a boreal catchment. Water Resour. Res. 2016, 52. [Google Scholar] [CrossRef]
- Liu, W.; Wei, X.; Li, Q.; Fan, H.; Duan, H.; Wu, J.; Giles-Hansen, K.; Zhang, H. Hydrological recovery in two large forested watersheds of southeastern China: Importance of watershed property in determining hydrological responses to reforestation. Hydrol Earth Syst. Sci. 2016, 20, 4747–4756. [Google Scholar] [CrossRef]
- Li, Q.; Wei, X.; Yang, X.; Giles-Hansen, K.; Zhang, M.; Liu, W. Topography significantly influencing low flows in snow-dominated watersheds. Hydrol. Earth Syst. Sci. 2018, 22, 1947. [Google Scholar] [CrossRef]
- Price, K. Effects of watershed topography, soils, land use, and climate on baseflow hydrology in humid regions: A review. Prog. Phys. Geog. 2011, 35, 465–492. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J.; Weiler, M.; Kendall, C.; McGlynn, B.L.; Welker, J.M.; Seibert, J. The role of topography on catchment-scale water residence time. Water Resour. Res. 2005, 41, 302–317. [Google Scholar] [CrossRef]
- Brown, A.E.; Zhang, L.; McMahon, T.A.; Western, A.W.; Vertessy, R.A. A review of paired catchment studies for determining changes in water yield resulting from alterations in vegetation. J. hydrol. 2005, 310, 28–61. [Google Scholar] [CrossRef]
- Gauthier, S.; Vaillancourt, M.A. Ecosystem Management in the Boreal Forest; Presses de I’Université du Québec: Quebec, QC, Canada, 2009. [Google Scholar]
- Liu, Q.; Yang, Z.; Cui, B.; Sun, T. Temporal trends of hydro-climatic variables and runoff response to climatic variability and vegetation changes in the yiluo river basin, China. Hydrol. Process. 2010, 23, 3030–3039. [Google Scholar] [CrossRef]
- Zheng, H.X.; Zhang, L.; Zhu, R.R.; Liu, C.M.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the yellow river basin. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Zhang, M.F.; Wei, X.H.; Sun, P.S.; Liu, S.R. The effect of forest harvesting and climatic variability on runoff in a large watershed: The case study in the upper Minjiang river of Yangtze river basin. J. Hydrol. 2012, 464, 1–11. [Google Scholar] [CrossRef]
- Shi, P.; Ma, X.; Hou, Y.; Li, Q.; Zhang, Z.; Qu, S.; Chen, C.; Cai, T.; Fang, X. Effects of land-use and climate change on hydrological processes in the upstream of Huai river, China. Water Resour. Manag. 2013, 27, 1263–1278. [Google Scholar] [CrossRef]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime. Bioscience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Poff, N.L.; Zimmerman, J.K.H. Ecological responses to altered flow regimes: A literature review to inform the science and management of environmental flows. Freshwater Biol. 2010, 55, 194–205. [Google Scholar] [CrossRef]
- Zanardo, S.; Harman, C.J.; Troch, P.A.; Rao, P.S.C.; Sivapalan, M. Intra-annual rainfall variability control on interannual variability of catchment water balance: A stochastic analysis. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Ellison, D.; Futter, M.N.; Bishop, K. On the forest cover–water yield debate: From demand- to supply-side thinking. Glob. Chang. Biol. 2012, 18, 806–820. [Google Scholar] [CrossRef]
- Valipour, M. Importance of solar radiation, temperature, relative humidity, and wind speed for calculation of reference evapotranspiration. Arch. Agron. Soil Sci. 2015, 61, 239–255. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. Trend analysis of reference evapotranspiration in northwest china: The roles of changing wind speed and surface air temperature. Hydrol. Process. 2013, 27, 3941–3948. [Google Scholar] [CrossRef]
- Valipour, M. Study of different climatic conditions to assess the role of solar radiation in reference crop evapotranspiration equations. Arch Agron. Soil Sci. 2015, 61, 679–694. [Google Scholar] [CrossRef]
- Kurylyk, B.L. Discussion of ‘a simple thaw-freeze algorithm for a multi-layered soil using the Stefan equation’ by Xie and Gough (2013). Permafrost Periglac. 2015, 26, 200–206. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; Hayashi, M.; Quinton, W.L.; McKenzie, J.M.; Voss, C.I. Influence of vertical and lateral heat transfer on permafrost thaw, peatland landscape transition, and groundwater flow. Water Resour. Res. 2016, 52, 1286–1305. [Google Scholar] [CrossRef]
- Wang, T.; Yang, H.; Yang, D.; Qin, Y.; Wang, Y. Quantifying the streamflow response to frozen ground degradation in the source region of the yellow river within the budyko framework. J. Hydrol. 2018, 558, 301–313. [Google Scholar] [CrossRef]
- Ding, Y.H.; Ren, G.Y.; Zhao, Z.C.; Xu, Y.; Luo, Y.; Li, Q.P.; Zhang, J. Detection, causes and projection of climate change over china: An overview of recent progress. Adv. Atmos. Sci. 2007, 24, 954–971. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuoxin, G.U.; Wang, X. Impact of simulated climate warming on the radial growth of larix gmelinii in northeast china. Acta Ecologica Sinica 2017, 37, 2684–2693. [Google Scholar]
- Jin, H.J.; Yu, Q.H.; Lii, L.Z.; Guo, D.X.; He, R.X.; Yu, S.P.; Sun, G.Y.; Li, Y.W. Degradation of permafrost in the Xing’anling mountains, northeastern china. Permafrost Periglac. 2007, 18, 245–258. [Google Scholar] [CrossRef]
- Chang, X.; Jin, H.; He, R.; Yang, S.; Yu, S.; Lv, L.; Guo, D.; Wang, S.; Kang, X. Advances in permafrost and cold regions environments studies in the da Xing’anling (Da Hinggan) mountains, northeastern China. J. Glaciol Geocryol 2008, 30, 176–182. [Google Scholar]
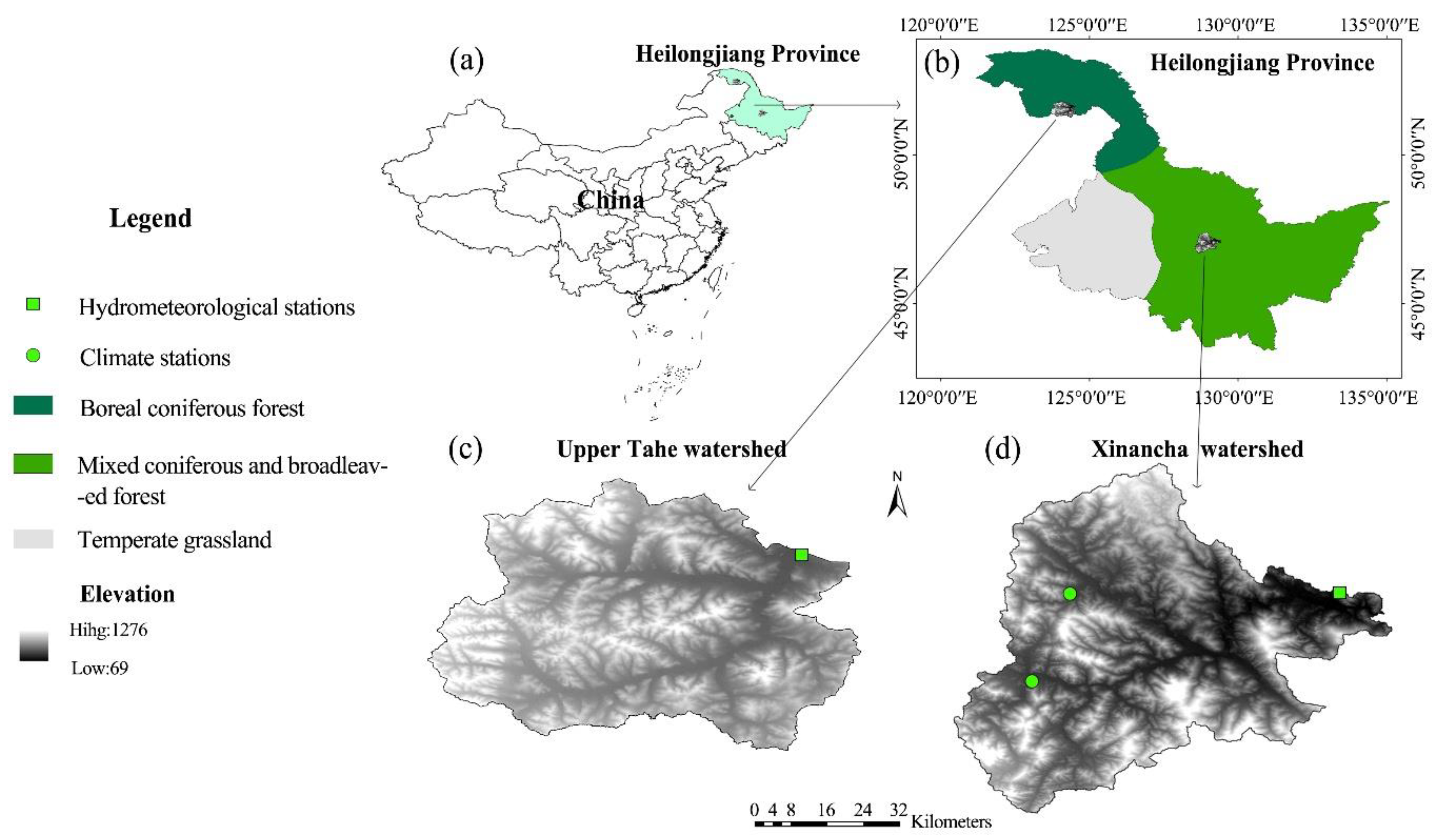
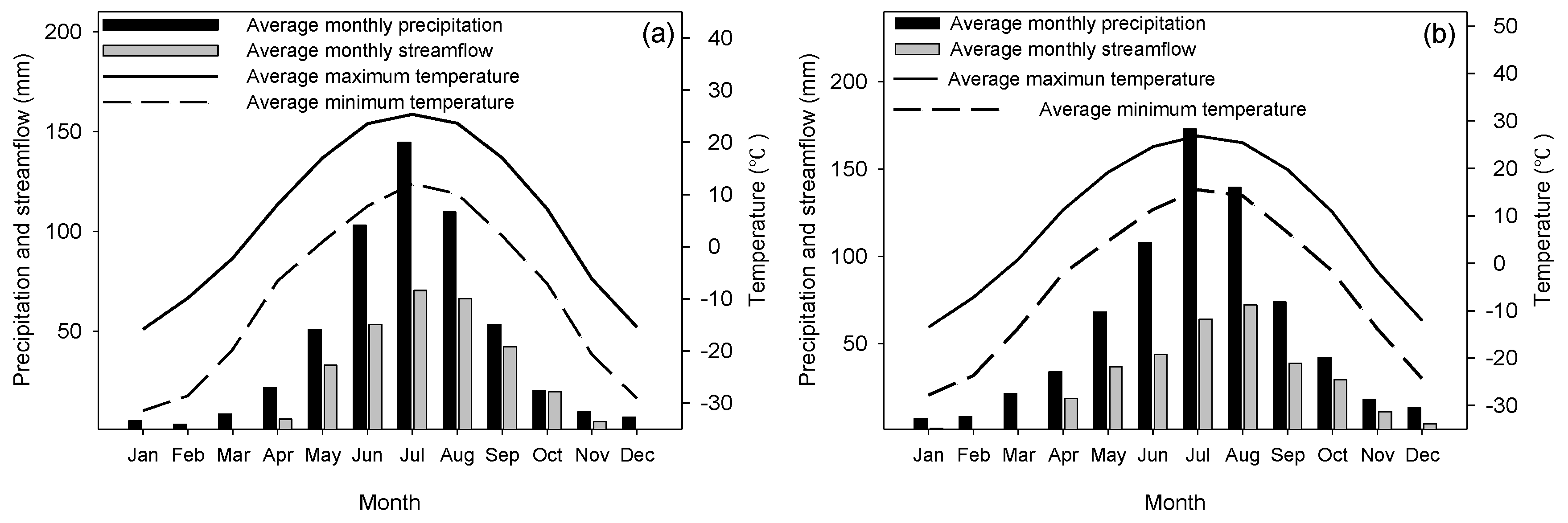
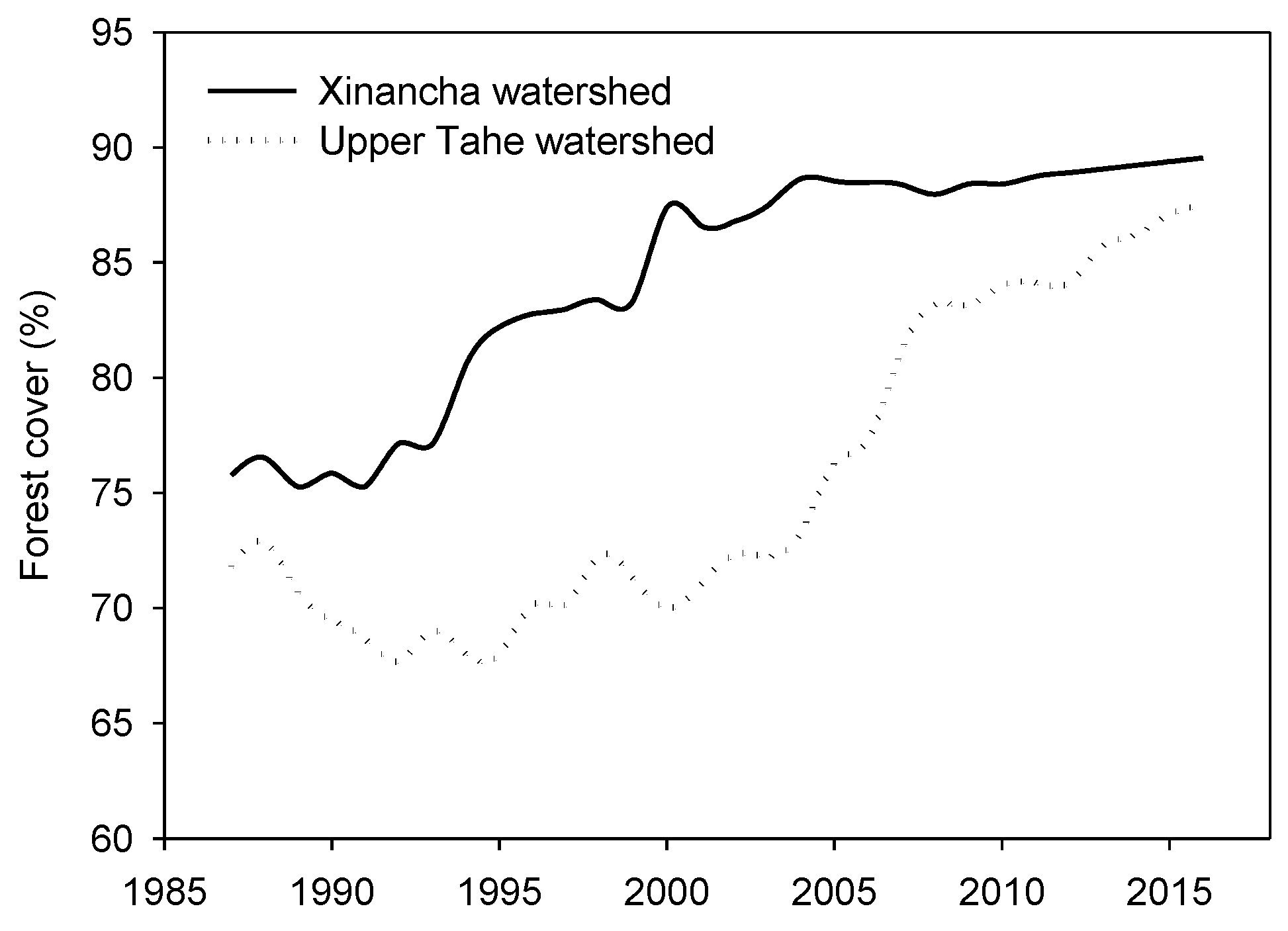
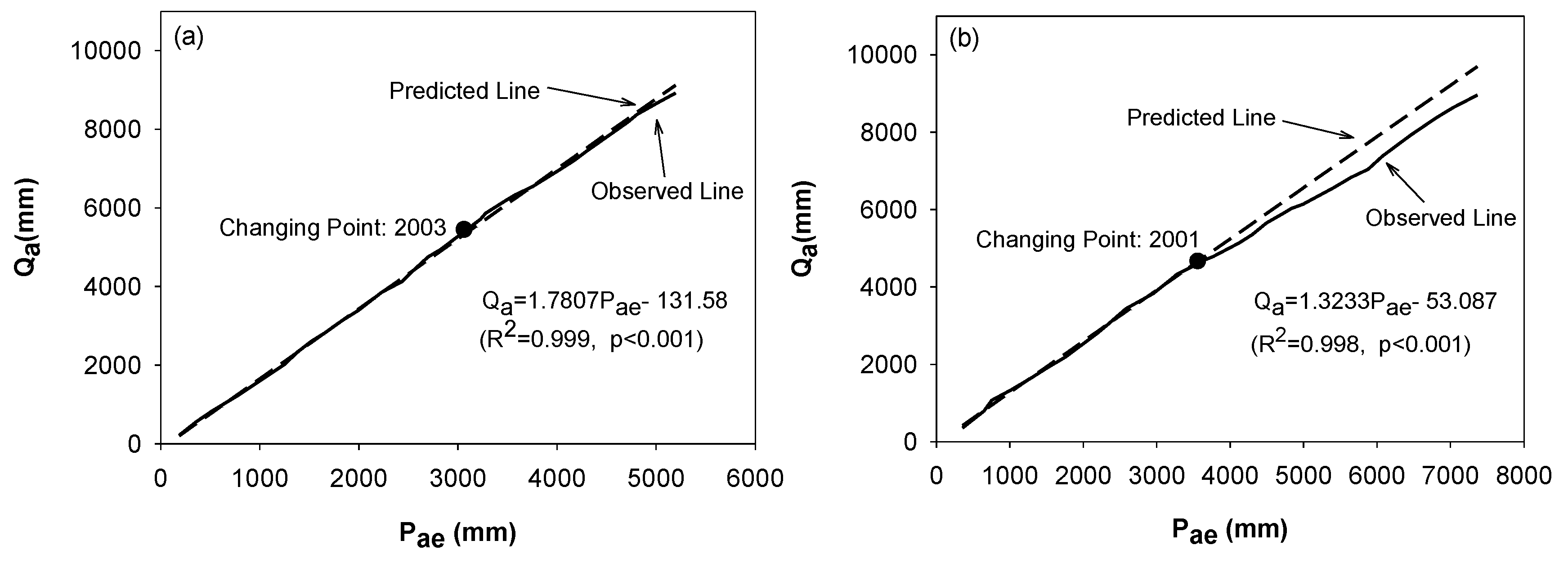
| Metrics | UTH Watershed | XNC Watershed |
|---|---|---|
| Drainage area (km2) | 2359 | 2582 |
| Mainstream length (km) | 83 | 82 |
| Average elevation (m) | 783 | 501 |
| Elevation range (m) | 432–1276 | 69–1226 |
| Average slope (°) | 12.5 | 13.4 |
| Soil type | Dark brown earths and brown coniferous forest soil | Dark brown earths and brown coniferous forest soil |
| Annual mean precipitation (mm) | 534.8 | 706.0 |
| Annual mean PET (mm) | 520.5 | 711.8 |
| Annual mean air temperature (°C) | −2.1 | 2.4 |
| Annual mean flow (mm) | 297.3 | 298.7 |
| Average forest cover (%) | 75.6 | 87.7 |
| Forest type | Boreal coniferous forest | Mixed coniferous and broadleaved forest |
| Hydrometric station | Xinlin | Nancha |
| Climate stations | Xinlin | Nancha, Xiaobai, Nanlie |
| Period | Watershed | Q | P | T | PET | ||||
|---|---|---|---|---|---|---|---|---|---|
| Slope 1 (mm/year) | p | Slope (mm/year) | p | Slope (°C/year) | p | Slope (mm/year) | p | ||
| Annual | UTH | −2.0 | 0.26 | −1.2 | 0.48 | 0.00 | 0.93 | 0.58 | 0.15 |
| XNC | −1.1 | 0.67 | 0.25 | 0.92 | 0.00 | 0.75 | 0.59 * | 0.01 | |
| Spring | UTH | 0.35 | 0.55 | 1.03 | 0.11 | 0.02 | 0.31 | 0.30 | 0.11 |
| XNC | 1.09 * | 0.02 | 2.36 * | 0.01 | 0.02 | 0.33 | 0.25 | 0.17 | |
| Summer | UTH | −1.88 | 0.32 | −1.90 | 0.32 | 0.02 | 0.16 | 0.58 | 0.08 |
| XNC | −0.04 | 1.00 | 0.31 | 0.97 | 0.03 | 0.07 | 0.47 | 0.11 | |
| Autumn | UTH | −0.29 | 0.62 | −0.16 | 0.86 | −0.02 | 0.41 | 0.00 | 0.94 |
| XNC | −0.63 | 0.50 | −1.67 | 0.18 | 0.01 | 0.72 | 0.10 | 0.27 | |
| Winter | UTH | −0.04 | 0.44 | −0.2 | 0.36 | −0.03 | 0.25 | −0.04 | 0.83 |
| XNC | −0.03 | 0.86 | 1.18 * | 0.02 | −0.04 | 0.38 | −0.11 | 0.55 | |
| Variables | Forest Cover of UTH (1,1,1) | Forest Cover of XNC (1,1,1) | ||||||
|---|---|---|---|---|---|---|---|---|
| ARIMA 1 Model | Cross-Correlation Coefficient | p | Lag | ARIMA Model | Cross-Correlation Coefficient | p | Lag | |
| Annual | (1,0,0) | −0.51 ** | 0.005 | 9 | (1,0,0) | −0.54 ** | 0.001 | 5 |
| Spring | (1,0,0) | 0.46 * | 0.019 | 4 | (0,0,1) | 0.41 * | 0.026 | 0 |
| Summer | (0,0,1) | −0.40 * | 0.038 | 10 | (1,0,0) | −0.46 ** | 0.007 | 5 |
| Autumn | (1,0,1) | −0.41 * | 0.017 | 9 | (0,0,1) | −0.40 * | 0.025 | 5 |
| Winter | (1,0,0) | −0.28 | 0.170 | 5 | (1,0,0) | 0.16 | 0.404 | 0 |
| Model Input | Model Structure | Parameter Estimation | |
|---|---|---|---|
| q(1) 1 | Ω 2 | ||
| Slope of MDMC 3 of UTH in Figure 4a | Interrupted ARIMA: (0,0,1), intervention at year 2003 | −0.73 (p < 0.05) | 0.52 (p < 0.05) |
| Slope of MDMC of XNC in Figure 4b | Interrupted ARIMA: (0,0,1), intervention at year 2001 | −0.76 (p < 0.05) | 0.73 (p < 0.05) |
| Watershed | Sub-Periods | P (mm) | PET (mm) | ΔP (mm) | ΔPET (mm) | β | γ | ΔQ (mm) | ΔQC (mm) | ΔQF (mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1987–2002 | 540.7 | 517.3 | ||||||||
| UTH | −11.3 | 7.0 | 0.58 | −0.33 | −23.9 | −8.8 | −15.1 | |||
| 2003–2016 | 529.5 | 524.3 | ||||||||
| 1987–2000 | 715.9 | 652.8 | ||||||||
| XNC | −7.7 | 7.9 | 0.60 | −0.36 | −46.5 | −7.5 | −39.0 | |||
| 2001–2016 | 708.2 | 660.7 |
| Method | UTH (from 1987–2002 to 2003–2016) | XNC (from 1987–2000 to 2001–2016) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Changes in Streamflow (mm) | Relative contributions (%) | Changes in Streamflow (mm) | Relative Contributions (%) | |||||||
| ΔQ | ΔQC | ΔQF | Climate | Forest | ΔQ | ΔQC | ΔQF | Climate | Forest | |
| MDMC 1 | −23.9 | −7.0 | −16.9 | 29.4 | 70.6 | −46.5 | −3.1 | −43.4 | 6.7 | 93.3 |
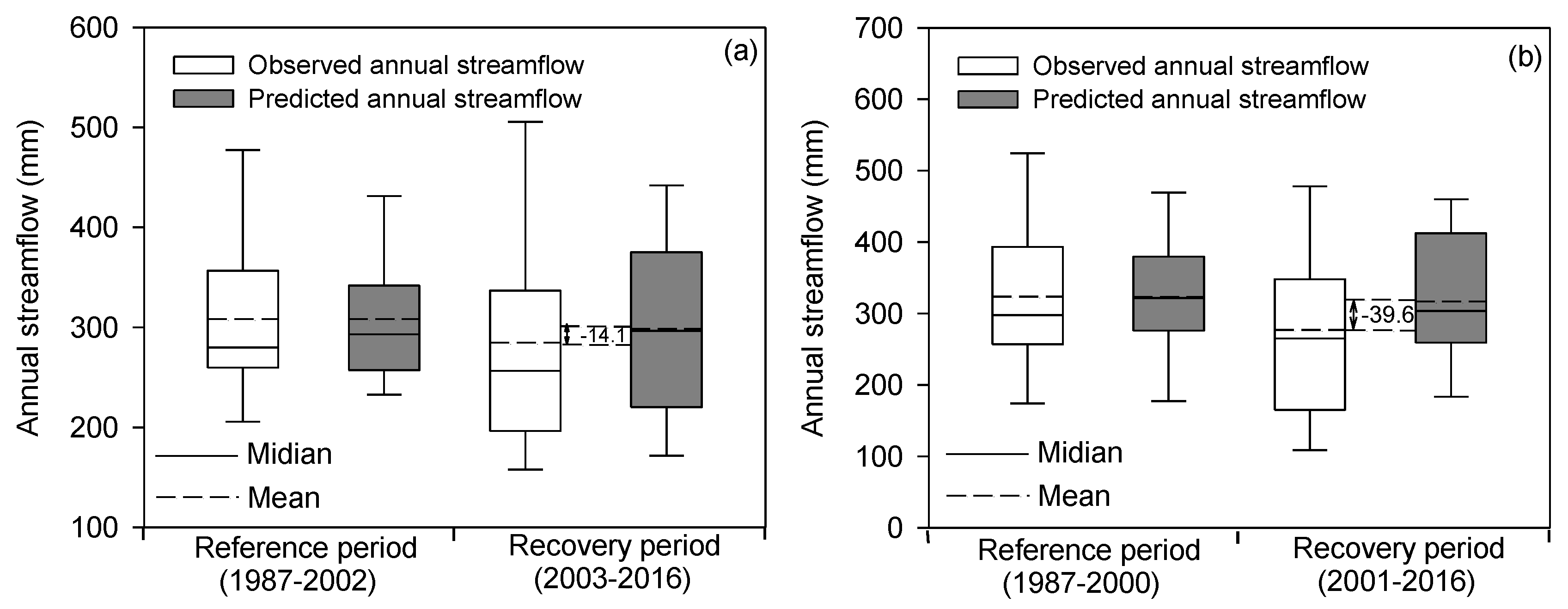
| TRA 2 | −9.8 | −14.1 | 40.9 | 59.1 | −6.9 | −39.6 | 14.9 | 85.1 | ||
| SBM 3 | −8.8 | −15.1 | 36.8 | 63.2 | −7.5 | −39.0 | 16.1 | 83.9 | ||
| Average | −8.5 | −15.4 | 35.7 | 64.3 | −7.2 | −40.7 | 12.6 | 87.4 | ||
| Watershed | Percentage of Watershed Area (%) | |||||
|---|---|---|---|---|---|---|
| Slope >40° | 20–40° | 15–20° | 10–15° | 5–10° | <5° | |
| UTH | 0.7 | 22.0 | 19.6 | 30.4 | 3.8 | 23.4 |
| XNC | 0.5 | 33.4 | 34.0 | 4.6 | 4.6 | 23.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, L.; Cai, T. Quantifying Impacts of Forest Recovery on Water Yield in Two Large Watersheds in the Cold Region of Northeast China. Forests 2018, 9, 392. https://doi.org/10.3390/f9070392
Duan L, Cai T. Quantifying Impacts of Forest Recovery on Water Yield in Two Large Watersheds in the Cold Region of Northeast China. Forests. 2018; 9(7):392. https://doi.org/10.3390/f9070392
Chicago/Turabian StyleDuan, Liangliang, and Tijiu Cai. 2018. "Quantifying Impacts of Forest Recovery on Water Yield in Two Large Watersheds in the Cold Region of Northeast China" Forests 9, no. 7: 392. https://doi.org/10.3390/f9070392
APA StyleDuan, L., & Cai, T. (2018). Quantifying Impacts of Forest Recovery on Water Yield in Two Large Watersheds in the Cold Region of Northeast China. Forests, 9(7), 392. https://doi.org/10.3390/f9070392





