Modeling Production Processes in Forest Stands: An Adaptation of the Solow Growth Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. The EcoSolow Model of Production Processes in the Forest Stand
2.2. Model Data
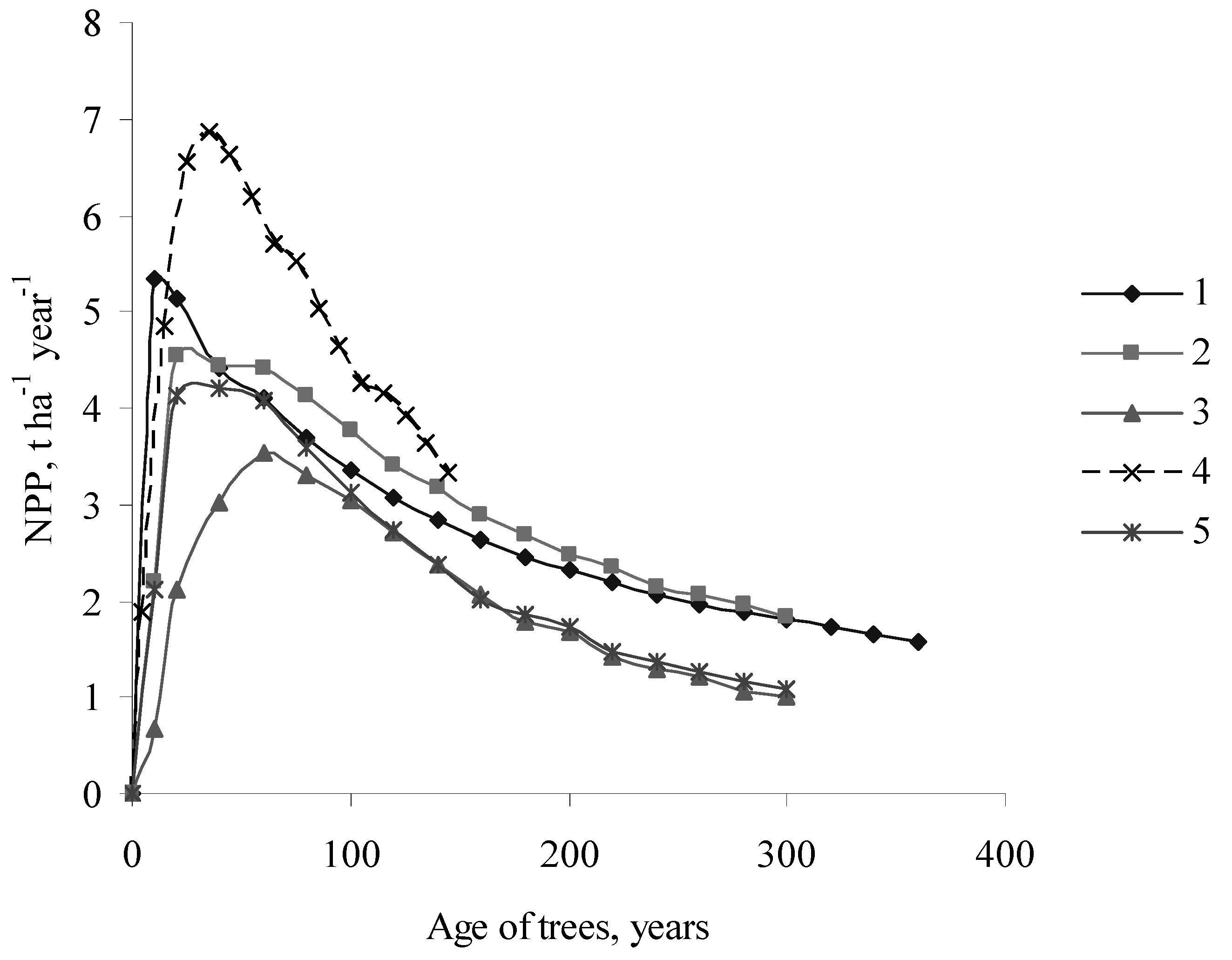
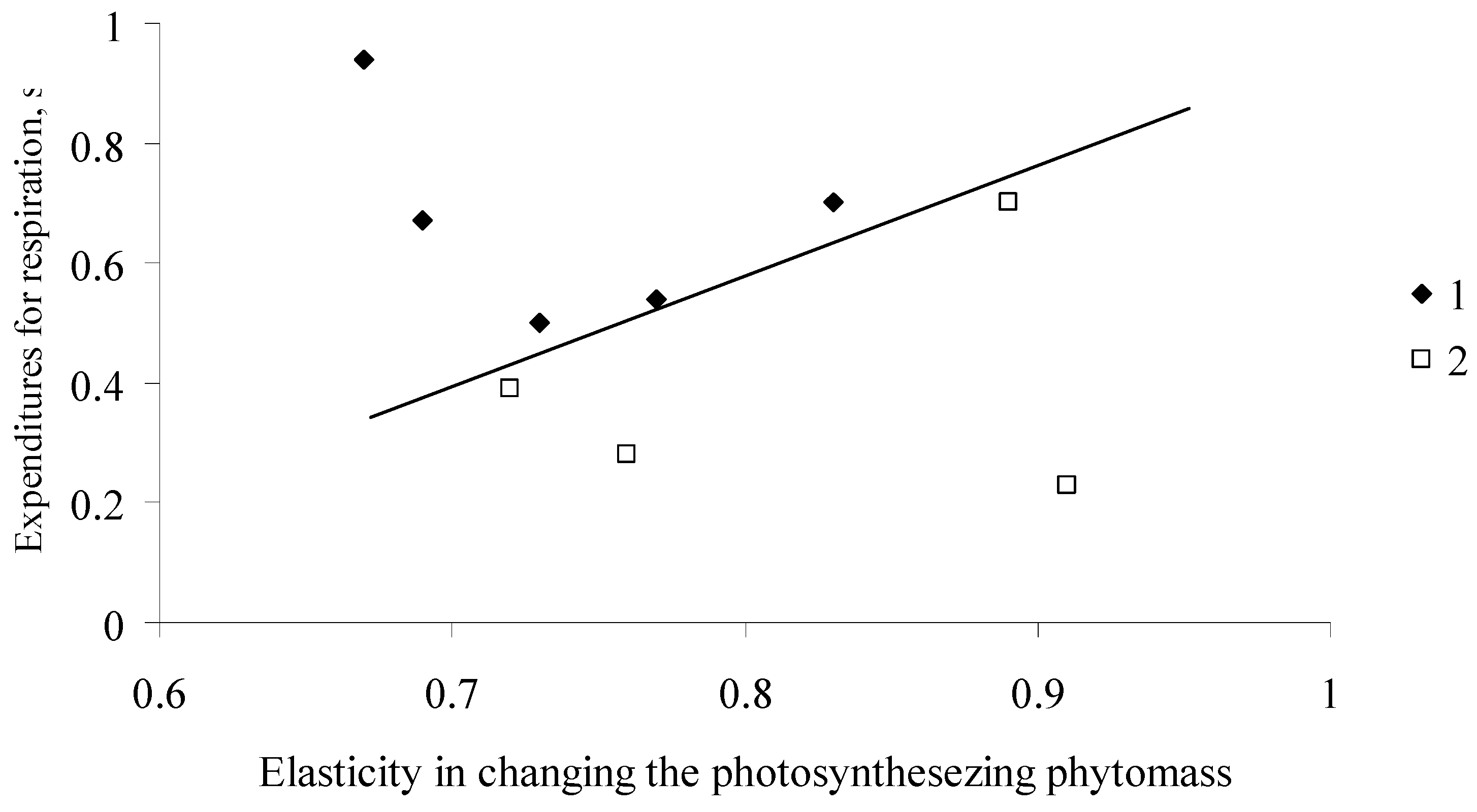
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
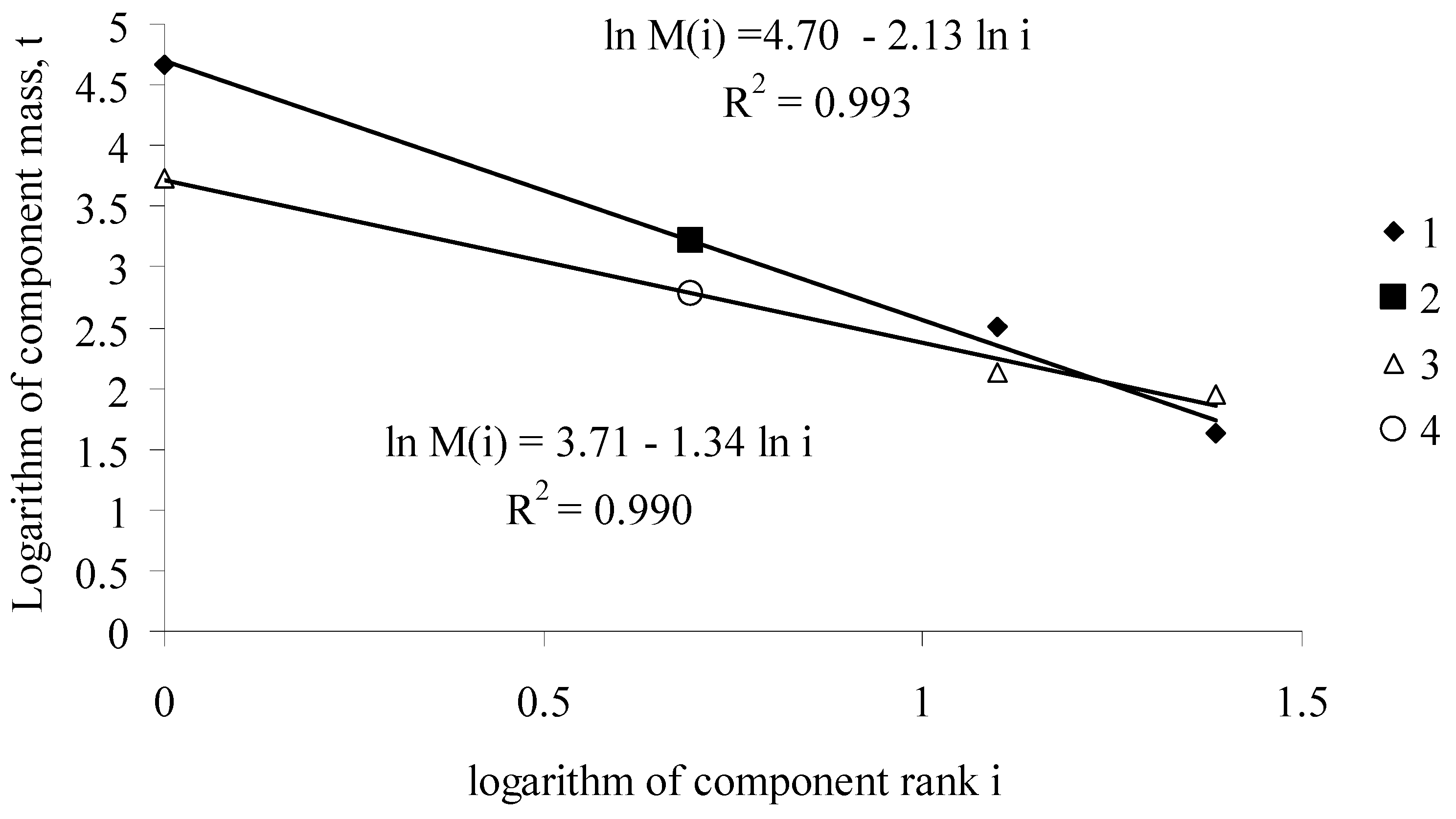
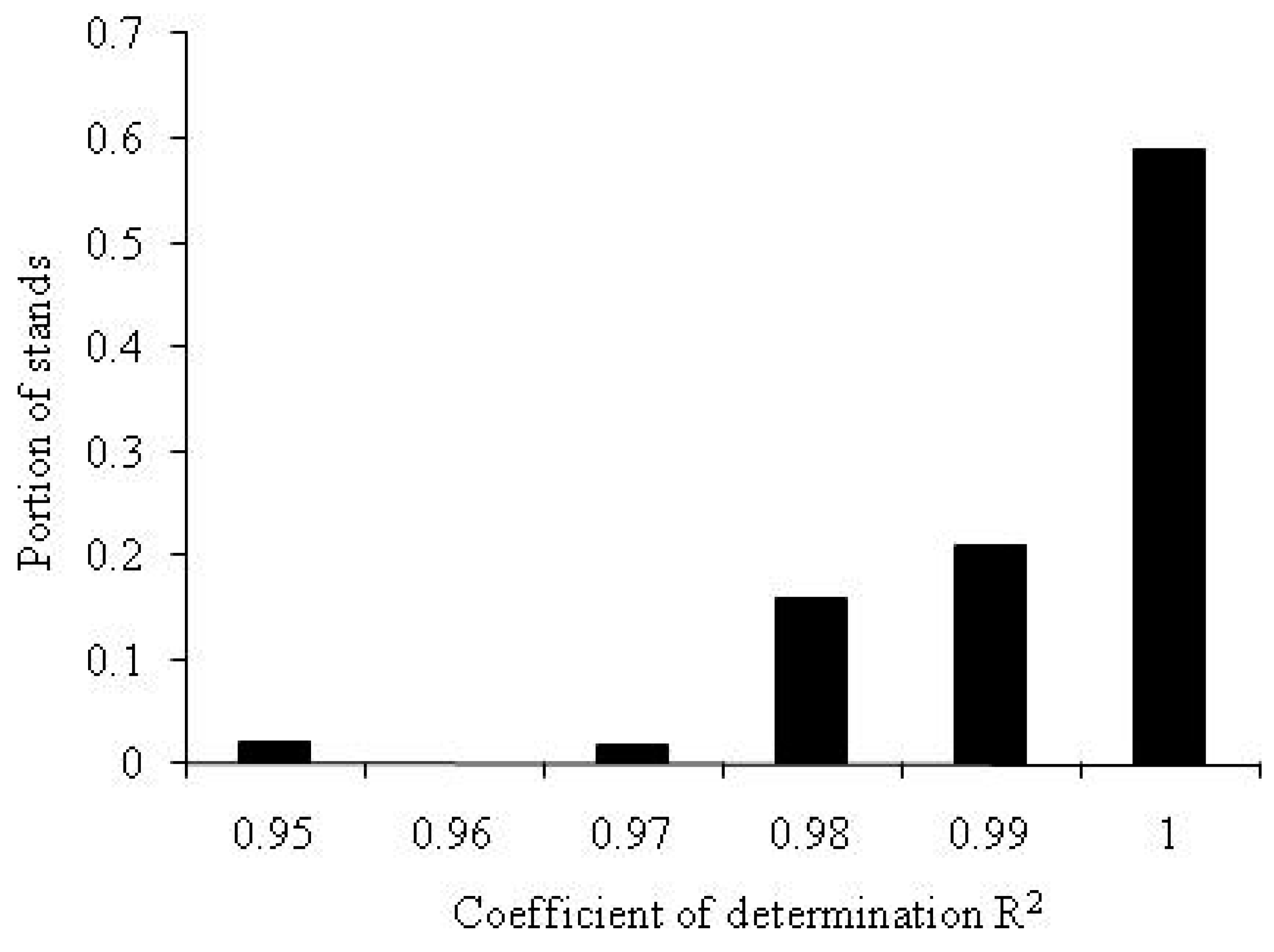
References
- Tjørve, E.; Tjørve, K.M.C. A unified approach to the Richards-model family for use in growth analyses: Why we need only two model forms. J. Theor. Biol. 2010, 267, 417–425. [Google Scholar] [CrossRef] [PubMed]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef]
- Khamanis, A.; Ismail, Z.; Haron, K.; Mohammed, A.T. Nonlinear growth models for modeling oil palm yield growth. J. Math. Stat. 2005, 1, 225–233. [Google Scholar]
- Skene, K.R. The energetics of ecological succession: A logistic model of entropic output. Ecol. Model. 2013, 250, 287–293. [Google Scholar] [CrossRef]
- Aspinall, R.J. Use of logistic regression for validation of maps of the spatial distribution of vegetation species derived from high spatial resolution hyperspectral remotely sensed data. Ecol. Model. 2002, 157, 301–312. [Google Scholar] [CrossRef]
- Kumar, R.; Nandy, S.; Agarwal, R.; Kushwaha, S.P.S. Forest cover dynamics analysis and prediction modeling using logistic regression model. Ecol. Indic. 2014, 45, 444–455. [Google Scholar] [CrossRef]
- Koralewski, T.E.; Wang, H.H.; Grant, W.E.; Byram, T.D. Plants on the move: Assisted migration of forest trees in the face of climate change. For. Ecol. Manag. 2015, 344, 30–37. [Google Scholar] [CrossRef]
- Acevedoa, M.A.; Marcanob, M.; Fletcher, R.J., Jr. A diffusive logistic growth model to describe forest recovery. Ecol. Model. 2012, 244, 13–19. [Google Scholar] [CrossRef]
- Odum, H.T. Systems Ecology: An Introduction; Wiley: New York, NY, USA, 1983; p. 644. [Google Scholar]
- Usoltsev, V.A. Phytomass of the Forests in North Eurasia: Database and Geography; Ural Branch of the Russian Academy of Sciences: Ekaterinburg, Russia, 2001; pp. 183–702. (In Russian) [Google Scholar]
- Usoltsev, V.A. Fitomassa i Pervichnaya Produktsiya Lesov Evrazii (Phytomass and Primary Production of Eurasian Forests); Ural Branch of the Russian Academy of Sciences: Yekaterinburg, Russia, 2010; pp. 18–512. (In Russian) [Google Scholar]
- Clark, D.A.; Brown, S.; Kicklighter, D.W.; Chambers, J.Q.; Thomlinson, J.R.; Ni, J. Measuring net primary production in forests: concepts and field methods. Ecol. Appl. 2001, 11, 356–370. [Google Scholar] [CrossRef]
- Kloeppel, B.D.; Harmon, M.E.; Fahey, T.J. Estimating aboveground net primary productivity in forest-dominated ecosystems. In Principles and Standards for Measuring Primary Production; Fahey, T.J., Knapp, A.K., Eds.; Oxford University Press: New York, NY, USA, 2007; pp. 63–81. [Google Scholar]
- Sala, O.E.; Biondini, M.E.; Lauenroth, W.K. Bias in estimates of primary production: An analytical solution. Ecol. Model. 1988, 44, 43–55. [Google Scholar] [CrossRef]
- Waring, R.H.; Landsberg, J.J.; Williams, M. Net primary production of forests: A constant fraction of gross primary production? Tree Physiol. 1998, 18, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Meng, S.; Jia, Q.; Zhou, G.; Zhou, H.; Lui, Q.; Yu, J. Fine Root Biomass and Its Relationship with Aboveground Traits of Larix gmelinii Trees in Northeastern China. Forests 2018, 9, 35. [Google Scholar] [CrossRef]
- Wang, B.; Li, M.; Fan, W.; Yu, Y.; Chen, J.M. Relationship between Net Primary Productivity and Forest Stand Age under Different Site Conditions and Its Implications for Regional Carbon Cycle Study. Forests 2018, 9, 5. [Google Scholar] [CrossRef]
- Sisay, K.; Thurnher, C.; Belay, B.; Lindner, G.; Hasenauer, H. Volume and Carbon Estimates for the Forest Area of the Amhara Region in Northwestern Ethiopia. Forests 2017, 8, 122. [Google Scholar] [CrossRef]
- Kolchugina, T.P.; Vinson, T.S. Equilibrium analysis of carbon pools and fluxes of forest biomes in the former Soviet Union. Can. J. For. Res. 1993, 23, 81–88. [Google Scholar] [CrossRef]
- Shvidenko, A.; Schepschenko, D.; Nilsson, S.; Bouloui, Y. Semi-empirical models for assessing biological productivity of Northern Eurasian forests. Ecol. Model. 2007, 204, 163–179. [Google Scholar] [CrossRef]
- Shvidenko, A.; Schepaschenko, D.; McCallum, I.; Nilsson, S. Can the uncertainty of full carbon accounting of forest ecosystems be made acceptable to policymakers? Clim. Chang. 2010, 103, 137–157. [Google Scholar] [CrossRef]
- Solow, R.M. A Contribution to the Theory of Economic Growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Houthakker, H.S. The Pareto Distribution and the Cobb–Douglas Production Function in Activity Analysis. Rev. Econ. Stud. 1955, 23, 27–31. [Google Scholar] [CrossRef]
- Cobb, C.W.; Douglas, P.H. A Theory of Production. Am. Econ. Rev. 1928, 18, 139–165. [Google Scholar]
- Jesus, F.; Gerard, A.F. The Estimation of the Cobb-Douglas Function: A Retrospective View. East. Econ. J. 2005, 31, 427–445. [Google Scholar]
- Jackson, R.B.; Canadell, J.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. A global analysis of root distributions for terrestrial biomes. Oecologia 1996, 108, 389–411. [Google Scholar] [CrossRef] [PubMed]
- Vogt, K.A.; Vogt, D.J.; Bloomfield, J. Analysis of some direct and indirect methods for estimating root biomass and production of forests at an ecosystem level. Plant Soil 1998, 200, 71–89. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Q.; Cihlar, J.; Bauhus, J.; Price, D.T. Estimating fine-root biomass and production of boreal and cool temperate forests using aboveground measurements: A new approach. Plant Soil 2004, 265, 31–46. [Google Scholar] [CrossRef]
- Curt, T.; Lucot, E.; Bouchaud, M. Douglas-fir root biomass and rooting profile in relation to soils in a mid-elevation area (Beaujolais Mounts, France). Plant Soil 2001, 233, 109–125. [Google Scholar] [CrossRef]
- Li, Z.; Kurz, W.A.; Apps, M.J.; Beukema, S.J. Belowground biomass dynamics in the carbon budget model of the Canadian forest sector: Recent improvements and implications for the estimation of NPP and NEP. Can. J. For. Res. 2003, 33, 126–136. [Google Scholar] [CrossRef]
- Sukhovolsky, V.G. Free competition of tree parts for resources and allometric correlations. J. Gen. Biol. 1997, 5, 80–88. (In Russian) [Google Scholar]
- Soukhovolsky, V.G.; Ivanova, J.D. Estimation of Forest Stand Net Primary Productivity Using Fraction Phytomass Distribution Model. Contemp. Probl. Ecol. 2013, 6, 700–707. [Google Scholar] [CrossRef]
- Ivanova, Y.; Soukhovolsky, V. Net primary production in forest ecosystem of middle siberia: Assessment using a model of tree component phytomass distribution. In Climate Change Impacts on High-Altitude Ecosystems; Ozturk, M., Hakeem, K.R., Faridah-Hanum, I., Efe, R., Eds.; Springer International Publishing: Basel, Switzerland, 2015; pp. 627–635. [Google Scholar]
- Ferrara, M.; Guerrini, L.; Mavilia, R. Modified Neoclassical Growth Models with Delay: A Critical Survey and Perspectives. Appl. Math. Sci. 2013, 7, 4249–4257. [Google Scholar] [CrossRef]
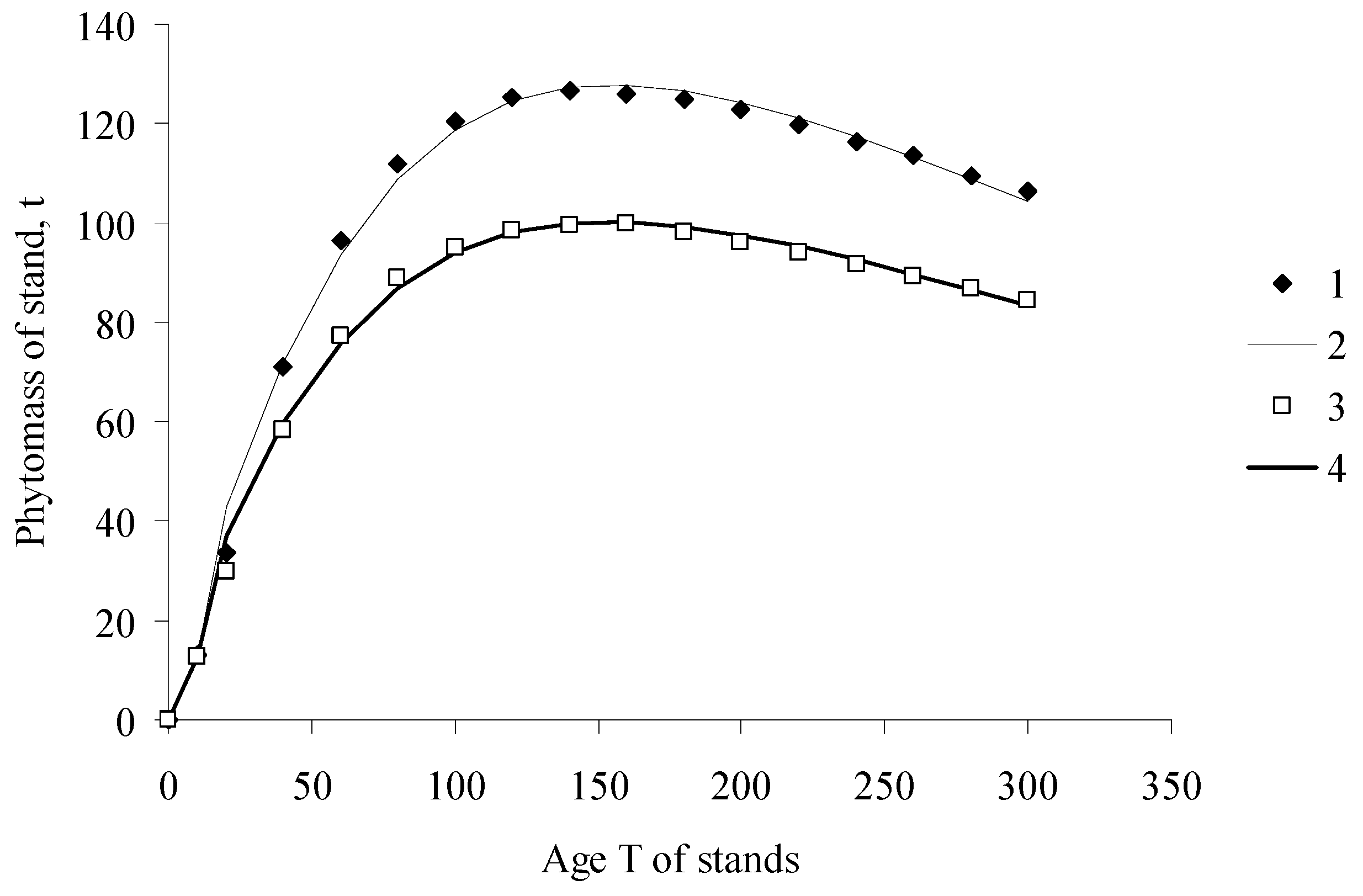
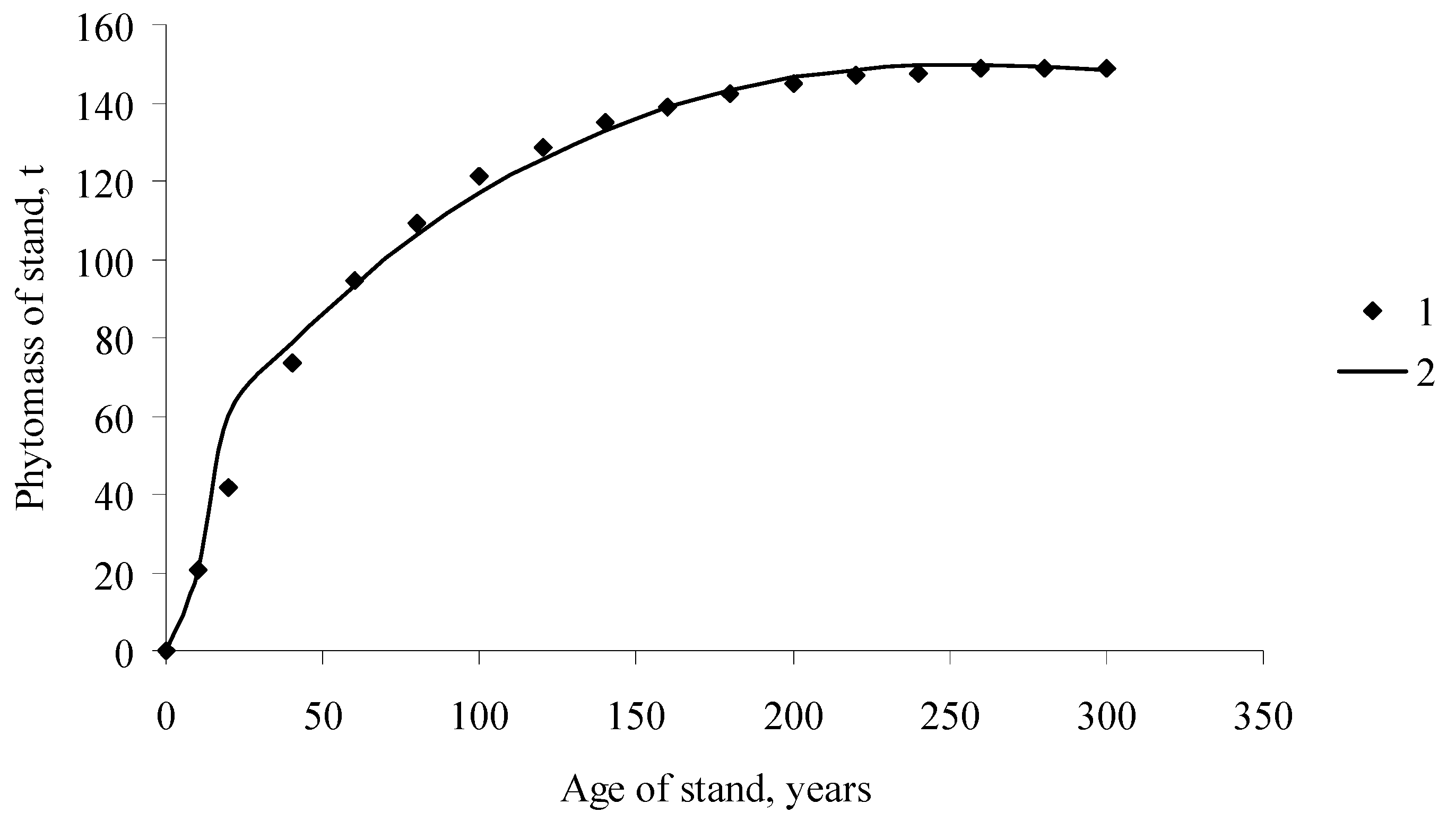



| Age, Years | Density, Trees/ha | Phytomass, t/ha | |||
|---|---|---|---|---|---|
| Stem with Bark | Needles | Branches | Roots * | ||
| 10 | 13,522 | 7.4 | 3.13 | 2.5 | 4.3 |
| 20 | 7528 | 25.7 | 3.64 | 4.2 | 8.9 |
| 40 | 3604 | 61.2 | 3.8 | 6.2 | 14.9 |
| 60 | 2167 | 85.4 | 3.71 | 7.4 | 18.0 |
| 80 | 1477 | 100.2 | 3.56 | 8.1 | 19.6 |
| 100 | 1075 | 108.3 | 3.41 | 8.6 | 20.4 |
| 120 | 827 | 113.1 | 3.27 | 8.9 | 20.8 |
| 140 | 656 | 114.4 | 3.13 | 9.1 | 20.8 |
| 160 | 542 | 113.8 | 3.0 | 9.2 | 20.6 |
| 180 | 453 | 112.6 | 2.89 | 9.3 | 20.4 |
| 200 | 382 | 110.7 | 2.78 | 9.4 | 20.1 |
| 220 | 331 | 107.7 | 2.68 | 9.4 | 19.7 |
| 240 | 289 | 104.5 | 2.59 | 9.4 | 19.2 |
| 260 | 255 | 101.5 | 2.51 | 9.4 | 18.7 |
| 280 | 226 | 97.8 | 2.42 | 9.3 | 18.3 |
| 300 | 202 | 94.7 | 2.35 | 9.3 | 17.9 |
| Woody Species, Location | ESM Parameters | ||
|---|---|---|---|
| A | α | s | |
| Pinus sylvestris L., 53°50′ N 92° E | 0.72 | 0.23 | 0.54 |
| Pinus sylvestris L., 51°45′ N 94°30′ E | 0.56 | 0.27 | 0.50 |
| Larix sibirica Ledeb., 54° N, 91°E | 1.60 | 0.09 | 0.23 |
| Larix sibirica Ledeb., 52° N, 95°30′ E | 1.39 | 0.17 | 0.70 |
| Picea obovata Ledeb., 56°35′ N, 57°40′ E | 1.10 | 0.11 | 0.70 |
| Picea obovata Ledeb., 59° N, 61° E | 0.73 | 0.28 | 0.39 |
| Abies sibirica Ledeb., 59° N, 93° E | 0.67 | 0.24 | 0.28 |
| Betula pendula Roth., 57° N, 93° E | 2.03 | 0.33 | 0.94 |
| Betula pendula Roth., 55°10′ N, 92° E | 1.83 | 0.31 | 0.67 |
| Pinus sylvestris L., 59°30′ N, 101°50′ E | 0.61 | 0.25 | 0.50 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soukhovolsky, V.; Ivanova, Y. Modeling Production Processes in Forest Stands: An Adaptation of the Solow Growth Model. Forests 2018, 9, 391. https://doi.org/10.3390/f9070391
Soukhovolsky V, Ivanova Y. Modeling Production Processes in Forest Stands: An Adaptation of the Solow Growth Model. Forests. 2018; 9(7):391. https://doi.org/10.3390/f9070391
Chicago/Turabian StyleSoukhovolsky, Vlad, and Yulia Ivanova. 2018. "Modeling Production Processes in Forest Stands: An Adaptation of the Solow Growth Model" Forests 9, no. 7: 391. https://doi.org/10.3390/f9070391
APA StyleSoukhovolsky, V., & Ivanova, Y. (2018). Modeling Production Processes in Forest Stands: An Adaptation of the Solow Growth Model. Forests, 9(7), 391. https://doi.org/10.3390/f9070391




