Neighbor and Height Effects on Crown Properties Associated with the Uniform-Stress Principle of Stem Formation
Abstract
1. Introduction
2. Lever Arm—Height to the Median of Leaf Area
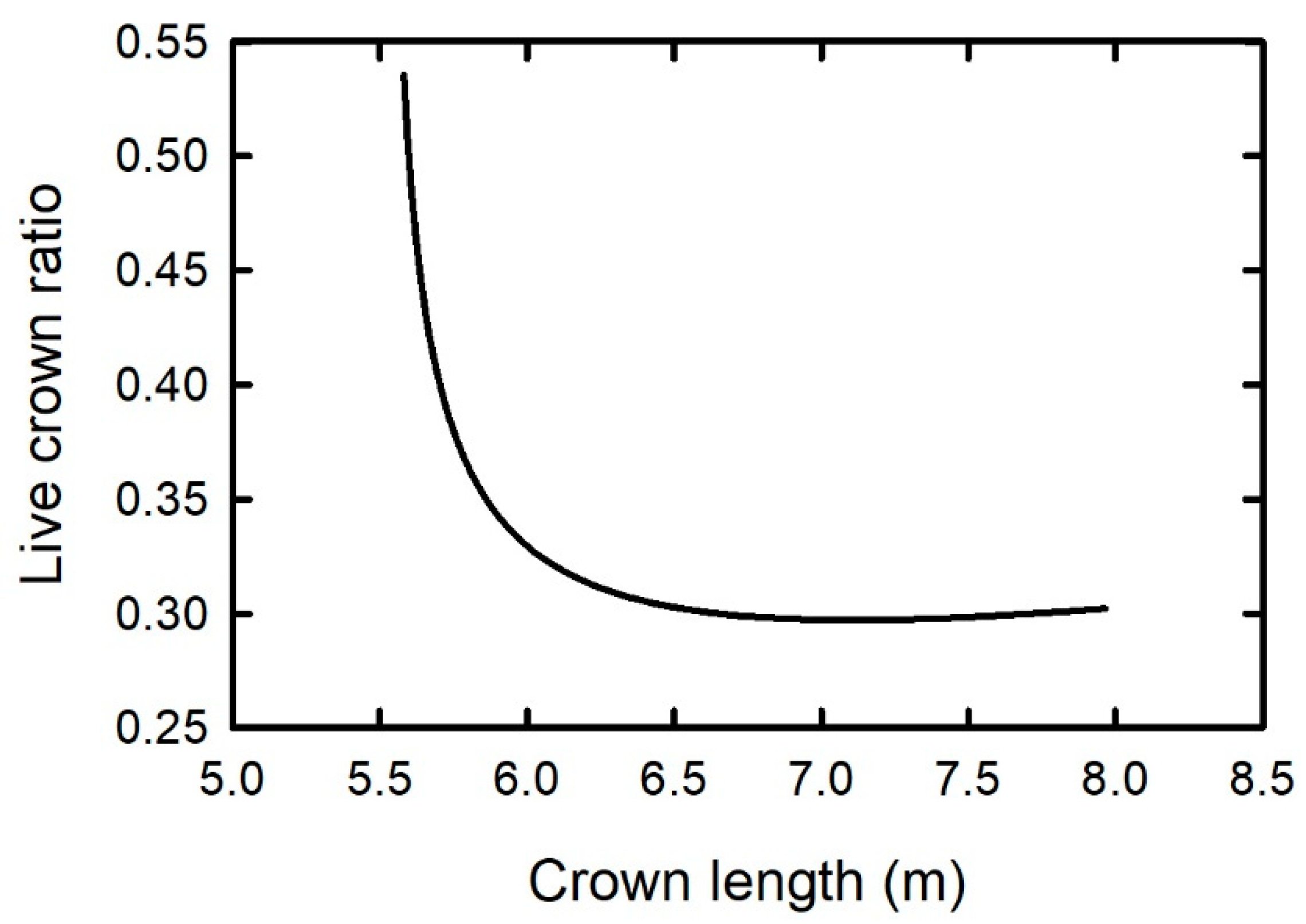
2.1. Height to the Base of the Live Crown
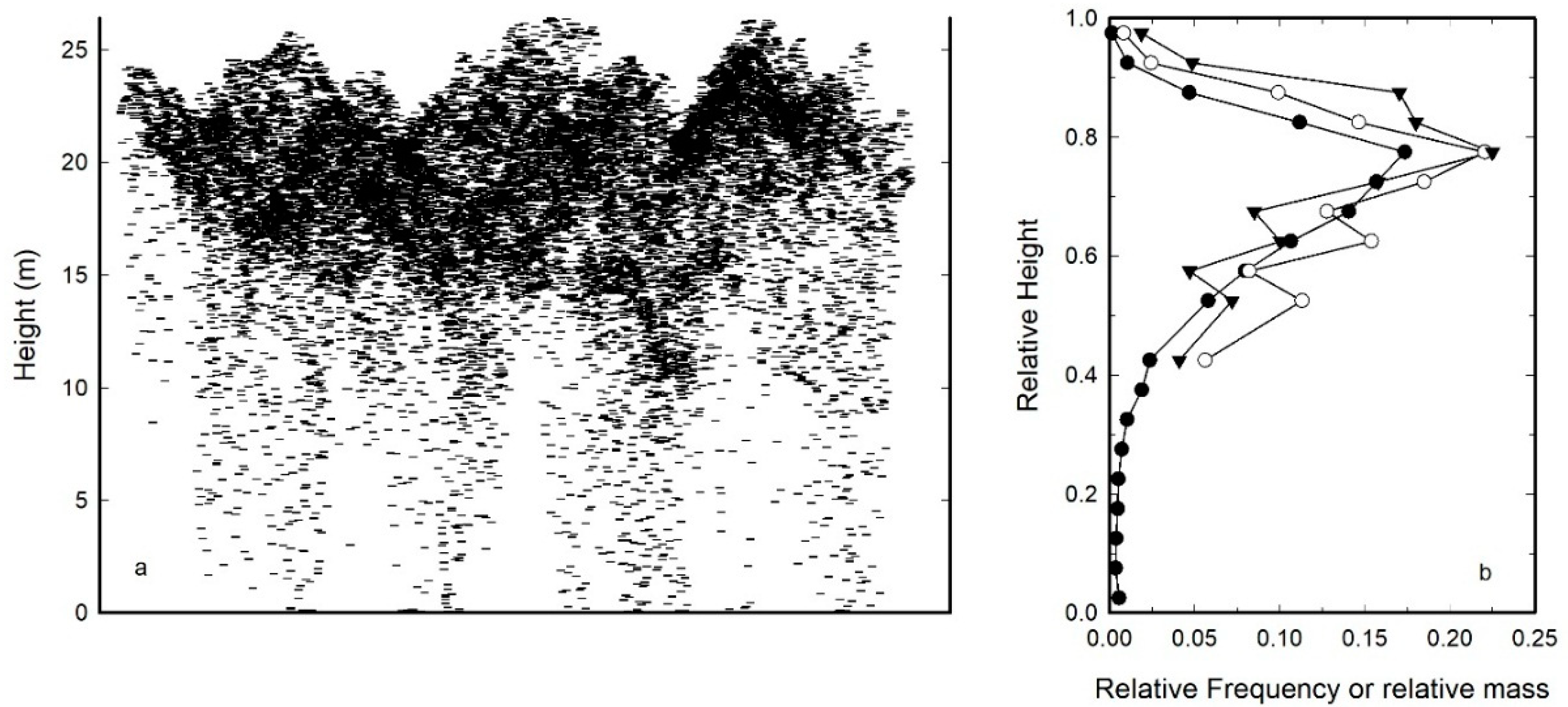
2.2. Height to Median Leaf Area
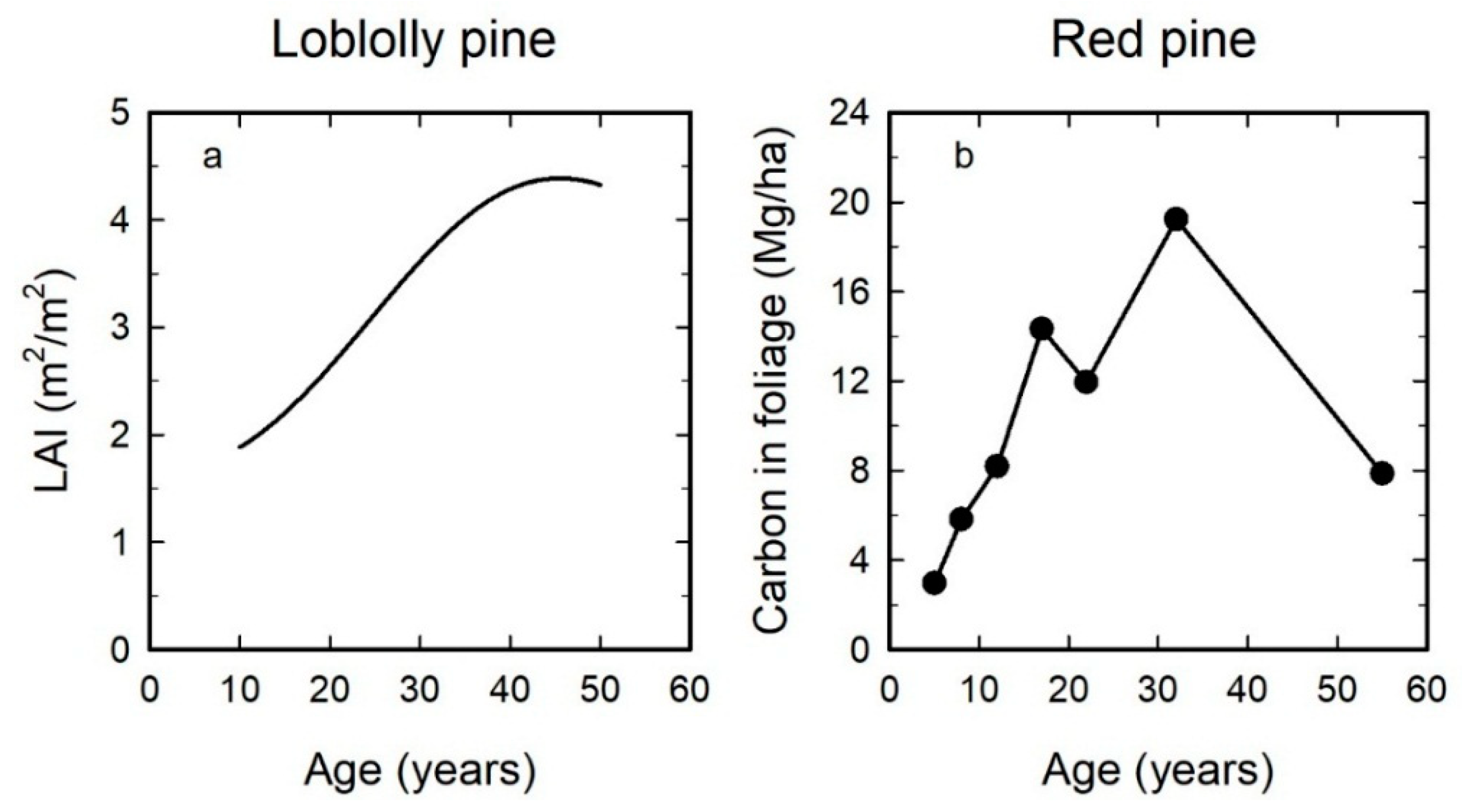
3. Mean Leaf Area per Tree
4. Potential for Including Physiological Processes in the Biomechanical Model
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Comstock, J.P.; Sperry, J.S. Theoretical considerations of optimal conduit length for water transport in vascular plants. New Phytol. 2000, 148, 195–218. [Google Scholar] [CrossRef]
- Sperry, J.S. Coordinating stomatal and xylem functioning—An evolutionary perspective. New Phytol. 2004, 162, 568–570. [Google Scholar] [CrossRef]
- Gardiner, B.; Byrne, K.; Hale, S.; Kamimura, K.; Mitchell, S.J.; Peltola, H.; Ruel, J.-C. A review of mechanistic modelling of wind damage risk to forests. Forestry 2008, 81, 447–463. [Google Scholar] [CrossRef]
- Moulia, B.; Coutand, C.; Julien, J.-L. Mechanosensitive control of plant growth: Bearing the load, sensing, transducing, and responding. Front. Plant Sci. 2015, 6, 52. [Google Scholar] [CrossRef] [PubMed]
- Valentine, H.T.; Amateis, R.L.; Gove, J.H.; Makela, A. Crown-rise and crown-length dynamics: Application to loblolly pine. Forestry 2013, 86, 371–375. [Google Scholar] [CrossRef]
- Mar:Möller, C. The effects of thinning, age, and site on foliage, increment, and loss of dry matter. J. For. 1947, 45, 393–404. [Google Scholar] [CrossRef]
- Madgwick, H.A.I.; Olson, D.F. Leaf area index and volume growth in thinned stands of Liriodendron tulipifera L. J. Appl. Ecol. 1974, 11, 575–579. [Google Scholar] [CrossRef]
- Martin, T.A.; Jokela, E.J. Stand development and production dynamics of loblolly pine under a range of cultural treatments in north-central Florida USA. For. Ecol. Manag. 2004, 192, 39–58. [Google Scholar] [CrossRef]
- Long, J.N.; Dean, T.J.; Roberts, S.D. Linkages between silviculture and ecology: Examination of several important conceptual models. For. Ecol. Manag. 2004, 200, 249–261. [Google Scholar] [CrossRef]
- Dean, T.J.; Baldwin, V.C. Crown management and stand density. In Growing Trees in a Greener World: Industrial Forestry in the 21st Century; 35th LSU Forestry Symposium; Carter, M.C., Ed.; Louisiana State University Agricultural Center, Louisiana Agricultural Experiment Station: Baton Rouge, LA, USA, 1996; pp. 148–159. [Google Scholar]
- Whitehead, D.; Edwards, W.R.N.; Jarvis, P.G. Conducting sapwood area, foliage area, and permeability in mature trees of Piceasitchensis and Pinuscontorta. Can. J. For. Res. 1984, 14, 940–947. [Google Scholar] [CrossRef]
- Long, J.N.; Smith, F.W.; Scott, D.R.W. The role of Douglas-fir stem sapwood and heartwood in the mechanical and physiological support of crown and development of stem form. Can. J. For. Res. 1981, 11, 459–464. [Google Scholar] [CrossRef]
- Mencuccini, M.; Grace, J.; Fioravanti, M. Biomechanical and hydraulic determinants of tree structure in Scots pine: Anatomical characteristics. Tree Physiol. 1997, 17, 105–113. [Google Scholar] [CrossRef] [PubMed]
- Woodrum, C.L.; Ewers, F.W.; Telewski, F.W. Hydraulic, biomechanical, and anatomical interactions of xylem from five species of Acer (Aceraceae). Am. J. Bot. 2003, 90, 693–699. [Google Scholar] [CrossRef] [PubMed]
- Dean, T.J.; Jerez, M.; Cao, Q.V. A simple stand growth model based on canopy dynamics and biomechanics. For. Sci. 2013, 59, 335–344. [Google Scholar] [CrossRef]
- Dean, T.J.; Long, J.N. Validity of constant-stress and elastic instability principles of stem formation in Pinus contorta and Trifolium pratense. Ann. Bot. 1986, 54, 833–840. [Google Scholar] [CrossRef]
- Metzger, K. Der Wind als massgebender Faktor für das Wachtsum der Bäume. Mundener Forstl. Hefte 1893, 3, 35–86. [Google Scholar]
- Assmann, E. The Principles of Forest Yield Study; Pergamon Press, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Jokela, E.J.; Harding, R.B.; Nowak, C.A. Long-term effects of fertilization on stem form, growth relations, and yield estimates of slash pine. For. Sci. 1989, 35, 832–842. [Google Scholar] [CrossRef]
- Morgan, J.; Cannell, M.G.R. Shape of tree stems—A re-examination of the uniform stress hypothesis. Tree Physiol. 1994, 14, 49–62. [Google Scholar] [CrossRef] [PubMed]
- Dean, T.J.; Roberts, S.D.; Gilmore, D.W.; Maguire, D.A.; Long, J.N.; O’Hara, K.L.; Seymour, R.S. An evaluation of the uniform stress hypothesis based on stem geometry in selected North American conifers. Trees Struct. Funct. 2002, 16, 559–568. [Google Scholar] [CrossRef]
- Cao, Q.V.; Dean, T.J. Predicting diameter at breast height from total height and crown length. In Proceedings of the 15th Bennial Southern Silvicultural Research Conference, SRS-GTR-17; Guldin, J.M., Ed.; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2013; pp. 201–205. [Google Scholar]
- Kidombo, S.D.; Dean, T.J. Growth of tree diameter and stem taper as affected by reduced leaf area on selected branch whorls. Can. J. For. Res. 2018, 48, 317–323. [Google Scholar] [CrossRef]
- West, P.W.; Jackett, D.R.; Sykes, S.J. Stresses in, and the shape of, tree stems in forest monoculture. J. Theor. Biol. 1989, 140, 327–343. [Google Scholar] [CrossRef]
- Niklas, K.J.; Spatz, H.C. Wind-induced stresses in cherry trees: Evidence against the hypothesis of constant stress levels. Trees Struct. Funct. 2000, 14, 230–237. [Google Scholar] [CrossRef]
- Minamino, R.; Tateno, M. Variation in susceptibility to wind along the trunk of an isolated Larix kaempferi (Pinaceae) tree. Am. J. Bot. 2014, 101, 1085–1091. [Google Scholar] [CrossRef] [PubMed]
- Dean, T.J. Effect of growth rate and wind sway on the relation between mechanical and water-flow properties in slash pine seedlings. Can. J. For. Res. 1991, 21, 1501–1506. [Google Scholar] [CrossRef]
- Valinger, E.; Lundqvist, L.; Sundberg, B. Mechanical stress during dormancy stimulates stem growth of scots pine seedlings. For. Ecol. Manag. 1994, 67, 299–303. [Google Scholar] [CrossRef]
- Lundqvist, L.; Valinger, E. Stem diameter growth of scots pine trees after increased mechanical load in the crown during dormancy and (or) growth. Ann. Bot. 1996, 77, 59–62. [Google Scholar] [CrossRef]
- Valentine, H.T.; Ludlow, A.R.; Furnival, G.M. Modeling crown rise in even-aged stands of Sitka spruce or loblolly pine. For. Ecol. Manag. 1994, 69, 189–197. [Google Scholar] [CrossRef]
- Long, J.N. A pratical approach to density management. For. Chron. 1985, 61, 23–27. [Google Scholar] [CrossRef]
- Dean, T.J.; Baldwin, V.C., Jr. Growth in loblolly pine plantations as a function of stand density and canopy properties. For. Ecol. Manag. 1996, 82, 49–58. [Google Scholar] [CrossRef]
- Beekhuis, J. Crown depth of radiata pine in relation to stand density and height. N. Z. J. For. 1965, 10, 43–61. [Google Scholar]
- Meng, S.X.; Rudnicki, M.; Lieffers, V.J.; Reid, D.E.B.; Silins, U. Preventing crown collisions increases the crown cover and leaf area of maturing lodgepole pine. J. Ecol. 2006, 94, 681–686. [Google Scholar] [CrossRef]
- Long, J.N.; Smith, F.W. Volume increment in Pinus contorta var. latifolia: The influence of stand development and crown dynamics. For. Ecol. Manag. 1992, 53, 53–64. [Google Scholar] [CrossRef]
- Putz, F.E. Mechanical abrasion and intercrown spacing. Am. Midl. Nat. 1984, 112, 24–28. [Google Scholar] [CrossRef]
- Ward, W.W. Live Crown Ratio and Stand Density in Young, Even-Aged, Red Oak Stands. For. Sci. 1964, 10, 56–65. [Google Scholar] [CrossRef]
- Dyer, M.E.; Burkhart, H.E. Compatible crown ratio and crown height models. Can. J. For. Res. 1987, 17, 572–574. [Google Scholar] [CrossRef]
- Hasenauer, H.; Monserud, R.A. A crown ratio model for Austrian forests. For. Ecol. Manag. 1996, 84, 49–60. [Google Scholar] [CrossRef]
- Dean, T.J. Using live-crown ratio to control wood quality: An example of quantitative silviculture. Presented at the Tenth Bennial Southern Silvicultural Research Conference, Shreveport, LA, USA, 16 February 1999; Haywood, J.D., Ed.; Gen. Tech. Rep. SRS-30. U.S. Department of Agriculture, Southern Research Station: Asheville, NC, USA, 1999; pp. 511–514. [Google Scholar]
- Zhao, D.; Kane, M.; Borders, B.E. Crown ratio and relative spacing relationships for Loblolly pine plantations. Open J. For. 2012, 2, 110–115. [Google Scholar] [CrossRef]
- Wilson, F.G. Numerical expression of stocking in terms of height. J. For. 1946, 44, 758–761. [Google Scholar]
- Hasenauer, H.; Monserud, R.A.; Gregoire, T.G. Using simultaneous regression techniques with individual-tree growth models. For. Sci. 1998, 44, 87–95. [Google Scholar] [CrossRef]
- Dean, T.J.; Long, J.N. Influence of leaf area and canopy structure on size-density relations in even-aged lodgepole pine stands. For. Ecol. Manag. 1992, 49, 109–117. [Google Scholar] [CrossRef]
- Smith, N.J. A model of stand allometry and biomass allocation during the self-thinning process. Can. J. For. Res. 1986, 16, 990–995. [Google Scholar] [CrossRef]
- Cao, Q.V.; Dean, T.J.; Baldwin, V.C., Jr. Modeling the size-density relationship in direct-seeded slash pine stands. For. Sci. 2000, 46, 317–324. [Google Scholar] [CrossRef]
- VanderSchaaf, C.L. Estimating individual stand size-density trajectories and a maximum size-density relationship species boundary line slope. For. Sci. 2010, 56, 327–335. [Google Scholar] [CrossRef]
- Hutchings, M.J.; Budd, C.S.J. Plant competition and its course through time. Bioscience 1981, 3, 640–645. [Google Scholar] [CrossRef]
- Gray, H.R. The Form and Taper of Forest-Tree Stems; Imperian Forestry Institute, University of Oxford: Oxford, UK, 1956. [Google Scholar]
- Wang, Y.P.; Jarvis, P.G. Influence of crown structural properties on PAR absorption, photosynthesis, and transpiration in sitka spruce—Application of a model (MAESTRO). Tree Physiol. 1990, 7, 297–316. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.W. Estimation of foliage denseness and foliage angle by inclined point quadrats. Aust. J. Bot. 1963, 11, 95–105. [Google Scholar] [CrossRef]
- Stenberg, P.; Kuuluvainen, T.; Kellomäki, S.; Jokela, E.J.; Gholz, H.L.; Gholz, H.L.; Linder, S.; McMurtrie, R.E. Crown structure, light interception, and productivity of pine trees and stands. Ecol. Bull. 1994, 43, 20–34. [Google Scholar]
- Stephens, G.R. Productivity of red pine, 1. Foliage distribution in tree crown and stand canopy. Agric. Meteorol. 1969, 6, 275–282. [Google Scholar] [CrossRef]
- Schreuder, H.T.; Swank, W.T. Coniferous Stands Characterized with The Weibull Distribution. Can. J. For. Res. 1974, 4, 518–523. [Google Scholar] [CrossRef]
- Xu, M.; Harrington, T.B.; Edwards, M.B. Responses of Loblolly Pine Biomass and Specific Leaf Area to Various Site Preparation Treatments; Edwards, M.B., Ed.; U.S.D.A., Forest Service, Southern Research Station: Ashsville, NC, USA, 1995; pp. 495–499.
- Jerez, M.; Dean, T.J.; Cao, Q.V.; Roberts, S.D. Describing leaf area distribution in loblolly pine trees with Johnson’s SB function. For. Sci. 2005, 51, 93–101. [Google Scholar] [CrossRef]
- Mori, S.; Hagihara, A. Crown profile of foliage area characterized with the weibull distribution in a hinoki (Chamaecyparis obtusa) stand. Trees Struct. Funct. 1991, 5, 149–152. [Google Scholar] [CrossRef]
- Maguire, D.A.; Bennett, W.S. Patterns in vertical distribution of foliage in young coastal Douglas-fir. Can. J. For. Res. 1996, 26, 1991–2005. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Zhao, F.; Yang, X.; Strahler, A.H.; Schaaf, C.L.; Yao, T.; Wang, Z.; Román, M.O.; Woodcock, C.E.; Ni-Meister, W.; Jupp, D.L.B.; et al. A comparison of foliage profiles in the Sierra National Forest obtained with a full-waveform under-canopy EVI lidar system with the foliage profiles obtained with an airborne full-waveform LVIS lidar system. Remote Sens. Environ. 2013, 136, 330–341. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. Lidar Remote Sensing of Forest Structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
- Parker, R.C.; Evans, D.L. An Application of Lidar in a Double-Sample Forest Inventory. West. J. Appl. For. 2004, 19, 95–101. [Google Scholar] [CrossRef]
- Evans, D.L.; Roberts, S.D.; Parker, R.C. LiDAR—A new tool for forest measurements? For. Chron. 2006, 82, 211–218. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Dean, T.J.; Cao, Q.V.; Roberts, S.D.; Evans, D.L. Measuring heights to crown base and crown median with LiDAR in a mature, even-aged loblolly pine stand. For. Ecol. Manag. 2009, 257. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A.T. Estimating canopy structure of Douglas-fir stands from discrete-return LiDAR. Trees Struct. Funct. 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Cao, Q.V.; Dean, T.J. Modeling crown structure from LiDAR data with statistical distributions. For. Sci. 2011, 57, 359–364. [Google Scholar]
- Baldwin, J.V.C. Is sapwood area a better predictor of loblolly pine crown biomass than bole diameter. Biomass 1989, 20, 177–185. [Google Scholar] [CrossRef]
- Roberts, S.D.; Dean, T.J.; Evans, D.L. Family influences on leaf area estimates derived from crown and tree dimensions in Pinus taeda. For. Ecol. Manag. 2003, 172, 261–270. [Google Scholar] [CrossRef]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manag. 2005, 213, 54–70. [Google Scholar] [CrossRef]
- Fang, H.; Xiao, Z.; Qu, Y.; Song, J. Leaf Area Index. In Advanced Remote Sensing; Liang, S., Li, X., Wang, J., Eds.; Academic Press: San Diego, CA, USA, 2012; pp. 347–381. ISBN 9780123859549. [Google Scholar]
- King, J.S.; Giardina, C.P.; Pregitzer, K.S.; Friend, A.L. Biomass partitioning in red pine (Pinus resinos) along a chronosequence in the Upper Peninsula of Michigan. Can. J. For. Res. 2007, 37, 93–102. [Google Scholar] [CrossRef]
- Gillespie, A.; Allen, H.; Vose, J.M. Amount and vertical distribution of foliage of young loblolly pine trees as affected by canopy position and silvicultural treatment. Can. J. For. Res. 1994, 24, 1337–1344. [Google Scholar] [CrossRef]
- Pearcy, R.W.; Yang, W.M. A three-dimensional crown architecture model for assessment of light capture and carbon gain by understory plants. Oecologia 1996, 108, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Albaugh, T.J.; Allen, H.L.; Fox, T.R. Individual tree crown and stand development in Pinus taeda under different fertilization and irrigation regimes. For. Ecol. Manag. 2006, 234, 10–23. [Google Scholar] [CrossRef]
- Kennedy, M. Functional–structural models optimize the placement of foliage units for multiple whole-canopy functions. Ecol. Res. 2010, 25, 723–732. [Google Scholar] [CrossRef]
- Sprugel, D.G. The relationship of evergreenness, crown architecture, and leaf size. Am. Nat. 1989, 133, 465–479. [Google Scholar] [CrossRef]
- Brix, H. Effects of thinning and nitrogen fertilization on growth of Douglas-fir: Relative contribution of foliage quantity and efficiency. Can. J. For. Res. 1983, 13, 167–175. [Google Scholar] [CrossRef]
- Teskey, R.O.; Gholz, H.L.; Cropper, W.P. Influence of climate and fertilization on net photosynthesis of mature slash pine. Tree Physiol. 1994, 14, 1215–1227. [Google Scholar] [CrossRef] [PubMed]
- Albaugh, T.J.; Allen, H.L.; Dougherty, P.M.; Kress, L.W.; King, J.S. Leaf area and above- and belowground growth responses of loblolly pine to nutrient and water additions. For. Sci. 1998, 44, 317–328. [Google Scholar]
- Jokela, E.J.; Dougherty, P.M.; Martin, T.A. Production dynamics of intensively managed loblolly pine stands in the southern United States: A synthesis of seven long-term experiments. For. Ecol. Manag. 2004, 192, 117–130. [Google Scholar] [CrossRef]
- Cieszewski, C.; Bailey, R.L. Generalized algebraic difference approach: Theory based derivation of dynamic site equations with polymorphism and variable asymptotes. For. Sci. 2000, 46, 116–126. [Google Scholar]
- Cieszewski, C.J. Three methods of deriving advanced dynamic site equations demonstrated on inland Douglas-fir site curves. Can. J. For. Res. 2001, 31, 165–173. [Google Scholar] [CrossRef]
- Gömöryova, E.; Gömory, D. Relationships between environmental factors and height growth and yield of Norway spruce stands: A factor-analytic approach. Forestry 1995, 68, 145–152. [Google Scholar] [CrossRef]
- Dean, T.J. Basal area increment and growth efficiency as functions of canopy dynamics and stem mechanics. For. Sci. 2004, 50, 106–116. [Google Scholar]
- Dean, T.J.; Baldwin, V.C., Jr. The relationship between Reineke’s stand-density index and physical stem mechanics. For. Ecol. Manag. 1996, 81, 25–34. [Google Scholar] [CrossRef]
- Jaffe, M.J. Thigmomorphogenesis: The response of plant growth and development to mechanical stimulation. Planta 1973, 114, 143–157. [Google Scholar] [CrossRef] [PubMed]
- Telewski, F.W.; Jaffe, M. Thigmomorphogenesis: Anatomical, morphological and mechanical analysis of genetically different sibs of Pinus taeda in response to mechanical pertubation. Physiol. Plant. 1986, 66, 219–226. [Google Scholar] [CrossRef] [PubMed]
- Telewski, F.W.; Pruyn, M.L. Thigmomorphogenesis: A dose response to flexing in Ulmus americana seedlings. Tree Physiol. 1998, 18, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Lundqvist, L.; Elfving, B. Influence of biomechanics and growing space on tree growth in young Pinus sylvestris stands. For. Ecol. Manag. 2010, 260, 2143–2147. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dean, T.J. Neighbor and Height Effects on Crown Properties Associated with the Uniform-Stress Principle of Stem Formation. Forests 2018, 9, 334. https://doi.org/10.3390/f9060334
Dean TJ. Neighbor and Height Effects on Crown Properties Associated with the Uniform-Stress Principle of Stem Formation. Forests. 2018; 9(6):334. https://doi.org/10.3390/f9060334
Chicago/Turabian StyleDean, Thomas J. 2018. "Neighbor and Height Effects on Crown Properties Associated with the Uniform-Stress Principle of Stem Formation" Forests 9, no. 6: 334. https://doi.org/10.3390/f9060334
APA StyleDean, T. J. (2018). Neighbor and Height Effects on Crown Properties Associated with the Uniform-Stress Principle of Stem Formation. Forests, 9(6), 334. https://doi.org/10.3390/f9060334




