Allometric Equations for Predicting Culm Surface Area of Three Bamboo Species (Phyllostachys spp.)
Abstract
:1. Introduction
- (1)
- Are the allometric equations site-specific?
- (2)
- Are the allometric equations species-specific?
- (3)
- What predictive variable is optimal for S prediction?
2. Materials and Methods
2.1. Study Sites
2.2. Field Measurements
2.3. Analyses Methods
3. Results and Discussion
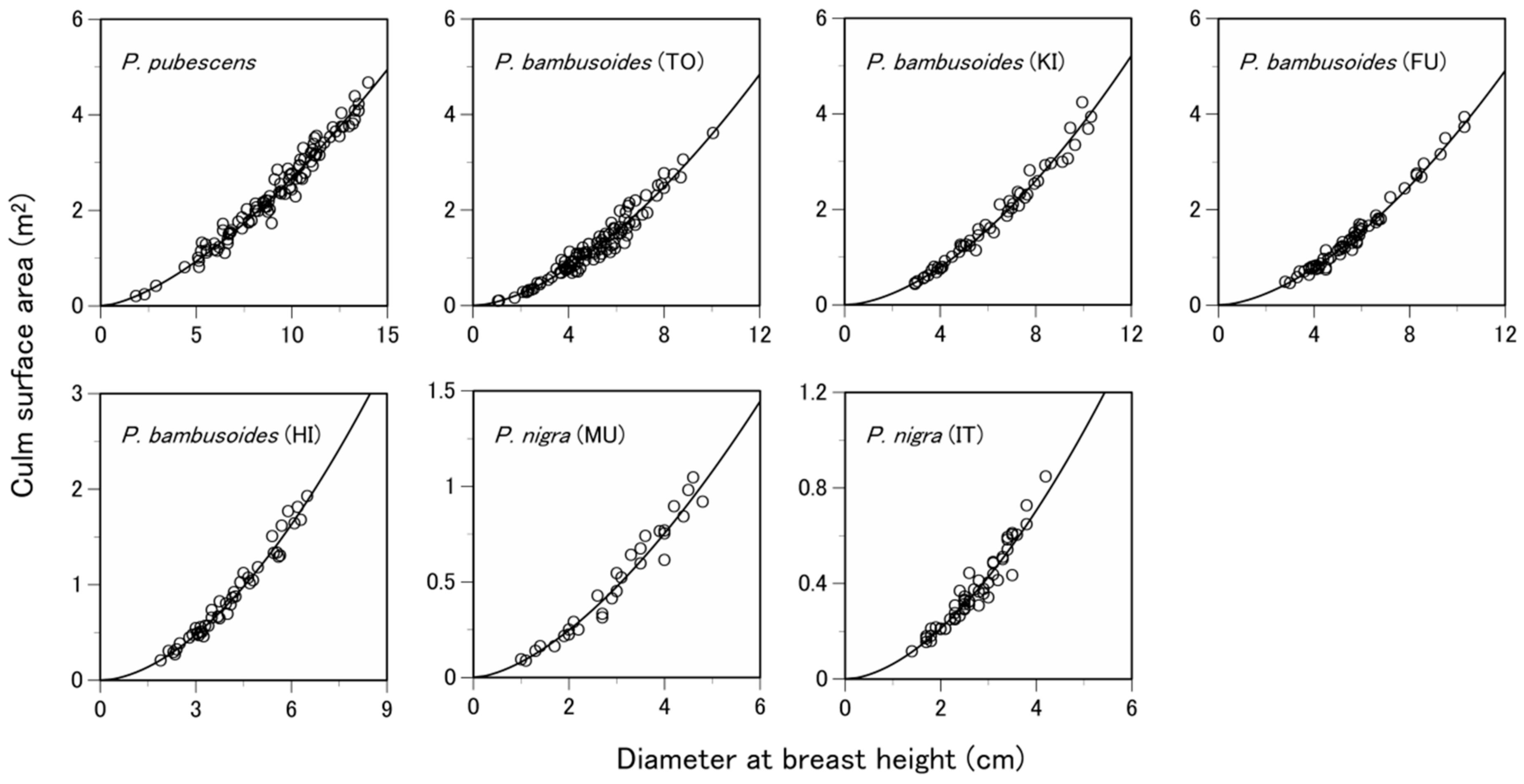
3.1. Are the Allometric Equations Site-Specific?
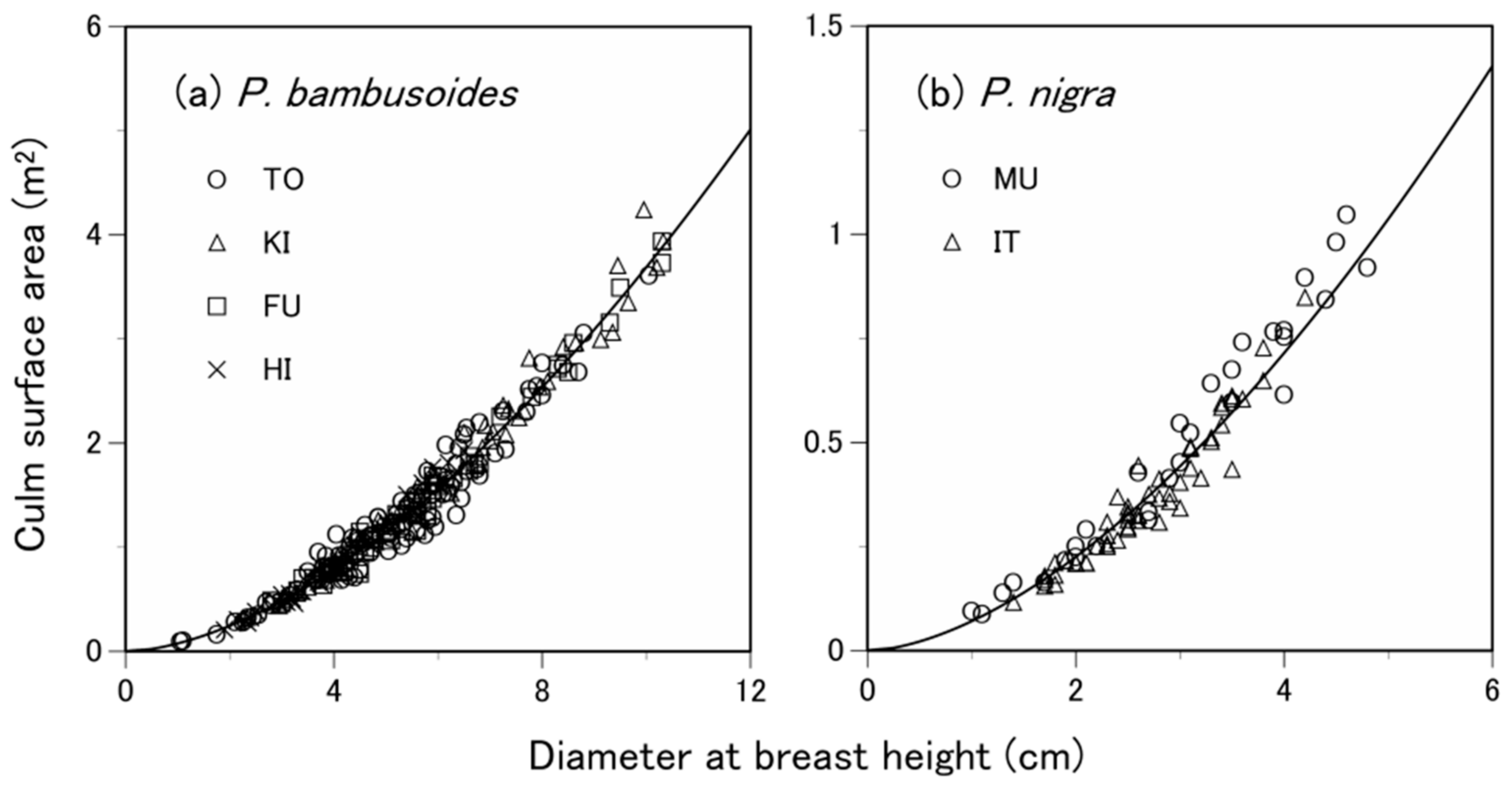
3.2. Are the Allometric Equations Species-Specific?
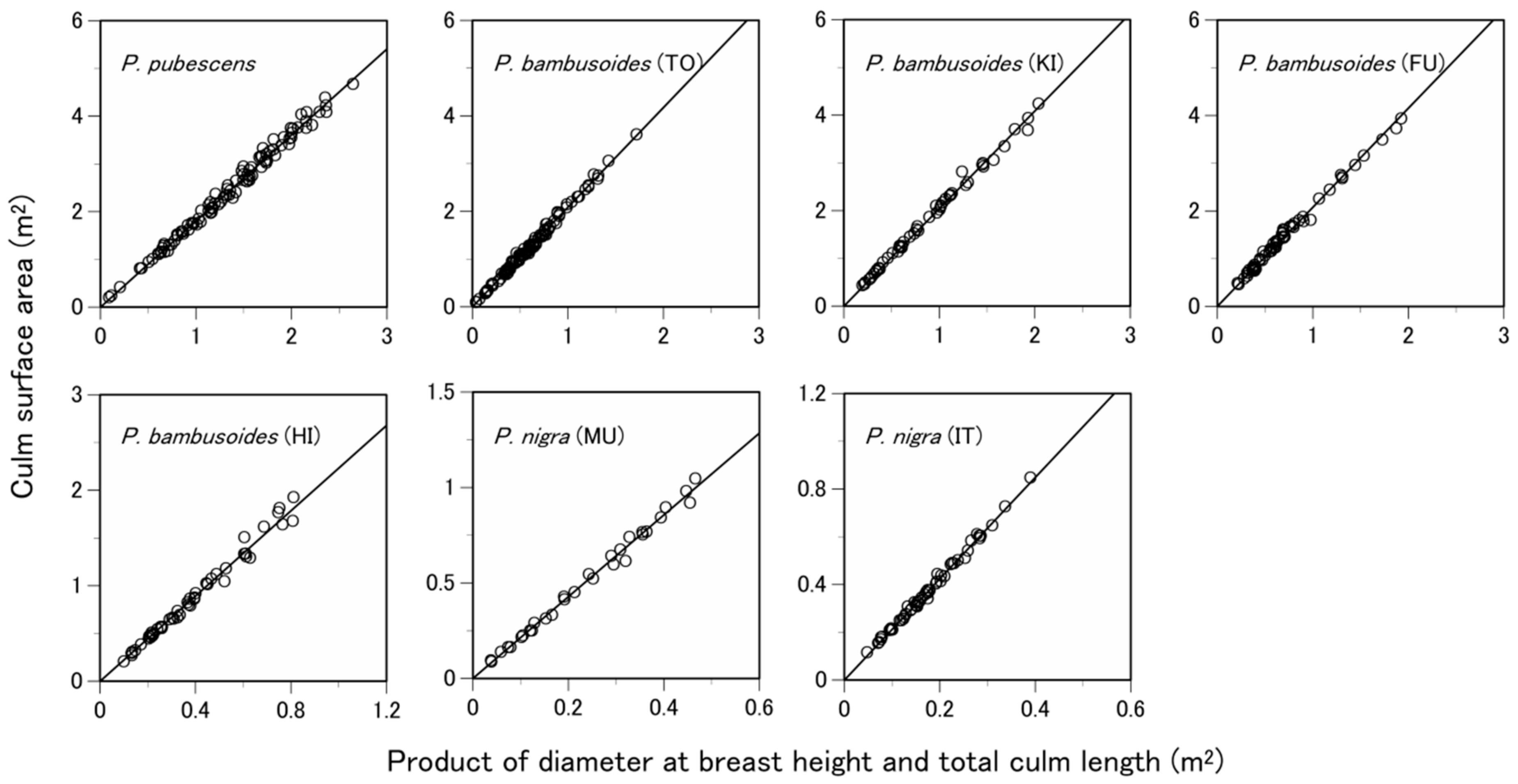
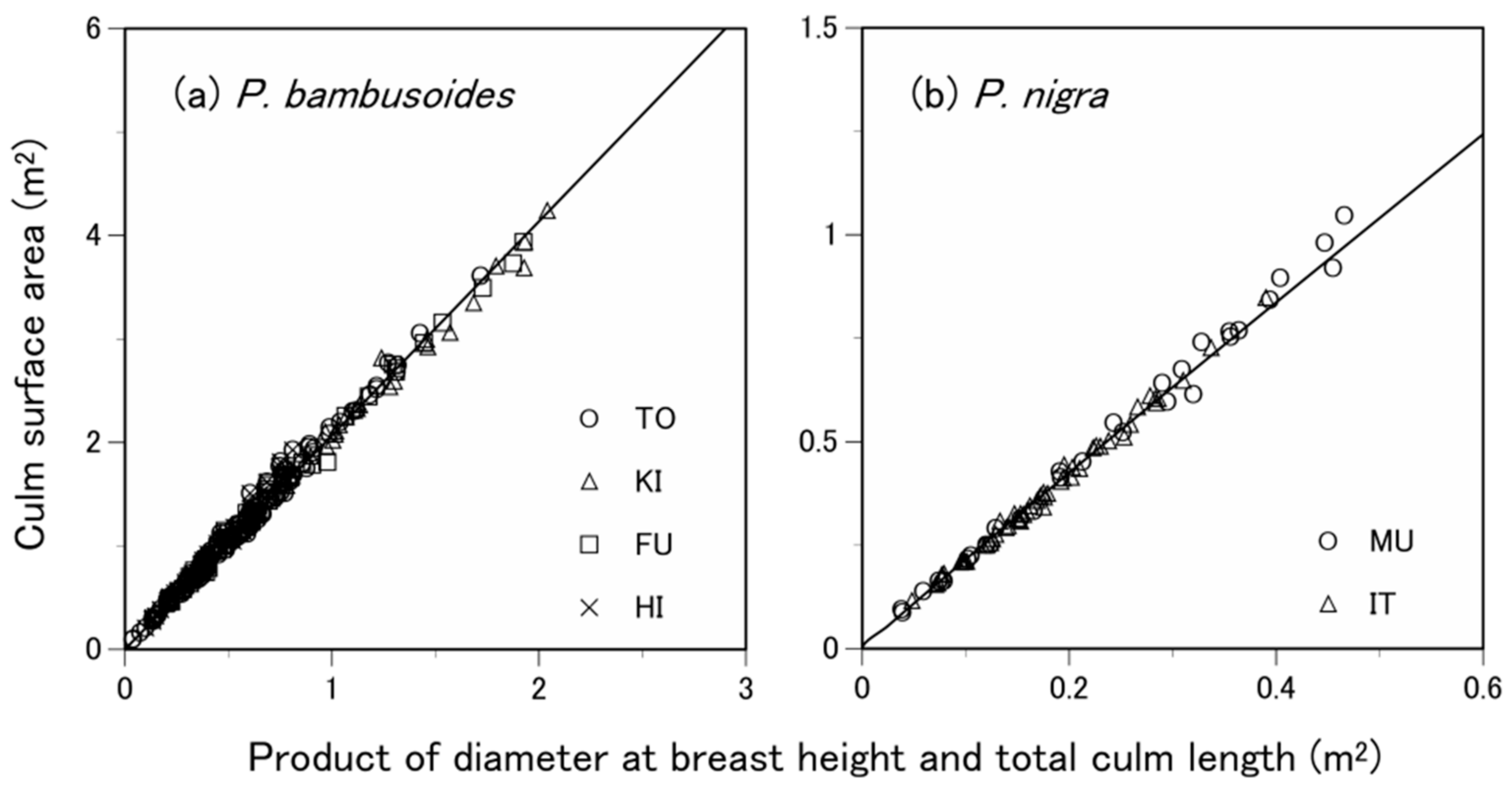
3.3. What Predictive Variable Is Optimal for S Prediction?
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lucas, S. Bamboo; Reaktion Books: London, UK, 2013. [Google Scholar]
- Clark, L.G.; Londoño, X.; Ruiz-Sanchez, E. Bamboo taxonomy and habitat. In Bamboo: The Plant and Its Uses; Liese, W., Köhl, M., Eds.; Springer: Cham, Switzerland, 2015; pp. 1–30. [Google Scholar]
- Kuehl, Y. Resource, yield, and volume of bamboos. In Bamboo: The Plant and Its Uses; Liese, W., Köhl, M., Eds.; Springer: Cham, Switzerland, 2015; pp. 91–111. [Google Scholar]
- Song, X.; Zhou, G.; Jiang, H.; Yu, S.; Fu, J.; Li, W.; Wang, W.; Ma, Z.; Peng, C. Carbon sequestration by Chinese bamboo forests and their ecological benefits: Assessment of potential, problems, and future challenge. Environ. Rev. 2011, 19, 418–428. [Google Scholar] [CrossRef]
- Song, X.; Peng, C.; Zhou, G.; Gu, H.; Li, Q.; Zhang, C. Dynamic allocation and transfer of non-structural carbohydrate, a possible mechanism for the explosive growth of Moso bamboo (Phyllostachys heterocycla). Sci. Rep. 2016, 6, 25908. [Google Scholar] [CrossRef] [PubMed]
- Yen, T.M. Culm height development, biomass accumulation and carbon storage in an initial growth stage for a fast-growing moso bamboo (Phyllostachys pubescens). Bot. Stud. 2016, 57, 10. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Zhou, G.; Du, H.; Lu, D.; Mo, L.; Xu, X.; Shi, Y.; Zhou, Y. Current and potential carbon stocks in Moso bamboo forests in China. J. Environ. Manag. 2015, 156, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Liu, Q.; Zhu, Z.; Shen, Y. Managing bamboo for carbon sequestration, bamboo stem and bamboo shoots. Small-Scale For. 2015, 14, 233–243. [Google Scholar] [CrossRef]
- Xu, L.; Shi, Y.; Zhou, G.; Xu, X.; Liu, E.; Zhou, Y.; Li, C.; Fang, H.; Deng, X. Temporal change in aboveground culms carbon stocks in the Moso bamboo forests and its driving factors in Zhejiang Province, China. Forests 2017, 8, 371. [Google Scholar] [CrossRef]
- Lin, M.Y.; Hsieh, I.F.; Lin, P.H.; Laplace, S.; Ohashi, M.; Chen, T.H.; Kume, T. Moso bamboo (Phyllostachys pubescens) forests as a significant carbon sink? A case study based on 4-year measurements in central Taiwan. Ecol. Res. 2017, 32, 845–857. [Google Scholar] [CrossRef]
- Yuen, J.Q.; Fung, T.; Ziegler, A.D. Carbon stocks in bamboo ecosystems worldwide: Estimates and uncertainties. For. Ecol. Manag. 2017, 393, 113–138. [Google Scholar] [CrossRef]
- Düking, R.; Gielis, J.; Liese, W. Carbon flux and carbon stock in a bamboo stand and their relevance for mitigating climate change. J. Am. Bamboo Soc. 2011, 24, 1–7. [Google Scholar]
- Zhou, G.; Meng, C.; Jiang, P.; Xu, Q. Review of carbon fixation in bamboo forests in China. Bot. Rev. 2011, 77, 262–270. [Google Scholar] [CrossRef]
- Zachariah, E.J.; Sabulal, B.; Nair, D.N.K.; Johnson, A.J.; Kumar, C.S.P. Carbon dioxide emission from bamboo culms. Plant Biol. 2016, 18, 400–405. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Jiang, P.; Wang, H.; Zhou, G.; Wu, J.; Yang, F.; Qian, X. Seasonal soil CO2 efflux dynamics after land use change from a natural forest to Moso bamboo plantations in subtropical China. For. Ecol. Manag. 2011, 262, 1131–1137. [Google Scholar] [CrossRef]
- Hsieh, I.F.; Kume, T.; Lin, M.Y.; Cheng, C.H.; Miki, T. Characteristics of soil CO2 efflux under an invasive species, Moso bamboo, in forests of central Taiwan. Trees 2016, 30, 1749–1759. [Google Scholar] [CrossRef]
- Tang, X.; Fan, S.; Qi, L.; Guan, F.; Du, M.; Zhang, H. Soil respiration and net ecosystem production in relation to intensive management in Moso bamboo forests. Catena 2016, 137, 219–228. [Google Scholar] [CrossRef]
- Isagi, Y. Carbon stock and cycling in a bamboo Phyllostachys bambusoides stand. Ecol. Res. 1994, 9, 47–55. [Google Scholar] [CrossRef]
- Isagi, Y.; Kawahara, T.; Kamo, K.; Ito, H. Net production and carbon cycling in a bamboo Phyllostachys pubescens stand. Plant Ecol. 1997, 130, 41–52. [Google Scholar] [CrossRef]
- Kim, M.H.; Nakane, K.; Lee, J.T.; Bang, H.S.; Na, Y.E. Stem/branch maintenance respiration of Japanese red pine stand. For. Ecol. Manag. 2007, 243, 283–290. [Google Scholar] [CrossRef]
- Harris, N.L.; Hall, C.A.S.; Lugo, A.E. Estimates of species- and ecosystem-level respiration of woody stems along an elevational gradient in the Luquillo Mountains, Puerto Rico. Ecol. Model. 2008, 216, 253–264. [Google Scholar] [CrossRef]
- Robertson, A.L.; Malhi, Y.; Farfan-Amezquita, F.; Aragão, L.E.O.C.; Silva Espejo, J.E.; Robertson, M.A. Stem respiration in tropical forests along an elevation gradient in the Amazon and Andes. Glob. Chang. Biol. 2010, 16, 3193–3204. [Google Scholar] [CrossRef]
- Zhao, K.; Dong, B.; Jia, Z.; Ma, L. Effect of climatic factors on the temporal variation of stem respiration in Larix principis-rupprechtii Mayr. Agric. For. Meteorol. 2018, 248, 441–448. [Google Scholar] [CrossRef]
- Damesin, C.; Ceschia, E.; Le Goff, N.; Ottorini, J.M.; Dufrêne, E. Stem and branch respiration of beech: From tree measurements to estimations at the stand level. New Phytol. 2002, 153, 159–172. [Google Scholar] [CrossRef]
- Inoue, A.; Sakamoto, M. Comparison of the methods for quantifying the culm surface area for bamboo, Phyllostachys pubescens. Ecol. Res. 2017, 32, 445–450. [Google Scholar] [CrossRef]
- Gavrikov, V.L. Stem Surface Area in Modeling of Forest Stands; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Inoue, A. Relationships of stem surface area to other stem dimensions for Japanese cedar (Cryptomeria japonica D. Don) and Japanese cypress (Chamaecyparis obtusa Endl.) trees. J. For. Res. 2004, 9, 45–50. [Google Scholar] [CrossRef]
- Pokorný, R.; Tomásková, I. Allometric relationships for surface area and dry mass of young Norway spruce aboveground organs. J. For. Sci. 2007, 53, 548–554. [Google Scholar] [CrossRef]
- Brantley, S.T.; Schulte, M.L.; Bolstad, P.V.; Miniat, C.F. Equations for estimating biomass, foliage area, and sapwood of small trees in the southern Appalachians. For. Sci. 2016, 62, 414–421. [Google Scholar] [CrossRef]
- Coletta, V.; Menguzzato, G.; Pellicone, G.; Veltri, A.; Marziliano, P.A. Effect of thinning on above-ground biomass accumulation in a Douglas-fir plantation in southern Italy. J. For. Res. 2016, 27, 1313–1320. [Google Scholar] [CrossRef]
- Marziliano, P.A.; Lafortezza, R.; Medicamento, U.; Lorusso, L.; Giannico, V.; Colangelo, C.; Sanesi, G. Estimating belowground biomass and root/shoot ratio of Phillyrea latifolia L. in the Mediterranean forest landscapes. Ann. For. Sci. 2015, 72, 585–593. [Google Scholar] [CrossRef]
- Nath, A.J.; Das, G.; Das, A.K. Above ground standing biomass and carbon storage in village bamboos in North East India. Biomass Bioenergy 2009, 33, 1188–1196. [Google Scholar] [CrossRef]
- Inoue, A.; Sakamoto, S.; Suga, H.; Kitahara, F. Estimation of culm volume for bamboo, Phyllostachys bambusoides, by two-way volume equation. Biomass Bioenergy 2011, 35, 2666–2673. [Google Scholar] [CrossRef]
- Inoue, A.; Sakamoto, S.; Kitazato, H.; Sakuta, K. Development of two-way volume equation for bamboo, Phyllostachys nigra. J. For. Plan. 2012, 18, 13–19. [Google Scholar] [CrossRef]
- Inoue, A.; Sakamoto, S.; Suga, H.; Kitazato, H.; Sakuta, K. Construction of one-way volume table for the three major useful bamboos in Japan. J. For. Res. 2013, 18, 323–334. [Google Scholar] [CrossRef]
- Suga, H.; Inoue, A.; Kitahara, F. Derivation of two-way volume equation for bamboo, Phyllostachys pubescens. J. For. Res. 2011, 16, 261–267. [Google Scholar] [CrossRef]
- Yuen, J.Q.; Fung, T.; Ziegler, A.D. Review of allometric equations for major land cover in SE Asia: Uncertainly and implications for above- and below-ground carbon estimates. For. Ecol. Manag. 2016, 360, 323–340. [Google Scholar] [CrossRef]
- Singnar, P.; Das, M.C.; Sileshi, G.W.; Brahma, B.; Nath, A.J.; Das, A.K. Allometric scaling, biomass accumulation and carbon stocks in different aged stands of thin-walled bamboos Schizostachyum dullooa, Pseudostachyum polymorphum and Melocanna baccifera. For. Ecol. Manag. 2017, 395, 81–91. [Google Scholar] [CrossRef]
- Inoue, A.; Suga, H. Relationships of culm surface area to other culm dimensions for bamboo, Phyllostachys pubescens. J. For. Res. 2009, 14, 236–239. [Google Scholar] [CrossRef]
- Yen, T.M.; Lee, J.S. Comparing aboveground carbon sequestration between moso bamboo (Phyllostachys heterocycla) and China fir (Cunninghamia lanceolata) forests based on the allometric model. For. Ecol. Manag. 2011, 261, 995–1002. [Google Scholar] [CrossRef]
- Uchimura, E. Utilization of Bamboo Resources into Modern Days; Soshinsya: Tokyo, Japan, 2009. (In Japanese) [Google Scholar]
- FAO. Global Forest Resources Assessment 2010: Main Report; FAO: Rome, Italy, 2010. [Google Scholar]
- Uchimura, E. A Flora of Bamboo Resources; Soshinsya: Tokyo, Japan, 2012. (In Japanese) [Google Scholar]
- Takano, K.T.; Hibino, K.; Numata, A.; Oguro, M.; Aiba, M.; Shiogama, H.; Takayabu, I.; Nakashizuka, T. Detecting latitudinal and altitudinal expansion of invasive bamboo Phyllostachys edulis and Phyllostachys bambusoides (Poaceae) in Japan to project potential habitats under 1.5 °C–4.0 °C global warming. Ecol. Evol. 2017, 7, 9848–9859. [Google Scholar] [CrossRef] [PubMed]
- Japan Meteorological Agency. Archives of the Past Meteorological Data (In Japanese). Available online: http://www.data.jma.go.jp/obd/stats/etrn/index.php (accessed on 31 March 2018).
- Ministry of Land, Infrastructure and Transport. National Land Policy (In Japanese). Available online: http://www.mlit.go.jp/kokudoseisaku/index.html (accessed on 16 May 2018).
- Inoue, A.; Tochihara, S.; Sato, M.; Shima, H. Universal node distribution in three bamboo species (Phyllostachys spp.). Trees 2017, 31, 1271–1278. [Google Scholar] [CrossRef]
- Zhao, H.L.; Denich, M.; Borsch, T. Growth behavior of Phyllostachys nigra var. henonis (Bambusoideae) in Central China. J. For. Res. 2005, 16, 163–168. [Google Scholar] [CrossRef]
- Gratani, L.; Crescente, M.F.; Varone, L.; Fabrini, G.; Digiulio, E. Growth pattern and photosynthetic activity of different bamboo species growing in the Botanical Garden of Rome. Flora 2008, 203, 77–84. [Google Scholar] [CrossRef]
- Ahmad, M.; Kamke, F.A. Analysis of Calcutta bamboo for structural composite materials: Physical and mechanical properties. Wood Sci. Technol. 2005, 39, 448–459. [Google Scholar] [CrossRef]
- Wang, X.; Ren, H.; Zhang, B.; Fei, B.; Burgert, I. Cell wall structure and formation of maturing fibers of moso bamboo (Phyllostachys pubescens) increase buckling resistance. J. R. Soc. Interface 2011, 9, 988–996. [Google Scholar] [CrossRef] [PubMed]
- Kleinn, C.; Morales-Hidalgo, D. An inventory of Guadua (Guadua angustifolia) bamboo in the coffee region of Colombia. Eur. J. For. Res. 2006, 125, 361–368. [Google Scholar] [CrossRef]
- Inoue, A.; Shimada, M.; Sato, M.; Shima, H. Estimation of culm volume reduction factor in five bamboo species (Phyllostachys spp.). J. For. Res. 2018, 29. in press. [Google Scholar]
- Aoki, T. On the volume table of Madake (Phyllostachys reticulate C. Koch) stem. Rep. Kyushu Univ. For. 1955, 5, 49–82, (In Japanese with English Summary). [Google Scholar]
- Inoue, A.; Kunisaki, T.; Kitahara, F.; Suga, H. Modeling height-diameter relationship for bamboo, Phyllostachys bambusoides. Bamboo J. 2011, 28, 1–9. [Google Scholar]
- Sharma, R.P.; Vacek, Z.; Vacek, S. Modeling individual tree height to diameter ratio for Norway spruce and European beech in Czech Republic. Trees 2016, 30, 1969–1982. [Google Scholar] [CrossRef]
- Inoue, A. A model for the relationship between form-factors for stem volume and those for stem surface area in coniferous species. J. For. Res. 2006, 11, 289–294. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; The R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: http://www.R-project.org/ (accessed on 31 March 2018).
- Liu, G.; Shi, P.; Xu, Q.; Dong, X.; Wang, F.; Wang, G.G.; Hui, C. Does the size-density relationship developed for bamboo species conform to the self-thinning rule? For. Ecol. Manag. 2016, 361, 339–345. [Google Scholar] [CrossRef]
- Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree height and tropical forest biomass estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
- Berger, A.; Gschwantner, T.; McRoberts, R.E.; Schadauer, K. Effects of measurement errors on individual tree stem volume estimates for the Austrian national forest inventory. For. Sci. 2014, 60, 14–24. [Google Scholar] [CrossRef]
- Mason, N.W.H.; Beets, P.N.; Payton, I.; Burrows, L.; Holdaway, R.J.; Carswell, F.E. Individual-based allometric equations accurately measure carbon storage and sequestration in shrublands. Forests 2014, 5, 309–324. [Google Scholar] [CrossRef]

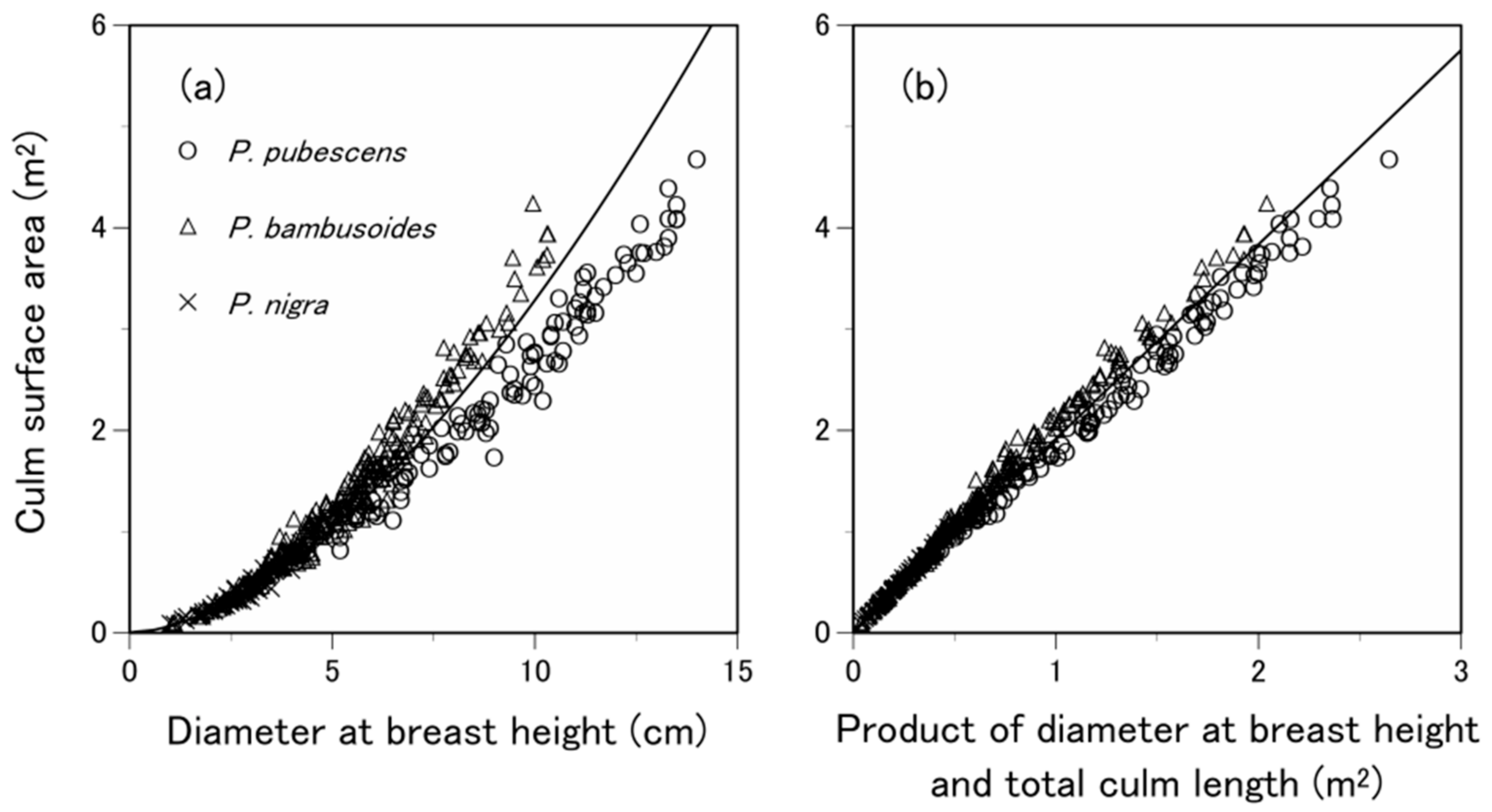
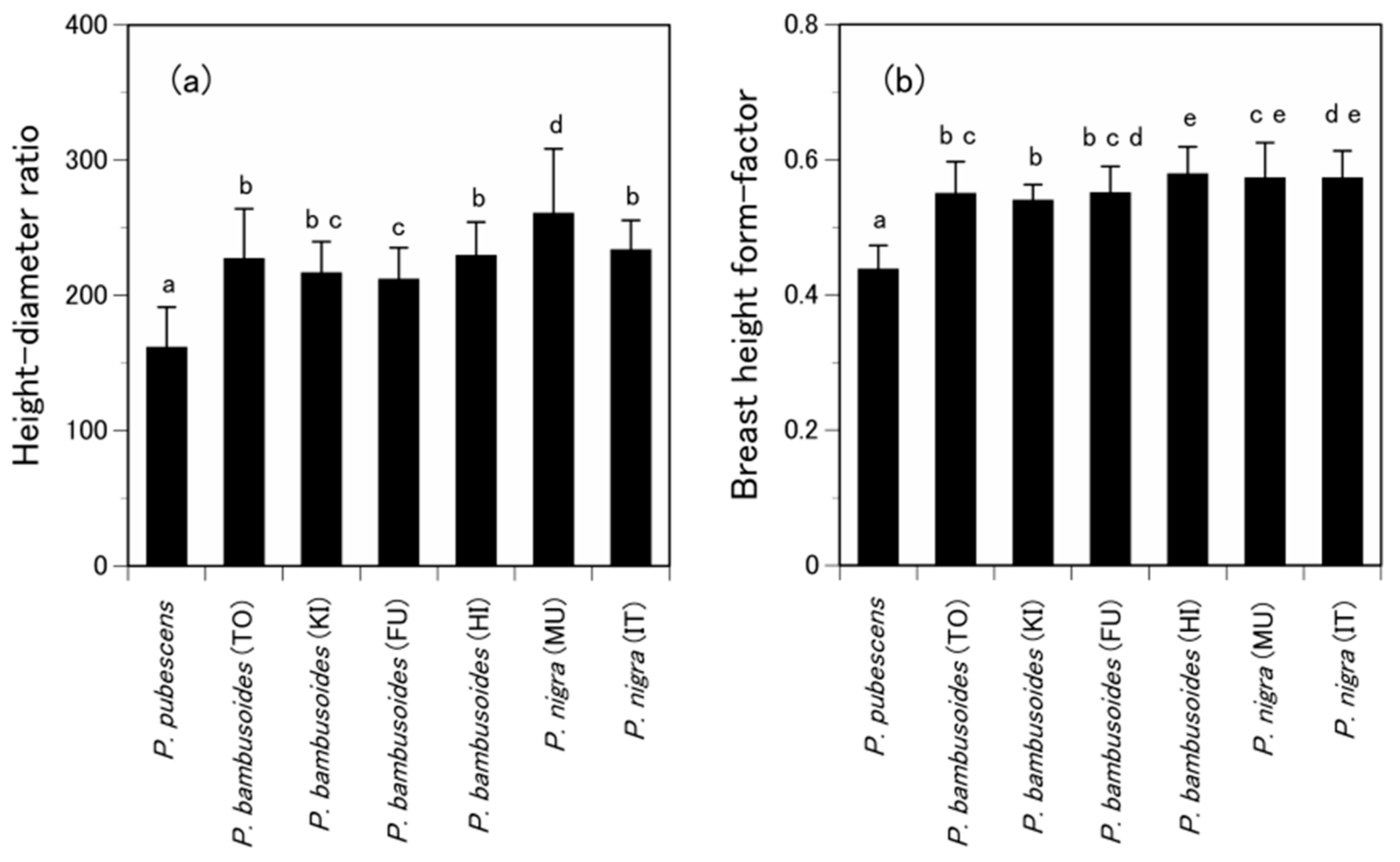
| Species | Site 1 | Number of Samples 2 | Soil Type 3 | Total Culm Height (m) 4 | Diameter at Breast Height (cm) 4 | Culm Surface Area (m2) 4 |
|---|---|---|---|---|---|---|
| P. pubescens | TO | 200 (100) | Ando soil | 14.1 ± 2.5 | 9.2 ± 2.7 | 2.46 ± 1.01 |
| P. bambusoides | TO | 200 (100) | Ando soil | 11.1 ± 3.0 | 5.0 ± 1.7 | 1.26 ± 0.70 |
| KI | 102 (51) | Brown forest soil or ando soil | 12.8 ± 3.4 | 6.2 ± 2.1 | 1.77 ± 1.00 | |
| FU | 122 (61) | Brown forest soil or ando soil | 11.8 ± 2.5 | 5.7 ± 1.7 | 1.50 ± 0.81 | |
| HI | 96 (48) | Brown forest soil or ando soil | 9.0 ± 2.1 | 4.1 ± 1.2 | 0.87 ± 0.46 | |
| P. nigra | MU | 60 (30) | Brown forest soil | 7.3 ± 2.0 | 2.9 ± 1.1 | 0.50 ± 0.30 |
| IT | 110 (55) | Gley soil or brown forest soil | 6.2 ± 1.5 | 2.7 ± 0.8 | 0.37 ± 0.19 |
| Equation | Species | Site 1 | Number of Samples 2 |
|---|---|---|---|
| Site-specific | P. bambusoides | TO | 200 |
| KI | 102 | ||
| FU | 122 | ||
| HI | 96 | ||
| P. nigra | MU | 60 | |
| IT | 110 | ||
| Species-specific | P. pubescens | TO | 200 |
| P. bambusoides | TO, KI, FU and HI | 520 | |
| P. nigra | MU and IT | 170 | |
| Common | P. bambusoides and P. nigra | TO, KI, FU, HI, MU and IT | 690 |
| Generic | P. pubescens, P. bambusoides and P. nigra | TO, KI, FU, HI, MU and IT | 890 |
| Equation | Species | Site 1 | Power Equation | Linear Equation | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| α | β | r2 | RMSE (m2) | AIC | γ | r2 | RMSE (m2) | AIC | |||
| Site-specific | P. bambusoides | TO | 159.03 | 1.65 | 0.97 | 0.155 | −83.25 | 2.08 | 0.99 | 0.051 | −306.68 |
| KI | 178.44 | 1.68 | 0.99 | 0.147 | −46.26 | 2.04 | 0.99 | 0.073 | −120.05 | ||
| FU | 184.19 | 1.70 | 0.98 | 0.089 | −115.35 | 2.07 | 0.99 | 0.068 | −150.95 | ||
| HI | 242.78 | 1.78 | 0.98 | 0.073 | −106.07 | 2.23 | 0.99 | 0.055 | −136.63 | ||
| P. nigra | MU | 143.52 | 1.63 | 0.97 | 0.060 | −79.96 | 2.14 | 0.99 | 0.025 | −134.44 | |
| IT | 263.16 | 1.83 | 0.94 | 0.039 | −191.73 | 2.12 | 0.99 | 0.011 | −322.93 | ||
| Species-specific | P. pubescens | 83.21 | 1.49 | 0.98 | 0.174 | −58.68 | 1.80 | 0.99 | 0.101 | −168.49 | |
| P. bambusoides | 179.50 | 1.69 | 0.98 | 0.131 | −315.58 | 2.07 | 0.99 | 0.069 | −649.89 | ||
| P. nigra | 239.91 | 1.79 | 0.95 | 0.051 | −260.28 | 2.13 | 0.99 | 0.017 | −441.90 | ||
| Common | P. bambusoides and P. nigra | 187.66 | 1.70 | 0.98 | 0.118 | −495.65 | 2.08 | 0.99 | 0.061 | −950.25 | |
| Generic | All species | 116.01 | 1.57 | 0.97 | 0.294 | −3.27 | 1.92 | 0.98 | 0.142 | −471.77 | |
| Equation | Species | Site 1 | Power Equation | Linear Equation | ||
|---|---|---|---|---|---|---|
| %AE (%) | %RMSE (%) | %AE (%) | %RMSE (%) | |||
| Site-specific | P. bambusoides | TO | −1.45 | 12.04 | −0.55 | 4.04 |
| KI | 2.06 | 6.17 | −1.95 | 2.73 | ||
| FU | −0.43 | 7.91 | −1.17 | 5.54 | ||
| HI | 0.95 | 9.44 | 1.12 | 7.86 | ||
| P. nigra | MU | −1.94 | 12.76 | −1.73 | 3.80 | |
| IT | −3.09 | 11.06 | −1.31 | 3.33 | ||
| Species-specific | P. pubescens | TO | 0.30 | 8.70 | −0.51 | 4.74 |
| P. bambusoides | TO | −1.42 | 11.30 | −0.88 | 4.10 | |
| KI | 0.05 | 5.78 | −0.28 | 3.16 | ||
| FU | 0.91 | 8.03 | −1.21 | 5.53 | ||
| HI | 0.73 | 9.19 | −5.77 | 9.94 | ||
| P. nigra | MU | −10.45 | 14.47 | −2.15 | 3.99 | |
| IT | 0.51 | 11.13 | −0.83 | 3.41 | ||
| Common | P. bambusoides | TO | −2.32 | 11.41 | −0.80 | 4.08 |
| KI | −0.46 | 5.91 | −0.20 | 3.21 | ||
| FU | 0.31 | 8.13 | −1.13 | 5.56 | ||
| HI | −0.48 | 9.25 | −5.70 | 9.89 | ||
| P. nigra | MU | −3.28 | 11.17 | −4.76 | 6.01 | |
| IT | 9.08 | 14.06 | −3.47 | 4.01 | ||
| Generic | P. pubescens | TO | 16.54 | 21.75 | 5.81 | 8.41 |
| P. bambusoides | TO | −8.39 | 19.40 | −8.48 | 10.30 | |
| KI | −9.59 | 15.81 | −7.92 | 7.77 | ||
| FU | −8.32 | 14.42 | −8.78 | 9.06 | ||
| HI | −4.62 | 14.10 | −12.99 | 16.34 | ||
| P. nigra | MU | −2.28 | 15.18 | −12.12 | 14.02 | |
| IT | −10.98 | 13.13 | −10.94 | 11.37 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoue, A.; Miyazawa, Y.; Sato, M.; Shima, H. Allometric Equations for Predicting Culm Surface Area of Three Bamboo Species (Phyllostachys spp.). Forests 2018, 9, 295. https://doi.org/10.3390/f9060295
Inoue A, Miyazawa Y, Sato M, Shima H. Allometric Equations for Predicting Culm Surface Area of Three Bamboo Species (Phyllostachys spp.). Forests. 2018; 9(6):295. https://doi.org/10.3390/f9060295
Chicago/Turabian StyleInoue, Akio, Yoshiyuki Miyazawa, Motohiro Sato, and Hiroyuki Shima. 2018. "Allometric Equations for Predicting Culm Surface Area of Three Bamboo Species (Phyllostachys spp.)" Forests 9, no. 6: 295. https://doi.org/10.3390/f9060295
APA StyleInoue, A., Miyazawa, Y., Sato, M., & Shima, H. (2018). Allometric Equations for Predicting Culm Surface Area of Three Bamboo Species (Phyllostachys spp.). Forests, 9(6), 295. https://doi.org/10.3390/f9060295





