Mixing Effects in Norway Spruce—European Beech Stands Are Modulated by Site Quality, Stand Age and Moisture Availability
Abstract
1. Introduction
- To compare the productivity of mixed and pure stands of Norway spruce and European beech along Switzerland’s large environmental gradients and to identify possible interactions between mixing effects and site, climate, age, and stand density. For this purpose, we focused on two hypotheses: (a) On average, mixed stands are more productive than pure stands, and (b) the positive effect decreases as the site conditions become more favorable for growth.
- To investigate whether mixing effects differ depending on the method employed to estimate BAmax (required for the calculation of species proportion by area). We hypothesized that (c) the methods employed lead to a different estimation of the mixing effect and the resulting over- or under-yielding.
2. Materials and Methods
2.1. Swiss NFI Sampling Design and Plot Selection
2.2. Species Proportions by Area
2.2.1. Self-Thinning Rule
2.2.2. Extended Competition Density Rule
2.3. Modelling the Stand Basal Area Increment
2.3.1. Climate Variables
2.3.2. Site Variables
2.3.3. Stand Variables
2.3.4. Model Fitting
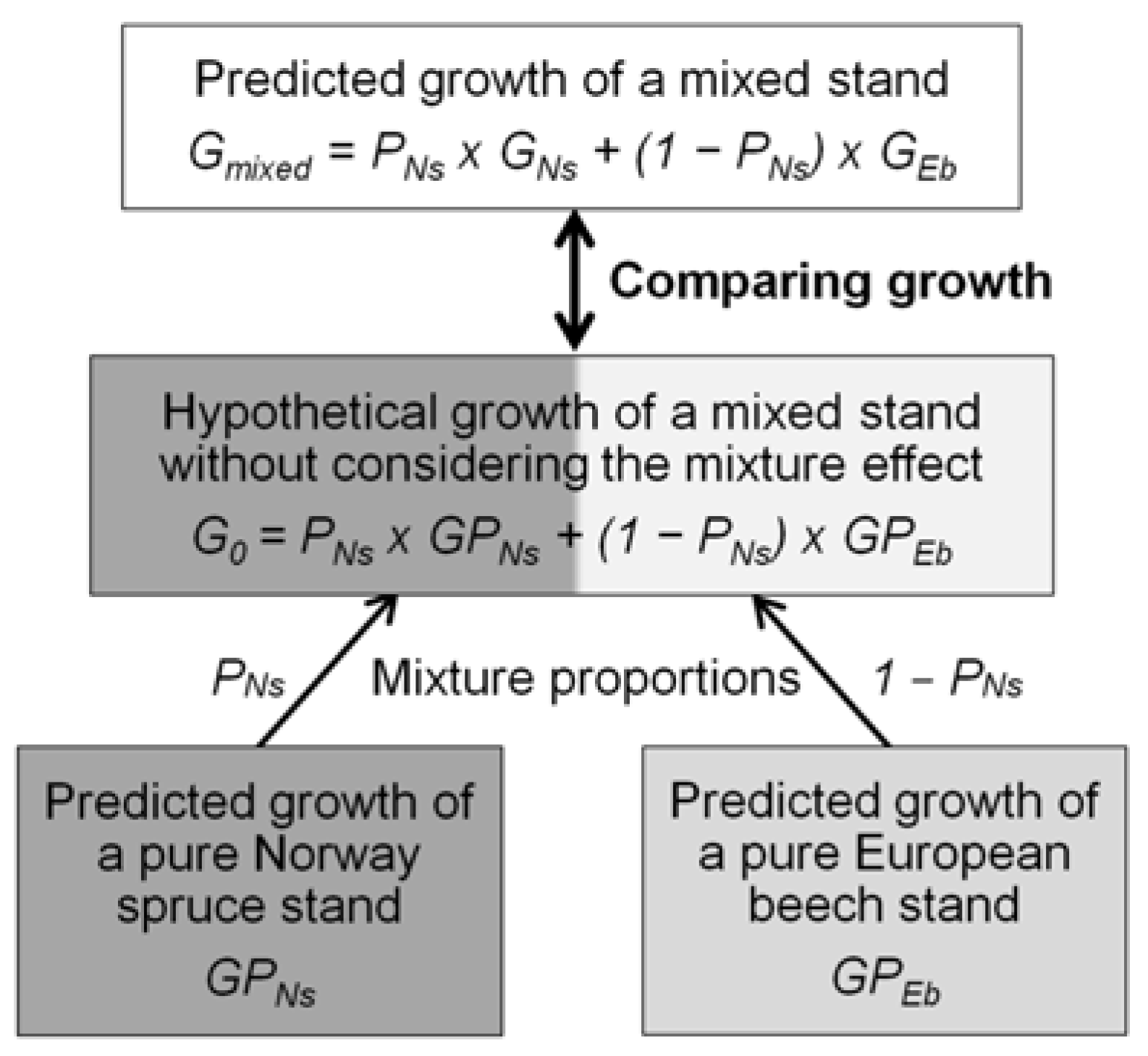
2.4. Comparison of the Productivity of Pure and Mixed Stands
2.5. Comparison of Mixing Effects Depending on the BAmax Alternative
3. Results
3.1. Calculation of the Maximum Basal Area and the Growth Index GI
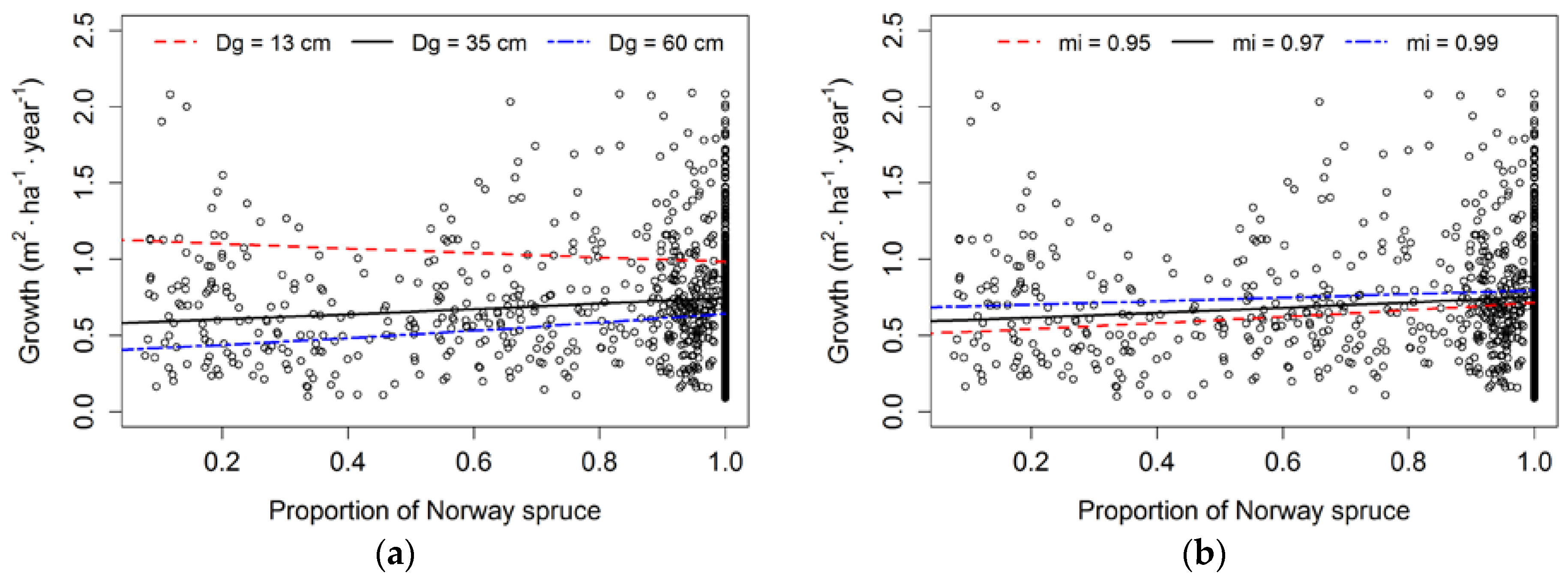
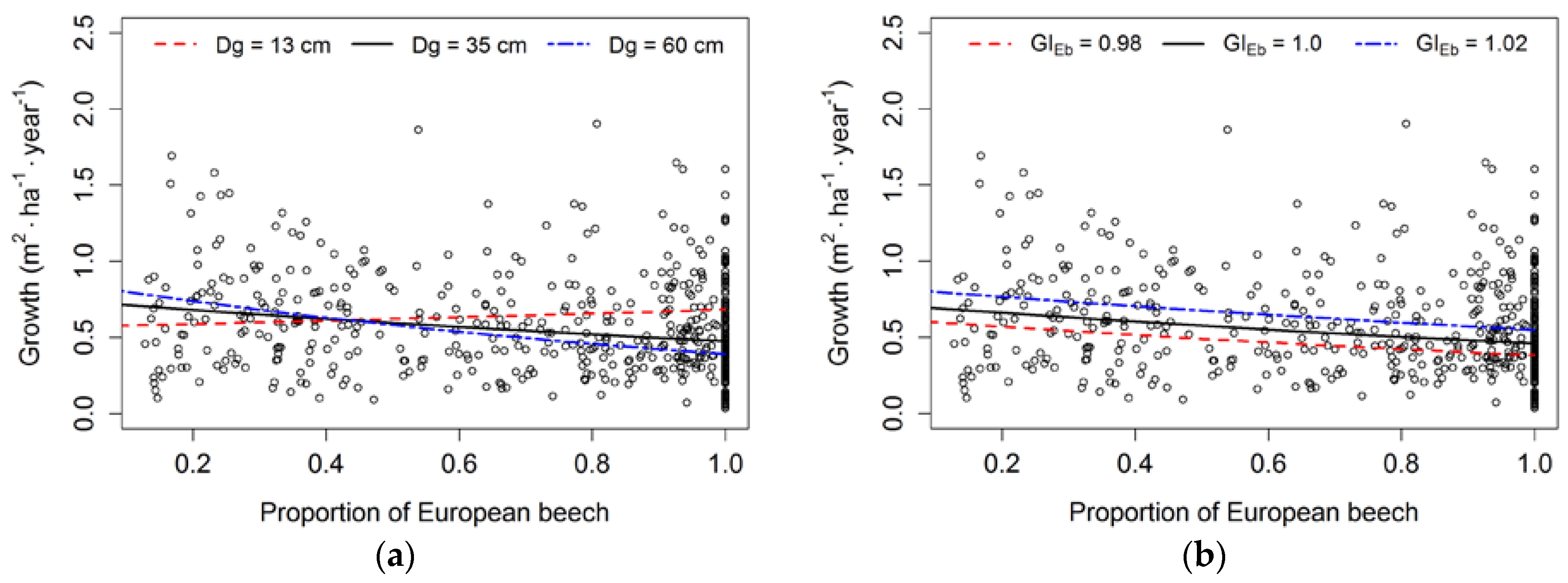
3.2. Stand Basal Area Increment Modelling
3.3. Productivity in Pure and Mixed Stands
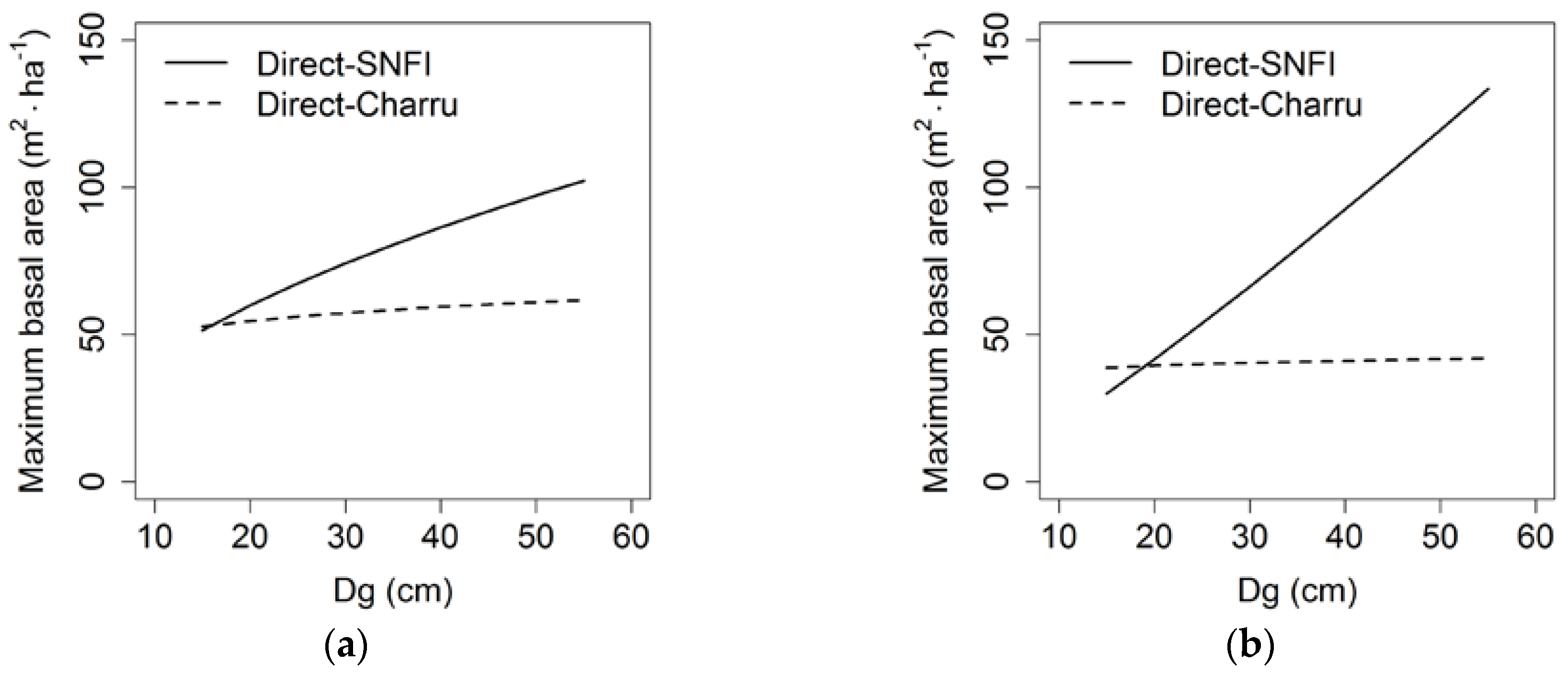
3.4. Comparison of Different Alternatives to Estimate BAmax
4. Discussion
4.1. Mixing Effects in Norway Spruce-European Beech Stands
4.2. Influence of Methodology on the Estimation of Mixing Effects
4.3. Other Methodological Aspects
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bravo-Oviedo, A.; Pretzsch, H.; Ammer, C.; Andenmatten, E.; Barbati, A.; Barreiro, S.; Brang, P.; Bravo, F.; Coll, L.; Corona, P.; et al. European Mixed Forests: Definition and research perspectives. For. Syst. 2014, 23, 518. [Google Scholar] [CrossRef]
- Gamfeldt, L.; Snäll, T.; Bagchi, R.; Jonsson, M.; Gustafsson, L.; Kjellander, P.; Ruiz-Jaen, M.C.; Fröberg, M.; Stendahl, J.; Philipson, C.D.; et al. Higher levels of multiple ecosystem services are found in forests with more tree species. Nat. Commun. 2013, 4, 1340. [Google Scholar] [CrossRef] [PubMed]
- Jactel, H.; Brockerhoff, E.; Duelli, P. A test of the biodiversity-stability theory: Meta-analysis of tree species diversity effects on insect pest infestations, and re-examination of responsible factors. In Forest Diversity and Function; Scherer-Lorenzen, M., Körner, C., Schulze, E.-D., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-22191-3. [Google Scholar]
- Knoke, T.; Ammer, C.; Stimm, B.; Mosandl, R. Admixing broadleaved to coniferous tree species: A review on yield, ecological stability and economics. Eur. J. For. Res. 2008, 127, 89–101. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G.; Uhl, E. Resistance of European tree species to drought stress in mixed versus pure forests: Evidence of stress release by inter-specific facilitation: Drought stress release by inter-specific facilitation. Plant Biol. 2013, 15, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Bauhus, J.; Forrester, D.I.; Gardiner, B.; Jactel, H.; Vallejo, R.; Pretzsch, H. Ecological stability of mixed-species forests. In Mixed-Species Forests; Pretzsch, H., Forrester, D.I., Bauhus, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 337–382. ISBN 978-3-662-54551-5. [Google Scholar]
- Keenan, R.J. Adaptation of forests and forest management to climate change: An editorial. Forests 2012, 3, 75–82. [Google Scholar] [CrossRef]
- Bauhus, J.; Puettmann, K.J.; Kühne, C. Close-to-nature forest management in Europe: Does it support complexity and adaptability of forest ecosystems? In Managing Forests as Complex Adaptive Systems: Building Resilience to the Challenge of Global Change; Messier, C.C., Puettmann, K.J., Coates, K.D., Eds.; Routledge: Abingdon, UK, 2013; pp. 187–213. ISBN 978-0-415-51977-9. [Google Scholar]
- Liang, J.; Crowther, T.W.; Picard, N.; Wiser, S.; Zhou, M.; Alberti, G.; Schulze, E.-D.; McGuire, A.D.; Bozzato, F.; Pretzsch, H.; et al. Positive biodiversity-productivity relationship predominant in global forests. Science 2016, 354, aaf8957. [Google Scholar] [CrossRef] [PubMed]
- Del Río, M.; Sterba, H. Comparing volume growth in pure and mixed stands of Pinus sylvestris and Quercus pyrenaica. Ann. For. Sci. 2009, 66, 502. [Google Scholar] [CrossRef]
- Huber, M.O.; Sterba, H.; Bernhard, L. Site conditions and definition of compositional proportion modify mixture effects in Picea abies—Abies alba stands. Can. J. For. Res. 2014, 44, 1281–1291. [Google Scholar] [CrossRef]
- Toïgo, M.; Vallet, P.; Perot, T.; Bontemps, J.-D.; Piedallu, C.; Courbaud, B. Overyielding in mixed forests decreases with site productivity. J. Ecol. 2015, 103, 502–512. [Google Scholar] [CrossRef]
- Pretzsch, H.; Block, J.; Dieler, J.; Dong, P.H.; Kohnle, U.; Nagel, J.; Spellmann, H.; Zingg, A. Comparison between the productivity of pure and mixed stands of Norway spruce and European beech along an ecological gradient. Ann. For. Sci. 2010, 67, 712. [Google Scholar] [CrossRef]
- Pretzsch, H.; Bielak, K.; Block, J.; Bruchwald, A.; Dieler, J.; Ehrhart, H.-P.; Kohnle, U.; Nagel, J.; Spellmann, H.; Zasada, M.; et al. Productivity of mixed versus pure stands of oak (Quercus petraea (Matt.) Liebl. and Quercus robur L.) and European beech (Fagus sylvatica L.) along an ecological gradient. Eur. J. For. Res. 2013, 132, 263–280. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-88306-7. [Google Scholar]
- Forrester, D.I.; Pretzsch, H. Tamm Review: On the strength of evidence when comparing ecosystem functions of mixtures with monocultures. For. Ecol. Manag. 2015, 356, 41–53. [Google Scholar] [CrossRef]
- Mina, M.; Huber, M.O.; Forrester, D.I.; Thürig, E.; Rohner, B. Multiple factors modulate tree growth complementarity in Central European mixed forests. J. Ecol. 2017. [Google Scholar] [CrossRef]
- Légaré, S.; Paré, D.; Bergeron, Y. The responses of black spruce growth to an increased proportion of aspen in mixed stands. Can. J. For. Res. 2004, 34, 405–416. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G. Transgressive overyielding in mixed compared with pure stands of Norway spruce and European beech in Central Europe: Evidence on stand level and explanation on individual tree level. Eur. J. For. Res. 2009, 128, 183–204. [Google Scholar] [CrossRef]
- Del Río, M.; Schütze, G.; Pretzsch, H. Temporal variation of competition and facilitation in mixed species forests in Central Europe. Plant Biol. 2014, 16, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Hein, S.; Dhôte, J.-F. Effect of species composition, stand density and site index on the basal area increment of oak trees (Quercus sp.) in mixed stands with beech (Fagus sylvatica L.) in northern France. Ann. For. Sci. 2006, 63, 457–467. [Google Scholar] [CrossRef]
- Forrester, D.I.; Benneter, A.; Bouriaud, O.; Bauhus, J. Diversity and competition influence tree allometric relationships—Developing functions for mixed-species forests. J. Ecol. 2017, 105, 761–774. [Google Scholar] [CrossRef]
- Dirnberger, G.F.; Sterba, H. A comparison of different methods to estimate species proportions by area in mixed stands. For. Syst. 2014, 23, 534. [Google Scholar] [CrossRef]
- Sterba, H.; del Río, M.; Brunner, A.; Condés, S. Effect of species proportion definition on the evaluation of growth in pure vs. mixed stands. For. Syst. 2014, 23, 547. [Google Scholar] [CrossRef]
- Reineke, L.H. Perfecting a stand-density index for even-aged forests. J. Agric. Res. 1933, 66, 627–638. [Google Scholar]
- Sterba, H. Estimating potential density from thinning experiments and inventory data. For. Sci. 1987, 33, 1022–1034. [Google Scholar]
- Vospernik, S.; Sterba, H. Do competition-density rule and self-thinning rule agree? Ann. For. Sci. 2015, 72, 379–390. [Google Scholar] [CrossRef]
- Charru, M.; Seynave, I.; Morneau, F.; Bontemps, J.-D. Recent changes in forest productivity: An analysis of national forest inventory data for common beech (Fagus sylvatica L.) in north-eastern France. For. Ecol. Manag. 2010, 260, 864–874. [Google Scholar] [CrossRef]
- Rohner, B.; Waldner, P.; Lischke, H.; Ferretti, M.; Thürig, E. Predicting individual-tree growth of central European tree species as a function of site, stand, management, nutrient, and climate effects. Eur. J. For. Res. 2017, 1–16. [Google Scholar] [CrossRef]
- Kaufmann, E. Estimation of standing timber, growth, and cut. In Swiss National Forest Inventory: Methods and Models of the Second Assessment; WSL Swiss Federal Research Institute: Birmensdorf, Switzerland, 2001; pp. 162–196. [Google Scholar]
- Brändli, U.-B.; Brassel, P.; Duc, P.; Keller, M.; Köhl, M.; Herold, A.; Kaufmann, E.; Lischke, H.; Paschedag, I.; Schnellbächer, H.-J.; et al. Swiss National Forest Inventory: Methods and Models of the Second Assessment; Brassel, P., Lischke, H., Eds.; WSL Swiss Federal Research Institute: Birmensdorf, Switzerland, 2001; ISBN 978-3-905620-99-3. [Google Scholar]
- Keller, M. Swiss National Forest Inventory. Manual of the Field Survey 2004–2007; Keller, M., Ed.; WSL Swiss Federal Research Institute: Birmensdorf, Switzerland, 2011. [Google Scholar]
- Düggelin, C.; Keller, M. Schweizerisches Landesforstinventar. Feldaufnahme-Anleitung 2017; Düggelin, C., Keller, M., Eds.; WSL Swiss Federal Research Institute: Birmensdorf, Switzerland, 2017. [Google Scholar]
- The Swiss National Forest Inventory NFI. Available online: https://www.lfi.ch/lfi/lfi-en.php (accessed on 8 February 2018).
- Sterba, H. The precision of species proportion by area when estimated by angle counts and yield tables. For. Int. J. For. Res. 1998, 71, 25–32. [Google Scholar] [CrossRef]
- Zhang, L.; Bi, H.; Gove, J.H.; Heath, L.S. A comparison of alternative methods for estimating the self-thinning boundary line. Can. J. For. Res. 2005, 35, 1507–1514. [Google Scholar] [CrossRef]
- Koenker, R. Quantreg: Quantile Regression. R Package Version 5.29. 2016. Available online: https://CRAN.R-project.org/package=quantreg (accessed on 3 April 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.r-project.org/ (accessed on 6 March 2017).
- Burkhart, H.E. Comparison of maximum size–density relationships based on alternate stand attributes for predicting tree numbers and stand growth. For. Ecol. Manag. 2013, 289, 404–408. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P. A re-evaluation of Reineke’s rule and stand density index. For. Sci. 2005, 51, 304–320. [Google Scholar]
- Rivoire, M.; Le Moguedec, G. A generalized self-thinning relationship for multi-species and mixed-size forests. Ann. For. Sci. 2012, 69, 207–219. [Google Scholar] [CrossRef]
- Condés, S.; del Río, M.; Sterba, H. Mixing effect on volume growth of Fagus sylvatica and Pinus sylvestris is modulated by stand density. For. Ecol. Manag. 2013, 292, 86–95. [Google Scholar] [CrossRef]
- Charru, M.; Seynave, I.; Morneau, F.; Rivoire, M.; Bontemps, J.-D. Significant differences and curvilinearity in the self-thinning relationships of 11 temperate tree species assessed from forest inventory data. Ann. For. Sci. 2012, 69, 195–205. [Google Scholar] [CrossRef]
- Kira, T.; Ogawa, H.; Sakazaki, N. Intrapecific competition among higher plants. I. Competition-yield-density interrelationship in regularly dispersed population. J. Inst. Polytech. Osaka City Univ. 1953, 4, 1–16. [Google Scholar]
- Assmann, E. Waldertragskunde: Organische Produktion, Struktur, Zuwachs und Ertrag von Waldbeständen; BLV: München, Germany, 1961. [Google Scholar]
- Remund, J.; von Arx, G.; Gallien, L.; Rebetez, M.; Huber, B.; Zimmermann, N.E. Klimawandel in der Schweiz—Entwicklung waldrelevanter Klimagrössen. In Wald im Klimawandel. Grundlagen für Adaptationsstrategien; Pluess, A.R., Augustin, S., Brang, P., Eds.; Haupt: Bern, Switzerland; Stuttgart, Germany; Wien, Austria, 2016; pp. 23–37. [Google Scholar]
- Keller, W. Mitteilungen der Eidgenössischen Forschungsanstalt für Wald, Schnee und Landschaft. In Einfacher Ertragskundlicher Bonitätsschlüssel für Waldbestände in der Schweiz; Kurt, A., Schmid-Haas, P., Eds.; Beer: Zürich, Switzerland, 1978; Volume 54. [Google Scholar]
- Trasobares, A.; Pukkala, T. Using past growth to improve individual-tree diameter growth models for uneven-aged mixtures of Pinus sylvestris L. and Pinus nigra Arn. in Catalonia, north-east Spain. Ann. For. Sci. 2004, 61, 409–417. [Google Scholar] [CrossRef]
- Berrill, J.-P.; O’Hara, K.L. Estimating site productivity in irregular stand structures by indexing the basal area or volume increment of the dominant species. Can. J. For. Res. 2014, 44, 92–100. [Google Scholar] [CrossRef]
- Dănescu, A.; Albrecht, A.T.; Bauhus, J.; Kohnle, U. Geocentric alternatives to site index for modeling tree increment in uneven-aged mixed stands. For. Ecol. Manag. 2017, 392, 1–12. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. R-Package Version 3.1-131. 2017. Available online: https://CRAN.R-project.org/package=nmle (accessed on 24 March 2017).
- Gregoire, T.G.; Schabenberger, O.; Barrett, J.P. Linear modelling of irregularly spaced, unbalanced, longitudinal data from permanent-plot measurements. Can. J. For. Res. 1995, 25, 135–156. [Google Scholar] [CrossRef]
- Bosela, M.; Tobin, B.; Šebeň, V.; Petráš, R.; Larocque, G.R. Different mixtures of Norway spruce, silver fir, and European beech modify competitive interactions in central European mature mixed forests. Can. J. For. Res. 2015, 45, 1577–1586. [Google Scholar] [CrossRef]
- Mina, M.; del Río, M.; Huber, M.O.; Thürig, E.; Rohner, B. The symmetry of competitive interactions in mixed Norway spruce, silver fir and European beech forests. J. Veg. Sci. 2018. under review. [Google Scholar]
- Bayer, D.; Seifert, S.; Pretzsch, H. Structural crown properties of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica (L.)) in mixed versus pure stands revealed by terrestrial laser scanning. Trees 2013, 27, 1035–1047. [Google Scholar] [CrossRef]
- Forrester, D.I.; Ammer, C.; Annighöfer, P.J.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; del Río, M.; Drössler, L.; et al. Predicting the spatial and temporal dynamics of species interactions in Fagus sylvatica and Pinus sylvestris forests across Europe. For. Ecol. Manag. 2017, 405, 112–133. [Google Scholar] [CrossRef]
- Longuetaud, F.; Piboule, A.; Wernsdörfer, H.; Collet, C. Crown plasticity reduces inter-tree competition in a mixed broadleaved forest. Eur. J. For. Res. 2013, 132, 621–634. [Google Scholar] [CrossRef]
- Bolte, A.; Kampf, F.; Hilbrig, L. Space sequestration below ground in old-growth spruce-beech forests—Signs for facilitation? Front. Plant Sci. 2013, 4, 322. [Google Scholar] [CrossRef] [PubMed]
- Schmid, I.; Kazda, M. Vertical distribution and radial growth of coarse roots in pure and mixed stands of Fagus sylvatica and Picea abies. Can. J. For. Res. 2001, 31, 539–548. [Google Scholar] [CrossRef]
- Bolte, A.; Villanueva, I. Interspecific competition impacts on the morphology and distribution of fine roots in European beech (Fagus sylvatica L.) and Norway spruce (Picea abies (L.) Karst.). Eur. J. For. Res. 2006, 125, 15–26. [Google Scholar] [CrossRef]
- Forrester, D.I. The spatial and temporal dynamics of species interactions in mixed-species forests: From pattern to process. For. Ecol. Manag. 2014, 312, 282–292. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G. Effect of tree species mixing on the size structure, density, and yield of forest stands. Eur. J. For. Res. 2016, 135, 1–22. [Google Scholar] [CrossRef]
- Vesterdal, L.; Clarke, N.; Sigurdsson, B.D.; Gundersen, P. Do tree species influence soil carbon stocks in temperate and boreal forests? For. Ecol. Manag. 2013, 309, 4–18. [Google Scholar] [CrossRef]
- Andivia, E.; Rolo, V.; Jonard, M.; Formánek, P.; Ponette, Q. Tree species identity mediates mechanisms of top soil carbon sequestration in a Norway spruce and European beech mixed forest. Ann. For. Sci. 2016, 73, 437–447. [Google Scholar] [CrossRef]
- Pinto, P.E.; Gégout, J.-C.; Hervé, J.-C.; Dhôte, J.-F. Respective importance of ecological conditions and stand composition on Abies alba Mill. dominant height growth. For. Ecol. Manag. 2008, 255, 619–629. [Google Scholar] [CrossRef]
- Condés, S.; Vallet, P.; Bielak, K.; Bravo-Oviedo, A.; Coll, L.; Ducey, M.J.; Pach, M.; Pretzsch, H.; Sterba, H.; Vayreda, J.; et al. Climate influences on the maximum size-density relationship in Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.) stands. For. Ecol. Manag. 2017, 385, 295–307. [Google Scholar] [CrossRef]
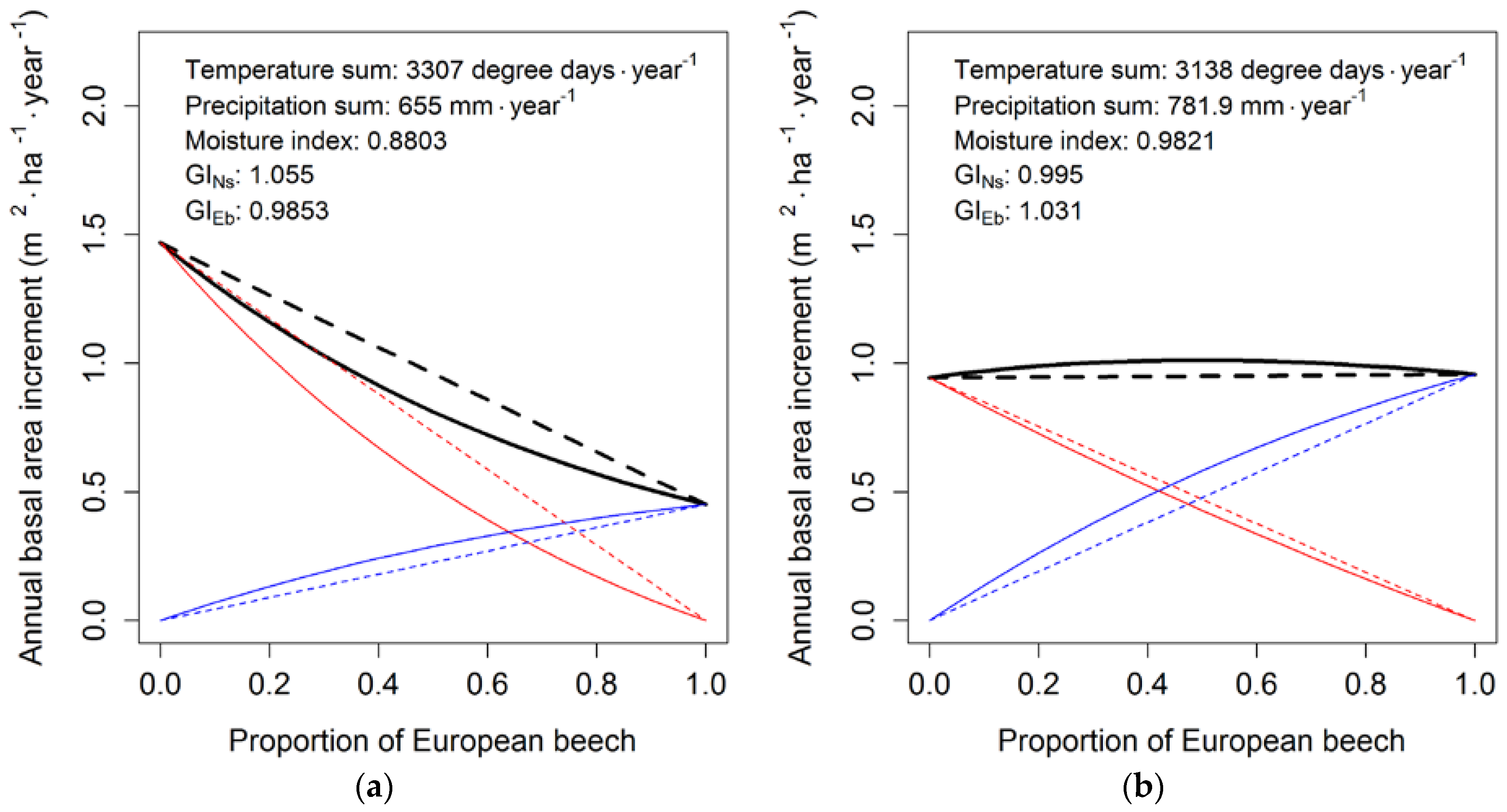
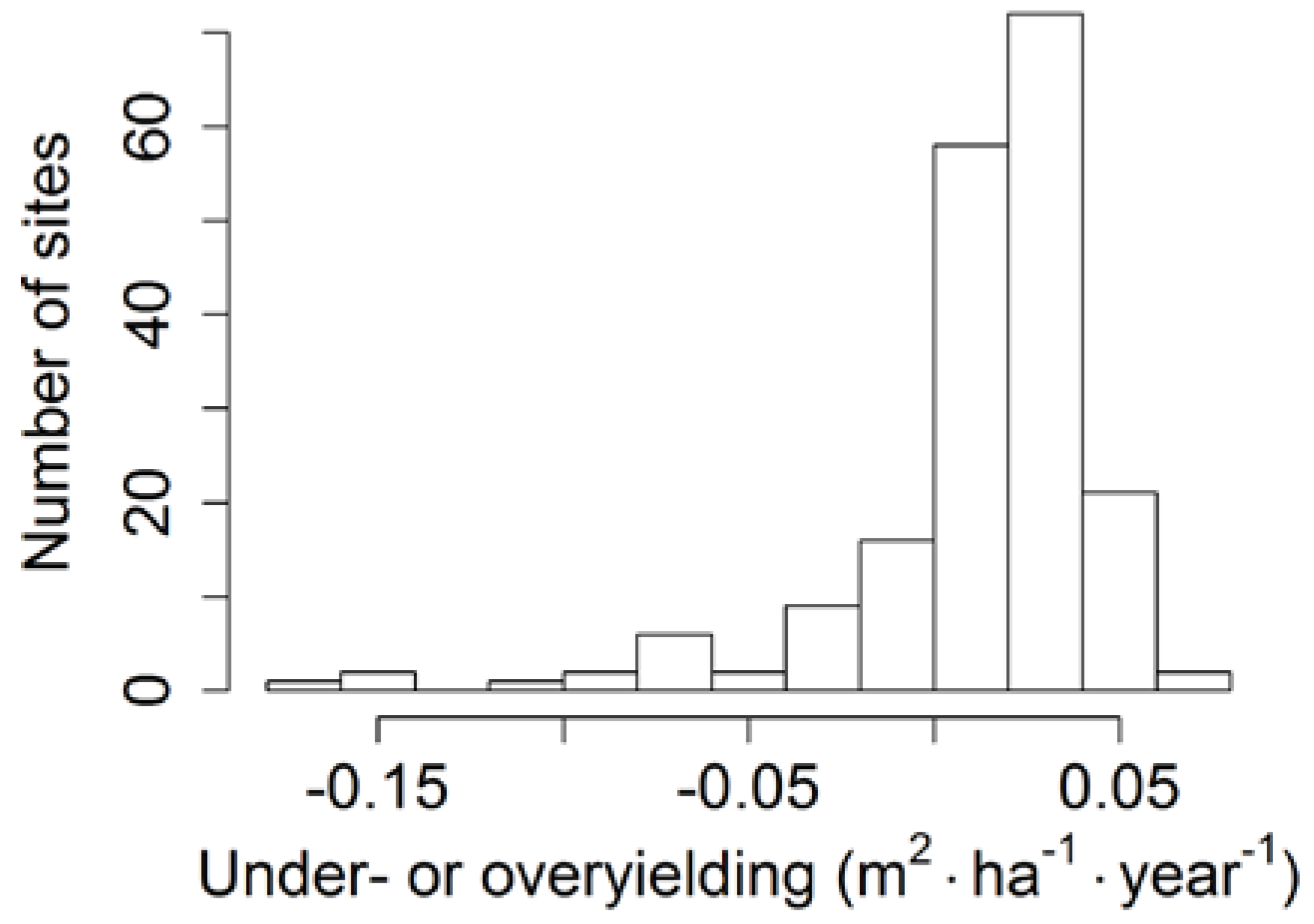
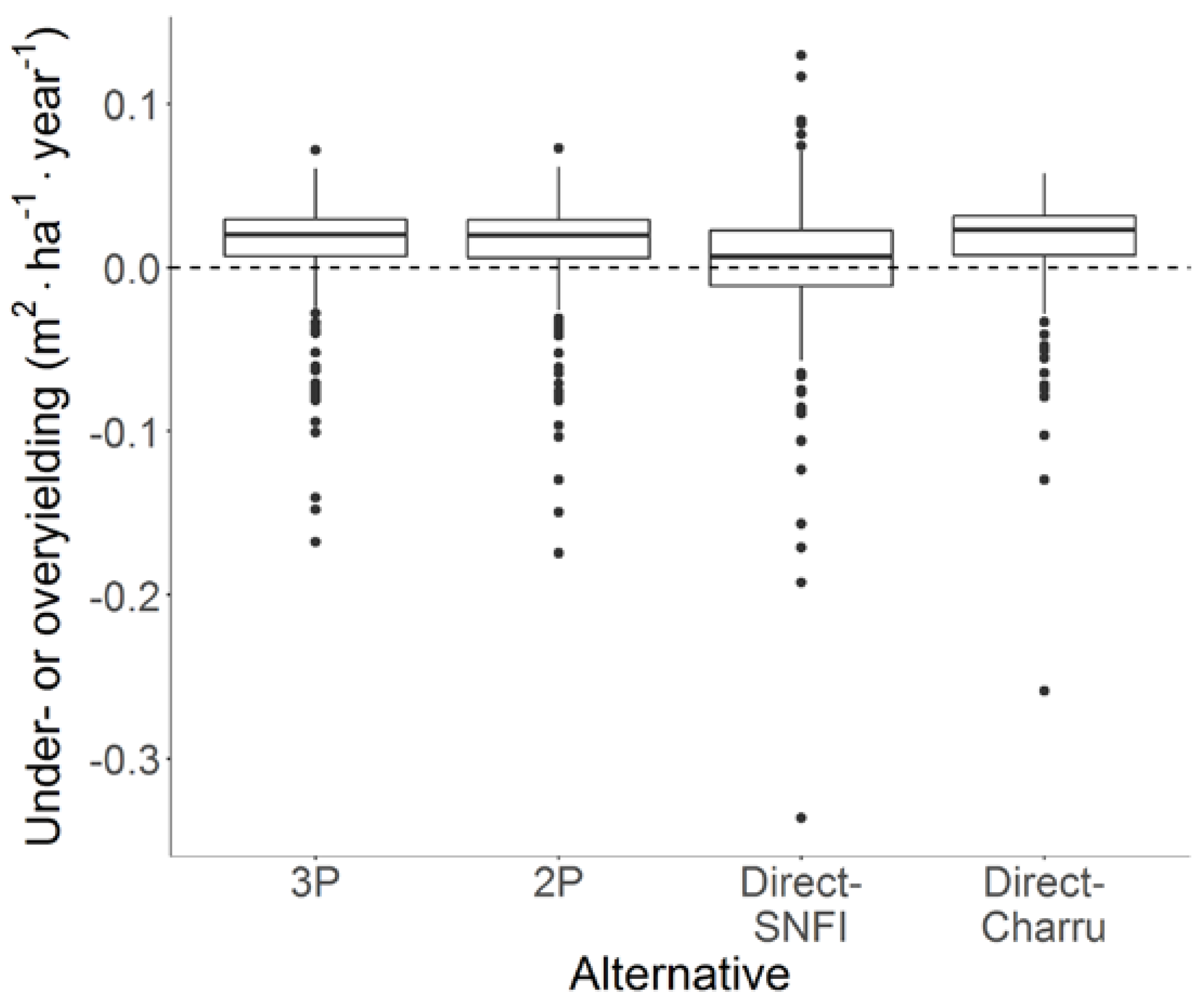
| Stand Type | n | iG | t | p | mi | GI | Dg | sd | P | |
|---|---|---|---|---|---|---|---|---|---|---|
| Norway spruce pure stands | 623 | Mean | 0.65 | 2034 | 849 | 0.98 | 1.000 | 36.5 | 0.64 | 0.99 |
| SD | 0.37 | 509 | 207 | 0.03 | 0.024 | 11.9 | 0.30 | 0.03 | ||
| Minimum | 0.09 | 935 | 243 | 0.64 | 0.934 | 12.5 | 0.02 | 0.87 | ||
| Maximum | 2.09 | 3922 | 1444 | 1.00 | 1.127 | 91.5 | 2.40 | 1.00 | ||
| Norway spruce mixed stands | 179 | Mean | 0.69 | 2602 | 903 | 0.97 | 0.996 | 34.9 | 0.66 | 0.48 |
| SD | 0.38 | 456 | 187 | 0.03 | 0.029 | 9.1 | 0.26 | 0.24 | ||
| Minimum | 0.10 | 1637 | 606 | 0.80 | 0.921 | 14.6 | 0.12 | 0.08 | ||
| Maximum | 2.08 | 3373 | 1649 | 1.00 | 1.185 | 59.9 | 1.48 | 0.87 | ||
| European beech pure stands | 145 | Mean | 0.52 | 2768 | 1036 | 0.96 | 0.998 | 31.7 | 0.75 | 0.98 |
| SD | 0.30 | 421 | 267 | 0.04 | 0.035 | 10.8 | 0.37 | 0.03 | ||
| Minimum | 0.03 | 1824 | 595 | 0.61 | 0.823 | 13.3 | 0.05 | 0.90 | ||
| Maximum | 1.65 | 3838 | 1826 | 1.00 | 1.132 | 60.8 | 2.84 | 1.00 | ||
| European beech mixed stands | 179 | Mean | 0.61 | 2610 | 900 | 0.97 | 0.999 | 35.2 | 0.66 | 0.52 |
| SD | 0.33 | 460 | 184 | 0.03 | 0.043 | 8.8 | 0.26 | 0.24 | ||
| Minimum | 0.09 | 1637 | 606 | 0.80 | 0.893 | 15.9 | 0.12 | 0.13 | ||
| Maximum | 1.90 | 3429 | 1649 | 1.00 | 1.324 | 59.9 | 1.39 | 0.92 |
| Alternative | BAmax Formula | STR-Coefficients Used |
|---|---|---|
| 3P | E from Swiss NFI data | |
| 2P | C and E from Swiss NFI data | |
| Direct-SNFI | C and E from Swiss NFI data | |
| Direct-Charru | C and E from Charru et al. [43] |
| Species | SNFI | Charru | ||||
|---|---|---|---|---|---|---|
| n | ln(C) | E | n | ln(C) | E | |
| Norway spruce | 550 | 11.96 (0.43) | −1.471 (0.123) | 1301 | 13.08 | −1.878 |
| European beech | 158 | 9.73 (0.46) | −0.848 (0.162) | 2409 | 12.95 | −1.941 |
| Parameter | Coeff | Norway Spruce | European Beech | ||||
|---|---|---|---|---|---|---|---|
| Value | SE | p-Value | Value | SE | p-Value | ||
| Intercept | ai | −5.966 | 1.356 | <0.0001 | −6.930 | 0.776 | <0.0001 |
| t | bi1 | 4.30 × 10−4 | 2.69 × 10−5 | <0.0001 | 5.67 × 10−4 | 4.23 × 10−5 | <0.0001 |
| p | bi3 | −2.44 × 10−4 | 6.72 × 10−5 | 0.0003 | −8.44 × 10−4 | 7.49 × 10−5 | <0.0001 |
| mi | bi5 | 7.440 | 1.283 | <0.0001 | 5.341 | 0.514 | <0.0001 |
| ln(GIi) | ci | 10.447 | 0.340 | <0.0001 | 6.976 | 0.697 | <0.0001 |
| ln(Dg) | di1 | −0.685 | 0.145 | <0.0001 | 0.280 | 0.152 | 0.0664 |
| ln(sd) | di2 | 0.610 | 0.020 | <0.0001 | 0.685 | 0.029 | <0.0001 |
| Pi | ei | 3.420 | 1.467 | 0.0201 | 1.834 | 0.645 | 0.0049 |
| mi × Pi | fi1 | −4.763 | 1.394 | 0.0007 | - | - | - |
| ln(GIi) × Pi | fi2 | - | - | - | 2.057 | 0.921 | 0.0266 |
| ln(Dg) × Pi | fi3 | 0.408 | 0.157 | 0.0095 | −0.644 | 0.183 | 0.0005 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Houpert, L.; Rohner, B.; Forrester, D.I.; Mina, M.; Huber, M.O. Mixing Effects in Norway Spruce—European Beech Stands Are Modulated by Site Quality, Stand Age and Moisture Availability. Forests 2018, 9, 83. https://doi.org/10.3390/f9020083
Houpert L, Rohner B, Forrester DI, Mina M, Huber MO. Mixing Effects in Norway Spruce—European Beech Stands Are Modulated by Site Quality, Stand Age and Moisture Availability. Forests. 2018; 9(2):83. https://doi.org/10.3390/f9020083
Chicago/Turabian StyleHoupert, Léa, Brigitte Rohner, David I. Forrester, Marco Mina, and Markus O. Huber. 2018. "Mixing Effects in Norway Spruce—European Beech Stands Are Modulated by Site Quality, Stand Age and Moisture Availability" Forests 9, no. 2: 83. https://doi.org/10.3390/f9020083
APA StyleHoupert, L., Rohner, B., Forrester, D. I., Mina, M., & Huber, M. O. (2018). Mixing Effects in Norway Spruce—European Beech Stands Are Modulated by Site Quality, Stand Age and Moisture Availability. Forests, 9(2), 83. https://doi.org/10.3390/f9020083





