Next Article in Journal
Sustained Biomass Carbon Sequestration by China’s Forests from 2010 to 2050
Previous Article in Journal
Long-Term Thinning Does not Significantly Affect Soil Water-Stable Aggregates and Diversity of Bacteria and Fungi in Chinese Fir (Cunninghamia lanceolata) Plantations in Eastern China
Previous Article in Special Issue
Assessing Ecosystem Services from the Forestry-Based Reclamation of Surface Mined Areas in the North Fork of the Kentucky River Watershed
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 9
Issue 11
10.3390/f9110688
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Climate Warming Alters Age-Dependent Growth Sensitivity to Temperature in Eurasian Alpine Treelines

by
Raúl Sanchez-Salguero
1,2,*,
J. Julio Camarero
2,
Emilia Gutiérrez
3,
Antonio Gazol
2,
Gabriel Sangüesa-Barreda
4,
Pavel Moiseev
5 and
Juan C. Linares
1
1
Departamento Sistemas Físicos, Químicos y Naturales, Universidad Pablo de Olavide, 41013 Sevilla, Spain
2
Instituto Pirenaico de Ecología (IPE-CSIC), 50192 Zaragoza, Spain
3
Departamento Biologia Evolutiva, Ecologia i Ciències Ambientals, Universidad Barcelona, Av. Diagonal 643, 08028 Barcelona, Spain
4
Departamento de Ciencias Agroforestales, EiFAB, iuFOR-Universidad de Valladolid, Campus Duques de Soria, 42004 Soria, Spain
5
Institute of Plant and Animal Ecology UD RAS, 8 Marta 202, Yekaterinburg 620144, Russia
*
Author to whom correspondence should be addressed.
Forests 2018, 9(11), 688; https://doi.org/10.3390/f9110688
Submission received: 1 September 2018 / Revised: 29 October 2018 / Accepted: 30 October 2018 / Published: 3 November 2018
(This article belongs to the Special Issue Forest Landscape Ecology: Linking Past, Present, and Future Data)
Browse Figures
Versions Notes

Abstract

:
Treeline ecotones are considered early-warning monitors of the effects of climate warming on terrestrial ecosystems, but it is still unclear how tree growth at treeline will track the forecasted temperature rise in these cold environments. Here, we address this issue by analysing and projecting growth responses to climate on two different cold-limited alpine treelines: Pinus uncinata Ram. in the Spanish Pyrenees and Larix sibirica Ledeb. in the Russian Polar Urals. We assess radial-growth changes as a function of tree age and long-term climate variability using dendrochronology and a process-based model of tree growth. Climate‒growth relationships were compared considering young (age < 50 years) and old trees (age > 75 years) separately. Warm summer conditions enhanced radial growth, particularly after the 1980s, in the Polar Urals sites, whereas growth was positively related to warm spring and winter conditions in the Pyrenees sites. These associations were stronger in young than in old trees for both tree species and regions. Forecasted warm conditions are expected to enhance growth rates in both regions, while the growing season is forecasted to lengthen in the Pyrenees treelines, mostly in young trees. The observed age-related responses to temperature also depend on the forecasted warming rates. Although the temperature sensitivity is overall increasing for young trees, those responses seem more divergent, or even reversed, throughout the contrasting emission scenarios. The RCP 8.5 emission scenario corresponding to the most pronounced warming and drier conditions (+4.8 °C) could also amplify drought stress in young trees from the Pyrenees treelines. Our modelling approach provides accessible tools to evaluate functional thresholds for tree growth in treeline ecotones under warmer conditions.

1. Introduction

Forecasted climate warming is projected to modify the productivity and distribution of forests and tree species, especially at cold-limited regions where warmer temperatures are predicted to enhance tree growth [1]. Rapid climate warming is expected to impact alpine and arctic treelines more intensely and rapidly than elsewhere, leading to enhanced growth and promoting upward treeline shifts or treeline encroachment, as has been already observed in several biomes [2,3,4,5].
At a global scale, seasonal temperatures correlate positively with treeline elevation [6]. However, climate effects on treeline position and tree growth depend not only on regional climate conditions but also on other local factors including treeline structure and tree age [7], both affecting tree sensitivity to climate [8]. Dendrochronological studies focused on climate‒growth relationships assume that, once the biological growth trend is removed, growth responses to climate are not dependent on tree age or size [9]. However, other studies have shown that trees respond to climate depending on their age [10,11,12,13,14]. Usually, old trees (age > 75 years) present greater growth sensitivity to climatic limitations than young trees (age < 50 years) [15,16].
Climate warming is spatially heterogeneous, with the highest rates of temperature increase observed in peripheral Eurasian regions such as the Polar Urals (larch treelines) and the Mediterranean Basin (mainly pine treelines) [17,18]. Temperature thresholds have been proposed to explain abrupt changes in radial growth across these different treeline types dominated by diverse conifer species [19,20]. However, upward treeline shifts have not always accompanied this growth stimulation, leading to a lag in treeline responses to climate [2,21]. Therefore, changes in radial growth seem to be a more consistent proxy of long-term treeline responses to climate warming than shifts in treeline elevation [22]. Nevertheless, a better understanding on growth responses to climate at treeline is required if we aim to use these ecotones as monitors of the effects of climate warming.
There is a research gap on how tree age affects climate‒growth relationships in multi-aged treeline populations where old and young trees differently respond to climate, and this different response may affect future treeline shifts [7]. The radial growth of treeline species is mainly limited by low air and soil temperatures during the growing season [18,23,24,25]. However, rising temperatures may selectively affect trees as a function of their ages, promoting the dominance of the most responsive age classes [12]. Therefore, it can be hypothesized that climate warming might benefit young trees more than old ones through an extended growing season because tree meristems may become less sensitive to temperature as trees age, enlarge and lose hydraulic and growth efficiency, i.e., as their sapwood to leaf area ratio decreases [26]. Older trees tend to have shorter vegetation periods and produce fewer but larger cells per ring compared to young trees, which results in slower and shorter xylogenesis, making older trees less responsive to temperature variations [27,28,29]. In addition, older trees can face hydraulic constraints due to tree height and a long root‒leaves path length, which can decrease the temperature correlations of certain individuals, particularly under favourable conditions [30]. In this sense, if climate warming relaxes the harsh environmental that constrains the growth at upper altitudinal limits, it can be expected that a “relaxation hypothesis” could selectively affect treeline shifts as a function of age [24].
The recent development of process-based forward models of tree-ring formation such as the well-validated Vaganov‒Shashkin-Lite model (hereafter the VS-Lite model [31,32]) offers a valuable tool for understanding age-dependent growth responses to climate warming at treeline [33,34]. The VS-Lite model is one of the simplest computational approaches for understanding growth responses to regional climate [35,36,37]. The age dependence of tree growth responses to climate warming at treeline could be better understood by calculating and modelling the relationships between past climate and radial growth and considering different age classes [8]. Such climate‒growth relationships can also be projected as a function of forecasted climate scenarios by using models of individual tree growth that allow for assessing future growth dynamics at the alpine treeline [7,33].
Here, we assess radial growth responses as a function of observed and forecasted climate under two emissions scenarios [38] using climate–growth correlations and the VS-Lite model, respectively. We compare treelines located in peripheral Eurasian regions dominated by different tree species such as the Mountain pine (Pinus uncinata Ram.) in the Spanish Pyrenees and the Siberian Larch (Larix sibirica Ledeb.) in the Russian Polar Urals (see [18] for more details of both sites). Our specific objectives are: (1) to compare the growth responses to climate as related to local climatic variability and tree age, (2) to characterize age-dependent thresholds of growth response to temperature using the VS-Lite model, and (3) to explore the warming-induced changes in treeline growth dynamics under different climatic scenarios. We assume that larch trees from the Ural treelines will be more sensitive to growing-season temperatures because they are deciduous and grow in a much colder region than pine trees forming the Pyrenean treelines. We expect that rising temperatures will lengthen the growing season at treelines, with young trees exhibiting the highest sensitivity to climate warming.

2. Materials and Methods

2.1. Study Area and Tree Species

Throughout this paper, the treeline is defined as the highest elevation of 2-m tall trees and the treeline ecotone is defined as the transition between the highest elevation of closed forest with >50% of tree cover and the treeline. We selected two treeline sites located in the Spanish Pyrenees (Table 1; Figure 1) previously characterized in extensive fieldwork [2,39]. The estimated maximum elevations of undisturbed treelines in the Pyrenees are 2200–2400 m a.s.l. [40]. The Ordesa site (hereafter OR) is an abrupt treeline influenced by strong winds shaping a dense krummholz belt, which explains the low elevation of this treeline, and subjected to cold and relatively dry conditions. The Tessó site (hereafter TE) is a diffuse treeline subjected to colder and wetter conditions. These treeline sites are located in the Mediterranean biome. Both sites have not been locally disturbed (logging, overgrazing, fire) for the past 50 years. The Pyrenean sites are dominated by Mountain pine (Pinus uncinata Ram.), which is a long-lived (it may reach 1000 years in age), slow-growing, evergreen and shade-intolerant conifer [41]. The species displays large ecological amplitude concerning topography and soil type [42]. Radial growth of P. uncinata starts in May and peaks in June–July, and latewood formation lasts from July to October [43]. Therefore, the growing season lasts from May to October. High-elevation Pyrenean P. uncinata forests usually form low-density, open-canopy stands located in steep, rocky and elevated sites and form the alpine treeline. The climate of the Pyrenees is strongly influenced by east–west and north–south gradients, with increasing Mediterranean conditions (e.g., warm and dry summers) eastwards and southwards, whereas continental conditions (e.g., cold winters) prevail in the Central Pyrenees [44]. Mediterranean summer drought is more important at OR than at TE site [45]. Mean annual temperature and total precipitation in the studied sites ranged from 2.0 to 4.9 °C and from 1200 (OR) to 2000 (TE) mm, respectively, with January and July as the coldest (mean −2.0 °C) and warmest (mean 12.5 °C) months, respectively [46]. Soils are mainly basic and acid in OR and TE sites, respectively.
We also selected two sites located at the Polar Urals forming the treeline ecotone between 220 m and 450 m a.s.l. and dominated by larch (Larix sibirica Ledeb.), a deciduous and shade-intolerant conifer, with some scattered birch trees (Betula tortuosa Ledeb.) and shrubby junipers. These treeline sites are located in the Polar biome. Here we studied two nearby site CH and UR study sites forming the treeline (CH) and the forest‒treeline transition (UR), respectively (Table 1; Figure 1). In these remote sites, the treeline has not been disturbed during at least the last two centuries [47]. Data of the Salekhard meteorological station (66.5° N, 66.7° E, 137 m a.s.l., located 55 km southeast of the CH and UR study sites) show a mean annual temperature of −6.4 °C, with July (+13.8 °C) and January (−24.4 °C) as the warmest and coldest months, respectively. According to climate–growth relationships and based on phenological field observations (needle and shoot elongation, stem wood formation), the growing season lasts from June to August [48]. Mean annual precipitation is 415 mm, with 50% falling as snow. The Ural study sites have been not locally disturbed by fires, logging or overgrazing for at least the last two centuries. Maximum snow depth is 200–250 cm [49]. Soils develop on ultramafic rocks (peridotites).

2.2. Field Sampling and Dendrochronological Methods

At each site, we selected trees at least 30 years old growing in the same site and located at least 5 m apart from each other across a rectangular area of 4200 m2 [7,18,41]. Two age groups were established based on previous analyses and considering old (age > 75 years) and young (age ≤ 50 years) trees. We sampled a minimum of 30 trees per age group for each site. We measured diameter at 1.3 m from the base (DBH) and height (H) of each tree using tapes (Table 2). Two cores per tree at 1.3 m height were collected with a Pressler increment borer along the perpendicular direction to maximum slope. The cores were air dried, sanded with sand paper of progressively finer grain until tree rings became clearly visible. Samples were visually cross-dated, and their ring width series were measured to the nearest 0.01 mm using a LINTABTM measuring device (Rinntech, Heidelberg, Germany). Cross-dating quality was checked using the program COFECHA [50] by comparing the consistency of the different ring-width series with mean site series of each age class using correlations. In cases of cores without pith, the rings to the pith was estimated by fitting a template of concentric circles with known radii to the innermost rings [51]. The number of growth rings in the missing radius was obtained by dividing the estimated length of the missing distance by the mean ring width obtained from the 20 innermost growth rings. Cores whose innermost rings were not close enough to the pith or did not curve were not used in the analyses of age effects.
To quantify climate‒growth relationships, tree-ring widths were converted into ring-width indices (TRWi) by standardizing and detrending ring-width data for each tree using the program ARSTAN v.44 (Tucson, AZ, USA) [52]. Each tree ring-width series was detrended fitting a 30-year long spline to retain high-frequency variability. Detrending allowed transforming ring widths to dimensionless growth indexes by dividing observed tree-ring widths by fitted values. The resulting series were pre-whitened by using autoregressive models to remove temporal autocorrelation. Finally, a biweight robust mean was computed to obtain a residual chronology for each age group for each site that was used in all subsequent analyses.
Lastly, to assess the quality of tree-ring width series several dendrochronological statistics were calculated considering the common period 1950–2012 [9]: the first-order autocorrelation of raw width data (AC), the mean sensitivity (MS) of indexed ring-width indices, the mean correlation between trees (rbt), the variance accounted for by the first principal component (PC1) and the Expressed Population Signal (EPS), which measures the statistical quality of the mean site chronology compared with a perfect infinitely replicated chronology [53]. The part of the site chronologies that reached EPS values equal to or higher than 0.85 were regarded as reliable enough for calculating climate‒growth correlations (Table 2).

2.3. Climate‒Growth Analysis and Projected Scenarios

Monthly temperature data were combined into three regional datasets using data from local meteorological stations, see [7,18]. In addition, the homogenized and quality-checked Climatic Research Unit-CRU (0.5° resolution) [55] and European Climate Assessment & Dataset project, E-OBS v. 14.0 climate data sets (0.25° resolution; [56]) were used to get monthly temperature data (maximum, mean and minimum temperatures) for 1950–2012. We analysed climatic trends in the study areas at a regional scale and also quantified climate–growth relationship using monthly climatic data (total precipitation and mean temperatures) from these combined climate datasets. Due to a decreasing number of instrumental station records together with an increasing amount of uncertainty associated with climate data before the 1950s [57], the statistical analyses (climate–growth correlations, models) were restricted to 1950–2012.
To quantify climate‒growth relationships between TRWi and monthly climate data, we calculated bootstrapped Pearson correlation coefficients for the common period 1950–2012. These correlations were calculated from previous August to current October, i.e., during the year of tree-ring formation, based on previous analyses of P. uncinata [43] and L. sibirica [18]. To assess whether these relationships were stable through time, we calculated 20-year long moving correlations overlapping by one year, taking into consideration those climate variables significantly (p < 0.05) correlated with TRWi. Comparisons of variables between age groups were assessed using one-way ANOVA.
The climate data projected for the 21st century was downscaled cf. [58] at a 0.25° spatial resolution from the fifth phase of the Coupled Model Intercomparison Project ensemble CMIP5 [59]; We selected two [38] AR5 (Fifth Assessment Report) scenarios, specifically the scenario (Representative Concentration Pathway, RCP 8.5) that most closely tracked recent historical emissions, and one lower-emission scenario (RCP 2.6) in which the increase in annual emissions is more gradual and declines after the mid-21st-century. These scenarios result in +4.8 °C (RCP 8.5) +0.3 °C (RCP 2.6) global warming rates, respectively, by the year 2100, relative to the late-20th-century baseline.

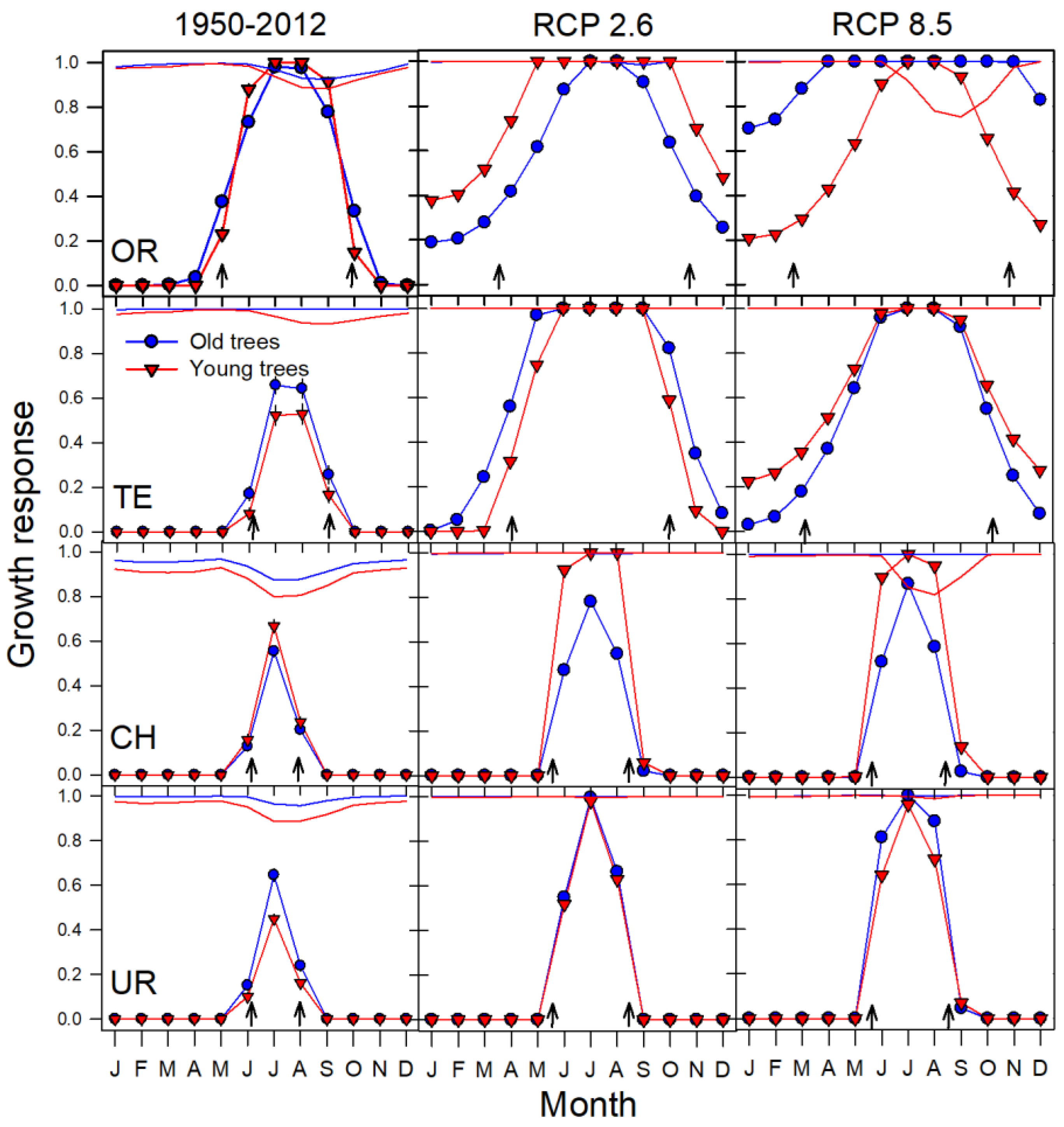
2.4. Temperature-Driven Growth Projections Based on the VS-Lite Model

We simulate TRWi as a function of climate using the VS-Lite model and a Bayesian parameter estimation approach [35]. The model estimates monthly soil moisture using the Leaky Bucket Model of hydrology where all precipitation is assumed to be liquid. For each year, the model simulates standardized tree-ring width anomalies from the minimum of the monthly growth responses to temperature (gT) and moisture (gM), modulated by insolation (gE). The growth response functions for temperature (gT) and moisture (gM) in VS-Lite involve only two parameters. The first parameter represents the temperature (T1) or moisture (M1) thresholds below which growth will not occur, whereas the second parameter is the optimal temperature (T2) or moisture (M2) thresholds above which growth is not limited by climate. The growth function parameters were estimated for each species using Bayesian calibration. Day length is determined from site latitude and does not vary between years. This scheme assumes normally distributed errors for the modelled TRWi values. The posterior median for each parameter was used to obtain the calibrated growth response for the selected age group for each site. Finally, the model was run over the entire period 1950–2012 using the calibrated parameters for each age group to produce a simulated tree-ring chronology (TRWiVSL) that represents an estimate of the age-site climate signal of tree growth [35]. The model was evaluated 10,000 times for each site using three parallel Markov Chain Monte Carlo chains with uniform prior distribution for each parameter and a white Gaussian noise model error [35]. To compute annual TRWi values with simulated TRWiVSL values, we integrated the overall simulated growth rates (gT, gM and gE) over the time window from August of the year prior to growth to October of the year of tree-ring formation. To evaluate the temporal stability of the calibrated growth response functions, we divided the period 1950–2012 into two intervals (1950–1975, 1975–2012), and withhold the second half for validation of the parameters estimated in the first half.
The climate‒growth relationships calculated using Pearson correlations were re-examined by applying stepwise multiple linear regressions to identify the effects of temperature on the observed TRWi data, and to project TRWi for the two age groups. Only those climate variables highly correlated with TRWi (r > |0.30|, p < 0.05) were considered in the temperature-driven TRWi projections under the abovementioned scenarios. Monthly temperatures for each site were transformed into normalized standard deviations to give them the same weight in the fitted models. Additionally, we evaluated the existence of multicollinearity among explanatory variables by calculating the variance inflation factor (VIF), which was lower than two, confirming no redundancy problems with the data. The selected models were run to forecast the TRWi of each site and age group (hereafter TRWip) for the 2013–2050 and 2050–2100 periods under the two emission scenarios. Finally, we conducted VS-Lite models on TRWip series over the same periods to estimate growth responses (gT, gM) and parameters (T1, T2, M1, M2) under future climate projections.
All analyses were conducted using the R statistical package [60]. We used the function dredge [61] of the R package MuMIn [60] using the lowest Akaike Information Criterion (AIC) for selecting the most parsimonious regression model [62]. The models were fitted using Generalized Least-Squares estimation (GLS) and the R package nlme [63].

3. Results

3.1. Age-Related Growth Responsiveness to Temperature

Warming trends during the 1901–2012 periods were stronger in the Pyrenean than in the Ural treelines (Figure 1). In contrast, the precipitation showed positive trends in Polar Urals. In terms of growth, we found significant (p < 0.01) higher ring-width values in young trees (mean 1.62 mm in P. uncinata and 1.09 mm in L. sibirica) than in old trees (mean 1.32 mm in P. uncinata and 0.62 mm in L. sibirica) (Table 2). Regarding dendrochronological statistics, young P. uncinata trees had the lowest values of first-order autocorrelation (AC), while old trees in both species presented the highest synchrony among trees (rbt) and the highest percentage of common variance (PC), except for old trees in the Urals CH site, suggesting a high responsiveness to climate (Table 2). Mean sensitivity was higher in young trees for P. uncinata and for old trees in L. sibirica. In all cases the EPS was above the 0.85 threshold usually considered for well-replicated chronologies or mean series (Table 2).
Warm summer conditions enhanced growth in the Ural treelines with stronger correlations in young trees. Specifically, higher June‒July temperatures were related to wider ring widths, particularly at the CH site (Figure 2). In contrast, warm current-spring and previous-winter conditions enhanced P. uncinata growth at Pyrenean treelines. These associations were also higher in young trees for OR and TE sites. Previous November temperature was also positively correlated with TRWi, with this correlation being higher in OR than in TE, particularly in old trees (Figure 2) (F = 2.86, p < 0.05).
Moving correlations between radial growth and the significant temperatures showed a noticeable shift in the 1980s with changes from negative to positive values for July minimum temperature in L. sibirica treelines, higher in young trees than in old ones (Figure 3). The influence of minimum May temperature on P. uncinata growth decreased more in OR than in TE Pyrenean treelines. In contrast, previous November temperatures were playing opposite roles by enhancing or decreasing growth since 1980s in OR and TE sites, respectively.

3.2. Process-Based Modelling of Tree Growth at Treeline

The VS-Lite model accurately predicted the year-to-year variability in TRWi during the 1950–2012 period for the two conifer species (Table 3; Figure 4). The modelled growth responses to temperature (gT) were higher in young trees for OR and CH sites (F = 6.75, p < 0.05), in contrast to the TE and UR sites (Figure 4). The mean growth response to temperature (gT) in the Pyrenean treelines peaked from April (May) to October in OR (TE) site, whilst the gT peaked from May to September in the Ural treelines in response to this extremely cold-limited environment. Tree growth was not limited by soil moisture (gM) as expected in response to high-elevation environment (Figure 5), except for OR site, where the growth constrains by low summer moisture, higher in young trees. The estimated minimum and optimal thresholds (T1, T2 and M1, M2) for growth confirmed the highest sensitivity of young P. uncinata trees and old L. sibirica trees to cold temperatures (maximum T2 value). The estimated higher value of M2 (optimal soil moisture conditions for growth) in P. uncinata confirmed the sensitivity to dry conditions in the Mediterranean treelines, especially in the OR site (Table 3; Figure 5).

3.3. Growth Projections at Treeline Based on Climate‒Growth Relationships

The selected climate-based models explained on average higher TRWi variance in old (69% OR, 47% TE) than in young (45% OR, 33% TE) P. uncinata trees. In the case of L. sibirica the explained variance (average 55%) was similar between age classes (Table 4). The climate predictors were similar to the most influential monthly climate variables detected in the analyses of climate‒growth relationships (Figure 2 and Figure 3). The predicted TRWi series based on GLS climate‒growth models were within the range of the observed values for the 1950–2012 period.

3.4. Age-Related Changes in the Projections of Climatic Thresholds

Under the climate scenarios (RCP 2.6 and RCP 8.5), growth at the Pyrenean and Ural studied treelines is forecasted to be increasingly favoured by rising temperatures, i.e., trees will show higher growth rates throughout a longer growing season (Figure 4 and Figure 5). In other words, growth at treeline will be less limited by cold conditions. The Pyrenean OR treeline would experience persistent warmer conditions through the year, causing that water shortage may limit growth in young trees (under RCP 8.5) (Figure 5). On the contrary, the Ural treelines are projected to show mainly higher growth rates, but similar growing season as nowadays (Figure 5). Warming would enhance growth, more in young trees than in old trees for the Ural CH site under both emission scenarios.
The minimum temperature threshold for growth (T1) will decrease in most sites, related to relaxation in temperature limitation during the onset of the growing season during the second half of the 21st-century (Table 4); and confirming that a marked advance of spring phenology could occur during the next decades. These decreases will be higher in young than in old trees. On the contrary the temperature at which growth is not limited (T2) will increase only in Pyrenean treeline sites (OR and TE), thus lengthening the growing season (Figure 5; Table 5). Thus, the forecasted warmer growing season would positively affect the growth of these treelines by enhancing their functional thresholds for optimal growth responses (i.e., gT), which are generally higher in young than in old trees (Figure 5).
The estimated optimal thresholds (T2, M2) for growth confirmed the highest sensitivity of young trees in the Pyrenean OR treeline to low soil moisture (maximum T2 and M2 values) under the RCP 8.5 scenario. We observed an increase of the minimum and optimum temperatures thresholds of growth (T1 and T2) and a decrease in minimum soil moisture (M1) for tree growth (Table 5). Consequently, growing conditions for young trees in the OR site under the RCP 8.5 scenario would sharply deteriorate because of declining soil water availability, with this limitation more pronounced in the former site than in TE.

4. Discussion

4.1. Growth Responsiveness to Rising Temperature at the Treeline

We found positive trends in growth responses to rising temperatures in Eurasian treelines located in different biomes, but such responses significantly varied with tree age [7,10,11]. These growth improvements are linked to recent temperature rising trends (Figure 1), suggesting climate warming may favour tree growth, expand growing season length and thus promote treeline advances [7,64].
Tree growth is strongly linked to recent inter-annual variability in growing season air temperature according to our results (Figure 2 and Figure 3; Table 4) [6]. Positive temperature‒growth relationships were observed in both young and old treeline individuals for both tree species suggesting a common response to warming regardless tree age, species or site [11]. However, younger individuals present a stronger linkage to growing season temperatures than older individuals as we hypothesized (Figure 2). These results may be explained by a relaxation of the thermal gradient within treeline ecotones under which the dependence of tree growth on temperature may decrease in response to recent warming trends at higher elevations [24]. Growth may still keep improving in response to warming despite local or regional differences while it relies mainly in young trees growth sensitivity [3,7].
Tree growth at alpine treelines from the Polar Urals (CH, UR) and the Pyrenees (OR, TE) responded more to growing season temperatures than to precipitation, and this response has been stable (Pyrenees) or strengthened (Polar Urals) after the 1980s, when temperatures started rising rapidly (Figure 3), see also [18,65]. Our results show that treeline growth is responding to climate warming by increasing growth rates and growing season, particularly at the Polar Urals where L. sibirica growth is mainly constrained by the short growing season and cold summer conditions [48]. However, at the Pyrenees study sites, warming trends after 1950 were more pronounced than in the Urals due to the contribution of increasingly warmer summer conditions [18]. This highlights that the typical representation featuring a straight northward or upward growth enhancement (e.g., in [5] for Scots pine) is more complex, with the role of precipitation that should not be overlooked at some drought-prone treelines [66,67]. In this context, we cannot discount the fact that rising atmospheric CO2 concentrations may ameliorate drought-induced growth reductions in lower latitudes (i.e., P. uncinata at OR treeline) subjected to warmer and drier climates [68].
The described patterns match those found in previous studies in the Pyrenees where most P. uncinata growth processes (shoot and needle elongation, tree-ring thickening and lignification) occur from May to October [69]. In this area P. uncinata radial growth at treeline is favoured by warmer May‒June conditions [24,69,70,71]. Warm temperatures at the end of the growing season (November) do not directly influence radial growth, but could enhance the synthesis of carbohydrates during late autumn that will be later allocated for earlywood formation the following year [72]. In the case of L. sibirica most growth processes occur from June to August [48,73] and its radial growth is favoured by warmer June and July temperatures (Figure 2 and Figure 4). In addition, the key role of summer temperature on the increasing growth rates of such Polar treelines might be also related to the snow amount, duration and cover [74]. Previous investigations across the Siberian subarctic treelines, including CH and UR study sites, found a delayed snow melt due to increasing winter precipitation [75]. Late snow melting could have postponed the onset of cambial activity, thus leading to slower growth and a loss of growth sensitivity to summer temperatures [23]. A similar detrimental effect of snow pack duration on growth has not been yet assessed for P. uncinata in the Pyrenees to the best of our knowledge. Those studies should consider the asymmetry of xylogenesis in P. uncinata, i.e., the fact that growth rates are much faster in the early (May–August) than in the late (September–November) growing season [43]. This implies that warm conditions early in the growing season may advance the spring cambial onset and determine the maximum growth rates for both treeline species, and possibly determine most of the final tree-ring width [23,76] (Figure 5). Other drivers such as changes in light availability [77], nitrogen deposition and rising CO2, biotic interactions, disturbance regime and local adaptations could also affect treeline growth, but their roles have to be further explored.

4.2. Climate Warming Influences Growth at Treeline Depending on Tree Age

The projected warming trends will have contrasting effects on the performance of P. uncinata and L. sibirica age groups at treeline (Figure 5; Table 4 and Table 5), which agrees with recent observations of growth increase in some of these sites [7,18]. We found evidence suggesting a notable growth improvement in cold-limited alpine treelines, which also agrees with previous findings [3,78]. These results suggest the existence of age-related changes in endogenous parameters possibly linked to the hydraulic conductivity and the tree carbon balance including vulnerability to winter desiccation [79]. Our results support the idea that rising spring to summer temperatures become more limiting for growth as trees become older as previously observed [16]. Such age dependence of tree growth responsiveness or sensitivity to climate could be explained by physiological changes (alterations in photosynthesis rates, changes in carbon or nutrient allocation to sinks or growing meristems, less efficient hydraulic architecture, etc.) as trees age and enlarge [80,81]. These ontogenetic changes affect xylogenesis [27] and modify growth–climate relationships [11] on these shade-intolerant conifer species. Additionally, old and usually large and dominant trees should display improved growth conditions by lowering sensitivity to competition despite increasing tree height leading to decreasing hydraulic conductance [82]. Hydraulic constraints are increasingly limiting as trees age, thus inducing stressful conditions in older individuals [26]. These include higher climate sensitivity in stressed trees and a more prominent growth-climate signal observed in tree-ring data [83]. Conversely, younger trees are able to face adverse weather conditions due to the longer lasting stomatal opening inducing higher assimilation rates and possibly improving their growth rate [84]. In harsh environmental conditions, this strategy, with regard to gas exchange and growth, could ensure a higher rate of tracheid production and, thus, a higher growth rate under rising temperatures, but perhaps at the cost of a greater mortality risk [80] and, from the dendroecological point of view, a weaker (more complacent) tree-ring record of climatic signals [11,29].
Our models forecast higher growth rates under future scenarios for younger treeline individuals (Figure 5). These individuals became established under higher temperatures and atmospheric CO2 concentrations than old individuals, which improves their growth and development [84]. Similar results were found by [68] that found a markedly higher growth of younger P. uncinata trees in the Pyrenees and attributed it to an increase in air temperature. It must be noted that old individuals tend also to display increasing growth rates despite expected constant growth under the theoretical logistic growth model [85]. Forecasted warmer conditions would lengthen the growing season of high-elevation mountain pine sites where growth enhancement is projected (Figure 5). The magnitude and speed at which these changes might occur are affected by tree age and, thus partially depend on non-climatic forcings, with fastest and greater growth shifts (Figure 5; Table 5) occurring under the most rapidly warming RCP 8.5 scenario [86]. The most substantial impacts on growth are predicted to be positive for young trees in the CH treeline site located at the Polar Urals, which agrees with 20th-century reports of warming-triggered growth responses in the Polar Urals [18]. Our projections confirm that growth improvements are linked to age-dependent temperature responses to rising trends, despite dry conditions in the OR treeline site, suggesting warming may favour tree growth (Figure 2) and promote treeline advances under forecasted 21st-climate scenarios (Figure 5) [3]. We projected high growth rates for young trees in both species under the moderately warmer RCP 2.6 and the warmest RCP 8.5 scenarios (Figure 5; Table 4), but also extended growing season in P. uncinata Pyrenean treelines [67]. We also expect that the OR site growing under the influence of Mediterranean dry conditions may be negatively influenced by warming-induced drought stress and will be most sensitive under the RCP 8.5 scenario [33], although the rises in atmospheric CO2 concentrations may help to avoid the forecasted drought-induced growth reductions [68]. This site is showing a rapid encroachment with abundant shrubby krummholz individuals, shaped by windy conditions and a shallow snowpack, suggesting a rapid growth enhancement in response to the warmer climate [7].
In general, climate projections forecast longer growing seasons in Pyrenees treeline and higher growth rates in the Polar Ural treeline (Figure 5), but other local factors such an extended snow-free period or wetter conditions could also explain the acceleration of growth rates in these cold places [49,87]. This would imply higher growth sensitivity to climate during the early growing season, suggesting a prominent advance of spring onset as already observed in xylogenesis investigations [88]. The minimum temperature threshold for growth (T1) will decrease in all sites, related to relaxation in temperature limitation during the onset of the growing season throughout the second half of the 21st-century (Table 4). This indicates that a marked advance of spring phenology could occur during the 21-st century [89]; although other studies have emphasized that snow depth and total precipitation also play an important role in regulating spring vegetation phenology in mountain ecosystems [74]. On the contrary, the temperature at which growth is not limited (T2) will increase in Pyrenean treeline sites, where a longer growing season is forecasted (Table 5). Therefore, the projected hotter and longer growing season would positively affect the growth of Eurasian treeline populations by enhancing their functional thresholds for optimal growth responses (i.e., gT) (Figure 5; Table 4). In contrast, cloudiness or a longer or deeper snowpack could greatly condition this growth improvement by reducing the growing season [87].
Although every modelling approach has limitations, assumptions and associated handicaps, our methodological framework provides robust results that are in accordance with what has been observed in field studies on treelines as monitors of climate warming [2,90]. Nevertheless, process-based models show limitations because climate constrains other demographic processes than growth not considered in our study (e.g., regeneration, mortality; see [5]). We focused on radial growth, but primary growth and leaf phenology are also prominent components of forest productivity and leaf flushing is expected to advance due to climate warming [91]. Further studies could integrate our approach based on a process-based growth model with other components of forest dynamics such as regeneration or mortality [7,92,93] to produce better and more realistic forecasts of treeline shifts in a warmer world.

5. Conclusions

We provide new evidences showing climate-induced growth changes for Mediterranean and Polar treelines located at the Spanish Pyrenees and the Russian Urals, respectively. We also present a novel approach by accounting for growth shifts in response to forecasted 21st-century climate warming scenarios. Our results support that the projected warming-induced responses at the treeline are contingent on tree age. This temperature-induced enhancement on radial growth is forecasted to strengthen under upcoming decades in young trees. The RCP 8.5 emission scenario corresponding to the most pronounced warming conditions (+4.8 °C) could also amplify drought stress in trees from drought-prone treelines, as might occur in some Pyrenean treelines. The use of a process-based growth model revealed changing growth responses to climate warming. These forecasts imply that a warmer climate would lead to increase growth in both treeline species, higher in young than in old trees, but also involves an extended growing season for P. uncinata treelines at the Pyrenees. Our approach provides accessible tools to evaluate functional thresholds for growth that may be used as “early-warning monitors” of climate change effects.

Author Contributions

R.S.-S. & J.J.C. conceived the idea and wrote the manuscript. All authors contributed to study design, discussion and to the final writing of the manuscript. J.J.C., E.G., A.G., G.S.-B., P.M. and J.C.L performed field dendrochronological sampling and analysis the tree-ring data. R.S.-S. & J.J.C. conducted the statistical analyses.

Funding

We are very grateful for several projects financed by “Organismo Autónomo de Parques Nacionales” (projects 12/2008 and 387/2011). This study was also supported by the following projects funded by the Spanish Ministry of Economy, Industry and Competitiveness: AMB95-0160, REN2002-04268-C02, CGL2011-26654, CGL2015-69186-C2-1-R (FunDiver), CGL2013-48843-C2-1-R (CoMo-ReAdapt); by the TreeClim ERA.Net RUS Pilot Joint Call for Collaborative S&T Projects (funded under the 7th European Framework Programme for Research and Development) and by the Russian Scientific Foundation under grant RSF-17-14-01112 in part connected with the Polar Urals data sampling and working with article text. RSS is supported by Spanish Ministry of Economy, Industry and Competitiveness Postdoctoral grant (IJCI-2015-25845, FEDER funds).

Acknowledgments

The authors thank J. Diego Galván for his help in site selection and field sampling. We also thank Andrea Hevia for help with statistical analysis. We thank the editor and three anonymous reviewers for the useful comments provided.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Albright, W.L.; Peterson, D.L. Tree growth and climate in the Pacific Northwest, North America: A broad-scale analysis of changing growth environments. J. Biogeogr. 2013, 40, 2119–2133. [Google Scholar] [CrossRef]
  2. Camarero, J.J.; Gutiérrez, E. Pace and pattern of recent treeline dynamics: Response of ecotones to climatic variability in the Spanish Pyrenees. Clim. Chang. 2004, 63, 181–200. [Google Scholar] [CrossRef]
  3. Harsch, M.A.; Hulme, P.E.; McGlone, M.S.; Duncan, R.P. Are treelines advancing? A global meta-analysis of treeline response to climate warming. Ecol. Lett. 2009, 12, 1040–1049. [Google Scholar] [CrossRef] [PubMed]
  4. Hallinger, M.; Manthey, M.; Wilmking, M. Establishing a missing link: Warm summers and winter snow cover promote shrub expansion into alpine tundra in Scandinavia. New Phytol. 2010, 186, 890–899. [Google Scholar] [CrossRef] [PubMed]
  5. Matías, L.; Jump, A.S. Asymmetric changes of growth and reproductive investment herald altitudinal and latitudinal range shifts of two woody species. Glob. Chang. Biol. 2015, 21, 882–896. [Google Scholar] [CrossRef] [PubMed]
  6. Paulsen, J.; Körner, C. A climate-based model to predict potential treeline position around the globe. Alpine Bot. 2014, 124, 1–12. [Google Scholar] [CrossRef]
  7. Camarero, J.J.; Linares, J.C.; García-Cervigón, A.I.; Batllori, E.; Martínez, I.; Gutiérrez, E. Back to the future: The responses of alpine treelines to climate warming are constrained by the current ecotone structure. Ecosystems 2017, 20, 683–700. [Google Scholar] [CrossRef]
  8. Liu, B.; Wang, Y.; Zhu, H.; Liang, E.; Camarero, J.J. Topography and age mediate the growth responses of Smith fir to climate warming in the southeastern Tibetan Plateau. Int. J. Climatol. 2016, 60, 1577–1587. [Google Scholar] [CrossRef] [PubMed]
  9. Fritts, H.C. Tree Rings and Climate; Blackburn Press: Caldwell/London, UK; New York, NY, USA, 2001; ISBN 0-12-268450-8. [Google Scholar]
  10. Szeicz, J.M.; MacDonald, G.M. Age-dependent tree-ring growth responses of subarctic white spruce to climate. Can. J. For. Res. 1994, 23, 120–132. [Google Scholar] [CrossRef]
  11. Carrer, M.; Urbinati, C. Age-dependent tree ring growth responses to climate of Larix decidua and Pinus cembra in the Italian Alps. Ecology 2004, 85, 730–740. [Google Scholar] [CrossRef]
  12. Rozas, V.; DeSoto, L.; Olano, J.M. Sex-specific, age-dependent sensitivity of tree-ring growth to climate in the dioecious tree Juniperus thurifera. New Phytol. 2009, 182, 687–697. [Google Scholar] [CrossRef] [PubMed]
  13. Li, X.; Liang, E.; Gričar, J.; Prislan, P.; Rossi, S.; Cufar, K. Age dependence of xylogenesis and its climatic sensitivity in Smith fir on the south-eastern Tibetan Plateau. Tree Physiol. 2013, 2013 33, 48–56. [Google Scholar] [CrossRef]
  14. Li, B.; Cheng, X.H.; Lv, L.X. Responses of radial growth to fire disturbance in alpine pine (Pinus densata) of different age classes in Nang County, Xizang, China. Chin. J. Plant Ecol. 2016, 40, 436–446. [Google Scholar]
  15. Yu, G.; Liu, Y.; Wang, X.; Ma, K. Age-dependent tree-ring growth responses to climate in Qilian juniper (Sabina przewalskii Kom.). Trees-Struct. Funct. 2008, 22, 197–204. [Google Scholar] [CrossRef]
  16. Linares, J.C.; Taïqui, L.; Sangüesa-Barreda, G.; Seco, J.I.; Camarero, J.J. Age-related drought sensitivity of Atlas cedar (Cedrus atlantica) in the Moroccan Middle Atlas forests. Dendrochronologia 2013, 31, 88–96. [Google Scholar] [CrossRef]
  17. Vautard, R.; Gobiet, A.; Sobolowski, S.; Kjellström, E.; Stegehuis, A.; Watkiss, P.; Mendlik, T.; Landgren, O.; Nikulin, G.; Teichmann, C.; et al. The European climate under a 2 °C global warming. Environ. Res. Lett. 2014, 9, 34006. [Google Scholar] [CrossRef] [Green Version]
  18. Pellizzari, E.; Camarero, J.J.; Gazol, A.; Granda, E.; Shetti, R.; Wilmking, M.; Moiseev, P.; Pividori, M.; Carrer, M. Diverging shrub and tree growth from the Polar to the Mediterranean biomes across the European continent. Glob. Chang. Biol. 2017, 23, 3169–3180. [Google Scholar] [CrossRef] [PubMed]
  19. Rolland, C.; Petitcolas, V.; Michalet, R. Change in radial tree growth for Picea abies, Larix decidua, Pinus cembra, and Pinus uncinata near the alpine timberline since 1750. Trees-Struct. Funct. 1998, 13, 40–53. [Google Scholar] [CrossRef]
  20. Salzer, M.W.; Hughes, M.K.; Bunn, A.G.; Kipfmueller, K.F. Recent unprecedented tree-ring growth in bristlecone pine at the highest elevations and possible causes. Proc. Natl. Acad. Sci. USA 2009, 106, 20348–20353. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  21. Kullman, L. Tree line population monitoring of Pinus sylvestris in the Swedish Scandes, 1973–2005: Implications for tree line theory and climate change ecology. J. Ecol. 2007, 95, 41–52. [Google Scholar] [CrossRef]
  22. Slatyer, R.O.; Noble, I.R. Dynamic of Montane Treelines. In Landscape Boundaries: Consequences for Biotic Diversity and Ecological Flows; Hansen, A.J., di Castri, F., Eds.; Springer: New York, NY, USA, 1992; pp. 346–359. ISBN 978-1-4612-7677-7. [Google Scholar]
  23. Kirdyanov, A.; Hughes, M.; Vaganov, E.; Schweingruber, F.; Silkin, P. The importance of early summer temperature and date of snow melt for tree growth in the Siberian Subarctic. Trees-Struct. Funct. 2003, 17, 61–69. [Google Scholar] [CrossRef]
  24. Tardif, J.; Camarero, J.J.; Ribas, M.; Gutiérrez, E. Spatiotemporal variability in tree growth in the central Pyrenees: Climatic and site influences. Ecol. Monogr. 2003, 73, 241–257. [Google Scholar] [CrossRef]
  25. Körner, Ch. Alpine Treelines; Springer: Basel, Switzerland, 2012; p. 220. ISBN 978-3-0348-0395-3. [Google Scholar]
  26. Mencuccini, M.; Grace, J. Climate influence the leaf-area sapwood ratio in Scots pine. Tree Physiol. 1995, 15, 1–10. [Google Scholar] [CrossRef] [PubMed]
  27. Rossi, S.; Deslauriers, A.; Anfodillo, T.; Carrer, M. Age-dependent xylogenesis in timberline conifers. New Phytol. 2008, 177, 199–208. [Google Scholar] [CrossRef] [PubMed]
  28. Carrer, M.; von Arx, G.; Castagnieri, D.; Petit, G. Distilling environmental information from time series of conduit size: The standardization issue and its relation to allometric and hydraulic constraints. Tree Physiol. 2015, 35, 27–33. [Google Scholar] [CrossRef] [PubMed]
  29. Konter, O.; Büntgen, U.; Carrer, M.; Esper, J. Testing for Climate Signal Age Effects at Two Treeline Sites in the European Alps and Tatra Mountains. In TRACE–Tree Rings in Archaeology, Climatology and Ecology; Wistuba, M., Cedro, A., Malik, I., Helle, G., Gärtner, H., Eds.; Scientific Technical Report STR; 17/04; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2017; Volume 15. [Google Scholar]
  30. Ryan, M.G.; Yoder, B.J. Hydraulic limits to tree height and tree growth. Bioscience 1997, 47, 235–242. [Google Scholar] [CrossRef]
  31. Vaganov, E.A.; Hughes, M.K.; Shashkin, A.V. Growth Dynamics of Conifer Tree Rings; Springer: Berlin, Germany, 2006; p. 358. ISBN 978-3-540-26086-8. [Google Scholar]
  32. Vaganov, E.A.; Anchukaitis, K.J.; Evans, M.N. How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. Dendroclimatology. In Developments in Paleoenvironmental Research; Hughes, M.K., Swetnam, T.W., Diaz, H.F., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 37–75. ISBN 978-1-4020-4010-8. [Google Scholar]
  33. Sánchez-Salguero, R.; Camarero, J.J.; Gutiérrez, E.; González Rouco, F.; Gazol, A.; Sangüesa-Barreda, G.; Andreu-Hayles, L.; Linares, J.C.; Seftigen, K. Assessing forest vulnerability to climate warming using a process-based model of tree growth: Bad prospects for rear-edges. Glob. Chang. Biol. 2017, 23, 2705–2719. [Google Scholar] [CrossRef] [PubMed]
  34. Sánchez-Salguero, R.; Camarero, J.J.; Carrer, M.; Gutiérrez, E.; Alla, A.Q.; Andreu-Hayles, L.; Hevia, A.; Koutavas, A.; Martínez-Sancho, E.; Nola, P.; et al. Climate extremes and predicted warming threaten Mediterranean Holocene firs forests refugia. Proc. Natl. Acad. Sci. USA 2017, 114, E10142–E10150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Tolwinski-Ward, S.E.; Anchukaitis, K.J.; Evans, M.N. Bayesian parameter estimation and interpretation for an intermediate model of tree-ring width. Clim. Past 2013, 9, 1481–1493. [Google Scholar] [CrossRef]
  36. Breitenmoser, P.; Bronnimann, S.; Frank, D. Forward modelling of tree-ring width and comparison with a global network of tree-ring chronologies. Clim. Past 2014, 10, 437–449. [Google Scholar] [CrossRef]
  37. Mina, M.; Martin-Benito, D.; Bugmann, H.; Cailleret, M. Forward modeling of tree-ring width improves simulation of forest growth responses to drought. Agric. For. Meteorol. 2016, 221, 13–33. [Google Scholar] [CrossRef]
  38. IPCC. Climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
  39. Batllori, E.; Gutiérrez, E. Regional tree line dynamics in response to global change in the Pyrenees. J. Ecol. 2008, 96, 1275–1288. [Google Scholar] [CrossRef] [Green Version]
  40. Ninot, J.M.; Carrillo, E.; Font, X.; Carreras, J.; Ferré, A.; Masalles, R.M.; Soriano, I.; Vigo, J. Altitude zonation in the Pyrenees. A geobotanic interpretation. Phytocoenologia 2007, 37, 371–398. [Google Scholar] [CrossRef]
  41. Camarero, J.J.; Gutiérrez, E. Structure and recent recruitment at alpine forest-pasture ecotones in the Spanish central Pyrenees. Ecoscience 1999, 6, 451–464. [Google Scholar] [CrossRef]
  42. Ceballos, L.; Ruiz de la Torre, J. Árboles y arbustos de la España Peninsular; Escuela Técnica Superior de Ingenieros de Montes: Madrid, Spain, 1979. ISBN 978847114 9688.
  43. Camarero, J.J.; Guerrero-Campo, J.; Gutiérrez, E. Tree-ring growth and structure of Pinus uncinata and Pinus sylvestris in the Central Spanish Pyrenees. Arct. Alp. Res. 1998, 30, 1–10. [Google Scholar] [CrossRef]
  44. López-Moreno, J.I.; García-Ruiz, J.M.; Beniston, M. Environmental Change and water management in the Pyrenees. Facts and future perspectives for Mediterranean mountains. Glob. Planet. Chang. 2008, 66, 300–312. [Google Scholar] [CrossRef]
  45. Balcells, E.; Gil Pelegrín, E. Consideraciones fenológicas de las biocenosis de altitud en el Parque Nacional de Ordesa y Monte Perdido, acompañadas y apoyadas mediante estudio preliminar de los datos meteorológicos obtenidos desde 1981 a 1989 en el observatorio de Góriz. Lucas Mallada 1992, 4, 71–162. [Google Scholar]
  46. Camarero, J.J. Growth and Regeneration Patterns and Processes in Pinus uncinata Ram. Treeline Ecotones in the Pyrenees and Anisolated Population in the Western Distribution Limit in Spain. Ph.D. Thesis, University of Barcelona, Barcelona, Spain, 1999. [Google Scholar]
  47. Shiyatov, S.G.; Terentev, M.M.; Fomin, V.V. Spatiotemporal dynamics of forest-tundra communities in the Polar Urals. Russ. J. Ecol. 2005, 36, 69–75. [Google Scholar] [CrossRef]
  48. Devi, N.; Hagedorn, F.; Moiseev, P.; Bugmann, H.; Shiyatov, S.; Mazepa, V.; Rigling, A. Expanding forests and changing growth forms of Siberian larch at the Polar Urals treeline during the 20th century. Glob. Chang. Biol. 2008, 14, 1581–1591. [Google Scholar] [CrossRef]
  49. Hagedorn, F.; Shiyatov, S.G.; Mazepa, V.S.; Devi, N.M.; Grigorèv, A.A.; Bartysh, A.A.; Fomin, V.V.; Kapralov, D.S.; Terentèv, M.; Bugman, H.; et al. Treeline advances along the Urals mountain range—Driven by improved winter conditions? Glob. Chang. Biol. 2014, 20, 3530–3543. [Google Scholar] [CrossRef] [PubMed]
  50. Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
  51. Duncan, R.P. An evaluation of errors in tree age estimates based on increment cores in kahikatea (Dacrycarpus dacrydioides). N. Z. Nat. Sci. 1989, 16, 31–37. [Google Scholar]
  52. Cook, E.R. A Time-Series Analysis Approach to Tree Ring Standardization. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
  53. Wigley, T.M.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Appl. Meteorol. Clim. 1984, 23, 201–213. [Google Scholar] [CrossRef]
  54. Quinn, G.P.; Keough, M.J. Experimental Design and Data Analysis for Biologists; Cambridge University Press: Cambridge, UK, 2002; p. 539. [Google Scholar]
  55. Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high resolution grids of monthly climatic observations–the CRU TS3. 10 Dataset. Int. J. Clim. 2013, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
  56. Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. Atmos. 2008, D20, 113. [Google Scholar] [CrossRef]
  57. Jones, P.D. The reliability of global and hemispheric surface temperature records. Adv. Atmos. Sci. 2016, 33, 269–282. [Google Scholar] [CrossRef] [Green Version]
  58. Moreno, A.; Hasenauer, H. Spatial downscaling of European climate data. Int. J. Climatol. 2016, 2016 36, 1444–1458. [Google Scholar] [CrossRef]
  59. Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
  60. R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; R Development Core Team: Vienna, Austria, 2018. [Google Scholar]
  61. Barton, K. MUMIn: Multi-model inference. R. package version 1.40.4. 2018. Available online: https://cran.r-project.org/web/packages/MuMIn/index.html (accessed on 1 June 2018).
  62. Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference; Springer: New York, NY, USA, 2002; p. 488. [Google Scholar]
  63. Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models, R package version 3.1-137; R Core Team: Vienna, Austria, 2018. [Google Scholar]
  64. Liu, B.; Liang, E.; Liu, K.; Camarero, J.J. Species- and elevation-dependent growth responses to climate warming of mountain forests in the Qinling Mountains, central China. Forests 2018, 9, 248. [Google Scholar] [CrossRef]
  65. Galván, D.; Camarero, J.J.; Gutiérrez, E. Seeing the trees for the forest: Drivers of individual growth responses to climate in Pinus uncinata mountain forests. J. Ecol. 2014, 102, 1244–1257. [Google Scholar] [CrossRef]
  66. González de Andrés, E.; Camarero, J.J.; Büntgen, U. Complex climate constraints of upper treeline formation in the Pyrenees. Trees-Struct. Funct. 2015, 29, 941–952. [Google Scholar] [CrossRef] [Green Version]
  67. Piper, F.; Viñegla, B.; Linares, J.C.; Camarero, J.J.; Cavieres, L.A.; Fajardo, A. Mediterranean and temperate treelines are controlled by different environmental drivers. J. Ecol. 2016, 104, 691–702. [Google Scholar] [CrossRef]
  68. Camarero, J.J.; Gazol, A.; Galván, J.D.; Sangüesa-Barreda, G.; Gutiérrez, E. Disparate effects of global-change drivers on mountain conifer forests: Warming-induced growth enhancement in young trees vs. CO2 fertilization in old trees from wet sites. Glob. Chang. Biol. 2015, 21, 738–749. [Google Scholar] [CrossRef] [PubMed]
  69. Guerrero-Campo, J.; Camarero, J.J.; Gutiérrez, E. Crecimiento estacional y caída de acículas en Pinus uncinata Ram. y Pinus sylvestris L. Investig. Agrar. Sist. Y Recur. For. 1998, 7, 155–172. [Google Scholar]
  70. Gutiérrez, E. Climate tree-growth relationships for Pinus uncinata Ram. in the Spanish pre-Pyrenees. Acta Oecol. 1991, 12, 213–225. [Google Scholar]
  71. Büntgen, U.; Frank, D.; Grudd, H.; Esper, J. Long-term summer temperature variations in the Pyrenees. Clim. Dyn. 2008, 31, 615–631. [Google Scholar] [CrossRef]
  72. Von Felten, S.; Hättenschwiler, S.; Saurer, M.; Siegwolf, R. Carbon allocation in shoots of alpine treeline conifers in a CO2 enriched environment. Trees Struct. Funct. 2007, 21, 283–294. [Google Scholar] [CrossRef] [Green Version]
  73. Jiao, L.; Jiang, Y.; Zhang, W.T.; Wang, M.C.; Zhang, L.N.; Zhao, S.D. Divergent responses to climate factors in the radial growth of Larix sibirica in the eastern Tianshan Mountains, northwest China. Trees-Struct. Funct. 2015, 29, 1673–1686. [Google Scholar] [CrossRef]
  74. Frost, G.V.; Epstein, H.E. Tall shrub and tree expansion in Siberian tundra ecotones since the 1960s. Glob. Chang. Biol. 2014, 20, 1264–1277. [Google Scholar] [CrossRef] [PubMed]
  75. Vaganov, E.A.; Hughes, M.K.; Kirdyanov, A.V.; Schweingruber, F.H.; Silkin, P.P. Influence of snowfall and melt timing on tree growth in subarctic Eurasia. Nature 1999, 400, 149–151. [Google Scholar] [CrossRef]
  76. Moser, L.; Fonti, P.; Buentgen, U.; Franzen, J.; Esper, J.; Luterbacher, J.; Frank, D. Timing and duration of European larch growing season along altitudinal gradients in the Swiss Alps. Tree Physiol. 2010, 30, 225–233. [Google Scholar] [CrossRef] [PubMed]
  77. Stine, A.R.; Huybers, P. Arctic tree rings as recorders of variations in light availability. Nat. Commun. 2014, 5, 3836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  78. Galván, J.D.; Camarero, J.J.; Sangüesa-Barreda, G.; Alla, A.Q.; Gutiérrez, E. Sapwood area drives growth in mountain conifer forests. J. Ecol. 2012, 100, 1233–1244. [Google Scholar] [Green Version]
  79. Mayr, S. Limits in water relations. In Trees at Their Upper Limit; Wieser, G., Tausz, M., Eds.; Springer: Berlin, Germany, 2007; pp. 145–162. [Google Scholar]
  80. Bond, B.J. Age-related changes in photosynthesis of woody plants. Trends Plant Sci. 2000, 5, 349–353. [Google Scholar] [CrossRef]
  81. Ryan, M.G.; Phillips, N.; Bond, B.J. The hydraulic limitation hypothesis revisited. Plant Cell Environ. 2006, 29, 367–381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  82. Domec, J.C.; Gartner, B.L. Age- and position-related changes in hydraulic versus mechanical dysfunction of xylem: Inferring the design criteria for Douglas-fir wood structure. Tree Physiol. 2002, 22, 91–104. [Google Scholar] [CrossRef] [PubMed]
  83. Shiyatov, S.G.; Mazepa, V.S.; Vaganov, E.A.; Schweingruber, F.H. Summer Temperature Variations Reconstructed by Tree-Ring Data at the Polar Timberline in Siberia. In Tree Rings, Environment and Humanity, Proceedings of the International Conference, Tucson, Arizona; Dean, J.S., Meko, D.M., Swetnam, T.W., Eds.; Radiocarbon Department of Geosciences University of Arizona: Tucson, AZ, USA, 1996; pp. 249–258. [Google Scholar]
  84. Phillips, N.G.; Buckley, T.N.; Tissue, D.T. Capacity of Old Trees to Respond to Environmental Change. J. Integr. Plant Biol. 2008, 50, 1355–1364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  85. Hunt, E.R.; Lavigne, M.B.; Franklin, S.E. Factors controlling the decline of net primary production with stand age for balsam fir in Newfoundland assessed using an ecosystem simulation model. Ecol. Mod. 1999, 122, 151–164. [Google Scholar] [CrossRef]
  86. Ruosch, M.; Spahni, R.; Joos, F.; Henne, P.D.; van der Knaap, W.O.; Tinner, W. Past and future evolution of Abies alba forests in Europe—Comparison of a dynamic vegetation model with Palaeo data and observations. Glob. Chang. Biol. 2016, 22, 727–740. [Google Scholar] [CrossRef] [PubMed]
  87. Lavergne, A.; Daux, V.; Villalba, R.; Barichivich, J. Temporal changes in climatic limitation of tree-growth at upper treeline forests: Contrasted responses along the west to-east humidity gradient in Northern Patagonia. Dendrochronologia 2015, 36, 49–59. [Google Scholar] [CrossRef]
  88. Yang, B.; He, M.; Shishov, V.; Tychkov, I.; Vaganov, E.H.; Rossi, S.; Ljungqvist, F.C.; Bräuning, A.; Grießinger, J. New perspective on spring vegetation phenology. Proc. Natl. Acad. Sci. USA 2017, 114, 6966–6971. [Google Scholar] [CrossRef] [PubMed]
  89. Badeck, F.; Bondeau, A.; Böttcher, K.; Doktor, D.; Lucht, W.; Schaber, J.; Sitch, S. Responses of spring phenology to climate change. New Phytol. 2004, 162, 295–309. [Google Scholar] [CrossRef] [Green Version]
  90. Shiyatov, S.G.; Terentév, M.M.; Fomin, V.V.; Zimmermann, N.E. Altitudinal and horizontal shifts of the upper boundaries of open and closed forests in the Polar Urals in the 20th century. Russ. J. Ecol. 2007, 38, 223–227. [Google Scholar] [CrossRef]
  91. Vitasse, Y.; Franc, C.; Delpierre, N.; Dufrêne, E.; Kremer, A.; Chuine, I.; Delzon, S. Assessing the effects of climate change on the phenology of European temperate trees. Agric. For. Meteorol. 2011, 151, 969–980. [Google Scholar] [CrossRef]
  92. Sangüesa-Barreda, G.; Camarero, J.J.; Esper, J.; Galván, D.; Büntgen, U. A millennium-long perspective on high-elevation pine recruitment in the Spanish central Pyrenees. Can. J. For. Res. 2018, 48, 1108–1113. [Google Scholar]
  93. Camarero, J.J.; García-Ruiz, J.M.; Sangüesa-Barreda, G.; Galván, J.D.; Alla, A.Q.; Sanjuán, Y.; Beguería, S.; Gutiérrez, E. Recent and intense dynamics in a formerly static treeline. Arct. Ant. Alp. Res. 2015, 47, 773–783. [Google Scholar] [CrossRef]
Forests 09 00688 g001 550
Figure 1. (a) Location of the sampled treelines in the Spanish Pyrenees (Pinus uncinata Ram.) and in the Russian Polar Urals (Larix sibirica Ledeb). The insets show the climatic diagram for each study site and below maps the distribution both species in Eurasia (Atlas Florae Europaeae). (b) Mean annual temperature and precipitation for the studied treelines during the 20th-century. The statistics show climatic trends (Pearson correlation coefficients, r) and the regression line for the temperature. Local, regional, and gridded data were used to build the climatic series (see [7]).
Figure 1. (a) Location of the sampled treelines in the Spanish Pyrenees (Pinus uncinata Ram.) and in the Russian Polar Urals (Larix sibirica Ledeb). The insets show the climatic diagram for each study site and below maps the distribution both species in Eurasia (Atlas Florae Europaeae). (b) Mean annual temperature and precipitation for the studied treelines during the 20th-century. The statistics show climatic trends (Pearson correlation coefficients, r) and the regression line for the temperature. Local, regional, and gridded data were used to build the climatic series (see [7]).
Forests 09 00688 g001
Forests 09 00688 g002 550
Figure 2. Pearson correlation coefficients calculated between P. uncinata and L. sibirica radial growth age groups (ring-width indexes) and the monthly mean, maximum and minimum temperatures for 1950–2012 in the Pyrenean treelines (OR, TE) and Ural treelines (CH, UR). Growth is related with climate data from the previous (months abbreviated by lowercase letters) and current (months and seasons (YR, annual; WI, winter; SP, spring; SU, summer) abbreviated by uppercase letters) years, the current year being that of tree-ring formation. The significance levels of correlation coefficients are indicated by dashed dark grey lines (p < 0.05) and light grey horizontal lines (p < 0.01).
Figure 2. Pearson correlation coefficients calculated between P. uncinata and L. sibirica radial growth age groups (ring-width indexes) and the monthly mean, maximum and minimum temperatures for 1950–2012 in the Pyrenean treelines (OR, TE) and Ural treelines (CH, UR). Growth is related with climate data from the previous (months abbreviated by lowercase letters) and current (months and seasons (YR, annual; WI, winter; SP, spring; SU, summer) abbreviated by uppercase letters) years, the current year being that of tree-ring formation. The significance levels of correlation coefficients are indicated by dashed dark grey lines (p < 0.05) and light grey horizontal lines (p < 0.01).
Forests 09 00688 g002
Forests 09 00688 g003 550
Figure 3. Temporal changes in bootstrapped correlation coefficients using 20-year long intervals shifted by one year for the period 1950–2012 (values are arranged for the last year of each 20-year long interval). Dashed horizontal lines indicate statistically significant correlation coefficients (p < 0.05) for previous maximum November temperature (lines) and current minimum May temperature (symbols) in Pinus uncinata Pyrenean treelines (OR, TE); current (year t) maximum July temperature (lines) and current minimum July temperature (symbols) in Urals Larix sibirica treelines (CH, UR). Sites’ codes are as in Table 1.
Figure 3. Temporal changes in bootstrapped correlation coefficients using 20-year long intervals shifted by one year for the period 1950–2012 (values are arranged for the last year of each 20-year long interval). Dashed horizontal lines indicate statistically significant correlation coefficients (p < 0.05) for previous maximum November temperature (lines) and current minimum May temperature (symbols) in Pinus uncinata Pyrenean treelines (OR, TE); current (year t) maximum July temperature (lines) and current minimum July temperature (symbols) in Urals Larix sibirica treelines (CH, UR). Sites’ codes are as in Table 1.
Forests 09 00688 g003
Forests 09 00688 g004 550
Figure 4. Observed (TRWi) and VS-Lite simulated ring-width chronologies (TRWiVSL) for each study site and age group in the four study treeline sites. Grey areas show the number of measured trees for each site. Sites’ codes are as in Table 1.
Figure 4. Observed (TRWi) and VS-Lite simulated ring-width chronologies (TRWiVSL) for each study site and age group in the four study treeline sites. Grey areas show the number of measured trees for each site. Sites’ codes are as in Table 1.
Forests 09 00688 g004
Forests 09 00688 g005 550
Figure 5. Simulated (1950–2012 period) and projected mean monthly growth response curves considering temperature (gT, symbols) and soil moisture (gM, lines) for each age group (blue, old trees; red, young trees) at the studied treeline sites. Projected growth response curves correspond to two IPCC AR5 emission scenarios (RCP 2.6 and RCP 8.5, with +0.3° and +4.8° C projected warming, respectively) and to the 2050–2100 period. The arrows show the estimated period with temperature above the minimum thresholds for growth (T1). Sites’ codes are as in Table 1.
Figure 5. Simulated (1950–2012 period) and projected mean monthly growth response curves considering temperature (gT, symbols) and soil moisture (gM, lines) for each age group (blue, old trees; red, young trees) at the studied treeline sites. Projected growth response curves correspond to two IPCC AR5 emission scenarios (RCP 2.6 and RCP 8.5, with +0.3° and +4.8° C projected warming, respectively) and to the 2050–2100 period. The arrows show the estimated period with temperature above the minimum thresholds for growth (T1). Sites’ codes are as in Table 1.
Forests 09 00688 g005
Table
Table 1. Main features of the studied Mediterranean (OR, TE) and Polar (CH, UR) treelines.
Table 1. Main features of the studied Mediterranean (OR, TE) and Polar (CH, UR) treelines.
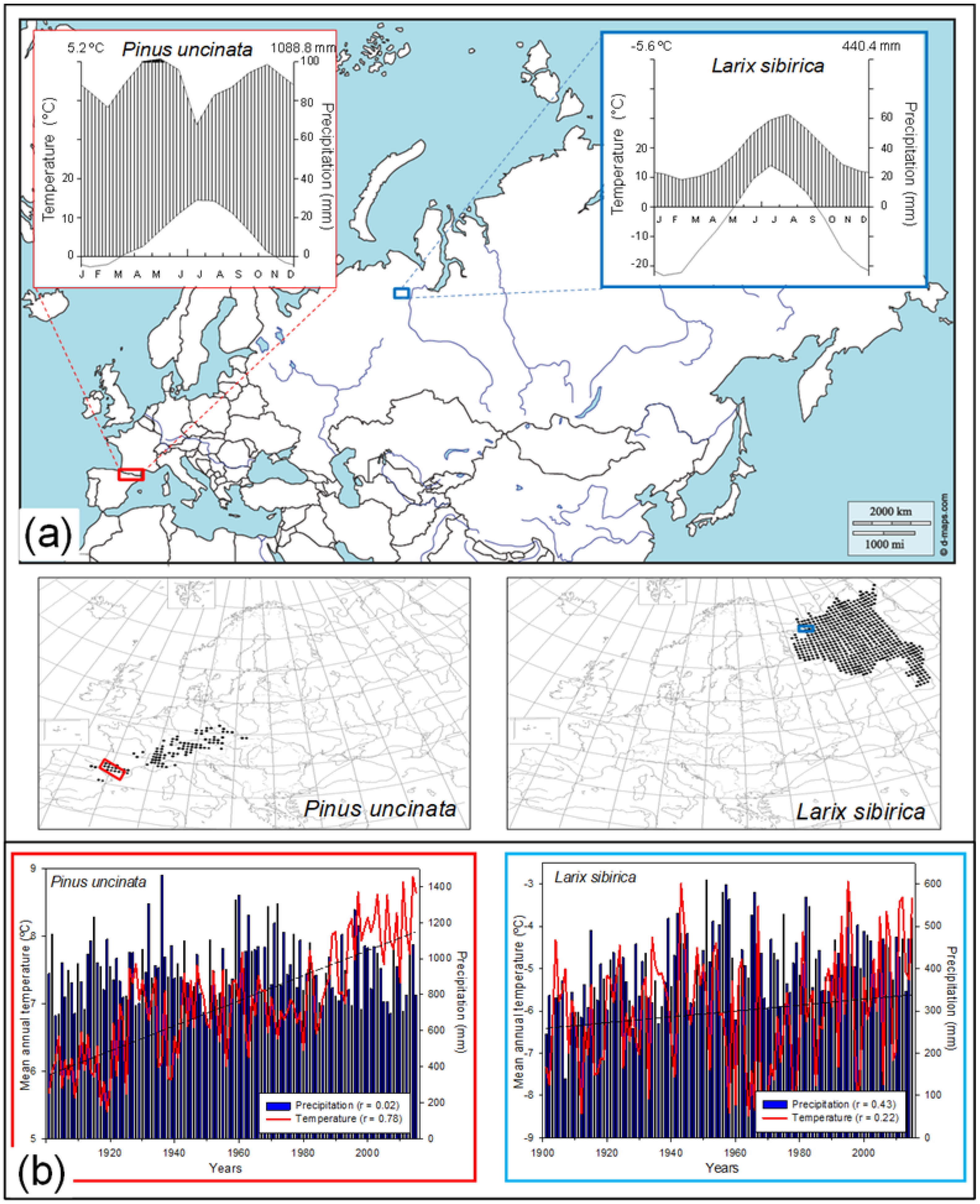
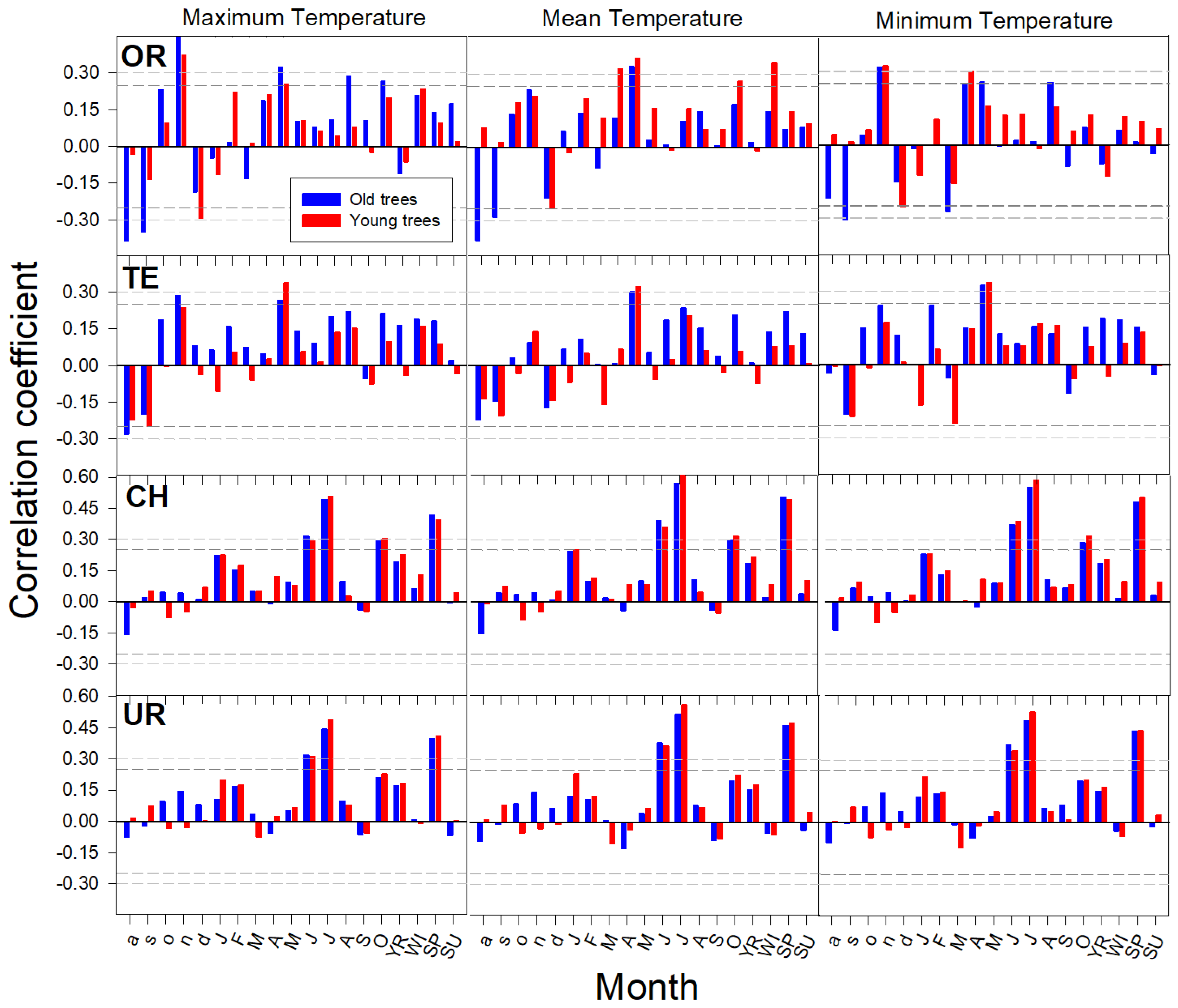
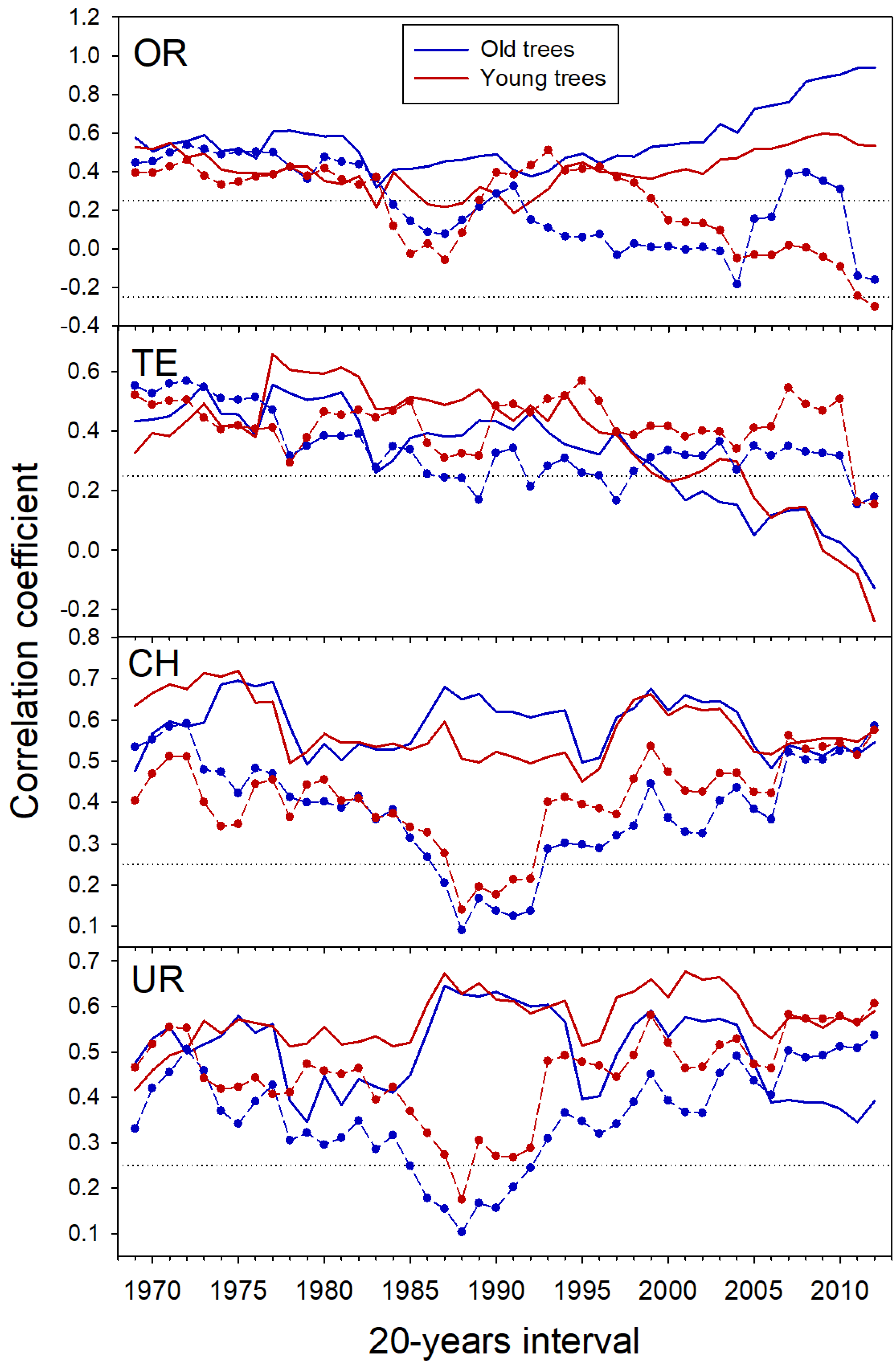
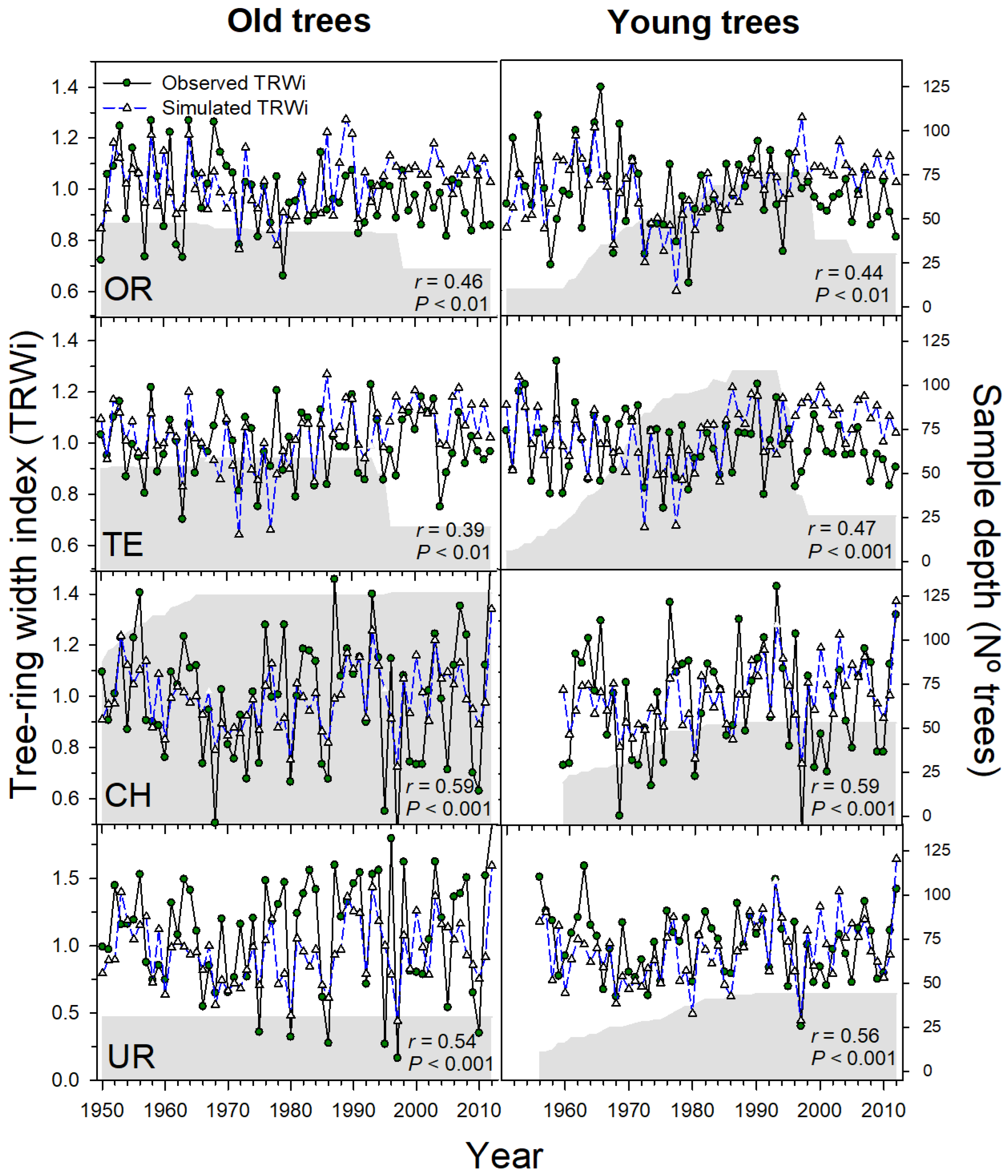
RangeSite (Code)Tree SpeciesLongitude (W/E)Latitude (N)Treeline‒Forest Limit Elevations (m a.s.l.)AspectSlope (°)
Spanish PyreneesOrdesa (OR)Mountain pine (Pinus uncinata)0°02′ W42°37′2130–2100S20
Tessó (TE)1° 03′ E42°36′2360–2330NE35
Russian Polar UralsUrals treeline (CH)Larch (Larix sibirica)66°40′ E66°32′450–320S-SW20
Urals treeline ecotone (UR)66°38′ E66°30′220–320S-SW15
Table
Table 2. Dendrochronological statistics calculated for the ring-width chronologies of each age group (old vs. young trees) for the period 1950–2012. Data are means ± standard error.
Table 2. Dendrochronological statistics calculated for the ring-width chronologies of each age group (old vs. young trees) for the period 1950–2012. Data are means ± standard error.
VariablesOrdesa (OR)Tessó (TE)Urals Treeline (CH)Urals Treeline Ecotone (UR)
OldYoungOldYoungOldYoungOldYoung
N° Trees487659108135533144
Diameter at breast height (cm)26.5 ± 0.9a10.5 ± 0.6b31.3 ± 1.9a9.2 ± 0.8b20.7 ± 0.9a9.8 ± 0.5b19.1 ± 0.7a9.5 ± 0.5b
Tree-ring width ± SD (mm) 11.11± 0.62b1.58 ± 0.89a1.52 ± 0.73b1.65 ± 0.81a0.88 ± 0.42b1.17 ± 0.53a0.43 ± 0.22b1.02 ± 0.49a
Age ± SD (years)108 ± 9a33 ± 2b115 ± 7a32 ± 1b97 ± 4a41 ± 3b120 ± 15a42 ± 2b
AC 20.76 ± 0.01a0.57 ± 0.03b0.79 ± 0.010.63 ± 0.020.54 ± 0.010.56 ± 0.020.64 ± 0.030.52 ± 0.02
MS0.24 ± 0.02b0.28 ± 0.01a0.20 ± 0.020.24 ± 0.010.36 ± 0.01a0.29 ± 0.01b0.45 ± 0.01a0.32 ± 0.01b
rbt0.58 ± 0.02a0.42 ± 0.02b0.47 ± 0.010.46 ± 0.010.71 ± 0.010.67 ± 0.010.81 ± 0.01a0.68 ± 0.01b
PC1 (%)36.230.735.131.854.957.167.756.3
EPS0.890.900.890.910.940.950.930.94
1 Different letters indicate significant (p < 0.05) differences between age groups (a,b) based on Mann‒Whitney U test [54]; SD, Standard deviation. 2 Variables abbreviations: AC, first-order autocorrelation; residual chronologies: MS, mean sensitivity; rbt, mean correlation among trees; PC1, variance in first eigenvector; EPS, expressed population signal.
Table
Table 3. Pearson correlation coefficients calculated between observed site series of tree-ring width indices (TRWi) and VS-Lite indices (TRWiVSL) for the calibration period (1950–2012); and for the sub-periods 1950–1975 and 1975–2012, also considering projected site series of tree-ring width indices (TRWip) and VS-Lite future indices (TRWip-VSL) for the periods 2013–2050 and 2050–2100 and two IPCC AR5 emission scenarios (RCP 2.6 and RC P 8.5). Correlation values higher than 0.25 are significant at p < 0.05.
Table 3. Pearson correlation coefficients calculated between observed site series of tree-ring width indices (TRWi) and VS-Lite indices (TRWiVSL) for the calibration period (1950–2012); and for the sub-periods 1950–1975 and 1975–2012, also considering projected site series of tree-ring width indices (TRWip) and VS-Lite future indices (TRWip-VSL) for the periods 2013–2050 and 2050–2100 and two IPCC AR5 emission scenarios (RCP 2.6 and RC P 8.5). Correlation values higher than 0.25 are significant at p < 0.05.
Ordesa (OR)Tessó (TE)Urals Treeline (CH)Urals Treeline Ecotone (UR)
PeriodIPCC ScenarioOldYoungOldYoungOldYoungOldYoung
1950–1975Observed0.440.610.360.280.550.540.430.56
1975–20120.390.380.350.380.600.580.570.62
1950–20120.460.440.390.470.590.590.540.56
2013–2050RCP 2.60.790.460.500.480.840.800.830.69
RCP 8.50.760.390.460.420.950.750.910.77
2050–2100RCP 2.60.440.320.300.290.750.580.800.60
RCP 8.50.910.860.500.480.980.890.950.93
Table
Table 4. Summary of the Generalized Least Squares Regressions (GLS) models used to forecast site chronologies of ring-width indices (TRWi). The percentage of variance explained by climate-based models is given by the adjusted coefficient of determination (R2adj). Abbreviations: p, precipitation; tm, mean temperature; tx, mean maximum temperature; ti, mean minimum temperature; sp, spring; su, summer. Numbers after climate variables indicate months, whereas the subscript “p” indicates the previous year.
Table 4. Summary of the Generalized Least Squares Regressions (GLS) models used to forecast site chronologies of ring-width indices (TRWi). The percentage of variance explained by climate-based models is given by the adjusted coefficient of determination (R2adj). Abbreviations: p, precipitation; tm, mean temperature; tx, mean maximum temperature; ti, mean minimum temperature; sp, spring; su, summer. Numbers after climate variables indicate months, whereas the subscript “p” indicates the previous year.
Site (Code)GroupR2adjF–Valuep-ValueEquations
Ordesa (OR)Old0.698.65<0.00011.01 + 0.05tx5 + 0.07tx7 + 0.07tx9 + 0.09tx12p + 0.04tm − 0.07Pwi + 0.03Psp
Young0.455.110.00020.98 + 0.04tx2 + 0.03tx5 − 0.03tm3 + 0.03tm4 − 0.04tmwi + 0.02P2
Tessó (TE)Old0.475.21<0.00010.99 − 0.06tx2 + 0.06tx9p − 0.03tx11p + 0.09ti2 + 0.07ti5 − 0.04ti9 − 0.04P1
Young0.335.460.00080.99 + 0.06tx5 − 0.04ti3 − 0.02tm6 − 0.03P1
Urals treeline (CH)Old0.559.96<0.00010.99 − 0.18tx6 − 0.11tsux + 0.05ti12p − 0.05tm4 + 0.33tm6 + 0.15tm7
Young0.5411.02<0.00010.98 − 0.11txsu + 0.12ti6 + 0.16tm7 − 0.04p3 + 0.04p7
Urals treeline ecotone (UR)Old0.579.56<0.00011.09 + 0.35tx8 − 0.16ti8-0.11tm4 + 0.60tm6 + 0.42tm7 + 0.11tm12p
Young0.538.91<0.00011.01 + 0.16tx7 + 0.06tisp + 0.13tm6 + 0.30tm7 − 0.06P3
Table
Table 5. Statistics of the Bayesian estimation of the VS-Lite growth response parameters (T1, T2, M1, and M2) of the three conifer species considering the 1950–2012 period, and two 21st-century periods and IPCC AR5 emission scenarios (RCP 2.6 and RCP 8.5).
Table 5. Statistics of the Bayesian estimation of the VS-Lite growth response parameters (T1, T2, M1, and M2) of the three conifer species considering the 1950–2012 period, and two 21st-century periods and IPCC AR5 emission scenarios (RCP 2.6 and RCP 8.5).
IPCC Emission Scenarios
ObservedRCP 2.6RCP 8.5
SiteAge Group 1Parameter (unit)1950–20122013–20502050–21002013–20502050–2100
Ordesa (OR)O/YT1 (°C)3.17/2.515.38/4.716.34/5.615.65/4.835.17/7.23
O/YT2 (°C)11.92/12.0320.78/20.7317.30/18.5514.20/21.5212.62/22.45
O/YM1 (v/v)0.080/0.0680.037/0.0180.014/0.0130.031/0.0370.027/0.011
O/YM2 (v/v)0.447/0.4720.294/0.3390.317/0.2700.232/0.1400.218/0.332
Tessó (TE)O/YT1 (°C)6.83/7.698.62/8.636.69/8.825.97/4.797.73/3.98
O/YT2 (°C)10.52/10.8915.88/18.2514.87/16.6214.09/17.0522.03/21.71
O/YM1 (v/v)0.011/0.0140.008/02130.024/0.0290.023/0.0560.087/0.035
O/YM2 (v/v)0.272/0.4360.213/0.3460.256/0.1390.247/0.4310.204/0.133
Urals treeline (CH)O/YT1 (°C)8.76/8.458.30/8.938.00/7.848.58/7.355.01/6.44
O/YT2 (°C)19.18/18.8620.14/10.6717.21/11.2618.89/14.3318.00/19.55
O/YM1 (v/v)0.030/0.0710.060/0.0580.073/0.0730.037/0.0840.002/0.040
O/YM2 (v/v)0.255/0.2660.224/0.2920.276/0.2410.167/0.3350.278/0.320
Urals treeline ecotone (UR)O/YT1 (°C)8.63/8.776.48/4.116.15/6.648.47/7.797.45/4.70
O/YT2 (°C)18.31/18.2011.06/11.6114.90/14.6115.09/17.3312.17/11.00
O/YM1 (v/v)0.072/0.0680.025/0.0120.043/0.0070.069/0.0870.009/0.025
O/YM2 (v/v)0.198/0.23740.267/0.3500.209/0.2730.274/0.2890.225/0.251
1 Abbreviations: O, old trees; Y, young trees.

Share and Cite

MDPI and ACS Style

Sanchez-Salguero, R.; Camarero, J.J.; Gutiérrez, E.; Gazol, A.; Sangüesa-Barreda, G.; Moiseev, P.; Linares, J.C. Climate Warming Alters Age-Dependent Growth Sensitivity to Temperature in Eurasian Alpine Treelines. Forests 2018, 9, 688. https://doi.org/10.3390/f9110688

AMA Style

Sanchez-Salguero R, Camarero JJ, Gutiérrez E, Gazol A, Sangüesa-Barreda G, Moiseev P, Linares JC. Climate Warming Alters Age-Dependent Growth Sensitivity to Temperature in Eurasian Alpine Treelines. Forests. 2018; 9(11):688. https://doi.org/10.3390/f9110688

Chicago/Turabian Style

Sanchez-Salguero, Raúl, J. Julio Camarero, Emilia Gutiérrez, Antonio Gazol, Gabriel Sangüesa-Barreda, Pavel Moiseev, and Juan C. Linares. 2018. "Climate Warming Alters Age-Dependent Growth Sensitivity to Temperature in Eurasian Alpine Treelines" Forests 9, no. 11: 688. https://doi.org/10.3390/f9110688

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop