Spatial Association and Diversity of Dominant Tree Species in Tropical Rainforest, Vietnam
Abstract
1. Introduction
2. Materials and Methods
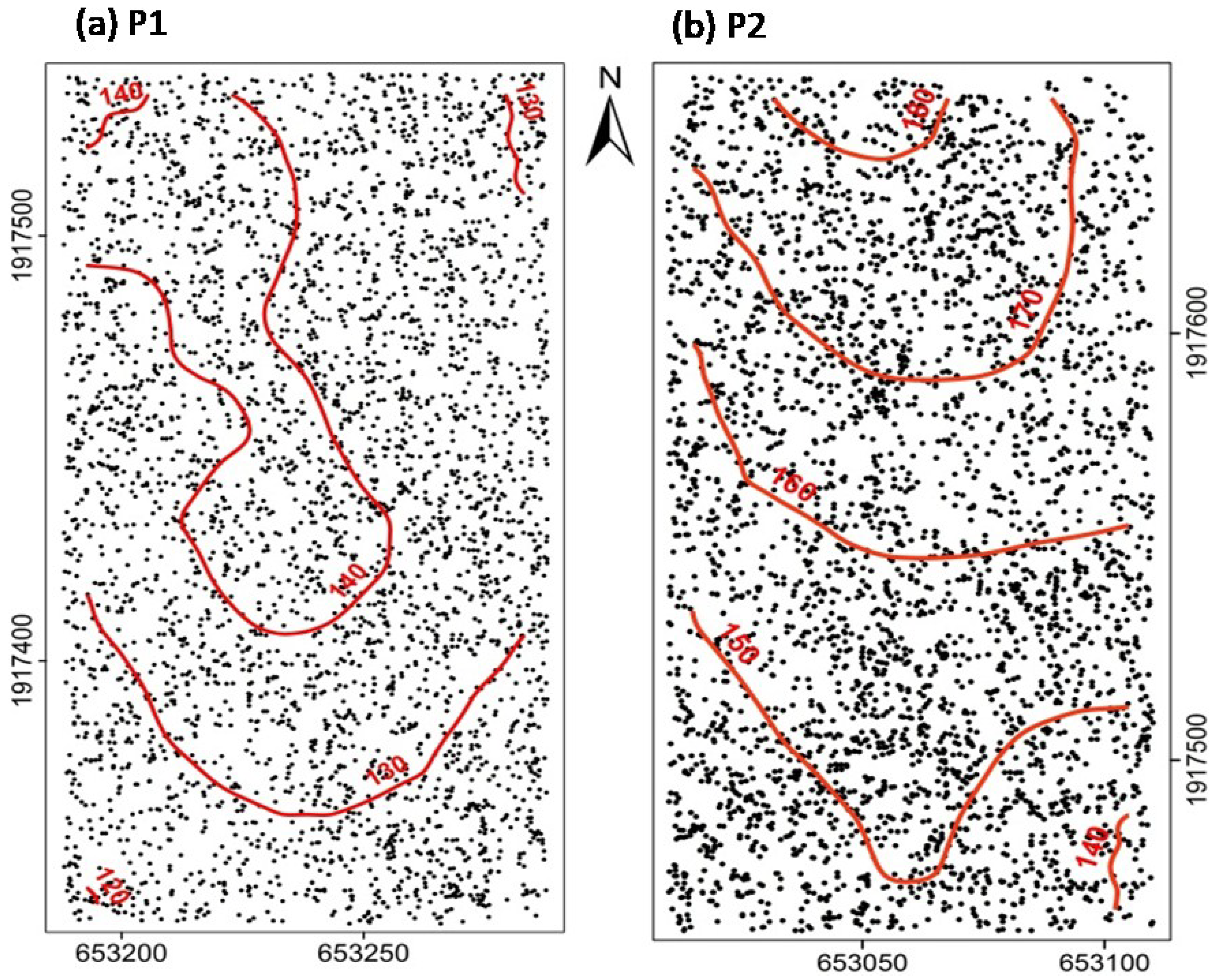
2.1.Study Site and Data Collection
2.2. Data Analysis
2.2.1. Uni- and Bivariate Pair Correlation Functions
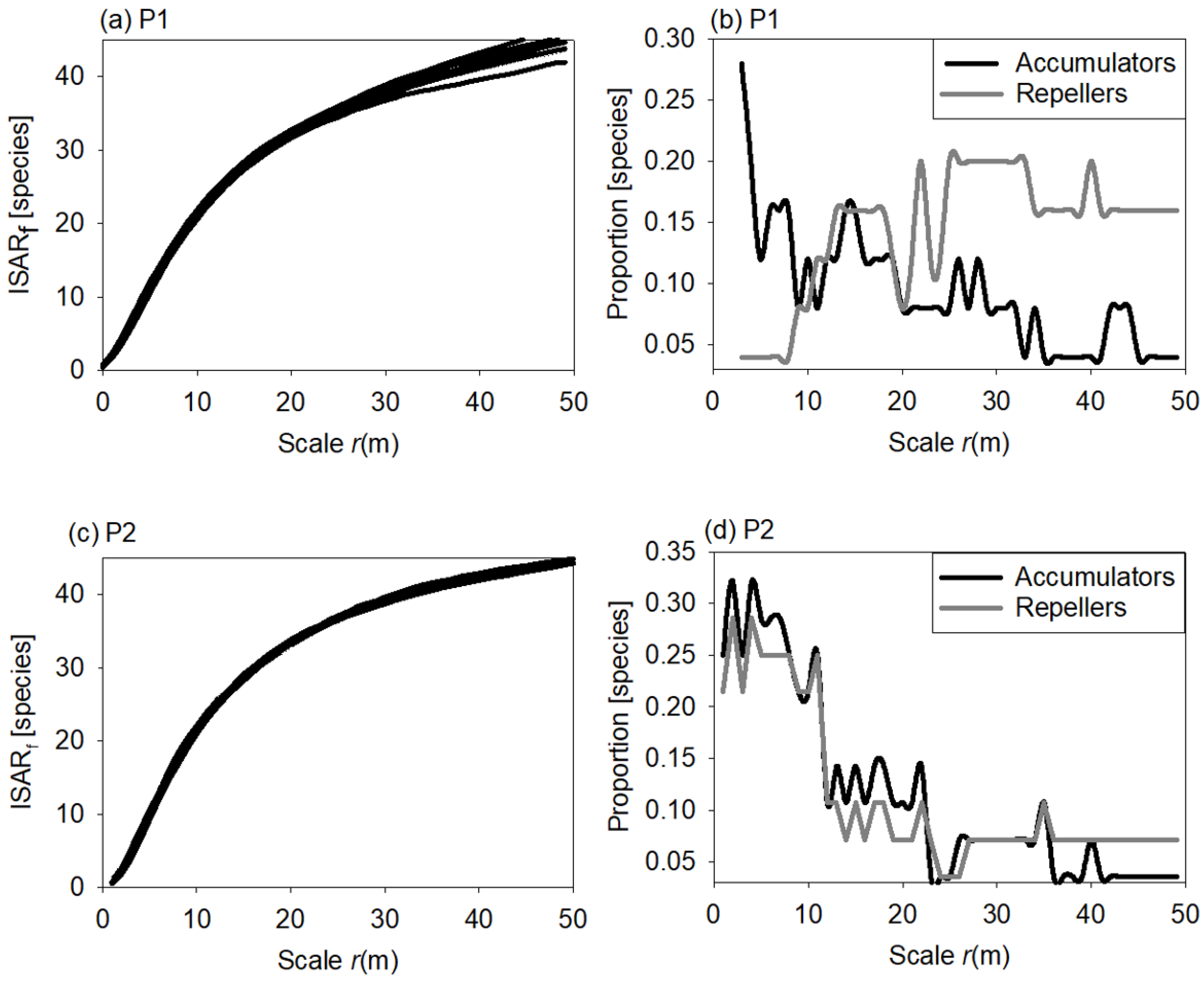
2.2.2. Individual Species—Area Relationship
2.2.3. Used Software Package
3. Results
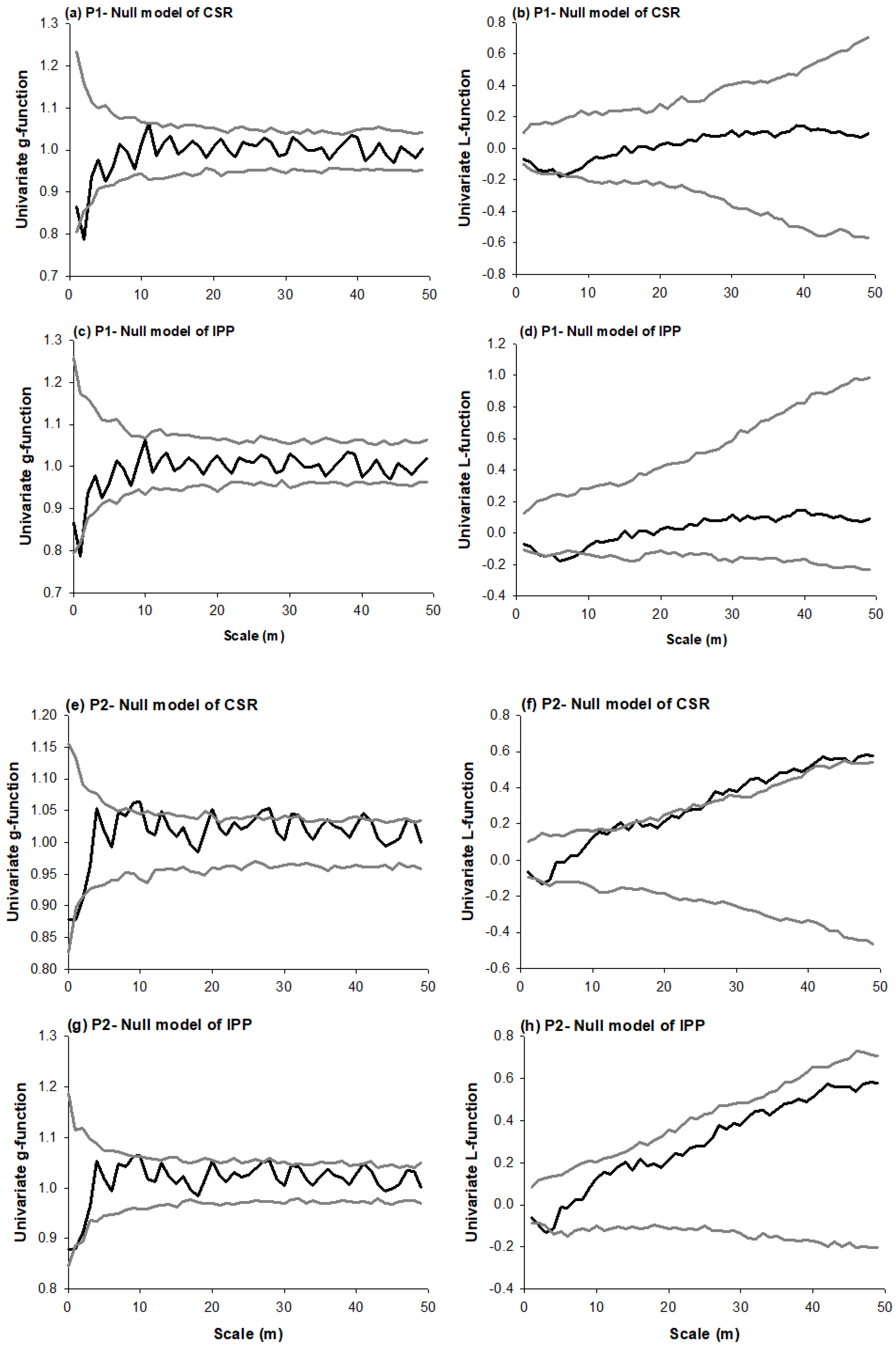
3.1. Species Distribution Patterns
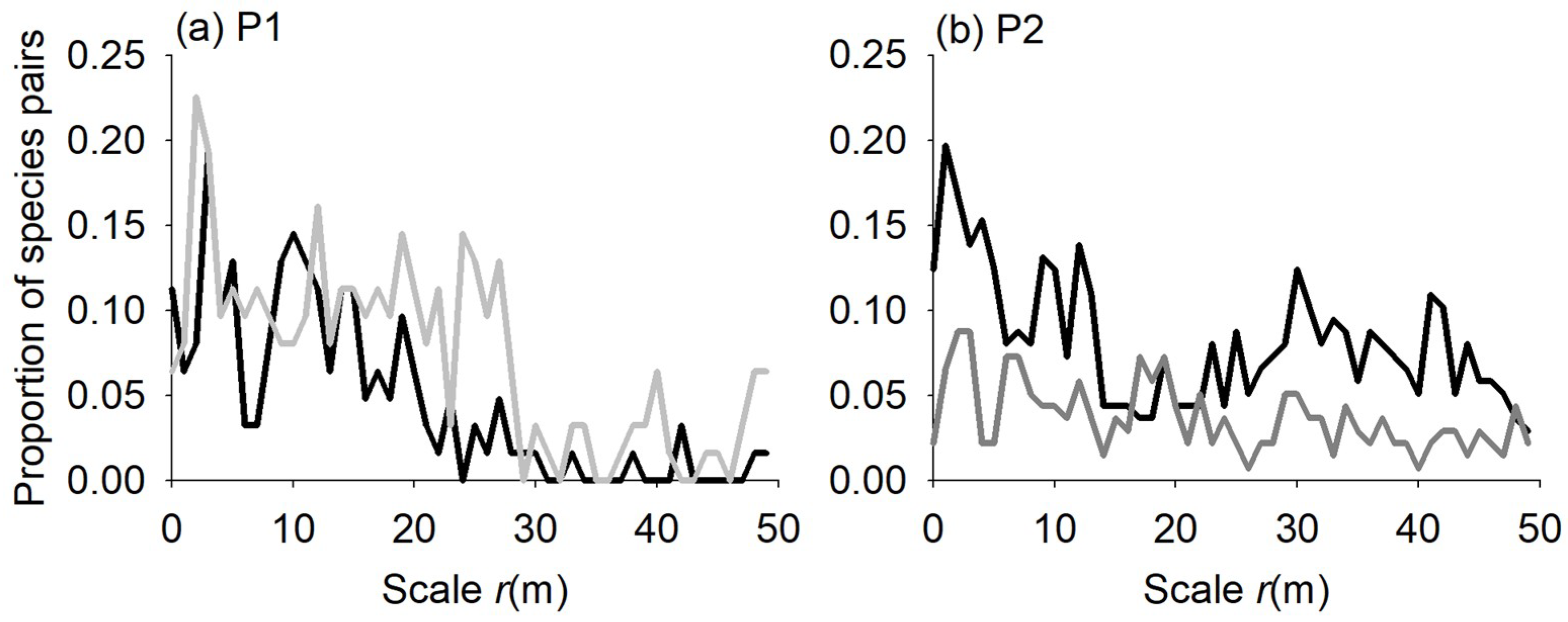
3.2. Species Associations
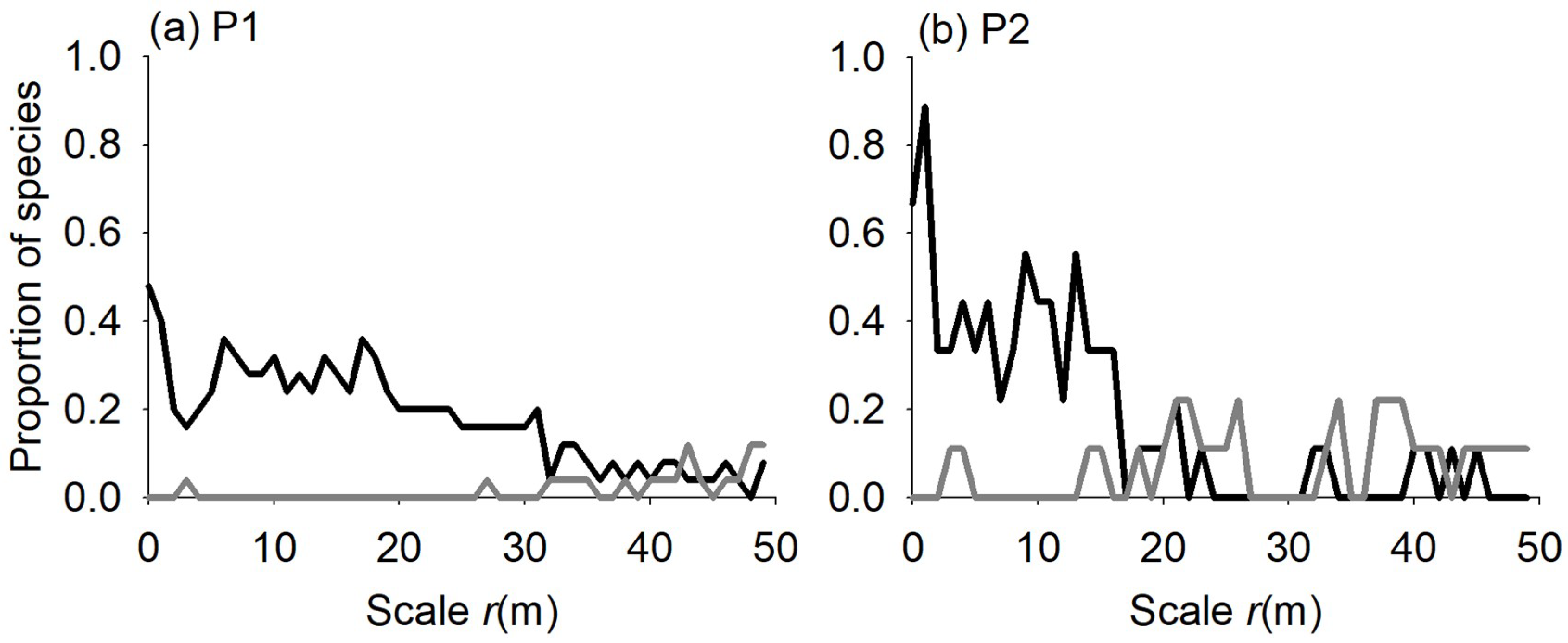
3.3. Individual Species Area Relationship
4. Discussion
4.1. Species Distribution Patterns
4.2. Species Associations
4.3. Individual Species—Area Relationship
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix
| No | Tree Species | P1 | P2 | Shade Tolerance | ||||
|---|---|---|---|---|---|---|---|---|
| N | DBH (cm) | IVI (%) | N | DBH (cm) | IVI (%) | |||
| 1 | Garuga pierrei Guillaumin | 282 | 10.08 ± 10.89 | 8.985 | 232 | 11.30 ± 13.26 | 7.72 | Tolerant |
| 2 | Tarrietia javanica Blume | 383 | 5.62 ± 6.39 | 7.285 | 330 | 4.52 ± 3.58 | 5.14 | Intolerant |
| 3 | Ormosia balansae Drake | 138 | 17.05 ± 12.97 | 7.26 | 187 | 14.75 ± 10.81 | 6.605 | Intolerant |
| 4 | Bursera tonkinensis Guillaumin | 384 | 6.15 ± 4.16 | 6.72 | 253 | 6.67 ± 4.12 | 4.41 | Medium |
| 5 | Paviesia annamensis Pierre. | 240 | 9.18 ± 7.64 | 6.025 | 239 | 6.94 ± 4.86 | 4.325 | Intolerant |
| 6 | Litsea glutinosa (Loureiro) C.B. Rob. | 229 | 8.06 ± 6.21 | 4.965 | 264 | 8.26 ± 6.70 | 5.495 | Intolerant |
| 7 | Castanopsis indica (Rox. ex Lin.) A. | 168 | 10.21 ± 8.27 | 4.65 | - | - | Intolerant | |
| 8 | Polyalthia nemoralis Aug.DC. | 303 | 5.02 ± 1.77 | 4.58 | 244 | 5.53 ± 1.88 | 3.78 | Intolerant |
| 9 | Syzygium wightianum Wall. ex Wig. & Arn. | 179 | 9.36 ± 7.04 | 4.405 | 81 | 11.56 ± 8.17 | 1.545 | Intolerant |
| 10 | Erythrophloeum fordii Oliver | 63 | 18.52 ± 15.35 | 3.96 | 36 | 19.33 ± 21.97 | 2.475 | Medium |
| 11 | Mallotus kurzii Hook.f. | 265 | 4.01 ± 0.98 | 3.76 | 114 | 3.71 ± 0.73 | 1.63 | Intolerant |
| 12 | Amoora dasyclada C.Y. Wu | 148 | 7.99 ± 6.73 | 3.285 | 96 | 8.89 ± 6.93 | 2.08 | Medium |
| 13 | Cinnamomun obtusifolium Nees | 100 | 10.71 ± 9.25 | 3.005 | 267 | 13.01 ± 10.59 | 8.51 | Intolerant |
| 14 | Vatica odorata (Griff.) Symington | 48 | 17.67 ± 15.90 | 2.945 | 48 | 23.46 ± 16.73 | 3.24 | Intolerant |
| 15 | Gironniera Subaequalis Planch | 92 | 9.71 ± 6.65 | 2.27 | 137 | 11.19 ± 9.28 | 3.73 | Medium |
| 16 | Endospermun sinensis Benth. | 54 | 11.77 ± 13.18 | 2.14 | 83 | 21.67 ± 13.33 | 4.63 | Intolerant |
| 17 | Sindora cochinchinensis auct. non Baill. | 41 | 16.52 ± 13.44 | 2.125 | 33 | 15.77 ± 14.19 | 2.77 | Intolerant |
| 18 | Garcinia oblongifolia Chanp. ex Benth. | 121 | 6.23 ± 4.08 | 2.115 | 67 | 6.22 ± 3.48 | 1.115 | Tolerant |
| 19 | Canarium album (Lour.) DC. | 46 | 15.01 ± 8.88 | 1.79 | 155 | 11.03 ± 6.04 | 3.685 | Intolerant |
| 20 | Koilodepas hainanense (Merr.) Croizat | 104 | 5.83 ± 2.61 | 1.685 | 80 | 8.41 ± 4.52 | 1.545 | Tolerant |
| 21 | Cassine glauca (Rottb.) Kuntze | 74 | 8.41 ± 5.51 | 1.59 | 89 | 8.69 ± 7.66 | 1.97 | Tolerant |
| 22 | Vitex trifolia L. | 33 | 14.83 ± 9.63 | 1.305 | - | - | Intolerant | |
| 23 | Litsea vang Lecomte | 71 | 6.54 ± 3.30 | 1.27 | 76 | 8.72 ± 4.67 | 1.5 | Intolerant |
| 24 | Symplocos laurina (Retz.) Wall. ex G. | 55 | 9.31 ± 5.61 | 1.255 | 145 | 11.81 ± 6.86 | 3.715 | Intolerant |
| 25 | Alangium ridleyi King | 40 | 7.89 ± 5.19 | 0.81 | 49 | 9.10 ± 6.27 | 1.045 | Tolerant |
| 26 | Engelhardtia roxburghiana Lindl. | - | - | 63 | 28.78 ± 11.91 | 4.845 | Tolerant | |
| 27 | Antheroporum pierrei Gagnep | - | - | 47 | 19.81 ± 7.39 | 2 | Intolerant | |
| 28 | Knema pierrei Warb. | - | - | 46 | 10.05 ± 4.86 | 0.99 | Tolerant | |
| 29 | Polyalthia cerasoides (Roxb.) Bedd. | - | - | 33 | 25.59 ± 20.80 | 1.4 | Intolerant | |
| 30 | Madhuca pasquieri (Dubard) H.J. Lam | - | - | 32 | 14.69 ± 9.76 | 1.07 | Medium | |
References
- Hai, N.H.; Wiegand, K.; Getzin, S. Spatial distributions of tropical tree species in northern Vietnam under environmentally variable site conditions. J. For. Res. 2014, 25, 257–268. [Google Scholar] [CrossRef]
- Hai, N.H.; Uria-Diez, J.; Wiegand, K. Spatial distribution and association patterns in a tropical evergreen broad-leaved forest of north-central Vietnam. J. Veg. Sci. 2016, 27, 318–327. [Google Scholar]
- Hubbell, S.P. Tree Dispersion, Abundance, and Diversity in a Tropical Dry Forest. Science 1979, 203, 1299–1309. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, T.; Gunatilleke, S.; Gunatilleke, N. Species associations in a heterogeneous Sri Lankan dipterocarp forest. Am. Nat. 2007, 170. [Google Scholar] [CrossRef] [PubMed]
- Getzin, S.; Wiegand, T.; Wiegand, K.; He, F. Heterogeneity influences spatial patterns and demographics in forest stands. J. Ecol. 2008, 96, 807–820. [Google Scholar] [CrossRef]
- Hubbell, S.P. Neutral theory in community ecology and the hypothesis of functional equivalence. Funct. Ecol. 2005, 19, 166–172. [Google Scholar] [CrossRef]
- Wiegand, T.; Savitri Gunatilleke, C.V.; Nimal Gunatilleke, I.A.U.; Huth, A. How individual species structure diversity in tropical forests. Proc. Natl. Acad. Sci. USA 2007, 104, 19029–19033. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.H.; Lin, Y.C.; Wiegand, T.; Nakazawa, T.; Su, S.H.; Hsieh, C.H.; Ding, T.S. Individual Species-Area Relationship of Woody Plant Communities in a Heterogeneous Subtropical Monsoon Rainforest. PloS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- McGill, B.J. Towards a unification of unified theories of biodiversity. Ecol. Lett. 2010, 13, 627–642. [Google Scholar] [CrossRef] [PubMed]
- Uriarte, M.; Condit, R.; Canham, C.D.; Hubbell, S.P. A spatially explicit model of sapling growth in a tropical forest: does the identity of neighbours matter? J. Ecol. 2004, 92, 348–360. [Google Scholar] [CrossRef]
- Wiegand, T.; Huth, A.; Getzin, S.; Wang, X.; Hao, Z.; Savitri Gunatilleke, C.V.; Nimal Gunatilleke, I.A.U. Testing the independent species’ arrangement assertion made by theories of stochastic geometry of biodiversity. Proc. R. Soc. B 2012, 279, 3312–3320. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wiegand, T.; Kraft, N.J.B.; Swenson, N.G.; Davies, S.J.; Hao, Z.; Howe, R.; Lin, Y.; Ma, K.; Mi, X.; et al. Stochastic dilution effects weaken deterministic effects of niche-based processes in species rich forests. Ecology 2016, 97, 347–360. [Google Scholar] [CrossRef] [PubMed]
- Hubbell, S.P.; Foster, R.B. Biology, Chance, and History and the Structure of Tropical Rain Forest Tree Communities. In Community Ecology; Diamond, J., Case, T.J., Eds.; Harper and Row Publishers: New York, NY, USA, 1986; pp. 314–329. [Google Scholar]
- Hubell, S. P. Neutral Theory and the Evolution of Ecological Equivalence. Ecology 2006, 87, 1387–1398. [Google Scholar] [CrossRef]
- Hubbell, S.P. The Unified Neutral Theory of Biodiversity and Biogeography (MPB-32); Princeton University Press: Princeton, NJ, USA, 2001. [Google Scholar]
- Wright, J.S. Plant diversity in tropical forests: A review of mechanisms of species coexistence. Oecologia 2002, 130, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Harms, K.E.; Condit, R.; Hubbell, S.P.; Foster, R.B. Habitat associations of trees and shrubs in a 50-ha neotropical forest plot. J. Ecol. 2001, 89, 947–959. [Google Scholar] [CrossRef]
- John, R.; Dalling, J.W.; Harms, K.E.; Yavitt, J.B.; Stallard, R.F.; Mirabello, M.; Hubbell, S.P.; Valencia, R.; Navarrete, H.; Vallejo, M.; et al. Soil nutrients influence spatial distributions of tropical tree species. Proc. Natl. Acad. Sci. USA. 2007, 104, 864–869. [Google Scholar] [CrossRef] [PubMed]
- Rayburn, A.P.; Wiegand, T. Individual species–area relationships and spatial patterns of species diversity in a Great Basin, semi-arid shrubland. Ecography 2012, 35, 341–347. [Google Scholar] [CrossRef]
- Stoyan, D.; Stoyan, H. Random Shapes and Point Fields: Methods of Geometrical Statistics; John Wiley & Sons: Chichester, UK, 1994. [Google Scholar]
- Wiegand, T.; Moloney, K.A. Handbook of Spatial Point-Pattern Analysis in Ecology; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Punchi-Manage, R.; Wiegand, T.; Wiegand, K.; Getzin, S.; Huth, A.; Savitri Gunatilleke, C.V.; Nimal Gunatilleke, I.A.U. Neighborhood diversity of large trees shows independent species patterns in a mixed dipterocarp forest in Sri Lanka. Ecology 2015, 96, 1823–1834. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, T.; Moloney, K.A. Rings, circles, and null-models for point pattern analysis in ecology. Oikos 2004, 104, 209–229. [Google Scholar] [CrossRef]
- Loosmore, N.B.; Ford, E.D. Statistical Inference Using the G or K Point Pattern Spatial Statistics. Ecology 2006, 87, 1925–1931. [Google Scholar] [CrossRef]
- Itoh, A.; Yamakura, T.; Ogino, K.; Lee, H.S.; Ashton, P.S. Spatial distribution patterns of two predominant emergent trees in a tropical rainforest in Sarawak, Malaysia. Plant Ecol. 1997, 132, 121–136. [Google Scholar] [CrossRef]
- Plotkin, J.B.; Potts, M.D.; Leslie, N.; Manokaran, N.; LaFrankie, J.; Ashton, P.S. Species-area Curves, Spatial Aggregation, and Habitat Specialization in Tropical Forests. J. Theor. Biol. 2000, 207, 81–99. [Google Scholar] [CrossRef] [PubMed]
- Dalling, J.W.; Hubbell, S.P.; Silvera, K. Seed dispersal, seedling establishment and gap partitioning among tropical pioneer trees. J. Ecol. 1998, 86, 674–689. [Google Scholar] [CrossRef]
- Chinh, N.N.; Dung, V.V.; Dai, T.D.; Dao, N.K; Hien, N.H; Lien, T.K. Vietnam Forest Trees; Agricultural Publishing House: Hanoi, Vietnam, 1996. [Google Scholar]
- Debski, I.; Burslem, D.F.R.P.; Palmiotto, P.A.; Lafrankie, J.V.; Lee, H.S.; Manokaran, N. Habitat Preferences of Aporosa in Two Malaysian Forests: Implications for Abundance and Coexistence. Ecology 2002, 83, 2005–2018. [Google Scholar] [CrossRef]
- Hurtt, G.C.; Pacala, S.W. The consequences of recruitment limitation: reconciling chance, history and competitive differences between plants. J. Theor. Biol. 1995, 176, 1–12. [Google Scholar] [CrossRef]
- Comita, L.S.; Hubbell, S.P. Local neighborhood and species’ shade tolerance influence survival in a diverse seedling bank. Ecology 2009, 90, 328–334. [Google Scholar] [CrossRef] [PubMed]
- Pacala, S.W.; Levin, S.A. Biologically Generated Spatial Pattern and the Coexistence of Competing Species. In Spatial Ecology: The Role of Space in Population Dynamics and Interspecific Interactions (MPB-30); Tilman, D., Kareiva, P., Eds.; Princeton University Press: Princeton, NJ, USA, 1997; pp. 204–232. [Google Scholar]
- Hubbell, S.P.; Ahumada, J.A.; Condit, R.; Foster, R.B. Local neighborhood effects on long-term survival of individual trees in a Neotropical forest. Ecol. Res. 2001, 16, 859–875. [Google Scholar] [CrossRef]
| Characteristic | Plot P1 | Plot P2 |
|---|---|---|
| Elevation (m): mean ± standard deviation (min–max) | 134 ± 6.3 (119–148) | 160 ± 11.1 (137–184) |
| Slope (degree):mean ± standard deviation (min–max) | 20 ± 6.6 (5–40) | 26 ± 7.5 (5–45) |
| Number of individuals | 3936 | 3731 |
| Total basal area (m2) | 48.4 | 64.6 |
| DBH (cm) (mean, min–max) | 8.6 (2.5–79.6) | 10.3 (2.5–95.5) |
| Number of species | 61 | 52 |
| Number of species with one individual | 13 | 7 |
| Number of species with ≥30 individuals | 25 | 28 |
| Number of shared species | 47 | 47 |
| Number of individuals from shared species | 3732 | 3698 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.H.; Erfanifard, Y.; Pham, V.D.; Le, X.T.; Bui, T.D.; Petritan, I.C. Spatial Association and Diversity of Dominant Tree Species in Tropical Rainforest, Vietnam. Forests 2018, 9, 615. https://doi.org/10.3390/f9100615
Nguyen HH, Erfanifard Y, Pham VD, Le XT, Bui TD, Petritan IC. Spatial Association and Diversity of Dominant Tree Species in Tropical Rainforest, Vietnam. Forests. 2018; 9(10):615. https://doi.org/10.3390/f9100615
Chicago/Turabian StyleNguyen, Hong Hai, Yousef Erfanifard, Van Dien Pham, Xuan Truong Le, The Doi Bui, and Ion Catalin Petritan. 2018. "Spatial Association and Diversity of Dominant Tree Species in Tropical Rainforest, Vietnam" Forests 9, no. 10: 615. https://doi.org/10.3390/f9100615
APA StyleNguyen, H. H., Erfanifard, Y., Pham, V. D., Le, X. T., Bui, T. D., & Petritan, I. C. (2018). Spatial Association and Diversity of Dominant Tree Species in Tropical Rainforest, Vietnam. Forests, 9(10), 615. https://doi.org/10.3390/f9100615






