Mapping Burn Severity of Forest Fires in Small Sample Size Scenarios
Abstract
1. Introduction
2. Study Areas and Data
2.1. Study Areas
2.2. Field Plots and Sub-Sampling
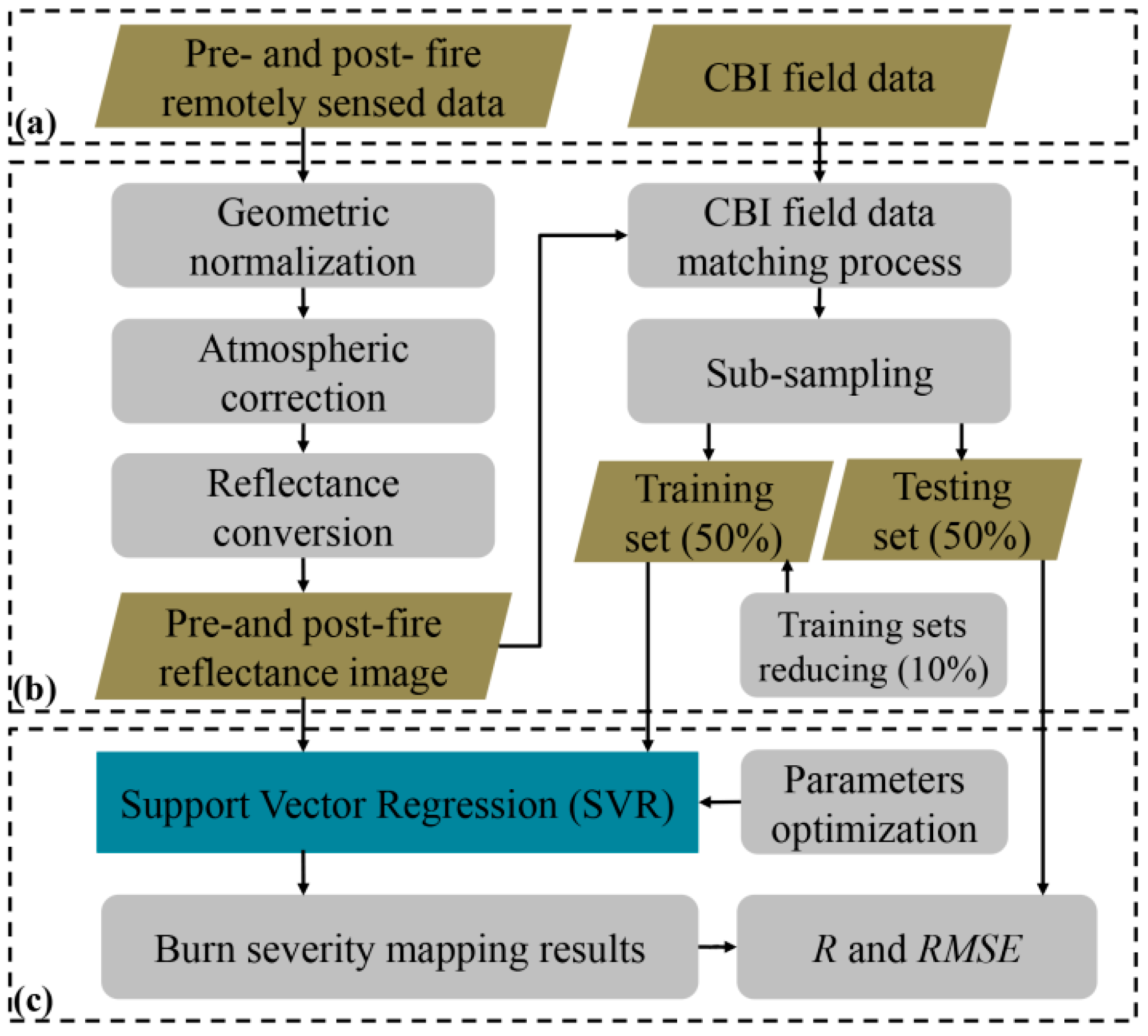
2.3. Imagery and Pre-Processing
3. Methods
3.1. Support Vector Regression
3.2. SVR Modeling
3.2.1. Kernel Parameters
3.2.2. Regularization Parameter
3.2.3. Parameter ε
- Different types of parameters are paired together within the assigned ranges of these parameters.
- With a selected pair of parameters in a search grid, the SVR are trained and then the common three-fold cross-validation precision (i.e., the root mean squared error (RMSE) between the predicted and the observed CBI values) is obtained and recorded.
- By altering the parameters pairs in other search grids, a series of cross-validation RMSEs are then returned too. Finally, the pair of key parameters of SVR (C and ε) with the minimum cross-validation RMSE value is selected.
3.3. Performance Evaluations
4. Results and Discussion
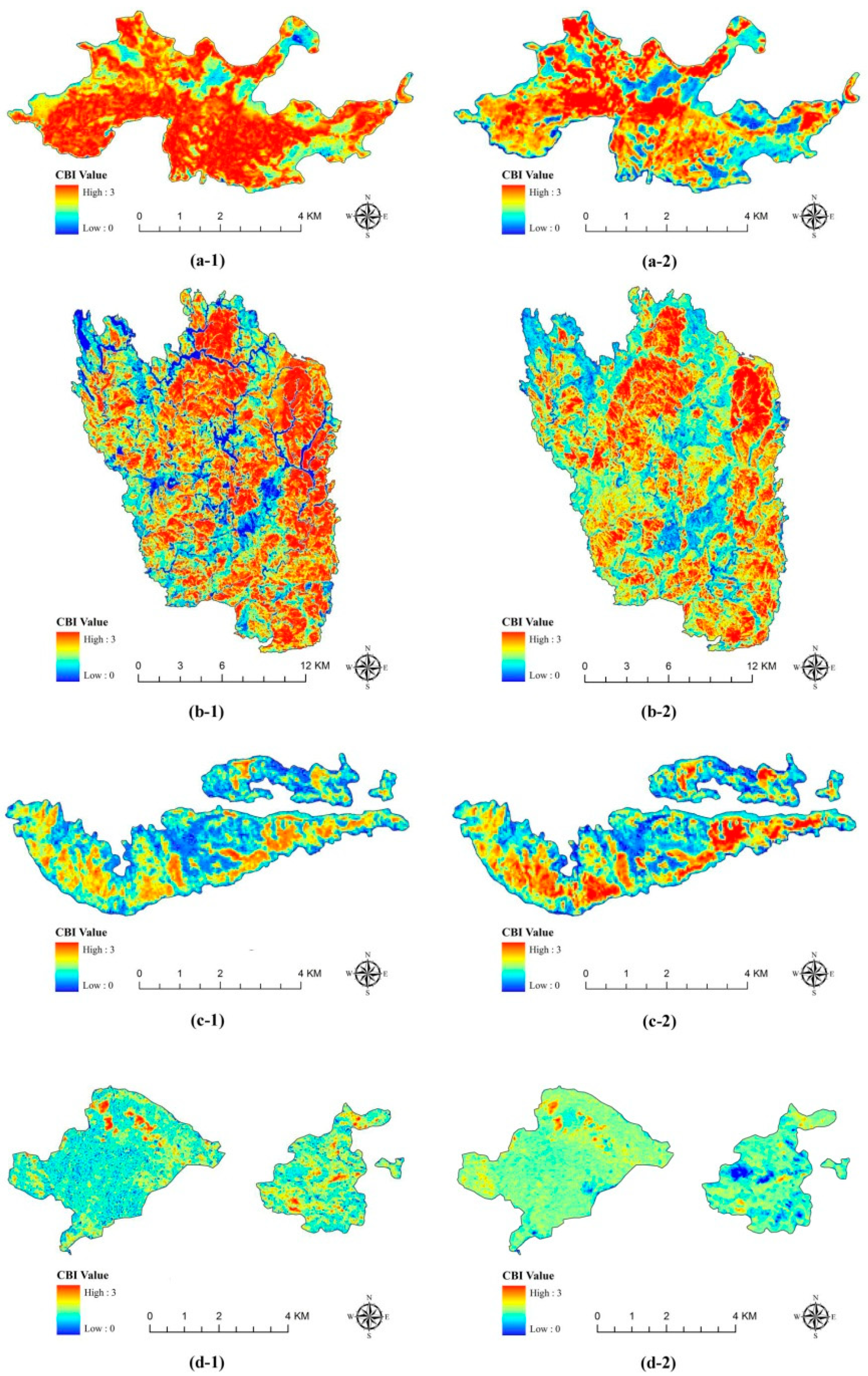
4.1. SVR-Based Burn Severity Mapping and Performance Evaluation
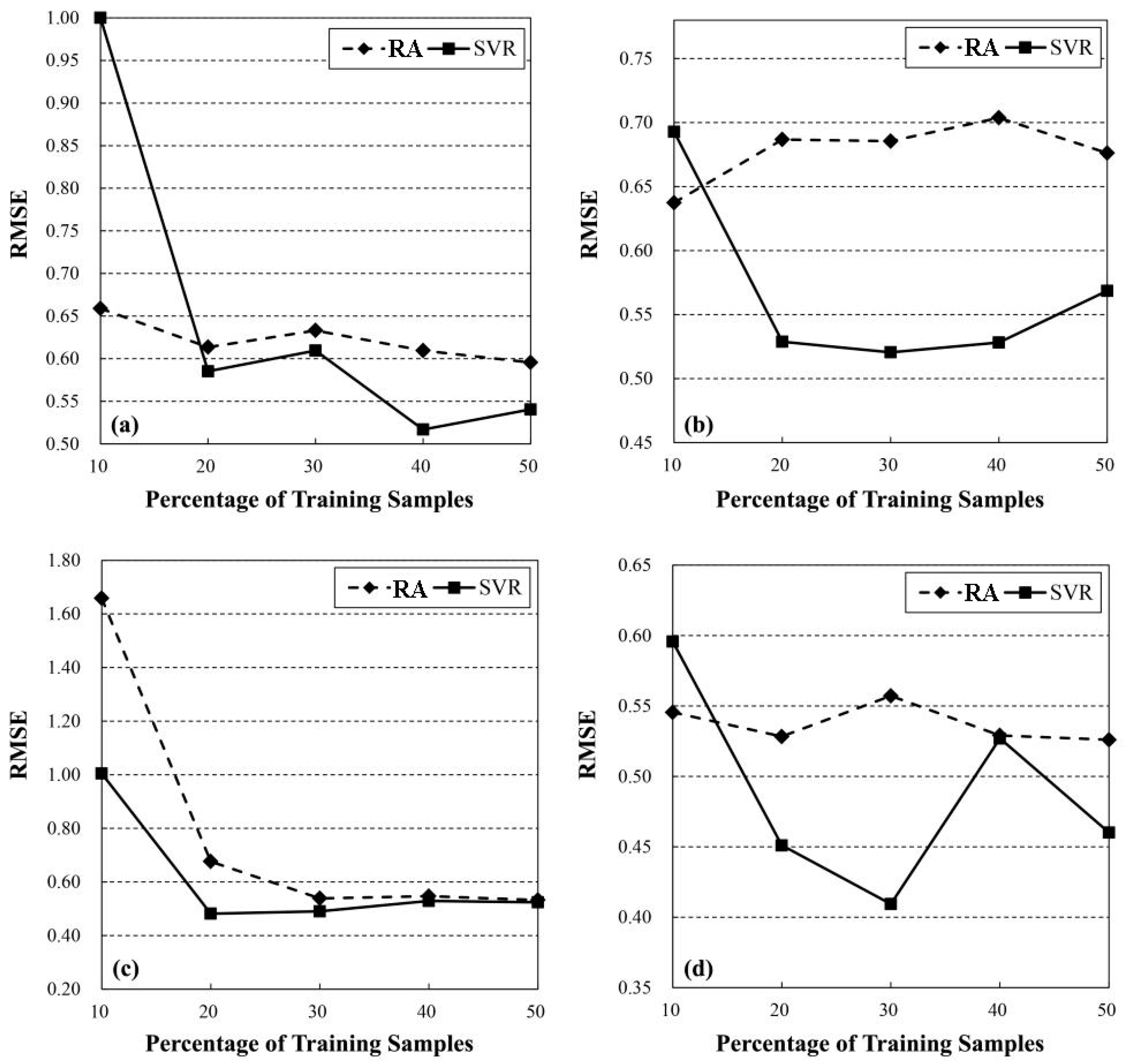
4.2. Burn Severity Mapping Accuracy Sensitivity to Training Samples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quintano, C.; Fernández-Manso, A.; Roberts, D.A. Multiple endmember spectral mixture analysis (mesma) to map burn severity levels from landsat images in mediterranean countries. Remote Sens. Environ. 2013, 136, 76–88. [Google Scholar] [CrossRef]
- Veraverbeke, S.; Hook, S.; Hulley, G. An alternative spectral index for rapid fire severity assessments. Remote Sens. Environ. 2012, 123, 72–80. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, W.; Li, S.; Zeng, Y. Forest fire spread simulating model using cellular automaton with extreme learning machine. Ecol. Model. 2017, 348, 33–43. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape Assessment (la): Sampling and Analysis Methods; Rocky Mountain Research Station, USDA, Forest Service: Fort Collins, CO, USA, 2006; pp. LA-1–LA-51.
- Veraverbeke, S.; Verstraeten, W.W.; Lhermitte, S.; Van De Kerchove, R.; Goossens, R. Assessment of post-fire changes in land surface temperature and surface albedo, and their relation with fire-burn severity using multitemporal modis imagery. Int. J. Wildl. Fire 2012, 21, 243–256. [Google Scholar] [CrossRef]
- Zheng, Z.; Zeng, Y.; Li, S.; Huang, W. A new burn severity index based on land surface temperature and enhanced vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 84–94. [Google Scholar] [CrossRef]
- Key, C.; Benson, N. Landscape assessment: Ground measure of severity, the composite burn index; and remote sensing of severity, the normalized burn ratio. In FIREMON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Keane, R.E., Caratti, J.F., Key, C.H., Benson, N.C., Gangi, L.J., Eds.; USDA Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; pp. CD:LA1–CD:LA51. [Google Scholar]
- De Santis, A.; Chuvieco, E. Geocbi: A modified version of the composite burn index for the initial assessment of the short-term burn severity from remotely sensed data. Remote Sens. Environ. 2009, 113, 554–562. [Google Scholar] [CrossRef]
- Schepers, L.; Haest, B.; Veraverbeke, S.; Spanhove, T.; Vanden Borre, J.; Goossens, R. Burned area detection and burn severity assessment of a heathland fire in belgium using airborne imaging spectroscopy (apex). Remote Sens. 2014, 6, 1803–1826. [Google Scholar] [CrossRef]
- Montealegre, A.; Lamelas, M.; Tanase, M.; De la Riva, J. Forest fire severity assessment using als data in a mediterranean environment. Remote Sens. 2014, 6, 4240–4265. [Google Scholar] [CrossRef]
- Parks, S.; Dillon, G.; Miller, C. A new metric for quantifying burn severity: The relativized burn ratio. Remote Sens. 2014, 6, 1827–1844. [Google Scholar] [CrossRef]
- Kasischke, E.S.; French, N.H. Locating and estimating the areal extent of wildfires in alaskan boreal forests using multiple-season avhrr ndvi composite data. Remote Sens. Environ. 1995, 51, 263–275. [Google Scholar] [CrossRef]
- Remmel, T.K.; Perera, A.H. Fire mapping in a northern boreal forest: Assessing avhrr/ndvi methods of change detection. For. Ecol. Manag. 2001, 152, 119–129. [Google Scholar] [CrossRef]
- Edwards, A.C.; Maier, S.W.; Hutley, L.B.; Williams, R.J.; Russell-Smith, J. Spectral analysis of fire severity in north australian tropical savannas. Remote Sens. Environ. 2013, 136, 56–65. [Google Scholar] [CrossRef]
- George, C.; Rowland, C.; Gerard, F.; Balzter, H. Retrospective mapping of burnt areas in central siberia using a modification of the normalised difference water index. Remote Sens. Environ. 2006, 104, 346–359. [Google Scholar] [CrossRef]
- Gerard, F.; Plummer, S.; Wadsworth, R.; Ferreruela Sanfeliu, A.; Iliffe, L.; Balzter, H.; Wyatt, B. Forest fire scar detection in the boreal forest with multitemporal spot-vegetation data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2575–2585. [Google Scholar] [CrossRef]
- Loboda, T.V.; French, N.H.F.; Hight-Harf, C.; Jenkins, L.; Miller, M.E. Mapping fire extent and burn severity in alaskan tussock tundra: An analysis of the spectral response of tundra vegetation to wildland fire. Remote Sens. Environ. 2013, 134, 194–209. [Google Scholar] [CrossRef]
- Murphy, K.A.; Reynolds, J.H.; Koltun, J.M. Evaluating the ability of the differenced normalized burn ratio (dnbr) to predict ecologically significant burn severity in alaskan boreal forests. Int. J. Wildl. Fire 2008, 17, 490–499. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Hao, X. Forest fire detection using the normalized multi-band drought index (nmdi) with satellite measurements. Agric. For. Meteorol. 2008, 148, 1767–1776. [Google Scholar] [CrossRef]
- Weber, K.T.; Seefeldt, S.S.; Norton, J.M.; Finley, C. Fire severity modeling of sagebrush-steppe rangelands in southeastern Idaho. GISci. Remote Sens. 2008, 45, 68–82. [Google Scholar] [CrossRef]
- Cocke, A.E.; Fulé, P.Z.; Crouse, J.E. Comparison of burn severity assessments using differenced normalized burn ratio and ground data. Int. J. Wildl. Fire 2005, 14, 189–198. [Google Scholar] [CrossRef]
- Epting, J.; Verbyla, D.; Sorbel, B. Evaluation of remotely sensed indices for assessing burn severity in interior Alaska using Landsat tm and ETM+. Remote Sens. Environ. 2005, 96, 328–339. [Google Scholar] [CrossRef]
- Escuin, S.; Navarro, R.; Fernandez, P. Fire severity assessment by using NBR (normalized burn ratio) and NDVI (normalized difference vegetation index) derived from Landsat tm/ETM images. Int. J. Remote Sens. 2008, 29, 1053–1073. [Google Scholar] [CrossRef]
- Garcia, M.L.; Caselles, V. Mapping burns and natural reforestation using thematic mapper data. Geocarto Int. 1991, 6, 31–37. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. The Normalized Burn Ratio (NBR): A Landsat tm Radiometric Measure of Burn Severity. Available online: http://www.nrmsc.usgs.gov/research/ndbr.htm (accessed on 22 January 2012).
- Van Wagtendonk, J.W.; Root, R.R.; Key, C.H. Comparison of aviris and Landsat ETM+ detection capabilities for burn severity. Remote Sens. Environ. 2004, 92, 397–408. [Google Scholar] [CrossRef]
- Miller, J.D.; Thode, A.E. Quantifying burn severity in a heterogeneous landscape with a relative version of the delta normalized burn ratio (DNBR). Remote Sens. Environ. 2007, 109, 66–80. [Google Scholar] [CrossRef]
- De Santis, A.; Chuvieco, E. Burn severity estimation from remotely sensed data: Performance of simulation versus empirical models. Remote Sens. Environ. 2007, 108, 422–435. [Google Scholar] [CrossRef]
- Hudak, A.T.; Morgan, P.; Bobbitt, M.J.; Smith, A.M.S.; Lewis, S.A.; Lentile, L.B.; Robichaud, P.R.; Clark, J.T.; McKinley, R.A. The relationship of multispectral satellite imagery to immediate fire effects. Fire Ecol. 2007, 3, 64–90. [Google Scholar] [CrossRef]
- Roy, D.P.; Boschetti, L.; Trigg, S.N. Remote sensing of fire severity: Assessing the performance of the normalized burn ratio. IEEE Geosci. Remote Sens. Lett. 2006, 3, 112–116. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Alvarez, F.; Han, T.; Rogan, J.; Hawkes, B. Characterizing boreal forest wildfire with multi-temporal Landsat and Lidar data. Remote Sens. Environ. 2009, 113, 1540–1555. [Google Scholar] [CrossRef]
- Patterson, M.W.; Yool, S.R. Mapping fire-induced vegetation mortality using landsat thematic mapper data: A comparison of linear transformation techniques. Remote Sens. Environ. 1998, 65, 132–142. [Google Scholar] [CrossRef]
- Brewer, C.K.; Winne, J.C.; Redmond, R.L.; Opitz, D.W.; Mangrich, M.V. Classifying and mapping wildfire severity: A comparison of methods. Photogramm. Eng. Remote Sens. 2005, 71, 1311–1320. [Google Scholar] [CrossRef]
- Quintano, C.; Fernandez-Manso, A.; Roberts, D.A. Burn severity mapping from landsat mesma fraction images and land surface temperature. Remote Sens. Environ. 2017, 190, 83–95. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L.; Rojo-Álvarez, J.L.; Melgani, F. Robust support vector regression for biophysical variable estimation from remotely sensed images. IEEE Geosci. Remote Sens. Lett. 2006, 3, 339–343. [Google Scholar] [CrossRef]
- Shao, Y.; Lunetta, R.S. Comparison of support vector machine, neural network, and cart algorithms for the land-cover classification using limited training data points. ISPRS-J. Photogramm. Remote Sens. 2012, 70, 78–87. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A.; Chicken, E. Nonparametric Statistical Methods; John Wiley & Sons: New York, NY, USA, 2013. [Google Scholar]
- Sadri, S.; Burn, D.H. Nonparametric methods for drought severity estimation at ungauged sites. Water Resour. Res. 2012, 48, W12505. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.S.; Townshend, J.R.G. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Standard precipitation index drought forecasting using neural networks, wavelet neural networks, and support vector regression. Appl. Comput. Intell. Soft Comput. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Osowski, S.; Garanty, K. Forecasting of the daily meteorological pollution using wavelets and support vector machine. Eng. Appl. Artif. Intell. 2007, 20, 745–755. [Google Scholar] [CrossRef]
- Hultquist, C.; Chen, G.; Zhao, K. A comparison of gaussian process regression, random forests and support vector regression for burn severity assessment in diseased forests. Remote Sens. Lett. 2014, 5, 723–732. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Perryman, B.L.; Olson, R.A.; Petersburg, S.; Naumann, T. Vegetation response to prescribed fire in Dinosaur National Monument. West. N. Am. Nat. 2002, 62, 414–422. [Google Scholar]
- Chen, X.; Vogelmann, J.E.; Rollins, M.; Ohlen, D.; Key, C.H.; Yang, L.; Huang, C.; Shi, H. Detecting post-fire burn severity and vegetation recovery using multitemporal remote sensing spectral indices and field-collected composite burn index data in a ponderosa pine forest. Int. J. Remote Sens. 2011, 32, 7905–7927. [Google Scholar] [CrossRef]
- Brown, P.M.; Sieg, C.H. Historical variability in fire at the ponderosa pine-Northern Great Plains prairie ecotone, southeastern Black Hills, South Dakota. Ecoscience 1999, 6, 539–547. [Google Scholar] [CrossRef]
- Smith, A.M.S.; Lentile, L.B.; Hudak, A.T.; Morgan, P. Evaluation of linear spectral unmixing and ΔNBR for predicting post-fire recovery in a North American ponderosa pine forest. Int. J. Remote Sens. 2007, 28, 5159–5166. [Google Scholar] [CrossRef]
- Berg, N.D.; Gese, E.M.; Squires, J.R.; Aubry, L.M. Influence of forest structure on the abundance of snowshoe hares in western Wyoming. J. Wildl. Manag. 2012, 76, 1480–1488. [Google Scholar] [CrossRef]
- Guarín, A.; Taylor, A.H. Drought triggered tree mortality in mixed conifer forests in Yosemite National Park, California, USA. For. Ecol. Manag. 2005, 218, 229–244. [Google Scholar] [CrossRef]
- Zhu, Z.; Key, C.; Ohlen, D.; Benson, N.C. Evaluate Sensitivities of Burn-Severity Mapping Algorithms for Different Ecosystems and Fire Histories in the United States; Final Report to the Joint Fire Science Program; Project: JFSP 01-1-4-12; USGS EROS: Sioux Falls, SD, USA, 2006.
- Shamshirband, S.; Gocic, M.; Petkovic, D.; Saboohi, H.; Herawan, T.; Mat Kiah, L.; Akib, S. Soft-Computing Methodologies for Precipitation Estimation: A Case Study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1353–1358. [Google Scholar] [CrossRef]
- Chuvieco, E.; Cocero, D.; Riano, D.; Martin, P.; Martınez-Vega, J.; de la Riva, J.; Pérez, F. Combining NDVI and surface temperature for the estimation of live fuel moisture content in forest fire danger rating. Remote Sens. Environ. 2004, 92, 322–331. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Introduction to statistical learning theory and support vector machines. Acta Autom. Sin. 2000, 26, 32–42. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- De Santis, A.; Asner, G.P.; Vaughan, P.J.; Knapp, D.E. Mapping burn severity and burning efficiency in California using simulation models and Landsat imagery. Remote Sens. Environ. 2010, 114, 1535–1545. [Google Scholar] [CrossRef]
- Soverel, N.O.; Perrakis, D.D.B.; Coops, N.C. Estimating burn severity from Landsat dNBR and RdNBR indices across western Canada. Remote Sens. Environ. 2010, 114, 1896–1909. [Google Scholar] [CrossRef]
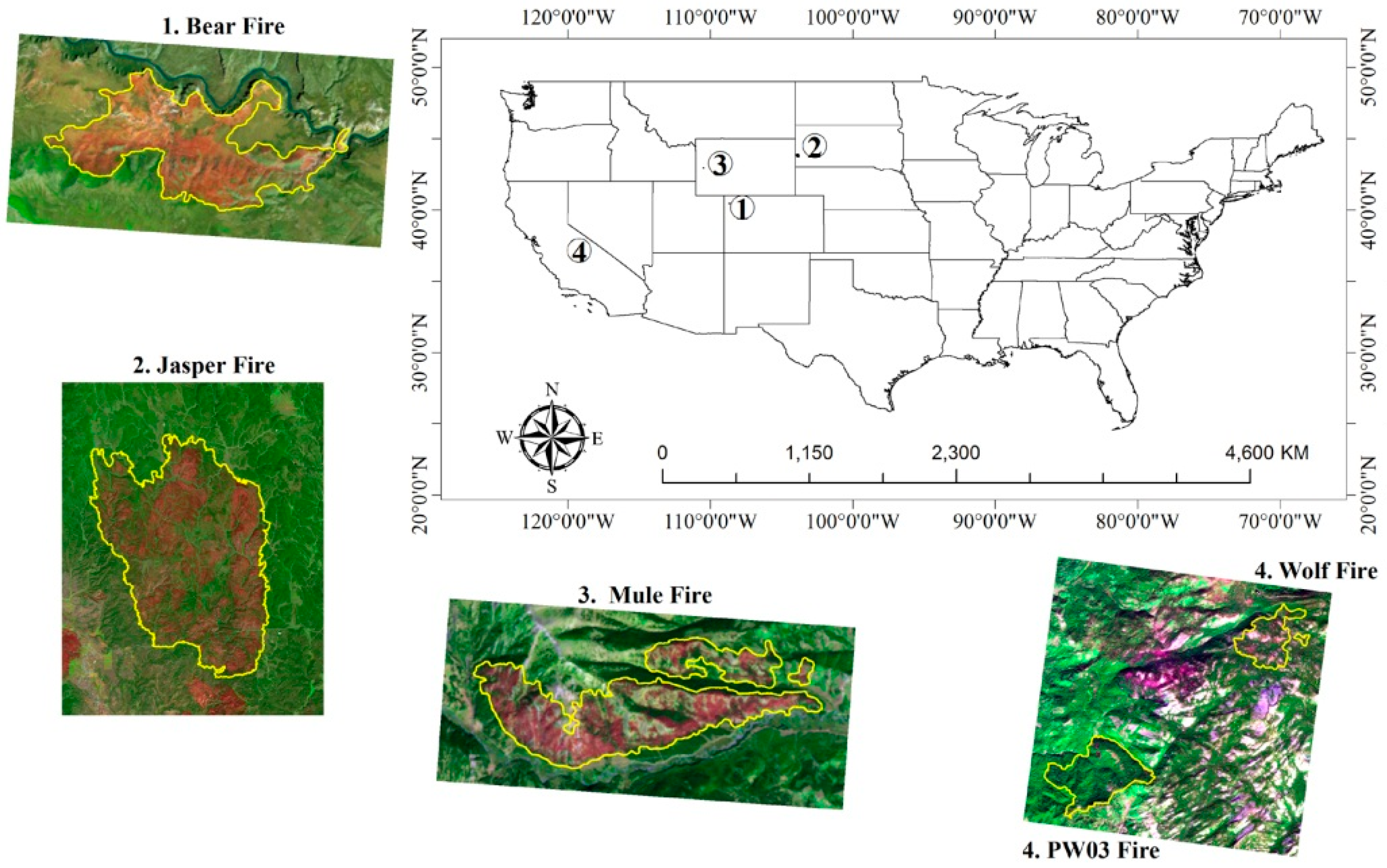
| Fire Name | Bear | Jasper | Mule | Pw03-Wolf |
|---|---|---|---|---|
| Regional Eco-Types | Southwest | Central | Northern Rockies | California |
| Alarm Date | 27 June 2002 | 24 August 2000 | 11 July 2002 | 3 Octorber 2002–11 July 2002 |
| Sensor | TM | TM and ETM+ | TM | ETM+ and TM |
| Pre-fire Image Date | 13 June 2002 | 1 May 2000 | 21 September 2001 | 18 Octorber 2001 |
| Post-fire Image Date | 31 May 2003 | 31 May 2002 | 27 September 2003 | 16 Octorber 2003 |
| Landsat Path/Row | 36/32 | 33/30 | 37/30 | 42/34 |
| CBI Field Plots Collected Date | 28 May–30 May 2003 | 14 May–26 May 2002 | 8 September–11 September 2003 | 15 August–30 Octorber 2003 |
| Fire Size (km2) | 18.62 | 336.37 | 11.86 | 13.61 |
| Fire Name | RA Parameters | RA 1 Precisions | SVR Parameters | SVR Precisions | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | R2 | R | RMSE | C | ε | R | RMSE | |
| Bear Fire | −15.22 | 9.53 | 1.35 | 0.52 | 0.82 | 0.60 | 16 | 0.22 | 0.85 | 0.54 |
| Jasper Fire | −4.39 | 5.77 | 0.82 | 0.68 | 0.73 | 0.68 | 29.86 | 0.03 | 0.83 | 0.57 |
| Mule Fire | −0.63 | 3.58 | 0.51 | 0.60 | 0.85 | 0.53 | 4 | 0.23 | 0.87 | 0.50 |
| Pw03-wolf Fire | −3.75 | 5.55 | 0.68 | 0.61 | 0.78 | 0.53 | 11.31 | 0.25 | 0.89 | 0.46 |
| Fire Name | Field Plots Number | RA Precisions | SVR Precisions | |||
|---|---|---|---|---|---|---|
| Training Samples | Testing Samples | R | RMSE | R | RMSE | |
| Bear Fire | 6 | 49 | 0.81 | 0.66 | 0.71 | 1.00 |
| 11 | 44 | 0.81 | 0.61 | 0.86 | 0.59 | |
| 17 | 38 | 0.80 | 0.63 | 0.80 | 0.61 | |
| 22 | 33 | 0.82 | 0.61 | 0.87 | 0.52 | |
| 28 | 27 | 0.82 | 0.60 | 0.85 | 0.54 | |
| Jasper Fire | 8 | 68 | 0.73 | 0.64 | 0.64 | 0.69 |
| 15 | 61 | 0.73 | 0.69 | 0.82 | 0.53 | |
| 23 | 53 | 0.72 | 0.69 | 0.83 | 0.52 | |
| 30 | 46 | 0.72 | 0.70 | 0.83 | 0.53 | |
| 38 | 38 | 0.73 | 0.68 | 0.83 | 0.57 | |
| Mule Fire | 6 | 49 | −0.19 | 1.66 | 0.00 | 1.00 |
| 11 | 44 | 0.83 | 0.68 | 0.89 | 0.48 | |
| 17 | 38 | 0.86 | 0.54 | 0.88 | 0.49 | |
| 22 | 33 | 0.86 | 0.55 | 0.87 | 0.53 | |
| 28 | 27 | 0.85 | 0.53 | 0.87 | 0.50 | |
| Pw03-wolf Fire | 8 | 70 | 0.78 | 0.55 | 0.77 | 0.60 |
| 16 | 62 | 0.78 | 0.53 | 0.84 | 0.45 | |
| 23 | 55 | 0.77 | 0.56 | 0.87 | 0.41 | |
| 31 | 47 | 0.78 | 0.53 | 0.87 | 0.53 | |
| 39 | 39 | 0.78 | 0.53 | 0.89 | 0.46 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Zeng, Y.; Li, S.; Huang, W. Mapping Burn Severity of Forest Fires in Small Sample Size Scenarios. Forests 2018, 9, 608. https://doi.org/10.3390/f9100608
Zheng Z, Zeng Y, Li S, Huang W. Mapping Burn Severity of Forest Fires in Small Sample Size Scenarios. Forests. 2018; 9(10):608. https://doi.org/10.3390/f9100608
Chicago/Turabian StyleZheng, Zhong, Yongnian Zeng, Songnian Li, and Wei Huang. 2018. "Mapping Burn Severity of Forest Fires in Small Sample Size Scenarios" Forests 9, no. 10: 608. https://doi.org/10.3390/f9100608
APA StyleZheng, Z., Zeng, Y., Li, S., & Huang, W. (2018). Mapping Burn Severity of Forest Fires in Small Sample Size Scenarios. Forests, 9(10), 608. https://doi.org/10.3390/f9100608






