Branch Development of Five-Year-Old Betula alnoides Plantations in Response to Planting Density
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site and Design
2.2. Measurements
2.3. Data Analysis
3. Results
3.1. Tree Growth Performance
3.2. Branch Quantity (Number, Proportion, Density)
3.3. Branch Morphology (Diameter, Length, Angle, the Largest Diameter)
3.4. Modeling and Simulation on Branch Attributes
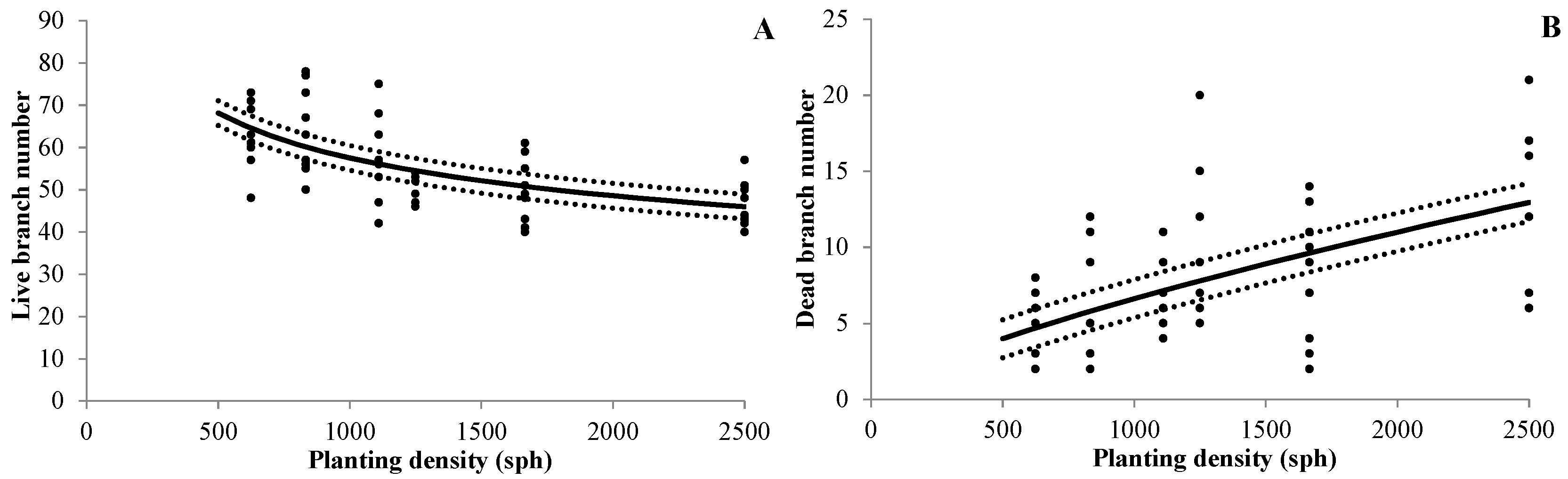
3.4.1. Branch Number
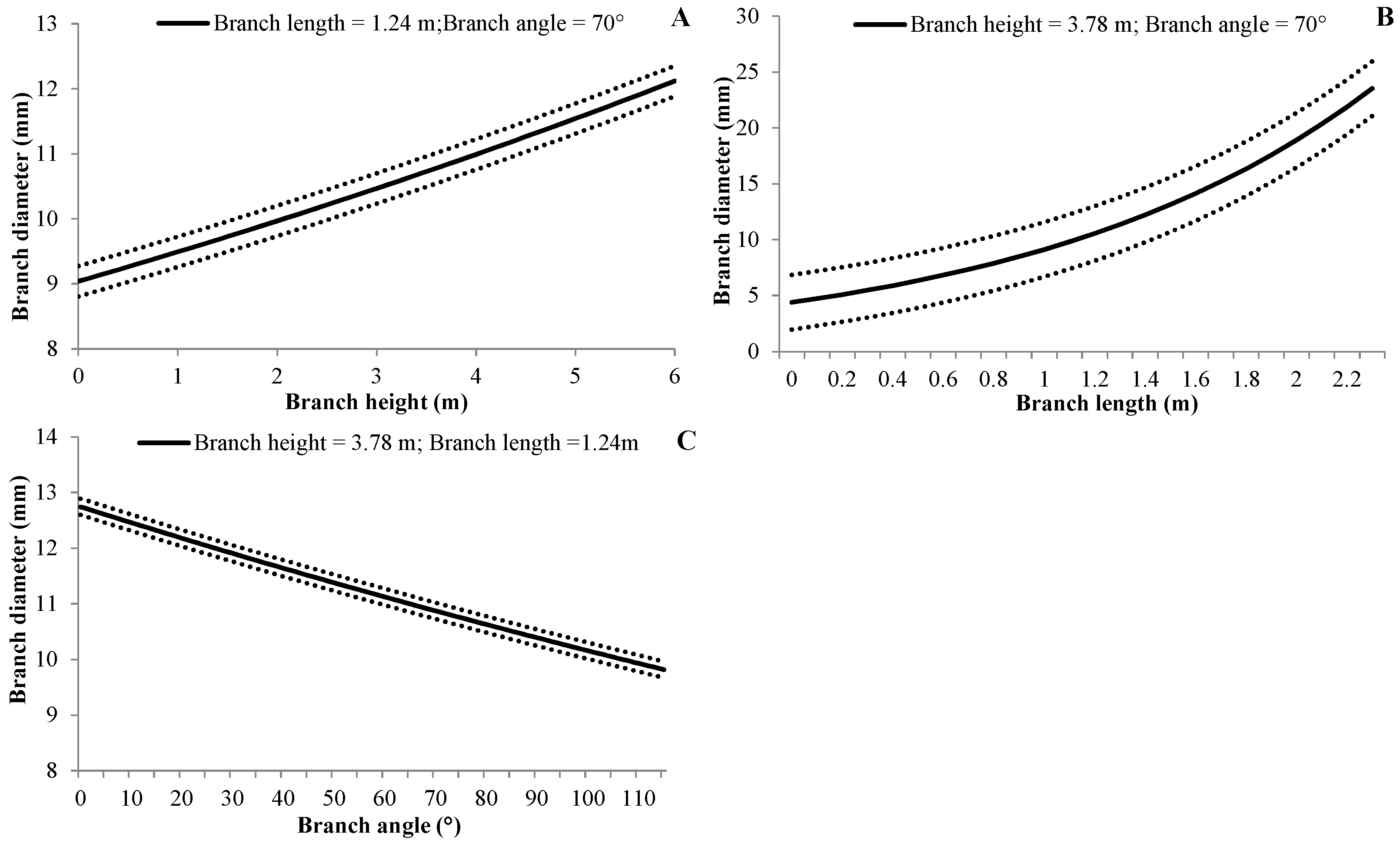
3.4.2. Branch Diameter
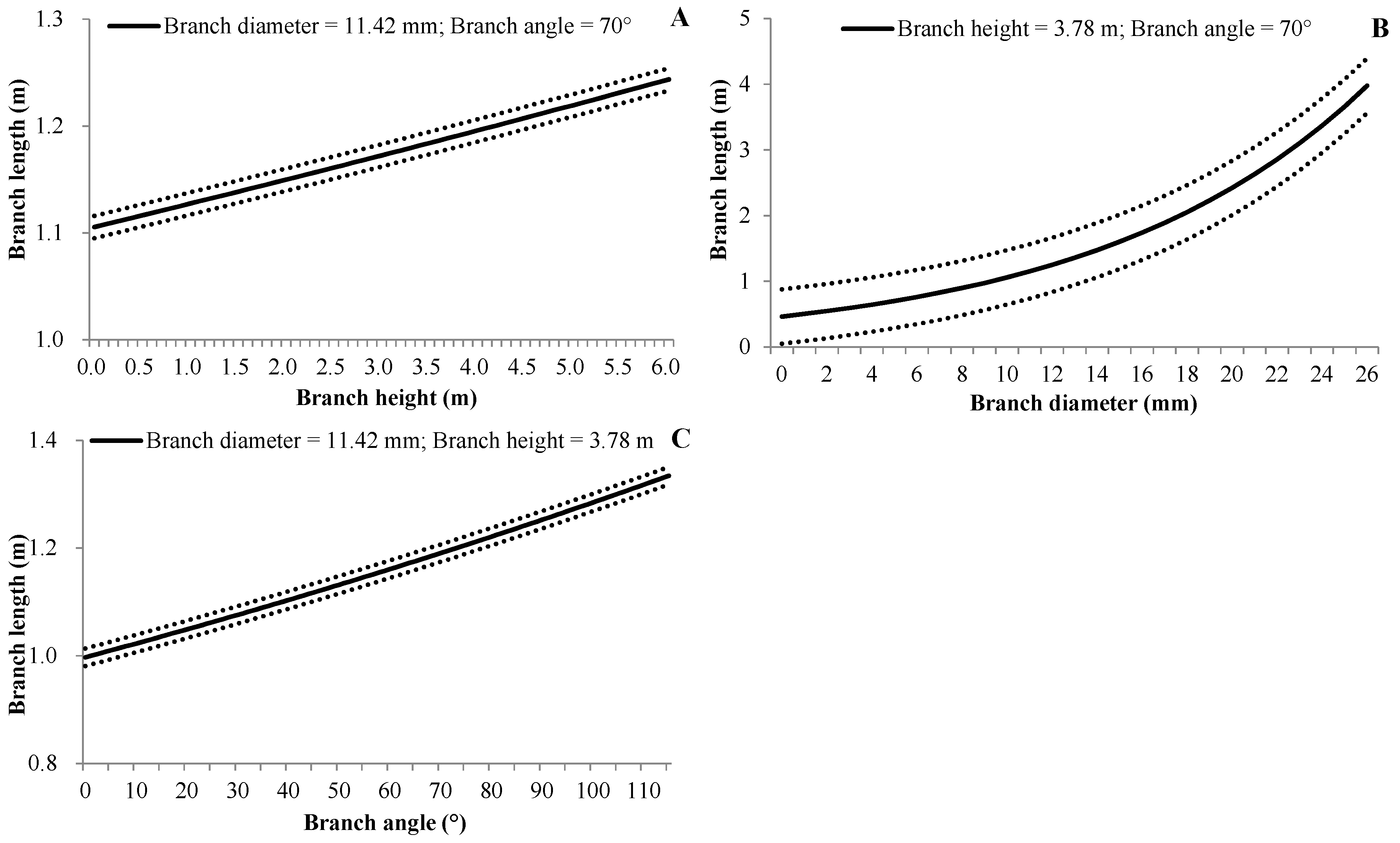
3.4.3. Branch Length
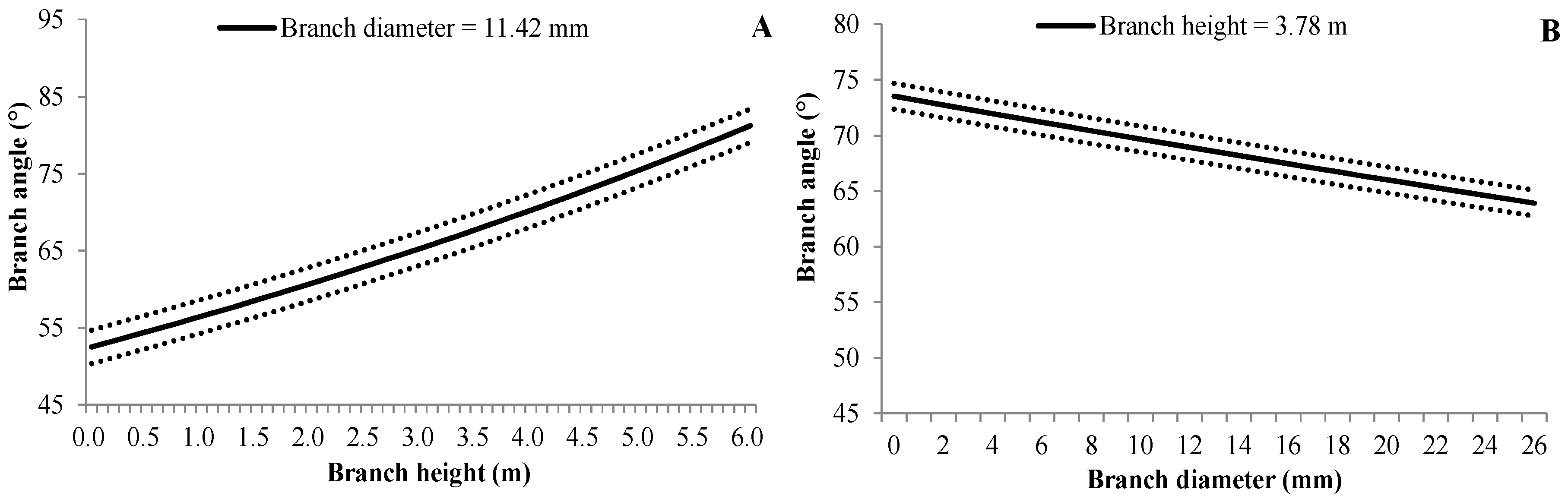
3.4.4. Branch Angle
4. Discussion
4.1. Tree Growth Performance
4.2. Branch Quantity
4.3. Branch Morphology
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zeng, J.; Zheng, H.S.; Weng, Q.J. Betula alnoides—A valuable tree species for tropical and warm-subtropical areas. For. Farm Commun. Tree Res. Rep. 1999, 4, 60–63. [Google Scholar]
- Wang, C.S.; Hein, S.; Zhao, Z.G.; Guo, J.J.; Zeng, J. Branch occlusion and discoloration of Betula alnoides under artificial and natural pruning. For. Ecol. Manag. 2016, 375, 200–210. [Google Scholar] [CrossRef]
- Zeng, J.; Zou, Y.P.; Bai, J.Y.; Zheng, H.S. RAPD analysis of genetic variation in natural populations of Betula alnoides from Guangxi, China. Euphytica 2003, 134, 33–41. [Google Scholar] [CrossRef]
- Mäkinen, H.; Verkasalo, E.; Tuimala, A. Effects of pruning in Norway spruce on tree growth and grading of sawn boards in Finland. Forestry 2014, 87, 417–424. [Google Scholar] [CrossRef]
- Macdonald, E.; Hubert, J. A review of the effects of silviculture on timber quality of Sitka spruce. Forestry 2002, 75, 107–138. [Google Scholar] [CrossRef]
- Dănescu, A.; Ehring, A.; Bauhus, J.; Albrecht, A.; Hein, S. Modelling discoloration and duration of branch occlusion following green pruning in Acer pseudoplatanus and Fraxinus excelsior. For. Ecol. Manag. 2015, 335, 87–98. [Google Scholar] [CrossRef]
- Hein, S. Knot attributes and occlusion of naturally pruned branches of Fagus sylvatica. For. Ecol. Manag. 2008, 256, 2046–2057. [Google Scholar] [CrossRef]
- Seeling, U.; Reck, P.; Becker, G.; Bücking, M. Quality of veneer and sawn timber, produced of pruned, high dimension Norway spruce trees with long crowns. Forst Holz 2004, 59, 63–68. [Google Scholar]
- Kearney, D.; James, R.; Montagu, K.; Smith, R.G.B. The effect of initial planting density on branching characteristics of Eucalyptus pilularis and E. grandis. Aust. For. 2007, 70, 262–268. [Google Scholar] [CrossRef]
- Wang, C.S.; Zhao, Z.G.; Hein, S.; Zeng, J.; Schuler, J.; Guo, J.J.; Guo, W.F.; Zeng, J. Effect of planting density on knot attributes and branch occlusion of Betula alnoides under natural pruning in southern China. Forests 2015, 6, 1343–1361. [Google Scholar] [CrossRef]
- DeBell, J.D.; Tappeiner, I.; John, C.; Krahmer, R.L. Branch diameter of western hemlock: Effects of precommercial thinning and implications for log grades. West. J. Appl. For. 1994, 9, 88–90. [Google Scholar]
- Mäkinen, H.; Saranpää, P.; Linder, S. Effect of nutrient optimization on branch characteristics in Picea abies (L.) Karst. Scand. J. For. Res. 2001, 16, 354–362. [Google Scholar] [CrossRef]
- Clair, J.B.S. Genetic variation in tree structure and its relation to size in Douglas-fir. II. Crown form, branch characters, and foliage characters. Can. J. For. Res. 1994, 24, 1236–1247. [Google Scholar] [CrossRef]
- Gort, J.; Zubizarreta-Gerendiain, A.; Peltola, H.; Kilpeläinen, A.; Pulkkinen, P.; Jaatinen, R.; Kellomäki, S. Differences in branch characteristics of Scots pine (Pinus sylvestris L.) genetic entries grown at different spacing. Ann. For. Sci. 2010, 67, 750. [Google Scholar] [CrossRef]
- Lowell, E.C.; Maguire, D.A.; Briggs, D.G.; Turnblom, E.C.; Jayawickrama, K.J.; Bryce, J. Effects of silviculture and genetics on branch/knot attributes of coastal Pacific Northwest Douglas-fir and implications for wood quality—a synthesis. Forests 2014, 5, 1717–1736. [Google Scholar] [CrossRef]
- Glencross, K.; Nichols, J.D.; Grant, J.C.; Sethy, M.; Smith, R.G.B. Spacing affects stem form, early growth and branching in young whitewood (Endospermum medullosum) plantations in Vanuatu. Int. For. Rev. 2012, 14, 442–451. [Google Scholar] [CrossRef]
- Briggs, D.; Ingaramo, L.; Turnblom, E. Number and diameter of breast-height region branches in a Douglas-fir spacing trial and linkage to log quality. For. Prod. J. 2007, 57, 28–34. [Google Scholar]
- Víquez, E.; Pérez, D. Effect of pruning on tree growth, yield, and wood properties of Tectona grandis plantations in Costa Rica. Silva Fenn. 2005, 39, 381–390. [Google Scholar] [CrossRef]
- Mäkinen, H. Effect of stand density on the branch development of silver birch (Betula pendula Roth) in central Finland. Trees-Struct. Funct. 2002, 16, 346–353. [Google Scholar]
- Newton, M.; Lachenbruch, B.; Robbins, J.M.; Cole, E.C. Branch diameter and longevity linked to plantation spacing and rectangularity in young Douglas-fir. For. Ecol. Manag. 2012, 266, 75–82. [Google Scholar] [CrossRef]
- Wang, C.S.; Zeng, J.; Hein, S.; Zhao, Z.G.; Guo, J.J.; Zeng, J. Crown and branch attributes of mid-aged Betula alnoides plantations in response to planting density. Scand. J. For. Res. 2017, 32, 679–687. [Google Scholar] [CrossRef]
- Hein, S.; Mäkinen, H.; Yue, C.; Kohnle, U. Modelling branch characteristics of Norway spruce from wide spacings in Germany. For. Ecol. Manag. 2007, 242, 155–164. [Google Scholar] [CrossRef]
- Mäkinen, H.; Hein, S. Effect of wide spacing on increment and branch properties of young Norway spruce. Eur. J. For. Res. 2006, 125, 239–248. [Google Scholar] [CrossRef]
- Niemistö, P. Influence of initial spacing and row-to-row distance on the crown and branch properties and taper of silver birch (Betula pendula). Scand. J. For. Res. 1995, 10, 235–244. [Google Scholar] [CrossRef]
- Umeki, K.; Kikuzawa, K. Patterns in individual growth, branch population dynamics, and growth and mortality of first-order branches of Betula platyphylla in northern Japan. Ann. For. Sci. 2000, 57, 587–598. [Google Scholar] [CrossRef]
- Umeki, K.; Seino, T. Growth of first-order branches in Betula platyphylla saplings as related to the age, position, size, angle, and light availability of branches. Can. J. For. Res. 2003, 33, 1276–1286. [Google Scholar] [CrossRef]
- Kint, V.; Hein, S.; Campioli, M.; Muys, B. Modelling self-pruning and branch attributes for young Quercus robur L. and Fagus sylvatica L. trees. For. Ecol. Manag. 2010, 260, 2023–2034. [Google Scholar] [CrossRef]
- Newman, M.C. Regression analysis of log-transformed data: Statistical bias and its correction. Environ. Toxicol. Chem. 1993, 12, 1129–1133. [Google Scholar] [CrossRef]
- Hummel, S. Height, diameter and crown dimensions of Cordia alliodora associated with tree density. For. Ecol. Manag. 2000, 127, 31–40. [Google Scholar] [CrossRef]
- Henskens, F.L.; Battaglia, M.; Cherry, M.L.; Beadle, C.L. Physiological basis of spacing effects on tree growth and form in Eucalyptus globulus. Trees-Struct Funct. 2001, 15, 365–377. [Google Scholar] [CrossRef]
- Akers, M.K.; Kane, M.; Zhao, D.; Teskey, R.O.; Daniels, R.F. Effects of planting density and cultural intensity on stand and crown attributes of mid-rotation loblolly pine plantations. For. Ecol. Manag. 2013, 310, 468–475. [Google Scholar] [CrossRef]
- Alcorn, P.J.; Pyttel, P.; Bauhus, J.; Smith, R.G.B.; Thomas, D.; James, R.; Nicotra, A. Effects of initial planting density on branch development in 4-year-old plantation grown Eucalyptus pilularis and Eucalyptus cloeziana trees. For. Ecol. Manag. 2007, 252, 41–51. [Google Scholar] [CrossRef]
- Pinkard, E.; Neilsen, W. Crown and stand characteristics of Eucalyptus nitens in response to initial spacing: Implications for thinning. For. Ecol. Manag. 2003, 172, 215–227. [Google Scholar] [CrossRef]
- Hein, S.; Weiskittel, A.R.; Kohnle, U. Branch characteristics of widely spaced Douglas-fir in south-western Germany: Comparisons of modelling approaches and geographic regions. For. Ecol. Manag. 2008, 256, 1064–1079. [Google Scholar] [CrossRef]
- Forrester, D.I.; Collopy, J.J.; Beadle, C.L.; Baker, T.G. Interactive effects of simultaneously applied thinning, pruning and fertiliser application treatments on growth, biomass production and crown architecture in a young Eucalyptus nitens plantation. For. Ecol. Manag. 2012, 267, 104–116. [Google Scholar] [CrossRef]
- Nelson, A.S.; Weiskittel, A.R.; Wagner, R.G. Development of branch, crown, and vertical distribution leaf area models for contrasting hardwood species in Maine, USA. Trees-Struct. Funct. 2014, 28, 17–30. [Google Scholar] [CrossRef]
- Kearney, D. Characterisation of Branching Patterns, Changes Caused by Variations in Initial Stocking and Implications for Silviculture, for E. grandis and E. pilularis Plantations in the North Coast Region of NSW. Bachelor’s Thesis, Department of Forestry, The Australian National University, Canberra, Australia, 1999. [Google Scholar]
- Neilsen, W.A.; Gerrand, A.M. Growth and branching habit of Eucalyptus nitens at different spacing and the effect on final crop selection. For. Ecol. Manag. 1999, 123, 217–229. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Maguire, D.A.; Monserud, R.A. Modeling crown structural responses to competing vegetation control, thinning, fertilization, and Swiss needle cast in coastal Douglas-fir of the Pacific Northwest, USA. For. Ecol. Manag. 2007, 245, 96–109. [Google Scholar] [CrossRef]
- Hein, S.; Weiskittel, A.R.; Kohnle, U. Effect of wide spacing on tree growth, branch and sapwood properties of young Douglas-fir [Pseudotsuga menziesii (Mirb.) Franco] in south-western Germany. Eur. J. For. Res. 2008, 127, 481–493. [Google Scholar] [CrossRef]
- Florence, R.G. Ecology and Silviculture of Eucalypt Forests; CSIRO: Collingwood, Australia, 2004; p. 413. [Google Scholar]
- Alcorn, P.J.; Forrester, D.I.; Rgb, S.; Thomas, D.S.; James, R.N.; Nicotra, A.B.; Bauhus, J. Crown structure and vertical foliage distribution in 4-year-old plantation-grown Eucalyptus pilularis and Eucalyptus cloeziana. Trees-Struct. Funct. 2013, 27, 555–566. [Google Scholar] [CrossRef]
| Abbreviation | Attributes Represent | Precision |
|---|---|---|
| Stand attributes | ||
| PD | Planting density treatments | / |
| Tree attributes | ||
| H | Tree height | 0.1 m |
| DBH | Stem diameter at breast height | 0.1 cm |
| Hcb | Height to crown base | 0.1 m |
| CW | Crown diameter | 0.1 m |
| NLB | Number of live branches | / |
| NDB | Number of dead branches | / |
| Branch attributes | ||
| BD | Branch diameter | 0.01 mm |
| BL | Branch length | 0.1 m |
| BA | Branch angle | 1° |
| BH | Branch height | 0.01 m |
| Model descriptors | ||
| a, b, c, d, e | Coefficients of fixed effects and intercepts | / |
| r, rp, rpt, rptb | Subscripts for replicate, plot, tree and branch | / |
| α, β, γ, δ | Variance components (random effects) | / |
| Φ | Dispersion parameter | / |
| ln() | Natural log-link | / |
| RMSE | Root mean squared error | / |
| R2(c), R2(m) | Conditional and marginal R2 | / |
| Planting Density (sph) | Spacing (Row × Tree) | DBH (cm) | H (m) | Hcb (m) | CD (m) | |
|---|---|---|---|---|---|---|
| Stand level | 625 | 4 m × 4 m | 6.85 (0.21)a | 5.16 (0.15)b | 1.46 (0.06)c | 3.33 (0.08)a |
| 833 | 4 m × 3 m | 6.51 (0.13)a | 5.00 (0.09)b | 1.40 (0.04)c | 3.07 (0.06)b | |
| 1111 | 3 m × 3 m | 6.70 (0.14)a | 5.33 (0.11)b | 1.59 (0.04)bc | 2.81 (0.05)c | |
| 1250 | 4 m × 2 m | 6.65 (0.14)a | 5.65 (0.10)a | 1.80 (0.06)ab | 2.64 (0.05)d | |
| 1667 | 3 m × 2 m | 6.93 (0.14)a | 5.69 (0.12)a | 1.94 (0.08)a | 2.63 (0.04)d | |
| 2500 | 2 m × 2 m | 6.46 (0.13)a | 5.21 (0.10)b | 1.89 (0.11)a | 2.43 (0.05)e | |
| Sampled dominant and co-dominant trees | 625 | 4 m × 4 m | 8.19 (0.48)a | 7.09 (0.26)a | 1.48 (0.09)b | 3.82 (0.15)a |
| 833 | 4 m × 3 m | 7.70 (0.21)a | 7.00 (0.28)a | 1.66 (0.25)ab | 3.56 (0.09)ab | |
| 1111 | 3 m × 3 m | 7.84 (0.28)a | 6.41 (0.16)a | 1.67 (0.10)ab | 3.42 (0.16)ab | |
| 1250 | 4 m × 2 m | 7.73 (0.24)a | 7.46 (0.20)a | 2.09 (0.09)a | 3.55 (0.09)ab | |
| 1667 | 3 m × 2 m | 7.79 (0.28)a | 7.46 (0.17)a | 1.97 (0.15)a | 3.34 (0.10)bc | |
| 2500 | 2 m × 2 m | 8.13 (0.41)a | 7.62 (0.16)a | 2.52 (0.19)a | 3.11 (0.09)c | |
| Branch Attributes | Planting Density (sph) | ||||||
|---|---|---|---|---|---|---|---|
| 625 | 833 | 1111 | 1250 | 1667 | 2500 | ||
| Branch number | Live | 63 (3)a | 64 (3)a | 57 (3)ab | 51 (1)bc | 50 (3)bc | 47 (2)c |
| Dead | 5 (1)d | 6 (1)cd | 6 (1)cd | 10 (2)b | 8 (1)bc | 13 (2)a | |
| Total | 68 (3)a | 70 (3)a | 64 (4)a | 61 (2)a | 58 (2)a | 61 (2)a | |
| Branch proportion | Live | 0.93 (0.01)a | 0.92 (0.02)a | 0.90 (0.01)ab | 0.84 (0.02)c | 0.86 (0.03)bc | 0.78 (0.03)d |
| Dead | 0.07 (0.01)d | 0.08 (0.02)d | 0.10 (0.01)cd | 0.16 (0.02)ab | 0.14 (0.03)bc | 0.22 (0.03)a | |
| Branch density | Live | 11.4 (0.9)a | 12.1 (0.8)a | 12.1 (0.6)a | 9.6 (0.5)b | 9.1 (0.5)b | 9.4 (0.5)b |
| Dead | 0.8 (0.1)d | 1.0 (0.2)cd | 1.3 (0.1)cd | 1.8 (0.3)b | 1.5 (0.3)bc | 2.6 (0.3)a | |
| Total | 12.3 (0.9)a | 13.2 (0.7)a | 13.4 (0.6)a | 11.4 (0.4)b | 10.6 (0.3)b | 11.9 (0.4)ab | |
| Branch diameter (mm) | 12.11 (0.21)a | 11.21 (0.19)a | 11.04 (0.21)a | 11.85 (0.24)a | 11.05 (0.22)a | 11.15 (0.25)a | |
| Branch angle (°) | 71.9 (0.6)a | 70.3 (0.7)a | 69.3 (0.7)a | 69.5 (0.8)a | 69.2 (1.0)a | 69.0 (0.9)a | |
| Branch length (m) | 1.31 (0.02)a | 1.23 (0.02)a | 1.21 (0.02)a | 1.26 (0.02)a | 1.23 (0.03)a | 1.18 (0.03)a | |
| The largest branch dimeter (mm) | 21.75 (0.69)a | 19.94 (0.64)ab | 19.05 (1.05)b | 19.35 (0.47)b | 18.06 (0.51)b | 18.45 (0.86)b | |
| Branch height of the largest branch (m) | 4.00 (0.39)b | 3.80 (0.26)b | 4.18 (0.06)ab | 4.91 (0.28)a | 4.72 (0.25)a | 4.90 (0.25)a | |
| Branch Attributes | Planting Density (sph) | ||||||
|---|---|---|---|---|---|---|---|
| 625 | 833 | 1111 | 1250 | 1667 | 2500 | ||
| Branch number | East | 12 (1) | 11 (1) | 10 (1) | 10 (0) | 7 (1) | 7 (1) |
| South | 11 (1) | 13 (1) | 11 (1) | 9 (1) | 9 (1) | 8 (1) | |
| West | 12 (1) | 10 (1) | 10 (1) | 8 (1) | 7 (1) | 7 (1) | |
| North | 11 (1) | 12 (0) | 11 (1) | 9 (1) | 8 (1) | 8 (1) | |
| Branch proportion | East | 0.26 (0.01) | 0.23 (0.01) | 0.24 (0.01) | 0.29 (0.01) | 0.23 (0.03) | 0.24 (0.02) |
| South | 0.23 (0.02) | 0.29 (0.02) | 0.27 (0.02) | 0.24 (0.02) | 0.29 (0.03) | 0.26 (0.02) | |
| West | 0.26 (0.02) | 0.22 (0.01) | 0.24 (0.02) | 0.21 (0.02) | 0.21 (0.03) | 0.23 (0.02) | |
| North | 0.24 (0.02) | 0.26 (0.01) | 0.25 (0.02) | 0.26 (0.02) | 0.26 (0.02) | 0.27(0.03) | |
| Equation | Response Variables | Regression Parameters | Predictor Variables | Estimate | Standard Error | Significance |
|---|---|---|---|---|---|---|
| (3) | NLB | a0 | Intercept | 5.738 | 0.2973 | <0.0001 |
| a1 | PD | −0.244 | 0.0421 | <0.0001 | ||
| Φ | 1.125 | |||||
| (4) | NDB | b0 | Intercept | −3.166 | 0.7910 | <0.0001 |
| b1 | PD | 0.732 | 0.1089 | <0.0001 | ||
| Φ | 2.051 | |||||
| (5) | BD | c0 | Intercept | 1.4341 | 0.0331 | <0.0001 |
| c1 | BH | 0.0489 | 0.0051 | <0.0001 | ||
| c2 | BL | 0.7283 | 0.0128 | <0.0001 | ||
| c3 | BA | −0.0023 | 0.0004 | <0.0001 | ||
| αbp | 0.0011 | 0.0006 | 0.041 | |||
| αbptb | 0.0440 | 0.0015 | <0.0001 | |||
| (6) | BL | d0 | Intercept | −1.0484 | 0.0423 | <0.0001 |
| d1 | BH | 0.0196 | 0.0058 | <0.0001 | ||
| d2 | BA | 0.0025 | 0.0004 | <0.0001 | ||
| d3 | BD | 0.0827 | 0.0016 | <0.0001 | ||
| βbp | 0.0017 | 0.0008 | 0.037 | |||
| βbptb | 0.0541 | 0.0018 | <0.0001 | |||
| (7) | BA | e0 | Intercept | 4.0002 | 0.0331 | <0.0001 |
| e1 | BH | 0.0726 | 0.0051 | <0.0001 | ||
| e2 | BD | −0.0054 | 0.0014 | <0.0001 | ||
| γbp | 0.0021 | 0.0010 | 0.027 | |||
| γbptb | 0.0466 | 0.0015 | <0.0001 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-S.; Tang, C.; Hein, S.; Guo, J.-J.; Zhao, Z.-G.; Zeng, J. Branch Development of Five-Year-Old Betula alnoides Plantations in Response to Planting Density. Forests 2018, 9, 42. https://doi.org/10.3390/f9010042
Wang C-S, Tang C, Hein S, Guo J-J, Zhao Z-G, Zeng J. Branch Development of Five-Year-Old Betula alnoides Plantations in Response to Planting Density. Forests. 2018; 9(1):42. https://doi.org/10.3390/f9010042
Chicago/Turabian StyleWang, Chun-Sheng, Cheng Tang, Sebastian Hein, Jun-Jie Guo, Zhi-Gang Zhao, and Jie Zeng. 2018. "Branch Development of Five-Year-Old Betula alnoides Plantations in Response to Planting Density" Forests 9, no. 1: 42. https://doi.org/10.3390/f9010042
APA StyleWang, C.-S., Tang, C., Hein, S., Guo, J.-J., Zhao, Z.-G., & Zeng, J. (2018). Branch Development of Five-Year-Old Betula alnoides Plantations in Response to Planting Density. Forests, 9(1), 42. https://doi.org/10.3390/f9010042





