Low Tree-Growth Elasticity of Forest Biomass Indicated by an Individual-Based Model
Abstract
1. Introduction
2. Data and Methods
2.1. Forest Inventory Data
2.2. Modelling
2.3. Study Design and Analysis
2.3.1. Calibration of Equations
2.3.2. Behaviour of Single-Stand Simulations
2.3.3. Scaling Relationships between Growth and Landscape-Scale Biomass Dynamics
2.3.4. Sensitivity Analysis
3. Results
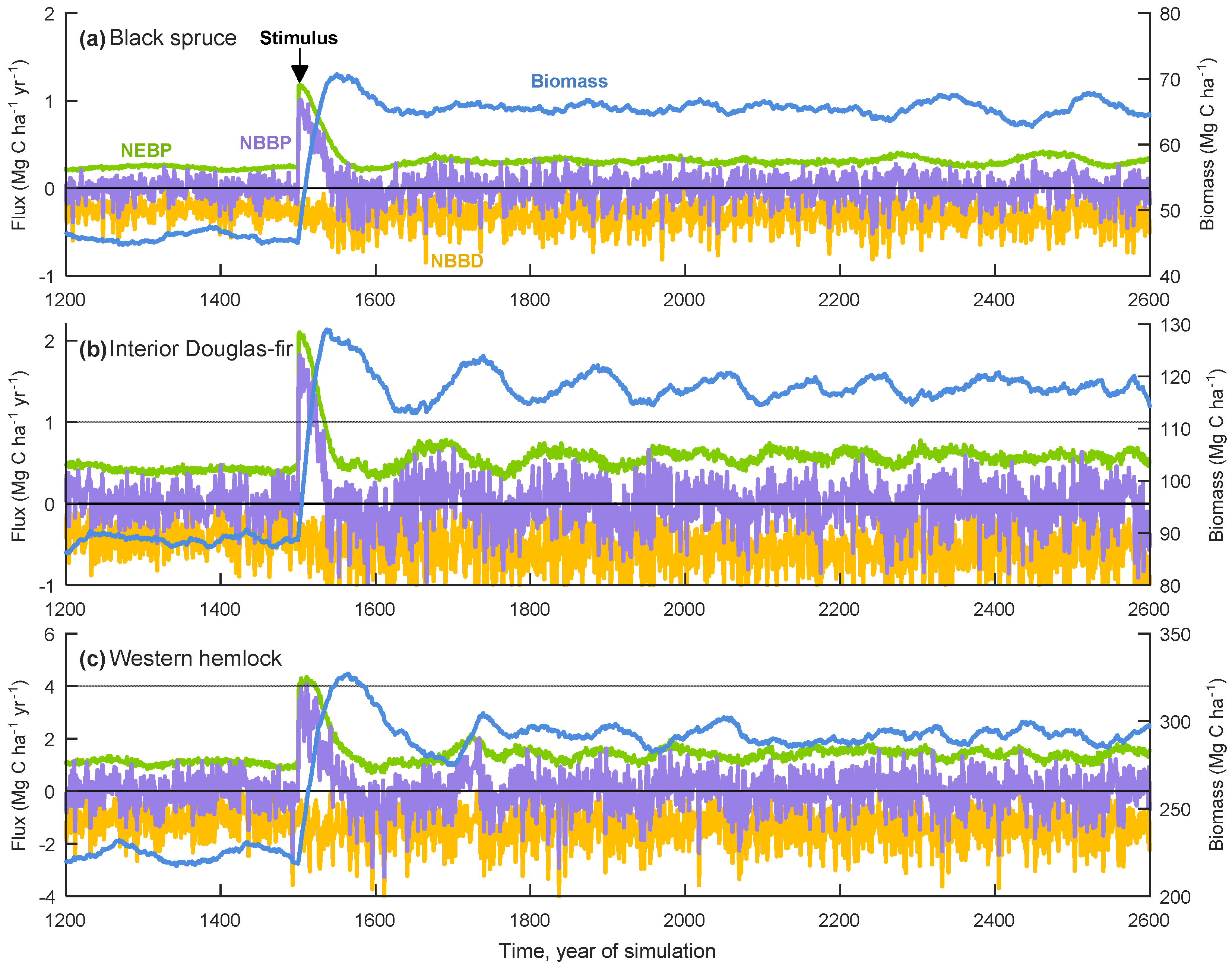
3.1. General Model Behaviour
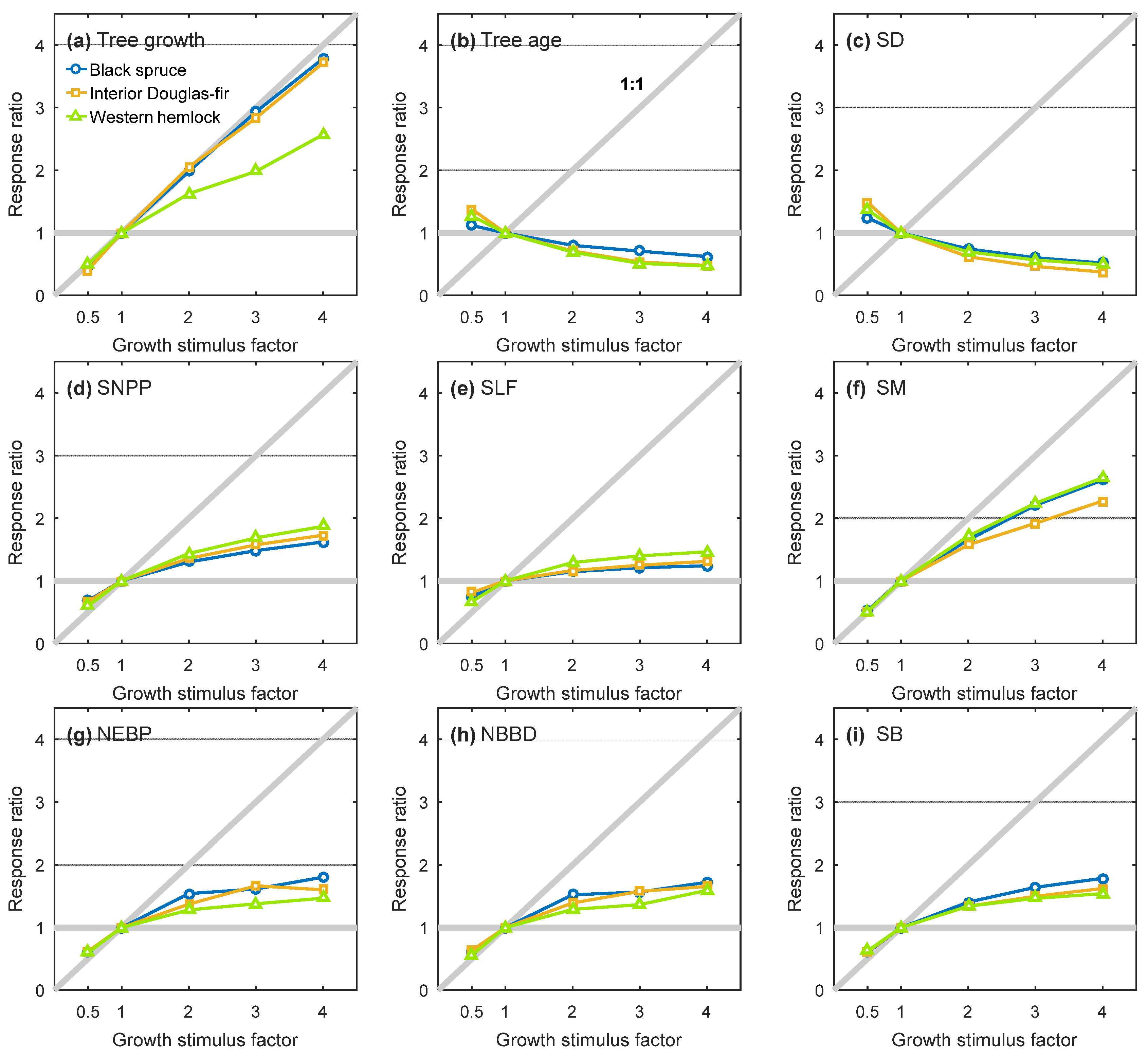
3.2. Equilibrium Responses to a Change in Tree Growth
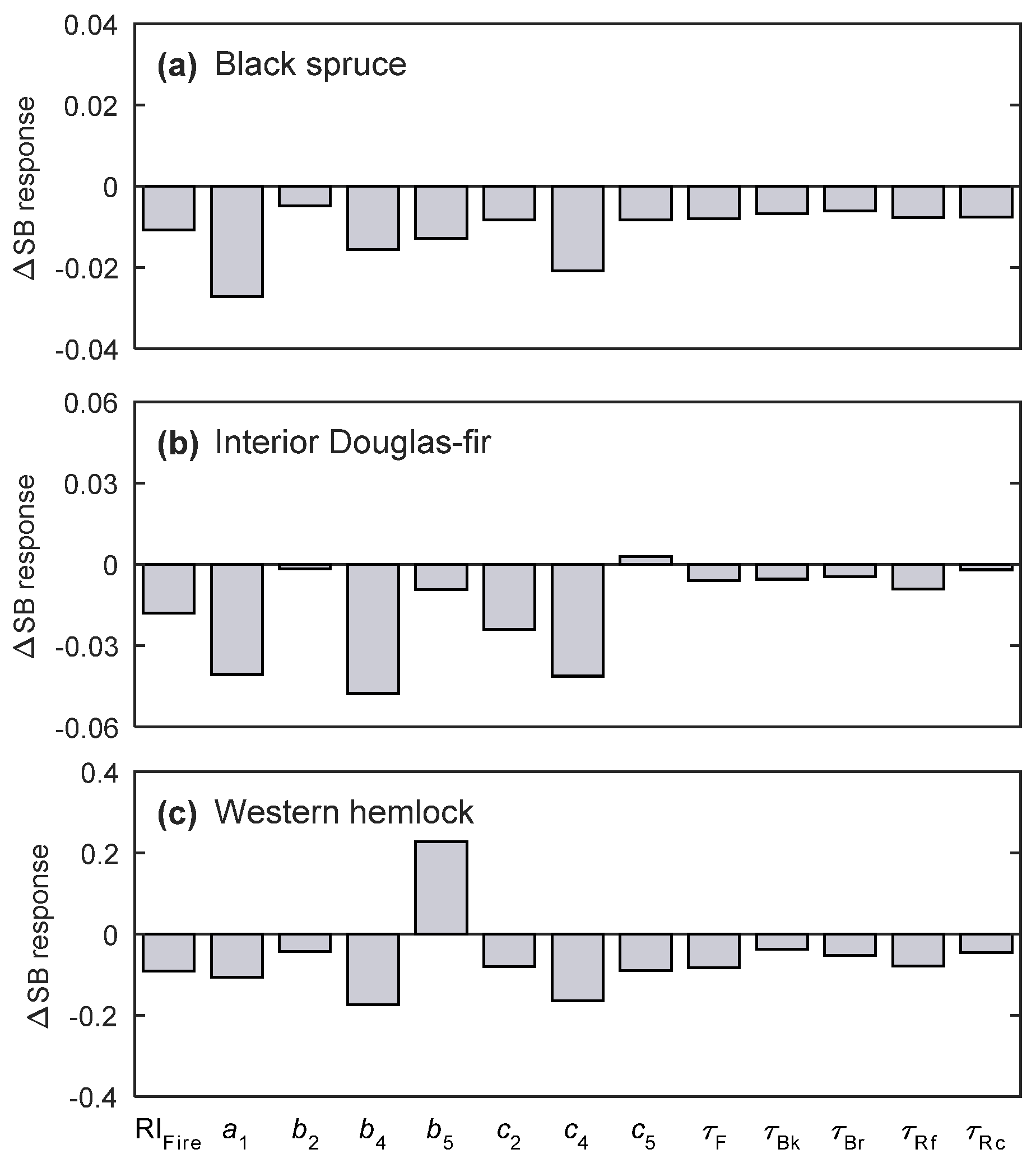
3.3. Sensitivity Analysis
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Galbraith, D.; Malhi, Y.; Affum-Baffoe, K.; Castanho, A.D.A.; Doughty, C.E.; Fisher, R.A.; Lewis, S.L.; Peh, K.S.-H.; Phillips, O.L.; Quesada, C.A.; et al. Residence times of woody biomass in tropical forests. Plant Ecol. Divers. 2013, 6, 139–157. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, Y.; Yu, G.; Zhang, L. Estimated carbon residence times in three forest ecosystems of eastern China: Applications of probabilistic inversion. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Zhou, X.; Zhou, T.; Luo, Y. Uncertainties in carbon residence time and NPP-driven carbon uptake in terrestrial ecosystems of the conterminous USA: A Bayesian approach. Tellus B Chem. Phys. Meteorol. 2012, 64, 17223. [Google Scholar] [CrossRef]
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V. Carbon and Other Biogeochemical Cycles. In Climate Change 2013: The Physical Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- King, A.; Dilling, L.; Zimmerman, G.; Fairman, D.; Houghton, R.; Marland, G.; Rose, A.; Wilbanks, T. The First State of the Carbon Cycle Report (SOCCR); U.S. Climate Change Science program Synthesis and Assessment product 2.2; 2007. Available online: http://cdiac.ess-dive.lbl.gov/SOCCR/pdf/sap2-2-final-all.pdf (accessed on 5 January 2018).
- Prentice, I.; Farquhar, G.; Fasham, M.; Goulden, M.; Heimann, M.; Jaramillo, V.; Kheshgi, H.; Le Quere, C.; Scholes, R.; Wallace, D. The Carbon Cycle and Atmospheric Carbon Dioxide. In Climate Change 2001: The Physical Science Basis; Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Fang, J.; Kato, T.; Guo, Z.; Yang, Y.; Hu, H.; Shen, H.; Zhao, X.; Kishimoto-Mo, A.W.; Tang, Y.; Houghton, R.A. Evidence for environmentally enhanced forest growth. Proc. Natl. Acad. Sci. USA 2014, 111, 9527–9532. [Google Scholar] [CrossRef] [PubMed]
- Hember, R.A.; Kurz, W.A.; Coops, N.C. Increasing net ecosystem biomass production of Canada’s boreal and temperate forests despite decline in dry climates. Glob. Biogeochem. Cycles 2017, 31, 134–158. [Google Scholar] [CrossRef]
- Kauppi, P.E.; Posch, M.; Pirinen, P. Large impacts of climatic warming on growth of boreal forests since 1960. PLoS ONE 2014, 9, e111340. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Pretzsch, H.; Biber, P.; Schütze, G.; Uhl, E.; Rötzer, T. Forest stand growth dynamics in Central Europe have accelerated since 1870. Nat. Commun. 2014, 5, 4967. [Google Scholar] [CrossRef] [PubMed]
- Drake, B.G.; Gonzàlez-Meler, M.A.; Long, S.P. More efficient plants: A consequence of rising atmospheric CO2? Annu. Rev. Plant Biol. 1997, 48, 609–639. [Google Scholar] [CrossRef] [PubMed]
- Idso, K.E.; Idso, S.B. Plant responses to atmospheric CO2 enrichment in the face of environmental constraints: A review of the past 10 years’ research. Agric. For. Meteorol. 1994, 69, 153–203. [Google Scholar] [CrossRef]
- LeBauer, D.S.; Treseder, K.K. Nitrogen limitation of net primary productivity in terrestrial ecosystems is globally distributed. Ecology 2008, 89, 371–379. [Google Scholar] [CrossRef] [PubMed]
- Norby, R.; Wullschleger, S.; Gunderson, C.; Johnson, D.; Ceulemans, R. Tree responses to rising CO2 in field experiments: Implications for the future forest. Plant Cell Environ. 1999, 22, 683–714. [Google Scholar] [CrossRef]
- Saxe, H.; Ellsworth, D.S.; Heath, J. Tree and forest functioning in an enriched CO2 atmosphere. New Phytol. 1998, 139, 395–436. [Google Scholar] [CrossRef]
- Way, D.A.; Oren, R. Differential responses to changes in growth temperature between trees from different functional groups and biomes: A review and synthesis of data. Tree Physiol. 2010, 30, 669–688. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Wan, S. Global response patterns of terrestrial plant species to nitrogen addition. New Phytol. 2008, 179, 428–439. [Google Scholar] [CrossRef] [PubMed]
- Bugmann, H.; Bigler, C. Will the CO2 fertilization effect in forests be offset by reduced tree longevity? Oecologia 2011, 165, 533–544. [Google Scholar] [CrossRef] [PubMed]
- Friend, A.D.; Lucht, W.; Rademacher, T.T.; Keribin, R.; Betts, R.; Cadule, P.; Ciais, P.; Clark, D.B.; Dankers, R.; Falloon, P.D.; et al. Carbon residence time dominates uncertainty in terrestrial vegetation responses to future climate and atmospheric CO2. Proc. Natl. Acad. Sci. USA 2014, 111, 3280–3285. [Google Scholar] [CrossRef] [PubMed]
- Manusch, C.; Bugmann, H.; Heiri, C.; Wolf, A. Tree mortality in dynamic vegetation models—A key feature for accurately simulating forest properties. Ecol. Model. 2012, 243, 101–111. [Google Scholar] [CrossRef]
- Körner, C. Plant CO2 responses: An issue of definition, time and resource supply. New Phytol. 2006, 172, 393–411. [Google Scholar] [CrossRef] [PubMed]
- Westoby, M. The Self-Thinning Rule. In Advances in Ecological Research; MacFadyen, A., Ford, E.D., Eds.; Academic Press: London, UK, 1984; pp. 167–225. [Google Scholar]
- Landsberg, J.; Sands, P. Physiological Ecology of Forest Production: Principles, Processes and Models, 1st ed.; Elsevier Inc.: Boston, MA, USA, 2011. [Google Scholar]
- Caspersen, J.P.; Vanderwel, M.C.; Cole, W.G.; Purves, D.W. How stand productivity results from size- and competition-dependent growth and mortality. PLoS ONE 2011, 6, e28660. [Google Scholar] [CrossRef] [PubMed]
- Hember, R.A.; Kurz, W.A.; Coops, N.C. Relationships between individual-tree mortality and water-balance variables indicate positive trends in water stress-induced tree mortality across North America. Glob. Chang. Biol. 2017, 23, 1691–1710. [Google Scholar] [CrossRef] [PubMed]
- Holzwarth, F.; Kahl, A.; Bauhus, J.; Wirth, C. Many ways to die—Partitioning tree mortality dynamics in a near-natural mixed deciduous forest. J. Ecol. 2013, 101, 220–230. [Google Scholar] [CrossRef]
- Lines, E.; Coomes, D.; Purves, D. Influences of forest structure, climate and species composition on tree mortality across the eastern US. PLoS ONE 2010, 5, e13212. [Google Scholar] [CrossRef] [PubMed]
- Muller-Landau, H.C.; Condit, R.S.; Chave, J.; Thomas, S.C.; Bohlman, S.A.; Bunyavejchewin, S.; Davies, S.; Foster, R.; Gunatilleke, S.; Gunatilleke, N.; et al. Testing metabolic ecology theory for allometric scaling of tree size, growth and mortality in tropical forests. Ecol. Lett. 2006, 9, 575–588. [Google Scholar] [CrossRef] [PubMed]
- Hember, R.A.; Coops, N.C.; Kurz, W.A. Statistical performance and behaviour of environmentally-sensitive composite models of lodgepole pine growth. For. Ecol. Manag. 2018, 408, 157–173. [Google Scholar] [CrossRef]
- Pokharel, B.; Dech, J.P. Mixed-effects basal area increment models for tree species in the boreal forest of Ontario, Canada using an ecological land classification approach to incorporate site effects. Forestry 2012, 85, 255–270. [Google Scholar] [CrossRef]
- Corcuera, L.; Camarero, J.J.; Sisó, S.; Gil-pelegrín, E. Radial-growth and wood-anatomical changes in overaged Quercus pyrenaica coppice stands: Functional responses in a new Mediterranean landscape. Trees 2006, 20, 91–98. [Google Scholar] [CrossRef]
- Pellizzari, E.; Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Carrer, M. Wood anatomy and carbon-isotope discrimination support long-term hydraulic deterioration as a major cause of drought-induced dieback. Glob. Chang. Biol. 2016, 22, 2125–2137. [Google Scholar] [CrossRef] [PubMed]
- Ryan, M.; Binkley, D.; Fownes, J. Age-related decline in forest productivity: Pattern and process. Adv. Ecol. Res. 1997, 27, 213–262. [Google Scholar]
- Ryan, M.G.; Phillips, N.; Bond, B.J. The hydraulic limitation hypothesis revisited. Plant Cell Environ. 2006, 29, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Norby, R.; Luo, Y. Evaluating ecosystem responses to rising atmospheric CO2 and global warming in a multi-factor world. New Phytol. 2004, 162, 281–293. [Google Scholar] [CrossRef]
- Landsberg, J. Modelling forest ecosystems: State of the art, challenges, and future directions. Can. J. For. Res. 2003, 33, 385–397. [Google Scholar] [CrossRef]
- Liu, J.; Ashton, P.S. Individual-based simulation models for forest succession and management. For. Ecol. Manag. 1995, 73, 157–175. [Google Scholar] [CrossRef]
- Monserud, R.A. Evaluating forest models in a sustainable forest management context. For. Biometry Model. Inf. Sci. 2003, 1, 35–47. [Google Scholar]
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A.; Vanclay, J.K. Tree-Level Models. In Forest Growth and Yield Modeling; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 69–84. [Google Scholar] [CrossRef]
- Lambert, M.C.; Ung, C.H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Ung, C.; Bernier, P.; Guo, X. Canadian national biomass equations: New parameter estimates that include British Columbia data. Can. J. For. Res. 2008, 38, 1123–1132. [Google Scholar] [CrossRef]
- Lamlom, S.H.; Savidge, R.A. A reassessment of carbon content in wood: Variation within and between 41 North American species. Biomass Bioenergy 2003, 25, 381–388. [Google Scholar] [CrossRef]
- Fortin, M.; DeBlois, J. Modeling Tree Recruitment with Zero-Inflated Models: The Example of Hardwood Stands in Southern Québec, Canada. For. Sci. 2007, 53, 529–539. [Google Scholar]
- Lexerød, N.L. Recruitment models for different tree species in Norway. For. Ecol. Manag. 2005, 206, 91–108. [Google Scholar] [CrossRef]
- Li, R.; Weiskittel, A.R.; Kershaw, J.A. Modeling annualized occurrence, frequency, and composition of ingrowth using mixed-effects zero-inflated models and permanent plots in the Acadian Forest Region of North America. Can. J. For. Res. 2011, 41, 2077–2089. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modelling regeneration and recruitment in a tropical rain forest. Can. J. For. Res. 1992, 22, 1235–1248. [Google Scholar] [CrossRef]
- Coops, N.C.; Waring, R.H. Estimating the vulnerability of fifteen tree species under changing climate in Northwest North America. Ecol. Model. 2011, 222, 2119–2129. [Google Scholar] [CrossRef]
- McKenney, D.W.; Pedlar, J.H.; Lawrence, K.; Campbell, K.; Hutchinson, M.F. Potential Impacts of Climate Change on the Distribution of North American Trees. BioScience 2007, 57, 939–948. [Google Scholar] [CrossRef]
- Nitschke, C.R.; Innes, J.L. A tree and climate assessment tool for modelling ecosystem response to climate change. Ecol. Model. 2008, 210, 263–277. [Google Scholar] [CrossRef]
- Worrall, J.J.; Rehfeldt, G.E. Recent declines of Populus tremuloides in North America linked to climate. For. Ecol. Manag. 2013, 299, 35–51. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. A basal area increment model for individual trees growing in even- and uneven-aged forest stands in Austria. For. Ecol. Manag. 1996, 80, 57–80. [Google Scholar] [CrossRef]
- Pretzsch, H.; Biber, P. Size-symmetric versus size-asymmetric competition and growth partitioning among trees in forest stands along an ecological gradient in central Europe. Can. J. For. Res. 2010, 40, 370–384. [Google Scholar] [CrossRef]
- Woods, A.J.; Heppner, D.; Kope, H.H.; Burleigh, J.; Maclauchlan, L. Forest health and climate change: A British Columbia perspective. For. Chron. 2010, 86, 412–422. [Google Scholar] [CrossRef]
- Kurz, W.A.; Dymond, C.C.; White, T.M.; Stinson, G.; Shaw, C.H.; Rampley, G.J.; Smyth, C.; Simpson, B.N.; Neilson, E.T.; Trofymow, J.A.; et al. CBM-CFS3: A model of carbon-dynamics in forestry and land-use change implementing IPCC standards. Ecol. Model. 2009, 220, 480–504. [Google Scholar] [CrossRef]
- Li, Z.; Kurz, W.; Apps, M.; Beukema, S. Belowground biomass dynamics in the Carbon Budget Model of the Canadian Forest Sector: Recent improvements and implications for the estimation of NPP and NEP. Can. J. For. Res. 2003, 33, 126–136. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Introductory Econometrics: A Modern Approach, 5th ed.; South-Western Cengage Learning: Mason, OH, USA, 2013. [Google Scholar]
- Stinson, G.; Kurz, W.A.; Smyth, C.E.; Neilson, E.T.; Dymond, C.C.; Metsaranta, J.M.; Boisvenue, C.; Rampley, G.J.; Li, Q.; White, T.M.; et al. An inventory-based analysis of Canada’s managed forest carbon dynamics, 1990 to 2008. Glob. Chang. Biol. 2011, 17, 2227–2244. [Google Scholar] [CrossRef]
- Trofymow, J.; Stinson, G.; Kurz, W. Derivation of a spatially explicit 86-year retrospective carbon budget for a landscape undergoing conversion from old-growth to managed forests on Vancouver Island, BC. For. Ecol. Manag. 2008, 256, 1677–1691. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate elasticity of streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Taylor, T.; Greenlaw, S. Elasticity. In Principles of Economics; OpenStax College: Houston, TX, USA, 2014; Chapter 5; pp. 99–113. [Google Scholar]
- Oliver, C.; Larson, B. Forest Stand Dynamics, 1st ed.; John Wiley and Sons: New York, NY, USA, 1996. [Google Scholar]
- Bormann, F.; Likens, G. Catastrophic disturbance and the steady-state in northern hardwood forests. Am. Sci. 1979, 67, 660–669. [Google Scholar]
- Whittaker, R.H.; Likens, G.E. Primary production: The biosphere and man. Hum. Ecol. 1973, 1, 357–369. [Google Scholar] [CrossRef]
- Wullschleger, S.D.; Post, W.M.; King, A.W. On the potential role for CO2 fertilization effect in forests: Estimates of the biotic growth factor based on 58 controlled-exposure studies. In Biotic Feedbacks in the Global Climatic System: Will the Warming Feed the Warming? Woodwell, G.M., Mackenzie, F.T., Eds.; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Peng, C.; Ma, Z.; Lei, X.; Zhu, Q.; Chen, H.; Wang, W.; Liu, S.; Li, W.; Fang, X.; Zhou, X. A drought-induced pervasive increase in tree mortality across Canada’s boreal forests. Nat. Clim. Chang. 2011, 1, 467–471. [Google Scholar] [CrossRef]
- Van Mantgem, P.J.; Stephenson, N.L.; Byrne, J.C.; Daniels, L.D.; Franklin, J.F.; Fule, P.Z.; Harmon, M.E.; Larson, A.J.; Smith, J.M.; Taylor, A.H.; et al. Widespread increase of tree mortality rates in the Western United States. Science 2009, 323, 521–524. [Google Scholar] [CrossRef] [PubMed]
- Bennett, A.C.; McDowell, N.G.; Allen, C.D.; Anderson-Teixeira, K.J. Larger trees suffer most during drought in forests worldwide. Nat. Plants 2015, 1, 15139. [Google Scholar] [CrossRef] [PubMed]
- D’Amato, A.W.; Bradford, J.B.; Fraver, S.; Palik, B.J. Effects of thinning on drought vulnerability and climate response in north temperate forest ecosystems. Ecol. Appl. 2013, 23, 1735–1742. [Google Scholar] [CrossRef] [PubMed]
- Fernández-de-Uña, L.; Cañellas, I.; Gea-Izquierdo, G. Stand Competition Determines How Different Tree Species Will Cope with a Warming Climate. PLoS ONE 2015, 10, e0122255. [Google Scholar] [CrossRef] [PubMed]
- Young, D.J.N.; Stevens, J.T.; Earles, J.M.; Moore, J.; Ellis, A.; Jirka, A.L.; Latimer, A.M. Long-term climate and competition explain forest mortality patterns under extreme drought. Ecol. Lett. 2017, 20, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Zang, C.; Pretzsch, H.; Rothe, A. Size-dependent responses to summer drought in Scots pine, Norway spruce and common oak. Trees 2012, 26, 557–569. [Google Scholar] [CrossRef]
- Flannigan, M.; Amiro, B.; Logan, K.; Stocks, B.; Wotton, B. Forest fires and climate change in the 21st century. Mitig. Adapt. Strateg. Glob. Chang. 2006, 11, 847–859. [Google Scholar] [CrossRef]
- Woods, A.J.; Coates, K.D.; Watts, M.; Foord, V.; Holtzman, E.I. Warning Signals of Adverse Interactions between Climate Change and Native Stressors in British Columbia Forests. Forests 2017, 8, 280. [Google Scholar] [CrossRef]
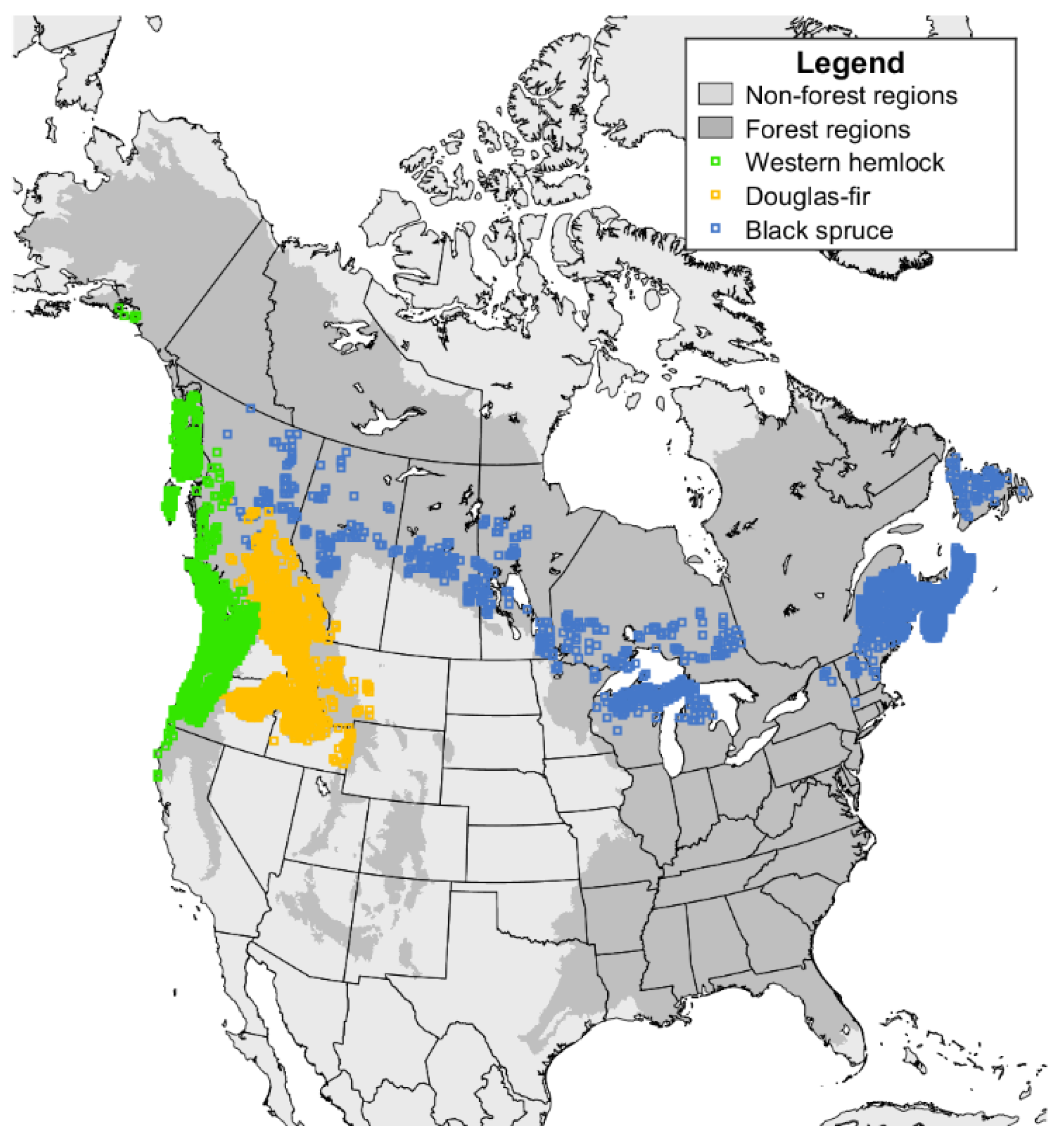
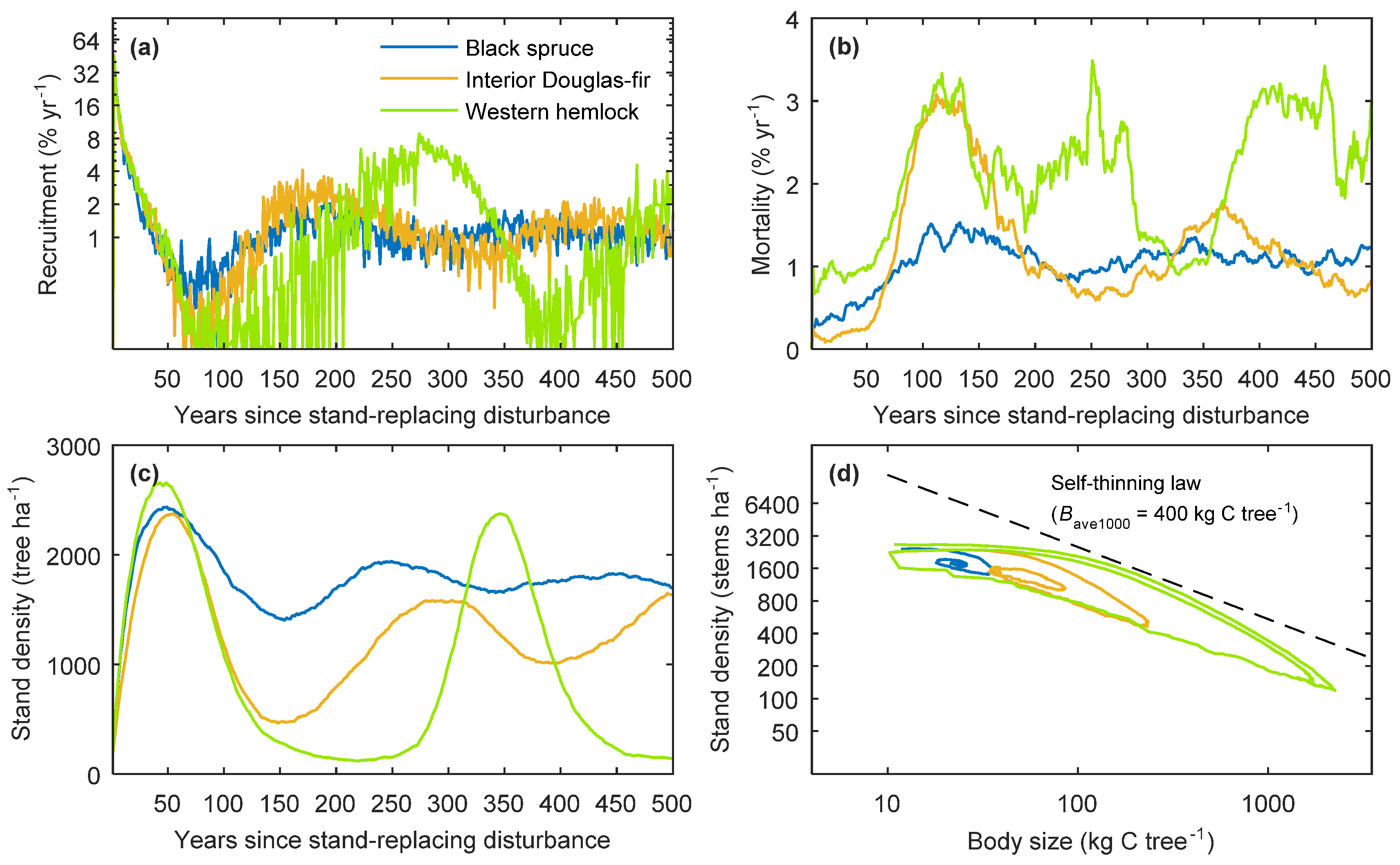
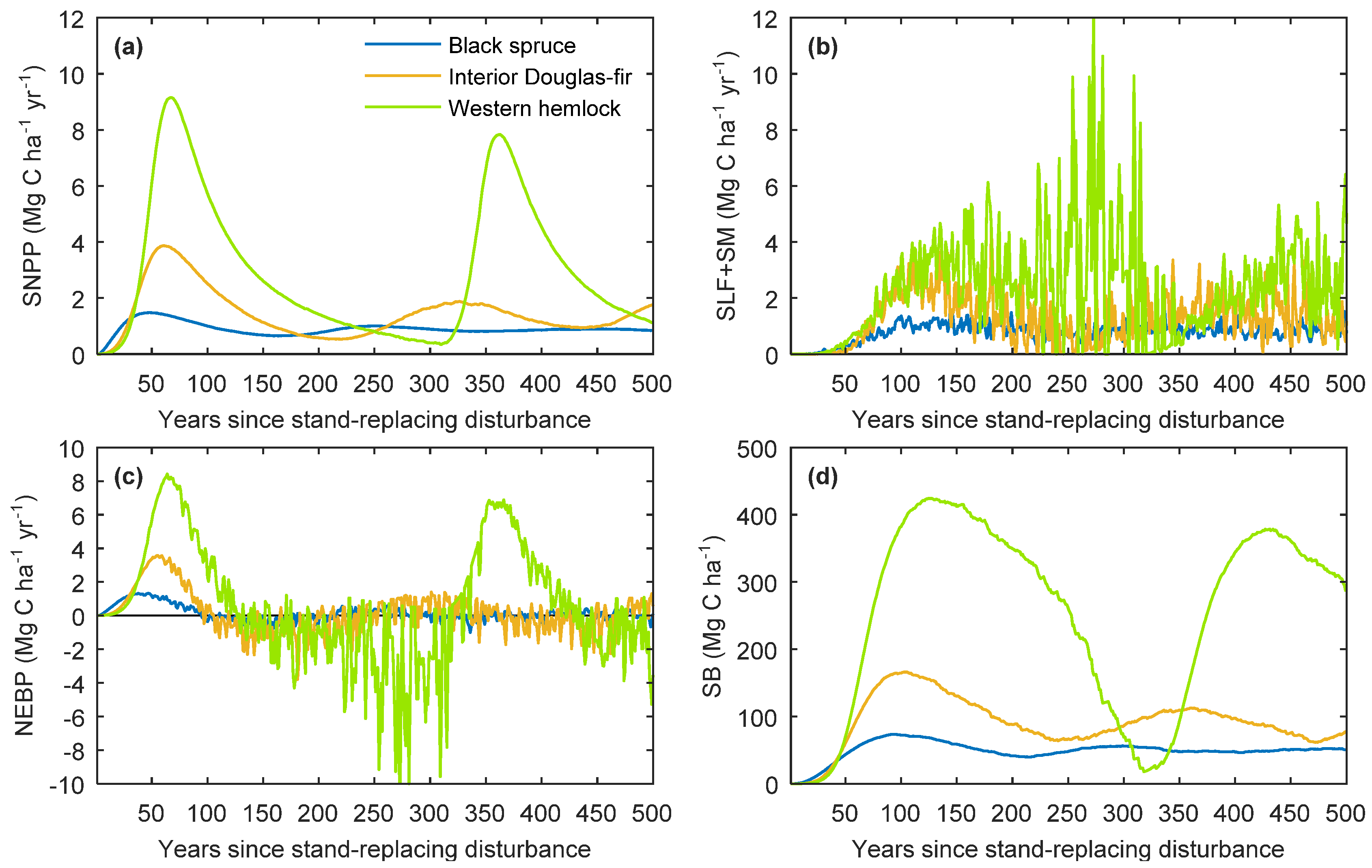
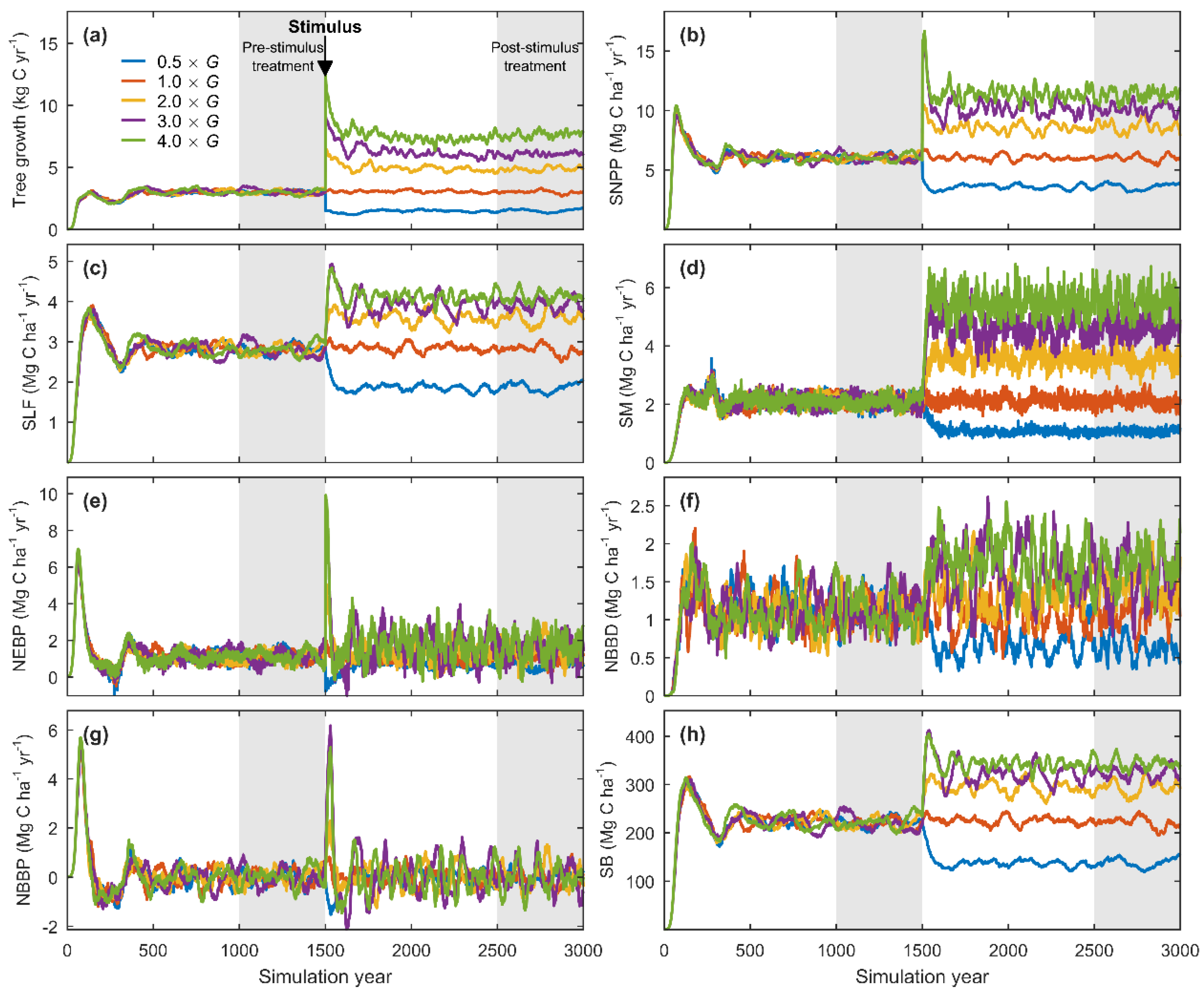
| Statistic | Black Spruce | Interior Douglas-Fir | Western Hemlock |
|---|---|---|---|
| Num. plots | 8206 | 5779 | 8024 |
| Num. observations | 304,850 | 335,518 | 436,053 |
| Time 1st percentile | 1965 | 1962 | 1947 |
| Time mean | 1992 | 1986 | 1982 |
| Time 99st percentile | 2012 | 2015 | 2013 |
| MAT 1st percentile | −3.4 | 1.3 | 3.4 |
| MAT mean | 1.8 | 5.2 | 8.0 |
| MAT 99st percentile | 6.9 | 8.8 | 10.5 |
| Wws 1st percentile | 45 | 8 | 65 |
| Wws mean | 175 | 59 | 163 |
| Wws 99st percentile | 200 | 183 | 200 |
| SA 1st percentile | 10 | 24 | 11 |
| SA mean | 71 | 74 | 45 |
| SA 99st percentile | 173 | 185 | 190 |
| Statistic | Black Spruce | Interior Douglas-Fir | Western Hemlock |
|---|---|---|---|
| a0 | −4.470 (0.014) | −6.020 (0.024) | −5.463 (0.029) |
| a1 | −0.901 (0.009) | −0.991 (0.007) | −1.600 (0.014) |
| Mean predicted Pr (Cond.) (% year−1) | 1.94 | 1.77 | 1.31 |
| Mean predicted Pr (Marg.) (% year−1) | 1.53 | 0.72 | 1.00 |
| AUC (Cond.) | 0.87 | 0.82 | 0.75 |
| AUC (Marg.) | 0.72 | 0.73 | 0.75 |
| Statistic | Black Spruce | Interior Douglas-Fir | Western Hemlock |
|---|---|---|---|
| b0 | −4.556 (0.014) | −4.194 (0.021) | −4.846 (0.024) |
| b1 | 0.090 (0.008) | −0.289 (0.010) | −0.068 (0.017) |
| b2 | −0.052 (0.009) | 0.163 (0.006) | 0.183 (0.010) |
| b3 | 0.331 (0.012) | 0.083 (0.011) | 0.040 (0.013) |
| b4 | 0.177 (0.012) | 0.642 (0.008) | 2.547 (0.019) |
| b5 | 0.131 (0.015) | 0.451 (0.010) | −2.217 (0.023) |
| Mean predicted Pm (Cond.) (% year−1) | 1.12 | 1.70 | 1.89 |
| Mean predicted Pm (Marg.) (% year−1) | 1.17 | 2.50 | 1.38 |
| AUC (Cond.) | 0.82 | 0.81 | 0.83 |
| AUC (Marg.) | 0.68 | 0.62 | 0.73 |
| Statistic | Black Spruce | Interior Douglas-Fir | Western Hemlock |
|---|---|---|---|
| c0 | −0.839 (0.008) | 0.343 (0.008) | 0.529 (0.010) |
| c1 | 0.492 (0.003) | 1.092 (0.002) | 1.556 (0.002) |
| c2 | −0.031 (0.002) | −0.198 (0.002) | −0.259 (0.001) |
| c3 | −0.127 (0.004) | −0.198 (0.005) | −0.030 (0.005) |
| c4 | −0.278 (0.003) | −0.487 (0.002) | −0.646 (0.003) |
| c5 | −0.060 (0.005) | −0.051 (0.004) | −0.135 (0.004) |
| Mean predicted Gag (Cond.) | 0.52 | 2.35 | 3.47 |
| Mean predicted Gag (Marg.) | 0.50 | 2.41 | 3.88 |
| MEC (Cond.) | 0.60 | 0.80 | 0.80 |
| MEC (Marg.) | 0.23 | 0.61 | 0.65 |
| Statistic | Pre-Stim. Mean | Post-Stim. Mean | Δ | Response Ratio | εG,X | p-Value |
|---|---|---|---|---|---|---|
| Tree growth (kg C tree−1 year−1) | ||||||
| Black spruce | 0.36 | 0.72 | 0.35 | 1.98 | N.A. | <0.001 |
| Interior Douglas-fir | 0.79 | 1.61 | 0.83 | 2.05 | N.A. | <0.001 |
| Western hemlock | 2.99 | 4.86 | 1.87 | 1.63 | N.A. | <0.001 |
| Mean | 1.38 | 2.40 | 1.02 | 1.89 | N.A. | <0.001 |
| Stand net primary production (Mg C ha−1 year−1) | ||||||
| Black spruce | 2.87 | 3.74 | 0.87 | 1.30 | 0.31 | <0.001 |
| Interior Douglas-fir | 2.94 | 4.00 | 1.05 | 1.36 | 0.34 | <0.001 |
| Western hemlock | 6.01 | 8.63 | 2.62 | 1.44 | 0.70 | <0.001 |
| Mean | 3.94 | 5.45 | 1.51 | 1.37 | 0.45 | <0.001 |
| Stand litterfall (Mg C ha−1 year−1) | ||||||
| Black spruce | 1.95 | 2.24 | 0.29 | 1.15 | 0.15 | <0.001 |
| Interior Douglas-fir | 1.35 | 1.57 | 0.22 | 1.16 | 0.16 | <0.001 |
| Western hemlock | 2.78 | 3.60 | 0.82 | 1.29 | 0.47 | <0.001 |
| Mean | 2.03 | 2.47 | 0.44 | 1.20 | 0.26 | <0.001 |
| Stand mortality (Mg C ha−1 year−1) | ||||||
| Black spruce | 0.71 | 1.18 | 0.47 | 1.65 | 0.66 | <0.001 |
| Interior Douglas-fir | 1.16 | 1.82 | 0.67 | 1.58 | 0.55 | <0.001 |
| Western hemlock | 2.06 | 3.55 | 1.48 | 1.72 | 1.15 | <0.001 |
| Mean | 1.31 | 2.18 | 0.87 | 1.65 | 0.79 | <0.001 |
| Stand biomass density (Mg C ha−1) | ||||||
| Black spruce | 47 | 66 | 19 | 1.41 | 0.41 | <0.001 |
| Interior Douglas-fir | 88 | 118 | 30 | 1.34 | 0.33 | <0.001 |
| Western hemlock | 219 | 294 | 75 | 1.34 | 0.55 | <0.001 |
| Mean | 118 | 159 | 41 | 1.36 | 0.43 | <0.001 |
| Stand density (tree ha−1) | ||||||
| Black spruce | 1802 | 1338 | −463 | 0.74 | −0.26 | <0.001 |
| Interior Douglas-fir | 1301 | 806 | −495 | 0.62 | −0.36 | <0.001 |
| Western hemlock | 1168 | 815 | −353 | 0.70 | −0.48 | <0.001 |
| Mean | 1424 | 986 | −437 | 0.69 | −0.37 | <0.001 |
| Residence time, ecosystem (years) | ||||||
| Black spruce | 65.5 | 55.7 | −9.8 | 0.85 | −0.15 | <0.001 |
| Interior Douglas-fir | 75.9 | 64.6 | −11.3 | 0.85 | −0.14 | <0.001 |
| Western hemlock | 106.1 | 82.9 | −23.2 | 0.78 | −0.35 | <0.001 |
| Mean | 82.5 | 67.7 | −14.7 | 0.83 | −0.21 | <0.001 |
| Residence time, biome (years) | ||||||
| Black spruce | 50.2 | 43.5 | −6.7 | 0.87 | −0.14 | <0.001 |
| Interior Douglas-fir | 55.3 | 48.6 | -6.7 | 0.88 | −0.11 | <0.001 |
| Western hemlock | 68.5 | 58.7 | −9.8 | 0.86 | −0.23 | <0.001 |
| Mean | 58.0 | 50.3 | −7.7 | 0.87 | −0.16 | <0.001 |
| Statistic | 50% Below Contemporary | Contemporary | Δ | Response Ratio | εG,X | p-Value |
|---|---|---|---|---|---|---|
| Tree growth (kg C tree−1 year−1) | ||||||
| Black spruce | 0.17 | 0.36 | 0.19 | 2.17 | N.A. | <0.001 |
| Interior Douglas-fir | 0.32 | 0.79 | 0.47 | 2.47 | N.A. | <0.001 |
| Western hemlock | 1.51 | 3.01 | 1.51 | 2.00 | N.A. | <0.001 |
| Mean | 0.66 | 1.39 | 0.72 | 2.21 | N.A. | <0.001 |
| Stand net primary production (Mg C ha−1 year−1) | ||||||
| Black spruce | 1.96 | 2.86 | 0.91 | 1.46 | 0.59 | <0.001 |
| Interior Douglas-fir | 1.96 | 2.95 | 0.99 | 1.50 | 0.56 | <0.001 |
| Western hemlock | 3.60 | 6.01 | 2.41 | 1.67 | 0.80 | <0.001 |
| Mean | 2.51 | 3.94 | 1.43 | 1.54 | 0.65 | <0.001 |
| Stand litterfall (Mg C ha−1 year−1) | ||||||
| Black spruce | 1.45 | 1.94 | 0.49 | 1.34 | 0.47 | <0.001 |
| Interior Douglas-fir | 1.10 | 1.36 | 0.25 | 1.23 | 0.31 | <0.001 |
| Western hemlock | 1.87 | 2.80 | 0.93 | 1.50 | 0.67 | <0.001 |
| Mean | 1.47 | 2.03 | 0.56 | 1.35 | 0.48 | <0.001 |
| Stand mortality (Mg C ha−1 year−1) | ||||||
| Black spruce | 0.36 | 0.69 | 0.33 | 1.91 | 0.88 | <0.001 |
| Interior Douglas-fir | 0.60 | 1.17 | 0.57 | 1.96 | 0.82 | <0.001 |
| Western hemlock | 1.06 | 2.08 | 1.02 | 1.96 | 0.98 | <0.001 |
| Mean | 0.67 | 1.31 | 0.64 | 1.94 | 0.89 | <0.001 |
| Stand biomass density (Mg C ha−1) | ||||||
| Black spruce | 28 | 46 | 18 | 1.66 | 0.74 | <0.001 |
| Interior Douglas-fir | 54 | 88 | 35 | 1.64 | 0.66 | <0.001 |
| Western hemlock | 138 | 221 | 83 | 1.60 | 0.75 | <0.001 |
| Mean | 73 | 118 | 45 | 1.64 | 0.72 | <0.001 |
| Stand density (tree ha−1) | ||||||
| Black spruce | 2246 | 1810 | −436 | 0.81 | −0.45 | <0.001 |
| Interior Douglas-fir | 1933 | 1297 | −636 | 0.67 | −0.82 | <0.001 |
| Western hemlock | 1582 | 1158 | −424 | 0.73 | −0.73 | <0.001 |
| Mean | 1920 | 1422 | −499 | 0.74 | −0.67 | <0.001 |
| Residence time, ecosystem (years) | ||||||
| Black spruce | 76.2 | 66.3 | −9.9 | 0.87 | −0.11 | <0.001 |
| Interior Douglas-fir | 90.1 | 75.7 | −14.4 | 0.84 | −0.11 | <0.001 |
| Western hemlock | 129.9 | 106.0 | −23.9 | 0.82 | −0.18 | <0.001 |
| Mean | 98.7 | 82.7 | −16.1 | 0.84 | −0.13 | <0.001 |
| Residence time, biome (years) | ||||||
| Black spruce | 54.5 | 49.2 | −5.3 | 0.90 | −0.08 | <0.001 |
| Interior Douglas-fir | 62.4 | 55.7 | −6.7 | 0.89 | −0.07 | <0.001 |
| Western hemlock | 81.7 | 68.8 | −12.9 | 0.84 | −0.16 | <0.001 |
| Mean | 66.2 | 57.9 | −8.3 | 0.88 | −0.10 | <0.001 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hember, R.A.; Kurz, W.A. Low Tree-Growth Elasticity of Forest Biomass Indicated by an Individual-Based Model. Forests 2018, 9, 21. https://doi.org/10.3390/f9010021
Hember RA, Kurz WA. Low Tree-Growth Elasticity of Forest Biomass Indicated by an Individual-Based Model. Forests. 2018; 9(1):21. https://doi.org/10.3390/f9010021
Chicago/Turabian StyleHember, Robbie A., and Werner A. Kurz. 2018. "Low Tree-Growth Elasticity of Forest Biomass Indicated by an Individual-Based Model" Forests 9, no. 1: 21. https://doi.org/10.3390/f9010021
APA StyleHember, R. A., & Kurz, W. A. (2018). Low Tree-Growth Elasticity of Forest Biomass Indicated by an Individual-Based Model. Forests, 9(1), 21. https://doi.org/10.3390/f9010021





