Tropical-Forest Structure and Biomass Dynamics from TanDEM-X Radar Interferometry
Abstract
:1. Introduction
2. Materials and Methods
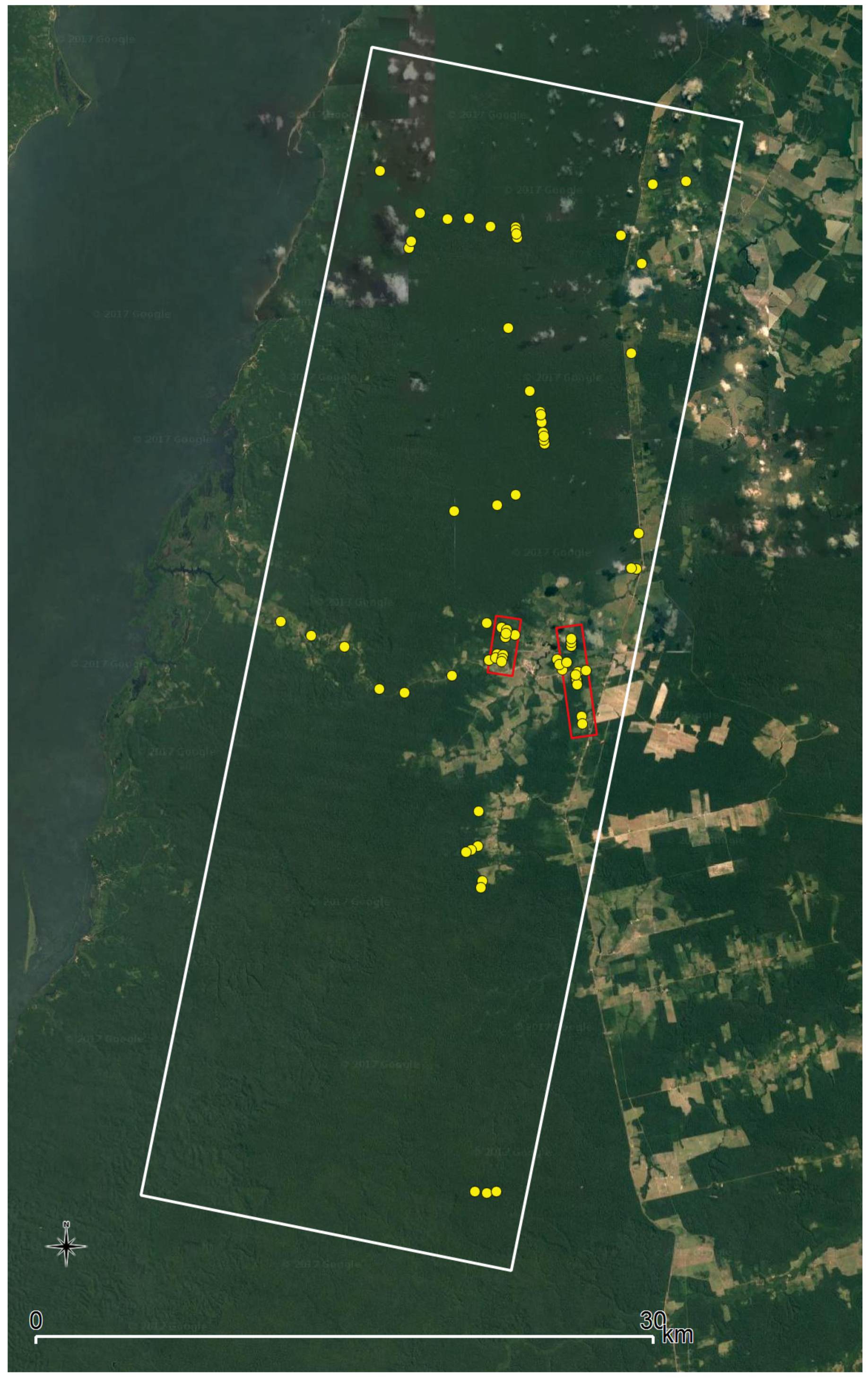
2.1. Tapajós National Forest and Field Measurements
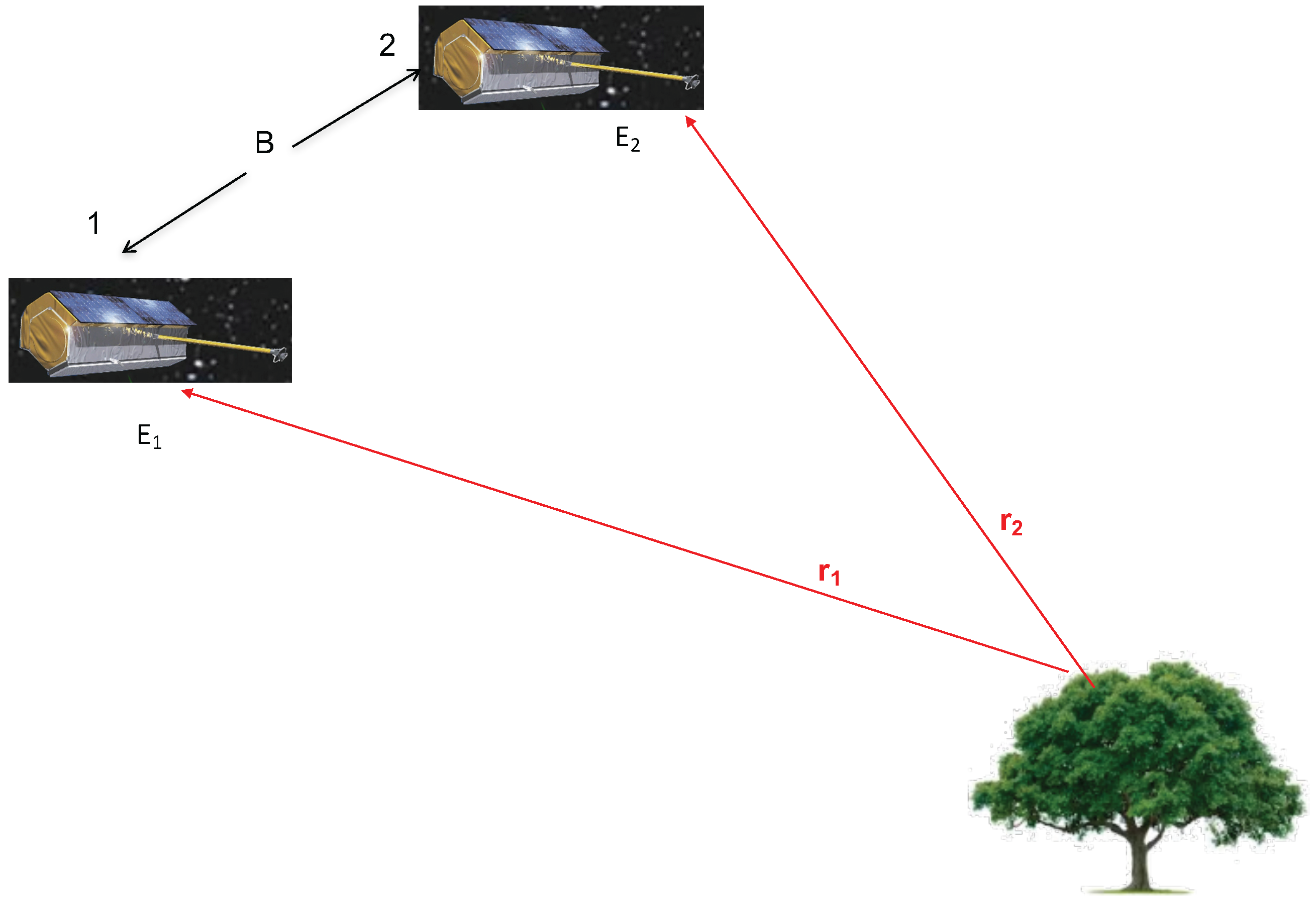
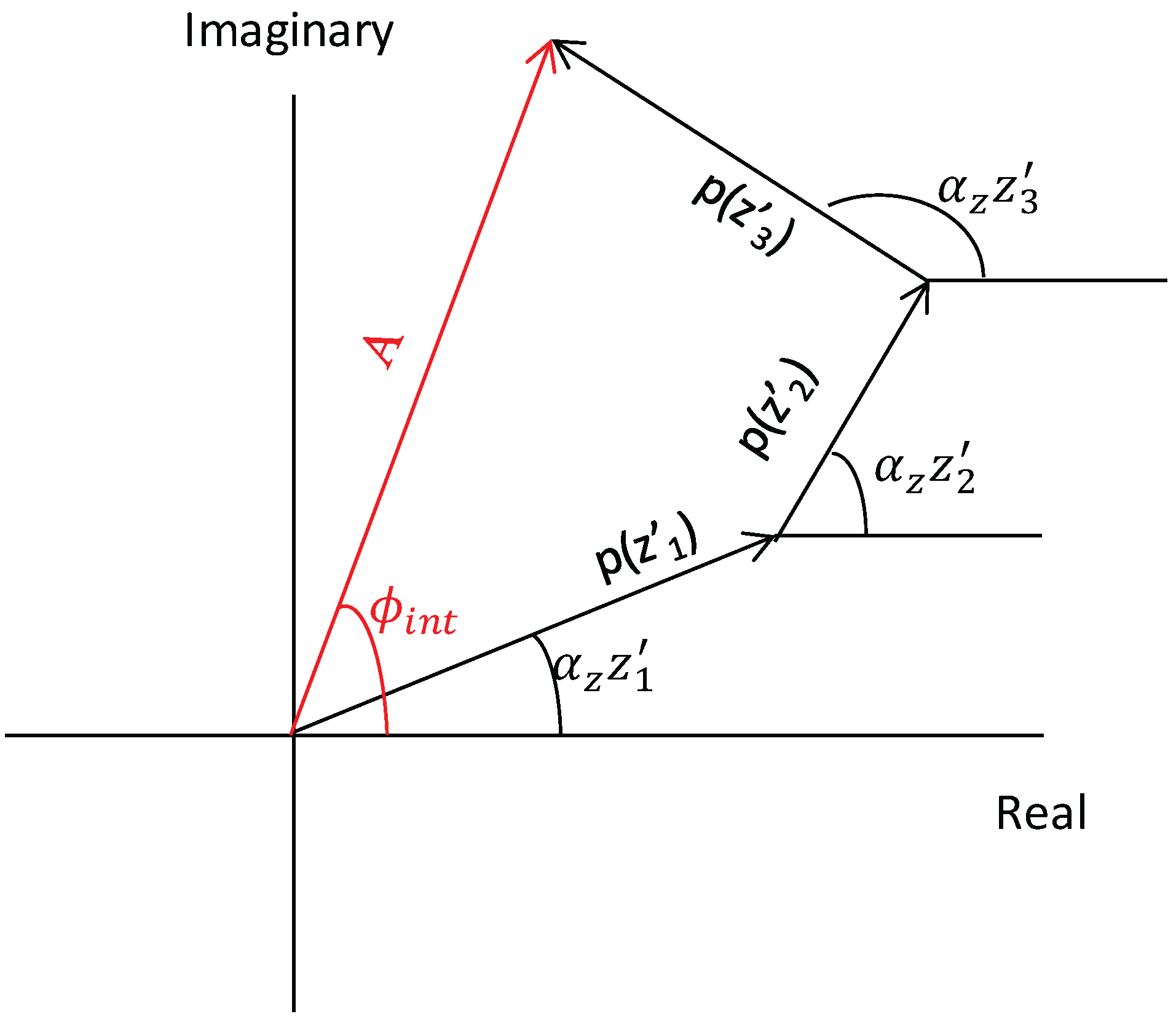
2.2. TanDEM-X, The Interferometric Phase-Height and Its Relation to Radar Power Vertical Profiles
2.3. The Relationship of Phase-Height to Mean Canopy Height and AGB
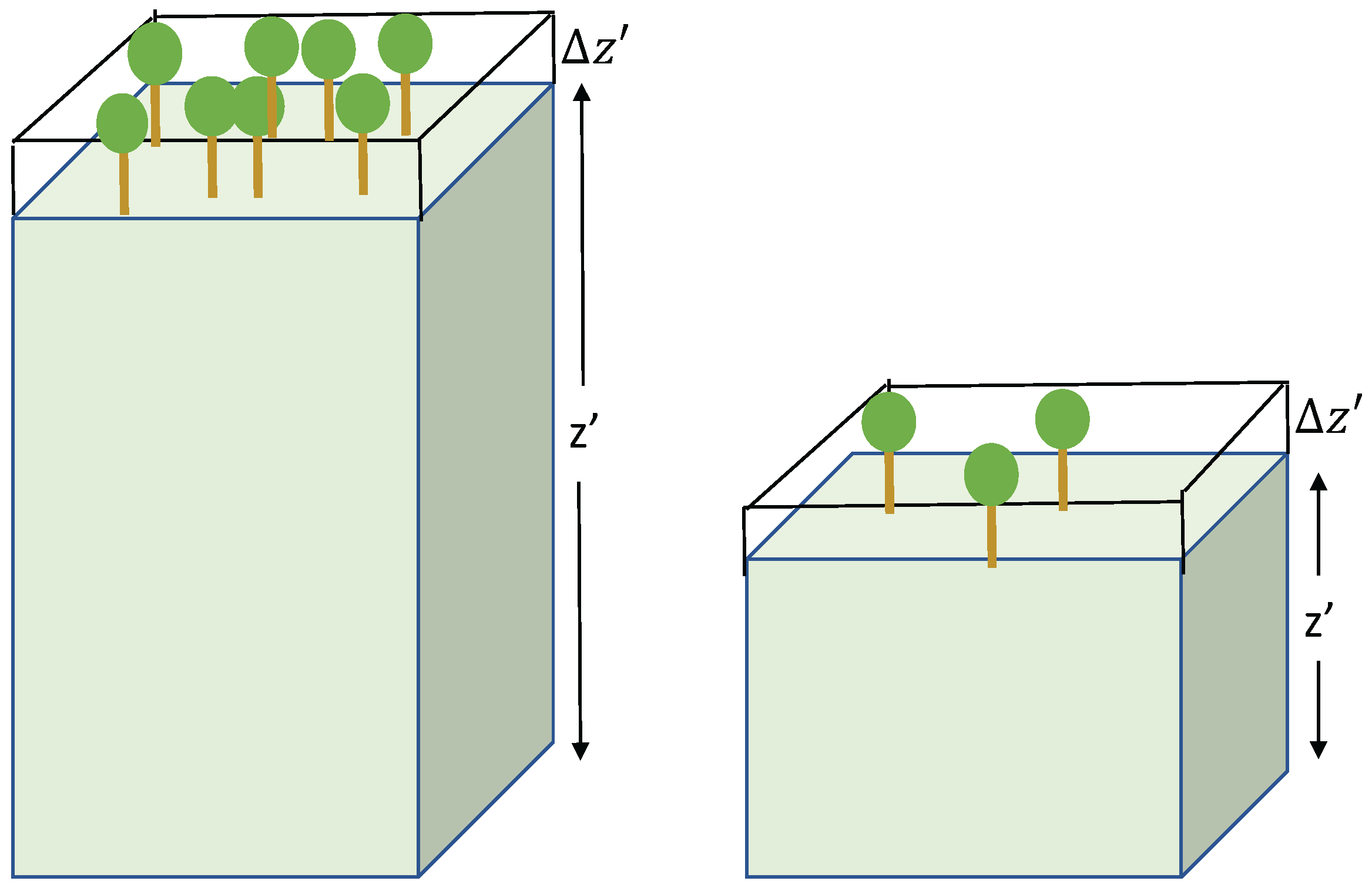
2.3.1. Qualitative Relationship Between Phase-Height and Mean Canopy Height
2.3.2. Quantitative Relationship Between Phase-Height and Mean Canopy Height: Conditions for Equality
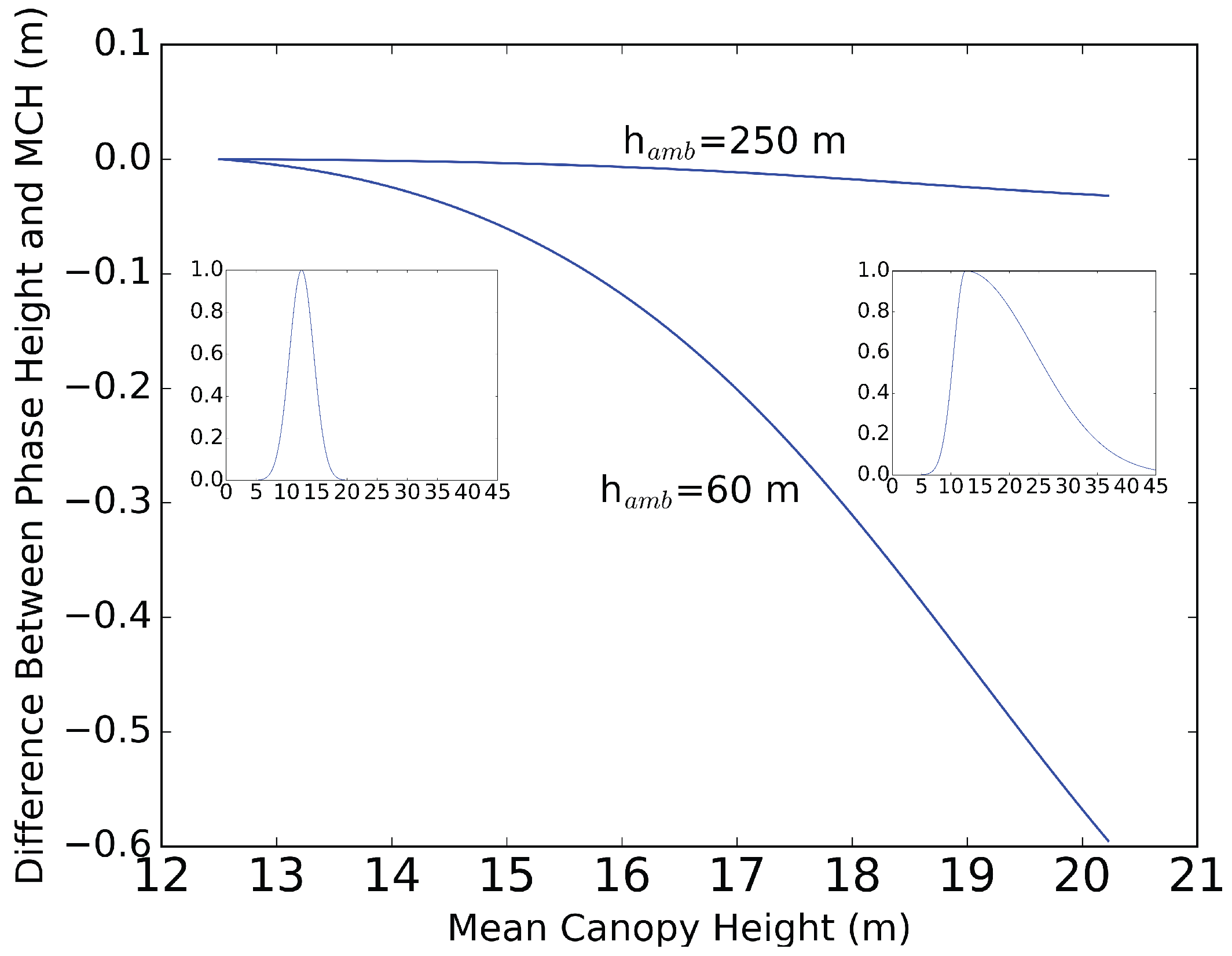
2.3.3. Quantitative Relationship: The Magnitude of Differences Between Phase-Height and Mean Canopy Height
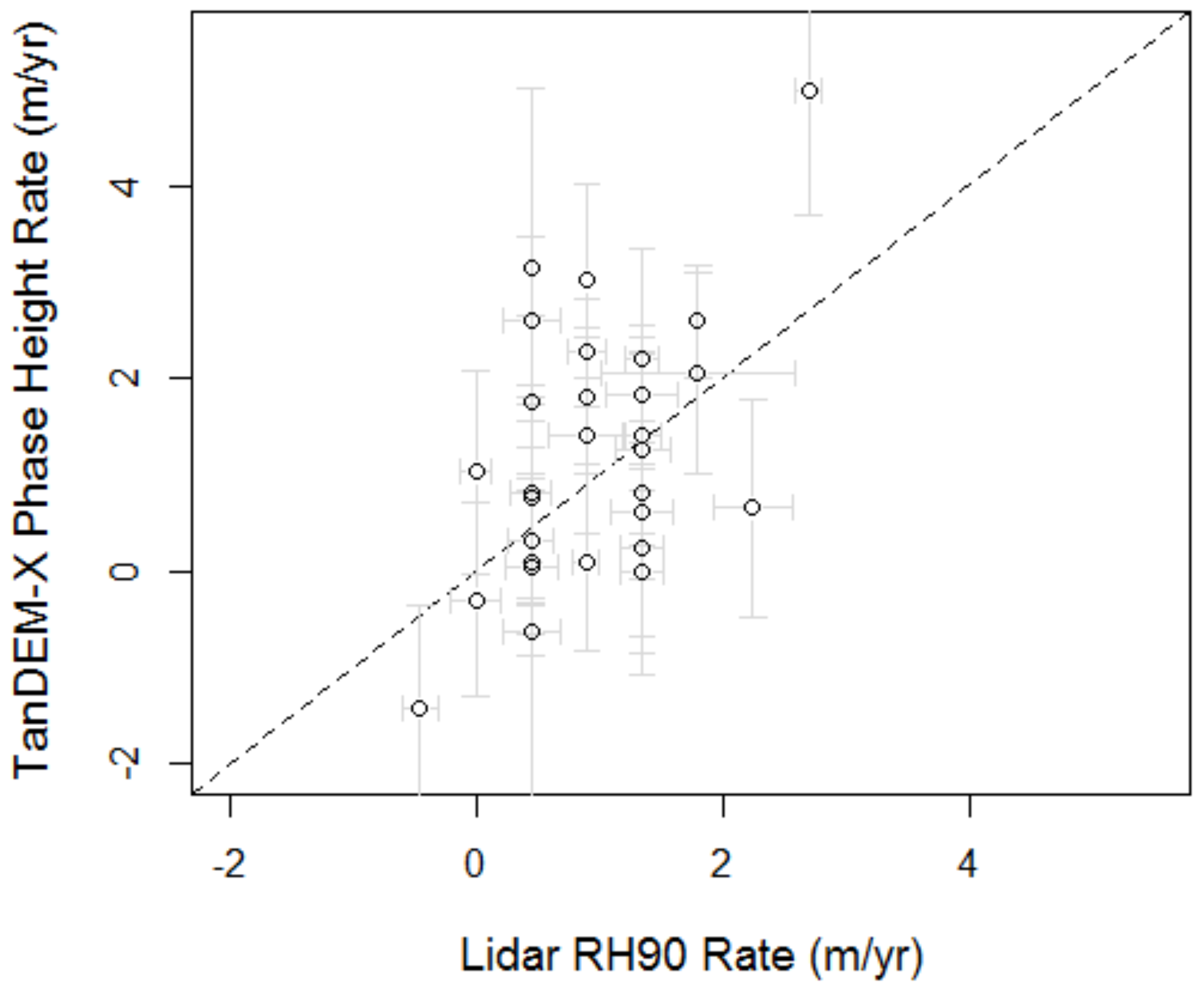
2.4. LiDAR Data for Phase-Height Rate Verification
3. Results: Time Series of Phase-Height and Aboveground Biomass
3.1. Phase-Height Rate from Raw Interferometric SAR Data
3.2. Removal of Systematic Trends in Phase-Height Data
3.3. Phase-Height Time Series and Rates
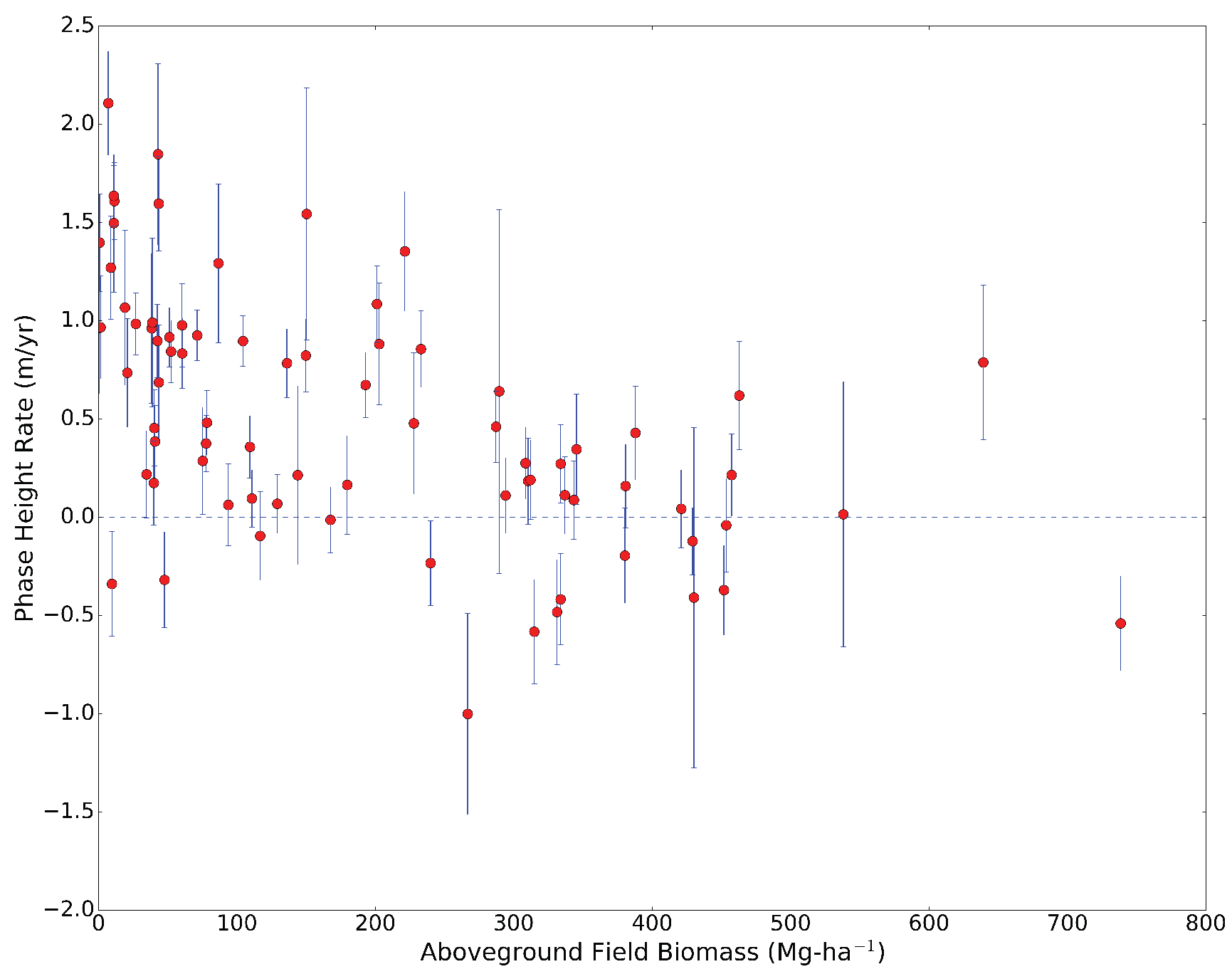
3.4. From Phase-Height Rate to AGB Rate
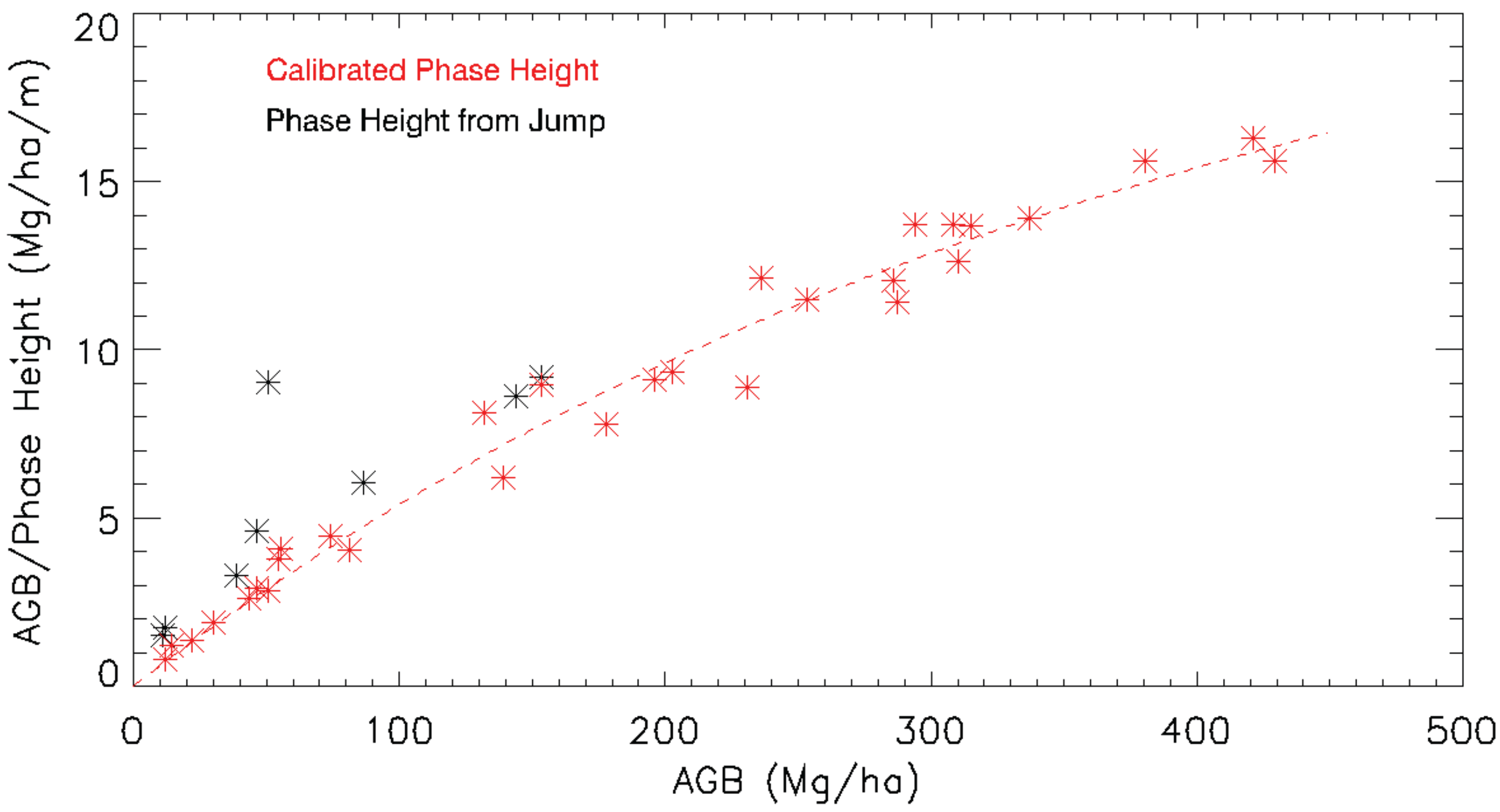
3.4.1. Model for Deriving Phase-Height-Rate to AGB Rate Conversion Factors
3.4.2. Applying Conversion Factors to Estimate AGB Rate
3.4.3. The Relative Accuracy of Single-Epoch and Differential (Rate) AGB Estimates
4. Discussion
4.1. X-Band Interferometry for Tropical-Forest Structure and Biomass
4.2. Using Phase-Height to Measure Tropical Forest Dynamics
4.3. The Performance of Phase-Height and AGB Rate and Future Enhancements
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| 1 | 2011 | 9 | 22 | 73.400 |
| 2 | 2011 | 6 | 15 | 57.900 |
| 3 | 2011 | 8 | 20 | 70.400 |
| 4 | 2011 | 10 | 14 | 83.000 |
| 5 | 2011 | 12 | 8 | 153.700 |
| 6 | 2011 | 12 | 30 | 154.400 |
| 7 | 2012 | 1 | 21 | 249.900 |
| 8 | 2012 | 2 | 12 | 252.500 |
| 9 | 2012 | 3 | 16 | 260.700 |
| 10 | 2012 | 3 | 27 | 246.500 |
| 11 | 2012 | 10 | 22 | 47.100 |
| 12 | 2012 | 11 | 2 | 49.300 |
| 13 | 2012 | 12 | 5 | 60.700 |
| 14 | 2013 | 3 | 25 | 194.200 |
| 15 | 2013 | 5 | 30 | 80.700 |
| 16 | 2013 | 7 | 13 | 117.300 |
| 17 | 2013 | 8 | 4 | 130.600 |
| 18 | 2013 | 8 | 26 | 72.500 |
| 19 | 2013 | 9 | 6 | 84.400 |
| 20 | 2013 | 9 | 28 | 95.000 |
| 21 | 2013 | 12 | 3 | 196.500 |
| 22 | 2013 | 12 | 14 | 169.300 |
| 23 | 2014 | 1 | 5 | 93.900 |
| 24 | 2014 | 2 | 7 | 71.300 |
| 25 | 2014 | 4 | 14 | 128.600 |
| 26 | 2014 | 5 | 6 | 83.300 |
| 27 | 2014 | 5 | 17 | 78.800 |
| 28 | 2014 | 5 | 28 | 78.900 |
| 29 | 2014 | 6 | 30 | 65.600 |
| 30 | 2014 | 7 | 22 | 69.500 |
| 31 | 2014 | 8 | 2 | 77.400 |
| 32 | 2014 | 9 | 15 | 134.300 |
| 1 | −3.130910 | −54.953098 | 0.454607 | 0.193582 | 0.000000 | 0.000 | 0.965 | 40.400 | |
| 2 | −3.133010 | −54.952702 | 0.784603 | 0.174644 | 0.000000 | 0.000 | 1.071 | 136.200 | |
| 3 | −3.133860 | −54.952599 | 0.068583 | 0.149540 | 0.000000 | 0.000 | 0.905 | 129.100 | |
| 4 | −3.027960 | −54.967098 | 0.856066 | 0.194395 | 0.000000 | 0.000 | 1.237 | 233.000 | |
| 5 | −3.029510 | −54.966900 | 0.478339 | 0.359500 | 0.000000 | 0.000 | 2.319 | 227.800 | |
| 6 | −3.024850 | −54.967499 | 0.110787 | 0.191887 | 0.000000 | 0.000 | 1.210 | 294.100 | |
| 7 | −3.020170 | −54.968201 | −0.194923 | 0.241532 | 0.000000 | 0.000 | 1.540 | 380.300 | |
| 8 | −2.937600 | −54.979401 | −0.581948 | 0.265151 | 0.000000 | 0.000 | 1.854 | 314.800 | |
| 9 | −2.936040 | −54.979599 | 0.275688 | 0.182756 | 0.000000 | 0.000 | 0.767 | 308.500 | |
| 10 | −2.934480 | −54.979801 | 0.043263 | 0.198722 | 0.000000 | 0.000 | 1.083 | 421.000 | |
| 11 | −2.939160 | −54.979198 | 0.112345 | 0.196660 | 0.000000 | 0.000 | 1.126 | 336.900 | |
| 12 | −3.026400 | −54.967300 | 0.673636 | 0.166502 | 0.000000 | 0.000 | 1.021 | 193.000 | |
| 13 | −3.017020 | −54.968601 | 0.460963 | 0.181941 | 0.000000 | 0.000 | 0.900 | 287.200 | |
| 14 | −3.135420 | −54.952400 | 0.481861 | 0.163645 | 0.000000 | 0.000 | 1.022 | 78.400 | |
| 15 | −3.015530 | −54.968899 | −0.121053 | 0.171038 | 0.000000 | 0.000 | 0.907 | 429.200 | |
| 16 | −3.152580 | −54.950001 | 1.543710 | 0.641120 | 2013.880371 | −17.113 | 1.947 | 150.400 | * |
| 17 | −3.149420 | −54.950401 | 0.844270 | 0.158688 | 0.000000 | 0.000 | 0.967 | 52.400 | |
| 18 | −3.115120 | −54.955200 | 0.686952 | 0.292748 | 2013.848145 | −8.752 | 1.093 | 43.600 | * |
| 19 | −3.116720 | −54.955002 | 0.926217 | 0.129313 | 0.000000 | 0.000 | 0.732 | 71.300 | |
| 20 | −3.118330 | −54.955002 | 0.184325 | 0.219348 | 0.000000 | 0.000 | 1.287 | 310.400 | |
| 21 | −3.112970 | −54.983601 | 1.270890 | 0.263002 | 2014.181519 | −8.050 | 1.278 | 8.900 | * |
| 22 | −3.114550 | −54.983799 | 1.067040 | 0.394613 | 2014.178345 | −6.581 | 1.057 | 19.100 | * |
| 23 | −3.111410 | −54.983299 | 1.609308 | 0.195239 | 0.000000 | 0.000 | 0.980 | 11.500 | |
| 24 | −3.125350 | −54.985401 | −0.317946 | 0.243731 | 2011.947632 | −5.442 | 0.814 | 47.800 | * |
| 25 | −3.123850 | −54.985100 | 0.984695 | 0.157564 | 0.000000 | 0.000 | 0.887 | 27.000 | |
| 26 | −3.122300 | −54.984901 | 0.916722 | 0.151511 | 0.000000 | 0.000 | 1.032 | 51.300 | |
| 27 | −3.056510 | −54.987499 | 0.640870 | 0.925907 | 0.000000 | 0.000 | 7.166 | 289.500 | |
| 28 | −2.930880 | −55.000099 | 0.345566 | 0.280541 | 0.000000 | 0.000 | 1.733 | 345.300 | |
| 29 | −2.943690 | −55.026299 | 1.353852 | 0.304138 | 0.000000 | 0.000 | 2.226 | 221.400 | |
| 30 | −2.934300 | −54.990601 | −0.417227 | 0.232297 | 0.000000 | 0.000 | 1.487 | 333.800 | |
| 31 | −3.124310 | −54.961102 | 1.397861 | 0.248493 | 0.000000 | 0.000 | 1.170 | 0.800 | |
| 32 | −3.128890 | −54.958900 | 0.961846 | 0.381249 | 2013.832886 | −10.488 | 1.304 | 38.500 | * |
| 33 | −3.110410 | −54.985600 | 2.107846 | 0.264627 | 0.000000 | 0.000 | 1.351 | 7.100 | |
| 34 | −3.357990 | −54.996601 | 0.087855 | 0.199023 | 0.000000 | 0.000 | 1.117 | 343.500 | |
| 35 | −3.358430 | −54.991402 | −0.040254 | 0.238347 | 0.000000 | 0.000 | 1.517 | 453.500 | |
| 36 | −3.358000 | −54.987400 | 0.272680 | 0.199662 | 0.000000 | 0.000 | 1.397 | 333.800 | |
| 37 | −3.138950 | −55.027802 | 0.882286 | 0.309965 | 0.000000 | 0.000 | 2.096 | 202.800 | |
| 38 | −3.118990 | −55.054199 | 1.847912 | 0.461109 | 0.000000 | 0.000 | 3.334 | 43.100 | |
| 39 | −3.107810 | −55.081902 | 0.964537 | 0.335342 | 0.000000 | 0.000 | 1.565 | 0.700 | |
| 40 | −3.059210 | −55.006500 | −0.233490 | 0.214971 | 0.000000 | 0.000 | 1.457 | 239.900 | |
| 41 | −2.950610 | −54.924702 | −0.095074 | 0.225523 | 0.000000 | 0.000 | 1.462 | 116.800 | |
| 42 | −2.915720 | −54.919899 | 0.966455 | 0.261321 | 0.000000 | 0.000 | 1.521 | 1.500 | |
| 43 | −2.914300 | −54.905399 | 0.218828 | 0.222246 | 0.000000 | 0.000 | 1.151 | 34.700 | |
| 44 | −3.114580 | −54.983799 | 1.497180 | 0.350418 | 2014.177979 | −7.178 | 1.100 | 11.100 | |
| 45 | −3.133010 | −54.952702 | 0.823535 | 0.186343 | 0.000000 | 0.000 | 1.141 | 149.800 | |
| 46 | −3.130910 | −54.953098 | 0.385443 | 0.184383 | 0.000000 | 0.000 | 0.941 | 40.800 | |
| 47 | −3.206300 | −54.995602 | 0.619866 | 0.275334 | 0.000000 | 0.000 | 1.619 | 462.900 | |
| 48 | −3.221620 | −54.993801 | 0.215504 | 0.209776 | 0.000000 | 0.000 | 1.290 | 457.400 | |
| 49 | −3.224370 | −54.994202 | 0.788685 | 0.393887 | 0.000000 | 0.000 | 2.555 | 639.200 | |
| 50 | −3.116710 | −54.955002 | 0.896724 | 0.129154 | 0.000000 | 0.000 | 0.811 | 104.400 | |
| 51 | −3.118320 | −54.955002 | 0.159074 | 0.213723 | 0.000000 | 0.000 | 1.219 | 380.800 | |
| 52 | −3.122100 | −54.987598 | 1.292980 | 0.403824 | 2013.798828 | −15.656 | 1.143 | 86.700 | * |
| 53 | −3.051970 | −54.979401 | 0.429349 | 0.238099 | 0.000000 | 0.000 | 1.541 | 387.900 | |
| 54 | −2.938070 | −54.933800 | −0.013126 | 0.167420 | 0.000000 | 0.000 | 0.954 | 167.600 | |
| 55 | −2.928430 | −55.021599 | 0.164560 | 0.251267 | 0.000000 | 0.000 | 1.638 | 179.700 | |
| 56 | −2.909920 | −55.039001 | 0.095907 | 0.145083 | 0.000000 | 0.000 | 1.026 | 110.800 | |
| 57 | −3.129750 | −54.952301 | 0.174746 | 0.213031 | 0.000000 | 0.000 | 1.100 | 40.000 | |
| 58 | −3.128970 | −54.948700 | 0.834410 | 0.178792 | 0.000000 | 0.000 | 1.095 | 60.500 | |
| 59 | −3.113640 | −54.979599 | 0.897366 | 0.187097 | 0.000000 | 0.000 | 1.158 | 42.600 | |
| 60 | −3.108400 | −54.992100 | 0.735734 | 0.276439 | 0.000000 | 0.000 | 1.719 | 20.900 | |
| 61 | −3.124500 | −54.990898 | −0.338942 | 0.266088 | 0.000000 | 0.000 | 1.441 | 9.700 | |
| 62 | −3.126430 | −54.960098 | 0.063191 | 0.208251 | 0.000000 | 0.000 | 1.489 | 93.800 | |
| 63 | −3.131600 | −55.007099 | 0.358451 | 0.158200 | 0.000000 | 0.000 | 0.972 | 109.400 | |
| 64 | −3.137290 | −55.039001 | −1.000995 | 0.511155 | 0.000000 | 0.000 | 3.598 | 266.800 | |
| 65 | −3.114210 | −55.068699 | 0.991243 | 0.428841 | 0.000000 | 0.000 | 2.641 | 38.900 | |
| 66 | −2.978960 | −54.982899 | −0.481809 | 0.266980 | 0.000000 | 0.000 | 1.697 | 331.300 | |
| 67 | −3.006480 | −54.973301 | 0.190774 | 0.202528 | 0.000000 | 0.000 | 1.307 | 312.100 | |
| 68 | −2.989900 | −54.929199 | 1.636473 | 0.153530 | 0.000000 | 0.000 | 0.958 | 11.000 | |
| 69 | −3.084400 | −54.926701 | 0.375553 | 0.143178 | 0.000000 | 0.000 | 1.118 | 77.800 | |
| 70 | −3.084200 | −54.928799 | 0.977014 | 0.212756 | 0.000000 | 0.000 | 1.323 | 60.400 | |
| 71 | −2.940900 | −55.025299 | 0.287384 | 0.272711 | 0.000000 | 0.000 | 1.799 | 75.300 | |
| 72 | −2.931070 | −55.009399 | 1.596654 | 0.240939 | 0.000000 | 0.000 | 1.673 | 43.500 | |
| 73 | −3.191080 | −54.995300 | −0.370769 | 0.228089 | 0.000000 | 0.000 | 1.386 | 451.900 | |
| 74 | −3.207900 | −54.998600 | −0.408313 | 0.865851 | 0.000000 | 0.000 | 5.597 | 430.200 | |
| 75 | −3.209040 | −55.000999 | −0.539660 | 0.240988 | 0.000000 | 0.000 | 1.836 | 738.400 | |
| 76 | −3.068920 | −54.925598 | 1.085426 | 0.194411 | 0.000000 | 0.000 | 1.312 | 201.200 | |
| 77 | −3.125470 | −54.957100 | 0.015487 | 0.675524 | 0.000000 | 0.000 | 4.816 | 538.100 | |
| 78 | −3.123570 | −54.987900 | 0.214025 | 0.454257 | 2013.909058 | −17.267 | 0.969 | 143.900 | * |
| 1 | 40.400 | 0.905 | 0.386 | 1.922 |
| 2 | 136.200 | 4.694 | 1.045 | 6.408 |
| 3 | 129.100 | 0.392 | 0.855 | 5.175 |
| 4 | 233.000 | 7.836 | 1.779 | 11.322 |
| 5 | 227.800 | 4.306 | 3.236 | 20.875 |
| 6 | 294.100 | 1.196 | 2.071 | 13.060 |
| 7 | 380.300 | −2.479 | 3.072 | 19.589 |
| 8 | 314.800 | −6.573 | 2.995 | 20.940 |
| 9 | 308.500 | 3.072 | 2.037 | 8.548 |
| 10 | 421.000 | 0.584 | 2.682 | 14.615 |
| 11 | 336.900 | 1.326 | 2.321 | 13.289 |
| 12 | 193.000 | 5.346 | 1.321 | 8.102 |
| 13 | 287.200 | 4.896 | 1.932 | 9.558 |
| 14 | 78.400 | 1.778 | 0.604 | 3.771 |
| 15 | 429.200 | −1.651 | 2.333 | 12.373 |
| 16 | 150.400 | 10.030 | 4.166 | 12.650 |
| 17 | 52.400 | 2.149 | 0.404 | 2.461 |
| 18 | 43.600 | 1.471 | 0.627 | 2.340 |
| 19 | 71.300 | 3.135 | 0.438 | 2.478 |
| 20 | 310.400 | 2.063 | 2.455 | 14.402 |
| 21 | 8.900 | 0.580 | 0.120 | 0.583 |
| 22 | 19.100 | 1.031 | 0.381 | 1.022 |
| 23 | 11.500 | 0.946 | 0.115 | 0.576 |
| 24 | 47.800 | −0.742 | 0.569 | 1.901 |
| 25 | 27.000 | 1.332 | 0.213 | 1.200 |
| 26 | 51.300 | 2.288 | 0.378 | 2.575 |
| 27 | 289.500 | 6.843 | 9.887 | 76.521 |
| 28 | 345.300 | 4.142 | 3.363 | 20.774 |
| 29 | 221.400 | 11.931 | 2.680 | 19.616 |
| 30 | 333.800 | −4.895 | 2.725 | 17.446 |
| 31 | 0.800 | 0.058 | 0.010 | 0.048 |
| 32 | 38.500 | 1.830 | 0.725 | 2.481 |
| 33 | 7.100 | 0.769 | 0.097 | 0.493 |
| 34 | 343.500 | 1.050 | 2.378 | 13.346 |
| 35 | 453.500 | −0.566 | 3.351 | 21.329 |
| 36 | 333.800 | 3.199 | 2.342 | 16.390 |
| 37 | 202.800 | 7.274 | 2.556 | 17.282 |
| 38 | 43.100 | 3.913 | 0.976 | 7.060 |
| 39 | 0.700 | 0.035 | 0.012 | 0.057 |
| 40 | 239.900 | −2.183 | 2.010 | 13.624 |
| 41 | 116.800 | −0.499 | 1.184 | 7.675 |
| 42 | 1.500 | 0.075 | 0.020 | 0.118 |
| 43 | 34.700 | 0.377 | 0.383 | 1.983 |
| 44 | 11.100 | 0.849 | 0.199 | 0.624 |
| 45 | 149.800 | 5.333 | 1.207 | 7.389 |
| 46 | 40.800 | 0.775 | 0.371 | 1.892 |
| 47 | 462.900 | 8.811 | 3.914 | 23.014 |
| 48 | 457.400 | 3.044 | 2.963 | 18.221 |
| 49 | 639.200 | 13.043 | 6.514 | 42.254 |
| 50 | 104.400 | 4.271 | 0.615 | 3.862 |
| 51 | 380.800 | 2.025 | 2.721 | 15.518 |
| 52 | 86.700 | 5.224 | 1.631 | 4.618 |
| 53 | 387.900 | 5.526 | 3.065 | 19.834 |
| 54 | 167.600 | −0.093 | 1.188 | 6.770 |
| 55 | 179.700 | 1.235 | 1.885 | 12.289 |
| 56 | 110.800 | 0.481 | 0.728 | 5.146 |
| 57 | 40.000 | 0.345 | 0.420 | 2.170 |
| 58 | 60.500 | 2.428 | 0.520 | 3.187 |
| 59 | 42.600 | 1.879 | 0.392 | 2.425 |
| 60 | 20.900 | 0.777 | 0.292 | 1.814 |
| 61 | 9.700 | −0.168 | 0.132 | 0.716 |
| 62 | 93.800 | 0.274 | 0.902 | 6.453 |
| 63 | 109.400 | 1.778 | 0.785 | 4.822 |
| 64 | 266.800 | −10.101 | 5.158 | 36.308 |
| 65 | 38.900 | 1.904 | 0.824 | 5.074 |
| 66 | 331.300 | −5.626 | 3.117 | 19.814 |
| 67 | 312.100 | 2.142 | 2.274 | 14.678 |
| 68 | 11.000 | 0.920 | 0.086 | 0.539 |
| 69 | 77.800 | 1.376 | 0.525 | 4.097 |
| 70 | 60.400 | 2.839 | 0.618 | 3.844 |
| 71 | 75.300 | 1.022 | 0.970 | 6.400 |
| 72 | 43.500 | 3.411 | 0.515 | 3.574 |
| 73 | 451.900 | −5.203 | 3.201 | 19.450 |
| 74 | 430.200 | −5.577 | 11.827 | 76.453 |
| 75 | 738.400 | −9.422 | 4.207 | 32.054 |
| 76 | 201.200 | 8.895 | 1.593 | 10.752 |
| 77 | 538.100 | 0.237 | 10.357 | 73.837 |
| 78 | 143.900 | 1.341 | 2.845 | 6.070 |
References
- Saugier, B.; Roy, J. Estimations of global terrestrial productivity: Converging toward a single number? In Terrestrial Global Productivity; Roy, J., Saugier, B., Mooney, H.A., Eds.; Academic Press: San Diego, CA, USA, 2001; p. 543. [Google Scholar]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Harding, D.J. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Schimel, D.; Stephens, B.B.; Fisher, J.B. Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl. Acad. Sci. USA 2015, 112, 436–441. [Google Scholar] [CrossRef] [PubMed]
- Houghton, R. Aboveground Forest Biomass and the Global Carbon Balance. Glob. Chang. Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Asner, G.P. Cloud cover in Landsat observations of the Brazilian Amazon. Int. J. Remote Sens. 2001, 22, 3855–3862. [Google Scholar] [CrossRef]
- Lynch, J.; Maslin, M.; Balzter, H.; Sweeting, M. Sustainability: Choose satellites to monitor deforestation. Nature 2013, 496, 293–294. [Google Scholar] [CrossRef] [PubMed]
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; Van Zyl, J.J. Vegetation characteristics and surface topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef] [Green Version]
- Treuhaft, R.N.; Gonçalves, F.G.; dos Santos, J.R.; Keller, M.; Palace, M.; Madsen, S.; Sullivan, F.; Graça, P. Tropical-Forest Biomass Estimation at X-band from the Spaceborne TanDEM-X Interferometer. IEEE Geosci. Remote Sens. Lett. 2015, 12, 239–243. [Google Scholar] [CrossRef]
- Solberg, S.; Lohne, T.P.; Karyanto, O. Temporal stability of InSAR height in a tropical rainforest. Remote Sens. Lett. 2015, 6, 209–217. [Google Scholar] [CrossRef]
- Askne, J.I.H.; Fransson, J.E.S.; Santoro, M.; Soja, M.J.; Ulander, L.M.H. Model-Based Biomass Estimation of a Hemi-Boreal Forest from Multitemporal TanDEM-X Acquisitions. Remote Sens. 2013, 5, 5574–5597. [Google Scholar] [CrossRef]
- Askne, J.I.H.; Soja, M.J.; Ulander, L.M.H. Biomass estimation in a boreal forest from TanDEM-X data, LiDAR DTM, and the interferometric water cloud model. Remote Sens. Environ. 2017, 196, 265–278. [Google Scholar] [CrossRef]
- Solberg, S.; Naesset, E.; Gobakken, T.; Bollandsas, O.M. Forest biomass change estimated from height change in interferometric SAR height models. Carbon Balance Manag. 2014, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Hansen, E.H.; Gobakken, T.; Solberg, S.; Kangas, A.; Ene, L.; Mauya, E.; Naesset, E. Relative efficiency of ALS and InSAR for biomass estimation in a Tanzanian rainforest. Remote Sens. 2015, 7, 9865–9885. [Google Scholar] [CrossRef] [Green Version]
- Solberg, S.; Hansen, E.H.; Gobakken, T.; Naessset, E.; Zahabu, E. Biomass and InSAR height relationship in a dense tropical forest. Remote Sens. Environ. 2017, 192, 169–175. [Google Scholar] [CrossRef]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and simulated GEDI LiDAR observations for forest structure mapping. Remote Sens. Environ. 2017, 187, 253–266. [Google Scholar] [CrossRef]
- Mascaro, J.; Asner, G.P.; Dent, D.H.; DeWalt, S.J.; Denslow, J.S. Scale-dependence of aboveground carbon accumulation in secondary forests of Panama: A test of the intermediate peak hypothesis. For. Ecol. Manag. 2012, 276, 62–70. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using LiDAR remote sensing at La Selva, Costa Rica. J. Geophys. Res. 2010, 115, G00E09. [Google Scholar] [CrossRef]
- Meyer, V.; Saatchi, S.S.; Chave, J.; Dalling, J.W.; Bohlman, S.; Fricker, G.A.; Robinson, C.; Neumann, M.; Hubbell, S. Detecting tropical forest biomass dynamics from repeated airborne LiDAR measurements. Biogeosciences 2013, 10, 5421–5438. [Google Scholar] [CrossRef]
- Woodhouse, I. Predicting Backscatter-Biomass and Height-Biomass Trends Using a Macroecology Model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 872–877. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Chapman, B.D.; dos Santos, J.R.; Gonçalves, F.G.; Dutra, L.V.; Graça, P.M.LA.; Drake, J.B. Vegetation profiles in tropical forests from multibaseline interferometric synthetic aperture radar, field, and LiDAR measurements. J. Geophys. Res. 2009, 114, D23. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Folster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, F.G.; Treuhaft, R.N.; Law, B.E.; Almeida, A.; Walker, W.; Baccini, A.; dos Santos, J.R.; Graça, P.M.L.A. Estimating Aboveground Biomass in Tropical Forests: Field Methods and Error Analysis for the Calibration of Remote Sensing Observations. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vielledent, G.; Vaudry, R.; Rasamoeline, M.; Hall, J.S.; van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Leitold, V.; Keller, M.; Morton, D.C.; Cook, B.D.; Shimabukuro, Y.E. Airborne LiDAR-based estimates of tropical forest structure in complex terrain: Opportunities and trade-offs for REDD+. Carbon Balance Manag. 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airbone laser scanning data using an area-based approach. Can. For. Serv. 2013, FI-X-010, 1–39. [Google Scholar]
- Gatelli, F.; Guarnieri, A.M.; Parizzi, F.; Pasquali, P.; Prati, C.; Rocca, F. The Wavenumber Shift in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1994, 32, 855–860. [Google Scholar] [CrossRef]
- Gonzalez, J.H.; Bachmann, M.; Krieger, G.; Fiedler, H. Development of the TanDEM-X Calibration Concept: Analysis of Systematic Errors. IEEE Trans. Geosci. Remote Sens. 2010, 48, 716–726. [Google Scholar] [CrossRef] [Green Version]
- Bevington, P.R. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill: New York, NY, USA, 1969; p. 93. [Google Scholar]
- Neeff, T.; dos Santos, J.R. A growth model for secondary forest in Central Amazonia. For. Ecol. Manag. 2005, 216, 270–282. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Prates-Clark, C.C.; Fernandes, E.C.M.; Riha, S.J. Secondary forest growth deviation from chronosequence predictions in Central Amazonia. Glob. Chang. Biol. 2007, 13, 967–979. [Google Scholar] [CrossRef]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating forest biomass to SAR data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. The calculated performance of forest structure and biomass estimates from interferometric radar. Waves Random Media 2004, 14, S345–S358. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.B.; Hunter, M.O.; Oliveira, R., Jr. Estimates of forest canopy height and aboveground biomass using ICEsat. Geophys. Res. Lett. 2005, 32, L22SO2. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley and Sons: New York, NY, USA, 1975; p. 291. [Google Scholar]
- Treuhaft, R.N.; Gonçalves, F.G.; Chapman, B.D.; Neumann, M.; dos Santos, J.R.; Graça, P.M.L.A. Relationships between remotely sensed forest structure and biomass: Fourier structure from LiDAR and InSAR and penetration at microwave frequencies. Rev. Bras. Cartogr. 2013, 65/4, 747–755. [Google Scholar]
- Askne, J.; Dammert, P.; Ulander, L.M.H.; Smith, G. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens. 1997, 35, 25–35. [Google Scholar] [CrossRef]
- De Zan, F.; Krieger, G.; Lopez-Dekker, P. On Some Spectral Properties of TanDEM-X Interferograms Over Forested Areas. IEEE Geosci. Remote Sens. Lett. 2013, 10, 71–75. [Google Scholar] [CrossRef] [Green Version]
- Treuhaft, R.N.; Siqueira, P.R. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-Baseline Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Kugler, F.; Schulze, D.; Hajnsek, I.; Pretzsch, H.; Papathanassiou, K. TanDEM-X Pol-InSAR Performance for Forest Height Estimation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar] [CrossRef]

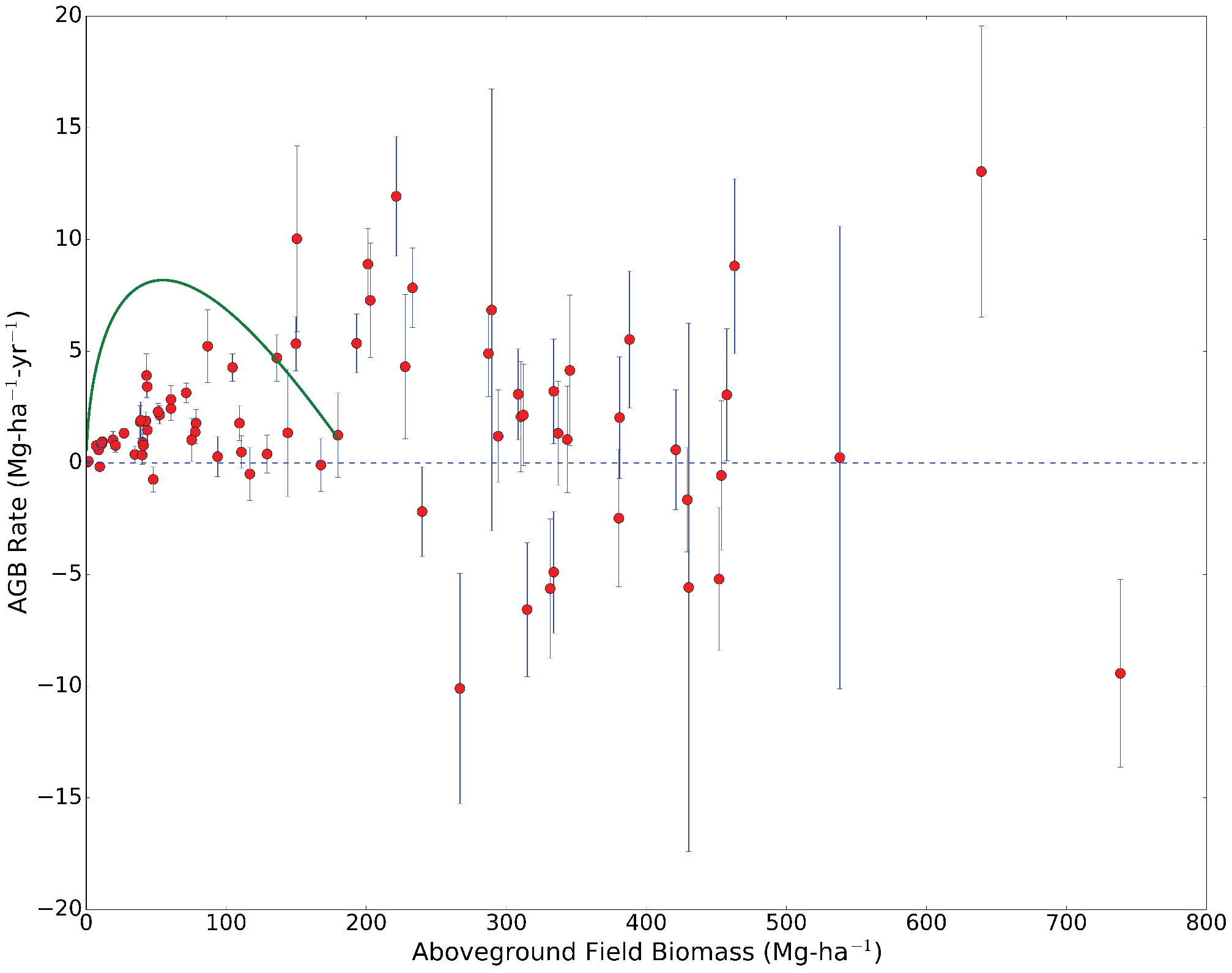
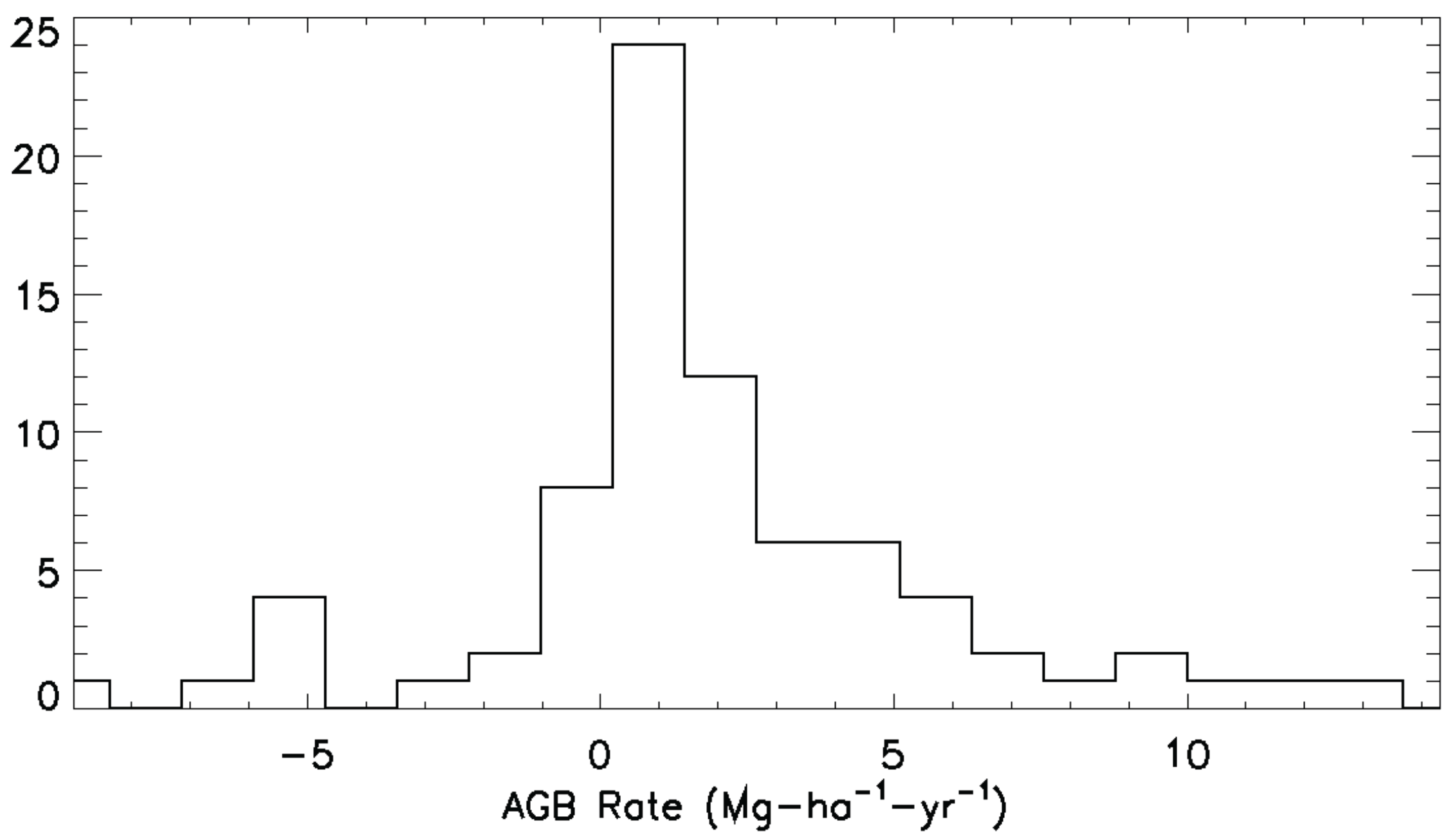
| Forest Type | Avg Phase-Height Rate (m-yr) | Standard Dev (m-yr) | Standard Dev of Mean (m-yr) |
|---|---|---|---|
| Secondary | 0.8 | 0.6 | 0.1 |
| Primary | 0.1 | 0.5 | 0.1 |
| All Plots | 0.5 | 0.6 | 0.1 |
| Forest Type | Avg AGB Rate (Mg-ha-yr) | Standard Dev (Mg-ha-yr) | Standard Dev of Mean (Mg-ha-yr) |
|---|---|---|---|
| Secondary Forest | 2.1 | 2.4 | 0.4 |
| Primary Forest | 1.1 | 5.2 | 0.9 |
| All Plots | 1.7 | 4.0 | 0.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Treuhaft, R.; Lei, Y.; Gonçalves, F.; Keller, M.; Santos, J.R.d.; Neumann, M.; Almeida, A. Tropical-Forest Structure and Biomass Dynamics from TanDEM-X Radar Interferometry. Forests 2017, 8, 277. https://doi.org/10.3390/f8080277
Treuhaft R, Lei Y, Gonçalves F, Keller M, Santos JRd, Neumann M, Almeida A. Tropical-Forest Structure and Biomass Dynamics from TanDEM-X Radar Interferometry. Forests. 2017; 8(8):277. https://doi.org/10.3390/f8080277
Chicago/Turabian StyleTreuhaft, Robert, Yang Lei, Fabio Gonçalves, Michael Keller, João Roberto dos Santos, Maxim Neumann, and André Almeida. 2017. "Tropical-Forest Structure and Biomass Dynamics from TanDEM-X Radar Interferometry" Forests 8, no. 8: 277. https://doi.org/10.3390/f8080277
APA StyleTreuhaft, R., Lei, Y., Gonçalves, F., Keller, M., Santos, J. R. d., Neumann, M., & Almeida, A. (2017). Tropical-Forest Structure and Biomass Dynamics from TanDEM-X Radar Interferometry. Forests, 8(8), 277. https://doi.org/10.3390/f8080277







