Tree Density and Forest Productivity in a Heterogeneous Alpine Environment: Insights from Airborne Laser Scanning and Imaging Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
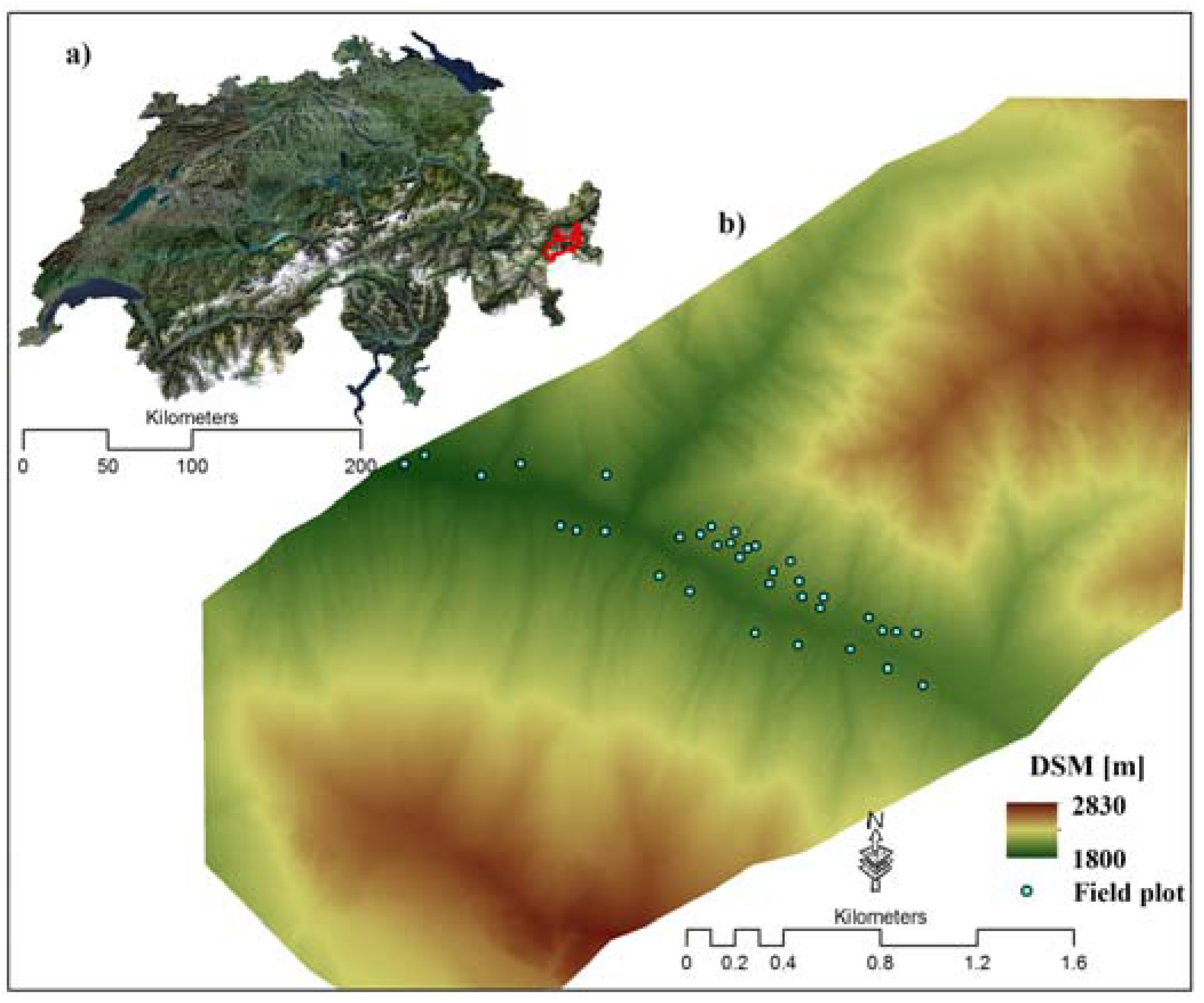
2.1. Study Area
2.2. Field Data
2.3. Airborne Imaging Spectroscopy Data
2.4. Airborne Laser Scanning Data
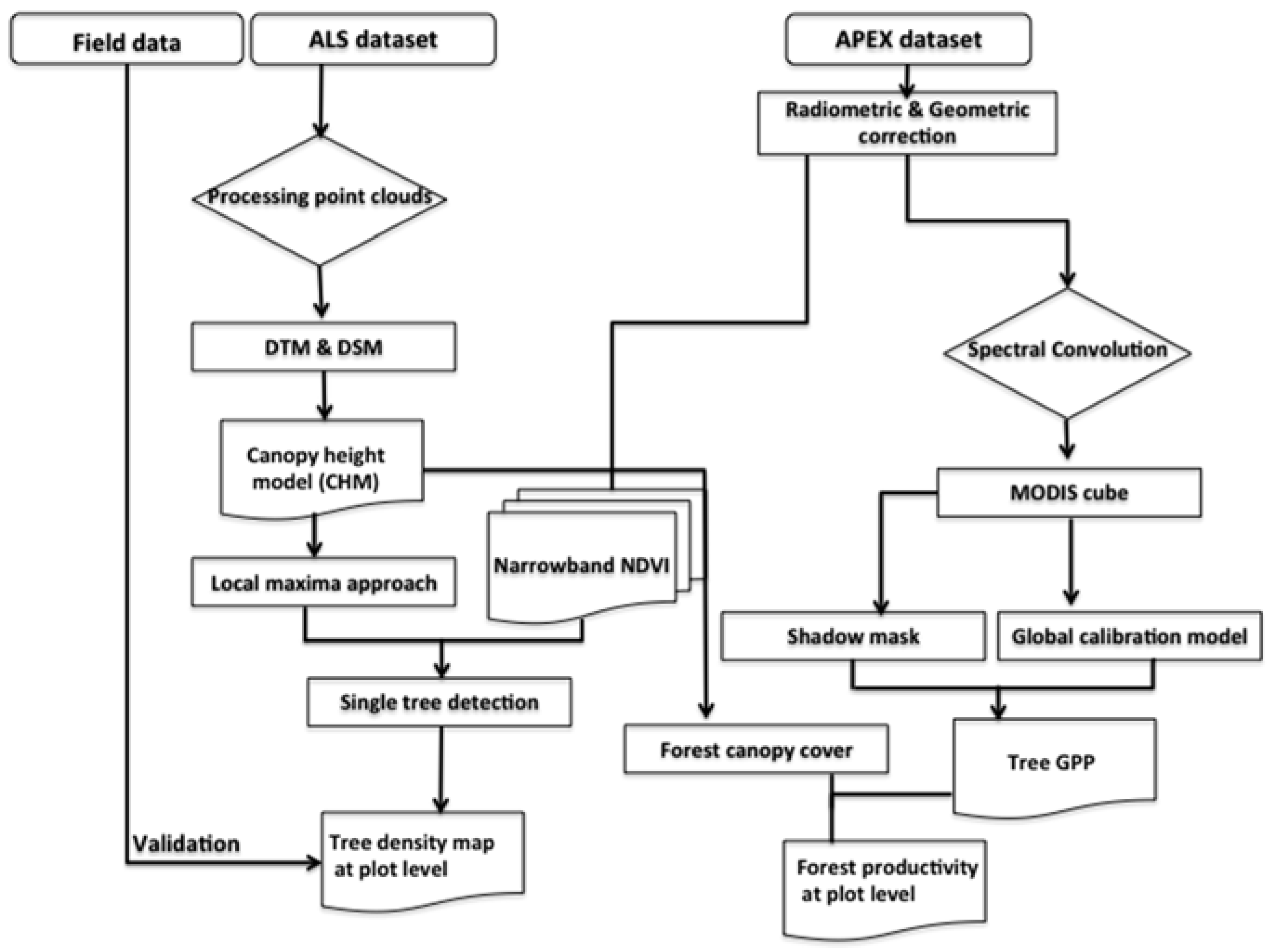
3. Methods
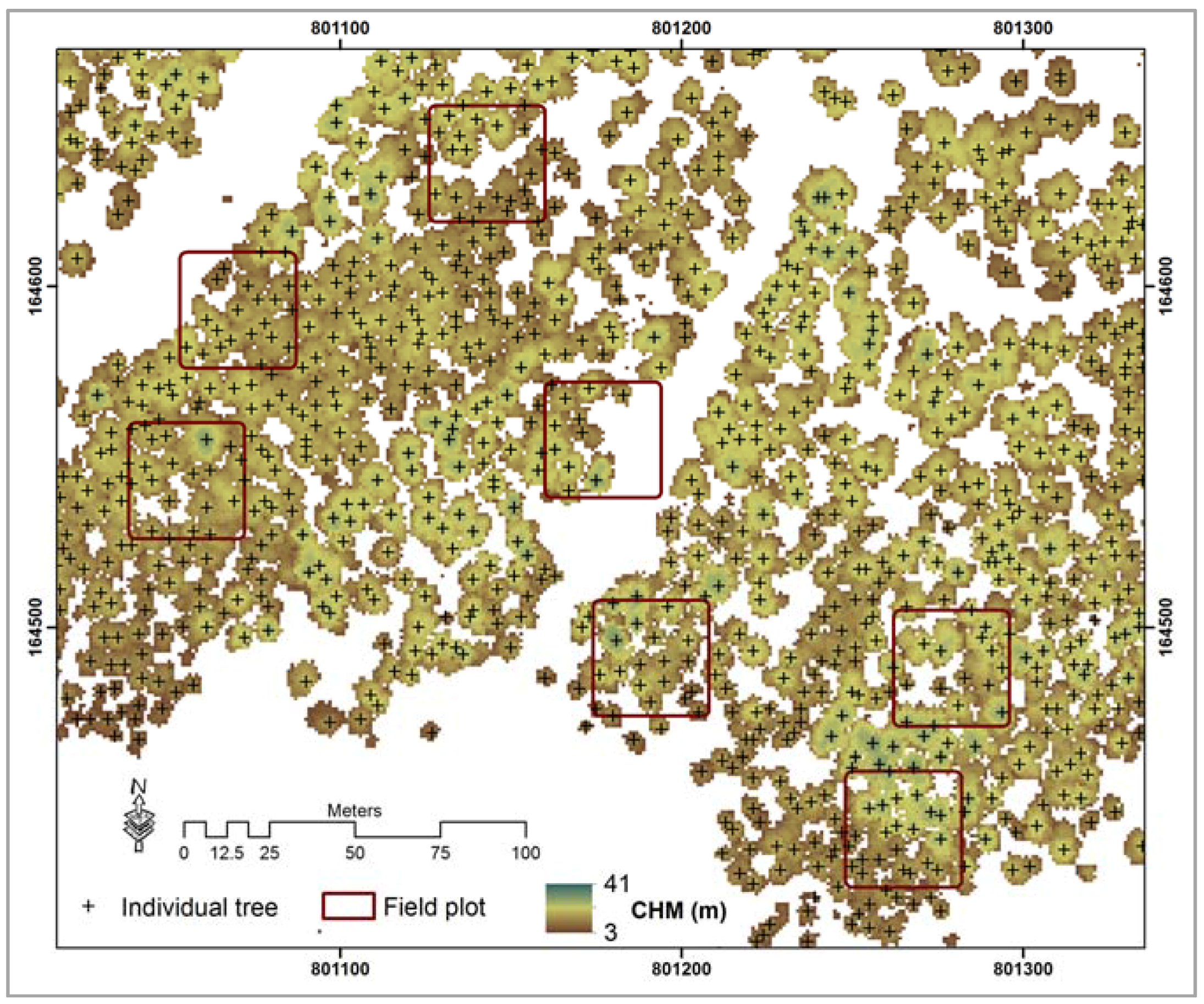
3.1. Local Maxima Approach to Estimate Tree Density Using ALS Data
3.2. Spatial Modeling of Forest Productivity Using APEX Data
3.3. Validation
4. Results
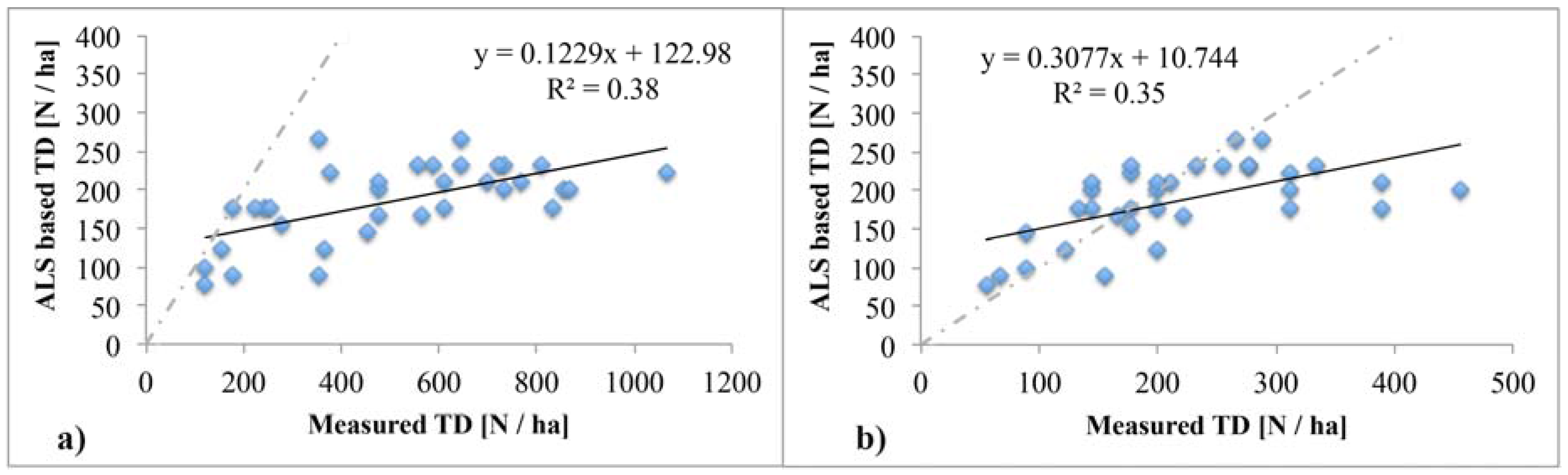
4.1. ALS Based Tree Density Estimation
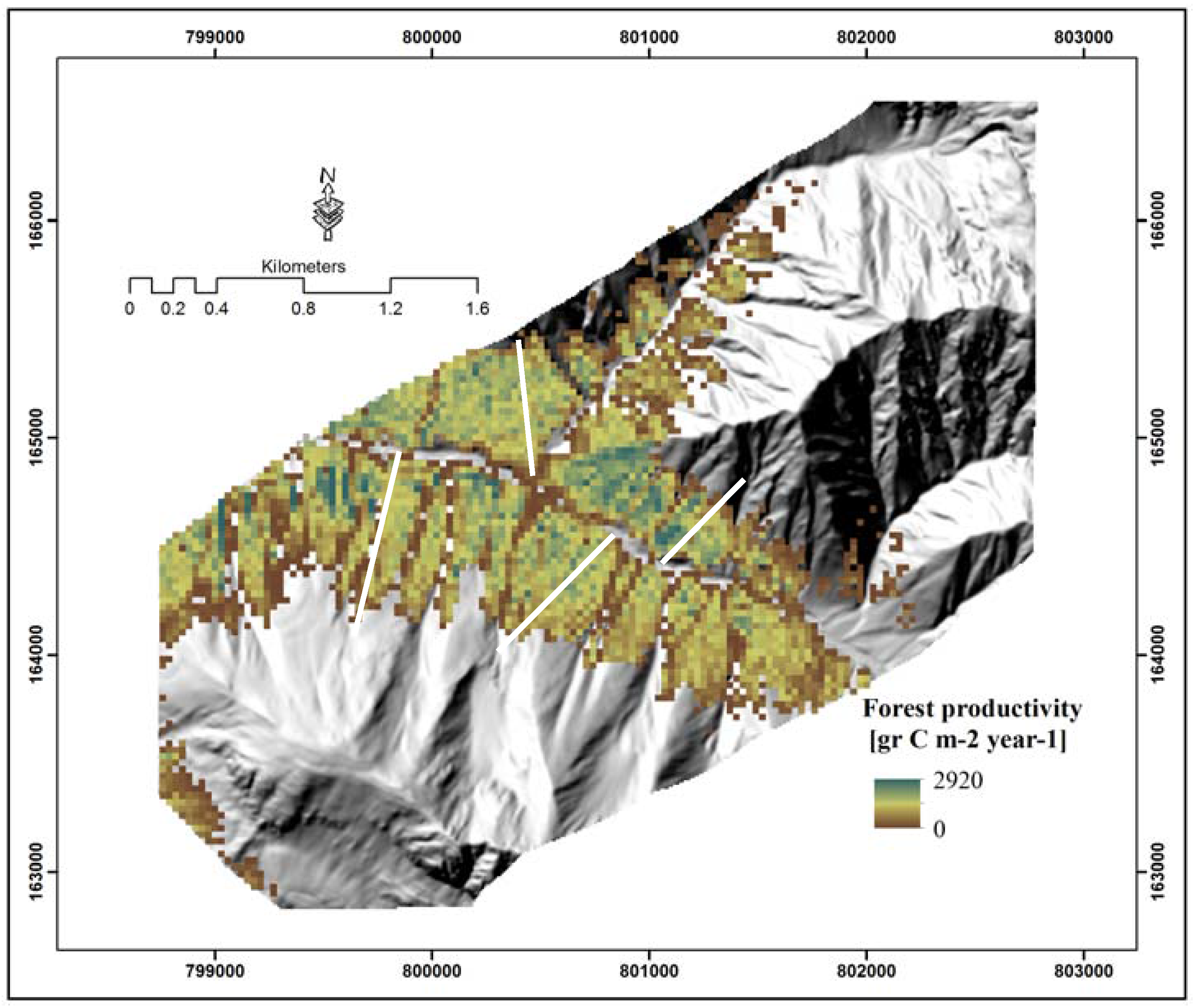
4.2. Spatial Distribution of Tree Density
4.3. Spatial Distribution of Forest Productivity
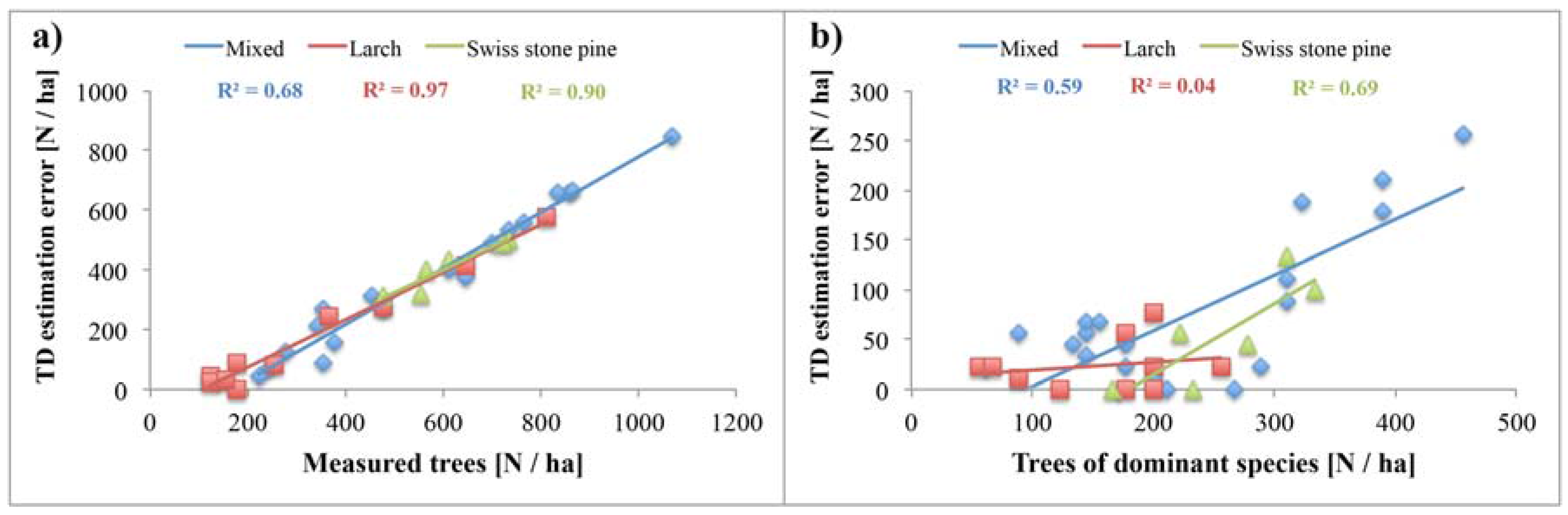
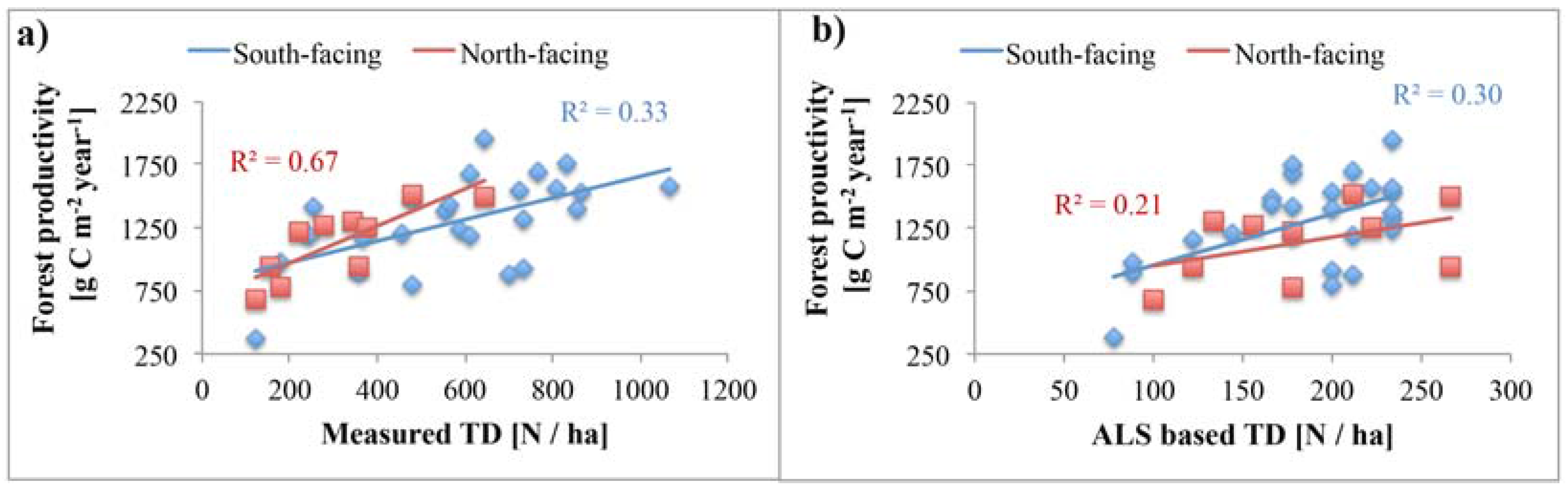
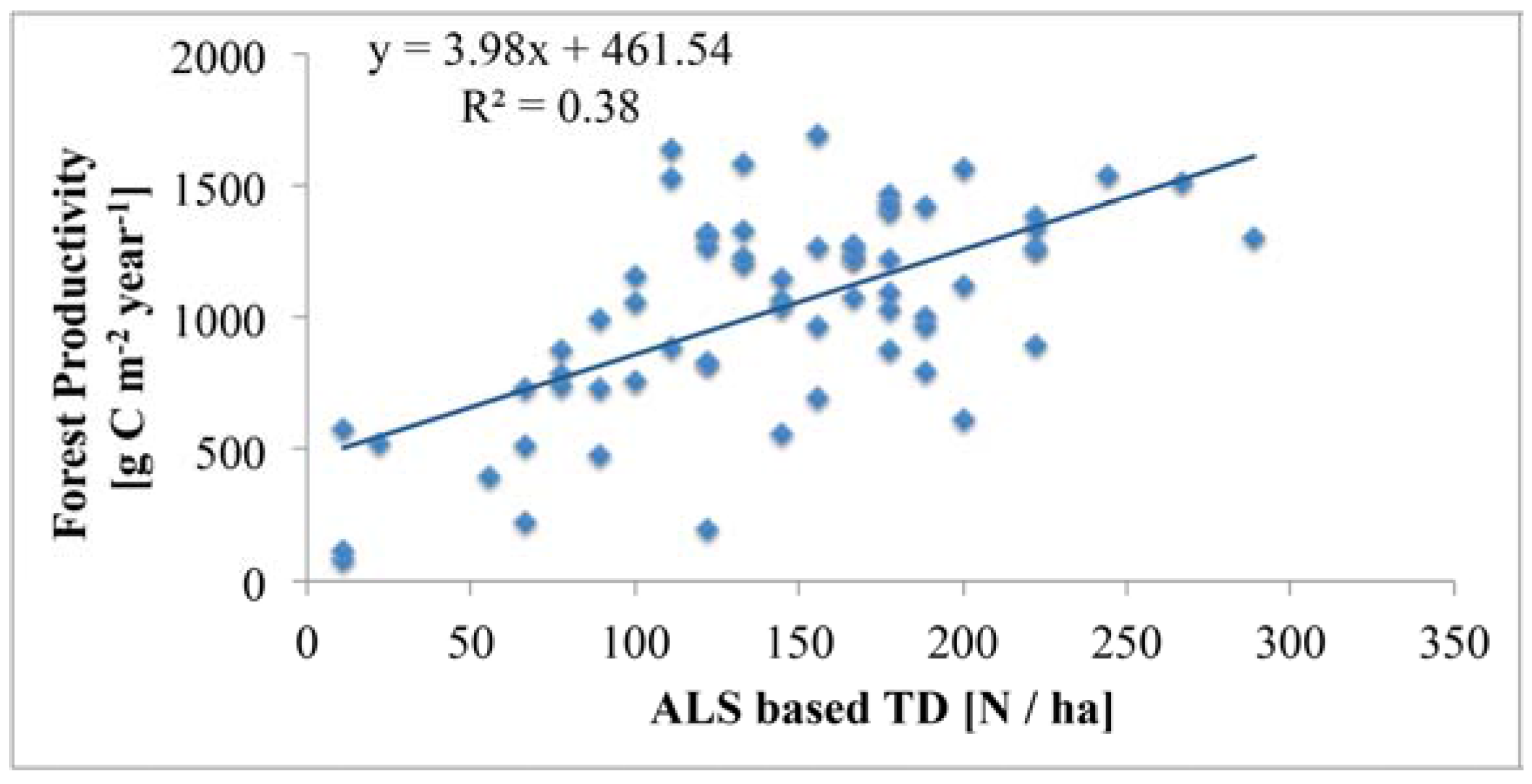
4.4. Relationship of Tree Density with Forest Productivity
5. Discussion
5.1. Reliability of Tree Density Retrieval
5.2. Reliability of Forest Productivity Retrieval
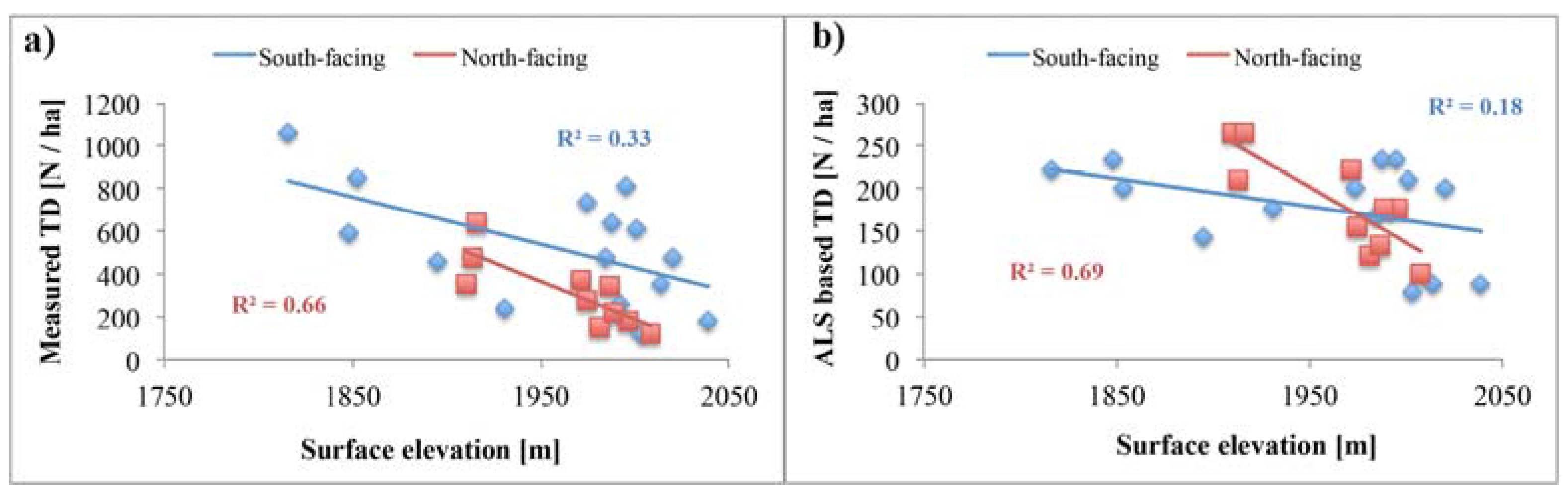
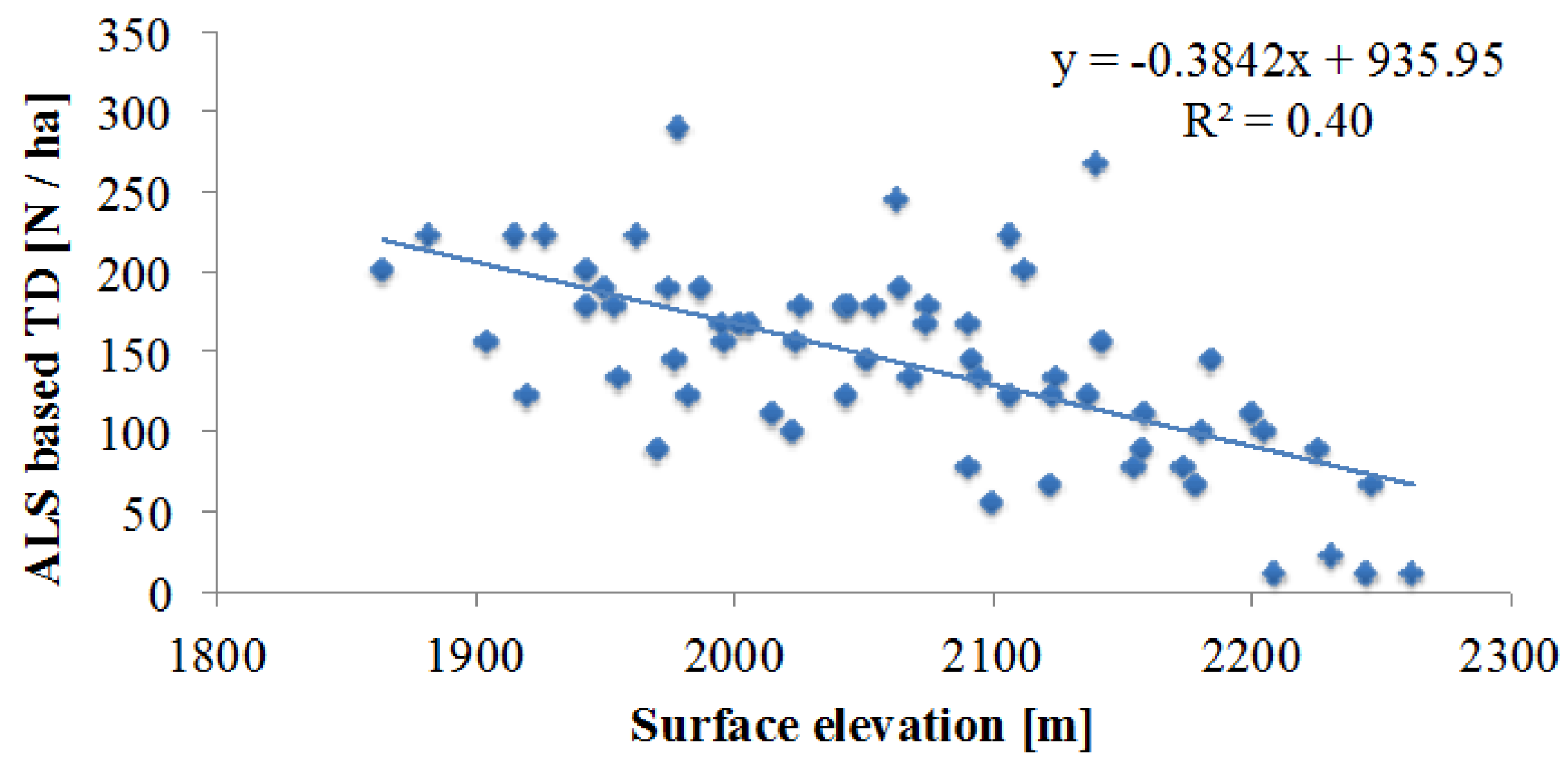
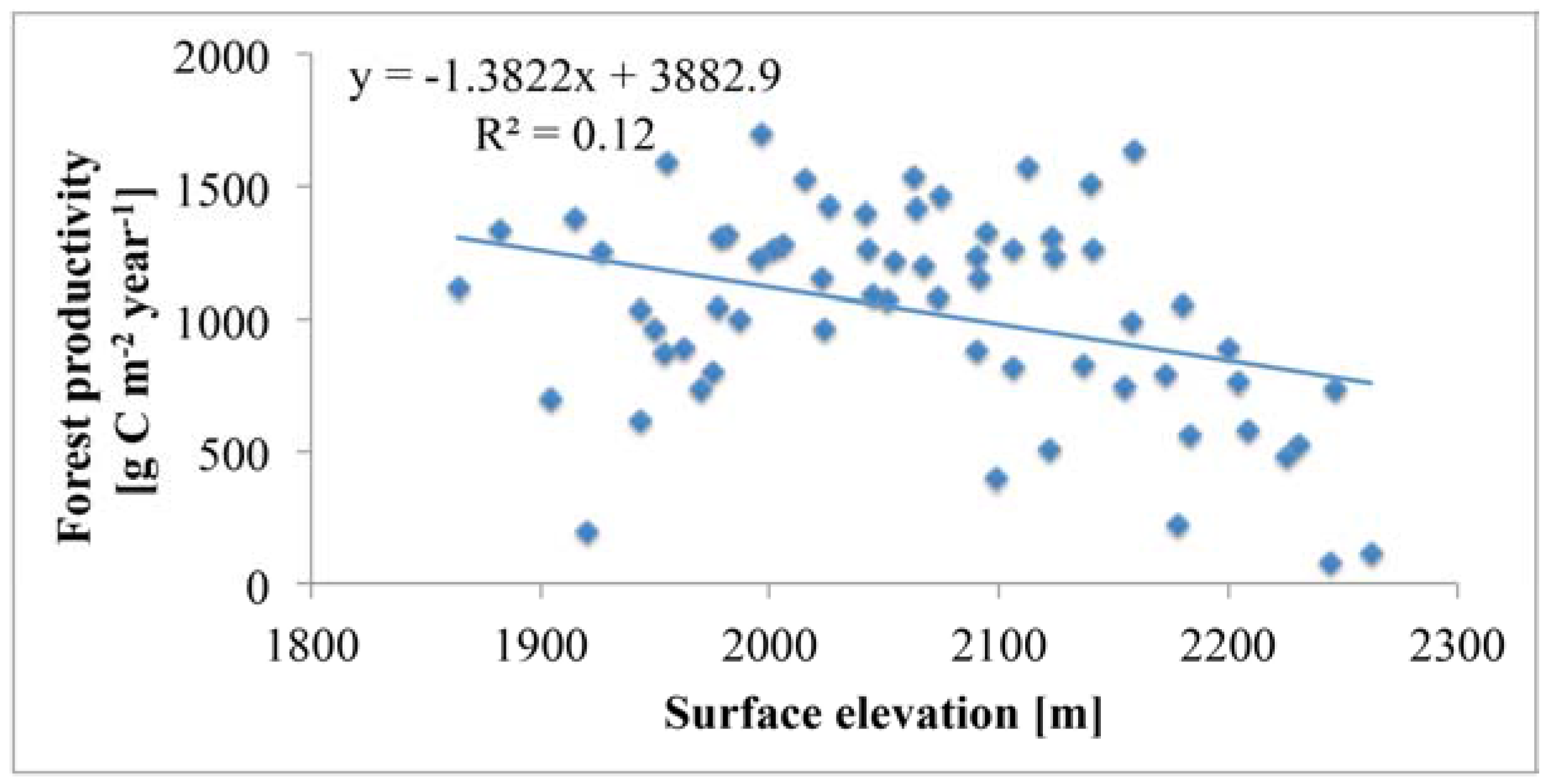
5.3. Topography Effects on Tree Density and Forest Productivity
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Johnson, P.E.; Shifley, S.R.; Rogers, R. The Ecology and Silviculture of Oaks; CABI: Wallingford, UK, 2009. [Google Scholar]
- Fatehi, P.; Damm, A.; Schaepman, M.E.; Kneubühler, M. Estimation of alpine forest structural variables from imaging spectrometer data. Remote Sens. 2015, 7, 16315–16338. [Google Scholar] [CrossRef]
- Tesfamichael, S.G.; Ahmed, F.; van Aardt, J.A.N.; Blakeway, F. A semi-variogram approach for estimating stems per hectare in Eucalyptus grandis plantations using discrete-return lidar height data. For. Ecol. Manag. 2009, 258, 1188–1199. [Google Scholar] [CrossRef]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. Biogeosciences 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Næsset, E.; Bjerknes, K.-O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner data. Remote Sens. Environ. 2001, 78, 328–340. [Google Scholar] [CrossRef]
- Capers, R.S.; Chazdon, R.L.; Brenes, A.R.; Alvarado, B.V. Successional dynamics of woody seedling communities in wet tropical secondary forests. J. Ecol. 2005, 93, 1071–1084. [Google Scholar] [CrossRef]
- Sproull, G.J.; Adamus, M.; Bukowski, M.; Krzyżanowski, T.; Szewczyk, J.; Statwick, J.; Szwagrzyk, J. Tree and stand-level patterns and predictors of Norway spruce mortality caused by bark beetle infestation in the Tatra Mountains. For. Ecol. Manag. 2015, 354, 261–271. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth, and Yield; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. Forestry 2008, 81, 13–31. [Google Scholar] [CrossRef]
- Rayan, M.G.; Binkley, D.; Fownes, J.H. Age-Related Decline in Forest Productivity: Pattern and Process. Adv. Ecol. Res. 1997, 27, 213–262. [Google Scholar]
- Goetz, S.J.; Prince, S.D. Remote sensing of net primary production in boreal forest stands. Agric. For. Meteorol. 1996, 78, 149–179. [Google Scholar] [CrossRef]
- Bontemps, J.-D.; Bouriaud, O. Predictive approaches to forest site productivity: Recent trends, challenges and future perspectives. Forestry 2013, 87, 109–128. [Google Scholar] [CrossRef]
- Maselli, F.; Papale, D.; Puletti, N.; Chirici, G.; Corona, P. Combining remote sensing and ancillary data to monitor the gross productivity of water-limited forest ecosystems. Remote Sens. Environ. 2009, 113, 657–667. [Google Scholar] [CrossRef]
- Crowther, T.W.; Glick, H.B.; Covey, K.R.; Bettigole, C.; Maynard, D.S.; Thomas, S.M.; Smith, J.R.; Hintler, G.; Duguid, M.C.; Amatulli, G.; et al. Mapping tree density at a global scale. Nature 2015, 525, 201–205. [Google Scholar] [CrossRef] [PubMed]
- Belote, R.T.; Prisley, S.; Jones, R.H.; Fitzpatrick, M.; de Beurs, K. Forest productivity and tree diversity relationships depend on ecological context within mid-Atlantic and Appalachian forests (USA). For. Ecol. Manag. 2011, 261, 1315–1324. [Google Scholar] [CrossRef]
- Bolton, D.K.; Coops, N.C.; Wulder, M.A. Measuring forest structure along productivity gradients in the Canadian boreal with small-footprint Lidar. Environ. Monit. Assess. 2013, 185, 6617–6634. [Google Scholar] [CrossRef] [PubMed]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Liu, J.; Yunhong, T.; Slik, J.W.F. Topography related habitat associations of tree species traits, composition and diversity in a Chinese tropical forest. For. Ecol. Manag. 2014, 330, 75–81. [Google Scholar] [CrossRef]
- Körner, C.; Farquhar, G.D.; Roksandic, Z. A global Survey of carbon Isotope Discrimination in Plants from High Altitude. Oecologia 2009, 74, 623–632. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Kryston, K.; Vaughn, N.; Knapp, D.E.; Bentley, L.P.; Shenkin, A.; Salinas, N.; Sinca, F.; et al. Scale dependence of canopy trait distributions along a tropical forest elevation gradient. New Phytol. 2017, 214, 973–988. [Google Scholar] [CrossRef] [PubMed]
- Coops, N.C.; Morsdorf, F.; Schaepman, M.E.; Zimmermann, N.E. Characterization of an alpine tree line using airborne LiDAR data and physiological modeling. Glob. Chang. Biol. 2013, 19, 3808–3821. [Google Scholar] [CrossRef] [PubMed]
- Hyyppä, J.; Hyyppä, H.; Inkinen, M.; Engdahl, M.; Linko, S.; Zhu, Y.-H. Accuracy comparison of various remote sensing data sources in the retrieval of forest stand attributes. For. Ecol. Manag. 2000, 128, 109–120. [Google Scholar] [CrossRef]
- Maselli, F.; Chiesi, M.; Mura, M.; Marchetti, M.; Corona, P.; Chirici, G. Combination of optical and LiDAR satellite imagery with forest inventory data to improve wall-to-wall assessment of growing stock in Italy. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 377–386. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of Individual Tree Crowns in Airborne Lidar Data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return lidar: An example from low density, fire prone ponderosa pine forests. For. Ecol. Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinen, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Falkowski, M.J.; Smith, A.M.; Gessler, P.E.; Morgan, P. Regression modeling and mapping of coniferous forest basal area and tree density from discrete-return lidar and multispectral satellite data. Can. J. Remote Sens. 2006, 32, 126–138. [Google Scholar] [CrossRef]
- Sivanpillai, R.; Smith, C.T.; Srinivasan, R.; Messina, M.G.; Wu, X.B. Estimation of managed loblolly pine stand age and density with Landsat ETM+ data. For. Ecol. Manag. 2006, 223, 247–254. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K.; Sobhan, I. Mapping beech (Fagus sylvatica L.) forest structure with airborne hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 201–211. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Brosofske, K.D.; Froese, R.E.; Falkowski, M.J.; Banskota, A. A Review of Methods for Mapping and Prediction of Inventory Attributes for Operational Forest Management. For. Sci. 2014, 60, 733–756. [Google Scholar] [CrossRef]
- Leiterer, R.; Mücke, W.; Morsdorf, F.; Hollaus, M.; Pfeifer, N.; Schapeman, M.E. Operational forest structure monitoring using airborne laser scanning. Photogramm. Fernerkund. Geoinf. 2013, 3, 173–184. [Google Scholar] [CrossRef]
- Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Wulder, M.A.; Coops, N.C.; Hudak, A.T.; Morsdorf, F.; Nelson, R.; Newnham, G.; Vastaranta, M. Status and prospects for LiDAR remote sensing of forested ecosystems. Can. J. Remote Sens. 2013, 39, 1–5. [Google Scholar] [CrossRef]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in Forest Inventory Using Airborne Laser Scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Tompalski, P.; Coops, N.C.; White, J.C.; Wulder, M.A. Enriching ALS-Derived Area-Based Estimates of Volume through Tree-Level Downscaling. Forests 2015, 6, 2608–2630. [Google Scholar] [CrossRef]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manag. 2005, 213, 54–70. [Google Scholar] [CrossRef]
- Vastaranta, M.; Saarinen, N.; Kankare, V.; Holopainen, M.; Kaartinen, H.; Hyyppä, J.; Hyyppä, H. Multisource Single-Tree Inventory in the Prediction of Tree Quality Variables and Logging Recoveries. Remote Sens. 2014, 6, 3475–3491. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkanen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
- Monteith, J.L.; Moss, C.J. Climate and the efficiency of crop production in Britain [and discussion]. Philos. Trans. R Soc. Lond. B Biol. Sci. 1977, 281, 227–294. [Google Scholar] [CrossRef]
- Waring, R.H.; Coops, N.C.; Fan, W.; Nightingale, J.M. MODIS enhanced vegetation index predicts tree species richness across forested ecoregions in the contiguous U.S.A. Remote Sens. Environ. 2006, 103, 218–226. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Maeirsperger, T.K.; Gower, S.T.; Kirschbaum, A.A.; Running, S.W.; Zhao, M.; Wofsy, S.C.; Dunn, A.L.; et al. Site-level evaluation of satellite-based global terrestrial gross primary production and net primary production monitoring. Glob. Chang. Biol. 2005, 11, 666–684. [Google Scholar] [CrossRef]
- Coops, N.C.; Ferster, C.J.; Waring, R.H.; Nightingale, J. Comparison of three models for predicting gross primary production across and within forested ecoregions in the contiguous United States. Remote Sens. Environ. 2009, 113, 680–690. [Google Scholar] [CrossRef]
- Schimel, D.; Pavlick, R.; Fisher, J.B.; Asner, G.P.; Saatchi, S.; Townsend, P.A.; Miller, C.; Frankenberg, C.; Hibbard, K.; Cox, P. Observing terrestrial ecosystems and the carbon cycle from space. Glob. Chang. Biol. 2015, 21, 1762–1776. [Google Scholar] [CrossRef] [PubMed]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- MeteoSwiss IDAweb. The Data Portal of MeteoSwiss for Research and Teaching. Available online: http://www.meteoschweiz.admin.ch/web/de/services/datenportal/idaweb.html (accessed on 3 November 2013).
- Hill, A.; Breschan, J.; Mandallaz, D. Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models. Forests 2014, 5, 2253–2275. [Google Scholar] [CrossRef]
- Schweiger, A.K.; Schütz, M.; Anderwald, P.; Schaepman, M.E.; Kneubühler, M.; Haller, R.; Risch, A.C. Foraging ecology of three sympatric ungulate species—Behavioural and resource maps indicate differences between chamois, ibex and red deer. Mov. Ecol. 2015, 3, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Risch, A.C.; Nagel, L.M.; Martin, S.; KrÜsi, B.O.; Kienast, F.; Bugmman, H. Structure and Long-Term Development of Subalpine Pinus montana Miller and Pinus cembra L. Forests in the Central European Alps. Forstwiss. Cent. 2003, 122, 219–230. [Google Scholar] [CrossRef]
- Kangas, A.; Maltamo, M. Forest Inventory Methodology and Applications; Springer: Berlin, Germany, 2006. [Google Scholar]
- Da Cunha, T.A.; Finger, C.A.G.; Hasenauer, H. Tree basal area increment models for Cedrela, Amburana, Copaifera and Swietenia growing in the Amazon rain forests. For. Ecol. Manag. 2016, 365, 174–183. [Google Scholar] [CrossRef]
- Leboeuf, A.; Beaudoin, A.; Fournier, R.A.; Guindon, L.; Luther, J.; Lambert, M. A shadow fraction method for mapping biomass of northern boreal black spruce forests using QuickBird imagery. Remote Sens. Environ. 2007, 110, 488–500. [Google Scholar] [CrossRef]
- Risch, A.C.; Jurgensen, M.F.; Page-Dumroese, D.S.; Wildi, O.; Schütz, M. Long-term development of above-and below-ground carbon stocks following land-use change in subalpine ecosystems of the Swiss National Park. J. For. 2008, 1602, 1590–1602. [Google Scholar] [CrossRef]
- Pretzsch, H. Canopy space filling and tree crown morphology in mixed-species stands compared with monocultures. For. Ecol. Manag. 2014, 327, 251–264. [Google Scholar] [CrossRef]
- Paulsen, J.; Körner, C. GIS-Analysis of Tree-Line Elevation in the Swiss Alps Suggests no Exposure Effect. J. Veg. Sci. 2011, 12, 817–824. [Google Scholar] [CrossRef]
- Schaepman, M.E.; Jehle, M.; Hueni, A.; D’Odorico, P.; Damm, A.; Weyermann, J.; Schneider, F.D.; Laurent, V.; Popp, C.; Seidel, F.C.; et al. Advanced radiometry measurements and Earth science applications with the Airborne Prism Experiment (APEX). Remote Sens. Environ. 2015, 158, 207–219. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R. Geo-atmospheric processing of airborne imaging spectrometry data. Part 1: Parametric orthorectification. Int. J. Remote Sens. 2002, 23, 2609–2630. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.J.; Alder-Golden, S.M.; Chetwynd, J.H.; Hoke, M.L.; et al. MODTRAN5: A reformulated atmospheric band model with auxiliary species and practical multiple scattering options. In Proceedings of the Society of Photo-Optical Instrumentation Engineer, International Society for Optics and Photonics, Bellingham, WA, USA, 20 January 2005; pp. 662–667. [Google Scholar]
- Wagner, W.; Hollaus, M.; Briese, C.; Ducic, V. 3D vegetation mapping using small-footprint full-waveform airborne laser scanners. Int. J. Remote Sens. 2008, 29, 1433–1452. [Google Scholar] [CrossRef]
- RIEGL Products. Airborne Scanning Datasheets. Available online: http://www.riegl.com (accessed on 4 June 2015).
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Hollaus, M.; Wagner, W.; Eberhöfer, C.; Karel, W. Accuracy of large-scale canopy heights derived from LiDAR data under operational constraints in a complex alpine environment. ISPRS J. Photogramm. Remote Sens. 2006, 60, 323–338. [Google Scholar] [CrossRef]
- Jakubowski, M.K.; Guo, Q.; Kelly, M. Tradeoffs between lidar pulse density and forest measurement accuracy. Remote Sens. Environ. 2013, 130, 245–253. [Google Scholar] [CrossRef]
- Brassel, P.; Lischke, H. Swiss National Forest Inventory: Methods and Models of the Second Assessment; WSL Swiss Federral Research Institute: Birmensdorf, Switzerland, 2001. [Google Scholar]
- Kankare, V.; Vastaranta, M.; Holopainen, M.; Räty, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Viitala, R. Retrieval of Forest Aboveground Biomass and Stem Volume with Airborne Scanning LiDAR. Remote Sens. 2013, 5, 2257–2274. [Google Scholar] [CrossRef]
- Leckie, D. Stand delineation and composition estimation using semi-automated individual tree crown analysis. Remote Sens. Environ. 2003, 85, 355–369. [Google Scholar] [CrossRef]
- Katoh, M.; Gougeon, F.A. Improving the Precision of Tree Counting by Combining Tree Detection with Crown Delineation and Classification on Homogeneity Guided Smoothed High Resolution (50 cm) Multispectral Airborne Digital Data. Remote Sens. 2012, 4, 1411–1424. [Google Scholar] [CrossRef]
- Lindberg, E.; Holmgren, J.; Olofsson, K.; Wallerman, J.; Olsson, H. Estimation of Tree Lists from Airborne Laser Scanning Using Tree Model Clustering and k-MSN Imputation. Remote Sens. 2013, 5, 1932–1955. [Google Scholar] [CrossRef]
- Wulder, M.; Niemann, K.O.; Goodenough, D.G. Local Maximum Filtering for the Extraction of Tree Locations and Basal Area from High Spatial Resolution Imagery. Remote Sens. Environ. 2000, 73, 103–114. [Google Scholar] [CrossRef]
- Kwak, D.-A.; Lee, W.-K.; Lee, J.-H.; Biging, G.S.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. For. Res. 2007, 12, 425–434. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
- Nightingale, J.M.; Fan, W.; Coops, N.C.; Waring, R.H. Predicting tree diversity across the United States as a function of modeled gross primary production. Ecol. Appl. 2008, 18, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, H.; Wang, W.; Milesi, C.; White, M.A.; Ganguly, S.; Gamo, M.; Hirata, R.; Myneni, R.B.; Nemani, R.R. Exploring Simple Algorithms for Estimating Gross Primary Production in Forested Areas from Satellite Data. Remote Sens. 2012, 4, 303–326. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Huang, N.; Niu, Z.; Zhan, Y.; Xu, S.; Tappert, M.C.; Wu, C.; Huang, W.; Gao, S.; Hou, X.; Cai, D. Relationships between soil respiration and photosynthesis-related spectral vegetation indices in two cropland ecosystems. Agric. For. Meteorol. 2012, 160, 80–89. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Liu, M.; Wang, C.; Xia, X. A hyperspectral index sensitive to subtle changes in the canopy chlorophyll content under arsenic stress. Int. J. Appl. Earth Obs. Geoinf. 2015, 36, 41–53. [Google Scholar] [CrossRef]
- Wang, T.; Skidmore, A.K.; Toxopeus, A.G.; Liu, X. Understory Bamboo Discrimination Using a Winter Image. Photogramm. Eng. Remote Sens. 2009, 75, 37–47. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Verhoef, W.; Schläpfer, D.; Garbari, S.; Schaepman, M.E. Impact of varying irradiance on vegetation indices and chlorophyll fluorescence derived from spectroscopy data. Remote Sens. Environ. 2015, 156, 202–215. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive Methods for Individual Tree Detection on Airborne Laser Based Canopy Height Model. In Proceedings of the ISPRS Workshop Laser-Scanners for Forest and Landscape Assessment, International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vienna, Austria, 3–6 October 2004; pp. 187–191. [Google Scholar]
- Jaskierniak, D.; Kuczera, G.; Benyon, R.; Wallace, L. Using tree detection algorithms to predict stand sapwood area, basal area and stocking density in Eucalyptus regnans forest. Remote Sens. 2015, 7, 7298–7323. [Google Scholar] [CrossRef]
- Casas, Á.; García, M.; Siegel, R.B.; Koltunov, A.; Ramírez, C.; Ustin, S. Burned forest characterization at single-tree level with airborne laser scanning for assessing wildlife habitat. Remote Sens. Environ. 2016, 175, 231–241. [Google Scholar] [CrossRef]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Heurich, M. Automatic recognition and measurement of single trees based on data from airborne laser scanning over the richly structured natural forests of the Bavarian Forest National Park. For. Ecol. Manag. 2008, 255, 2416–2433. [Google Scholar] [CrossRef]
- Freitas, S.R.; Mello, M.C.S.; Cruz, C.B.M. Relationships between forest structure and vegetation indices in Atlantic Rainforest. For. Ecol. Manag. 2005, 218, 353–362. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Smith, A.M.S.; Gessler, P.E.; Hudak, A.T.; Vierling, L.A.; Evans, J.S. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens. 2008, 34, 338–350. [Google Scholar] [CrossRef]
- Torabzadeh, H.; Morsdorf, F.; Leiterer, R.; Schaepman, M.E. Fusing imaging spectrometry and airborne laser scanner data for tree species discrimination. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2014), Quebec City, QC, Canada, 13–18 July 2014; pp. 1253–1256. [Google Scholar]
- Gatziolis, D.; Fried, J.S.; Monleon, V.S. Challenges to estimating tree height via LiDAR in closed-canopy forests: A parable from Western Oregon. For. Sci. 2010, 56, 139–155. [Google Scholar]
- Yu, X.; Litkey, P.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Assessment of Low Density Full-Waveform Airborne Laser Scanning for Individual Tree Detection and Tree Species Classification. Forests 2014, 5, 1011–1031. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; Monson, R.K.; et al. On the use of MODIS EVI to assess gross primary productivity of North American ecosystems. J. Geophys. Res. Biogeosci. 2006, 111, 1–16. [Google Scholar] [CrossRef]
- Jahan, N.; Gan, T.Y. Developing a gross primary production model for coniferous forests of northeastern USA from MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 11–20. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1923. [Google Scholar] [CrossRef]
- Zielis, S.; Etzold, S.; Zweifel, R.; Eugster, W.; Haeni, M.; Buchmann, N. NEP of a Swiss subalpine forest is significantly driven not only by current but also by previous year’s weather. Biogeosciences 2014, 11, 1627–1635. [Google Scholar] [CrossRef]
- Wolf, S.; Eugster, W.; Ammann, C.; Häni, M.; Zielis, S.; Hiller, R.; Stieger, J.; Imer, D.; Merbold, L.; Buchmann, N. Contrasting response of grassland versus forest carbon and water fluxes to spring drought in Switzerland. Environ. Res. Lett. 2013, 8, 35007. [Google Scholar] [CrossRef]
- Damm, A.; Elber, J.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A.; et al. Remote sensing of sun-induced fluorescence to improve modeling of diurnal courses of gross primary production (GPP). Glob. Chang. Biol. 2010, 16, 171–186. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Lee, J.-E.; Berry, J.A.; van der Tol, C.; Yang, X.; Guanter, L.; Damm, A.; Baker, I.; Frankenberg, C. Simulations of chlorophyll fluorescence incorporated into the Community Land Model version 4. Glob. Chang. Biol. 2015, 21, 3469–3477. [Google Scholar] [CrossRef] [PubMed]
- Parazoo, N.C.; Bowman, K.; Fisher, J.B.; Frankenberg, C.; Jones, D.B.A.; Cescatti, A.; Pérez-Priego, Ó.; Wohlfahrt, G.; Montagnani, L. Terrestrial gross primary production inferred from satellite fluorescence and vegetation models. Glob. Chang. Biol. 2014, 20, 3103–3121. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.-E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327-33. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; van der Tol, C.; Magnani, F.; Sabater, N.; Rivera, J.P.; Mohammed, G.; Moreno, J. Evaluating the predictive power of sun-induced chlorophyll fluorescence to estimate net photosynthesis of vegetation canopies: A SCOPE modeling study. Remote Sens. Environ. 2016, 176, 139–151. [Google Scholar] [CrossRef]
- Paulsen, J.; Weber, U.M.; Körner, C. Tree growth near treeline: Abrupt or gradual reduction with altitude? Arct. Antarct. Alp. Res. 2000, 32, 14–20. [Google Scholar] [CrossRef]
- Whittaker, R.H.; Bormann, F.H.; Likens, G.E. The Hubbard Brook ecosystem study: Forest biomass and production. Ecol. Monogr. 1974, 44, 233–254. [Google Scholar] [CrossRef]
- Tateno, R.; Takeda, H. Forest structure and tree species distribution in relation to topography-mediated heterogeneity of soil nitrogen and light at the forest floor. Ecol. Res. 2003, 18, 559–571. [Google Scholar] [CrossRef]
- Pinno, B.D.; Paré, D.; Guindon, L.; Bélanger, N. Predicting productivity of trembling aspen in the Boreal Shield ecozone of Quebec using different sources of soil and site information. For. Ecol. Manag. 2009, 257, 782–789. [Google Scholar] [CrossRef]
- Köhl, M.; Magnussen, S.; Marchetti, M. Sampling Methods, Remote Sensing and GIS Multiresource Forest Inventory; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]

| Parameter | DBH > 5 cm | DBH > 12 cm | DBH > 20 cm | DBH > 30 cm | South-Facing | North-Facing |
|---|---|---|---|---|---|---|
| Number of plots [-] | 35 | 35 | 35 | 35 | 25 | 10 |
| Number of trees [-] | 1598 | 1360 | 1103 | 691 | 1314 | 284 |
| Tree density [N/ha] | ||||||
| Mean | 507 | 432 | 350 | 219 | 584 | 316 |
| Minimum | 122 | 122 | 89 | 56 | 122 | 122 |
| Maximum | 1067 | 755 | 600 | 456 | 1067 | 644 |
| Standard deviation | 249 | 189 | 141 | 96 | 238 | 161 |
| Measured Trees | Detected Trees | Detection Rate [%] | |||
|---|---|---|---|---|---|
| All DBHs | DBH > 12 | DBH > 20 | DBH > 30 | ||
| 1598 | 581 | 36 | 43 | 53 | 84 |
| Plots | All Trees | DBH > 12 | DBH > 20 | DBH > 30 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | RMSE% | R2 | RMSE | RMSE% | R2 | RMSE | RMSE% | R2 | RMSE | RMSE% | |
| All | 0.39 | 389 | 77 | 0.40 | 294 | 68 | 0.42 | 201 | 57 | 0.35 | 87 | 40 |
| North | 0.68 | 176 | 56 | 0.68 | 124 | 44 | 0.74 | 101 | 39 | 0.80 | 68 | 33 |
| South | 0.52 | 447 | 77 | 0.58 | 339 | 69 | 0.53 | 229 | 59 | 0.27 | 93 | 42 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatehi, P.; Damm, A.; Leiterer, R.; Pir Bavaghar, M.; Schaepman, M.E.; Kneubühler, M. Tree Density and Forest Productivity in a Heterogeneous Alpine Environment: Insights from Airborne Laser Scanning and Imaging Spectroscopy. Forests 2017, 8, 212. https://doi.org/10.3390/f8060212
Fatehi P, Damm A, Leiterer R, Pir Bavaghar M, Schaepman ME, Kneubühler M. Tree Density and Forest Productivity in a Heterogeneous Alpine Environment: Insights from Airborne Laser Scanning and Imaging Spectroscopy. Forests. 2017; 8(6):212. https://doi.org/10.3390/f8060212
Chicago/Turabian StyleFatehi, Parviz, Alexander Damm, Reik Leiterer, Mahtab Pir Bavaghar, Michael E. Schaepman, and Mathias Kneubühler. 2017. "Tree Density and Forest Productivity in a Heterogeneous Alpine Environment: Insights from Airborne Laser Scanning and Imaging Spectroscopy" Forests 8, no. 6: 212. https://doi.org/10.3390/f8060212
APA StyleFatehi, P., Damm, A., Leiterer, R., Pir Bavaghar, M., Schaepman, M. E., & Kneubühler, M. (2017). Tree Density and Forest Productivity in a Heterogeneous Alpine Environment: Insights from Airborne Laser Scanning and Imaging Spectroscopy. Forests, 8(6), 212. https://doi.org/10.3390/f8060212






