Quantification of Phosphorus Exports from a Small Forested Headwater-Catchment in the Eastern Ore Mountains, Germany
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site Description
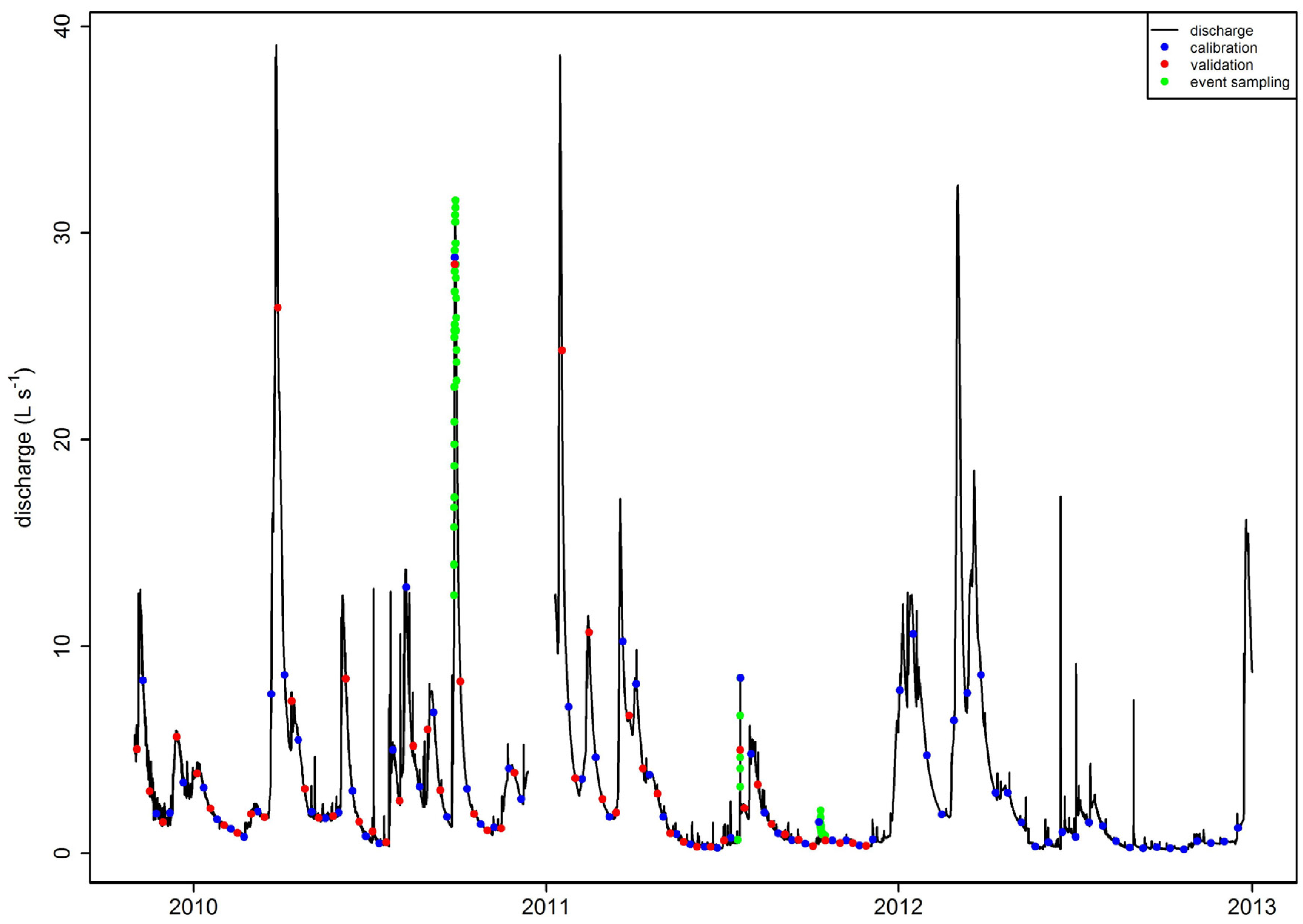
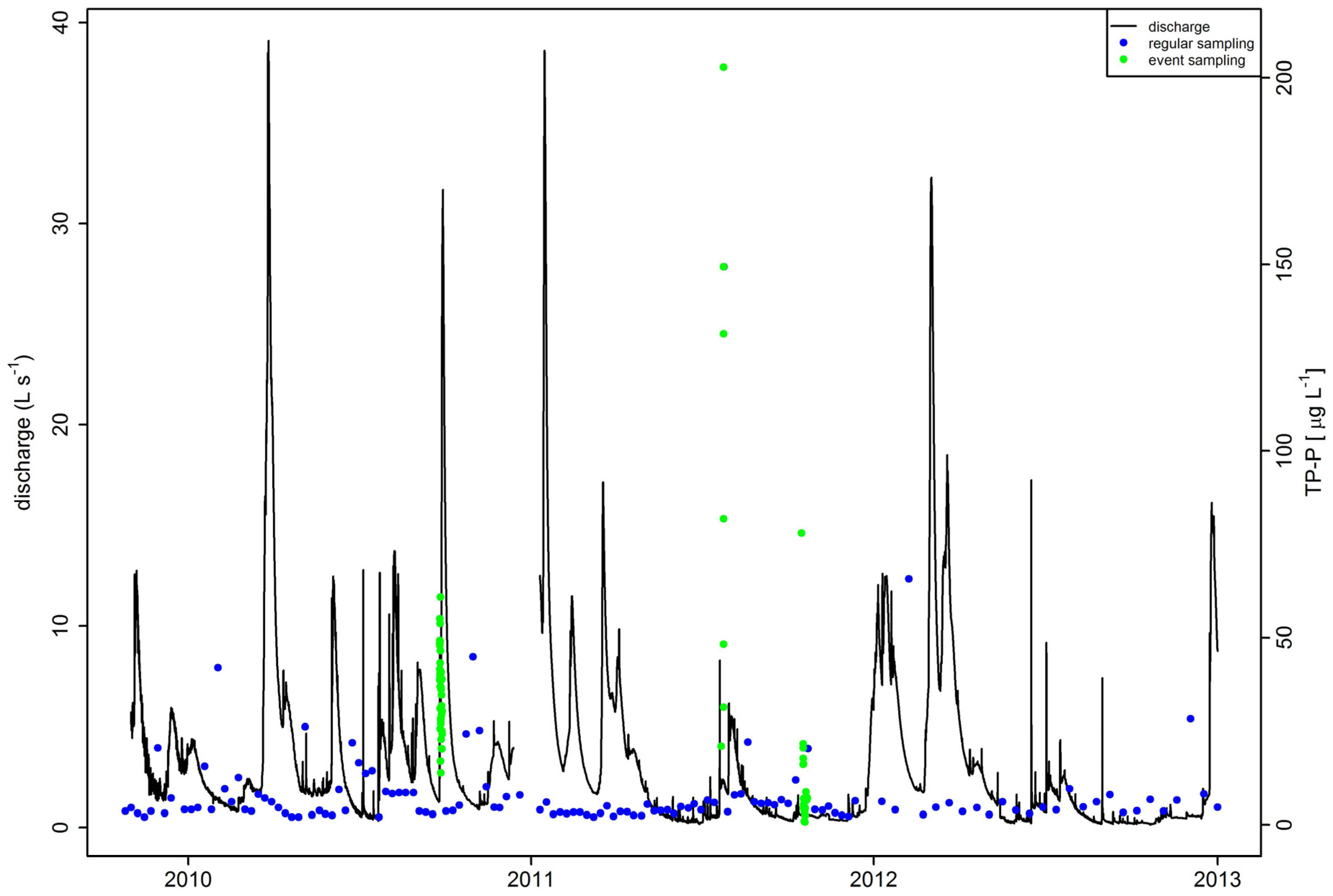
2.2. Water Sampling and Chemical Analysis
2.3. Load Calculations
3. Results and Discussion
3.1. Phosphorus Concentrations
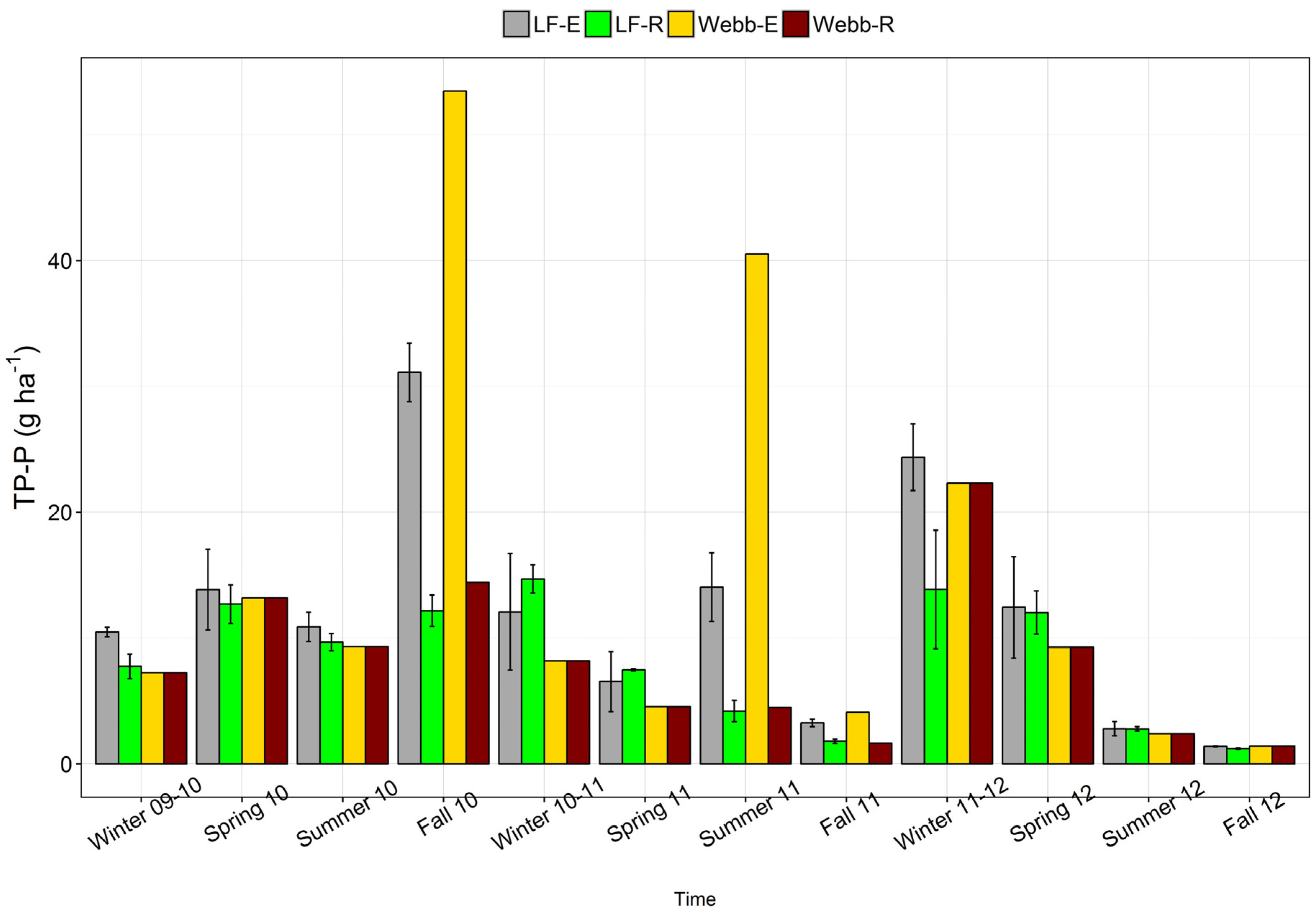
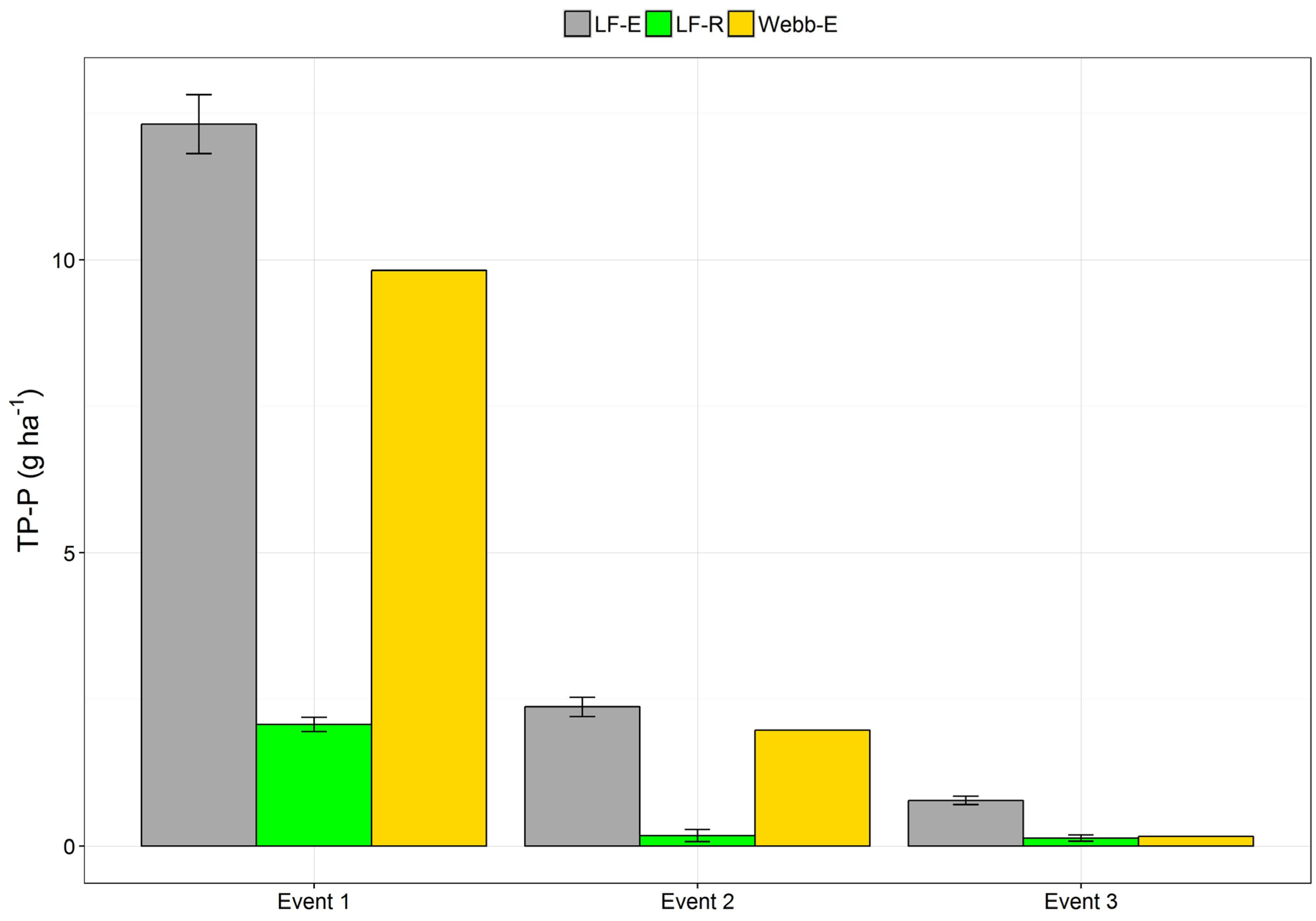
3.2. Phosphorus Fluxes
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lang, F.; Bauhus, J.; Frossard, E.; George, E.; Kaiser, K.; Kaupenjohann, M.; Krüger, J.; Matzner, E.; Polle, A.; Prietzel, J.; et al. Phosphorus in forest ecosystems: New insights from an ecosystem nutrition perspective. J. Plant Nutr. Soil Sci. 2016, 179, 129–135. [Google Scholar] [CrossRef]
- Walker, T.W.; Syers, J.K. The fate of phosphorus during pedogenesis. Geoderma 1976, 15, 1–19. [Google Scholar] [CrossRef]
- Haygarth, P.M.; Hepworth, L.; Jarvis, S.C. Forms of phosphorus transfer in hydrological pathways from soil under grazed grassland. Eur. J. Soil Sci. 1998, 49, 65–72. [Google Scholar] [CrossRef]
- Vuorenmaa, J.; Rekolainen, S.; Lepistö, A.; Kenttämies, K.; Kauppila, P. Losses of Nitrogen and Phosphorus from Agricultural and Forest Areas in Finland during the 1980s and 1990s. Environ. Monit. Assess. 2002, 76, 213–248. [Google Scholar] [CrossRef] [PubMed]
- Verheyen, D.; Gaelen, N.V.; Ronchi, B.; Batelaan, O.; Struyf, E.; Govers, G.; Merckx, R.; Diels, J. Dissolved phosphorus transport from soil to surface water in catchments with different land use. AMBIO 2015, 44, 228–240. [Google Scholar] [CrossRef] [PubMed]
- Bol, R.; Julich, D.; Brödlin, D.; Siemens, J.; Kaiser, K.; Dippold, M.A.; Spielvogel, S.; Zilla, T.; Mewes, D.; von Blanckenburg, F.; et al. Dissolved and colloidal phosphorus fluxes in forest ecosystems—an almost blind spot in ecosystem research. J. Plant Nutr. Soil Sci. 2016, 179, 425–438. [Google Scholar] [CrossRef]
- van der Heijden, G.; Legout, A.; Pollier, B.; Bréchet, C.; Ranger, J.; Dambrine, E. Tracing and modeling preferential flow in a forest soil—Potential impact on nutrient leaching. Geoderma 2013, 195–196, 12–22. [Google Scholar] [CrossRef]
- Julich, D.; Julich, S.; Feger, K.-H. Phosphorus in Preferential Flow Pathways of Forest Soils in Germany. Forests 2016, 8, 19. [Google Scholar] [CrossRef]
- Kerr, J.G.; Eimers, M.C.; Yao, H. Estimating stream solute loads from fixed frequency sampling regimes: The importance of considering multiple solutes and seasonal fluxes in the design of long-term stream monitoring networks. Hydrol. Process. 2016, 30, 1521–1535. [Google Scholar] [CrossRef]
- Yanai, R.D.; Tokuchi, N.; Campbell, J.L.; Green, M.B.; Matsuzaki, E.; Laseter, S.N.; Brown, C.L.; Bailey, A.S.; Lyons, P.; Levine, C.R.; et al. Sources of uncertainty in estimating stream solute export from headwater catchments at three sites. Hydrol. Process. 2015, 29, 1793–1805. [Google Scholar] [CrossRef]
- Harmel, R.D.; Cooper, R.J.; Slade, R.M.; Haney, R.L.; Arnold, J.G. Cumulative uncertainty in measured streamflow and water quality data for small watersheds. Trans. ASABE 2006, 49, 689–701. [Google Scholar] [CrossRef]
- Horowitz, A.J. A Review of Selected Inorganic Surface Water Quality-Monitoring Practices: Are We Really Measuring What We Think, and If So, Are We Doing It Right? Environ. Sci. Technol. 2013, 47, 2471–2486. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, J.W.; Feng, X.; Neal, C.; Robson, A.J. The fine structure of water-quality dynamics: The (high-frequency) wave of the future. Hydrol. Process. 2004, 18, 1353–1359. [Google Scholar] [CrossRef]
- Ullrich, A.; Volk, M. Influence of different nitrate–N monitoring strategies on load estimation as a base for model calibration and evaluation. Environ. Monit. Assess. 2010, 171, 513–527. [Google Scholar] [CrossRef] [PubMed]
- Webb, B.W.; Phillips, J.M.; Walling, D.E.; Littlewood, I.G.; Watts, C.D.; Leeks, G.J.L. Load estimation methodologies for British rivers and their relevance to the LOIS RACS(R) programme. Sci. Total Environ. 1997, 194–195, 379–389. [Google Scholar] [CrossRef]
- Palviainen, M.; Finér, L.; Laurén, A.; Launiainen, S.; Piirainen, S.; Mattsson, T.; Starr, M. Nitrogen, Phosphorus, Carbon, and Suspended Solids Loads from Forest Clear-Cutting and Site Preparation: Long-Term Paired Catchment Studies from Eastern Finland. AMBIO 2013, 43, 218–233. [Google Scholar] [CrossRef] [PubMed]
- Kunimatsu, T.; Hamabata, E.; Sudo, M.; Hida, Y. Comparison of nutrient budgets betwen three forested mountain watersheds on granite bedrock. Water Sci. Technol. 2001, 44, 129–140. [Google Scholar] [PubMed]
- Ide, J.; Chiwa, M.; Higashi, N.; Maruno, R.; Mori, Y.; Otsuki, K. Determining storm sampling requirements for improving precision of annual load estimates of nutrients from a small forested watershed. Environ. Monit. Assess. 2012, 184, 4747–4762. [Google Scholar] [CrossRef] [PubMed]
- Benning, R.; Schua, K.; Schwärzel, K.; Feger, K.H. Fluxes of Nitrogen, Phosphorus, and Dissolved Organic Carbon in the inflow of the Lehnmühle reservoir (Saxony) as compared to streams draining three main land-use types in the catchment. Adv. Geosci. 2012, 32, 1–7. [Google Scholar] [CrossRef]
- Appling, A.P.; Leon, M.C.; McDowell, W.H. Reducing bias and quantifying uncertainty in watershed flux estimates: The R package loadflex. Ecosphere 2015, 6, 1–25. [Google Scholar] [CrossRef]
- Verma, S.; Markus, M.; Cooke, R.A. Development of error correction techniques for nitrate-N load estimation methods. J. Hydrol. 2012, 432–433, 12–25. [Google Scholar] [CrossRef]
- Lorenz, D.; Runkel, R. Rloadest: River Load Estimation; U.S. Geological Survey: Mounds View, MN, USA, 2015.
- Runkel, R. Revisions to LOADEST; U.S. Geological Survey: Reston, VA, USA, 2013.
- Runkel, R.; Crawford, C.; Cohn, T. Load Estimator (LOADEST): A FORTRAN Program for Estimating Constituent Loads in Streams and Rivers; Techniques and Methods Book 4; U.S. Geological Survey: Reston, VA, USA, 2004.
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Dinh, M.-V.; Schramm, T.; Spohn, M.; Matzner, E. Drying–rewetting cycles release phosphorus from forest soils. J. Plant Nutr. Soil Sci. 2016, 179, 670–678. [Google Scholar] [CrossRef]
- Julich, D.; Julich, S.; Feger, K.-H. Phosphorus fractions in preferential flow pathways and soil matrix in hillslope soils in the Thuringian Forest (Central Germany). J. Plant Nutr. Soil Sci. 2017, 180, 407–417. [Google Scholar] [CrossRef]
- Barthold, F.K.; Woods, R.A. Stormflow generation: A meta-analysis of field evidence from small, forested catchments. Water Resour. Res. 2015, 51, 3730–3753. [Google Scholar] [CrossRef]
- Heller, K.; Kleber, A. Hillslope runoff generation influenced by layered subsurface in a headwater catchment in Ore Mountains, Germany. Environ. Earth Sci. 2016, 75, 943. [Google Scholar] [CrossRef]
- Hübner, R.; Heller, K.; Günther, T.; Kleber, A. Monitoring hillslope moisture dynamics with surface ERT for enhancing spatial significance of hydrometric point measurements. Hydrol. Earth Syst. Sci. 2015, 19, 225–240. [Google Scholar] [CrossRef]
- Worrall, F.; Howden, N.J.K.; Burt, T.P. Assessment of sample frequency bias and precision in fluvial flux calculations—An improved low bias estimation method. J. Hydrol. 2013, 503, 101–110. [Google Scholar] [CrossRef]
| Method | Abbreviation | Reference |
|---|---|---|
| Discharge-weighted Flux estimation | Webb | Method E in [15] |
| Linear Interpolation | Lin. I. | [20] |
| Triangular Interpolation | Triang. I. | [20,21] |
| Rectangular Interpolation | Rect. I. | [20,21] |
| Spline Interpolation | Spl. I. | [20] |
| Smooth Spline Interpolation | Sm. Spl. I. | [20] |
| Distance Weighted Interpolation | Dist. Weigh I. | [20] |
| Linear Model | Lin. Mod. | [20] |
| Loadest Regression Model 1 | Reg. Mod. 1 | [22,23,24] |
| Loadest Regression Model 2 | Reg. Mod. 2 | [22,23,24] |
| Loadest Regression Model 3 | Reg. Mod. 3 | [22,23,24] |
| Loadest Regression Model 4 | Reg. Mod. 4 | [22,23,24] |
| Loadest Regression Model 5 | Reg. Mod. 5 | [22,23,24] |
| Loadest Regression Model 6 | Reg. Mod. 6 | [22,23,24] |
| Loadest Regression Model 7 | Reg. Mod. 7 | [22,23,24] |
| Loadest Regression Model 8 | Reg. Mod. 8 | [22,23,24] |
| Loadest Regression Model 9 | Reg. Mod. 9 | [22,23,24] |
| Season | Tot. Discharge (L·s−1) | Samp. Discharge (L·s−1) | TP-P (µg·L−1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mn. | Md. | Min | Max | Mn. | Md. | Min | Max | Mn. | Md. | |
| Winter 09–10 | 0.8 | 6.0 | 2.4 | 2.0 | 0.8 | 5.6 | 2.4 | 1.9 | 3.0 | 42.0 | 10.9 | 6.0 |
| Spring 10 | 1.4 | 39.1 | 5.6 | 2.2 | 1.7 | 26.4 | 5.2 | 2.0 | 2.0 | 26.2 | 6.3 | 3.9 |
| Summer 10 | 0.3 | 13.8 | 3.6 | 2.7 | 0.5 | 12.9 | 3.9 | 3.0 | 2.0 | 21.8 | 9.7 | 8.5 |
| Fall 10 | 0.9 | 31.7 | 4.1 | 2.5 | 1.1 | 9.5 | 3.6 | 3.0 | 2.7 | 44.9 | 12.0 | 4.6 |
| Winter 10–11 | 2.4 | 38.6 | 7.2 | 4.5 | 2.6 | 24.3 | 7.4 | 4.1 | 2.5 | 8.4 | 4.6 | 3.5 |
| Spring 11 | 0.4 | 17.2 | 3.5 | 2.3 | 0.4 | 10.2 | 3.4 | 2.0 | 2.0 | 5.4 | 3.3 | 3.4 |
| Summer 11 | 0.2 | 8.3 | 1.4 | 0.7 | 0.3 | 4.8 | 1.4 | 0.7 | 3.3 | 22.0 | 8.0 | 5.8 |
| Fall 11 | 0.3 | 1.6 | 0.6 | 0.6 | 0.3 | 0.9 | 0.6 | 0.6 | 2.2 | 21.0 | 7.4 | 5.2 |
| Winter 11–12 | 0.3 | 12.6 | 4.4 | 3.0 | 0.5 | 10.6 | 4.2 | 3.3 | 2.6 | 65.7 | 16.4 | 5.3 |
| Spring 12 | 0.2 | 32.3 | 5.7 | 3.1 | 0.3 | 8.6 | 4.0 | 2.9 | 2.6 | 6.0 | 4.3 | 4.1 |
| Summer 12 | 0.2 | 17.3 | 1.1 | 0.9 | 0.3 | 1.5 | 0.9 | 0.8 | 2.9 | 9.5 | 5.6 | 4.7 |
| Fall 12 | 0.1 | 1.1 | 0.4 | 0.3 | 0.2 | 0.6 | 0.3 | 0.3 | 3.1 | 28.2 | 8.6 | 5.0 |
| Event | Discharge (L·s−1) | TP-P (µg·L−1) | ||||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Mn. | Md. | Min | Max | Mn. | Md. | |
| Event 1 | 12.5 | 31.6 | 25.8 | 26.4 | 2.7 | 60.9 | 34.3 | 36.8 |
| Event 2 | 0.6 | 8.5 | 4.7 | 4.6 | 21.0 | 202.8 | 95.1 | 81.9 |
| Event 3 | 0.9 | 2.1 | 1.1 | 1.0 | b.d. | 78.0 | 11.4 | 6.5 |
| Method | R² | MAE | ||
|---|---|---|---|---|
| TP-P | TP-P | |||
| R | E | R | E | |
| Lin. I. | 0.44 | 0.96 | 0.05 | 0.12 |
| Triang. I. | 0.62 | 0.97 | 0.06 | 0.14 |
| Rect. I. | 0.41 | 0.91 | 0.06 | 0.15 |
| Spl. I. | 0.46 | 0.94 | 0.05 | 0.13 |
| Sm. Spl. I. | 0.61 | 0.36 | 0.06 | 0.27 |
| Dist. Weigh I. | 0.50 | 0.97 | 0.05 | 0.12 |
| Lin. Mod. | 0.61 | 0.37 | 0.05 | 0.26 |
| Reg. Mod. 1 | 0.60 | 0.37 | 0.05 | 0.26 |
| Reg. Mod. 2 | 0.55 | 0.37 | 0.06 | 0.26 |
| Reg. Mod. 3 | 0.60 | 0.36 | 0.05 | 0.26 |
| Reg. Mod. 4 | 0.67 | 0.60 | 0.05 | 0.24 |
| Reg. Mod. 5 | 0.56 | 0.37 | 0.06 | 0.26 |
| Reg. Mod. 6 | 0.56 | 0.60 | 0.05 | 0.24 |
| Reg. Mod. 7 | 0.66 | 0.60 | 0.05 | 0.24 |
| Reg. Mod. 8 | 0.57 | 0.59 | 0.06 | 0.24 |
| Reg. Mod. 9 | 0.57 | 0.60 | 0.06 | 0.24 |
| Year | LF-R | LF-E | Webb-R | Webb-E | ||||
|---|---|---|---|---|---|---|---|---|
| Mn. | Std.Dev. | Mn. | Std.Dev. | Mn. | Std.Dev. | Mn. | Std.Dev. | |
| 2010 | 42.3 | 1.1 | 66.3 | 1.8 | 44.2 | n.a. | 83.2 | n.a. |
| 2011 | 28.2 | 0.6 | 35.9 | 2.5 | 18.9 | n.a. | 57.3 | n.a. |
| 2012 | 29.9 | 1.7 | 41.0 | 1.8 | 35.4 | n.a. | 35.4 | n.a. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Julich, S.; Benning, R.; Julich, D.; Feger, K.-H. Quantification of Phosphorus Exports from a Small Forested Headwater-Catchment in the Eastern Ore Mountains, Germany. Forests 2017, 8, 206. https://doi.org/10.3390/f8060206
Julich S, Benning R, Julich D, Feger K-H. Quantification of Phosphorus Exports from a Small Forested Headwater-Catchment in the Eastern Ore Mountains, Germany. Forests. 2017; 8(6):206. https://doi.org/10.3390/f8060206
Chicago/Turabian StyleJulich, Stefan, Raphael Benning, Dorit Julich, and Karl-Heinz Feger. 2017. "Quantification of Phosphorus Exports from a Small Forested Headwater-Catchment in the Eastern Ore Mountains, Germany" Forests 8, no. 6: 206. https://doi.org/10.3390/f8060206
APA StyleJulich, S., Benning, R., Julich, D., & Feger, K.-H. (2017). Quantification of Phosphorus Exports from a Small Forested Headwater-Catchment in the Eastern Ore Mountains, Germany. Forests, 8(6), 206. https://doi.org/10.3390/f8060206







