How Similar Are Forest Disturbance Maps Derived from Different Landsat Time Series Algorithms?
Abstract
:1. Introduction
- How do the map products derived from the seven algorithms (Table 1) agree in terms of aggregate area disturbed over six Landsat scenes distributed across diverse forested regions of the conterminous US? Similarly, how do these compare with disturbance area estimates determined from an independent probability sample where disturbance was identified by human interpretation using the TimeSync-based methodology [22]?
- How much agreement is there at the pixel level among the map products in their spatial depictions of forest disturbance over time?
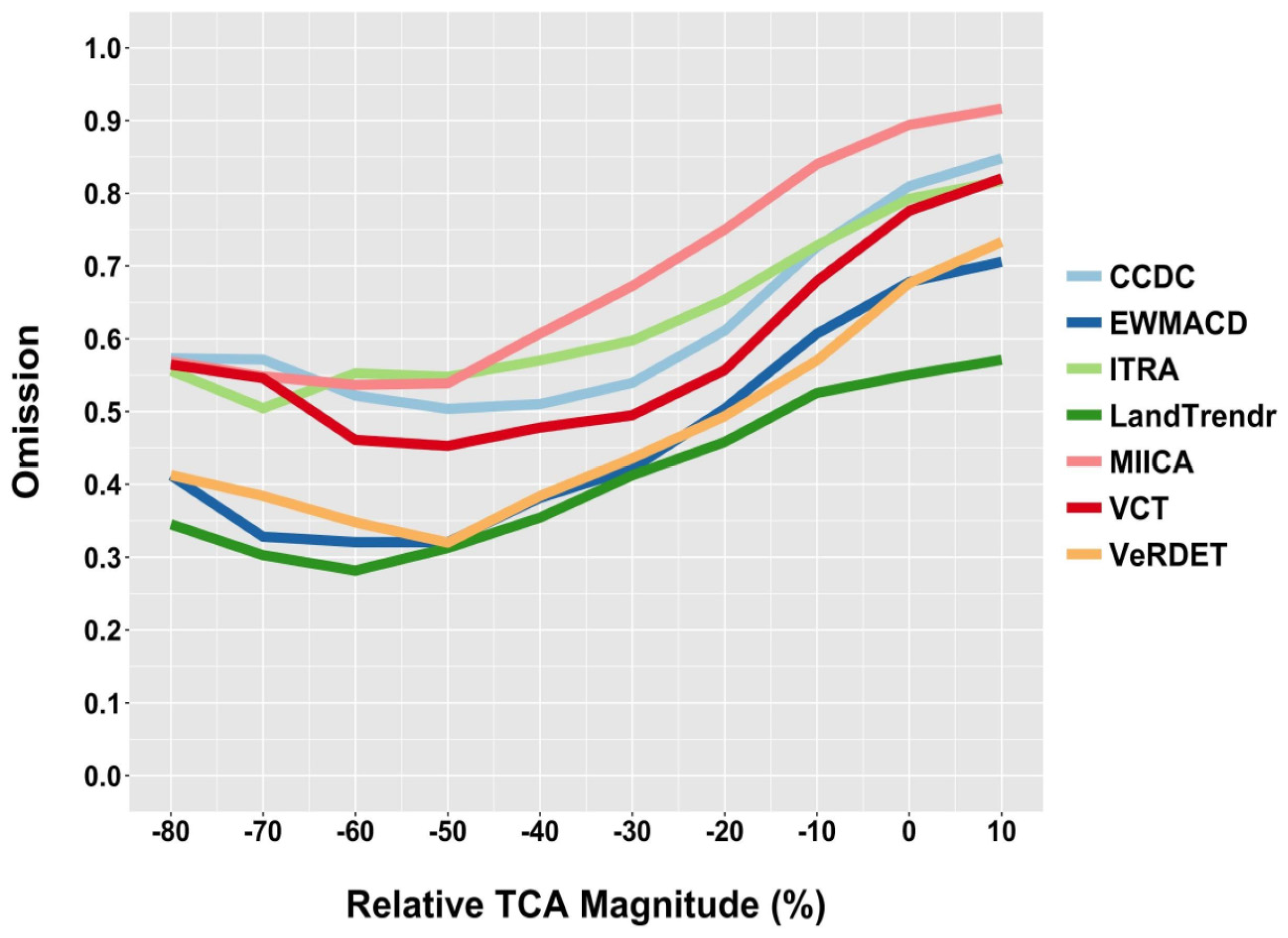
- Compared to a reference dataset, how do mapped disturbance omission and commission differ among the map products, and how closely related are these to the spectral change magnitude?
2. Materials and Methods
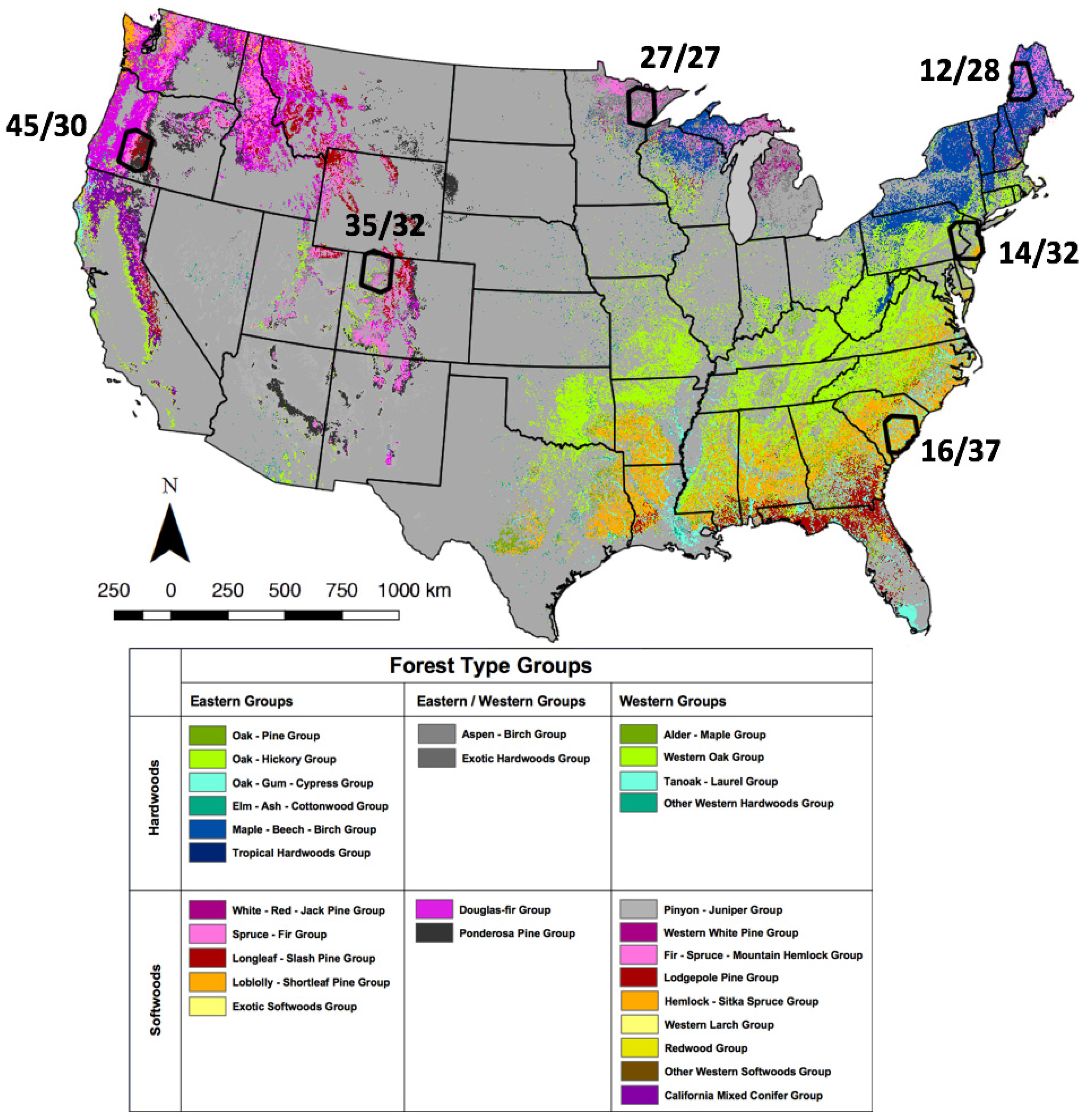
2.1. Study Scenes
2.2. Landsat Images, Synthetic Images, and Map Products
2.3. Reference Data
2.4. Aggregate Disturbance Rates (Question 1)
2.5. Map-to-Map Agreement (Question 2)
2.6. Map-to-Reference Data Agreement (Question 3)
3. Results
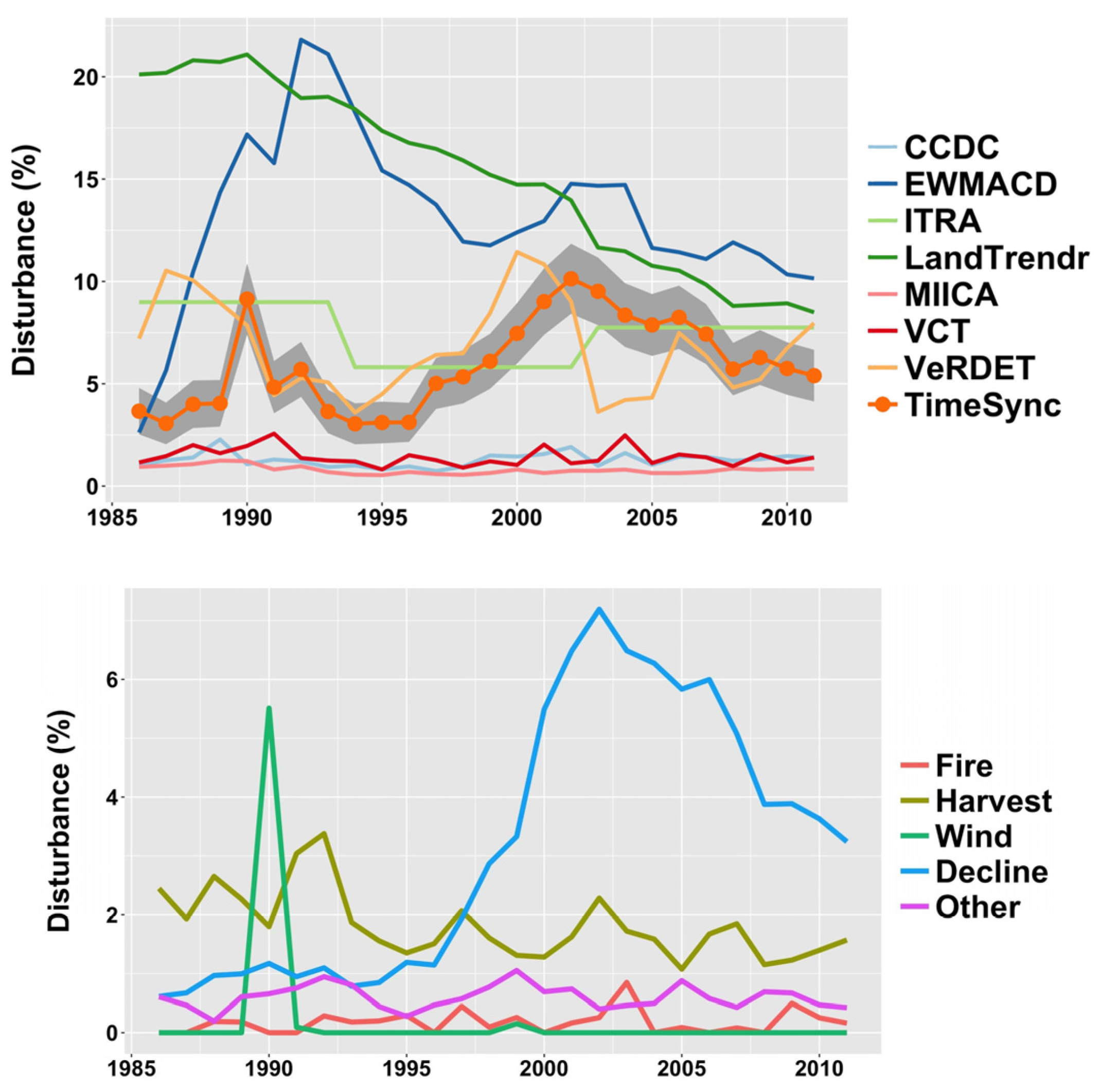
3.1. Aggregate Disturbance Rates (Question 1)
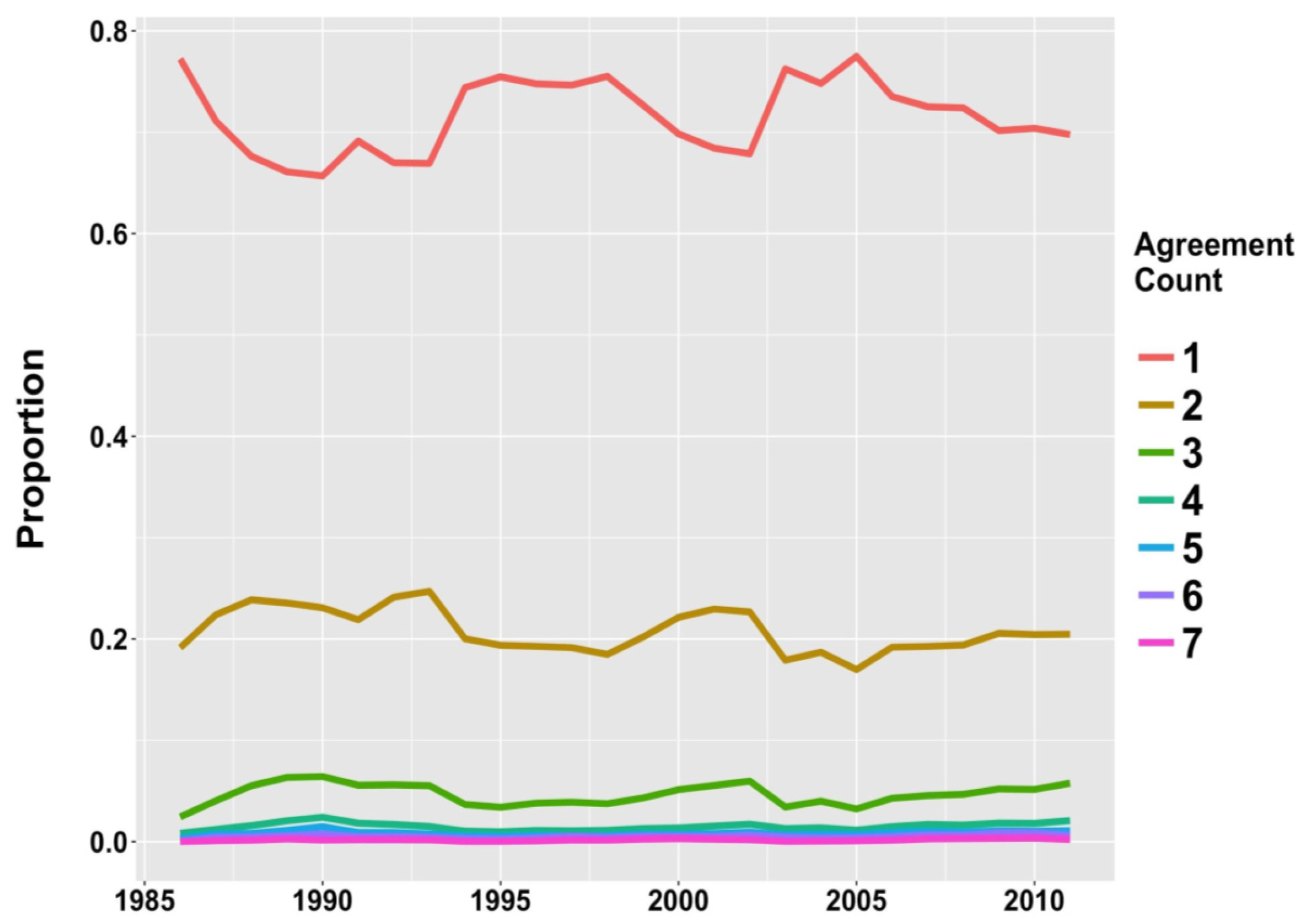
3.2. Map-to-Map Agreement (Question 2)
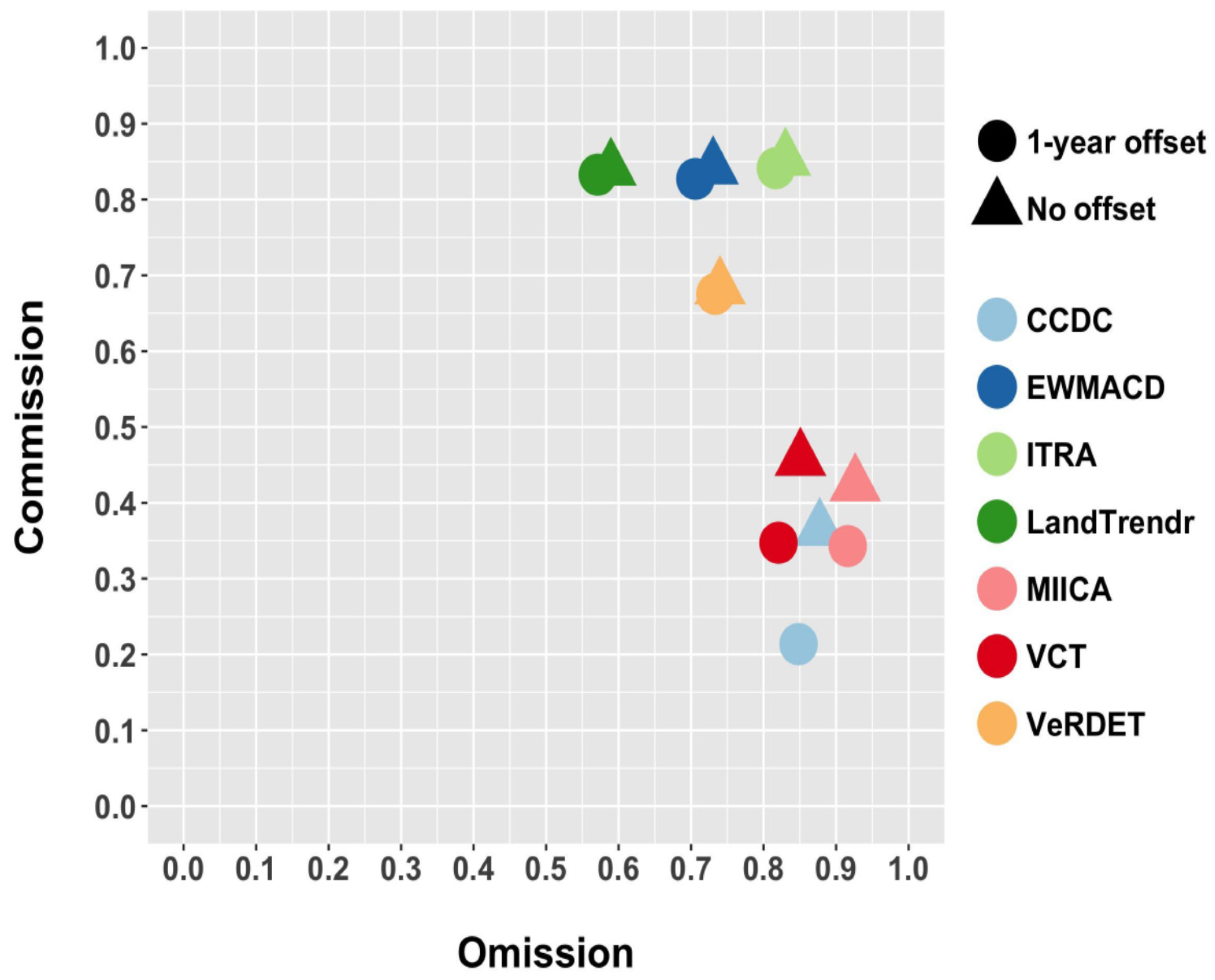
3.3. Map-to-Reference Data Agreement (Question 3)
4. Discussion
4.1. Disagreement among Disturbance Maps
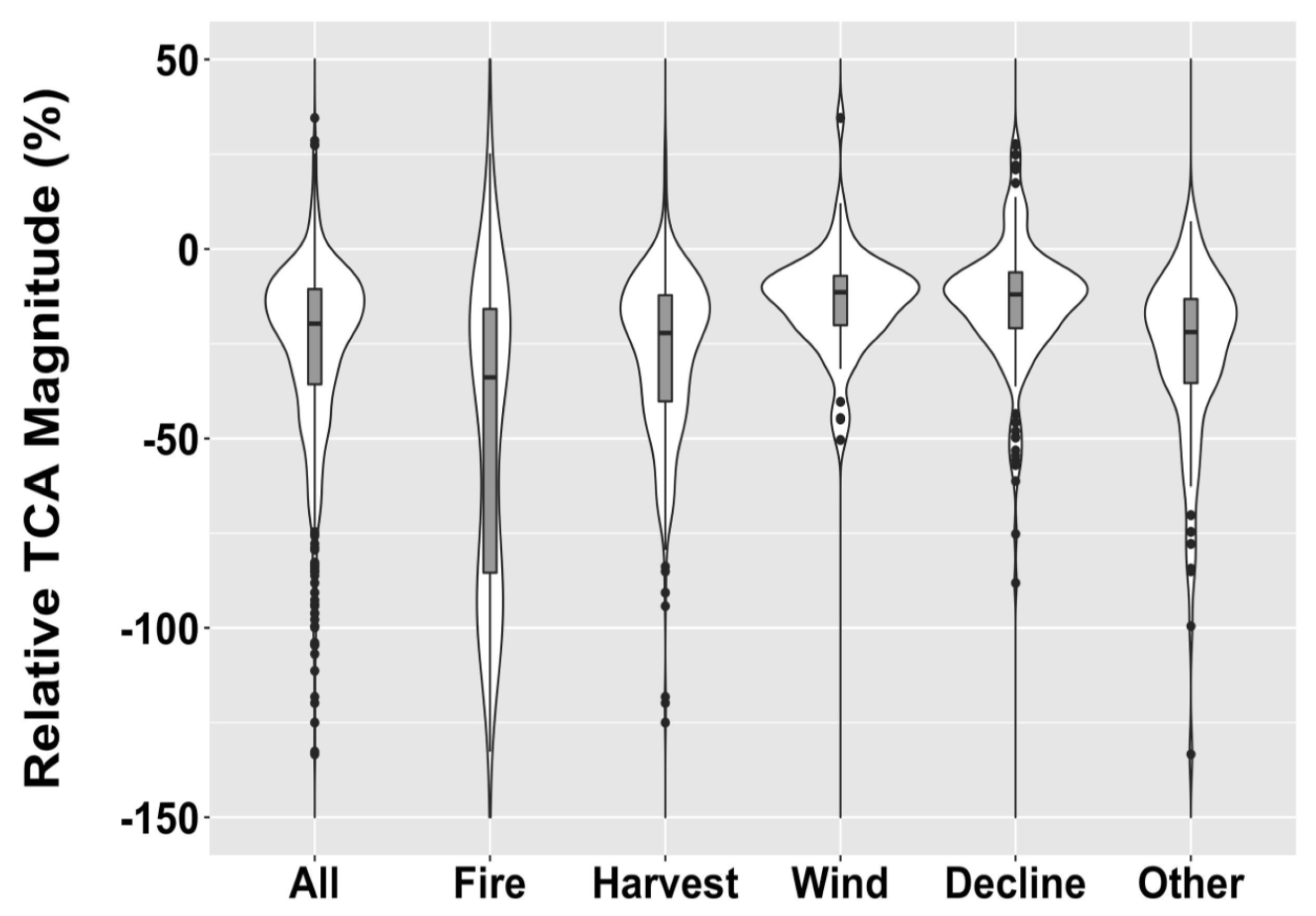
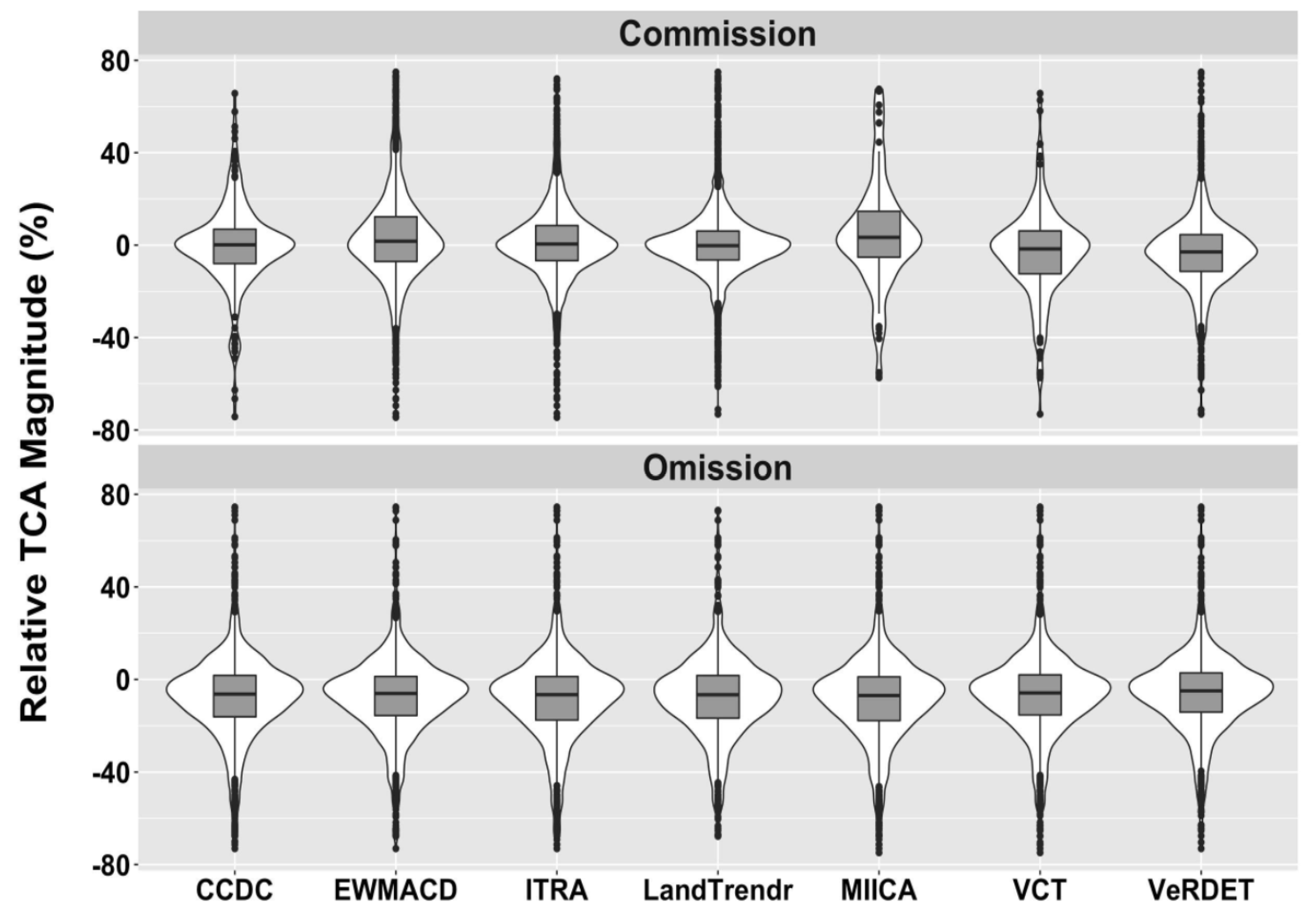
4.2. Disturbance Magnitude
4.3. Why Are the Maps So Different?
5. Conclusions
- Spectral change magnitudes associated with forest disturbance are highly variable, with a population likely to be skewed towards lower-magnitude occurrences. Such disturbances are challenging to map because they are often difficult to distinguish from spectral noise common in temporal trajectories of spectral signals.
- Landsat disturbance maps derived from automated algorithms are likely to be quite dissimilar. This is true both of the maps themselves and of aggregate rates of disturbance mapped over time.
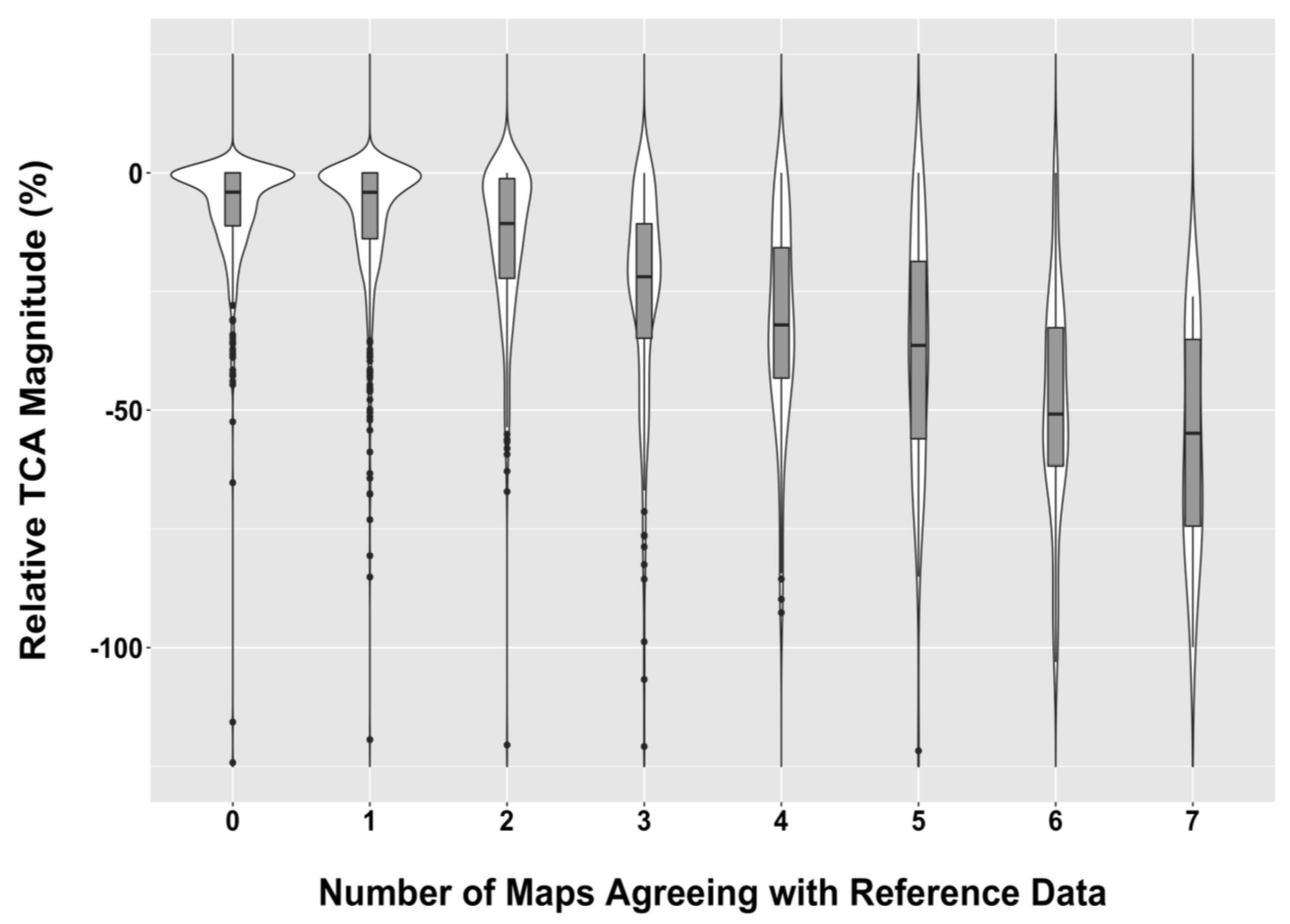
- Maps from different algorithms are more likely to agree with each other about the location and timing of forest disturbance as the change magnitude becomes greater.
- Algorithms that target a broader set of disturbance magnitudes are likely to have more commission and less omission errors than algorithms that target mostly greater magnitude disturbances.
- A spectral change magnitude threshold (~50% relative TCA) was identified; for changes with a magnitude smaller than this threshold, the omission error increases. Algorithms that attempt to detect these lesser-magnitude disturbances are likely to exhibit greater levels of mapping commission.
- Users of forest disturbance maps now have choices among several maps, each derived from different algorithms. Given the strengths and weaknesses of each map with respect to the omission and commission errors and target disturbance populations, a user should be cautious and endeavor to understand how well these maps will suit their needs. It would be irresponsible to assume a given map is by default highly accurate and to not consider how errors might influence use in a variety of contexts.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Seidl, R.; Schelhaas, M.-J.; Rammer, W.; Verkerk, P.J. Increasing forest disturbance in Europe and their impacts on carbon storage. Nat. Clim. Chang. 2014, 4, 806–810. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.G. Disturbance and landscape dynamics in a changing world. Ecology 2010, 91, 2833–2849. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.; Coops, N.C.; Beck, P.S.A.; Chambers, J.Q.; Gongodagamage, C.; Hicke, J.A.; Huang, C.; Kennedy, R.; Krofcheck, D.J.; Litvak, M.; et al. Global satellite monitoring of climate-induced vegetation disturbances. Trends Plant Sci. 2015, 20, 114–123. [Google Scholar] [CrossRef] [PubMed]
- Schwantes, A.M.; Swenson, J.J.; Jackson, R.B. Quantifying drought-induced tree mortality in the open canopy woodlands of central Texas. Remote Sens. Environ. 2016, 181, 54–64. [Google Scholar] [CrossRef]
- Brooks, E.B.; Wynne, R.H.; Thomas, V.A.; Blinn, C.E.; Coulston, J.W. On-the-fly massively multitemporal change detection using statistical quality control charts and Landsat data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3316–3332. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Stehman, S.V.; Schroeder, T.A.; Bell, D.M.; Masek, J.G.; Huang, C.; Meigs, G.W. Forest disturbance in the conterminous US from 1985–2012: The emerging dominance of forest decline. For. Ecol. Manag. 2016, 360, 242–252. [Google Scholar] [CrossRef]
- Cohen, W.B.; Goward, S.N. Landsat’s role in ecological applications of remote sensing. BioScience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 1–55. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B.; Pfaff, E.; Braaten, J.; Nelson, P. Spatial and temporal patterns of forest disturbance and regrowth within the area of the Northwest Forest Plan. Remote Sens. Environ. 2012, 122, 117–133. [Google Scholar] [CrossRef]
- Mildrexler, D.; Yang, Z.; Cohen, W.B. A forest vulnerability index based on drought and high temperatures. Remote Sens. Environ. 2016, 173, 314–325. [Google Scholar] [CrossRef]
- Sulle-Menashe, D.; Kennedy, R.E.; Yang, Z.; Braaten, J.; Krankina, O.; Friedl, M.A. Detecting forest disturbance in the Pacific Northwest from MODIS time series using temporal segmentation. Remote Sens. Environ. 2014, 151, 114–123. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Andréfouët, S.; Cohen, W.B.; Gómez, C.; Griffiths, P.; Hais, M.; Healey, S.P.; Helmer, E.; Hostert, P.; Lyons, M.B.; et al. Bringing an ecological view of change to Landsat- based remote sensing. Front. Ecol. Environ. 2014, 12, 339–346. [Google Scholar] [CrossRef]
- Banskota, A.; Kayastha, N.; Falkowski, M.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest monitoring using Landsat time-series data—A review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Xian, G.; Homer, C.; Tolk, B. Monitoring gradual ecosystem change using Landsat time series analyses: Case studies in selected forest and rangeland ecosystems. Remote Sens. Environ. 2012, 122, 92–105. [Google Scholar] [CrossRef]
- Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ. 2010, 114, 183–198. [Google Scholar] [CrossRef]
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the National Land Cover Database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic Landsat images based on all available Landsat data: Predicting Landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
- Hughes, M.J. New Remote Sensing Methods for Detecting and Quantifying Forest Disturbance and Regeneration in the Eastern United States. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2014. [Google Scholar]
- Cohen, W.B.; Yang, Z.; Kennedy, R.E. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync—Tools for calibration and validation. Remote Sens. Environ. 2010, 114, 2911–2924. [Google Scholar] [CrossRef]
- Schleeweis, K.; Goward, S.N.; Huang, C.; Masek, J.G.; Moisen, G.G.; Kennedy, R.E.; Thomas, N.E. Regional dynamics of forest canopy change and underlying causal processes in the contiguous U.S. J. Geophys. Res. Biogeosci. 2013, 118, 1035–1053. [Google Scholar] [CrossRef]
- Reufenacht, B.; Finco, M.V.; Nelson, M.D.; Czaplewski, R.; Helmer, E.H.; Blackard, J.A.; Holden, G.R.; Lister, A.J.; Salajanu, D.; Weyerman, D.; Winterberger, K. Conterminous U.S. and Alaska forest type mapping using forest inventory and analysis data. Photogramm. Eng. Remote Sens. 2008, 74, 1379–1388. [Google Scholar] [CrossRef]
- United State Geological Survey (USGS). Product Guide: Landsat 4–7 Climate Data Record (CDR) Surface Reflectance. 2016. Available online: http://landsat.usgs.gov/documents/cdr_sr_product_guide.pdf (accessed on 12 December 2016).
- Masek, J.G.; Vermote, E.F.; Saleous, N.; Wolfe, R.; Hall, F.G.; Huemmrich, F.; Gao, F.; Kutler, J.; Lim, T.K. A Landsat Surface Reflectance Data Set for North America, 1990–2000. Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.E. Comparison between Landsat-derived disturbance history and lidar to predict current forest structure. Remote Sens. Environ. 2012, 122, 146–165. [Google Scholar] [CrossRef]
- Masek, J.G.; Goward, S.N.; Kennedy, R.E.; Cohen, W.B.; Moisen, G.G.; Schleeweis, K.; Huang, C. United States forest disturbance trends observed using Landsat time series. Ecosystems 2013, 16, 1087–1104. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Schroeder, T.A.; Healey, S.P.; Moisen, G.G.; Frescino, T.; Cohen, W.B.; Huang, C.; Kennedy, R.E.; Yang, Z. Improving estimates of forest disturbance by combining observa-tions from Landsat time series with US Forest Service Forest Inventory and Analysis data. Remote Sens. Environ. 2014, 154, 61–73. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1977; p. 428. [Google Scholar]
- Avitabile, V.; Herold, M.; Henry, M.; Schmullius, C. Mapping biomass with remote sensing: A comparison of methods for the case study of Uganda. Carbon Balance Manag. 2011, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Pflugmacher, D.; Krankina, O.N.; Cohen, W.B.; Friedl, M.; Sulla-Menashe, D.; Kennedy, R.; Nelson, P.; Loboda, T.; Kuemmerle, T.; Dyukarev, E.; et al. Comparison and assessment of coarse resolution land cover maps for Northern Eurasia. Remote Sens. Environ. 2011, 115, 3539–3553. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; Baccini, A.; Asner, G.P.; Goetz, S.J.; Harris, N.L.; Brown, S. Uncertainty in the spatial distribution of tropical forest biomass: A comparison of pan-tropical maps. Carbon Balance Manag. 2013, 8, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cohen, W.B.; Spies, T.A.; Alig, R.J.; Oetter, D.R.; Maiersperger, T.K.; Fiorella, M. Characterizing 23 years (1972–1995) of stand replacement disturbance in western Oregon forests with Landsat imagery. Ecosystems 2002, 5, 122–137. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Spies, T.A.; Moeur, M.; Pflugmacher, D.; Whitley, M.G.; Lefsky, M.A. The Relative Impact of Harvest and Fire upon Landscape-Level Dynamics of Older Forests: Lessons from the Northwest Forest Plan. Ecosystems 2008, 11, 1106–1119. [Google Scholar] [CrossRef]
- Dale, V.H.; Joyce, L.A.; McNulty, S.; Neilson, R.P.; Ayres, M.P.; Flannigan, M.D.; Hanson, P.J.; Irland, L.C.; Lugo, A.E.; Peterson, C.J.; et al. Climate change and forest disturbances. BioScience 2001, 51, 723–734. [Google Scholar] [CrossRef]
- Espírito-Santo, F.D.B.; Gloor, M.; Keller, M.; Malhi, Y.; Saatchi, S.; Nelson, B.; Junior, R.C.O.; Pereira, C.; Lloyd, J.; Frolking, S.; et al. Size and frequency of natural forest disturbances and the Amazon forest carbon balance. Nat. Commun. 2014, 5, 3434. [Google Scholar] [PubMed]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-resolution global maps of 21st-century forest cover change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
| Algorithm | Citations | Disturbance Target Population | Bands/Indices, This Study | Basic Approach |
|---|---|---|---|---|
| LandTrendr (Landsat-based detection of Trends in Disturbance and Recovery) | [15] | Discrete events and gradual trends; broad range of disturbance magnitudes; forests only | NBR | Temporal segmentation of annual series; pixel as analysis unit |
| ITRA (Image Trends from Regression Analysis) | [16] | Gradual trends; broad range disturbance magnitudes; all woody vegetation | NDVI | Slope of annual series over multi-year epochs; pixel as analysis unit |
| VCT (Vegetation Change Tracker) | [17] | Discrete events; limited range of disturbance magnitudes; forests only | Forestness Index | Multi-year departure of annual series from previous year; pixel as analysis unit |
| EWMACD (Exponentially Weighted Moving Average Change Detection) | [5] | Discrete events; broad range of disturbance magnitudes; forests only | NDVI | Multi-year departure from phenology model based on every clear observation from previous years; pixel as analysis unit |
| MIICA (Multi-index Integrated Change Analysis) | [18] | Discrete events; limited range of disturbance magnitudes; all land cover types | NBR, NDVI, Change Vector, Relative Change Vector | Bi-temporal differencing of annual series; pixel as analysis unit |
| CCDC (Continuous Change Detection and Classification) | [19,20] | Discrete events; limited range of disturbance magnitudes; all land cover types | Bands 2–5, 7 | Multi-year departure from phenology model based on every clear observation from previous years; pixel as analysis unit |
| VeRDET (Vegetation Regeneration and Disturbance Estimates Through Time) | [21] | Discrete events and gradual trends; broad range of disturbance magnitudes; forests only | NDMI | Temporal segmentation of annual series; pixel as analysis unit (after initial spatial segmentation) |
| Area (ha) per Landsat Path/Row | |||||||
|---|---|---|---|---|---|---|---|
| Forest Type Group | 12/28 | 14/32 | 16/37 | 27/27 | 35/32 | 45/30 | Total |
| White/Red/Jack Pine Group | 644 | 94 | 0 | 35,288 | 0 | 0 | 36,025 |
| Spruce/Fir Group | 661,588 | 19 | 0 | 430,213 | 0 | 0 | 1,091,819 |
| Longleaf/Slash Pine Group | 0 | 0 | 5631 | 0 | 0 | 0 | 5631 |
| Loblolly/Shortleaf Pine Group | 0 | 163,956 | 1,069,100 | 0 | 0 | 0 | 1,233,056 |
| Pinyon/Juniper Group | 0 | 6600 | 0 | 0 | 168,969 | 8131 | 183,700 |
| Douglas-fir Group | 0 | 0 | 0 | 0 | 2388 | 445,938 | 448,325 |
| Ponderosa Pine Group | 0 | 0 | 0 | 0 | 3119 | 597,481 | 600,600 |
| Western White Pine Group | 0 | 0 | 0 | 0 | 0 | 388 | 388 |
| Fir/Spruce/Mountain Hemlock Group | 0 | 0 | 0 | 0 | 267,994 | 401,731 | 669,725 |
| Lodgepole Pine Group | 0 | 0 | 0 | 0 | 82,356 | 367,031 | 449,388 |
| Hemlock/Sitka Spruce Group | 0 | 0 | 0 | 0 | 0 | 350 | 350 |
| Other Western Softwood Group | 0 | 0 | 0 | 0 | 94 | 75 | 169 |
| California Mixed Conifer Group | 0 | 0 | 0 | 0 | 0 | 631 | 631 |
| Exotic Softwoods Group | 0 | 38 | 0 | 0 | 0 | 0 | 38 |
| Oak/Pine Group | 0 | 14,231 | 37,681 | 38 | 0 | 0 | 51,950 |
| Oak/Hickory Group | 0 | 408,519 | 41,188 | 256 | 0 | 0 | 449,963 |
| Oak/Gum/Cypress Group | 0 | 10,625 | 454,731 | 0 | 0 | 0 | 465,356 |
| Elm/Ash/Cottonwood Group | 81 | 14,506 | 10,606 | 9356 | 1056 | 0 | 35,606 |
| Maple/Beech/Birch Group | 673,650 | 37,350 | 0 | 14,581 | 0 | 0 | 725,581 |
| Aspen/Birch Group | 24,188 | 925 | 0 | 1,023,113 | 359,781 | 231 | 1,408,238 |
| Alder/Maple Group | 0 | 0 | 0 | 0 | 0 | 6 | 6 |
| Western Oak Group | 0 | 0 | 0 | 0 | 120,150 | 369 | 120,519 |
| Tanoak/Laurel Group | 0 | 0 | 0 | 0 | 0 | 19 | 19 |
| Other Western Hardwoods Group | 0 | 0 | 0 | 0 | 100 | 0 | 100 |
| Total Forest Area | 1,360,150 | 656,863 | 1,618,938 | 1,512,844 | 1,006,006 | 1,822,381 | 7,977,181 |
| Total Non-Forest Area | 121,700 | 1,407,844 | 314,000 | 287,844 | 1,074,863 | 164,625 | 3,370,876 |
| Total Scene Area | 1,481,850 | 2,064,706 | 1,932,938 | 1,800,688 | 2,080,869 | 1,987,006 | 11,348,056 |
| Percent Forest | 91.8 | 31.8 | 83.8 | 84.0 | 48.3 | 91.7 | 70.3 |
| Harvest | Fire | Decline | Wind | Other | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Map | Omission (%) | Standard Error (%) | Omission (%) | Standard Error (%) | Omission (%) | Standard Error (%) | Omission (%) | Standard Error (%) | Omission (%) | Standard Error (%) |
| CCDC | 63.6 | 2.7 | 66.5 | 6.1 | 98.2 | 0.3 | 86.9 | 0.6 | 83.1 | 4.9 |
| EWMACD | 59.9 | 7.2 | 53.7 | 7.4 | 80.4 | 6.1 | 57.3 | 2.0 | 60.2 | 10.6 |
| ITRA | 68.8 | 7.1 | 62.8 | 12.8 | 93.0 | 2.5 | 85.2 | 0.7 | 64.9 | 6.6 |
| LandTrendr | 53.3 | 1.2 | 40.7 | 4.2 | 58.7 | 6.2 | 70.4 | 1.4 | 61.3 | 8.2 |
| MIICA | 82.0 | 3.2 | 66.5 | 13.0 | 99.5 | 0.2 | 96.7 | 0.2 | 84.6 | 6.6 |
| VCT | 58.0 | 1.9 | 62.8 | 8.5 | 97.6 | 0.8 | 83.6 | 0.8 | 78.1 | 7.8 |
| VeRDET | 53.3 | 7.8 | 44.2 | 4.3 | 89.3 | 3.4 | 64.1 | 3.0 | 60.6 | 9.1 |
| Mean | 62.7 | 4.4 | 56.7 | 8.1 | 88.1 | 2.8 | 77.7 | 1.2 | 70.4 | 7.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cohen, W.B.; Healey, S.P.; Yang, Z.; Stehman, S.V.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Huang, C.; Hughes, M.J.; Kennedy, R.E.; et al. How Similar Are Forest Disturbance Maps Derived from Different Landsat Time Series Algorithms? Forests 2017, 8, 98. https://doi.org/10.3390/f8040098
Cohen WB, Healey SP, Yang Z, Stehman SV, Brewer CK, Brooks EB, Gorelick N, Huang C, Hughes MJ, Kennedy RE, et al. How Similar Are Forest Disturbance Maps Derived from Different Landsat Time Series Algorithms? Forests. 2017; 8(4):98. https://doi.org/10.3390/f8040098
Chicago/Turabian StyleCohen, Warren B., Sean P. Healey, Zhiqiang Yang, Stephen V. Stehman, C. Kenneth Brewer, Evan B. Brooks, Noel Gorelick, Chengqaun Huang, M. Joseph Hughes, Robert E. Kennedy, and et al. 2017. "How Similar Are Forest Disturbance Maps Derived from Different Landsat Time Series Algorithms?" Forests 8, no. 4: 98. https://doi.org/10.3390/f8040098
APA StyleCohen, W. B., Healey, S. P., Yang, Z., Stehman, S. V., Brewer, C. K., Brooks, E. B., Gorelick, N., Huang, C., Hughes, M. J., Kennedy, R. E., Loveland, T. R., Moisen, G. G., Schroeder, T. A., Vogelmann, J. E., Woodcock, C. E., Yang, L., & Zhu, Z. (2017). How Similar Are Forest Disturbance Maps Derived from Different Landsat Time Series Algorithms? Forests, 8(4), 98. https://doi.org/10.3390/f8040098










