Biophysical and Economic Analysis of Black Spruce Regeneration in Eastern Canada Using Global Climate Model Productivity Outputs
Abstract
:1. Introduction
2. Methods
2.1. Overview
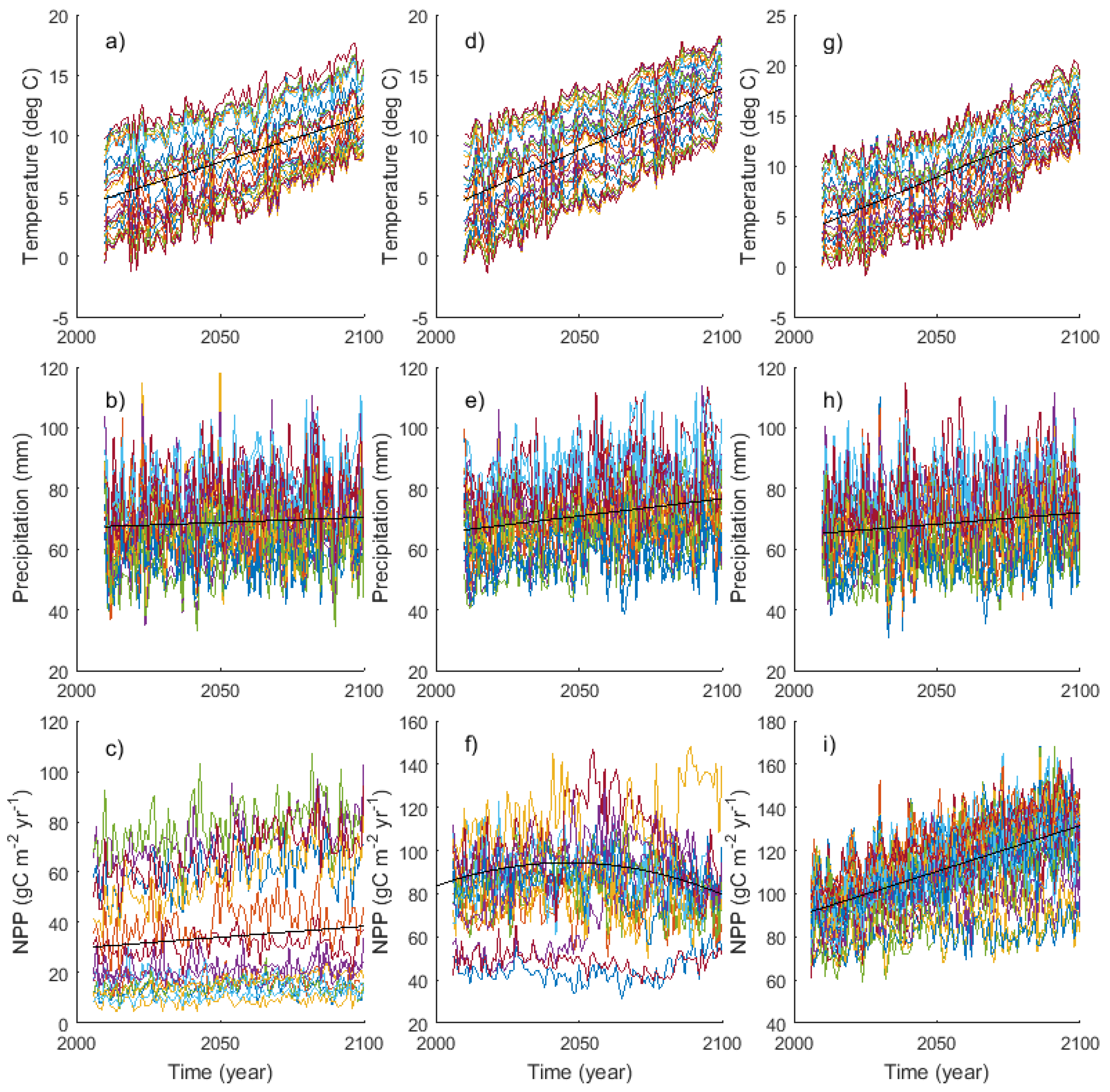
2.2. GCM-Simulated Forest Productivity Estimates
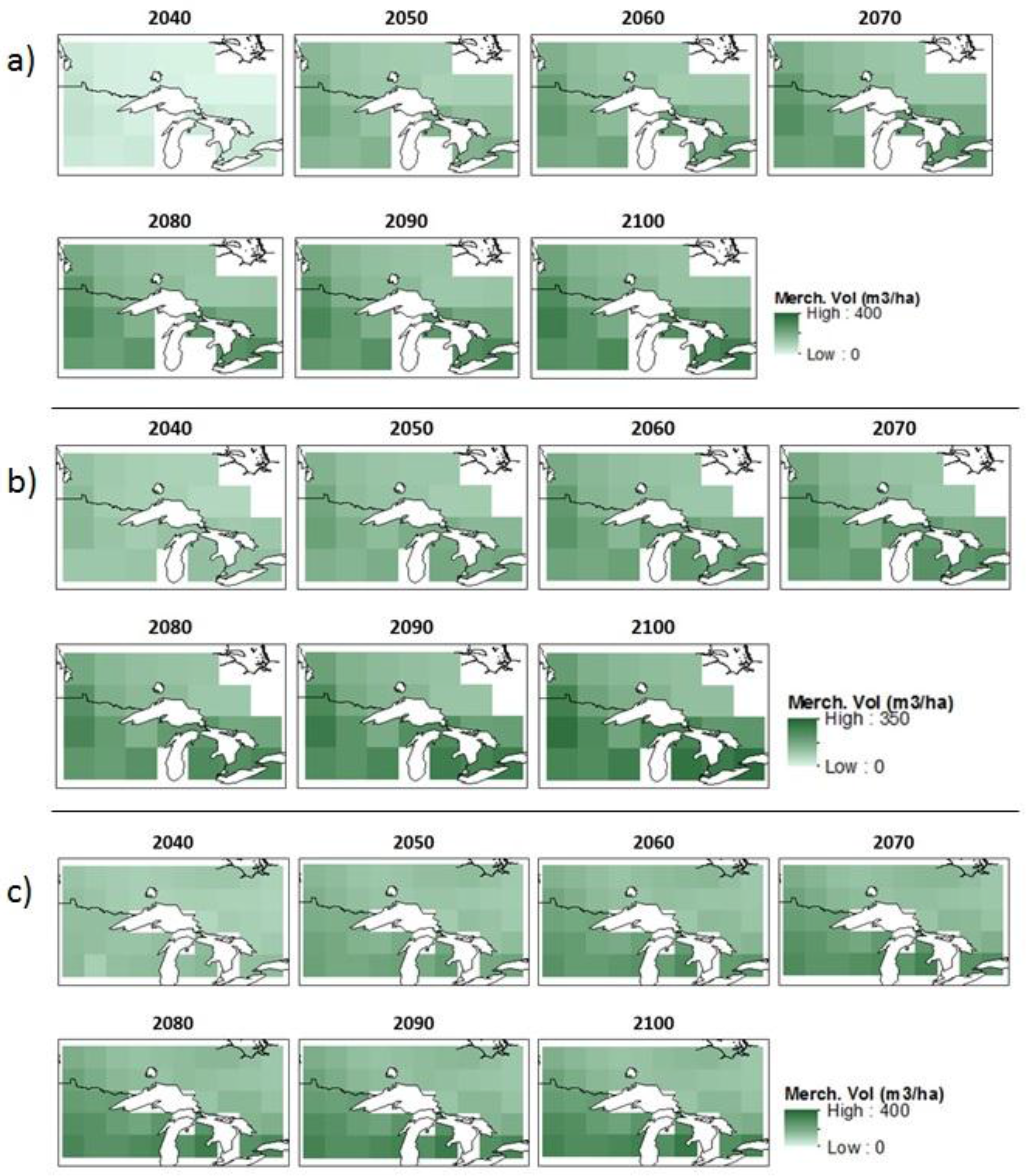
2.3. Growth and Yield Estimates and NPP Adjustments
2.4. Economic Calculations
2.4.1. Wood-Only Calculations
2.4.2. Wood and Carbon Sequestration Calculations
2.5. Sensitivity Analysis
3. Results and Discussion
3.1. Climate, NPP, and Growth Projections
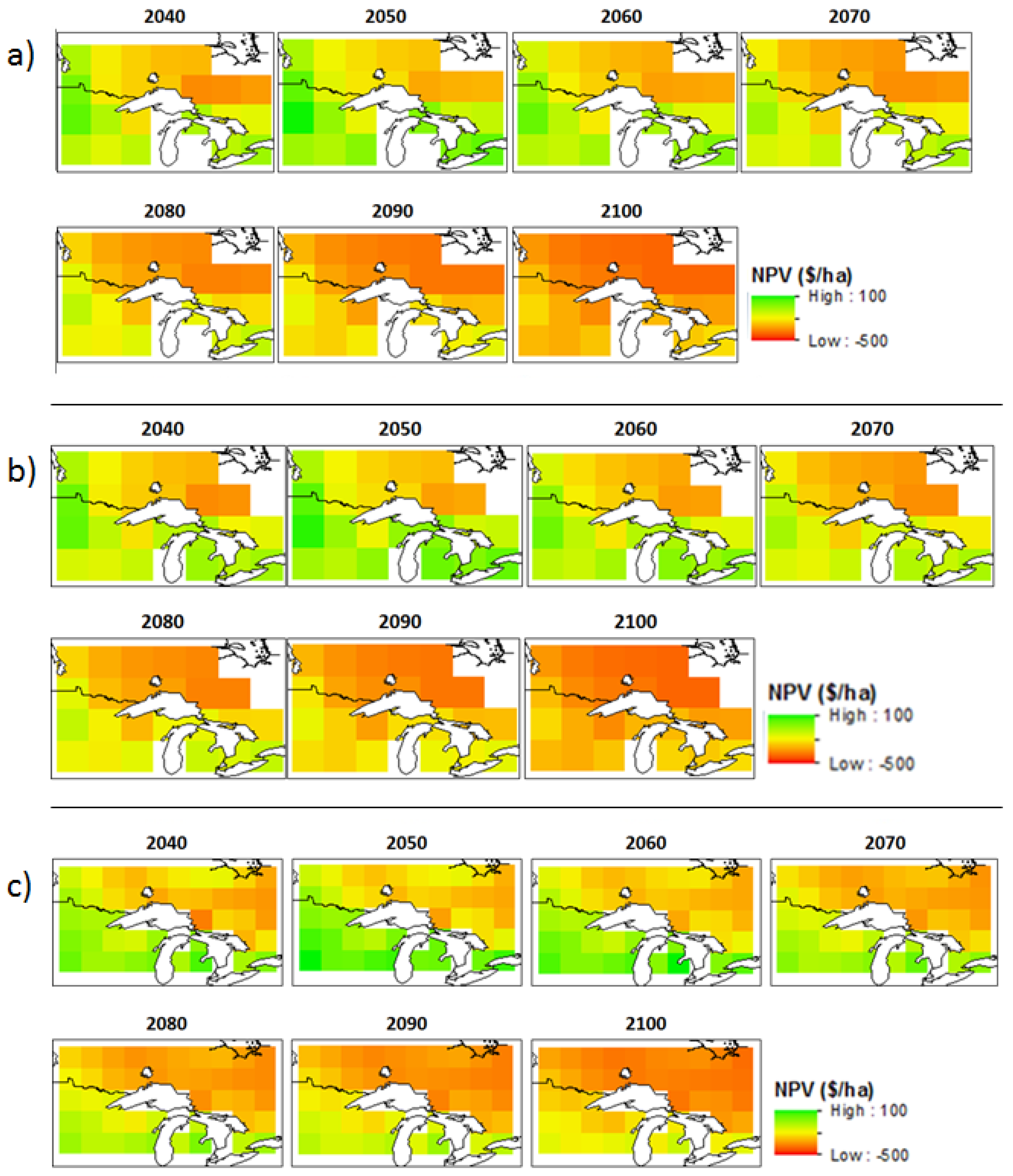
3.2. Economic Benefits
3.3. Sensitivity Analyses
4. Conclusions and Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Food and Agriculture Organization. Global Forest Resources Assessment 2015. How Are the World’s Forests Changing? Food Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Jackson, R.B. The Structure, Distribution, and Biomass of the World’s Forests. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 592–622. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.T.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Kurz, W.A.; Dymond, C.C.; Stinson, G.; Rampley, G.J.; Neilson, E.T.; Safranyik, L. Mountain pine beetle and forest carbon feedback to climate change. Nature 2008, 452, 987–990. [Google Scholar] [CrossRef] [PubMed]
- Van Kooten, G.C.; Binkley, C.S.; Delcourt, G. Effect of Carbon Taxes and Subsidies on Optimal Forest Rotation Age and Supply of Carbon Services. Am. J. Agric. Econ. 1995, 77, 365–374. [Google Scholar] [CrossRef]
- McKenney, D.W.; Yemshanov, D.; Fox, G.; Ramlal, E. Cost estimates for carbon sequestration from fast growing poplar plantations in Canada. For. Policy Econ. 2004, 6, 345–358. [Google Scholar] [CrossRef]
- Yemshanov, D.; McKenney, D.W.; Hatton, T.; Fox, G. Investment Attractiveness of Afforestation in Canada Inclusive of Carbon Sequestration Benefits. Can. J. Agric. Econ. 2005, 53, 307–323. [Google Scholar] [CrossRef]
- Yemshanov, D.; McKenney, D.; Fraleigh, S.; D’Eon, S. An integrated spatial assessment of the investment potential of three species in southern Ontario, Canada inclusive of carbon benefits. For. Policy Econ. 2007, 10, 48–59. [Google Scholar] [CrossRef]
- Kula, E.; Gunalay, Y. Carbon sequestration, optimum forest rotation and their environmental impact. Environ. Impact Assess. Rev. 2012, 37, 18–22. [Google Scholar] [CrossRef]
- EPA. Climate Impacts on Forests. Available online: http://www.epa.gov/climatechange/impacts-adaptation/forests.html (accessed on 16 January 2017).
- Hoen, H. The Faustmann rotation in the presence of a positive CO2 price. J. For. Econ. 1993, 35, 278–287. [Google Scholar]
- Hoen, H.; Solberg, B. CO2-taxing, timber rotations, and market implications. Econ. Carbon Sequestration For. 1997, 27, 151–162. [Google Scholar] [CrossRef]
- Stainback, G.; Alavalapati, J. Economic analysis of slash pine forest carbon sequestration in the southern U.S. J. For. Econ. 2002, 8, 105–117. [Google Scholar] [CrossRef]
- Asante, P.; Armstrong, G. Optimal forest harvest age considering carbon sequestration in multiple carbon pools: A comparative statics analysis. J. For. Econ. 2012, 18, 145–156. [Google Scholar] [CrossRef]
- Plantinga, A.; Bridsey, R. Optimal forest stand management when benefits are derived from carbon. Nat. Resour. Model. 1994, 8, 373–387. [Google Scholar]
- Englin, J.; Callaway, J. Environmental impacts of sequestering carbon through forestation. Clim. Chang. 1995, 31, 37–78. [Google Scholar] [CrossRef]
- Enzinger, S.; Jeffs, C. Economics of forests as carbon sinks: An Australian perspective. J. For. Econ. 2000, 6, 227–249. [Google Scholar]
- Ontario Ministry of Natural Resources. Annual Report on Forest Management 2012–2013; Ontario Ministry of Natural Resources: Ottawa, ON, Canada, 2013.
- Intergovernmental Panel on Climate Change. Climate Change 2014: Impacts, Adaptation, and Vulnerability. A Special Report of Working Groups I and II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; 1132p. [Google Scholar]
- Faustmann, M. Calculation of the Value which Forest Land and Immature Stands Possess for Forestry. J. For. Econ. 1996, 1, 7–44. [Google Scholar]
- Hartman, R. The harvesting decision when a standing forest has value. Econ. Inq. 1976, 14, 52–58. [Google Scholar] [CrossRef]
- Pretzsch, H. Forest Dynamics, Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- He, L.; Chen, J.; Pan, Y.; Birdsey, R.; Kattge, J. Relationships between net primary productivity and forest stand age in U.S. forests. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Arora, V.; Boer, G. Uncertainties in the 20th century carbon budget associated with land use change. Glob. Chang. Biol. 2010, 16, 3327–3348. [Google Scholar] [CrossRef]
- Arora, V.; Boer, G. Terrestrial ecosystems response to future changes in climate and atmospheric CO2 concentration. Biogeosciences 2014, 11, 4157–4171. [Google Scholar] [CrossRef]
- Watanabe, S.; Hajima, T.; Sudo, K.; Nagashima, T.; Takemura, T.; Okajima, H.; Nozawa, T.; Kawase, H.; Abe, M.; Yokohata, T.; et al. MIROC-ESM: Model description and basic results of CMIP5–20c3m experiments. Geosci. Model Dev. Discuss. 2011, 4, 1063–1128. [Google Scholar] [CrossRef]
- Giorgetta, M.; Jungclaus, J.; Reick, C.; Legutke, S.; Bader, J.; Bottinger, M.; Stevens, B. Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the coupled model intercomparison project phase 5. J. Adv. Model. Earth Syst. 2013, 5, 572–597. [Google Scholar] [CrossRef]
- Reick, C.; Raddatz, T.; Brovkin, V.; Gayler, V. The representation of natural and anthropogenic land over change in MPI-ESM. J. Adv. Model. Earth Syst. 2013, 5, 459–482. [Google Scholar] [CrossRef]
- Taylor, K.; Stouffer, R.; Meehl, G. A summary of the CMIP5 experimental design. World 2009, 4, 1–33. [Google Scholar] [CrossRef]
- Shao, P.; Zeng, X.; Sakaguchi, K.; Monson, R.; Zeng, X. Terrestrial carbon cycle: Climate relations in eight CMIP5 Earth System models. J. Clim. 2013, 26, 8744–8764. [Google Scholar] [CrossRef]
- Moss, R.; Edmonds, J.; Hibbard, K.; Manning, M.; Rose, S.; van Vuuren, D.; Carter, T.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Ung, C.H.; Bernier, P.Y.; Guo, X.J.; Lambert, M.C. A simple growth and yield model for assessing changes in standing volume across Canada’s forests. For. Chron. 2009, 85, 57–64. [Google Scholar] [CrossRef]
- Duan, N. Smearing estimate: A nonparametric retransformation method. J. Am. Stat. Assoc. 1983, 78, 605–610. [Google Scholar] [CrossRef]
- McKenney, D.W.; Hutchinson, M.F.; Papadopol, P.; Lawrence, K.; Pedlar, J.; Campbell, K.; Milewska, E.; Hopkinson, R.F.; Price, D.; Owen, T. Customized Spatial Climate Models for North America. Bull. Am. Meteorol. Soc. 2011, 92, 1611–1622. [Google Scholar] [CrossRef]
- Samuleson, P. Economics of forestry in an evolving society. Econ. Inq. 1976, 14, 466–492. [Google Scholar] [CrossRef]
- California Carbon Dashboard. Carbon Price. Available online: http://calcarbondash.org (accessed on 14 May 2016).
- Johansson, P.; Lofgren, K. The Economics of Forestry and Natural Resources; Basil Blackwell Ltd.: London, UK, 1985. [Google Scholar]
- Cairns, R. Faustmann’s Formulae for Forest Capital; McGill University: Montreal, QC, Canada, 2012; pp. 1–23. [Google Scholar]
- Jessome, A. Forest Tech. Report No. 21: Strength and Related Properties of Woods Grown in Canada; Government of Canada: Ottawa, ON, Canada, 1977.
- Liu, J.; Chen, J.; Cihlar, J.; Chen, W. Net primary productivity mapped for Canada at 1-km resolution. Glob. Ecol. Biogeogr. 2002, 11, 115–129. [Google Scholar] [CrossRef]
- Skidmore, A. Environmental Modelling with GIS and Remote Sensing; Taylor & Francis: New York, NY, USA, 2002. [Google Scholar]
- Rossi, S.; Morin, H.; Deslauriers, A.; Plourde, P. Predicting xylem phenology in black spruce under climate change. Glob. Chang. Biol. 2011, 17, 614–625. [Google Scholar] [CrossRef]
- Rossi, S.; Girard, M.; Morin, H. Lengthening of the duration of xylogenesis engenders disproportionate increases in xylem production. Glob. Chang. Biol. 2014, 20, 2261–2271. [Google Scholar] [CrossRef] [PubMed]
- Girardin, M.; Hogg, E.; Bernier, P.; Kurz, W.; Guo, X.; Cyr, G. Negative impacts of high temperatures on growth of black spruce forests intensify with the anticipated climate warming. Glob. Chang. Biol. 2016, 627–643. [Google Scholar] [CrossRef] [PubMed]
- Gennaretti, F.; Arseneault, D.; Nicault, A.; Perreault, L.; Begin, Y. Volcano-induced regime shifts in millennial tree-ring chronologies from northeastern North America. Proc. Natl. Acad. Sci. USA 2014, 111, 10077–10082. [Google Scholar] [CrossRef] [PubMed]
- Ueyama, M.; Kudo, S.; Iwama, C.; Nagano, H.; Kobayashi, H.; Harazono, Y.; Yoshikawa, K. Does summer warming reduce black spruce productivity in interior Alaska? J. For. Res. 2015, 20, 52–59. [Google Scholar] [CrossRef]
- Way, D.; Sage, R. Thermal acclimation of photosynthesis in black spruce [Picea mariana (Mill.) B.S.P.]. Plant. Cell Environ. 2008, 31, 1250–1262. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Kimball, J.; Hogg, E.; Zhao, M.; Oechel, W.; Cassano, J.; Running, S. Satellite-based model detection of recent climate-driven changes in northern high-latitude vegetation productivity. J. Geophys. Res. Biogeosci. 2008, 113, 1179–1183. [Google Scholar] [CrossRef]
- Girardin, M.; Bouriaud, O.; Hogg, E.; Kurz, W.; Zimmermann, N.; Metsaranta, J.; Jong, R.; Frank, D.; Esper, J.; Buntgen, U.; et al. No growth simulation of Canada’s boreal forest under half-century of combined warming and CO2 fertilization. Proc. Natl. Acad. Sci. USA 2016, 113, E8406–E8414. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Piao, S.; Tang, Z.; Peng, C.; Ji, W. Interannual variability in net primary production and precipitation. Science 2001, 293, 1723. [Google Scholar] [CrossRef] [PubMed]
- Del Grosso, S.; Parton, W.; Stohlgren, T.; Zheng, D.; Bachelet, D.; Prince, S.; Hibbard, K.; Olson, R. Global potential net primary production predicted from vegetation class, precipitation, and temperature. Ecology 2008, 89, 2117–2126. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Southworth, J. Disentangling the relationships between net primary production and precipitation in Southern Africa savannas using satellite observations from 1982 to 2010. Remote Sens. 2013, 5, 3803–3825. [Google Scholar] [CrossRef]
- Plonski, W.L. Normal Yield Tables for Black Spruce, Jack Pine, Aspen, and White Birch in Northern Ontario; Ontario Department of Lands and Forests: Ottawa, ON, Canada, 1956.
- Payandeh, B. Plonski’s (metric) yield tables formulated. For. Chron. 1991, 5, 545–546. [Google Scholar] [CrossRef]
- Fowells, H. Silvics of Forest Trees of the United States; Agriculture Handbook No. 271; U.S. Department of Agriculture: Washington, DC, USA, 1965.
- Yang, J.; McKenney, D.; Weersink, A. Should climate change make us think more about the economics of forest management? For. Chron. 2015, 91, 23–31. [Google Scholar] [CrossRef]
- Johnstone, J.; Hollingsworth, T.; Chapin, F.; Mack, M. Changes in fire regime break the legacy lock on successional trajectories in Alaskan boreal forest. Glob. Chang. Biol. 2010, 16, 1281–1295. [Google Scholar] [CrossRef]
- Beck, P.; Juday, G.; Alix, C.; Barber, V.; Winslow, S.; Sousa, E.; Heiser, P.; Herriges, J.; Goetz, S. Changes in forest productivity across Alaska consistent with biome shift. Ecol. Lett. 2011, 14, 373–379. [Google Scholar] [CrossRef] [PubMed]
- Stern, N. The Economics of Climate Change. The Stern Review; Cabinet Office: Cambridge, UK, 2007.
- Nordhaus, W. A Question of Balance; Yale University Press: London, UK, 2008. [Google Scholar]
- Rydge, J. Implementing Effective Carbon Pricing; New Climate Economy: London, UK; Washington, DC, USA, 2015. [Google Scholar]
- Coleman, J.S.M.; Rogers, J.C. Ohio River Valley winter moisture conditions associated with the Pacific-North American teleconnection pattern. J. Clim. 2003, 16, 969–981. [Google Scholar] [CrossRef]
- Payandeh, B.; Wang, Y. Variable stocking version of Plonski’s yield tables formulated. For. Chron. 1996, 72, 181–184. [Google Scholar] [CrossRef]
- Martell, D. The use of historical fire weather data for prescribed burn planning. For. Chron. 1978, 54, 96–98. [Google Scholar] [CrossRef]
- Daigneault, A.; Miranda, M.; Sohngen, B. Optimal forest management with carbon sequestration credits and endogenous fire risk. Land Econ. 2010, 86, 155–172. [Google Scholar] [CrossRef]
- Boulanger, Y.; Gauthier, S.; Gray, D.; Le Goff, H.; Lefort, P.; Morissette, J. Fire regime zonation under current and future climate over eastern Canada. Ecol. Appl. 2013, 23, 904–923. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Value |
|---|---|
| Discount rate (%) | 4, (2, 8) * |
| Establishment costs ($·ha−1) | 500, (0, 200, 1000) * |
| Timber price ($·m−3) | 20, (50) * |
| Price for carbon ($·ton−1·CO2) | 5, (10, 20) * |
| Model | Scenario | OHA * | Northwest Ontario | Northeast Ontario | Southern Ontario | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max. | Min. | Std. | Mean | Max. | Min. | Std. | Mean | Max. | Min. | Std. | |||
| Can-ESM2 | W * | 2049 | −136 | 33 | −221 | 99 | −265 | −220 | −300 | 33 | −51 | 29 | −128 | 67 |
| W + C * | 2052 | 430 | 503 | 345 | 100 | 305 | 347 | 272 | 31 | 522 | 607 | 445 | 70 | |
| MIROC | W | 2048 | −137 | 38 | −228 | 103 | −269 | −226 | −307 | 33 | −39 | 18 | −130 | 68 |
| W + C | 2054 | 424 | 592 | 337 | 96 | 304 | 345 | 274 | 29 | 471 | 600 | 443 | 68 | |
| MPI | W | 2048 | −226 | −105 | −297 | 61 | −263 | −208 | −330 | 39 | −90 | 57 | −258 | 120 |
| W + C | 2052 | 341 | 459 | 282 | 60 | 306 | 353 | 248 | 35 | 485 | 628 | 321 | 118 | |
| CanESM2 | MIROC | MPI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenarios | r = 2% (46) | r = 4% (39) | r = 8% (33) | r = 2% (45) | r = 4% (38) | r = 8% (33) | r = 2% (46) | r = 4% (38) | r = 8% (32) | |||
| NW | 666 | −136 | −430 | 661 | −137 | −424 | 391 | −226 | −444 | |||
| NE | 267 | −265 | −456 | 261 | −269 | −454 | 277 | −263 | −453 | |||
| S | 1012 | −51 | −416 | 1047 | −39 | −409 | 900 | −90 | −419 | |||
| Scenarios | C = $0 (33) | C = $200 (35) | C = $500 (39) | C = $1000 (46) | C = $0 (34) | C = $200 (36) | C = $500 (38) | C = $1000 (45) | C = $0 (33) | C = $200 (36) | C = $500 (38) | C = $1000 (46) |
| NW | 534 | 262 | −136 | −762 | 334 | 257 | −137 | −759 | −51 | −132 | −226 | −841 |
| NE | 398 | 125 | −265 | −876 | 196 | 122 | −269 | −876 | −84 | −171 | −263 | −873 |
| S | 604 | 332 | −51 | −663 | 410 | 346 | −39 | −653 | 92 | −2 | −90 | −696 |
| Scenarios | P = $20 (39) | P = $50 (34) | P = $20 (38) | P = $50 (36) | P = $20 (38) | P = $50 (36) | ||||||
| NW | −136 | 660 | −137 | 643 | −226 | 418 | ||||||
| NE | −265 | 316 | −269 | 306 | −263 | 322 | ||||||
| S | −51 | 824 | −39 | 864 | −90 | 744 | ||||||
| CanESM2 | MIROC | MPI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenarios | r = 2% (49) | r = 4% (42) | r = 8% (35) | r = 2% (47) | r = 4% (44) | r = 8% (35) | r = 2% (49) | r = 4% (42) | r = 8% (35) | |||
| NW | 1276 | 430 | 108 | 1285 | 424 | 109 | 1000 | 341 | 90 | |||
| NE | 880 | 305 | 81 | 880 | 304 | 81 | 887 | 306 | 82 | |||
| S | 1631 | 522 | 122 | 1662 | 529 | 125 | 1518 | 485 | 115 | |||
| Scenarios | C = $0 (35) | C = $200 (39) | C = $500 (42) | C = $1000 (49) | C = $0 (35) | C = $200 (38) | C = $500 (44) | C = $1000 (49) | C = $0 (36) | C = $200 (38) | C = $500 (42) | C = $1000 (51) |
| NW | 885 | 811 | 430 | −177 | 886 | 812 | 424 | −175 | 789 | 723 | 341 | −251 |
| NE | 748 | 682 | 305 | −285 | 748 | 679 | 304 | −286 | 755 | 686 | 306 | −280 |
| S | 955 | 896 | 522 | −80 | 969 | 909 | 529 | −68 | 943 | 858 | 485 | −111 |
| Scenarios | P = $20 (42) | P = $50 (38) | P = $20 (44) | P = $50 (35) | P = $20 (42) | P = $50 (36) | ||||||
| NW | 430 | 1184 | 424 | 1216 | 341 | 978 | ||||||
| NE | 305 | 851 | 304 | 871 | 306 | 882 | ||||||
| S | 522 | 1391 | 529 | 1424 | 485 | 1304 | ||||||
| Scenarios | Pcs = $5 (42) | Pcs = $10 (42) | Pcs = $20 (51) | Pcs = $5 (44) | Pcs = $10 (45) | Pcs = $20 (56) | Pcs = $5 (42) | Pcs = $10 (46) | Pcs = $20 (60) | |||
| NW | 430 | 504 | 675 | 424 | 502 | 680 | 341 | 420 | 624 | |||
| NE | 305 | 379 | 573 | 304 | 384 | 589 | 306 | 387 | 601 | |||
| S | 522 | 596 | 773 | 529 | 608 | 783 | 485 | 565 | 745 | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; McKenney, D.W.; Pedlar, J.H.; Arain, M.A. Biophysical and Economic Analysis of Black Spruce Regeneration in Eastern Canada Using Global Climate Model Productivity Outputs. Forests 2017, 8, 106. https://doi.org/10.3390/f8040106
Lee J, McKenney DW, Pedlar JH, Arain MA. Biophysical and Economic Analysis of Black Spruce Regeneration in Eastern Canada Using Global Climate Model Productivity Outputs. Forests. 2017; 8(4):106. https://doi.org/10.3390/f8040106
Chicago/Turabian StyleLee, Jung, Daniel W. McKenney, John H. Pedlar, and M. Altaf Arain. 2017. "Biophysical and Economic Analysis of Black Spruce Regeneration in Eastern Canada Using Global Climate Model Productivity Outputs" Forests 8, no. 4: 106. https://doi.org/10.3390/f8040106
APA StyleLee, J., McKenney, D. W., Pedlar, J. H., & Arain, M. A. (2017). Biophysical and Economic Analysis of Black Spruce Regeneration in Eastern Canada Using Global Climate Model Productivity Outputs. Forests, 8(4), 106. https://doi.org/10.3390/f8040106






