Prevalence of Inter-Tree Competition and Its Role in Shaping the Community Structure of a Natural Mongolian Scots Pine (Pinus sylvestris var. mongolica) Forest
Abstract
:1. Introduction
2. Materials and Methods
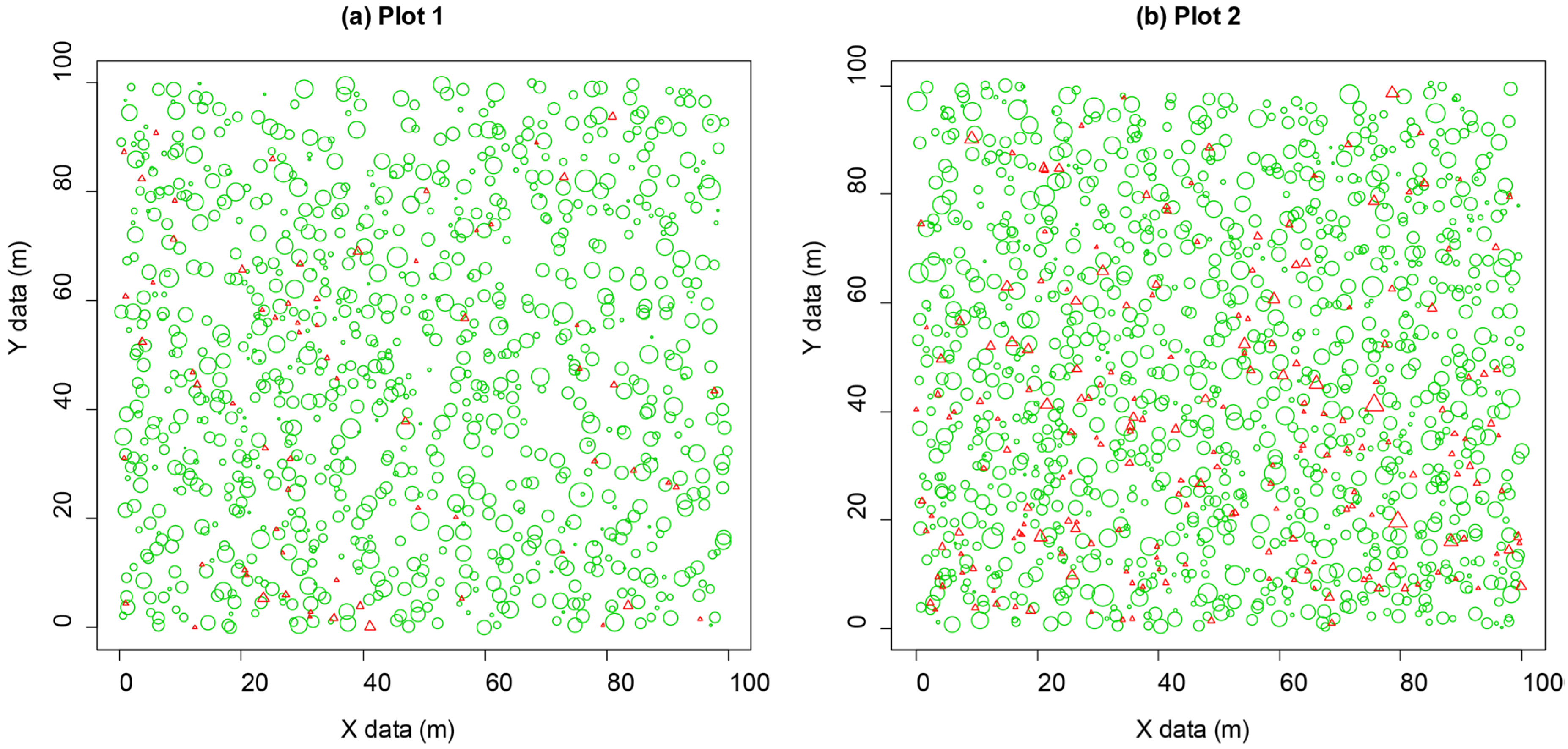
2.1. Study Site and Tree Data
2.2. Nearest Neighbour Analysis
2.3. Spatial Pattern Analysis
2.3.1. Pair Correlation Function
2.3.2. Mark Differentiation Function
3. Results
3.1. Non-Spatial Stand Structure Characteristics
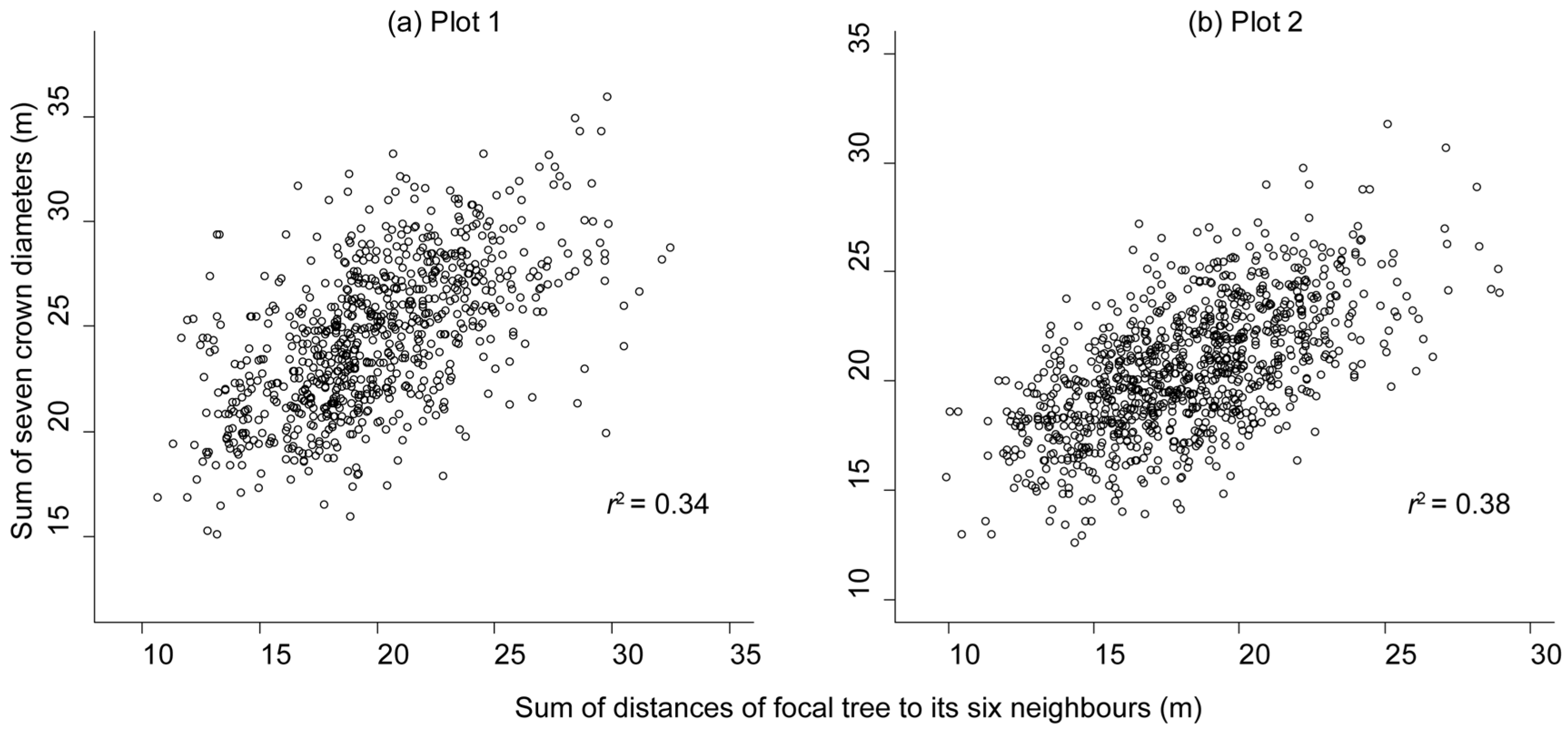
3.2. Reduction in Tree Size Caused by Competition
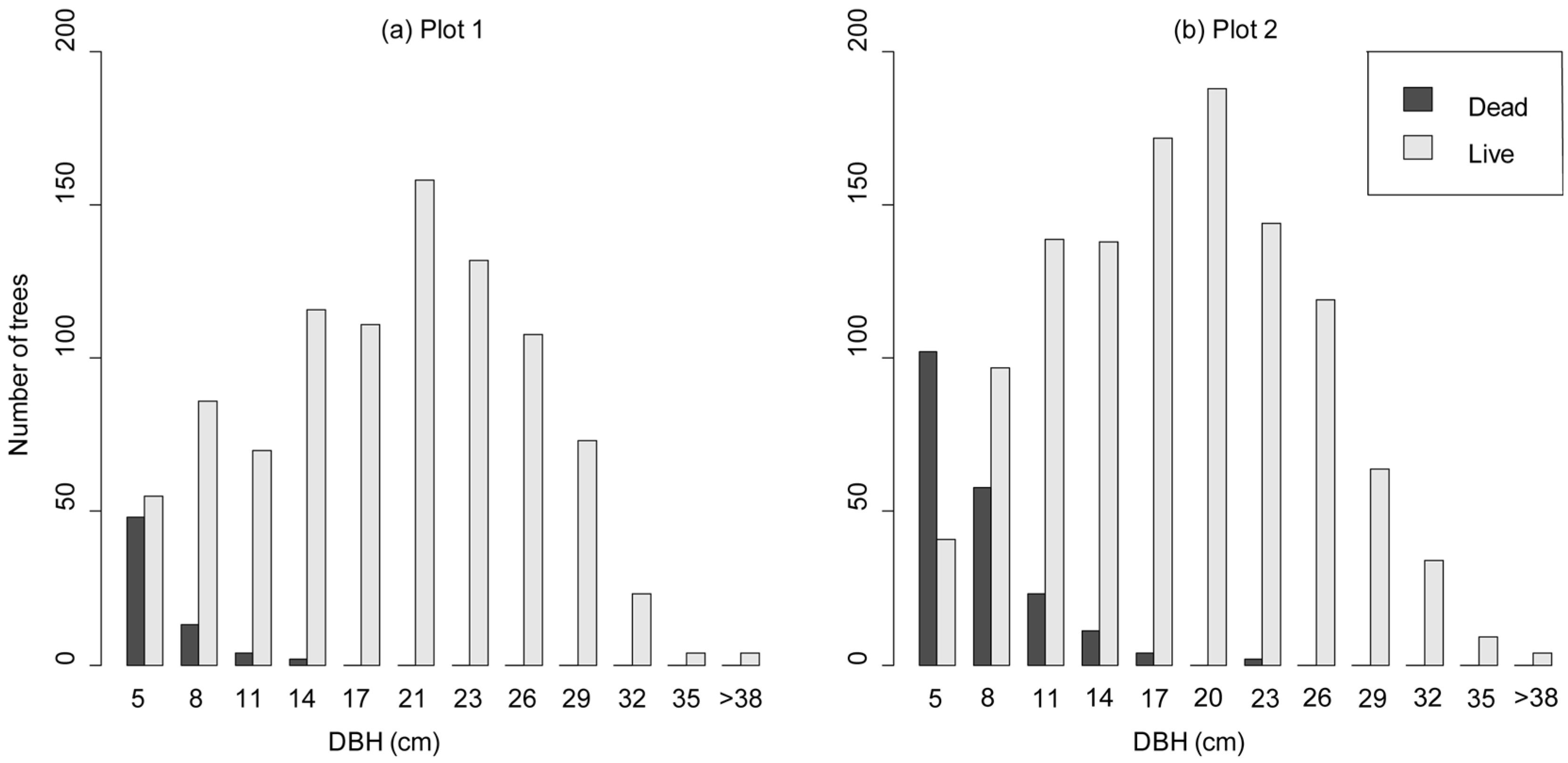
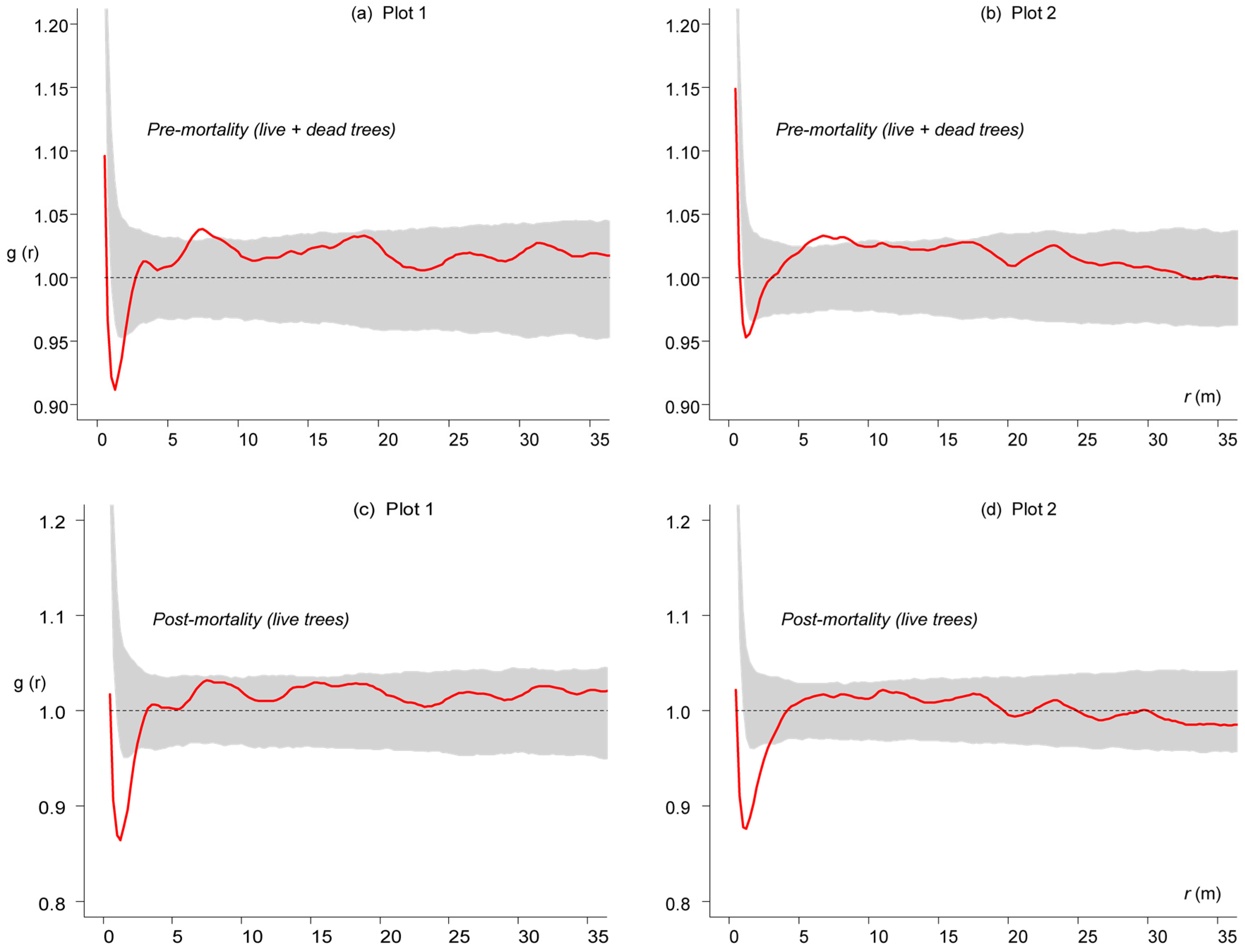
3.3. Competition-Induced Tree Mortality
3.4. Competition-Induced Size Variation
4. Discussion
4.1. Competition and Tree Growth
4.2. Competition and Regular Spacing
4.3. Competition and Tree Size Inequality
4.4. Implications for Management
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brown, J.H.; Mehlman, D.W.; Stevens, G.C. Spatial variation in abundance. Ecology 1995, 76, 2028–2043. [Google Scholar] [CrossRef]
- Wright, J.S. Plant diversity in tropical forests: A review of mechanisms of species coexistence. Oecologia 2002, 130, 1–14. [Google Scholar] [CrossRef]
- Bravo-Oviedo, A.; Sterba, H.; del Río, M.; Bravo, F. Competition-induced mortality for Mediterranean Pinus pinaster Ait. and P. sylvestris L. For. Ecol. Manag. 2006, 222, 88–98. [Google Scholar] [CrossRef]
- Das, A.; Battles, J.; Stephenson, N.L.; van Mantgem, P.J. The contribution of competition to tree mortality in old-growth coniferous forests. For. Ecol. Manag. 2011, 261, 1203–1213. [Google Scholar] [CrossRef]
- Getzin, S.; Dean, C.; He, F.; A Trofymow, J.; Wiegand, K.; Wiegand, T. Spatial patterns and competition of tree species in a Douglas-fir chronosequence on Vancouver Island. Ecography 2006, 29, 671–682. [Google Scholar] [CrossRef]
- Meyer, K.M.; Ward, D.; Wiegand, K.; Moustakas, A. Multi-proxy evidence for competition between savanna woody species. Perspect. Plant Ecol. Evol. Syst. 2008, 10, 63–72. [Google Scholar] [CrossRef]
- Wolf, A. Fifty year record of change in tree spatial patterns within a mixed deciduous forest. For. Ecol. Manag. 2005, 215, 212–223. [Google Scholar] [CrossRef]
- Peet, R.K.; Christensen, N.L. Competition and tree death. Bioscience 1987, 37, 586–595. [Google Scholar] [CrossRef]
- Pillay, T.; Ward, D. Competitive effect and response of savanna tree seedlings: Comparison of survival, growth and associated functional traits. J. Veg. Sci. 2014, 25, 226–234. [Google Scholar] [CrossRef]
- Potvin, C.; Dutilleul, P. Neighborhood effects and size-asymmetric competition in a tree plantation varying in diversity. Ecology 2009, 90, 321–327. [Google Scholar] [CrossRef] [PubMed]
- Pretzsch, H. Forest dynamics, growth, and yield. In Forest Dynamics, Growth and Yield; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–39. [Google Scholar]
- Shackleton, C. Nearest-neighbour analysis and the prevelance of woody plant competition in South African savannas. Plant Ecol. 2002, 158, 65–76. [Google Scholar] [CrossRef]
- Fraver, S.; D’Amato, A.W.; Bradford, J.B.; Jonsson, B.G.; Jönsson, M.; Esseen, P.A. Tree growth and competition in an old-growth Picea abies forest of boreal Sweden: Influence of tree spatial patterning. J. Veg. Sci. 2014, 25, 374–385. [Google Scholar] [CrossRef]
- Franklin, J.F.; Van Pelt, R. Spatial aspects of structural complexity in old-growth forests. J. For. 2004, 102, 22–28. [Google Scholar]
- Pillay, T.; Ward, D. Spatial pattern analysis and competition between Acacia karroo trees in humid savannas. Plant Ecol. 2012, 213, 1609–1619. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.-Y.; Niu, P.-X.; Chu, G.-M. Spatial pattern formation and intraspecific competition of Anabasis aphylla L. population in the diluvial fan of junggar basin, NW China. Pak. J. Bot. 2015, 47, 543–550. [Google Scholar]
- He, F.; Duncan, R.P. Density-dependent effects on tree survival in an old-growth Douglas fir forest. J. Ecol. 2000, 88, 676–688. [Google Scholar] [CrossRef]
- Moustakas, A.; Wiegand, K.; Getzin, S.; Ward, D.; Meyer, K.M.; Guenther, M.; Mueller, K.-H. Spacing patterns of an Acacia tree in the Kalahari over a 61-year period: How clumped becomes regular and vice versa. Acta Oecol. 2008, 33, 355–364. [Google Scholar] [CrossRef]
- Peterson, C.J.; Squiers, E.R. An unexpected change in spatial pattern across 10 years in an aspen-white pine forest. J. Ecol. 1995, 847–855. [Google Scholar] [CrossRef]
- Piao, T.; Chun, J.H.; Yang, H.M.; Cheon, K. Negative density dependence regulates two tree species at later life stage in a temperate forest. PLoS ONE 2014, 9, e103344. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.H.; Halpern, C.B. The structure and dynamics of Abies magnifica forests in the southern Cascade Range, USA. J. Veg. Sci. 1991, 2, 189–200. [Google Scholar] [CrossRef]
- Walters, M.B.; Reich, P.B. Are shade tolerance, survival, and growth linked? Low light and nitrogen effects on hardwood seedlings. Ecology 1996, 77, 841–853. [Google Scholar] [CrossRef]
- Zhao, Q.; Zeng, D.; Lee, D.; He, X.; Fan, Z.; Jin, Y. Effects of Pinus sylvestris var. mongolica afforestation on soil phosphorus status of the Keerqin Sandy Lands in China. J. Arid Environ. 2007, 69, 569–582. [Google Scholar] [CrossRef]
- Zhu, J.; Kang, H.; Tan, H.; Xu, M. Effects of drought stresses induced by polyethylene glycol on germination of Pinus sylvestris var. mongolica seeds from natural and plantation forests on sandy land. J. For. Res. 2006, 11, 319–328. [Google Scholar] [CrossRef]
- Han, G.; Zhang, G.; Yang, W. Quantitative analysis on principle eco-climatic factors of limiting natural reforestation of Pinus sylvestris var. mongolica on sandy land. Sci. Silvae Sin. 1998, 35, 22–27. [Google Scholar]
- Peters, H.A. Neighbour-regulated mortality: The influence of positive and negative density dependence on tree populations in species-rich tropical forests. Ecol. Lett. 2003, 6, 757–765. [Google Scholar] [CrossRef]
- Wills, C.; Condit, R.; Foster, R.B.; Hubbell, S.P. Strong density-and diversity-related effects help to maintain tree species diversity in a neotropical forest. Proc. Natl. Acad. Sci. USA 1997, 94, 1252–1257. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, R.; Henrys, P.A.; Brown, P.E.; Burslem, D.F.; Diggle, P.J.; Gunatilleke, C.; Gunatilleke, I.; Kassim, A.R.; Law, R.; Noor, S. Spatial patterns reveal negative density dependence and habitat associations in tropical trees. Ecology 2011, 92, 1723–1729. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, T.; A Moloney, K. Rings, circles, and null-models for point pattern analysis in ecology. Oikos 2004, 104, 209–229. [Google Scholar] [CrossRef]
- Kenkel, N. Pattern of self-thinning in jack pine: Testing the random mortality hypothesis. Ecology 1988, 69, 1017–1024. [Google Scholar] [CrossRef]
- Gonçalves, C.; Batalha, M. Towards testing the “honeycomb rippling model” in cerrado. Braz. J. Biol. 2011, 71, 401–408. [Google Scholar] [PubMed]
- Velázquez, J.; Allen, R.B.; Coomes, D.A.; Eichhorn, M.P. Asymmetric competition causes multimodal size distributions in spatially structured populations. Proc. R. Soc. B 2016, 283, 20152404. [Google Scholar] [CrossRef] [PubMed]
- Weiner, J.; Stoll, P.; Muller-Landau, H.; Jasentuliyana, A. The effects of density, spatial pattern, and competitive symmetry on size variation in simulated plant populations. Am. Nat. 2001, 158, 438–450. [Google Scholar] [CrossRef] [PubMed]
- Weiner, J. Asymmetric competition in plant populations. Trends Ecol. Evol. 1990, 5, 360–364. [Google Scholar] [CrossRef]
- Ford, E. Competition and stand structure in some even-aged plant monocultures. J. Ecol. 1975, 63, 311–333. [Google Scholar] [CrossRef]
- Suzuki, S.N.; Kachi, N.; Suzuki, J.-I. Development of a local size hierarchy causes regular spacing of trees in an even-aged Abies forest: Analyses using spatial autocorrelation and the mark correlation function. Ann. Bot. 2008, 102, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Reed, D.D.; Burkhart, H.E. Spatial autocorrelation of individual tree characteristics in loblolly pine stands. For. Sci. 1985, 31, 575–587. [Google Scholar]
- Hui, G.; Pommerening, A. Analysing tree species and size diversity patterns in multi-species uneven-aged forests of Northern China. For. Ecol. Manag. 2014, 316, 125–138. [Google Scholar] [CrossRef]
- Pommerening, A.; Gonçalves, A.C.; Rodríguez-Soalleiro, R. Species mingling and diameter differentiation as second-order characteristics. Allg. Forst Jagdztg. 2011, 182, 115–129. [Google Scholar]
- Ling, L.; Yanbo, H.; Qianxue, W.; Hongxiang, W.; Jili, Z.; Chunlai, W.; Zhonghua, Z. Structure characters of Pinus sylvestris var. mongolica natural forest on sandy land. For. Res. 2016, 29, 623–629. [Google Scholar]
- Liu, Y.; Bao, G.; Song, H.; Cai, Q.; Sun, J. Precipitation reconstruction from Hailar pine (Pinus sylvestris var. mongolica) tree rings in the Hailar region, Inner Mongolia, China back to 1865 AD. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 282, 81–87. [Google Scholar] [CrossRef]
- Kahle, D.; Wickham, H. ggmap: A Package for Spatial Visualization with Google Maps and OpenStreetMap, R package version 2.3; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Wiegand, T.; Moloney, K.A. Handbook of Spatial Point-Pattern Analysis in Ecology; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Pommerening, A. Arne Pommerening’s Forest Biometrics Lab. Available online: http://pommerening.org (accessed on 29 July 2015).
- Baddeley, A.; Turner, R. Spatstat: An R package for analyzing spatial point patterns. J. Stat. Softw. 2005, 12, 1–42. [Google Scholar] [CrossRef]
- Eddelbuettel, D.; François, R.; Allaire, J.; Chambers, J.; Bates, D.; Ushey, K. Rcpp: Seamless R and C++ integration. J. Stat. Softw. 2011, 40, 1–18. [Google Scholar] [CrossRef]
- Gates, D. Competition and skewness in plantations. J. Theor. Biol. 1982, 94, 909–922. [Google Scholar] [CrossRef]
- Smith, T.M.; Grant, K. The role of competition in the spacing of trees in a Burkea africana-Terminalia sericea savanna. Biotropica 1986, 18, 219–223. [Google Scholar] [CrossRef]
- Aakala, T.; Fraver, S.; Palik, B.J.; D’Amato, A.W. Spatially random mortality in old-growth red pine forests of northern Minnesota. Can. J. For. Res. 2012, 42, 899–907. [Google Scholar] [CrossRef]
- Larson, A.J.; Lutz, J.A.; Donato, D.C.; Freund, J.A.; Swanson, M.E.; HilleRisLambers, J.; Sprugel, D.G.; Franklin, J.F. Spatial aspects of tree mortality strongly differ between young and old-growth forests. Ecology 2015, 96, 2855–2861. [Google Scholar] [CrossRef] [PubMed]
- D’Amato, A.W.; Bradford, J.B.; Fraver, S.; Palik, B.J. Effects of thinning on drought vulnerability and climate response in north temperate forest ecosystems. Ecol. Appl. 2013, 23, 1735–1742. [Google Scholar] [CrossRef] [PubMed]
- Zheng, D.; Jiang, F.; Fan, Z. Stability of Mongolian pine plantation on sandy land. Chin. J. Appl. Ecol. 1996, 7, 337–343. (In Chinese) [Google Scholar]
- Gele, D.; Guoping, Z.; Xinxing, W.; Jifeng, D.; Guodong, D.; Yuanyuan, Z.; Zhenhua, M. Effects of stand density on stand structure and understory vegetation of Pinus sylvestris plantations in Mu Us sandland. Bull. Soil Water Conserv. 2015, 35, 86–91. [Google Scholar]



| Plot Number | Slope (°) | Canopy Cover | Tree Density (trees/ha) | Mean Basal Area (m2/ha) | Mean DBH (cm) | Number of Dead Stems | Mortality Percentage (%) |
|---|---|---|---|---|---|---|---|
| Plot 1 | <3 | 0.7 | 940 | 33.6 | 21.3 | 67 | 7 |
| Plot 2 | <3 | 0.7 | 1149 | 39.8 | 21.0 | 200 | 17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wan, P.; Wang, Q.; Liu, L.; Zhang, G.; Hui, G. Prevalence of Inter-Tree Competition and Its Role in Shaping the Community Structure of a Natural Mongolian Scots Pine (Pinus sylvestris var. mongolica) Forest. Forests 2017, 8, 84. https://doi.org/10.3390/f8030084
Wang H, Wan P, Wang Q, Liu L, Zhang G, Hui G. Prevalence of Inter-Tree Competition and Its Role in Shaping the Community Structure of a Natural Mongolian Scots Pine (Pinus sylvestris var. mongolica) Forest. Forests. 2017; 8(3):84. https://doi.org/10.3390/f8030084
Chicago/Turabian StyleWang, Hongxiang, Pan Wan, Qianxue Wang, Ling Liu, Gongqiao Zhang, and Gangying Hui. 2017. "Prevalence of Inter-Tree Competition and Its Role in Shaping the Community Structure of a Natural Mongolian Scots Pine (Pinus sylvestris var. mongolica) Forest" Forests 8, no. 3: 84. https://doi.org/10.3390/f8030084
APA StyleWang, H., Wan, P., Wang, Q., Liu, L., Zhang, G., & Hui, G. (2017). Prevalence of Inter-Tree Competition and Its Role in Shaping the Community Structure of a Natural Mongolian Scots Pine (Pinus sylvestris var. mongolica) Forest. Forests, 8(3), 84. https://doi.org/10.3390/f8030084





