Evaluating the Effects of Carbon Prices on Trade-Offs between Carbon and Timber Management Objectives in Forest Spatial Harvest Scheduling Problems: A Case Study from Northeast China
Abstract
:1. Introduction
2. Materials and Methods
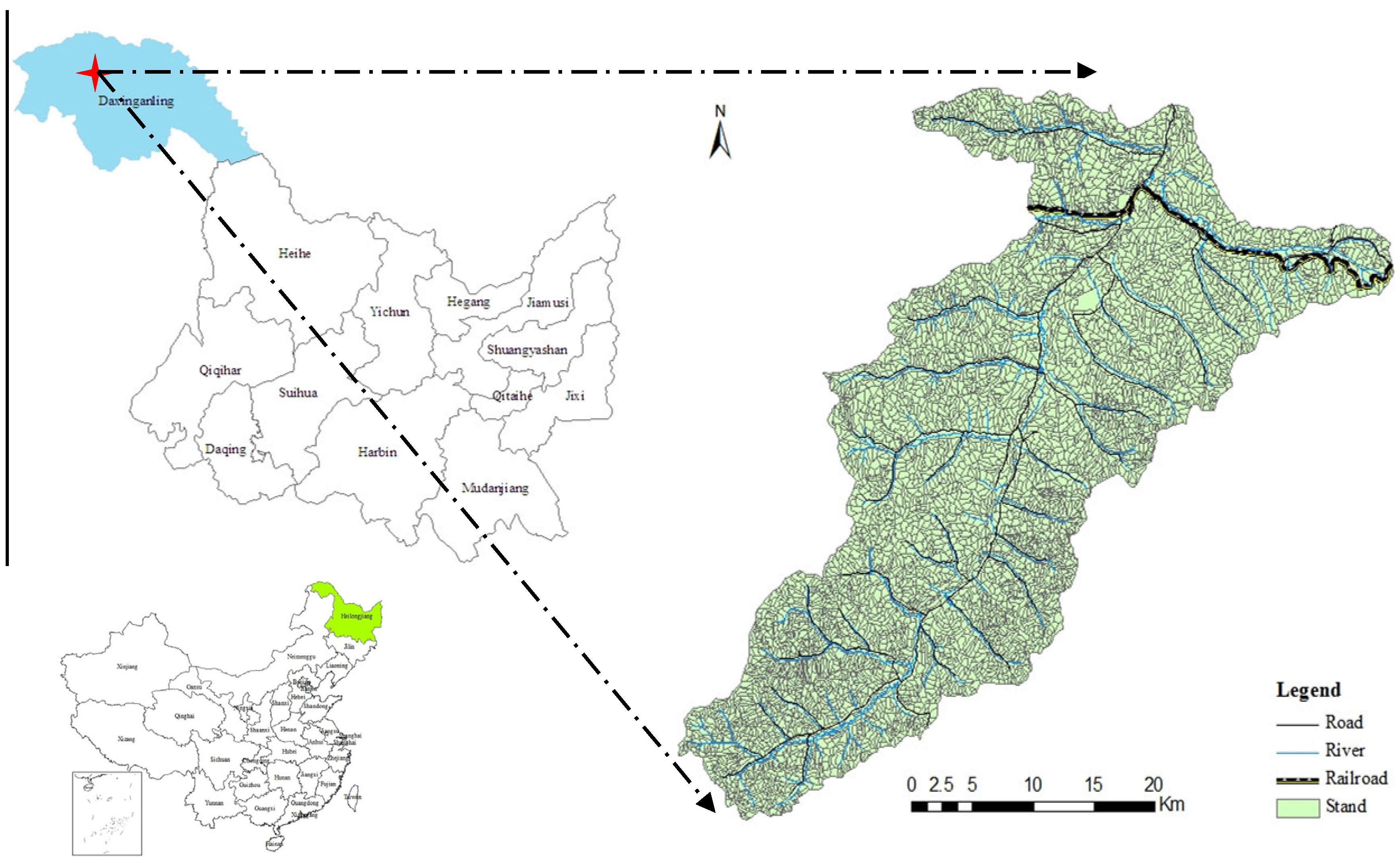
2.1. Forest Planning Data Sets
2.2. Forest Planning Problems
2.3. Forest Planning Process
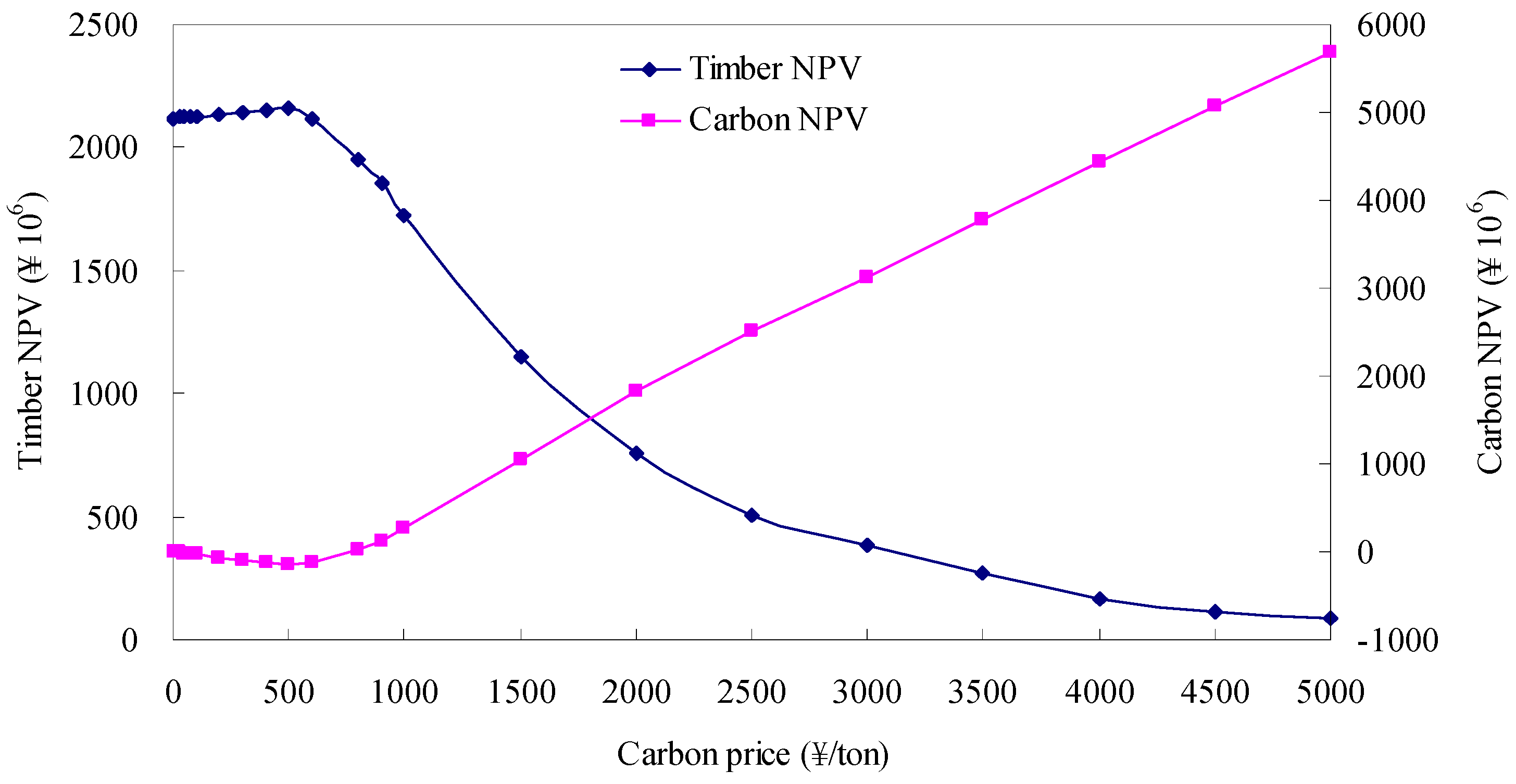
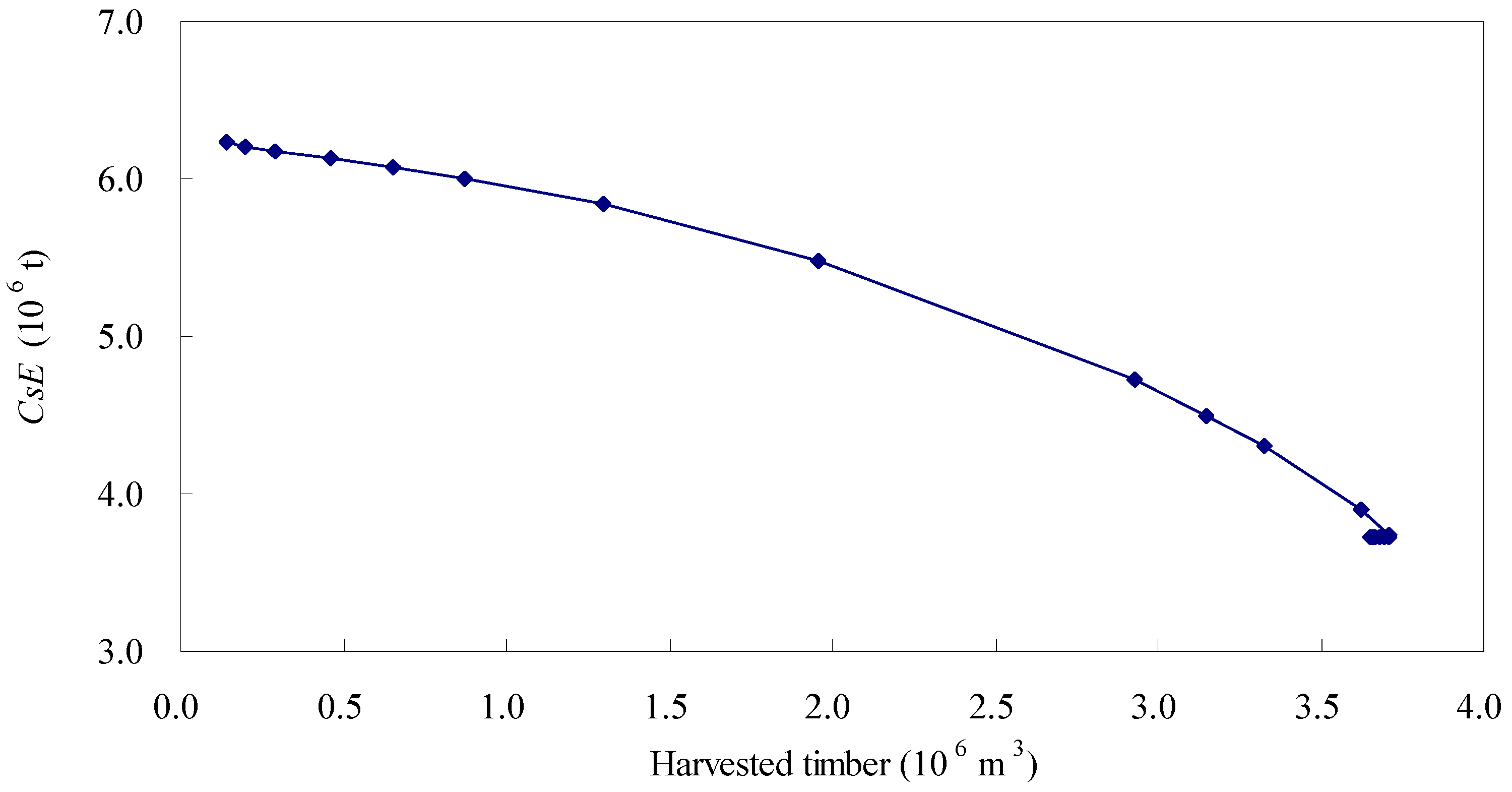
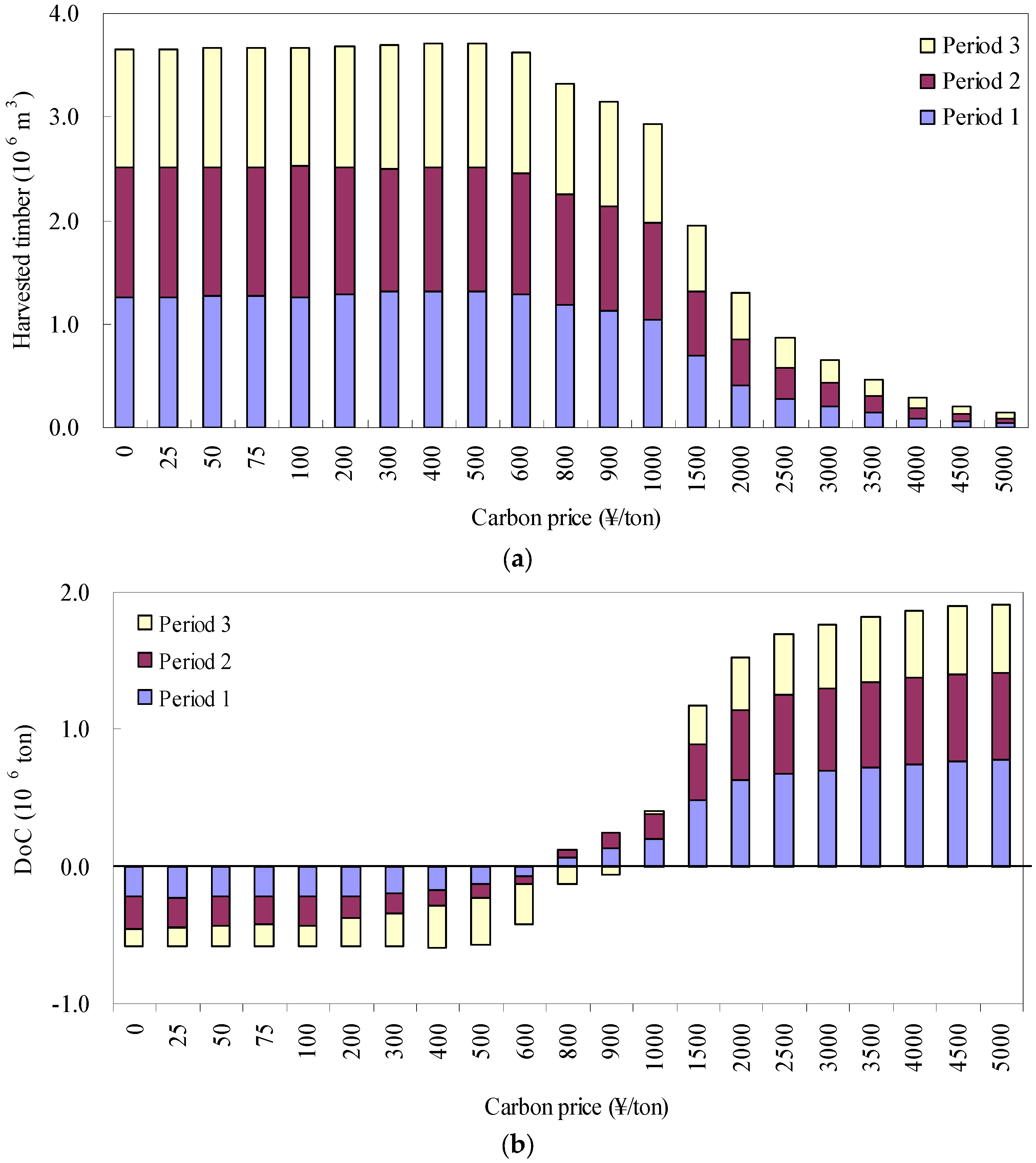
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Backéus, S.; Wikström, P.; Lämås, T. Modelling carbon sequestration and timber production in a regional case study. Silva Fenn. 2006, 40, 615–629. [Google Scholar] [CrossRef]
- State Forestry Bureau. Forest Resources Statistics of China for 2009–2013; Chinese Forestry Press: Beijing, China, 2014. (In Chinese)
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Carbon Dioxide Information Analysis Centre. World’s countries Ranked by 2011 Total Fossil-Fuel CO2 Emissions from Fossil-Fuel Burning, Cement Production, and Gas Flaring. Available online: http://cdiac.ornl.gov/ (accessed on 17 November 2016).
- Krcmar, E.; Kooten, G.C.V.; Vertinsky, I. Managing forest and marginal agricultural land for multiple tradeoffs: Compromising on economic, carbon and structural diversity objectives. Ecol. Model. 2005, 185, 451–468. [Google Scholar] [CrossRef]
- Saunders, M.; Tobin, B.; Black, K.; Gioria, M.; Nieuwenhuis, M.; Osborne, B.A. Thinning effects on the net ecosystem carbon exchange of a Sitka spruce forest are temperature-dependent. Agric. For. Meteorol. 2012, 157, 1–10. [Google Scholar] [CrossRef]
- Liu, Q.; Cai, H.; Jin, G. Effects of selective cutting on the carbon density and net primary productivity of a mixed broadleaved-Korean pine forest in northeast China. Chin. J. Appl. Ecol. 2013, 24, 2709–2716. [Google Scholar]
- Bravo-Oviedo, A.; Ruiz-Peinado, R.; Modrego, P.; Alonso, R.; Montero, G. Forest thinning impact on carbon stock and soil condition in Southern European populations of P. sylvestris L. For. Ecol. Manag. 2015, 357, 259–267. [Google Scholar] [CrossRef]
- Jandl, R.; Lindner, M.; Vesterdal, L.; Bauwens, B.; Baritz, R.; Hagedorn, F.; Johnson, D.W.; Minkkinen, K.; Byme, K.A. How strongly can forest management influence soil carbon sequestration? Geoderma 2007, 137, 253–268. [Google Scholar] [CrossRef]
- Ruiz-Peinado, R.; Bravo-Oviedo, A.; López-Senespleda, E.; Montero, G.; Rio, M. Do thinning influence biomass and soil carbon stocks in Mediterranean maritime pinewoods? Eur. J. For. Res. 2013, 132, 253–262. [Google Scholar] [CrossRef]
- Primicia, I.; Artázcoz, R.; Imbert, J.B.; Puertas, F.; Traver, M.D.C.; Castillo, F.J. Influence of thinning intensity and canopy type on Scots pine stand and growth dynamics in a mixed managed forest. For. Syst. 2016, 25, e057. [Google Scholar] [CrossRef]
- Johnson, D.W.; Curtis, P.S. Effects of forest management on soil C and N storage: Metaanalysis. For. Ecol.Manag. 2001, 140, 227–238. [Google Scholar] [CrossRef]
- Campbell, J.; Alberti, G.; Martin, J.; Law, B.E. Carbon dynamics of a ponderosa pine plantation following a thinning treatment in the northern Sierra Nevada. For. Ecol. Manag. 2009, 257, 453–463. [Google Scholar] [CrossRef]
- Eriksson, E.; Gillespie, A.R.; Gustavsson, L.; Langvall, O.; Olsson, M.; Sathre, R.; Stendahl, J. Integrated carbon analysis of forest management practices and wood substitution. Can. J. For. Res. 2007, 37, 671–681. [Google Scholar] [CrossRef]
- Kurttila, M.; Pukkala, T.; Loikkanen, J. The performance of alternative spatial objective types in forest planning calculations: A case for flying squirrel and moose. For. Ecol. Manag. 2002, 166, 245–260. [Google Scholar] [CrossRef]
- Baskent, E.Z.; Keles, S. Developing alternative forest management planning strategies incorporating timber, water and carbon values: An examination of their interactions. Environ. Model. Assess. 2009, 14, 467–480. [Google Scholar] [CrossRef]
- Başkent, E.Z.; Küçüker, D.M. Incorporating water production and carbon sequestration into forest management planning: A case study in Yalnızçam planning unit. For. Syst. 2010, 19, 98–111. [Google Scholar] [CrossRef]
- Bourque, C.P.A.; Neilson, E.T.; Gruenwald, C.; Perrin, S.F.; Hiltz, J.C.; Blin, Y.A.; Horsman, G.V.; Parker, M.S.; Thorburn, C.B.; Corey, M.M.; et al. Optimizing carbon sequestration in commercial forests by integrating carbon management objectives in wood supply modeling. Mitig. Adapt. Strateg. Glob. Chang. 2007, 12, 1253–1275. [Google Scholar] [CrossRef]
- Annkristin, R.; Terje, G.; Birger, S.; Hans-Fredrik, H.; Even, B. A forest optimization model including carbon flows: Application to a forest in Norway. For. Ecol. Manag. 2009, 258, 579–589. [Google Scholar]
- Dahlin, B.; Sallnas, O. Harvest scheduling under adjacency constraints-A case study from the Swedish sub-alpine region. Scand. J. For. Res. 1993, 8, 281–290. [Google Scholar] [CrossRef]
- Boston, K.; Bettinger, P. An economic and landscape evaluation of the green-up rules for California, Oregon, and Washington (USA). For. Policy Econ. 2006, 8, 251–266. [Google Scholar] [CrossRef]
- Sustainable Forestry Initiative. SFI 2015–2019 Forest Management Standard; Sustainable Forestry Initiative Inc.: Washington, DC, USA, 2015. [Google Scholar]
- Borges, P.; Bergseng, E.; Eid, T.; Gobakken, T. Impact of maximum opening area constraints on profitability and biomass availability in forest-a large, real world case. Silva Fenn. 2015, 49, 1347. [Google Scholar] [CrossRef]
- Dong, L.; Bettinger, P.; Liu, Z.; Qin, H. Spatial forest harvest scheduling for areas involving carbon and timber management goals. Forests 2015, 6, 1362–1379. [Google Scholar] [CrossRef]
- Murray, A.T. Spatial restrictions in harvest scheduling. For. Sci. 1999, 45, 45–52. [Google Scholar]
- Chen, B.; Gadow, K.V. Timber harvest planning with spatial objectives, using the method of simulated annealing. Eur. J. Oper. Res. 2002, 121, 25–34. [Google Scholar]
- World Bank, Ecofys. State and Trends of Carbon Pricing; World Bank, Ecofys: Washington, DC, USA, 2015. [Google Scholar]
- State Development Planning Commission; State Forestry Bureau. The Ecological Protection and Economic Transformation Plans of Great Xing’an Mountain in 2010–2020; Chinese Forestry Press: Beijing, China, 2010. (In Chinese)
- Wang, H. Dynamic Simulating System for Stand Growth of Forests in Northeast China. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2012. [Google Scholar]
- State Forestry Bureau. The Technical Regulations of National Forest Investigation; Chinese Forestry Press: Beijing, China, 2003. (In Chinese)
- Lei, X.; Lu, Y.; Peng, C.; Zhang, X.; Chang, J.; Hong, L. Growth and structure development of semi-natural larch-spruce-fir (Larix olgensis-Picea jezoensis-Abies nephrolepis) forests in northeast China: 12-year results after thinning. For. Ecol. Manag. 2007, 240, 165–177. [Google Scholar] [CrossRef]
- Website of China Carbon Emission and Trading. Available online: http://www.tanpaifang.com/ (accessed on 17 November 2016).
- McDill, M.E.; Rebain, S.A.; Braze, J. Harvest scheduling with area-based adjacency constraints. For. Sci. 2002, 48, 631–642. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1101. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Pukkala, T.; Heinonen, T. Optimizing heuristic search in forest planning. Nonlinear Anal.: Real World Appl. 2006, 7, 1284–1297. [Google Scholar] [CrossRef]
- Boston, K.; Bettinger, P. An analysis of Monte-Carlo integer programming simulated annealing and tabu search heuristics for solving spatial harvest scheduling problems. For. Sci. 1999, 45, 292–301. [Google Scholar]
- Fu, H.; Yan, W.; Chen, J. Forest carbon storage and its dynamics in Daxing’an Mountains of Inner Mongolia. J. Arid Land Resour. Environ. 2013, 27, 166–170. (In Chinese) [Google Scholar]
- Wei, Y.; Zhou, W.; Zhou, L.; Qin, S.; Dai, L. Carbon storage and its distribution pattern in the natural larix gmelinii forest on Daxing’an Mountains. Acta Ecol. Sin. 2015, 35, 189–195. (In Chinese) [Google Scholar]
- Dong, L. Developing Individual and Stand-Level Biomass Equations in NortheastChina Forest Area. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2015. [Google Scholar]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Gonzalo, J.; Pukkala, T.; Borges, J.G. Integrating fire risk in stand management scheduling: An application to Maritime pine stands in Portugal. Ann. Oper. Res. 2014, 219, 379–395. [Google Scholar] [CrossRef]
- Bettinger, P.; Siry, J.; Merry, K. Forest management planning technology issues posed by climate change. For. Sci. Technol. 2013, 9, 9–19. [Google Scholar] [CrossRef]
- Hu, H.; Wei, S.; Sun, L. Estimation of carbon emissions due to forest fire in Daxing’an Mountains from 1965 to 2010. Chin. J. Plant Ecol. 2012, 36, 629–644. (In Chinese) [Google Scholar] [CrossRef]
- Peter, B.; Nelson, J. Estimating harvest schedules and profitability under the risk of fire disturbance. Can. J. For. Res. 2005, 35, 1378–1388. [Google Scholar] [CrossRef]
- Couture, S.; Reynaud, A. Forest management under fire risk when forest carbon sequestration has value. Ecol. Econ. 2011, 70, 2002–2011. [Google Scholar] [CrossRef]
- Garcia-Gonzalo, J.; Borges, J.G.; Palma, J.H.N.; Zubizarreta-Gerendiain, A. A decision support system for management planning of Eucalyptus plantations facing climate change. Ann. For. Sci. 2014, 71, 187–199. [Google Scholar] [CrossRef]
- Borges, P.; Martins, I.; Berseng, E.; Eid, T.; Gobakken, T. Effects of site productivity on forest harvest scheduling subject to green-up and maximum area restriction. Scand. J. For. Res. 2015, 31, 507–516. [Google Scholar] [CrossRef]
- Nalle, D.J.; Arthur, J.L.; Montgomery, C.A. Economic impacts of adjacency and green-up constraints on timber production at a landscape scale. J. For. Econ. 2005, 10, 189–205. [Google Scholar] [CrossRef]
| Period (a) | Prescription (b) | Carbon Price (¥/ton) | |||||
|---|---|---|---|---|---|---|---|
| 0 | 50 | 500 | 800 | 1000 | 5000 | ||
| −1 | −1 | 4.36 | 4.36 | 4.36 | 4.36 | 4.36 | 4.36 |
| 0 | 0 | 0.22 | 0.23 | 0.40 | 5.44 | 9.61 | 88.40 |
| 1 | 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.47 |
| 2 | 0.51 | 0.34 | 0.30 | 1.76 | 3.82 | 0.44 | |
| 3 | 42.19 | 41.68 | 39.90 | 32.08 | 26.15 | 0.19 | |
| 2 | 1 | 0.00 | 0.00 | 0.00 | 0.25 | 0.70 | 2.27 |
| 2 | 0.02 | 0.03 | 0.03 | 3.36 | 7.09 | 0.16 | |
| 3 | 29.81 | 30.09 | 27.91 | 22.92 | 16.57 | 0.03 | |
| 3 | 1 | 0.00 | 0.03 | 0.09 | 5.26 | 8.91 | 3.69 |
| 2 | 0.37 | 0.45 | 0.93 | 8.47 | 13.88 | 0.00 | |
| 3 | 22.52 | 22.78 | 26.07 | 16.09 | 8.91 | 0.00 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Dong, L.; Huang, Y. Evaluating the Effects of Carbon Prices on Trade-Offs between Carbon and Timber Management Objectives in Forest Spatial Harvest Scheduling Problems: A Case Study from Northeast China. Forests 2017, 8, 43. https://doi.org/10.3390/f8020043
Qin H, Dong L, Huang Y. Evaluating the Effects of Carbon Prices on Trade-Offs between Carbon and Timber Management Objectives in Forest Spatial Harvest Scheduling Problems: A Case Study from Northeast China. Forests. 2017; 8(2):43. https://doi.org/10.3390/f8020043
Chicago/Turabian StyleQin, Huiyan, Lingbo Dong, and Yingli Huang. 2017. "Evaluating the Effects of Carbon Prices on Trade-Offs between Carbon and Timber Management Objectives in Forest Spatial Harvest Scheduling Problems: A Case Study from Northeast China" Forests 8, no. 2: 43. https://doi.org/10.3390/f8020043
APA StyleQin, H., Dong, L., & Huang, Y. (2017). Evaluating the Effects of Carbon Prices on Trade-Offs between Carbon and Timber Management Objectives in Forest Spatial Harvest Scheduling Problems: A Case Study from Northeast China. Forests, 8(2), 43. https://doi.org/10.3390/f8020043





