Forest Planning Heuristics—Current Recommendations and Research Opportunities for s-Metaheuristics
Abstract
:1. Introduction
2. Recommendations
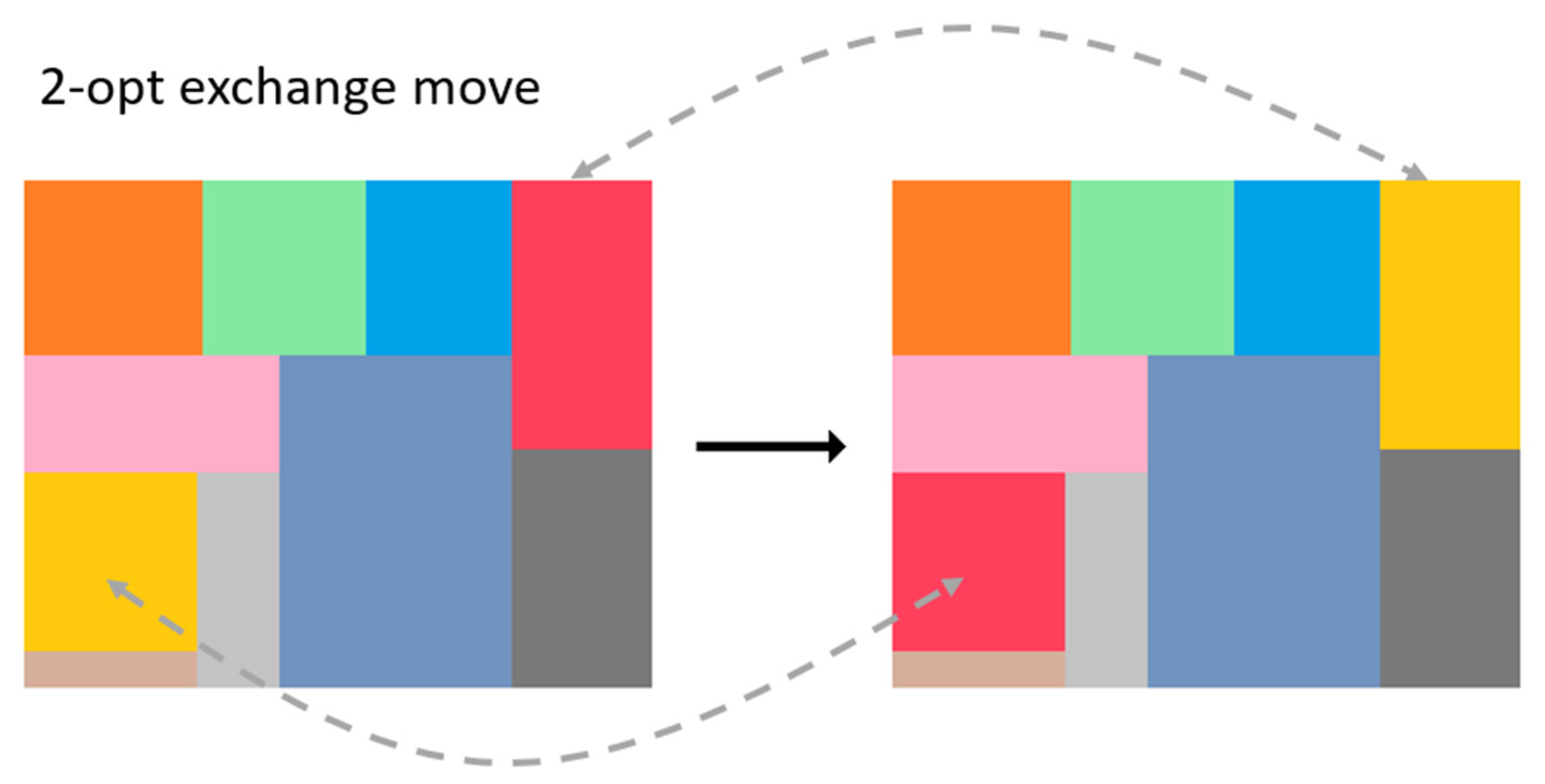
2.1. Process Improvements to s-Metaheuristics
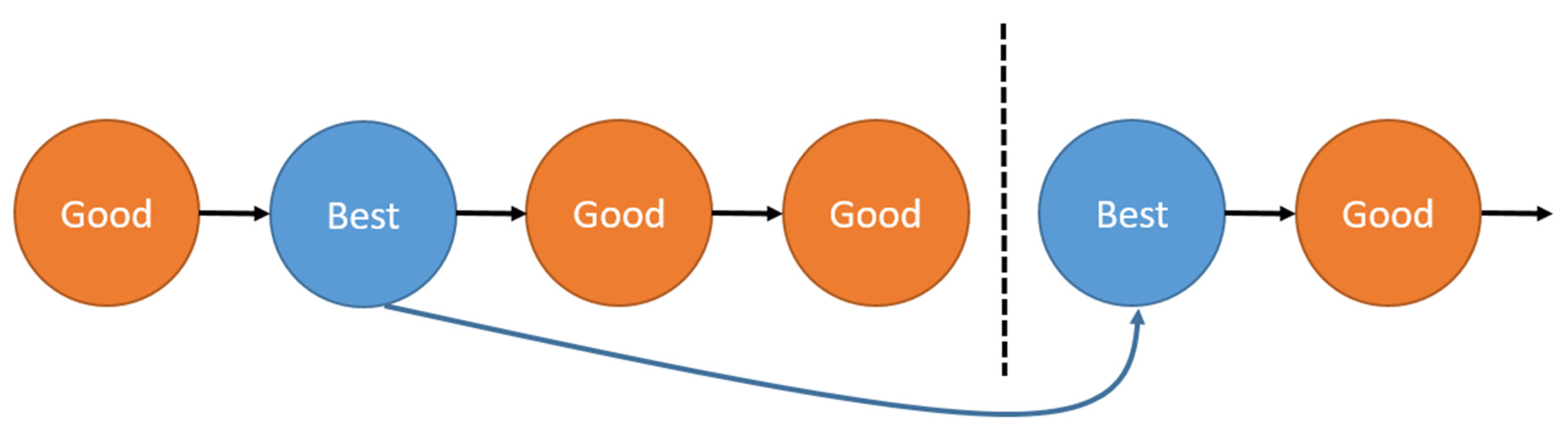
2.2. Search Reversion Strategies
2.3. Search Destruction and Reconstruction Strategies
2.4. Intelligent and Dynamic Parameterization of a Search Process
2.5. Intelligent Termination or Integration Criteria for a Search Process
2.6. Seeding the Search with a High-Quality Solution
3. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bettinger, P.; Boston, K.; Siry, J.P.; Grebner, D.L. Forest Management and Planning, 2nd ed.; Academic Press: New York, NY, USA, 2017; ISBN 978-0-128-09476-1. [Google Scholar]
- Nocentini, S.; Buttoud, G.; Ciancio, O.; Corona, P. Managing forests in a changing world: The need for a systemic approach: A review. For. Syst. 2017, 26. [Google Scholar] [CrossRef]
- Reyer, C.P.O.; Bugmann, H.; Nabuurs, G.-J.; Hanewinkel, M. Models for adaptive forest management. Reg. Environ. Chang. 2015, 15, 1483–1487. [Google Scholar] [CrossRef]
- Boston, K.; Sessions, J. Development of a spatial harvest scheduling system to promote the conservation between indigenous and exotic forests. Int. For. Rev. 2006, 8, 297–306. [Google Scholar] [CrossRef]
- Ding, T.; Sun, K.; Yang, Q.; Khan, A.W.; Bie, Z. Mixed integer second order cone relaxation with dynamic simulation for proper power system islanding operations. IEEE J. Emerg. Sel. Top. C 2017, 7, 295–306. [Google Scholar] [CrossRef]
- Bettinger, P.; Sessions, J.; Boston, K. Using Tabu search to schedule timber harvests subject to spatial wildlife goals for big game. Ecol. Model. 1997, 94, 111–123. [Google Scholar] [CrossRef]
- Bettinger, P.; Sessions, J.; Johnson, K.N. Ensuring the compatibility of aquatic habitat and commodity production goals in eastern Oregon with a Tabu search procedure. For. Sci. 1998, 44, 96–112. [Google Scholar]
- Talbi, E.-G. Metaheuristics: From Design to Implementation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 978-0-470-27858-1. [Google Scholar]
- De León-Aldaco, S.E.; Calleja, H.; Alquicira, J.A. Metaheuristic optimization methods applied to power converters: A review. IEEE Trans. Power Electr. 2015, 30, 6791–6803. [Google Scholar] [CrossRef]
- Bettinger, P.; Boston, K.; Sessions, J. Intensifying a heuristic forest harvest scheduling search procedure with 2-opt decision choices. Can. J. For. Res. 1999, 29, 1784–1792. [Google Scholar] [CrossRef]
- Heinonen, T.; Pukkala, T. A comparison of one- and two-compartment neighbourhoods in heuristic search with spatial forest management goals. Silva Fenn. 2004, 38, 319–332. [Google Scholar] [CrossRef]
- Dong, L.; Bettinger, P.; Liu, Z.; Qin, H. A comparison of a neighborhood search technique for forest spatial harvest scheduling problems: A case study of the simulated annealing algorithm. For. Ecol. Manag. 2015, 356, 124–135. [Google Scholar] [CrossRef]
- Bachmatiuk, J.; Garcia-Gonzalo, J.; Borges, J.G. Analysis of the performance of different implementations of a heuristic method to optimize forest harvest scheduling. Silva Fenn. 2015, 49. [Google Scholar] [CrossRef]
- Glover, F. Finding a best traveling salesman 4-opt move in the same time as a best 2-opt move. J. Heuristics 1996, 2, 169–179. [Google Scholar] [CrossRef]
- Montiel, L.; Dimitrakopoulos, R. A heuristic approach for the stochastic optimization of mine production schedules. J. Heuristics 2017, 23, 397–415. [Google Scholar] [CrossRef]
- Ding, H.; Lim, A.; Rodrigues, B.; Zhu, Y. New heuristics for over-constrained flight to gate assignments. J. Oper. Res. Soc. 2004, 55, 760–768. [Google Scholar] [CrossRef]
- Grasas, A.; Juan, A.A.; Faulin, J.; de Armas, J.; Ramalhinho, H. Biased randomization of heuristics using skewed probability distributions: A survey and some applications. Comput. Ind. Eng. 2017, 110, 216–228. [Google Scholar] [CrossRef]
- López, C.L. Heuristics as Markov chains. Ann. Math. Artif. Intell. 2015, 73, 275–309. [Google Scholar] [CrossRef]
- Bettinger, P.; Demirci, M.; Boston, K. Search reversion within s-metaheuristics: Impacts illustrated with a forest planning problem. Silva Fenn. 2015, 49. [Google Scholar] [CrossRef]
- Akbulut, R.; Bettinger, P.; Ucar, Z.; Obata, S.; Boston, K.; Siry, J. Spatial forest plan development using heuristic processes seeded with a relaxed linear programming solution. For. Sci. 2017, 63, 518–528. [Google Scholar] [CrossRef]
- Bettinger, P.; Zhu, J. A new heuristic for solving spatially constrained forest planning problems based on mitigation of infeasibilities radiating outward from a forced choice. Silva Fenn. 2006, 40, 315–333. [Google Scholar] [CrossRef]
- Zhu, J.; Bettinger, P.; Li, R. Additional insight into the performance of a new heuristic for solving spatially constrained forest planning problems. Silva Fenn. 2007, 41, 687–698. [Google Scholar] [CrossRef]
- Schrimpf, G.; Schneider, J.; Stamm-Wilbrandt, H.; Dueck, G. Record breaking optimization results using the ruin and recreate principle. J. Comput. Phys. 2000, 159, 139–171. [Google Scholar] [CrossRef]
- Lozano, M.; García-Martínez, C.; Rodríguez, F.J.; Trujillo, H.M. Optimizing network attacks by artificial bee colony. Inf. Sci. 2017, 377, 30–50. [Google Scholar] [CrossRef]
- Rojas-Morales, N.; Riff Rojas, M.-C.; Ureta, E.M. A survey and classification of opposition-based metaheuristics. Comput. Ind. Eng. 2017, 110, 424–435. [Google Scholar] [CrossRef]
- Glover, F. Ejection chains, reference structures and alternating path methods for traveling salesman problems. Discret. Appl. Math. 1996, 65, 223–253. [Google Scholar] [CrossRef]
- Derigs, U.; Vogel, U. Experience with a framework for developing heuristics for solving rich vehicle routing problems. J. Heuristics 2014, 20, 75–106. [Google Scholar] [CrossRef]
- Almeida, F.; Giménez, D.; López-Espín, J.J.; Pérez-Pérez, M. Parameterized schemes of metaheuristics: Basic ideas and applications with genetic algorithms, scatter search, and GRASP. IEEE Trans. Syst. Man Cybern. A 2013, 43, 570–586. [Google Scholar] [CrossRef]
- Bettinger, P. SOFIE (Scheduling of Forest Investment Endeavors), Version 1.0. U.S. Copyright Registration Number TXu 2-008-943. 20 June 2016. [Google Scholar]
- Pukkala, T.; Heinonen, T. Optimizing heuristic search in forest planning. Nonlinear Anal. Real World Appl. 2006, 7, 1284–1297. [Google Scholar] [CrossRef]
- Nickabadi, A.; Ebadzadeh, M.M.; Safabakhsh, R. A novel particle swarm optimization algorithm with adaptive inertial weight. Appl. Soft Comput. 2011, 11, 3658–3670. [Google Scholar] [CrossRef]
- Zabinsky, Z.B.; Bulger, D.; Khompatraporn, C. Stopping and restarting strategy for stochastic sequential search in global optimization. J. Glob. Optim. 2010, 46, 273–286. [Google Scholar] [CrossRef]
- Ribeiro, C.C.; Rosseti, I.; Souza, R.C. Probabilistic stopping rules for GRASP heuristics and extensions. Int. Trans. Oper. Res. 2013, 20, 301–323. [Google Scholar] [CrossRef]
- Li, R.; Bettinger, P.; Boston, K. Informed development of meta heuristics for spatial forest planning problems. Open Oper. Res. J. 2010, 4, 1–11. [Google Scholar] [CrossRef]
- Golden, B.L.; Alt, F.B. Interval estimation of a global optimum for large combinatorial problems. Nav. Res. Logist. Q. 1979, 26, 69–77. [Google Scholar] [CrossRef]
- Los, M.; Lardinois, C. Combinatorial programming, statistical optimization and the optimal transportation network problem. Transp. Res. B-Meth. 1982, 16, 89–124. [Google Scholar] [CrossRef]
- Rojas, J.M.; Fraser, G.; Arcuri, A. Seeding strategies in search-based unit test generation. Softw. Test. Verif. Reliab. 2016, 26, 366–401. [Google Scholar] [CrossRef]
- Esmailzadeh, A.; Rahnamayan, S. Center-point-based simulated annealing. In Proceedings of the 25th IEEE Canadian Conference on Electrical and Computer Engineering, Montreal, QC, Canada, 29 April–2 May 2012; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Manfrini, F.A.L.; Bernardino, H.S.; Barbosa, H.J.C. On heuristics for seeding the initial population of Cartesian genetic programming applied to combinational logic circuits. In Proceedings of the 2016 Conference on Genetic and Evolutionary Computation Conference Companion, Denver, CO, USA, 20–24 July 2016; Association of Computing Machinery: New York, NY, USA, 2016; pp. 105–106. [Google Scholar] [CrossRef]
- Calvet, L.; de Armas, J.; Masip, D.; Juan, A.A. Learnheuristics: hybridizing metaheuristics with machine learning for optimization with dynamic inputs. Open Math. 2017, 15, 261–280. [Google Scholar] [CrossRef]
- Bettinger, P. Distributing geographic information systems capabilities to field offices: Benefits and challenges. J. Forest. 1999, 97, 22–26. [Google Scholar]
- Bettinger, P.; Boston, K. A conceptual model for describing decision-making situations in integrated natural resource planning and modeling projects. Environ. Manag. 2001, 28, 1–7. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bettinger, P.; Boston, K. Forest Planning Heuristics—Current Recommendations and Research Opportunities for s-Metaheuristics. Forests 2017, 8, 476. https://doi.org/10.3390/f8120476
Bettinger P, Boston K. Forest Planning Heuristics—Current Recommendations and Research Opportunities for s-Metaheuristics. Forests. 2017; 8(12):476. https://doi.org/10.3390/f8120476
Chicago/Turabian StyleBettinger, Pete, and Kevin Boston. 2017. "Forest Planning Heuristics—Current Recommendations and Research Opportunities for s-Metaheuristics" Forests 8, no. 12: 476. https://doi.org/10.3390/f8120476
APA StyleBettinger, P., & Boston, K. (2017). Forest Planning Heuristics—Current Recommendations and Research Opportunities for s-Metaheuristics. Forests, 8(12), 476. https://doi.org/10.3390/f8120476





