1. Introduction
Airborne scanning lidar technology (henceforth referred to as simply lidar) provides vegetation measurements which are highly related to forest attributes needed for forest inventory and monitoring. Some examples of forest attributes which are highly related to lidar measurements include stem volume, basal area, quadratic mean diameter, and above-ground biomass [
1,
2,
3]. The lidar vegetation measurements can be obtained with high precision over large areas enabling wall-to-wall measurements and predictions of vegetation attributes, as well as precise estimates of population parameters. Despite demonstrated advantages to using lidar for inventory and monitoring, there are also omissions from most analyses which inhibit common usage. One of the limitations of typical lidar research studies, is that they do not directly evaluate prediction of tree diameter distributions.
The distribution of diameters at breast height (dbh) is an important component of most forest inventory, management, and monitoring strategies. Dbhs are needed to describe stand properties because variables such as growth, volume, market value, conversion-cost, product specifications, and future forest prescriptions are dependent on trees’ dbhs. The use of single-tree level growth and yield models almost always requires dbh distributions. Dbhs are also used to assess forest sustainability based on whether the quantity and sizes of growing stock are suited to replace the current population of harvestable trees [
4]. Information about dbhs also informs the type and timing of management strategies and economic value of the stand [
5]. Ecological analyses also use dbh density information including, for example, assessments of vegetative diversity [
6], insect disturbance mechanics [
7], habitat suitability [
8], and suitability and distribution of parent stock for coarse woody debris [
9].
Dbh distributions are often simplified using a mathematical function with parameters that can be estimated or recovered using lidar measurements or other ancillary data. Dbh distribution functions can be predicted with both parametric and non-parametric strategies. Parametric strategies are based on the assumption that the dbh density can be characterized by a theoretical probability density function. A variety of theoretical functions have been tested including the beta [
10], Weibull [
11,
12] and Johnson’s SB [
13,
14]. Two methods have been used to predict parameters of theoretical functions, the parameter prediction method and the parameter recovery method [
15]. As the name indicates, in the parameter prediction method stand attributes (or remote sensing data) are used to predict parameters of the probability density function. In the parameter recovery method moments or percentiles of dbh distribution are predicted or measured using stand variables. The parameters of a theoretical distribution are then recovered by leveraging the known relationships between the predicted attributes and the distributional parameters.
Non-parametric strategies attempt to predict percentiles of empirical distributions [
16,
17] or directly predict dbh bins or classes. While parametric strategies are advantageous in being able to represent a complete distribution with a few parameters when the empirical distribution is unimodal, they may have limited ability to represent complex and mixed species stands that may not have unimodal densities [
18]. Empirical strategies which retain the original data or relative densities by dbh bins provide more flexibility to accommodate many types of stand tables [
17], however, some prediction strategies for multiple dbh percentiles can result in illogical behavior, benefitting from the introduction of constraints [
19].
Various strategies for predicting dbh distributions with lidar have been evaluated. Gobakken and Næsset [
20] compared parameter prediction and parameter recovery methods in the prediction of stem number and basal area distributions. The underlying probability theoretical distribution was a two-parameter Weibull distribution. The precision was slightly better for the parameter recovery method than for the parameter prediction method. Mehtatalo et al. [
21] also used the parameter recovery approach, however, they proposed a method where the parameters of the assumed dbh distribution and height-dbh curve are determined in such a manner that they are compatible with the predictions of stand attributes. Maltamo et al. [
22] proposed another approach to obtain a compatible stand description. First the parameters of a Weibull distribution and stand volume are predicted with lidar. Then, the estimated stem number distribution is modified to correspond to the volume obtained in the previous step by using the calibration estimation approach proposed by Deville and Sarndal [
23].
Percentiles of dbh distributions have also been predicted with lidar. Maltamo et al. [
24] predicted 12 percentile points in semi-natural forests in Finland. Bollandsås and Naesset [
25] predicted 10 percentiles in uneven-sized Norway spruce stands. Breidenbach et al. [
26] used a generalized linear model (GLM) to estimate parameters of theoretical distributions with lidar. A benefit of GLM is that they can be a one-step procedure, without the need to first fit a distribution and then predict its parameters. Thomas et al. [
27] studied the prediction of both unimodal and bimodal dbh distributions using a finite mixture model approach. They successfully predicted the parameters of separate Weibull functions, but because there was no lidar-based method for separation of distribution type (unimodal or bimodal), the applicability of the method is somewhat limited for lidar inventory.
An alternative strategy to predict dbh distribution with lidar is using k-nearest-neighbor (k-NN) imputation. An advantage of k-NN is that the k-NN model can be used to simultaneously predict a suite of response variables, including a list of individual trees records (tree-list). k-NN also provides compatible stand if stand attributes are predicted simultaneously with tree-lists. This was the motivation for the work by Packalén and Maltamo [
28]. They predicted stand attributes and tree-lists simultaneously for Scots pine, Norway spruce, and deciduous trees and compared the performance of a tree-list approach to the use of a Weibull distribution approach. The k-NN tree-list strategy was able to mimic bimodal dbh distributions of Norway Spruce (the only shade tolerant tree species in the study area) and in general provided clearly lower error index values. Maltamo et al. [
29] examined the performance of a k-NN tree-list approach without considering tree species. Their objectives were to investigate the effect of different predictor and response variables and to examine the influence of reduced numbers of training plots. The results indicated that response variables must be selected very carefully in order to obtain accurate predictions of dbh distributions and stand attributes. They also reported that with a low number of training plots (approx. 100) precise predictions of dbh distributions could be produced in their study area.
When a diameter prediction strategy is evaluated, inference is typically made on differences between the observed and predicted distribution using hypothesis or goodness of fit tests, such as the Kolmogorov-Smirnov test. However, for reasons described extensively in Reynolds et al. [
30] including that the
p-values can be wildly inaccurate (for fewer than 40 trees per plot), these types of tests are problematic for many of the same reasons that the statistical community discourages
p-value based inference in hypothesis testing (e.g., Halsey et al. [
31]). Reynolds et al. [
30] instead proposed an index based upon absolute deviations in the units of the response. This index is often referred to as the “Reynolds error index” in the literature. Reynolds et al. [
30] also described methodologies for formal statistical inference using their error index.
In this study we wished to understand tradeoffs between various lidar and k-NN based dbh prediction strategies (e.g., numbers of neighbors, distance metrics, and others). While studies have examined dbh predictions with lidar, only a subset of prediction strategies were examined, and the indices used by studies are difficult to generalize to other designs and areas. To overcome these limitations, we propose two indices and use them to examine a variety of dbh predictions strategies. The proposed indices are based on the well-known coefficient of determination (R2), and root mean squared deviation (RMSD) which simplifies their interpretation by users and readers.
Initially, we graphically demonstrate the behavior of the two proposed indices using simulations. We then use the indices to describe the relative performances of a variety of lidar and k-NN diameter distribution prediction strategies. Given the large number of components of a k-NN and lidar prediction strategy, clarity is needed on which k-NN configurations work best with lidar for dbh distribution predictions. Components that we examine include distance metrics (e.g., Euclidean vs. Mahalanobis), numbers of neighbors (the k in k-NN), presence or absence of stratification, and sensitivity of predictions to the choice of response and predictor variables. Based on our findings using the proposed indices, we conclude with recommendations on effective diameter distribution predictions strategies with lidar and k-NN.
2. Materials and Methods
2.1. Study Site
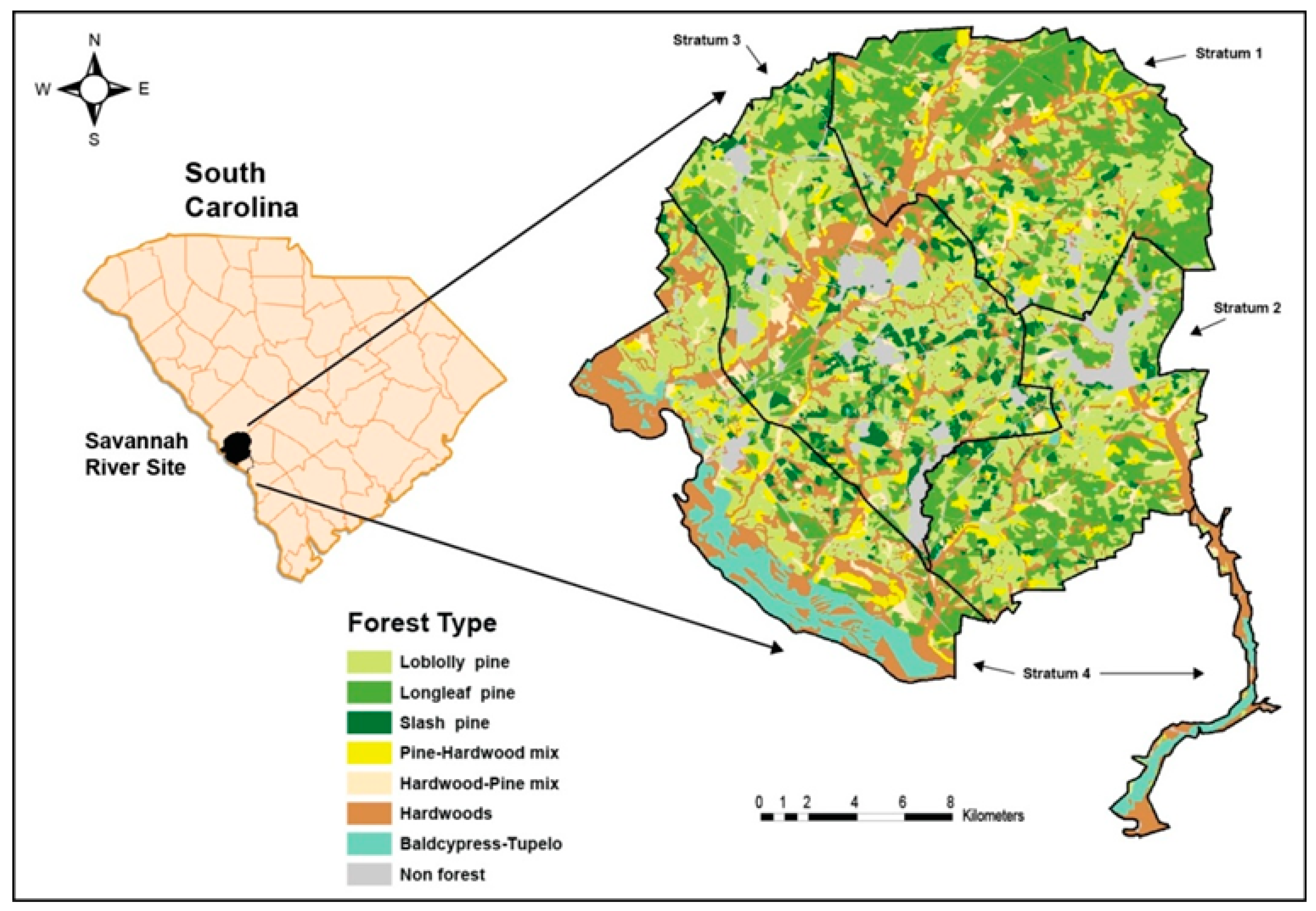
The study was conducted at the U. S. Department of Energy’s Savannah River Site, an 80,267 ha National Environmental Research Park in Aiken and Barnwell counties, South Carolina USA (
Figure 1). The Savannah River Site is characterized by sandy soils and gently sloping hills dominated by pines, with hardwoods occurring in riparian areas. Prior to acquisition by the Department of Energy in 1951, the majority of Savannah River Site uplands were agricultural fields or had recently been harvested for timber. The U.S. Department of Agriculture Forest Service has managed the natural resources of the Savannah River Site since 1952 and reforested the majority of the uplands with loblolly (
P. taeda), longleaf (
P. palustris), and slash (
P. elliottii) pines. These pine stands are actively managed for timber and wildlife habitat.
2.2. Ground Data Collection
Plot measurements were performed on a grid of fixed radius circular plots designed for modeling forest attributes with auxiliary lidar data. The plot design consisted of two concentric nested fixed area circular measurement plots. The innermost 0.004 ha plot was used to measure trees between 2.5 and 7.4 cm in dbh. Larger trees were measured on a 0.04 ha plot if there were at least 8 dominant or co-dominant trees, otherwise trees larger than 7.4 cm dbh were measured on a 0.081 ha plot. The heights, dbhs, heights to crown base, and species were recorded for trees on the two concentric plots, and additionally trees between 2.5 and 7.4 cm were tallied on a 0.04 ha plot.
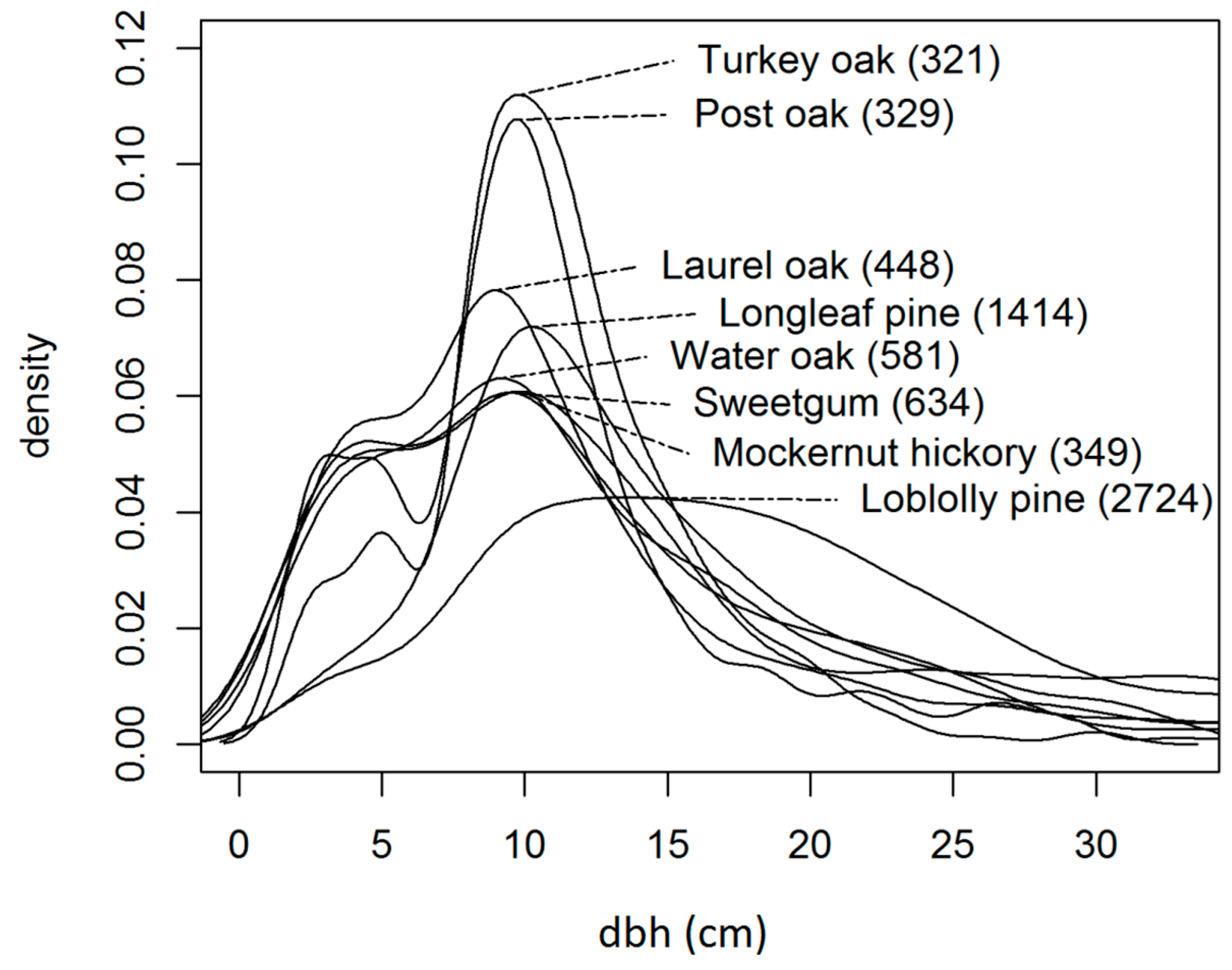
Plot locations were selected purposively to cover the range of tree sizes and stand compositions that occur on the Savannah River Site. Field measurements were taken on 194 field plot locations selected purposively to sample across multiple vegetation classes and sizes. Of the 194 plots, 4 were dropped because it was determined that they were measured in locations outside of our target population. A summary of the tree and plot variables used for this study is provided in
Table 1. Additionally, a visual representation of the empirical dbh density functions for the 8 most common species occurring on plots is shown in
Figure 2. Additional forest attributes (besides dbh) used in our analyses included trees per hectare (TPH), basal area per hectare (m
2/ha, BA), Lorey’s height (m, Lor.), and total cubic stem volume (m
3/ha, Vol.).
Plot locations were surveyed using L1/L2 GLONASS enabled survey-grade GPS receivers. The receiver was placed at each plot’s center on a 3 m pole and a minimum of 600 1-second-epoch satellite fixes were collected and differentially corrected. We expect the horizontal RMSE for surveyed plot center positions to be less than 1 m in the pine forest types at the Savannah River Site, based upon our previous experience with positional accuracy using these receivers in a variety of forest types (e.g., Andersen et al. [
32]).
Plots were assigned to post-strata using the dominant species group for the stand in which the plot was measured (the most common dominant types include: Hardwood—29 plots; Loblolly P.—76 plots; Longleaf P.—54 plots). All of the hardwood species were combined into a single stratum. Forestry staff for the site developed a tract-wide map of species groups by visually classifying stands in the field. Plots were assigned to strata by intersecting plot locations with the strata map.
2.3. Lidar Data
Lidar data were collected from 21 February to 2 March 2009 with two Leica ALS50-II lidar sensors in leaf-off conditions.
Table 2 provides acquisition parameters.
Point cloud data were processed to create predictor variables for this study using the cloudmetrics executable included with FUSION software [
33]. This executable computes a large number of statistics from lidar including, but not limited to, height percentiles (e.g., 90th, 50th, and 30th percentile heights in
Table 3) and lidar cover (the percent of returns above a threshold, in our case 1.50 m). We also examined fraction without foliage (fwof), a modeled variable which used normalized intensity to suggest the proportion of the leaf-off lidar which did not intersect live foliage.
2.4. k-NN Tree-List Imputation
In k-NN imputation, response variables from measured sites are shared or imputed with sites without measurements based on the degree of similarity in their auxiliary variables. The “similarity” in auxiliary variables is evaluated using a distance metric, e.g., Euclidean distance, where a large number of distance metrics have been demonstrated in the k-NN literature. The distance metrics are functions which determine how one or more auxiliary variables should be weighted and combined. The coefficients of the weight function can also depend on the observed association between response and predictor variables, theoretically weighting predictors which can better predict the response variable(s). If more than one nearest neighbor (k greater than one) is used, then a rule must be formulated to average (continuous) and select (categorical) donor response values. This procedure can be used to simultaneously impute a large number of response variables in a single step.
Procedurally, the process is as follows: (1) a distance metrics is computed between measured and unmeasured (response) observations, then (2) the k observations with the smallest distances (donors) are transferred (imputed) to the observation without a measured response (target).
For this study we relied upon the yaImpute package [
34] implemented in R [
35] for k-NN imputation. The identities of the donor plots (nearest neighbors) were used to impute tree-lists, as yaImpute is not currently set up to directly impute tree-lists. Based on the donors’ identities, all of the tree records from the imputed donor plots were copied to the target observation. Each copied tree was then distance weighted to generate a tree-list for the target observation. The distance weighted tree-lists from the k neighbors then became the basis for prediction of the empirical dbh density for the target observation. The choice of a weighting function for the K imputed neighbors has been shown to have limited effect on performance [
28].
2.5. k-NN Imputation Strategy Components
We examined the effects of 4 components of a k-NN tree-list imputation strategy including (1) the choice of distance metric, (2) the selected predictors, (3) the set of response variables, and (4) the effect of post-stratification. The distance metrics evaluated include Euclidean distance (EUC.), Mahalanobis distance (MAH), most similar neighbors (MSN), and random forest (RF). MSN and RF distances both use response variables for measured observations in computing distances. Additional details for how these distances are defined can be found in the yaImpute package documentation [
34]. The effect of post-stratification on k-NN performance was evaluated by stratifying the data, and predicting separately within strata. Strata with fewer than 10 response measurements were imputed from the pool of all observation.
2.6. Dbh Densities
The proportions of trees falling in diameter bins (the empirical dbh density, or just “dbh density”) were computed by first binning lists of trees into 2.54 cm (1 inch) dbh bins and computing the proportions of all trees in the dbh classes. In the case of imputed tree-lists, weighted dbh densities were computed using the distance weights from the imputed plots. The bin proportions were then smoothed with a 3-bin moving average centered on the target bins. The smoothing function was applied to emphasize major trends, and de-emphasize fine-scale fluctuations. Individual plot densities can have spikes, pits, and other characteristics that we did not wish to examine.
2.7. Measures of Performance
Evaluation of k-NN predictions strategies were performed using Leave One Out (LOO) validation in combination with indices. In LOO, models are iteratively fit to the data while omitting one plot at a time. After fitting a given model, the data are then tested against the omitted plot. The errors in prediction for the omitted plots then serve as the basis for indices of performance. Our first suggested measure of performance is index H.
Index H is equivalent to the coefficient of determination (or, commonly, R2) which has a straight-forward interpretation—the proportion of variability explained. The index has an advantage over alternative measures of performance that we examined in that it provides a relative measure of performance. The baseline level of variability comes from plot variation in dbh densities around the mean dbh density within a dbh class for all of the plots. As with R2, smaller prediction error relative to baseline variability will yield index H values closer to one. Larger prediction residuals will in general cause index H to approach zero, and negative values of H are possible if the prediction strategy is inferior to prediction with the means model. Our inferences for this index are similar to those that would be made from R2. We rely heavily on index H for inferences about different k-NN dbh prediction strategies. While the H values are suggestive of general trends in performance, the index is not suited for identifying a single best prediction strategy.
A limitation of index H is that it is only meaningful in comparisons if the baseline variability is similar between compared strategies. In many cases this property will not hold. We expect, for example, to have greater variability amongst variable radius plots than amongst fixed radius plots for the same area; comparing their index H values then would be meaningless. To compare prediction strategies from two different inventory designs or two study areas with different levels of baseline variability, it is important to have an absolute measure of performance. A second limitation to index H is that the index is unitless, and it is often desirable to have an index in the same units as the attribute of interest. To support inferences from multiple designs in the units of the response, we propose a second index, I, which is an absolute measure of performance:
Index I is equivalent to the Root Mean Squared Deviation (RMSD) by plot (rather than by bin). The units for this index are the same as for the attribute of interest. As with RMSD, a smaller value of index I indicates better prediction performance. Index I can be used to compare performance across sites, designs, and project areas.
While we do not use p-values in this analysis, we recognize that some users will wish to use p-values. p-value can be fairly easily generated for the suggest indices with simulations. One simulation-based approach to obtain p-value is to randomly assign tree-lists to plots several thousand times, and compute index values for each randomization. This will yield a distribution of index values for the null model where lidar and k-NN provide no explanatory power. The distribution can then be compared to the observed index value for a particular lidar and k-NN configuration. The proportion of values which are as extreme as the observed index value will serve as the simulation-based p-value.
2.8. Index Demonstration
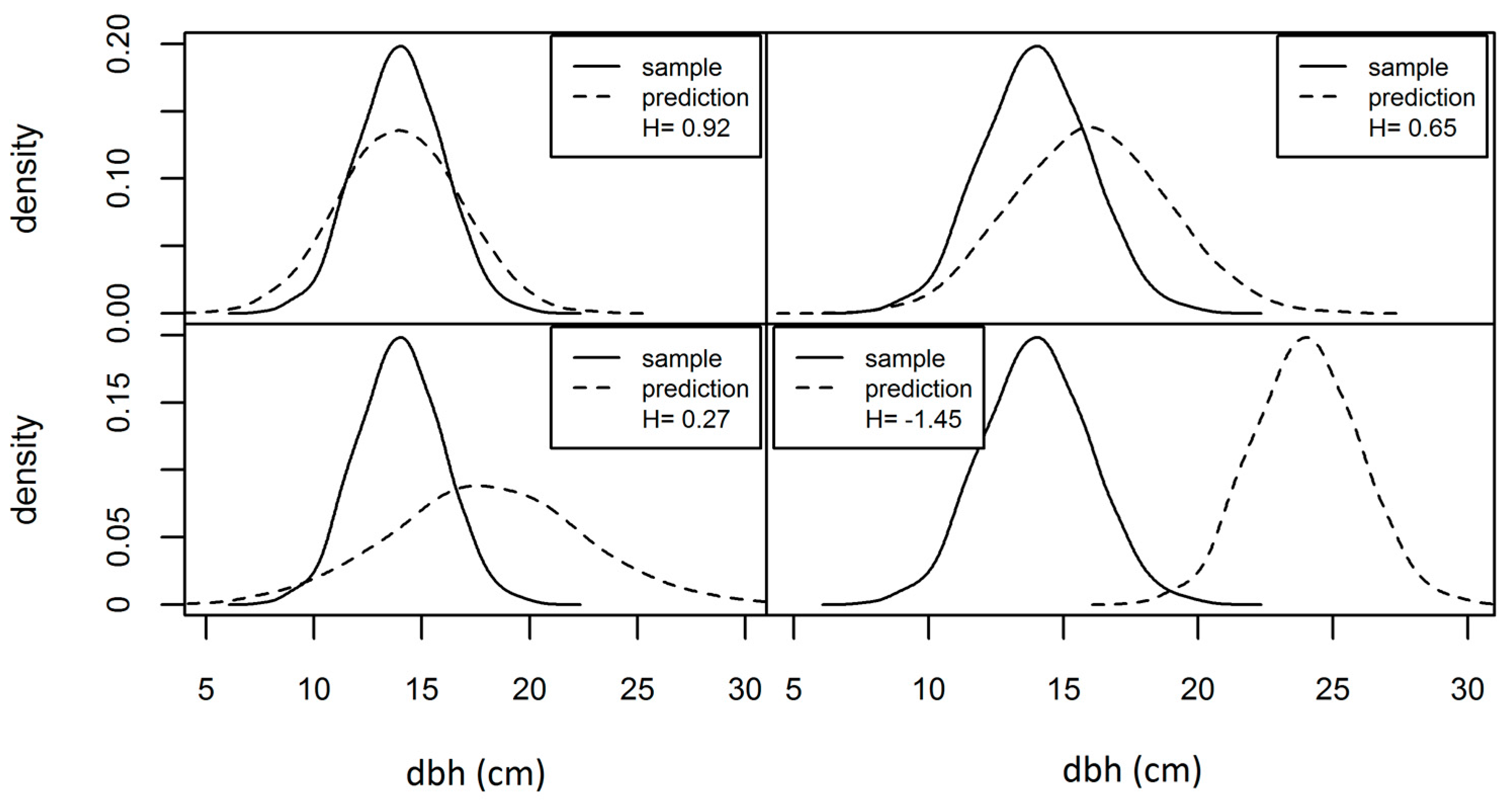
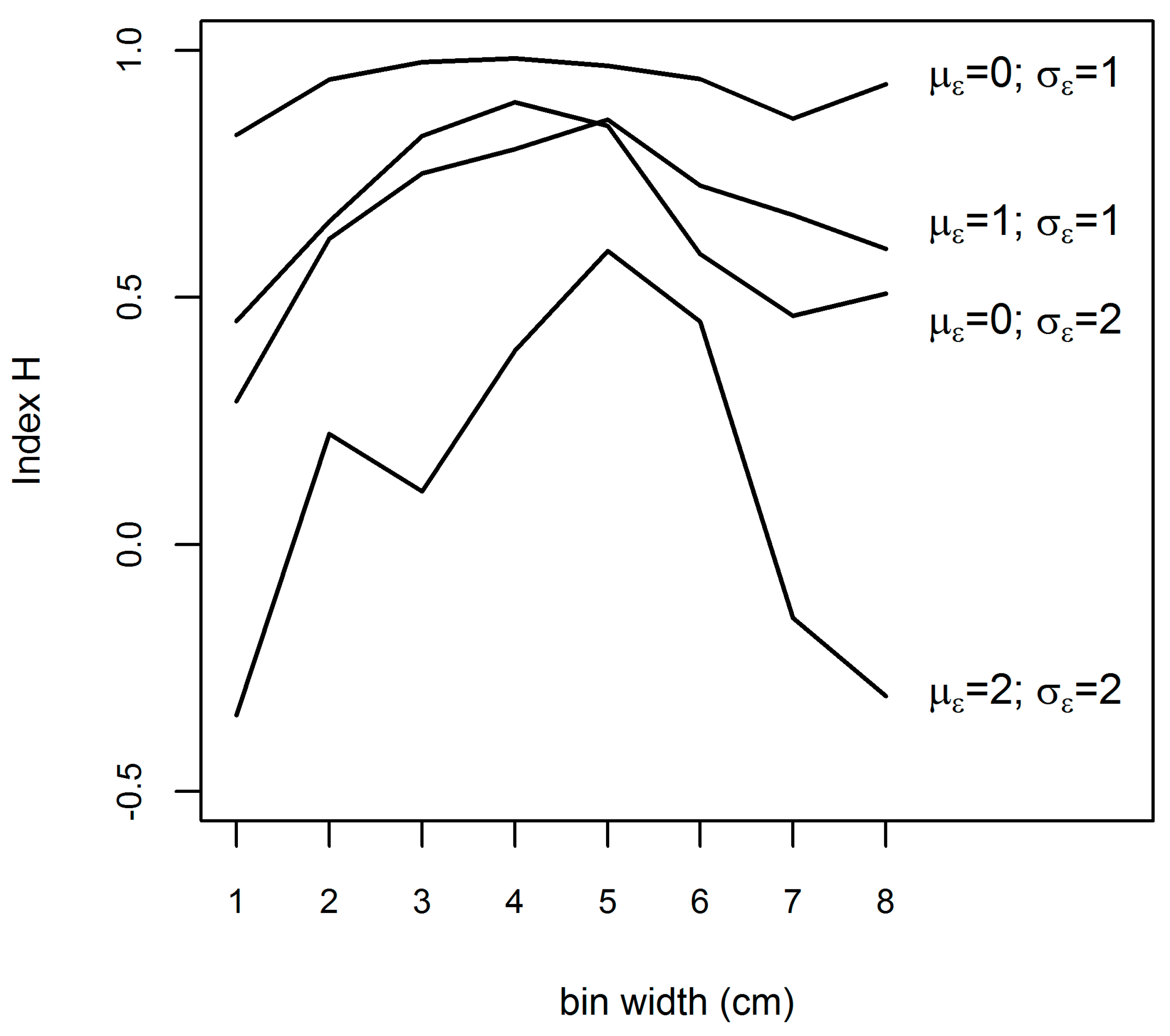
To provide a sense of the behavior of our indices as a function of prediction performance, we provide a visual calibration image which shows H values for various levels of departure from agreement between a sample and a prediction (
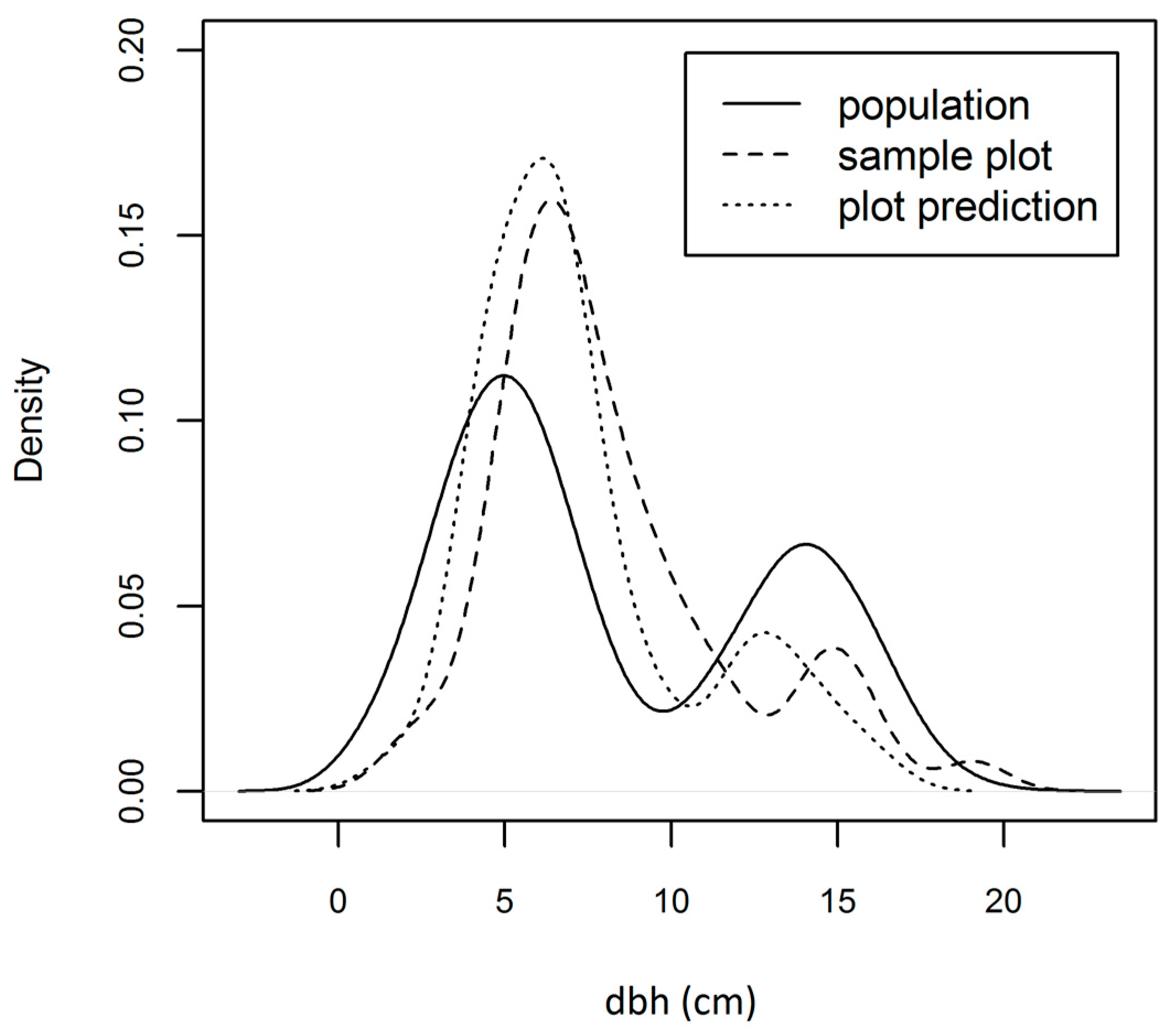
Figure 3). Our quantitative examination of the properties of H relative to prediction properties used simulated dbhs. Our simulated population is a mixture distribution composed of two normal distributions (the solid line in
Figure 4). For our examination, we took 100 clustered sample plots of 50 trees from the simulated population, and compared these with “predictions” for the samples. In
Figure 4 we can see all three cases: (1) the underlying population, (2) the distribution observed on a plot, and (3) the prediction for the plot. For the purposes of demonstration, predictions were obtained by taking the original sample data and introducing Gaussian noise with parameters (
). In our simulations, we look at various dbh bin widths and four types of errors in our predictions, where the four types of prediction errors are represented as four separate lines and labeled with the parameters of their error distributions. Larger values of index H suggest better prediction performance, where H is bounded by one on its upper end. A value less than zero indicates that the mean by bins (as obtained from all sample plots) is a better predictor of the sample distribution than the prediction strategy under examination.