Variation of Drying Strains between Tangential and Radial Directions in Asian White Birch
Abstract
:1. Introduction
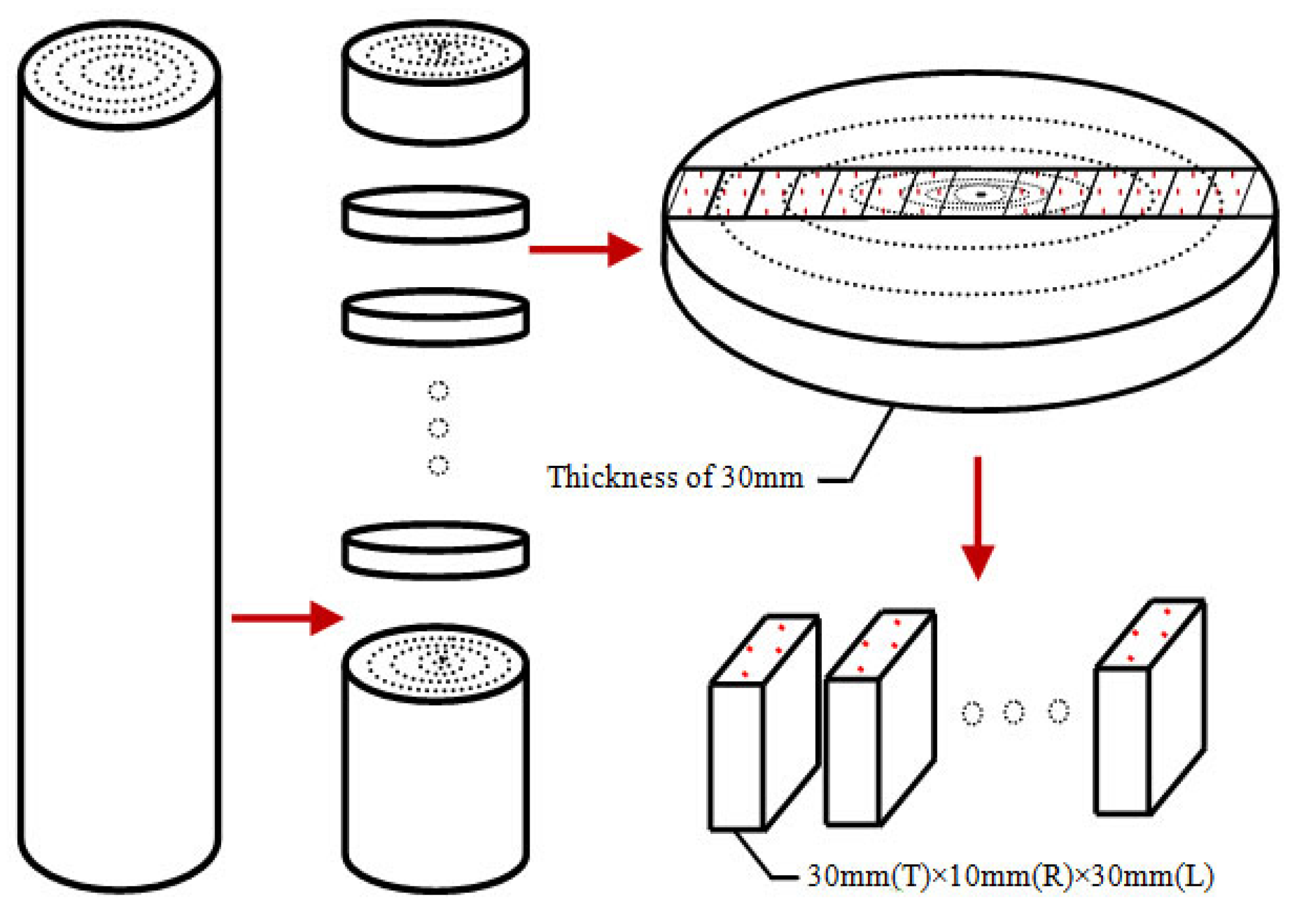
2. Materials and Methods
3. Results and Discussion
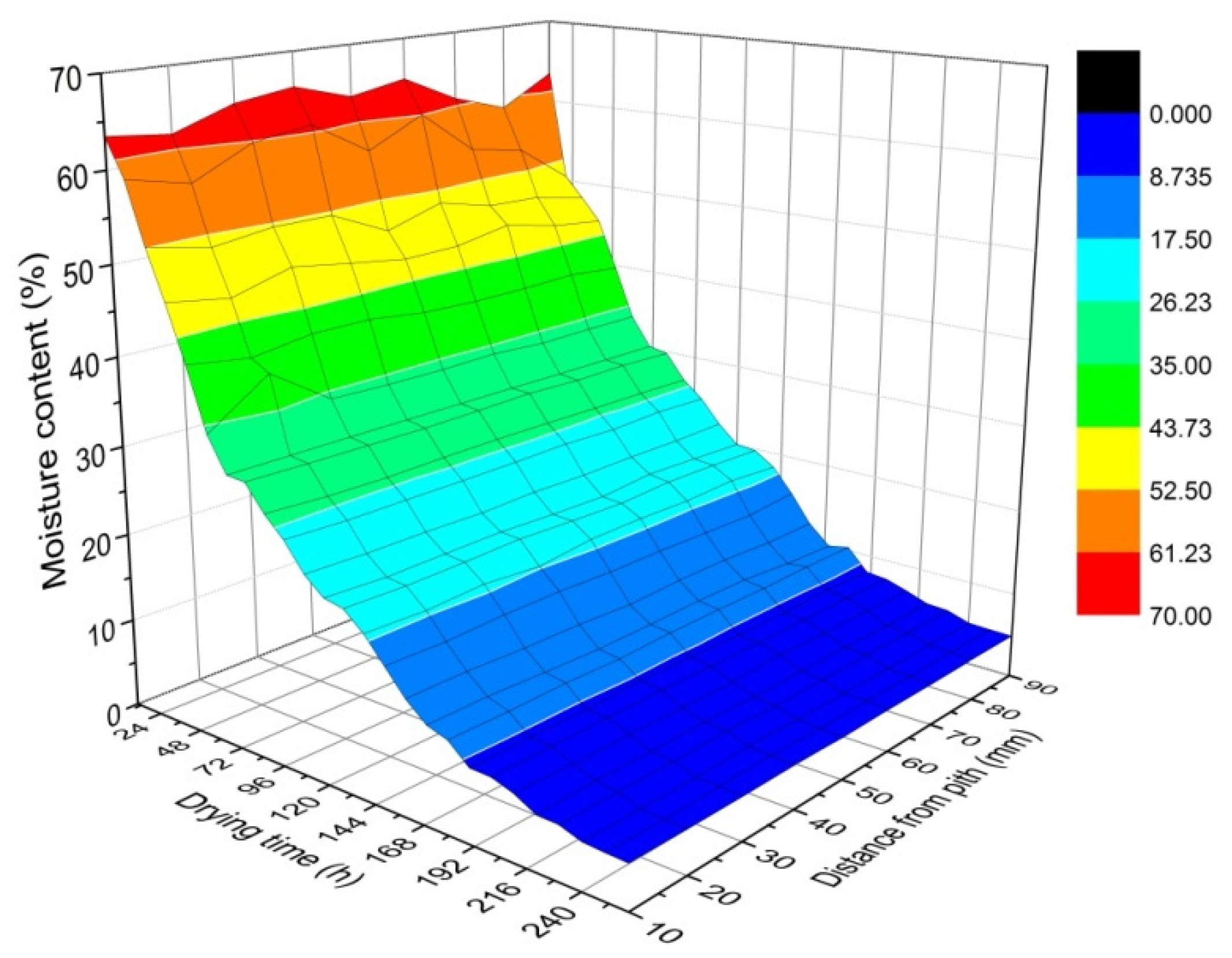
3.1. Moisture Content History
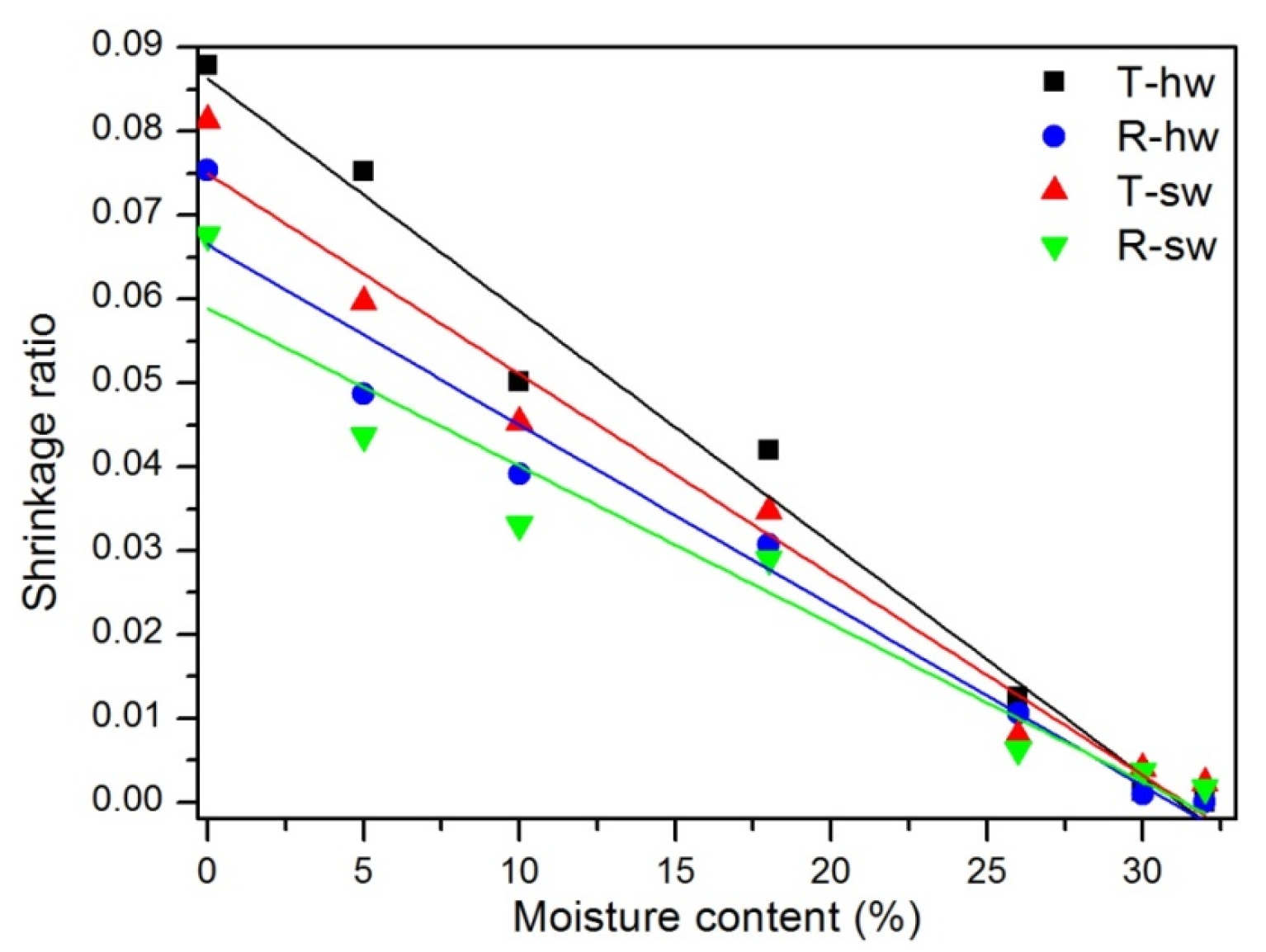
3.2. Difference of Shrinkage Ratios between the Tangential and Radial Directions
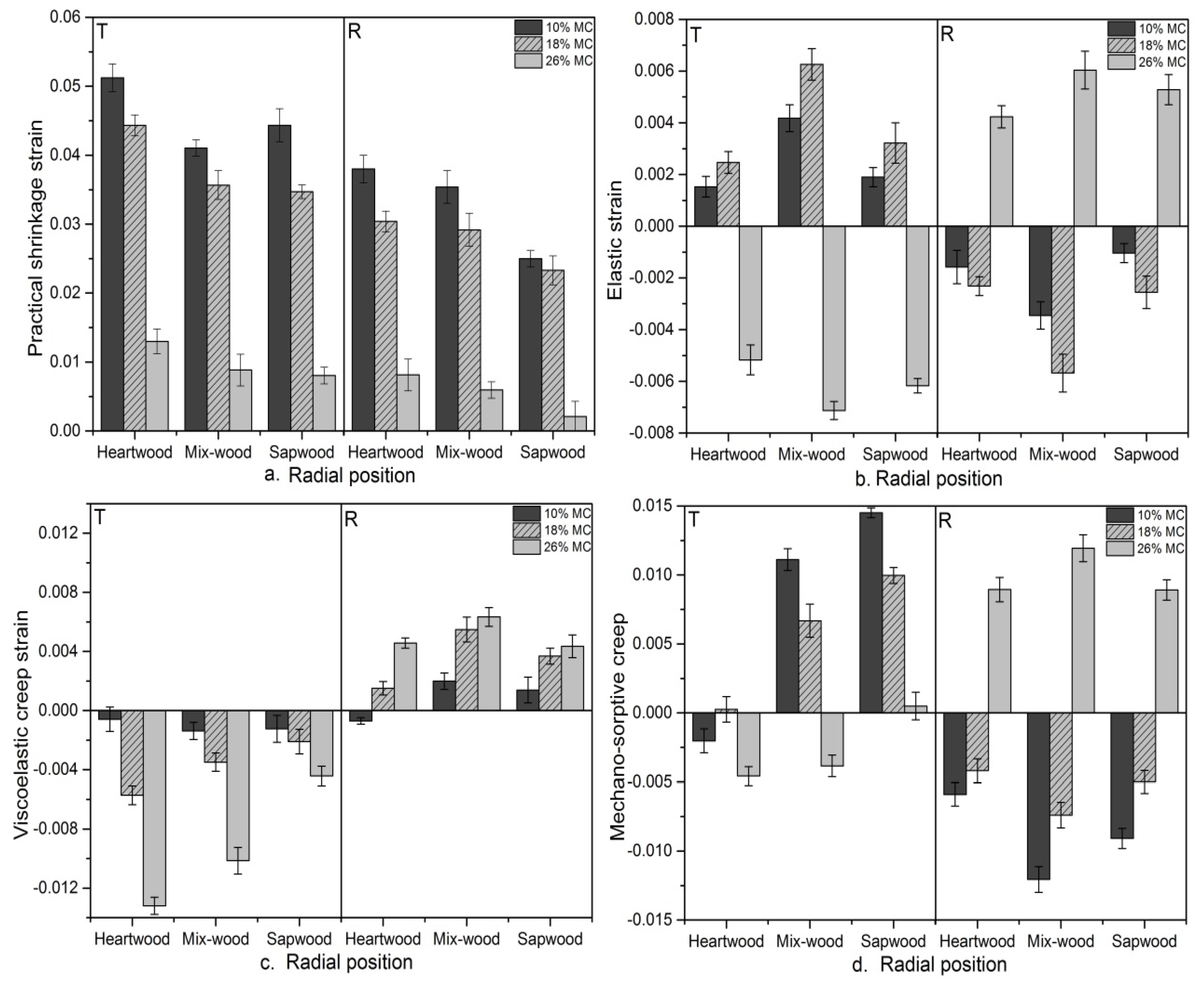
3.3. Variations of Drying Strains between the Tangential and Radial Directions
3.3.1. Practical Shrinkage Strain
3.3.2. Elastic Strain
3.3.3. Viscoelastic Creep Strain
3.3.4. Mechano-Sorptive (MS) Creep
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| MS | Mechano-sorptive |
| MC | Moisture content |
References
- Lee, N.H.; Hayashi, K. Effect of end-covering and low pressure steam explosion treatment on drying rate and checking during radio-frequency/vacuum drying of Japanese cedar log cross sections. For. Prod. J. 2000, 50, 73–78. [Google Scholar]
- Armstrong, L.D.; Kingston, R.S.T. Effect of moisture changes on creep in wood. Nature 1960, 185, 862–863. [Google Scholar] [CrossRef]
- Rice, R.W.; Youngs, R.L. The mechanism and development of creep during drying of red oak. Holz Roh Werkst. 1990, 48, 73–79. [Google Scholar] [CrossRef]
- Wu, Q.; Milota, M.R. Rheological behavior of Douglas-fir perpendicular to the grain at elevated temperatures. Wood Fiber Sci. 1995, 27, 285–295. [Google Scholar]
- Wu, Q.; Milota, M.R. Mechano-sorptive deformation of Douglas-fir specimens under tangential tensile stress during moisture adsorption. Wood Fiber Sci. 1996, 28, 128–132. [Google Scholar]
- Takahashi, C.; Ishimaru, Y.; Iida, I.; Furuta, Y. The creep of wood destabilized by change in moisture content. Part I: The creep behaviors of wood during and immediately after drying. Holzforschung 2004, 58, 261–267. [Google Scholar] [CrossRef]
- Perré, P.; Passard, J. A physical and mechanical model able to predict the stress field in wood over a wide range of drying conditions. Dry. Technol. 2004, 22, 27–44. [Google Scholar] [CrossRef]
- Lazarescu, C.; Avramidis, S. Drying related strain development in restrained wood. Dry. Technol. 2008, 26, 544–551. [Google Scholar] [CrossRef]
- Peng, M.K.; Chui, Y.H.; Ho, Y.C.; Wang, W.C.; Zhou, Y.T. Investigation of shrinkage in softwood using digital image correlation method. Appl. Mech. Mater. 2011, 83, 157–161. [Google Scholar] [CrossRef]
- Peng, M.K.; Ho, Y.C.; Wang, W.C.; Chui, Y.H.; Gong, M. Measurement of wood shrinkage in jack pine using three dimensional digital image correlation (DIC). Holzforschung 2012, 66, 639–643. [Google Scholar] [CrossRef]
- Zhan, J.F.; Avramidis, S. Mechanosorptive creep of hemlock under conventional drying: I. The determination of free shrinkage strain. Dry. Technol. 2011, 29, 789–796. [Google Scholar] [CrossRef]
- Zhan, J.F.; Avramidis, S. Mechanosorptive creep of hemlock under conventional drying: II. Description of actual creep behavior in drying lumber. Dry. Technol. 2011, 29, 1140–1149. [Google Scholar] [CrossRef]
- Larsen, F.; Ormarsson, S. Numerical and experimental study of moisture-induced stress and strain field developments in timber logs. Wood Sci. Technol. 2013, 47, 837–852. [Google Scholar] [CrossRef]
- Larsen, F.; Ormarsson, S. Experimental and finite element study of the effect of temperature and moisture on the tangential tensile strength and fracture behavior in timber logs. Holzforschung 2014, 68, 133–140. [Google Scholar] [CrossRef]
- Fu, Z.Y.; Cai, Y.C.; Zhao, J.Y.; Huan, S.Q. The effect of shrinkage anisotropy on tangential rheological properties of Asian white birch disks. BioResources 2013, 8, 5235–5243. [Google Scholar] [CrossRef]
- Fu, Z.Y.; Zhao, J.Y.; Cai, Y.C. Investigation of tangential strain caused by shrinkage anisotropy using image analytical method. Eng. Sci. 2014, 12, 25–29. [Google Scholar]
- Dahlblom, O.; Petersson, H.; Ormarsson, S. Characterization of Shrinkage. European Project FAIR CT 96–1915, Improved Spruce Timber Utilization; Final Rep. Sub-Task AB1.5; Division of Structural Mechanics, Lund Institute of Technology, Lund University: Scania, Sweden, 1999. [Google Scholar]
- Samuel, V.G.; Samuel, L.Z. Moisture Relations and Physical Properties of Wood; Wood Handbook; U.S. Deptartment of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010; Chapter 4; pp. 4–6.
- Booker, R.E.; Evans, J.M. The effect of drying schedule on the radial permeability of pinus radiae. Holz Roh Werkst. 1994, 52, 26–39. [Google Scholar] [CrossRef]
- Lazarescu, C.; Avramidis, S.; Oliveira, L. Modeling shrinkage response to tensile stresses in wood drying: I. Shrinkage-moisture interaction in stress-free specimens. Dry. Technol. 2009, 27, 1183–1191. [Google Scholar] [CrossRef]
- Pang, S.S.; Herritsch, A. Physical properties of earlywood and latewood of Pinus radiate D. Don: Anisotropic shrinkage, equilibrium moisture content and fibre saturation point. Holzforschung 2005, 59, 654–661. [Google Scholar] [CrossRef]
| Moisture Content (%) | Dry Bulb Temperature (°C) | Wet Bulb Temperature (°C) | Relative Humidity (%) | Equilibrium Moisturecontent (%) |
|---|---|---|---|---|
| MC > 50 | 40 | 38 | 88 | 18.3 |
| 40 | 40 | 37 | 82 | 16 |
| 35 | 40 | 36 | 76 | 14.1 |
| 30 | 40 | 35 | 71 | 12.7 |
| 25 | 40 | 34 | 66 | 11.5 |
| 20 | 40 | 32 | 57 | 9.6 |
| 15 | 40 | 30 | 48 | 8.2 |
| 10 | 40 | 29 | 44 | 7.6 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Zhao, J.; Yang, Y.; Cai, Y. Variation of Drying Strains between Tangential and Radial Directions in Asian White Birch. Forests 2016, 7, 59. https://doi.org/10.3390/f7030059
Fu Z, Zhao J, Yang Y, Cai Y. Variation of Drying Strains between Tangential and Radial Directions in Asian White Birch. Forests. 2016; 7(3):59. https://doi.org/10.3390/f7030059
Chicago/Turabian StyleFu, Zongying, Jingyao Zhao, Yeli Yang, and Yingchun Cai. 2016. "Variation of Drying Strains between Tangential and Radial Directions in Asian White Birch" Forests 7, no. 3: 59. https://doi.org/10.3390/f7030059
APA StyleFu, Z., Zhao, J., Yang, Y., & Cai, Y. (2016). Variation of Drying Strains between Tangential and Radial Directions in Asian White Birch. Forests, 7(3), 59. https://doi.org/10.3390/f7030059





