Genetic Improvement of Wood Properties in Pinus kesiya Royle ex Gordon for Sawn Timber Production in Malawi
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Genetic Materials
2.2. Growth Data
2.3. Wood Sample Processing and Measurement
2.4. Statistical Analysis
3. Results and Discussion
3.1. Heritability and Genetic Gains
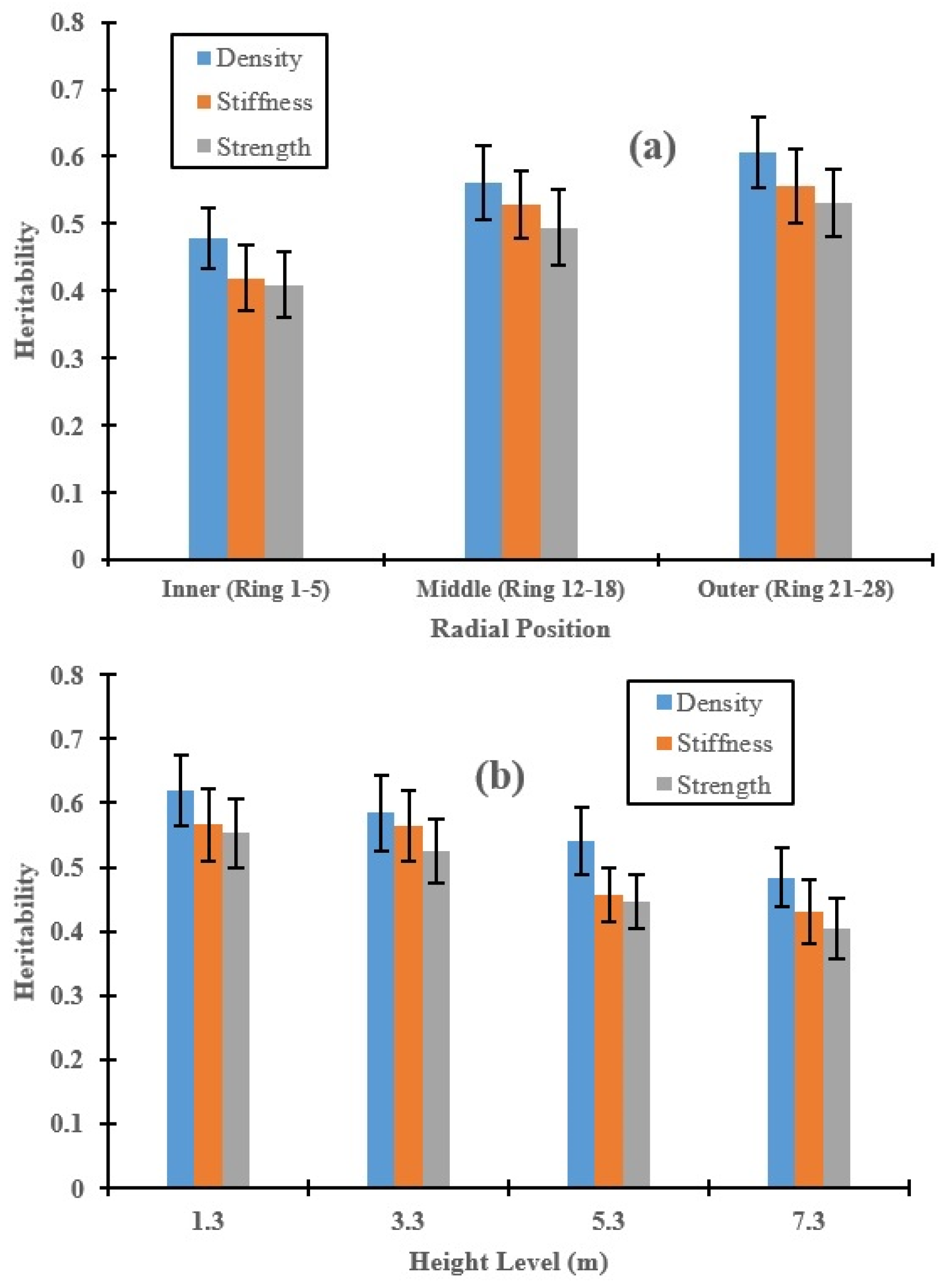
3.2. Genetic Control of Wood Properties along the Radial Direction and Stem Height
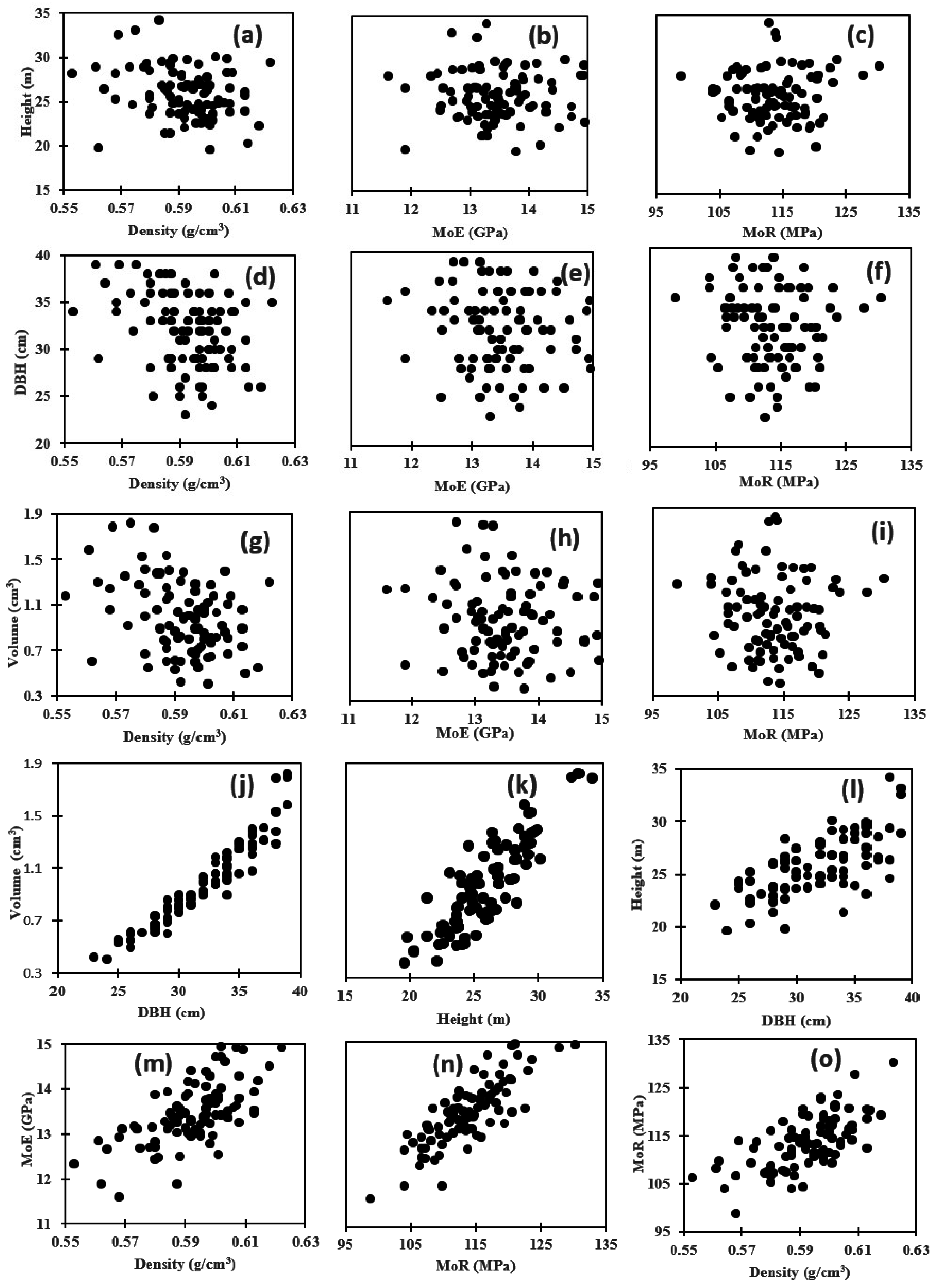
3.3. Genetic Correlation among Wood Properties
3.4. Genetic Correlation between Wood Properties and Growth Traits
3.5. Correlated Response
3.6. Implication of Tree Improvement of Pinus kesiya in Malawi
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DBH | Diameter at breast height |
| HGT | Total tree height |
| MFA | Microfibril angle |
| MoE | Modulus of Elasticity |
| MoR | Modulus of Rupture |
| PROC | Procedure |
| SAS | Statistical Analysis System |
References
- Gogoi, B.R.; Sharma, M.; Sharma, C.L. Ring width variations of Khasi pine (Pinus kesiya Royle ex Gordon) at breast height. J. Indian Acad. Wood Sci. 2014, 11, 87–92. [Google Scholar] [CrossRef]
- Missio, R.F.; Silva, A.M.; Dias, L.A.S.; Moraes, M.L.T.; Resende, M.D.V. Estimates of genetic parameters and prediction of additive genetic values in Pinus kesiya progenies. Crop. Breed. Appl. Biotechnol. 2005, 5, 394–401. [Google Scholar] [CrossRef]
- Missanjo, E.; Kamanga-Thole, G. Impact of site disturbances from harvesting and logging on soil physical properties and Pinus kesiya tree growth. Int. Sch. Res. Not. 2014, 2014, 323626. [Google Scholar]
- Missanjo, E.; Mwale, G. A mixed effect height-diameter model for Pinus kesiya in Malawi. J. Biodivers. Manag. For. 2014, 3. [Google Scholar] [CrossRef]
- Johnson, G.R.; Gartner, B.L. Genetic variation in basic density and modulus of elasticity of coastal Douglas-fir. Tree Genet. Genomes 2006, 3, 25–33. [Google Scholar] [CrossRef]
- Steffenrema, A.; Saranpää, P.; Lundqvistc, S.; Skrøppa, T. Variation in wood properties among five full-sib families of Norway spruce (Picea abies). Ann. For. Sci. 2007, 64, 799–806. [Google Scholar] [CrossRef]
- Zobel, B.J.; van Buijtenen, J.P. Wood Variation: Its Causes and Control; Springer: Berlin, Germany, 1989. [Google Scholar]
- Kollmann, F.F.P.; Côté, W.A., Jr. Principles of Wood Science and Technology I Solid Wood; Springer: Berlin, Germany, 1968. [Google Scholar]
- Guller, B.; Isik, K.; Centinay, S. Genetic variation in Pinus brutia Ten.: Wood density traits. BioResources 2011, 6, 4012–4027. [Google Scholar]
- Hannrup, B.; Ekberg, I.; Persson, A. Genetic correlation among wood, growth capacity and stem traits in Pinus sylvestris. Scand. J. For. Res. 2000, 15, 161–170. [Google Scholar] [CrossRef]
- Ivkovich, M.; Namkoong, G.; Koshy, M. Genetic variation in wood properties of interior spruce I growth, latewood percentage and wood density. Can. J. For. Res. 2002, 32, 2116–2127. [Google Scholar] [CrossRef]
- Apiolaza, L.A. Very early selection for wood quality: Screening for early winners. Ann. For. Sci. 2009, 66, 601–610. [Google Scholar] [CrossRef]
- Apiolaza, L.A.; Shakti, S.C.; Walker, J.C.F. Genetic control of very early compression and opposite wood in Pinus radiata and its implications for selection. Tree Genet. Genomes 2011, 7, 563–571. [Google Scholar] [CrossRef]
- Zobel, B.J.; Jett, J.B. Genetics of Wood Formation; Springer: Berlin, Germany, 1995. [Google Scholar]
- Lenz, P.; Cloutier, A.; Mackay, J.; Beaulieu, J. Genetic control of wood properties in Picea glauca—An analysis of trends with cambial age. Can. J. For. Res. 2010, 40, 703–715. [Google Scholar] [CrossRef]
- Lenz, P.; Auty, D.; Achim, A.; Beaulieu, J.; Mackay, J. Genetic Improvement of White Spruce Mechanical Wood Traits—Early Screening by means of Acoustic Velocity. Forests 2013, 4, 575–594. [Google Scholar] [CrossRef]
- Ingram, C.L.; Chipompha, N.W.S. The Silvicultural Guide Book of Malawi, 2nd ed.; FRIM: Zomba, Malawi, 1987. [Google Scholar]
- Missanjo, E.; Matsumura, J. Wood density and mechanical properties of Pinus kesiya Royle ex Gordon in Malawi. Forests 2016, 7, 135. [Google Scholar] [CrossRef]
- SAS Institute Inc. Qualification Tools User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2004. [Google Scholar]
- Falconer, D.S.; Mackay, T.F.C. Introduction to Quantitative Genetics, 4th ed.; Longman Group Ltd.: Essex, UK, 1996. [Google Scholar]
- Hong, Z.; Fries, A.; Wu, H.X. High negative genetic correlations between growth traits and wood properties suggest incorporating multiple traits selection including economic weights for the future Scots pine breeding programs. Ann. For. Sci. 2014, 71, 463–472. [Google Scholar] [CrossRef]
- Cornelius, J. Heritabilities and additive genetic coefficients of variations in forest trees. Can. J. For. Res. 1994, 24, 372–379. [Google Scholar] [CrossRef]
- Yildirim, K.; Ozturk, H.; Siklar, S.; Kaya, Z. Inheritance of wood specific gravity and its genetic correlation and its growth traits in young Pinus brutia progenies. In Proceedings of the IUFRO-Division 2 Joint Conference: Low Input Breeding and Genetic Conservation of Forest Tee species, Antalya, Turkey, 9–13 October 2006.
- Vargas-Hernandez, J.; Adams, W.T. Age-Age correlation and early selection for wood density in young coastal Douglas-fir. For. Sci. 1992, 38, 467–478. [Google Scholar]
- Hylen, G. Age trends in genetic parameters of wood density in young Norway spruce. Can. J. For. Res. 1999, 29, 135–143. [Google Scholar] [CrossRef]
- Li, L.; Wu, H.X. Efficiency of early selection for rotation-aged growth and wood density traits in Pinus radiata. Can. J. For. Res. 2005, 35, 2019–2029. [Google Scholar]
- Gaspar, M.J.; Louzada, J.L.; Silva, M.E.; Aguiar, A.; Almeida, M.H. Age trends in genetic parameters of wood density components in 46 half-sibling families of Pinus pinaster. Can. J. For. Res. 2008, 38, 1470–1477. [Google Scholar] [CrossRef]
- Moura, V.P.G.; Dvorak, W.S. Provenance and family variation of Pinus caribaea var. hondurensis from Guatemala and Honduras grown in Brazil, Columbia and Venezuela. Pesqui. Agropecu. Bras. 2001, 36, 225–234. [Google Scholar]
- Hodge, G.R.; Purnell, R.C. Genetic parameter estimates for wood density, transition age, and radial growth in splash pine. Can. J. For. Res. 1993, 23, 1881–1891. [Google Scholar] [CrossRef]
- Nicholls, J.W.; Morris, J.D.; Pederick, L.A. Heritability estimates of density characteristics in juvenile Pinus radiata wood. Silv. Genet. 1980, 29, 54–61. [Google Scholar]
- Louzada, J.L.P.C.; Fonseca, F.M.A. The heritability of wood density components in Pinus pinaster Ait. and implications for tree breeding. Ann. For. Sci. 2002, 59, 867–873. [Google Scholar] [CrossRef]
- Kumar, S.; Dungey, H.S.; Matheson, A.C. Genetic parameters and strategies for genetic improvement of stiffness in Radiata pine. Silv. Genet. 2006, 55, 77–84. [Google Scholar]
- Wright, J.W. Introduction to Forest Genetics; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Zobel, B.J.; Sprague, J.R. Juvenile Wood in Forest Trees; Springer: Berlin, Germany, 1998. [Google Scholar]
- Fukatsu, E.; Hiraoka, Y.; Matsunaga, K.; Tsubomura, M.; Nakada, R. Genetic relationship between wood properties and growth traits in Larix kaempferi obtained from a diallel mating test. J. Wood Sci. 2015, 61, 10–18. [Google Scholar] [CrossRef]
- Hung, T.D.; Brawner, J.T.; Meder, R.; Lee, D.J.; Southerton, S.; Thinh, H.H.; Dieters, M.J. Estimates of genetic parameters for growth and wood properties un Eucalyptus pellita F. Muell. to support tree breeding in Vietnam. Ann. For. Sci. 2015, 72, 205–217. [Google Scholar] [CrossRef]
- Hai, P.H. Genetic Improvement of Plantation-Grown Acacia auriculiformis for Sawn Timber Production. Ph.D. Thesis, Swedish University of Agricultural Sciences, Uppsala, Sweden, September 2009. [Google Scholar]
- Kumar, S.; Jayawickrama, K.J.S.; Lee, J.; Lausberg, M. Direct and indirect measures of stiffness and strength show high heritability in a wind-pollinated radiata pine progeny test in New Zealand. Silv. Genet. 2002, 51, 256–261. [Google Scholar]
- Wu, H.X.; Ivković, M.; Gapare, W.J.; Matheson, A.C.; Baltunis, B.S.; Powell, M.B.; McRae, T.A. Breeding for wood quality and profit in Pinus radiata: A review of genetic parameter estimates and implications for breeding and deployment. N. Z. J. For. Sci. 2008, 38, 56–87. [Google Scholar]
- Ivković, M.; Wu, H.X.; McRae, T.A.; Powell, M.B. Developing breeding objectives for radiata pine structural wood production I. Bioeconomic model and economic weights. Can. J. For. Res. 2006, 36, 2920–2931. [Google Scholar] [CrossRef]
- Gapare, W.J.; Baltunis, B.S.; Ivković, M.; Wu, H.X. Genetic correlations among juvenile wood quality and growth traits and implication for selection strategy in Pinus radiata D. Don. Ann. For. Sci. 2009, 66, 606. [Google Scholar] [CrossRef]
| Traits | Among Families | Within Families | ||
|---|---|---|---|---|
| h2 (s.e.) | Gs (%) | h2 (s.e.) | Gs (%) | |
| Wood Properties | ||||
| Density (g/cm3) | 0.595 (0.055) | 22.6 | 0.367 (0.100) | 13.2 |
| MoE (GPa) | 0.559 (0.038) | 16.7 | 0.317 (0.095) | 9.01 |
| MoR (MPa) | 0.542 (0.091) | 15.8 | 0.295 (0.092) | 8.20 |
| Growth Traits | ||||
| Total height (m) | 0.469 (0.048) | 7.11 | 0.177 (0.078) | 2.42 |
| DBH (cm) | 0.400 (0.042) | 6.05 | 0.133 (0.073) | 1.63 |
| Volume (cm3) | 0.483 (0.053) | 19.4 | 0.187 (0.079) | 7.55 |
| Traits | Correlation (Standard Error) | ||
|---|---|---|---|
| Phenotypic | Genetic | Residual | |
| Between Growth Traits and Wood Properties | |||
| Height vs. Density | −0.248 (0.010) * | −0.386 (0.057) | −0.052 (0.006) |
| Height vs. MoE | −0.013 (0.001 ) ns | −0.309 (0.056) | −0.036 (0.002) |
| Height vs. MoR | 0.041 (0.003) ns | −0.366 (0.082) | −0.019 (0.009) |
| DBH vs. Density | −0.338 (0.011) * | −0.496 (0.049) | −0.097 (0.004) |
| DBH vs. MoE | −0.112 (0.006) ns | −0.473 (0.046) | −0.298 (0.083) |
| DBH vs. MoR | −0.093 (0.004) ns | −0.468 (0.071) | −0.149 (0.089) |
| Volume vs. Density | −0.358 (0.010) * | −0.458 (0.052) | −0.290 (0.061) |
| Volume vs. MoE | 0.099 (0.002) ns | −0.399 (0.051) | −0.224 (0.058) |
| Volume vs. MoR | −0.056 (0.005) ns | −0.488 (0.071) | −0.272 (0.086) |
| Among Growth Traits | |||
| Height vs. DBH | 0.688 (0.077) ** | 0.935 (0.009) | 0.545 (0.052) |
| Height vs. Volume | 0.850 (0.056) ** | 0.684 (0.040) | 0.550 (0.052) |
| DBH vs. Volume | 0.955 (0.031) ** | 0.987 (0.002) | 0.921 (0.011) |
| Among Wood Properties | |||
| Density vs. MoE | 0.790 (0.019) ** | 0.735 (0.025) | 0.213 (0.053) |
| Density vs. MoR | 0.793 (0.019) ** | 0.539 (0.060) | 0.521 (0.061) |
| MoE vs. MoR | 0.818 (0.018) ** | 0.464 (0.061) | 0.475 (0.060) |
| Selection Traits | Correlated Response (%) for Target Traits | ||
|---|---|---|---|
| MoE | MoR | Volume | |
| Wood properties | |||
| Density | 12.6 | 8.85 | −9.78 |
| MoE | 16.7 * | 7.43 | −8.30 |
| MoR | 7.62 | 15.8 * | −9.96 |
| Growth traits | |||
| DBH | −6.68 | −6.32 | 17.3 |
| Height | −4.74 | −5.37 | 13.0 |
| Volume | −6.18 | −7.23 | 19.4 * |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Missanjo, E.; Matsumura, J. Genetic Improvement of Wood Properties in Pinus kesiya Royle ex Gordon for Sawn Timber Production in Malawi. Forests 2016, 7, 253. https://doi.org/10.3390/f7110253
Missanjo E, Matsumura J. Genetic Improvement of Wood Properties in Pinus kesiya Royle ex Gordon for Sawn Timber Production in Malawi. Forests. 2016; 7(11):253. https://doi.org/10.3390/f7110253
Chicago/Turabian StyleMissanjo, Edward, and Junji Matsumura. 2016. "Genetic Improvement of Wood Properties in Pinus kesiya Royle ex Gordon for Sawn Timber Production in Malawi" Forests 7, no. 11: 253. https://doi.org/10.3390/f7110253
APA StyleMissanjo, E., & Matsumura, J. (2016). Genetic Improvement of Wood Properties in Pinus kesiya Royle ex Gordon for Sawn Timber Production in Malawi. Forests, 7(11), 253. https://doi.org/10.3390/f7110253






