Automating Plot-Level Stem Analysis from Terrestrial Laser Scanning
Abstract
:1. Introduction
2. Materials Preparation
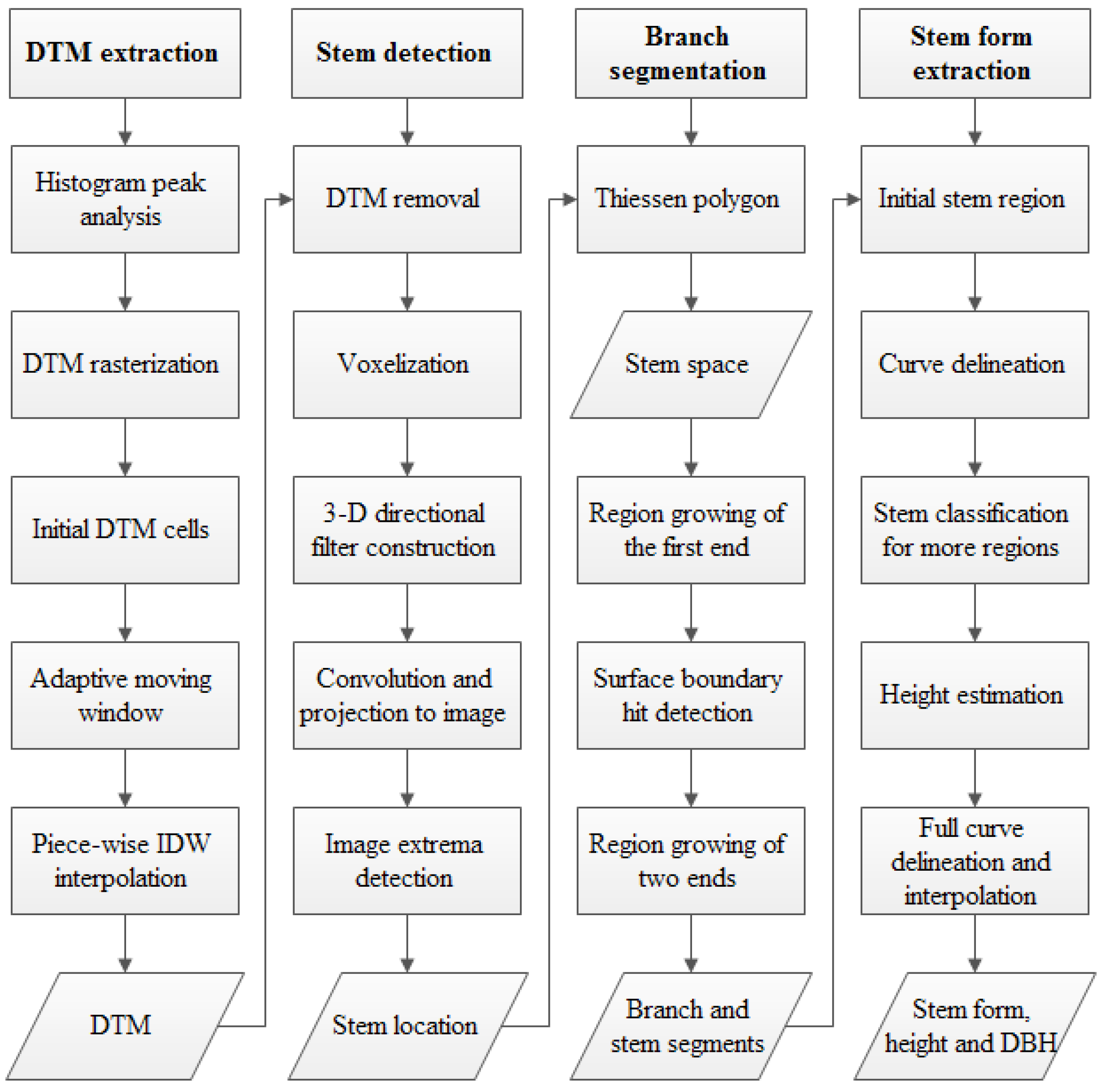
3. Methodology
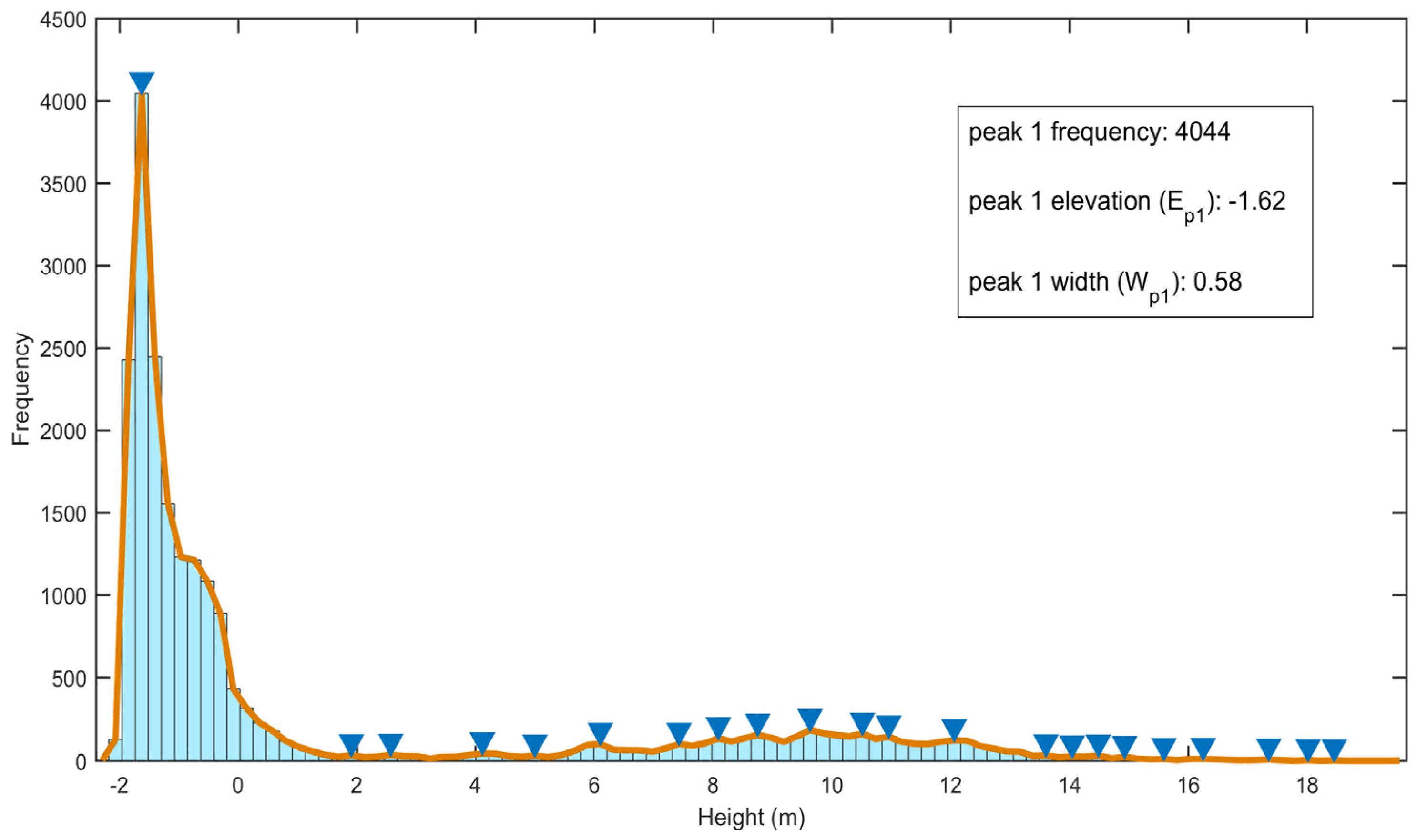
3.1. DTM Extraction
3.2. Stem Location Extraction and Isolation
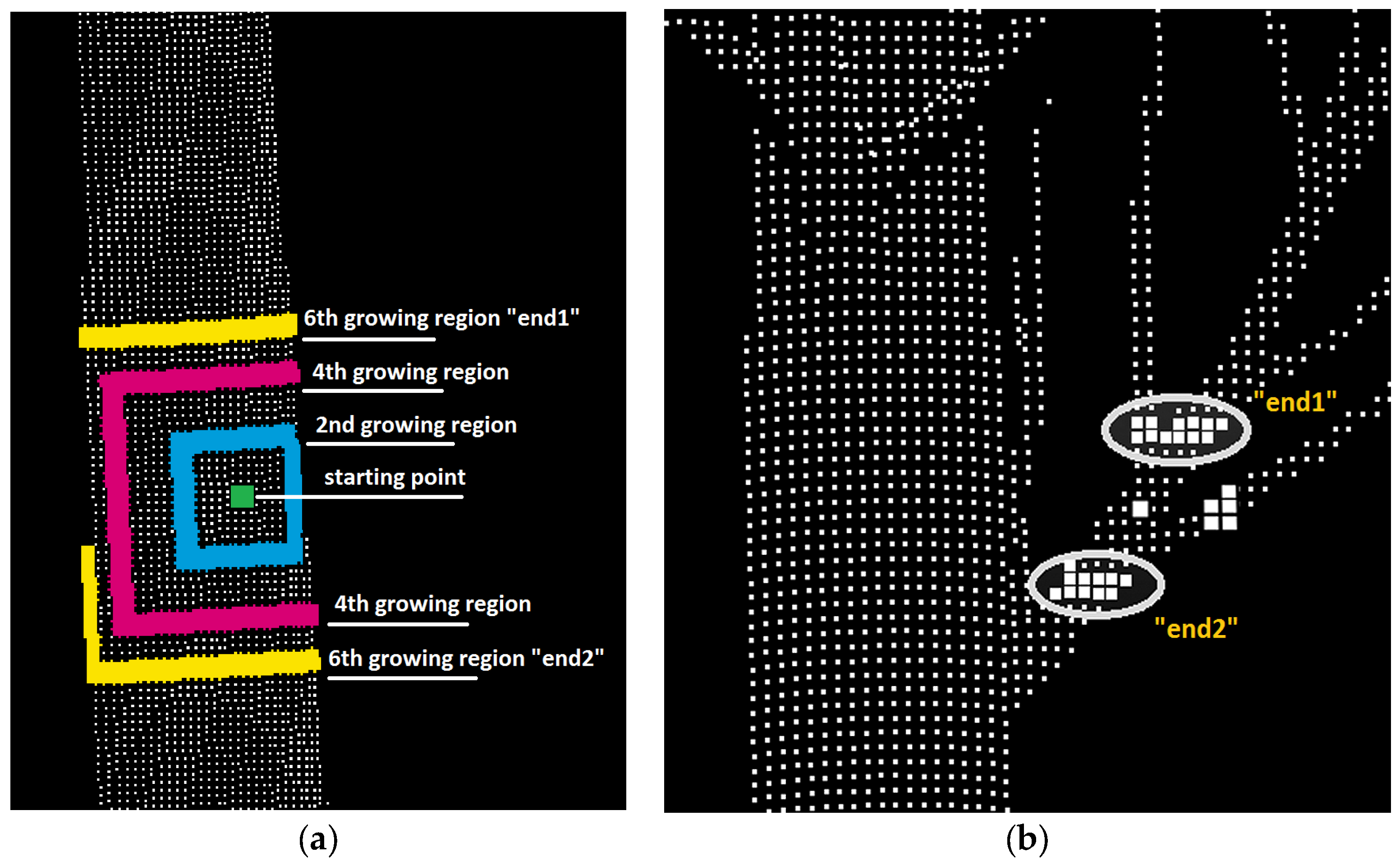
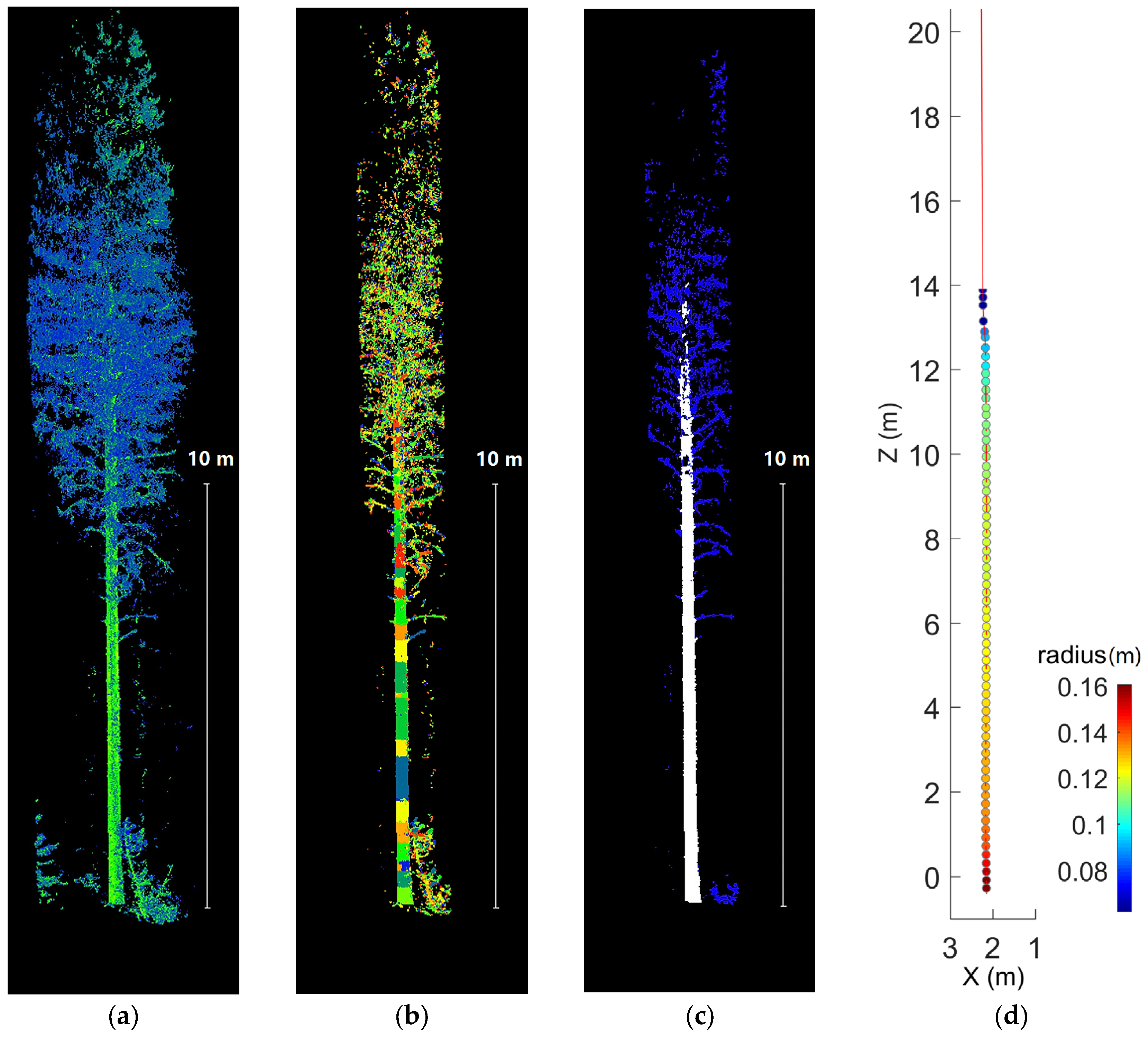
3.3. Stem Form Extraction: Segmentation
| Algorithm 1. Description of point cloud segmentation using region growing method. | ||
| Input: | ||
| Output: | ||
| Parameters: | , ,, | |
| 1 | ; | |
| 2 | ||
| 3 | ||
| 4 | ; ; ; | |
| 5 | ||
| 6 | ; ; | |
| 7 | ; | |
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 | | |
| 21 | ||
| 22 | | |
| 23 | ||
| 24 | ||
| 25 | ||
| 26 | | |
| 27 | ||
| 28 | ||
3.4. Stem Form Extraction: Classification
3.5. Validation
4. Results and Discussion
4.1. DTM Extraction
4.2. Stem Location Extraction and Isolation
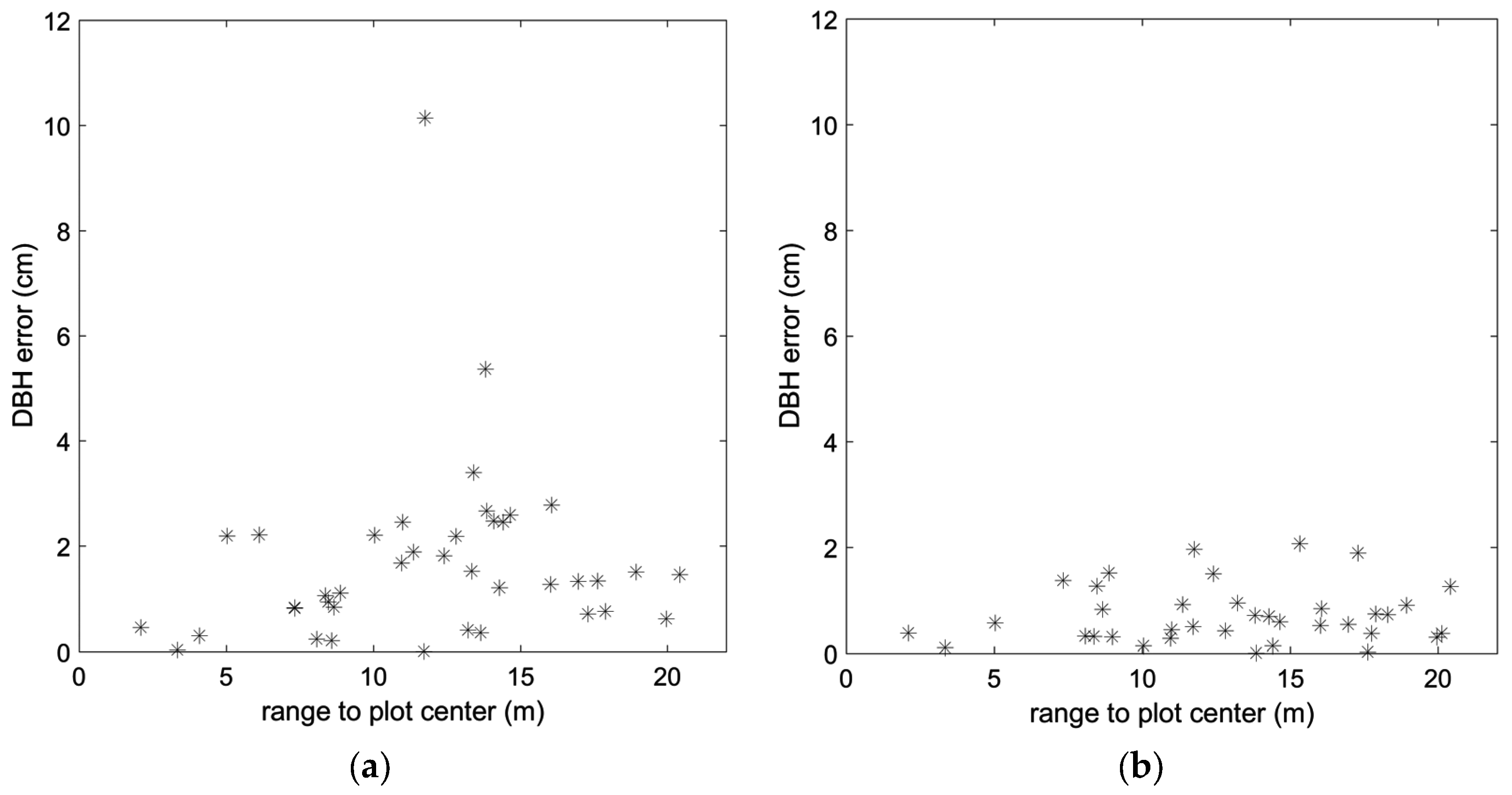
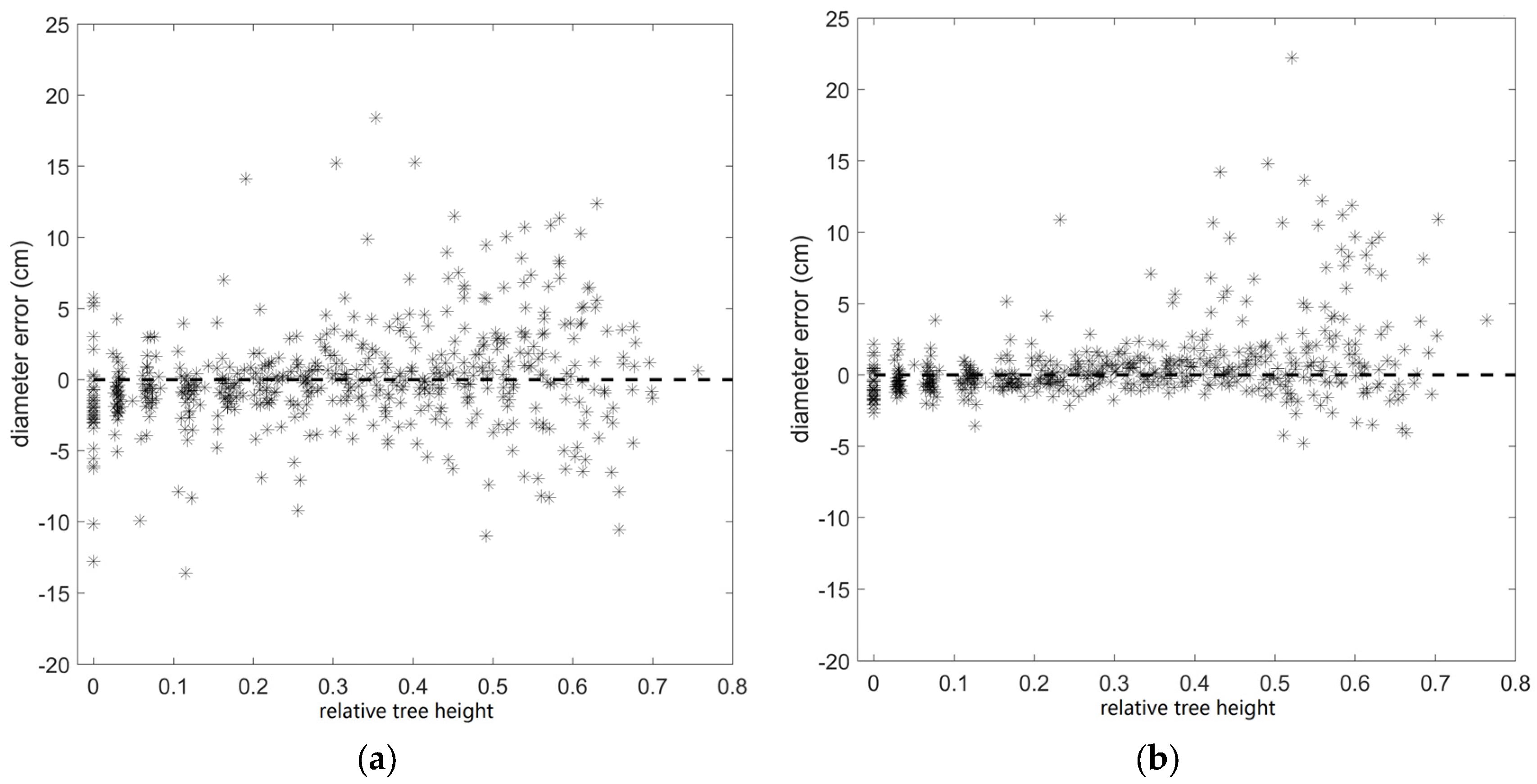
4.3. Stem Form Extraction
4.4. Time Efficiency
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Penman, J.; Gytarsky, M.; Hiraishi, T.; Krug, T.; Kruger, D.; Pipatti, R.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. Good Practice Guidance for Land Use, Land-Use Change and Forestry; Institute for Global Environmental Strategies IGES: Kanagawa, Japan, 2003; Available online: http://hdl.handle.net/123456789/6871 (Accessed on 07 July 2016).
- Kangas, A.; Maltamo, M. Forest Inventory: Methodology and Applications; Springer Science & Business Media: Berlin, Germany, 2006; Volume 10. [Google Scholar]
- Luther, J.E.; Skinner, R.; Fournier, R.A.; Van Lier, O.R.; Bowers, W.W.; Coté, J.-F.; Hopkinson, C.; Moulton, T. Predicting wood quantity and quality attributes of balsam fir and black spruce using airborne laser scanner data. Forestry 2013. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompaski, P.; Nijland, W.; Rickbeil, G.J.M.; Nielsen, S.E.; Bater, C.W.; Stadt, J.J. A forest structure habitat index based on airborne laser scanning data. Ecol. Indic. 2016, 67, 346–357. [Google Scholar] [CrossRef]
- Chen, J.M.; Ju, W.; Cihlar, J.; Price, D.; Liu, J.; Chen, W.; Pan, J.; Black, A.; Barr, A. Spatial distribution of carbon sources and sinks in Canada’s forests. Tellus B 2003, 55, 622–641. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J.; Pitkänen, J.; Packalén, P. Preharvest measurement of marked stands using airborne laser scanning. For. Sci. 2007, 53, 653–661. [Google Scholar]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Blanchette, D.; Fournier, R.A.; Luther, J.E.; Cote, J.-F. Predicting wood fiber attributes using local-scale metrics from terrestrial lidar data: A case study of Newfoundland conifer species. For. Ecol. Manag. 2015, 347, 116–129. [Google Scholar] [CrossRef]
- Jennings, S.; Brown, N.; Sheil, D. Assessing forest canopies and understorey illumination: Canopy closure, canopy cover and other measures. Forestry 1999, 72, 59–74. [Google Scholar] [CrossRef]
- Peterson, D.W.; Reich, P.B. Prescribed fire in oak savanna: Fire frequency effects on stand structure and dynamics. Ecol. Appl. 2001, 11, 914–927. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic principles of forest fuel reduction treatments. For. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Berger, A.; Gschwantner, T.; McRoberts, R.E.; Schadauer, K. Effects of measurement errors on individual tree stem volume estimates for the austrian national forest inventory. For. Sci. 2014, 60, 14–24. [Google Scholar] [CrossRef]
- Schreuder, H.T.; Wood, G.B.; Gregoire, T.G. Sampling Methods for Multiresource Forest Inventory; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Rice, B.; Weiskittel, A.R.; Wagner, R.G. Efficiency of alternative forest inventory methods in partially harvested stands. Eur. J. For. Res. 2014, 133, 261–272. [Google Scholar] [CrossRef]
- Wulder, M. Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters. Prog. Phys. Geogr. 1998, 22, 449–476. [Google Scholar] [CrossRef]
- Gillis, M.; Omule, A.; Brierley, T. Monitoring Canada’s forests: The national forest inventory. For. Chron. 2005, 81, 214–221. [Google Scholar] [CrossRef]
- Chasmer, L.; Hopkinson, C.; Treitz, P. Investigating laser pulse penetration through a conifer canopy by integrating airborne and terrestrial lidar. Can. J. Remote Sens. 2006, 32, 116–125. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Young-Pow, C.; Treitz, P. Assessing forest metrics with a ground-based scanning lidar. Can. J. For. Res. 2004, 34, 573–583. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.B.; Culvenor, D.S.; Coops, N.C. Using airborne and ground-based ranging lidar to measure canopy structure in australian forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Van Leeuwen, M.; Hilker, T.; Coops, N.C.; Frazer, G.; Wulder, M.A.; Newnham, G.J.; Culvenor, D.S. Assessment of standing wood and fiber quality using ground and airborne laser scanning: A review. For. Ecol. Manag. 2011, 261, 1467–1478. [Google Scholar] [CrossRef]
- Hilker, T.; Van Leeuwen, M.; Coops, N.C.; Wulder, M.A.; Newnham, G.J.; Jupp, D.L.; Culvenor, D.S. Comparing canopy metrics derived from terrestrial and airborne laser scanning in a douglas-fir dominated forest stand. Trees 2010, 24, 819–832. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial lidar technology in forest science: Application fields, benefits and challenges. Ann. For Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Henning, J.G.; Radtke, P.J. Detailed stem measurements of standing trees from ground-based scanning lidar. For. Sci. 2006, 52, 67–80. [Google Scholar]
- Liang, X.; Litkey, P.; Hyyppä, J.; Kaartinen, H.; Kukko, A.; Holopainen, M. Automatic plot-wise tree location mapping using single-scan terrestrial laser scanning. Photogramm. J. Finl. 2011, 22, 37–48. [Google Scholar]
- Rutzinger, M.; Pratihast, A.K.; Oude Elberink, S.J.; Vosselman, G. Tree modelling from mobile laser scanning data-sets. Photogramm. Rec. 2011, 26, 361–372. [Google Scholar] [CrossRef]
- Liang, X.; Kankare, V.; Yu, X.; Hyyppä, J.; Holopainen, M. Automated stem curve measurement using terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1739–1748. [Google Scholar] [CrossRef]
- Kankare, V.; Joensuu, M.; Vauhkonen, J.; Holopainen, M.; Tanhuanpää, T.; Vastaranta, M.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Rikala, J. Estimation of the timber quality of scots pine with terrestrial laser scanning. Forests 2014, 5, 1879–1895. [Google Scholar] [CrossRef]
- Kretschmer, U.; Kirchner, N.; Morhart, C.; Spiecker, H. A new approach to assessing tree stem quality characteristics using terrestrial laser scans. Silva Fenn. 2013, 47, 14. [Google Scholar] [CrossRef]
- Bienert, A.; Scheller, S.; Keane, E.; Mullooly, G.; Mohan, F. Application of terrestrial laser scanners for the determination of forest inventory parameters. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36(part 5). [Google Scholar]
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Aschoff, T.; Spiecker, H. Algorithms for the automatic detection of trees in laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Pueschel, P.; Newnham, G.; Rock, G.; Udelhoven, T.; Werner, W.; Hill, J. The influence of scan mode and circle fitting on tree stem detection, stem diameter and volume extraction from terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 77, 44–56. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Aschoff, T.; Thies, M.; Spiecker, H. Describing forest stands using terrestrial laser-scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 237–241. [Google Scholar]
- Pueschel, P. The influence of scanner parameters on the extraction of tree metrics from faro photon 120 terrestrial laser scans. ISPRS J. Photogramm. Remote Sens. 2013, 78, 58–68. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.-W. Terrestrial laser scanning as an effective tool to retrieve tree level height, crown width, and stem diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef]
- Pfeifer, N.; Winterhalder, D. Modelling of tree cross sections from terrestrial laser scanning data with free-form curves. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Liang, X.; Hyyppä, J. Automatic stem mapping by merging several terrestrial laser scans at the feature and decision levels. Sensors 2013, 13, 1614–1634. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Watt, P.; Donoghue, D. Measuring forest structure with terrestrial laser scanning. Int. J. Remote Sens. 2005, 26, 1437–1446. [Google Scholar] [CrossRef]
- Tansey, K.; Selmes, N.; Anstee, A.; Tate, N.; Denniss, A. Estimating tree and stand variables in a corsican pine woodland from terrestrial laser scanner data. Int. J. Remote Sens. 2009, 30, 5195–5209. [Google Scholar] [CrossRef]
- Dassot, M.; Colin, A.; Santenoise, P.; Fournier, M.; Constant, T. Terrestrial laser scanning for measuring the solid wood volume, including branches, of adult standing trees in the forest environment. Comput. Electron. Agric. 2012, 89, 86–93. [Google Scholar] [CrossRef]
- Huang, H.; Li, Z.; Gong, P.; Cheng, X.; Clinton, N.; Cao, C.; Ni, W.; Wang, L. Automated methods for measuring dbh and tree heights with a commercial scanning lidar. Photogramm. Eng. Remote Sens. 2011, 77, 219–227. [Google Scholar] [CrossRef]
- Brolly, G.B. Locating and Parameter Retrieval of Individual Trees from Terrestrial Laser Scanner Data. Ph.D. Thesis, University of West Hungary, Sopron, Hungary, 2013; p. 104. Available online: http://ilex.efe. hu/PhD/emk/brollygabor/disszertacio. pdf (accessed on 30 January 2016). [Google Scholar]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Strahler, A.H.; Jupp, D.L.B.; Woodcock, C.E.; Schaaf, C.B.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground-based lidar instrument (echidna®). Can. J. Remote Sens. 2008, 34, S426–S440. [Google Scholar] [CrossRef]
- Lovell, J.; Jupp, D.; Newnham, G.; Culvenor, D. Measuring tree stem diameters using intensity profiles from ground-based scanning lidar from a fixed viewpoint. ISPRS J. Photogramm. Remote Sens. 2011, 66, 46–55. [Google Scholar] [CrossRef]
- Schilling, A.; Schmidt, A.; Maas, H.-G. Automatic tree detection and diameter estimation in terrestrial laser scanner point clouds. In Proceedings of the 16th Computer Vision Winter Workshop, Mitterberg, Austria, 2–4 February 2011; pp. 75–83.
- Wezyk, P.; Koziol, K.; Glista, M.; Pierzchalski, M. Terrestrial laser scanning versus traditional forest inventory: First results from the polish forests. In Proceedings of the ISPRS Workshop ‘Laser Scanning 2007 and SilviLaser 2007’, Espoo, Finland, 12 September 2007–14 September 2007; pp. 12–14.
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface lidar remote sensing of basal area and biomass in deciduous forests of eastern maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Huang, H.; Gong, P.; Cheng, X.; Clinton, N.; Cao, C.; Ni, W.; Li, Z.; Wang, L. Forest structural parameter extraction using terrestrial LiDAR. In Proceedings of American Geophysical Union Fall Meeting, San Francisco, CA, USA, 15–19 September 2008.
- Thies, M.; Spiecker, H. Evaluation and future prospects of terrestrial laser scanning for standardized forest inventories. Forest 2004, 2, 1. [Google Scholar]
- Bienert, A.; Scheller, S.; Keane, E.; Mohan, F.; Nugent, C. Tree detection and diameter estimations by analysis of forest terrestrial laserscanner point clouds. In Proceedings of the ISPRS Workshop ‘Laser Scanning 2007 and SilviLaser 2007’, Espoo, Finland, 12–14 September 2007; pp. 50–55.
- Ducey, M.J.; Astrup, R. Adjusting for nondetection in forest inventories derived from terrestrial laser scanning. Can. J. Remote Sens. 2013, 39, 410–425. [Google Scholar]
- Litkey, P.; Puttonen, E.; Liang, X. Comparison of point cloud data reduction methods in single-scan TLS for finding tree stems in forest. In Proceedings of SilviLaser, Hobart, Australia, 16–19 October 2011.
- Yang, X.; Strahler, A.H.; Schaaf, C.B.; Jupp, D.L.B.; Yao, T.; Zhao, F.; Wang, Z.; Culvenor, D.S.; Newnham, G.J.; Lovell, J.L.; et al. Three-dimensional forest reconstruction and structural parameter retrievals using a terrestrial full-waveform lidar instrument (Echidna®). Remote Sens. Environ. 2013, 135, 36–51. [Google Scholar] [CrossRef]
- Hyyppa, J.; Liang, X. Project Benchmarking on Terrestrial Laser Scanning for forestry Applications. Available online: http://www.eurosdr.net/research/project/project-benchmarking-terrestrial-laser-scanning-forestry-applications (accessed on 20 September 2015).
- Kobler, A.; Pfeifer, N.; Ogrinc, P.; Todorovski, L.; Oštir, K.; Džeroski, S. Repetitive interpolation: A robust algorithm for dtm generation from aerial laser scanner data in forested terrain. Remote Sens. Environ. 2007, 108, 9–23. [Google Scholar] [CrossRef]
- Douillard, B.; Underwood, J.; Kuntz, N.; Vlaskine, V.; Quadros, A.; Morton, P.; Frenkel, A. On the segmentation of 3d lidar point clouds. In Proceedings of the 2011 IEEE International Conference Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2798–2805.
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A progressive morphological filter for removing nonground measurements from airborne lidar data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Brunelli, R.; Poggiot, T. Template matching: Matched spatial filters and beyond. Pattern Recognit. 1997, 30, 751–768. [Google Scholar] [CrossRef]
- Nixon, M. Feature Extraction & Image Processing; Academic Press: Pittsburgh, Pennsylvania, PA, USA, 2008. [Google Scholar]
- Masutani, Y.; Masamune, K.; Dohi, T. Region-growing based feature extraction algorithm for tree-like objects. In Proceedings of the 4th International Conference Visualization in Biomedical Computing, vbc’96 Hamburg, Germany, 22–25 September 1996; Höhne, K.H., Kikinis, R., Eds.; Springer: Berlin, Germany, 1996; pp. 159–171. [Google Scholar]
- Roggero, M. Object segmentation with region growing and principal component analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 289–294. [Google Scholar]
- Gander, W.; Golub, G.H.; Strebel, R. Least-squares fitting of circles and ellipses. BIT Numer. Math. 1994, 34, 558–578. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Yu, X. The use of a mobile laser scanning system for mapping large forest plots. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1504–1508. [Google Scholar] [CrossRef]
- Raumonen, P.; Casella, E.; Calders, K.; Murphy, S.; Åkerblom, M.; Kaasalainen, M. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 189. [Google Scholar] [CrossRef]
- Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly accurate tree models derived from terrestrial laser scan data: A method description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef]
- Hackenberg, J.; Wassenberg, M.; Spiecker, H.; Sun, D. Non destructive method for biomass prediction combining TLS derived tree volume and wood density. Forests 2015, 6, 1274–1300. [Google Scholar] [CrossRef]
- Litkey, P.; Liang, X.; Kaartinen, H.; Hyyppä, J.; Kukko, A.; Holopainen, M.; Hill, R.; Rosette, J.; Suárez, J. Single-scan TLS methods for forest parameter retrieval. In Proceedings of SilviLaser 2008, 8th international conference on LiDAR applications in forest assessment and inventory, Heriot-Watt University, Edinburgh, UK, 17–19 September 2008; pp. 295–304.
- Côté, J.-F.; Fournier, R.A.; Egli, R. An architectural model of trees to estimate forest structural attributes using terrestrial LiDAR. Environ. Model. Softw. 2011, 26, 761–777. [Google Scholar] [CrossRef]
- Livny, Y.; Yan, F.; Olson, M.; Chen, B.; Zhang, H.; El-Sana, J. Automatic Reconstruction of Tree Skeletal Structures from Point Clouds; ACM Transactions on Graphics (TOG); ACM: New York, NY, USA, 2010; p. 151. [Google Scholar]
- Newnham, G.J.; Armston, J.D.; Calders, K.; Disney, M.I.; Lovell, J.L.; Schaaf, C.B.; Strahler, A.H.; Danson, F.M. Terrestrial laser scanning for plot-scale forest measurement. Curr. For. Rep. 2015, 1, 239–251. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Schilling, A.; Maas, H. Automatic reconstruction of skeletal structures from TLS forest scenes. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 321. [Google Scholar] [CrossRef]
- Yang, B.; Dai, W.; Dong, Z.; Liu, Y. Automatic forest mapping at individual tree levels from terrestrial laser scanning point clouds with a hierarchical minimum cut method. Remote Sens. 2016, 8, 372. [Google Scholar] [CrossRef]
- Eysn, L.; Pfeifer, N.; Ressl, C.; Hollaus, M.; Grafl, A.; Morsdorf, F. A practical approach for extracting tree models in forest environments based on equirectangular projections of terrestrial laser scans. Remote Sens. 2013, 5, 5424–5448. [Google Scholar] [CrossRef]




| 1. DTM extraction | ||
| DTM resolution | 0.2 (m) | |
| * | Local elevation tolerance in a moving window | 0.5 (m) |
| Minimum initial ground points in a moving window | 10 | |
| * | DTM upper threshold factor | 5 |
| 2. Stem detection | ||
| Horizontal resolution for voxelization | 0.1 (m) | |
| Vertical resolution for voxelization | 0.5 (m) | |
| * | Cylindrical filter width s (roughly close to DBH) | 0.2 (m) |
| Cylindrical filter height b | 1 (m) | |
| Maximally-allowed cylindrical filter leaning angle | 20° | |
| * | Cylindrical filter value (larger value creates more peaks) | 1 |
| Filtered peak detection strength (larger value detects weaker peaks) | 0.5 | |
| 3. Branch and stem segmentation | ||
| * | Region growing step | 0.02 (m) |
| Point gap tolerance | 0.01 (m) | |
| * | Maximum branch width increase ratio | 0.8 |
| Maximum branch direction change | 60° | |
| 4. Stem curve extraction | ||
| Stem node interval | 0.2 (m) | |
| * | Stem radius tolerance | 1.3 |
| RMSE | r2 | |
| DBH (SS) | 2.4 cm | 0.81 |
| DBH (MS) | 0.9 cm | 0.97 |
| Height (SS) | 1.7 m | 0.58 |
| Height (MS) | 1.7 m | 0.68 |
| Average RMSEs | Average r2 s | |
| Diameter (SS) | 3.2 cm | 0.58 |
| Diameter (MS) | 2.4 cm | 0.76 |
| Process | SS | MS |
|---|---|---|
| Reading point cloud | 1 | 4 |
| (sppm) * | (2.5) | (2.2) |
| Extracting and removing DTM | 1 | 4 |
| (sppm) | (2.5) | (2.2) |
| Extracting stem location | 0.2 | 1 |
| (sppm) | (0.5) | (0.5) |
| Isolating stem space | 1 | 4 |
| (sppm) | (2.5) | (2.2) |
| Extracting stem form | 24 | 135 |
| (sppm) | (61.1) | (72.9) |
| Overall | 27 | 148 |
| (sppm) | (68.7) | (80.0) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, Z.; Hopkinson, C.; Chasmer, L. Automating Plot-Level Stem Analysis from Terrestrial Laser Scanning. Forests 2016, 7, 252. https://doi.org/10.3390/f7110252
Xi Z, Hopkinson C, Chasmer L. Automating Plot-Level Stem Analysis from Terrestrial Laser Scanning. Forests. 2016; 7(11):252. https://doi.org/10.3390/f7110252
Chicago/Turabian StyleXi, Zhouxin, Christopher Hopkinson, and Laura Chasmer. 2016. "Automating Plot-Level Stem Analysis from Terrestrial Laser Scanning" Forests 7, no. 11: 252. https://doi.org/10.3390/f7110252
APA StyleXi, Z., Hopkinson, C., & Chasmer, L. (2016). Automating Plot-Level Stem Analysis from Terrestrial Laser Scanning. Forests, 7(11), 252. https://doi.org/10.3390/f7110252







