Loblolly Pine Productivity and Water Relations in Response to Throughfall Reduction and Fertilizer Application on a Poorly Drained Site in Northern Florida
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Design
- (1)
- Control (C): ambient throughfall, no fertilizer application
- (2)
- Throughfall Reduction (TR): 30% throughfall reduction, no fertilizer application
- (3)
- Fertilizer application (F): ambient throughfall, fertilizer application
- (4)
- Fertilizer application and Throughfall Reduction (TR+F): 30% throughfall reduction, fertilizer application.
2.2. Throughfall Exclusion Design
2.3. Meteorological and Soil Measurements
2.4. Leaf Area Index, Specific Needle Area, and ANPP
2.5. Sap Flow and Transpiration
2.6. Canopy-Level Stomatal Conductance
2.7. Statistical Analysis
3. Results
3.1. Soil Bulk Density, Texture, and Moisture
3.2. LAI, Needlefall, and Growth
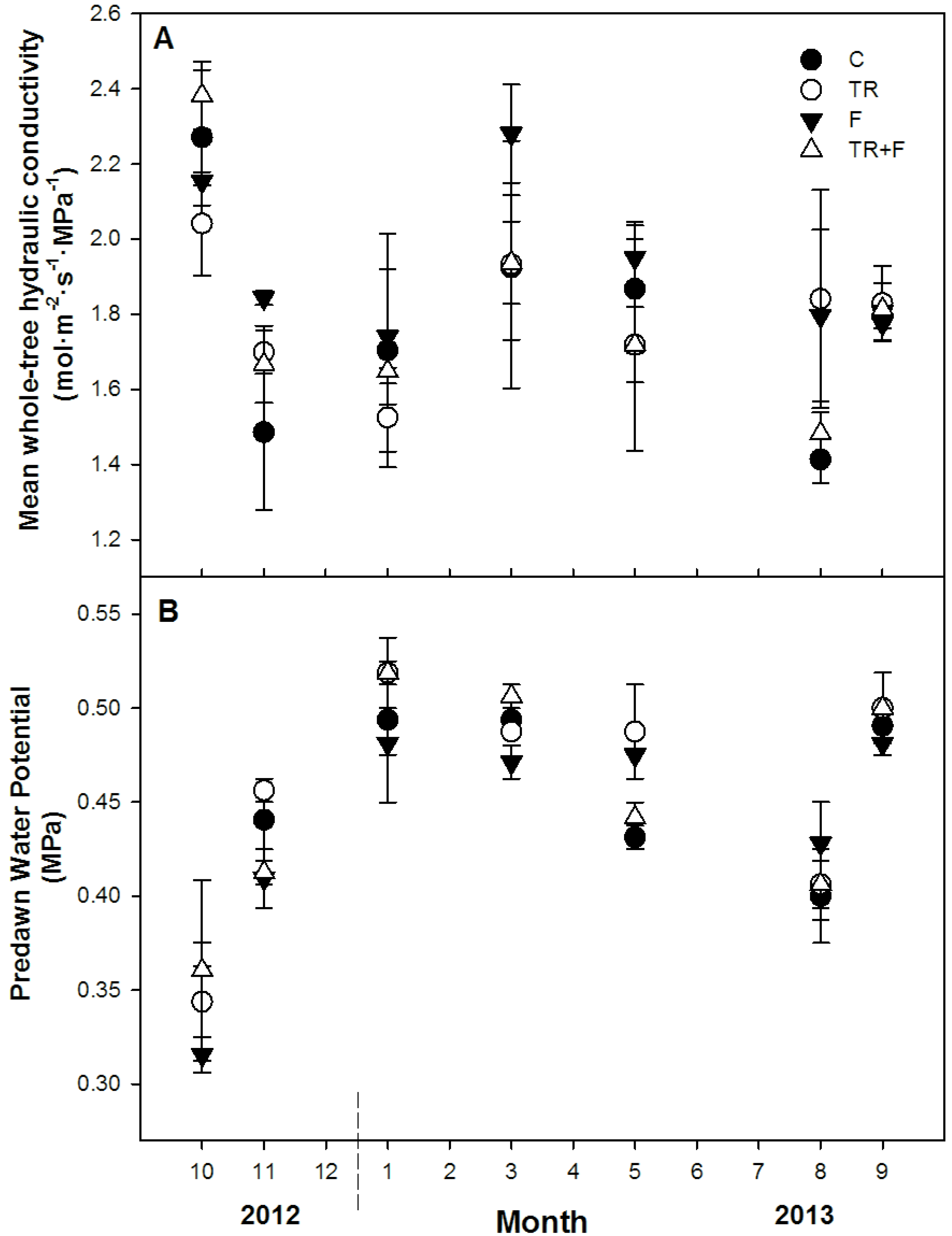
3.3. Whole-Tree Hydraulic Conductance
3.4. Radial Variation in Sap Flow
3.5. Transpiration
3.6. Canopy Conductance
4. Discussion
4.1. Whole-Tree Hydraulic Conductance
4.2. LAI and ANPP
4.3. Sap Flow and Transpiration
4.4. Canopy Conductance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CO2 | Carbon Dioxide |
| PPM | Parts per million |
| D | Vapor Pressure Deficit (kPa) |
| U.S. | Unites States |
| LAI | Leaf Area Index |
| C | Control Treatment |
| TR | Throughfall reduction treatment |
| F | Fertilizer application Treatment |
| TR+F | Throughfall reduction + fertilizer application treatment |
| As | Sapwood Area |
| DBH | Diameter at breast height (1.37m) |
| PPFD | Photosynthetic photon flux density |
| TIG | Tungsten inert gas |
| θ0–20 | Volumetric water content of 0–20cm soil horizon |
| θ0–30 | Volumetric water content of 0–30 cm soil horizon |
| θ0–60 | Volumetric water content of 0–60cm soil horizon |
| θ0–84 | Volumetric water content of 0–84cm soil horizon |
| θ30–60 | Volumetric water content of 30–60cm soil horizon |
| θ60–84 | Volumetric water content of 60–84cm soil horizon |
| ANPP | Aboveground net primary productivity |
| BAG | Basal area growth |
| ΔT | Temperature difference |
| ΔTm | Maximum temperature difference |
| JS | Sap flux density (JS, g∙m−2∙s−1) |
| ECOR | Corrected transpiration estimates |
| E20 | Uncorrected transpiration estimates from outer 20mm of sapwood |
| EMax | Maximum daily transpiration |
| EDay | Daily transpiration rate |
| EMonth | Monthly transpiration rate |
| EYear | Yearly transpiration rate |
| GC | Canopy stomatal conductance |
| GCref | Maximum canopy stomatal conductance in mmol∙m−2∙s−1 at vapor pressure Deficit = 1 kPa |
| δ | The slope of the boundary line of the relationship between canopy stomatal conductance and the natural logarithm of vapor pressure deficit |
| 3-PG | Physiological Principles in Predicting Growth model |
| MaxCond | Maximum canopy stomatal conductance in m∙s−1 at vapor pressure deficit = 0 kPa |
| CoeffCond | Defines stomatal response to vapor pressure deficit in mb−1 |
| KS | Whole-tree hydraulic conductance |
| ΨL | Leaf water potential |
References
- Siegenthaler, U.; Stocker, T.F.; Monnin, E.; Lüthi, D.; Schwander, J.; Stauffer, B.; Raynaud, D.; Barnola, J.-M.; Fischer, H.; Masson-Delmotte, V.; et al. Stable carbon cycle–climate relationship during the late pleistocene. Science 2005, 310, 1313–1317. [Google Scholar] [CrossRef] [PubMed]
- Bala, G. Digesting 400 ppm for global mean CO2 concentration. Curr. Sci. 2013, 104, 47–48. [Google Scholar]
- Kunkel, K.E.; Stevens, L.E.; Stevens, S.E.; Sun, L.; Janssen, E.; Wuebbles, D.; Konrad, C.E.; Fuhrman, C.M.; Keim, B.D.; Kruk, M.C.; et al. Regional climate trends and Scenarios for the U.S. national climate assessment; Climate of the Southeast U.S.; NOAA Technical Report NESDIS 142-2; NOAA National Climatic Data Center: Asheville, NC, USA, 2013; p. 94.
- Schultz, R.P. Loblolly Pine: The ecology and Culture of Loblolly Pine (Pinus taeda L.); USDA Agric. Handb.713; U.S. Government Publishing Office: Washington, DC, USA, 1997.
- McKeand, S.; Mullin, T.; Byram, T.; White, T. Deployment of genetically improved loblolly and slash pines in the south. J. For. 2003, 101, 32–37. [Google Scholar]
- Smith, W.B.; Miles, P.B.; Perry, C.H.; Pugh, S.A. Forest Resources of the United States, 2007; General Technical Report WO-78; USDA Forest Service: Washington, DC, USA, 2009; p. 336.
- Han, F.X.; Plodinec, M.J.; Su, Y.; Monts, D.L.; Li, Z. Terrestrial carbon pools in southeast and south-central United States. Clim. Change 2007, 84, 191–202. [Google Scholar] [CrossRef]
- Anderson, C.J.; Lockaby, B.G. The effectiveness of forestry best management practices for sediment control in the southeastern United States: A literature review. South. J. Appl. For. 2011, 35, 170–177. [Google Scholar]
- McLaughlin, D.L.; Kaplan, D.A.; Cohen, M.J. Managing forests for increased regional water yield in the southeastern U.S. Coastal Plain. J. Am. Water Resour. Assoc. 2013, 49, 953–965. [Google Scholar] [CrossRef]
- Wear, D.N.; Greis, J.G. Southern Forest Resource Assessment: Summary Report; General Technical Report SRS-54; USDA Forest Service Southern Research Station: Asheville, NC, USA, 2002; p. 103.
- Fox, T.R.; Jokela, E.J.; Allen, H.L. The Development of Pine Plantation Silviculture in the Southern United States. J. For. 2007, 105, 337–347. [Google Scholar]
- Albaugh, T.J.; Allen, H.L.; Dougherty, P.M.; Kress, L.W.; King, J.S. Leaf area and above- and belowground growth responses of loblolly pine to nutrient and water additions. For. Sci. 1998, 44, 317–328. [Google Scholar]
- Jokela, E.J.; Martin, T.A.; Vogel, J.G. Twenty-five years of intensive forest management with southern pines: important lessons learned. J. For. 2010, 108, 338–347. [Google Scholar]
- Ewers, B.E.; Oren, R.; Albaugh, T.J.; Dougherty, P.M. Carry-over effects of water and nutrient supply on water use of Pinus taeda. Ecol. Appl. 1999, 9, 513–525. [Google Scholar] [CrossRef]
- Ewers, B.E.; Oren, R.; Sperry, J.S. Influence of nutrient versus water supply on hydraulic architecture and water balance in Pinus taeda. Plant Cell Environ. 2000, 23, 1055–1066. [Google Scholar] [CrossRef]
- Samuelson, L.J.; Farris, M.G.; Stokes, T.A.; Coleman, M.D. Fertilization but not irrigation influences hydraulic traits in plantation-grown loblolly pine. For. Ecol. Manag. 2008, 255, 3331–3339. [Google Scholar] [CrossRef]
- Sun, G.; Arumugam, S.; Caldwell, P.V.; Conrads, P.A.; Covich, A.P.; Cruise, J.; Feldt, J.; Georgakakos, A.P.; McNider, R.T.; McNulty, S.G.; et al. Impacts of climate change and variability on water resources in the Southeast USA. In Climate of the Southeast United States: Variability, Change, Impacts, and Vulnerability; Ingram, K.T., Dow, K., Carter, L., Anderson, J., Eds.; Island Press: Washington, DC, USA, 2013; pp. 210–236. [Google Scholar]
- Roth, B.E.; Jokela, E.J.; Martin, T.A.; Huber, D.A.; White, T.L. Genotype × environment interactions in selected loblolly and slash pine plantations in the Southeastern United States. For. Ecol. Manag. 2007, 238, 175–188. [Google Scholar] [CrossRef]
- Gonzalez-Benecke, C.A.; Martin, T.A. Water availability and genetic effects on water relations of loblolly pine (Pinus taeda) stands. Tree Physiol. 2010, 30, 376–392. [Google Scholar] [CrossRef] [PubMed]
- Aspinwall, M.J.; King, J.S.; Domec, J.-C.; McKeand, S.E.; Isik, F. Genetic effects on transpiration, canopy conductance, stomatal sensitivity to vapour pressure deficit, and cavitation resistance in loblolly pine. Ecohydrology 2011, 4, 168–182. [Google Scholar] [CrossRef]
- Tang, Z.; Sayer, M.A.S.; Chambers, J.L.; Barnett, J.P. Interactive effects of fertilization and throughfall exclusion on the physiological responses and whole-tree carbon uptake of mature loblolly pine. Can. J. Bot. 2004, 82, 850–861. [Google Scholar] [CrossRef]
- Will, R.E.; Fox, T.; Akers, M.; Domec, J.-C.; Gonzalez-Benecke, C.; Jokela, E.; Kane, M.; Laviner, A.; Lokuta, G.; Markewitz, D.; et al. A range-wide experiment to investigate nutrient and soil moisture interactions in loblolly pine plantations. Forests 2015, 6, 2014–2028. [Google Scholar] [CrossRef]
- Soil Survey Staff, Natural Resources Conservation Service, United States Department of Agriculture. Web Soil Survey. Available online: http://websoilsurvey.nrcs.usda.gov/ (accessed on 21 January 2012).
- Karl, T.R.; Melillo, J.M.; Peterson, T.C. Global Climate Change Impacts in the United States; Cambridge University Press: New York, NY, USA, 2009; p. 188. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Gee, G.W.; Bauder, J.W. Particle-size analysis. In Methods of Soil Analysis, 2nd ed.; Klute, A., Ed.; American Society of Agronomy: Madison, WI, USA, 1986; pp. 383–411. [Google Scholar]
- Martin, T.A.; Jokela, E.J. Developmental patterns and nutrition impact radiation use efficiency components in southern pine stands. Ecol. Appl. 2004, 14, 1839–1854. [Google Scholar] [CrossRef]
- Gonzalez-Benecke, C.A.; Gezan, S.A.; Albaugh, T.J.; Allen, H.L.; Burkhart, H.E.; Fox, T.R.; Jokela, E.J.; Maier, C.A.; Martin, T.A.; Rubilar, R.A.; Samuelson, L.J. Local and general above-stump biomass functions for loblolly pine and slash pine trees. For. Ecol. Manag. 2014, 334, 254–276. [Google Scholar] [CrossRef]
- Granier, A. Une nouvelle méthode pour la mesure du flux de sève brute dans le tronc des arbres. Ann. Sci. For. 1985, 42, 193–200. [Google Scholar] [CrossRef]
- Granier, A. Evaluation of transpiration in a Douglas-fir stand by means of sap flow measurements. Tree Physiol. 1987, 3, 309–320. [Google Scholar] [CrossRef] [PubMed]
- Clearwater, M.J.; Meinzer, F.C.; Andrade, J.L.; Goldstein, G.; Holbrook, N.M. Potential errors in measurement of nonuniform sap flow using heat dissipation probes. Tree Physiol. 1999, 19, 681–687. [Google Scholar] [CrossRef] [PubMed]
- Čermák, J.; Kučera, J.; Nadezhdina, N. Sap flow measurements with some thermodynamic methods, flow integration within trees and scaling up from sample trees to entire forest stands. Trees 2004, 18, 529–546. [Google Scholar] [CrossRef]
- Samuelson, L.J.; Stokes, T.A.; Coleman, M.D. Influence of irrigation and fertilization on transpiration and hydraulic properties of Populus deltoides. Tree Physiol. 2007, 27, 765–774. [Google Scholar] [CrossRef] [PubMed]
- Ewers, B.E.; Oren, R. Analyses of assumptions and errors in the calculation of stomatal conductance from sap flux measurements. Tree Physiol. 2000, 20, 579–589. [Google Scholar] [CrossRef] [PubMed]
- Ewers, B.E.; Oren, R.; Johnsen, K.H.; Landsberg, J.J. Estimating maximum mean canopy stomatal conductance for use in models. Can. J. For. Res. 2001, 31, 198–207. [Google Scholar] [CrossRef]
- Landsberg, J.J.; Waring, R.H. A generalized model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. For. Ecol. Manag. 1997, 95, 209–228. [Google Scholar] [CrossRef]
- Gonzalez-Benecke, C.A.; Jokela, E.J.; Cropper, W.P.; Bracho, R.; Leduc, D.J. Parameterization of the 3-PG model for Pinus elliottii stands using alternative methods to estimate fertility rating, biomass partitioning and canopy closure. For. Ecol. Manag. 2014, 327, 55–75. [Google Scholar] [CrossRef]
- Wullschleger, S.D.; Meinzer, F.C.; Vertessy, R.A. A review of whole-plant water use studies in tree. Tree Physiol. 1998, 18, 499–512. [Google Scholar] [CrossRef] [PubMed]
- National Oceanic & Atmospheric Administration (NOAA). Monthly Summaries of the Global Historical Climatology Network-Daily (GHCN-D) Subset: USC00087025; NOAA National Climatic Data Center: Asheville, NC, USA, 2014.
- Gonzalez-Benecke, C.A.; Martin, T.A.; Wendell, C.P. Whole-tree water relations of co-occurring mature Pinus palustris and Pinus elliottii var. elliottii. Can. J. For. Res. 2011, 41, 509–523. [Google Scholar] [CrossRef]
- McCarthy, J.W.; Stone, E.L. Changes in soil water tables following phosphorus fertilization of young slash pine. Soil Sci. Soc. Am. J. 1991, 55, 1440. [Google Scholar] [CrossRef]
- Teskey, R.O.; Gholz, H.L.; Cropper, W.P. Influence of climate and fertilization on net photosynthesis of mature slash pine. Tree Physiol. 1994, 14, 1215–1227. [Google Scholar] [CrossRef] [PubMed]
- Gholz, H.L.; Clark, K.L. Energy exchange across a chronosequence of slash pine forests in Florida. Agric. For. Meteorol. 2002, 112, 87–102. [Google Scholar] [CrossRef]
- Powell, T.L.; Gholz, H.L.; Clark, K.L.; Starr, G.; Cropper, W.P.; Martin, T.A. Carbon exchange of a mature, naturally regenerated pine forest in north Florida. Glob. Change Biol. 2008, 14, 2523–2538. [Google Scholar] [CrossRef]
- Van Rees, K.C.J.; Comerford, N.B. Vertical root distribution and strontium uptake of a slash pine stand on a Florida Spodosol. Soil Sci. Soc. Am. J. 1986, 50, 1042. [Google Scholar] [CrossRef]
- Torreano, S.J.; Morris, L.A. Loblolly pine root growth and distribution under water stress. Soil Sci. Soc. Am. J. 1998, 62, 818. [Google Scholar] [CrossRef]
- Albaugh, T.J.; Allen, H.L.; Kress, L.W. Root and stem partitioning of Pinus taeda. Trees 2006, 20, 176–185. [Google Scholar] [CrossRef]
- Bracho, R.; Starr, G.; Gholz, H.L.; Martin, T.A.; Cropper, W.P.; Loescher, H.W. Controls on carbon dynamics by ecosystem structure and climate for southeastern U.S. slash pine plantations. Ecol. Monogr. 2012, 82, 101–128. [Google Scholar] [CrossRef]
- Domec, J.-C.; Noormets, A.; King, J.S.; Sun, G.; Mcnulty, S.G.; Gavazzi, M.J.; Boggs, J.L.; Treasure, E.A. Decoupling the influence of leaf and root hydraulic conductances on stomatal conductance and its sensitivity to vapour pressure deficit as soil dries in a drained loblolly pine plantation. Plant Cell Environ. 2009, 32, 980–991. [Google Scholar]
- Bartkowiak, S.M.; Samuelson, L.J.; McGuire, M.A.; Teskey, R.O. Fertilization increases sensitivity of canopy stomatal conductance and transpiration to throughfall reduction in an 8-year-old loblolly pine plantation. For. Ecol. Manag. 2015, 354, 87–96. [Google Scholar] [CrossRef]
- Teskey, R.O.; Bongarten, B.C.; Cregg, B.M.; Dougherty, P.M.; Hennessey, T.C. Physiology and genetics of tree growth response to moisture and temperature stress: An examination of the characteristics of loblolly pine (Pinus taeda L.). Tree Physiol. 1987, 3, 41–61. [Google Scholar] [CrossRef] [PubMed]
- Ward, E.J.; Domec, J.-C.; Laviner, M.A.; Fox, T.R.; Sun, G.; McNulty, S.; King, J.; Noormets, A. Fertilization intensifies drought stress: Water use and stomatal conductance of Pinus taeda in a midrotation fertilization and throughfall reduction experiment. For. Ecol. Manag. 2015, 355, 72–82. [Google Scholar] [CrossRef]
- Phillips, N.; Oren, R.; Zimmermann, R. Radial patterns of xylem sap flow in non-, diffuse- and ring-porous tree species. Plant Cell Environ. 1996, 19, 983–990. [Google Scholar] [CrossRef]
- Ford, C.R.; McGuire, M.A.; Mitchell, R.J.; Teskey, R.O. Assessing variation in the radial profile of sap flux density in Pinus species and its effect on daily water use. Tree Physiol. 2004, 24, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Spicer, R.; Gartner, B.L. The effects of cambial age and position within the stem on specific conductivity in Douglas-fir (Pseudotsuga menziesii) sapwood. Trees 2001, 15, 222–229. [Google Scholar] [CrossRef]
- Domec, J.-C.; Pruyn, M.L.; Gartner, B.L. Axial and radial profiles in conductivities, water storage and native embolism in trunks of young and old-growth ponderosa pine trees. Plant Cell Environ. 2005, 28, 1103–1113. [Google Scholar]
- Mark, W.R.; Crews, D.L. Heat-pulse velocity and bordered pit condition in living Engelmann spruce and lodgepole pine trees. For. Sci. 1973, 19, 291–296. [Google Scholar]
- Sperry, J.S.; Perry, A.H.; Sullivan, J.E.M. Pit membrane degradation and air-embolism formation in ageing xylem vessels of Populus tremuloides Michx. J. Exp. Bot. 1991, 42, 1399–1406. [Google Scholar] [CrossRef]
- Dye, P.J.; Olbrich, B.W.; Poulter, A.G. The Influence of growth rings in Pinus patula on heat pulse velocity and sap flow measurement. J. Exp. Bot. 1991, 42, 867–870. [Google Scholar] [CrossRef]
- Jiménez, M.S.; Nadezhdina, N.; Čermák, J.; Morales, D. Radial variation in sap flow in five laurel forest tree species in Tenerife, Canary Islands. Tree Physiol. 2000, 20, 1149–1156. [Google Scholar] [CrossRef] [PubMed]
- Phillips, N.; Oren, R. intra- and inter-annual variation in transpiration of a pine forest. Ecol. Appl. 2001, 11, 385–396. [Google Scholar] [CrossRef]
- Samuelson, L.J.; Stokes, T.A. Transpiration and canopy stomatal conductance of 5-year-old loblolly pine in response to intensive management. For. Sci. 2006, 52, 313–323. [Google Scholar]
- Ewers, B.E.; Oren, R.; Phillips, N.; Strömgren, M.; Linder, S. Mean canopy stomatal conductance responses to water and nutrient availabilities in Picea abies and Pinus taeda. Tree Physiol. 2001, 21, 841–850. [Google Scholar] [CrossRef] [PubMed]
- Bryars, C.; Maier, C.; Zhao, D.; Kane, M.; Borders, B.; Will, R.; Teskey, R. Fixed physiological parameters in the 3-PG model produced accurate estimates of loblolly pine growth on sites in different geographic regions. For. Ecol. Manag. 2013, 289, 501–514. [Google Scholar] [CrossRef]
- Gonzalez-Benecke, C.A.; Teskey, R.O.; Martin, T.A.; Jokela, E.J.; Fox, T.R.; Kane, M.B.; Noormets, A. Regional validation and improved parameterization of the 3-PG model for Pinus taeda stands. For. Ecol. Manag. 2015, 36, 237–256. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]


| DBH (cm) | |||
|---|---|---|---|
| Treatment | Minimum | Maximum | Mean |
| C | 10 | 19.1 | 14.9 |
| TR | 8.6 | 19.5 | 15.0 |
| F | 9.6 | 19.3 | 14.8 |
| TR+F | 9 | 19.6 | 15.3 |
| Treatment | p-Value | ||||||
|---|---|---|---|---|---|---|---|
| C | TR | F | TR+F | F | TR | F×TR | |
| ANPP 2013 (Mg∙ha−1∙year−1) | 26.5 a | 28.1 ac | 32.3 b | 30.2 bc | <0.001 | 0.736 | 0.049 |
| BAG 2012 (m2∙ha−1∙year−1) | 4.2 | 4.0 | 5.0 | 4.7 | 0.007 | 0.230 | 0.789 |
| BAG 2013 (m2∙ha−1∙year−1) | 3.4 | 3.5 | 4.3 | 3.9 | 0.033 | 0.576 | 0.314 |
| LAI 2012 (Projected) | 2.0–3.4 | 1.9–3.3 | 1.9–3.6 | 1.9–3.7 | 0.037 | 0.938 | 0.308 |
| LAI 2013 (Projected) | 2.3–3.6 | 2.3–3.6 | 2.7–4.1 | 2.7–4.2 | <0.001 | 0.452 | 0.478 |
| Needlefall 2013 (Mg∙ha−1∙year−1) | 5.5 | 5.6 | 6.4 | 6.6 | <0.001 | 0.383 | 0.536 |
| Treatment | p Value | ||||||
|---|---|---|---|---|---|---|---|
| C | TR | F | TR+F | F | TR | FxTR | |
| EYear (mm∙year−1) | 535 | 547 | 596 | 546 | 0.349 | 0.545 | 0.334 |
| EMax (mm∙day−1) | 2.60 | 2.70 | 3.08 | 2.76 | 0.125 | 0.517 | 0.229 |
| −δ (mmol∙m−2∙s−1∙ln(kPa)−1) | 81.37 | 79.93 | 77.56 | 73.49 | 0.635 | 0.687 | 0.793 |
| GCref (mmol∙m−2∙s−1) | 138.38 | 139.9 | 137.19 | 126.2 | 0.587 | 0.663 | 0.573 |
| MaxCond (m∙s−1) | 0.0065 | 0.0063 | 0.0060 | 0.0057 | 0.178 | 0.630 | 0.897 |
| CoeffCond (mbar−1) | 0.061 | 0.058 | 0.055 | 0.063 | 0.998 | 0.502 | 0.130 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wightman, M.G.; Martin, T.A.; Gonzalez-Benecke, C.A.; Jokela, E.J.; Cropper, W.P., Jr.; Ward, E.J. Loblolly Pine Productivity and Water Relations in Response to Throughfall Reduction and Fertilizer Application on a Poorly Drained Site in Northern Florida. Forests 2016, 7, 214. https://doi.org/10.3390/f7100214
Wightman MG, Martin TA, Gonzalez-Benecke CA, Jokela EJ, Cropper WP Jr., Ward EJ. Loblolly Pine Productivity and Water Relations in Response to Throughfall Reduction and Fertilizer Application on a Poorly Drained Site in Northern Florida. Forests. 2016; 7(10):214. https://doi.org/10.3390/f7100214
Chicago/Turabian StyleWightman, Maxwell G., Timothy A. Martin, Carlos A. Gonzalez-Benecke, Eric J. Jokela, Wendell P. Cropper, Jr., and Eric J. Ward. 2016. "Loblolly Pine Productivity and Water Relations in Response to Throughfall Reduction and Fertilizer Application on a Poorly Drained Site in Northern Florida" Forests 7, no. 10: 214. https://doi.org/10.3390/f7100214
APA StyleWightman, M. G., Martin, T. A., Gonzalez-Benecke, C. A., Jokela, E. J., Cropper, W. P., Jr., & Ward, E. J. (2016). Loblolly Pine Productivity and Water Relations in Response to Throughfall Reduction and Fertilizer Application on a Poorly Drained Site in Northern Florida. Forests, 7(10), 214. https://doi.org/10.3390/f7100214








