1. Introduction
Airborne laser scanning (ALS) is increasingly being used in forest mapping [
1,
2,
3]. In certain types of mature stands, even individual trees can be inventoried using ALS data [
4,
5,
6]. This kind of individual-tree-level inventory is usually based on the detection of trees from an ALS point cloud. The estimation of the tree variables is based on ALS-derived point cloud metrics and ground-truth data corresponding to the same trees [
7,
8,
9], thus creating a geodatabase for accurate tree inventory.
In Finland, 96% of annual timber felling in standing sales on privately-owned forestland is done using harvesters [
10]. As part of the harvesting process, a harvester collects detailed data on the logged trees, such as length of the utilizable stem part and stem diameter at intervals of 10 cm; and the length, top diameter, and volume of each log [
11]. The majority of harvesters are equipped with a global navigation satellite system (GNSS), in addition to having onboard geographic information system (GIS) software. Currently, the location of a harvester under the forest canopy is recorded with an accuracy of about 3 m [
12], but the location of the harvester head,
i.e., the location of the processed tree, is not recorded. However, only the roundwood trade and haulage are based on these harvester measurements.
Information collected by means of the harvester head could partly replace the field measurements needed for calibrating remotely-sensed inventory data, and thereby provide both less costly and more detailed reference data required in various forest inventory and mapping applications. Holopainen
et al. [
13] proposed that after harvesting a few trees, local inventory data can be updated in real time. However, the positional accuracy of the current harvester-based tree data is not sufficient to match the trees detected by ALS and therefore harvester head positioning requires technical improvements. There are technical solutions that could be used for positioning the harvester head relative to the harvester, but so far there have not been enough incentives for machine manufacturers to add this new functionality to new machines. If the harvester is also equipped with a MLS (Mobile Laser Scanning) system, then trees possessing the desired characteristics could be selected using the stem curve information available from the MLS data. Moreover, the direct georeferencing solution of GNSS/IMU sensors could be used in the positioning of such a harvester.
Thus, improved performance in forest inventory is expected to be achieved if the position of the harvester head is known so that the harvested trees and the ALS data can be linked. Some studies have been conducted explaining the usability of the approach. Peuhkurinen
et al. [
6] conducted the first tests where ALS data were used in making pre-harvest measurements. An inventory based on individual tree crowns (ITC) was carried out in two mature conifer stands (density ~465 stems per hectare) prior to logging. The major problem in ITC is deemed to be tree detection (e.g., [
14,
15]), but on a managed forest site tested in the study the number of harvestable trees was underestimated by less than 3%. In general, the ITC approach is at its best in single-layered mature stands. Holmgren
et al. [
16] showed that if the harvester measurements are used as reference data for ALS-based tree-level inventories, highly accurate estimates can be obtained. Their imputation accuracies (root mean squared error percentage RMSE-%) for stem volume, mean tree height, mean stem diameter, and stem density were 11%, 8%, 12%, and 19%, respectively. These validations were executed using aggregated plots, which suggests that stand-level estimates would be even more accurate. Since tree positions were missing from operational harvester data, Holmgren
et al. [
16] used manual measurements to match the logged trees with the ALS data. Holmgren
et al. [
16], like Holopainen
et al. [
13], also stated that a future operational system could continuously receive stem data sent from the operating harvester and these data could be used to continuously update an ALS-based reference database, and thereby enable improved prediction of stem attributes for stands not yet harvested. Melkas
et al. [
17] studied forest resource data updating using a harvester’s species-specific timber volume data. In that study, the pre-thinning ALS-derived accuracies (RMSE-%) were 21.6% and 21.7% for an area-based ALS inventory (see [
18]) and ITC-based inventory, respectively (validated pre-felling by means of field-measured plots). Following the thinning operation, the timber volume data were updated based on the harvester data, and the corresponding RMSE-% values were 29.4% and 31.6%. However, the absolute RMSE values remained at the pre-felling level. Melkas
et al. [
17] concluded that harvester data have potential for updating stand-level data. If sophisticated databases showing the locations and species of individual trees are available, tree-level harvest scheduling can be optimized; e.g., by using a species-mingling index as suggested by Bettinger and Tang [
19].
The aim in this study was to test the accuracy of various instruments utilizing GNSS mounted on machinery in motion under forest canopies of varying densities to enable us to understand the current state-of-the-art in GNSS-based positioning under forest canopies. The tested GNSS devices include a low-cost, consumer handheld navigator, two single-frequency receivers with external mini-antennas, and a geodetic dual-frequency receiver with an external antenna. Both real-time positioning and post-processed positioning with and without inertial measurement unit (IMU) data were analyzed to find out what kind of equipment could be added to the harvesters to achieve the required positioning performance for reliable tree matching. In the future, the stem data collected by means of harvesters could be used for enhancing pre-harvest inventory data to predict logging yields from forest stands. There is a high operational requirement for these kind of high-resolution forest data. Modern wood flow optimization tools could be used more efficiently and provide savings through precision forestry.
2. Positioning in the Forest
2.1. Global Navigation Satellite Systems (GNSS)
Satellite-based positioning includes deriving the location of a user’s receiver based on radio frequency signals transmitted by satellite systems. Current fully-operational GNSS applications include the US Navstar GPS (Global Positioning System) and the Russian GLONASS (GLObalnaja NAvigatsionnaja Sputnikovaja Sistema). Satellite-based positioning is based on accurate time determination: the time difference between the transmitted and the received radio signal denotes the signal travel time, which reveals the distance between the satellite and the user’s antenna. Utilizing these measurements of the distance between the user antenna and a minimum of four different satellites, the receiver can obtain three-dimensional receiver coordinates in a global reference frame and the time difference between the receiver and the satellite’s clocks.
Satellite-based positioning is undergoing a period of rapid change. There is a need to reform the GPS and GLONASS systems due to the increasing number of applications, more demanding requirements from users, and the need to mitigate interference and disturbances to the radio signals used by these systems. Both of these systems are being modernized to better serve the challenging present-day applications in obstructed signal conditions. These modernizations include an increasing the number of transmission frequencies and changes to signal components. In addition, the European Galileo and the Chinese BeiDou systems are under development. There is a determined intention to design the future, modernized systems to be resistant to interference, as well as to be more accurate and available over a wider range of conditions. Also, the use of multiple systems for positioning increases the accuracy and reliability of positioning even further [
20].
2.1.1. GPS
The GPS is maintained and financed by the US Department of Defense and currently consists of 31 operational satellites orbiting at an altitude of about 20,200 km [
21]. These satellites transmit signals primarily at two frequencies called L1 and L2. In the future, GPS satellites will also transmit a signal called L5. Two types of pseudorandom codes are modulated in GPS signal transmission onto the carrier signal: a civilian Coarse Acquisition (C/A) code is modulated to carrier L1 and this is used for coarse positioning, and Precise (P) code is modulated to carriers L1 and L2 for precision positioning. In addition, a navigation message is modulated to the signal containing information about the satellites’ orbits, clocks, and health status. Generally, only the C/A code is utilized in civilian receivers for obtaining the satellite-to-user distances and then the user location. Because the true difference between the satellite’s and receiver’s clocks is not known, the measured distance is called pseudorange. The C/A code enables the code’s pseudorange to be derived with an accuracy of about 3 m. When the phase of the carrier signal is used, the phase pseudorange can be determined with an accuracy of a millimeter, but then the number of full waves, the ambiguity, must be either resolved by using the code pseudorange or estimated. The loss of signal lock between a GPS satellite and the receiver is referred to as cycle slip, following which the ambiguity must be resolved. The use of a dual frequency receiver, utilizing both L1 and L2, allows the removal of the first-order effects of the ionosphere. [
22] The more precise P code is mostly intended for military purposes. A GPS receiver obtains and processes signals simultaneously from multiple satellites. When the satellite locations can be determined from the navigation message modulated to the signal, the different satellite-to-user distance measurements provide the means for calculating the user’s receiver’s position, velocity, and time [
20].
2.1.2. GLONASS
Following the recent years’ vigorous maintenance and reformation efforts, Russia’s satellite navigation system GLONASS is again fully operational. GLONASS differs from GPS especially as regards the scheme used for signal transmissions; each GLONASS satellite has its own transmission frequency and they orbit at an altitude of about 19,000 km. Currently, GLONASS has 24 operational satellites. GLONASS, like GPS, was originally designed for military purposes, but nowadays its applications have spread to uses such as land and sea traffic, and gradually to other consumer products. GLONASS continues to undergo modernization, and in the future GLONASS will also use code division technology in its signal transmissions like GPS (
i.e., all of the satellites will transmit on the same carrier frequency). New signals and codes are also being added to GLONASS in order to enable improved accuracy and interoperability with other systems [
20].
2.1.3. Emerging Systems: Galileo and BeiDou
The European satellite navigation system, Galileo, is intended for civilian use and it has been under development for almost a decade. Problems in financing, design, and interoperability (with, for example, the US GPS) have delayed the plans for and deployment of the new system. One of the foremost motives for developing Galileo has been the goal of making it independent from the military-operated systems. Dependency on the other systems is considered to adversely impact European security and to bring about too much insecurity for all of the applications and services currently depending on satellite-based navigation. Two test satellites have already been in orbital operation since 2005 and 2008, and in October 2011 two of the first in-orbit validation satellites were launched successfully to their planned orbits, and a year later two more were launched. The Galileo system will consist of a total of 30 satellites orbiting at an altitude of about 23,000 km [
23]. Galileo is expected to be fully operational around 2018–2020, and Galileo satellites will be transmitting signals on the same frequencies as GPS, but modulated using different code techniques [
20].
The Chinese satellite navigation system under development,
i.e., BeiDou (COMPASS) Navigation Satellite System, is somewhat similar in design to the US GPS. BeiDou will consist of 35 satellites, five of which will orbit in geostationary orbits. The geostationary part will transmit differential error corrections related to GNSS signals. BeiDou is estimated to be operational in 2020 at the latest [
20].
2.2. Positioning Accuracy and Augmentation Systems
The accuracy achievable using GNSS ranges from a few millimeters to tens of meters depending on the operating environment and receiver technology used (e.g., single- or dual-frequency use, code- or carrier-phase measurements, and static or kinematic receivers). Better positioning accuracy can be achieved using more complicated and thus more expensive technology. Millimeter accuracy can only be achieved in good, unobstructed signal conditions, such as those in open, outdoor areas, utilizing differential GNSS (DGNSS). The basic concept of DGNSS is the use of a minimum of two receivers, one at a known location and one at an unknown position, which can see common GNSS satellites. By fixing the location of one of the receivers, the other location can be found either by computing corrections to the position of the unknown receiver or by computing corrections to the pseudoranges. Satellite signals are generally noisy, especially in environments where signals are attenuated and reflected, which is also called multi-pathing, due to obstacles in the proximity, such as buildings or trees.
Augmentation of GNSS means improving the navigation system’s performance, such as accuracy, reliability, and availability, through the integration of external data into the positioning computation. Some systems transmit additional data on sources of error (such as clock drift, ephemeris, or ionospheric delay), others provide direct measurements of how much the signal is off, while a third group provides additional vehicle data for integration into the computation process.
A satellite-based augmentation system (SBAS) is a system that supports augmentation through the use of additional satellite-broadcast messages. Such systems are commonly composed of multiple ground stations, located at precisely-surveyed points. The ground stations take measurements of one or more of the GNSS satellites, the satellite signals, or other environmental factors, which may impact the signal received by the users. Using these observations, correction messages are created and sent to one or more satellites to be broadcast to the end users. SBAS is sometimes synonymous with WADGNSS, wide-area DGNSS. Examples of SBAS are the Wide Area Augmentation System (WAAS), operated by the United States Federal Aviation Administration (FAA) and the European Geostationary Navigation Overlay Service (EGNOS), operated by the European Satellite Services Provider (ESSP).
Ground-based augmentation systems (GBAS) and ground-based regional augmentation systems (GRAS) support augmentation through the use of messages transmitted by radio or mobile data networks. As with the satellite based augmentation systems detailed above, ground-based augmentation systems are commonly composed of one or more precisely-surveyed ground stations (references), which take measurements concerning the GNSS, and the data are transmitted directly to the end user (rover). The distance between the reference and the rover, i.e., baseline, has a major influence on the achievable accuracy. Examples of GBAS utilizing DGNSS are real-time kinematic (RTK) measurements, where correction messages are typically received from one reference station, and the virtual reference station (VRS) service, where a network of reference stations is used to compute a virtual reference for a location close to the rover.
The augmentation can also include additional information being blended into the position computation. Often the additional positioning instruments used operate using principles that complement GNSS positioning. These instruments provide independent and uncorrelated data that are not necessarily subject to the same sources of error or interference. The additional sensors may include sensors such as an IMU, an electronic compass and an odometer.
2.3. Post-Processing of GNSS Data
If raw satellite observations of the reference and the rover are stored, the position of the rover can be computed in post-processing using DGNSS. Another method is to use only the data logged at the rover and precise point processing (PPP). The PPP approach utilizes precise clocks and orbits, two of the most significant error sources of GNSS positioning. GPS satellite ephemerides, satellite and ground station clocks and GLONASS satellite ephemerides can be downloaded from International GNSS Service (IGS). These data are typically available after a couple of days (GPS) or two weeks (GLONASS) after the observation session [
24]. Post-processing often results in better positioning accuracy, but, as a real-time method, it is highly dependent on the satellite visibility, instrumentation,
etc. Data logged with additional sensors, such as an IMU and an odometer, can be used to improve the accuracy and reliability of the post-processed position solution.
2.4. GNSS in under Forest Canopies
There are many studies focusing on positioning under forest canopies using various GNSS devices and processing techniques, and the results show that a dense forest canopy can reduce the accuracy of the GNSS device. In these cases, the measurements were obtained during static sessions of varying length, and the positioning accuracy varied from a few centimeters to several meters, depending on the instrumentation, length of data observation period, and processing.
Næsset and Gjevestad [
25] studied the performance of a GPS PPP application under coniferous forest canopies. A 20-channel, dual-frequency GPS receiver collecting pseudorange and carrier phase observations was used as a stand-alone receiver to determine the positional accuracy of 19 points under coniferous forest canopies. The mean positional accuracy ranged from 0.27 to 0.88 m for an observation period of 120 min, and 0.95 to 3.48 m for 15 min. In the case of the 15 min observation period, the computed positions could not be found for 8 to 44 percent of the locations. The accuracy increased as the forest stand density decreased. The stand basal area and number of trees correlated significantly with the expected positioning accuracy.
The accuracies of recreational-grade and survey-grade GPS receivers were evaluated by Andersen
et al. [
26] across a range of forest conditions in the Tanana Valley of interior Alaska. High-accuracy check points were then used to evaluate the accuracy of positions acquired in stands representing different forest types using a recreational-grade GPS unit and a GLONASS-enabled survey-grade unit, over a range of acquisition and post-processing alternatives, including distance to base station, or baseline length (0–10, 10–50, 50–100, and >100 km), use of GLONASS satellites, and data observation periods (5, 10, and 20 min). The accuracy of the recreational-grade GPS was 3–7 m across all sites. As regards the survey-grade units, their accuracy was influenced by the forest type and baseline length, with smaller errors observed in more open stands and with shorter baseline lengths. The use of GLONASS satellites improved positioning accuracy by a small but appreciable amount, and longer observation periods (20 min) resulted in more reliable and accurate positions across all sites. In general, these results indicate that if forest inventory plots in interior Alaska and other high-latitude regions of the world were occupied for 20 min by survey-grade instruments, positioning accuracy below 1 m errors can be consistently obtained across a wide range of conditions.
Danskin
et al. [
27] confirmed that survey-grade receivers provide higher horizontal positioning accuracy than consumer-grade receivers, better horizontal positioning accuracy during leaf-off forest conditions (
i.e., winter), and that differential correction can improve horizontal positioning accuracy, and WAAS, when available, can improve horizontal positioning accuracy.
Even centimeter-level accuracy can be achieved using differential computation and static observations, but usually this requires open-sky conditions [
28,
29].
However, positioning while moving is a more complex problem as satellite visibility changes arbitrarily and the collecting of positional reference data is challenging. There are some studies addressing the positioning accuracy of a moving device evaluated under a forest canopy. Tachiki
et al. [
30] studied GPS-related positional errors produced when monitoring a mobile device under the forest canopy on two test sites: a deciduous forest stand and a coniferous forest stand with mean stand tree heights 8.4 and 8.9 m, and mean basal areas 41.1 and 38.4 m
3/ha, respectively. Two GPS receivers were used, one of navigation-grade and the other of survey-grade, both with and without real-time differential correction. The mean horizontal accuracy (STD) was about 4.1 m for the navigation-grade receiver and about 2.7 m for the survey-grade receiver. Differential correction did not improve the accuracy for either receiver. The researchers concluded that a higher stand density causes a larger positional error when the basal area is about the same. Ucar
et al. [
31] studied the dynamic accuracy of recreational-grade GPS receivers in an oak-hickory forest by measuring the area of the test plot (0.9 ha) defined by eight ground-based control points. They concluded that the average area agreement was 93% during the winter season (leaf-off), and 84% during the summer season (leaf-on). In the study by Liang
et al. [
32], the accuracy of estimation of the location of the tree stems when using a mobile laser scanning system setup in a backpack was 0.38 m. The main error source was in the positioning of the system. The study area was a homogenous mature pine forest and an IMU was used and post-processing was implemented.
Past studies have concentrated on the positioning accuracy of GNSS in forest environments and on techniques for improving GNSS accuracy. In 2001, Holden
et al. [
33] used skyward-looking photography in conjunction with GPS data in an attempt to develop a quantitative method of classifying forest canopies and of relating this classification to the degradation of carrier phase differential GPS (DGPS) performance. This technique led to a definite correlation between canopy obstruction and DGPS performance with the
R2 value increasing up to 0.74 when fitting a trend line to their findings. In 1999, Sigrist and Hermy [
34] found that with 300 GPS fixes, the Position Dilution of Precision (PDOP) is not as good an indicator of positional accuracy under a forest canopy as has been generally acclaimed. The study focused on the quantitative analysis of GPS accuracy under different forest canopy types and how PDOP affects positional accuracy as well as how foliage relates to signal blockage. The most significant conclusions presented in this paper were as follows: as canopy density increased, the signal attenuation increased; PDOP is not a good indicator of position precision; and the usability of skyward photography techniques as a measure of canopy closure. Bettinger and Merry [
35] also found moderate correlation between average positional error and some forest structure attributes in their study on the influence of the juxtaposition of trees on consumer-grade GPS positioning quality. In 1998, Axelrad and Behre [
36] demonstrated that NMEA (National Marine Electronics Association) messages in GPS receivers included individual SV (space vehicle, satellite) signal to noise ratios and are capable of showing significant signal attenuation based on the angle of the SV from the zenith. This particular research was measuring this signal attenuation from space-based platforms and so the attenuation was mainly attributed to the atmosphere. It is, therefore, rational to assume that the addition of forest canopy between the SV and antenna attenuates the signal further. The technique of signal-to-noise ratios from each SV can provide us with the data from each SV and the SV location relative to the antenna regarding the effect of forest canopy density and the effect of the signal propagation of as caused by the forest.
4. Results
The results for positioning accuracy under forest canopies are shown in
Table 7. As regards NVS and NovAtel, both the real-time autonomous single-point solution and the post-processed differential solution are given. As can be seen, the real-time accuracy of single-frequency devices is superior to that of geodetic dual-frequency device equipped with a less sensitive antenna-receiver combination optimized for differential solution under better satellite visibility. High-sensitivity receivers are able to track weaker signals, which results in a larger number of tracked satellites, but the signals are subject to interference and multipathing due to disturbance caused by forest canopies. Geodetic receivers are also subject to interference and multipathing, but the tracked signals are of better quality in terms of frequency spectrum and measurement noise thanks to the purpose-designed antenna and signal-processing techniques. High-sensitivity receivers are mostly used in navigators and smartphones, and geodetic receivers have been adopted by professionals for geodetic purposes. When post-processing is applied, the accuracy of NovAtel improves notably and is superior to real-time solutions. With IMU data also available, the accuracy was 0.7 m (reference trajectory). During the data acquisition along Trajectory 2, there were five visible satellites more than were available for Trajectory 1, and this probably partly explains the better accuracy obtained with the real-time systems.
Table 7.
The positioning accuracy under forest canopies.
Table 7.
The positioning accuracy under forest canopies.
| Device (No. of Observations Traj.1/Traj.2) | RMSE (m) | Combined |
|---|
| Traj.1 | Traj.2 |
|---|
| Garmin eTrex 30 (823/690) | 10.2 | 6.6 | 8.4 |
| u-blox MAX-M5Q (823/690) | 4.9 | 4.6 | 4.7 |
| NVS single point (642/N/A) | 6.2 | N/A | N/A |
| NVS post-proc. GPS only (660/N/A) | 6.7 | N/A | N/A |
| NovAtel single point (768/654) | 45.6 | 17.5 | 31.5 |
| NovAtel post-proc. (556/400) | 1.7 | 1.9 | 1.8 |
On analyzing accuracy under different forest conditions, it appeared that the accuracy of single-frequency GNSS devices is less dependent on forest conditions, whereas the performance of the tested geodetic dual-frequency receiver is very sensitive to satellite visibility (
Table 8). This can also be seen in the post-processed solution for NovAtel; the accuracy deteriorated with increasing basal area, mean height, and stem volume.
Table 8.
The positioning accuracy under different forest stand conditions and the resultant ANOVA values.
Table 8.
The positioning accuracy under different forest stand conditions and the resultant ANOVA values.
| Device | RMSE (m), Mean of Two Runs (No. of Observations) | ANOVA |
|---|
| Young Pine | Young Spruce | Mature Pine | Mature Spruce | F | p-Value |
|---|
| Garmin eTrex 30 | 9.3 (277) | 8.5 (249) | 8.2 (709) | 7.7 (278) | 20.0 | <0.001 |
| u-blox MAX-M5Q | 4.2 (277) | 4.8 (249) | 4.7 (709) | 4.6 (278) | 10.0 | <0.001 |
| NVS single point | 5.5 (123) | 6.8 (76) | 6.1 (336) | 6.8 (118) | 3.00 | 0.030 |
| NVS post-proc. GPS only | 5.9 (124) | 7.7 (84) | 6.6 (338) | 6.9 (114) | 2.85 | 0.036 |
| NovAtel single point | 7.6 (272) | 31.4 (229) | 27.2 (672) | 49.3 (249) | 4.01 | 0.007 |
| NovAtel post-proc. | 0.8 (249) | 1.3 (145) | 1.9 (524) | 2.7 (123) | 71.63 | <0.001 |
5. Discussion and Conclusions
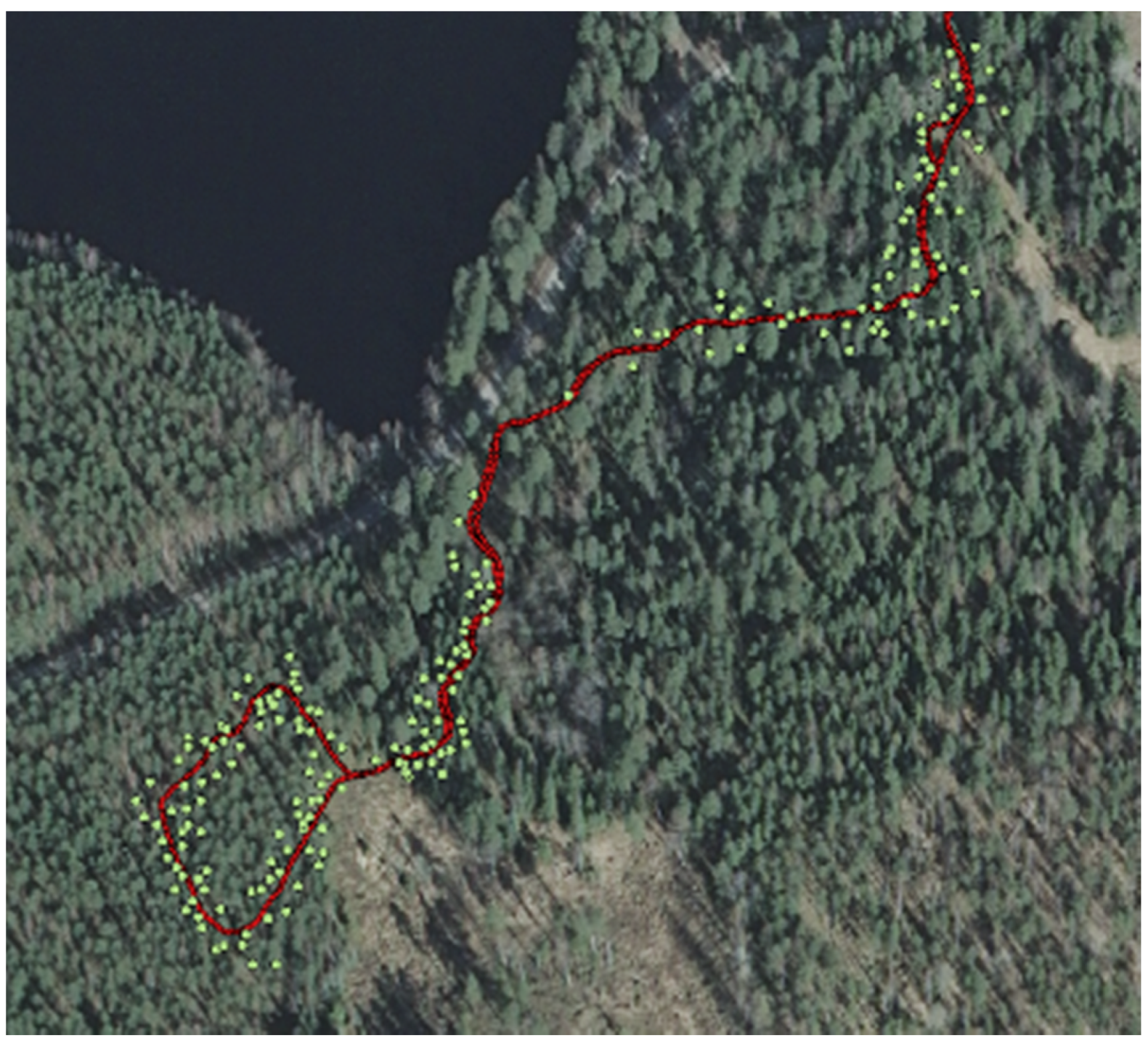
The aim of this study was to investigate the positioning accuracy of novel GNSS devices under forest canopies representing varying forest conditions. The study was carried out to simulate the accuracy that could be obtained when using a harvester. The acquisition of detailed and spatially accurate tree data is required in forest inventories based on remote sensing for ground-based truth, and a harvester in motion is one potential data source for such data [
4,
9,
15,
39,
40].
Based on the results, the required accuracy level of 1 m for tree matching cannot be achieved when using stand-alone GNSS devices, but when differential GNSS (real-time or post-processed) together with IMU data are applied, accuracy of even less than 1 m can be achieved, e.g., in this study this was 0.6–0.8 m. Thus, in theory, if high-precision GNSS + IMU units are mounted onto a harvester, then the collected stem data can be linked to remote-sensing data and further utilized in forest-inventory applications. However, the fusion of harvester data and remote-sensing data warrants further research. The present study addressed only the positional problem studied using an ATV instead of a harvester. In practice, unlike the ATV in this study, the harvester is not constantly on the move, and the satellite antenna is located higher above the ground [
41], and consequently improved accuracy in real-life scenario can be expected under similar forest conditions. On the other hand, satellite geometry is continually changing, and (even though the test data were collected at different times of the day) positioning accuracy may improve or deteriorate from what is reported here as “satellite conditions” change. The remote sensing part of the method has been studied by Holmgren
et al. [
16], who looked into the prediction of basic stand variables, such as stem volume, mean tree height, diameter, and stem density, and used manually taken measurements to match the logged trees with the ALS data since the harvesters cannot provide the needed positioning.
The RMSE of real-time 2D GNSS positioning for single-frequency receivers varied between 4 and 9 m in mature and thinning stands. This level of accuracy is not adequate to enable the accurate determination of the real-time position of a moving vehicle within the forest. However, the accuracy improves when the harvester remains stationary for longer periods. It seems that the accuracy of novel single-frequency GNSS devices is not so dependent on the forest conditions, whereas the performance of the tested geodetic dual-frequency receiver appears to be more sensitive to satellite visibility. In situations where post-processing and dual-frequency satellite data can be applied, accuracy of up to 2 m can be obtained for a slowly moving vehicle.