Timing of Drought Triggers Distinct Growth Responses in Holm Oak: Implications to Predict Warming-Induced Forest Defoliation and Growth Decline
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites and Species
2.2. Field Sampling
2.3. Climate Data
2.4. Primary Growth and Phenology
2.5. Remote Sensing Data: Vegetation Indices
2.6. Secondary Growth
2.7. Spanish Defoliation Data
2.8. Statistical Analyses
3. Results
3.1. Climate Trends and Long-Term Tree-Ring Responses to Droughts
3.2. Primary Growth Responses to Drought

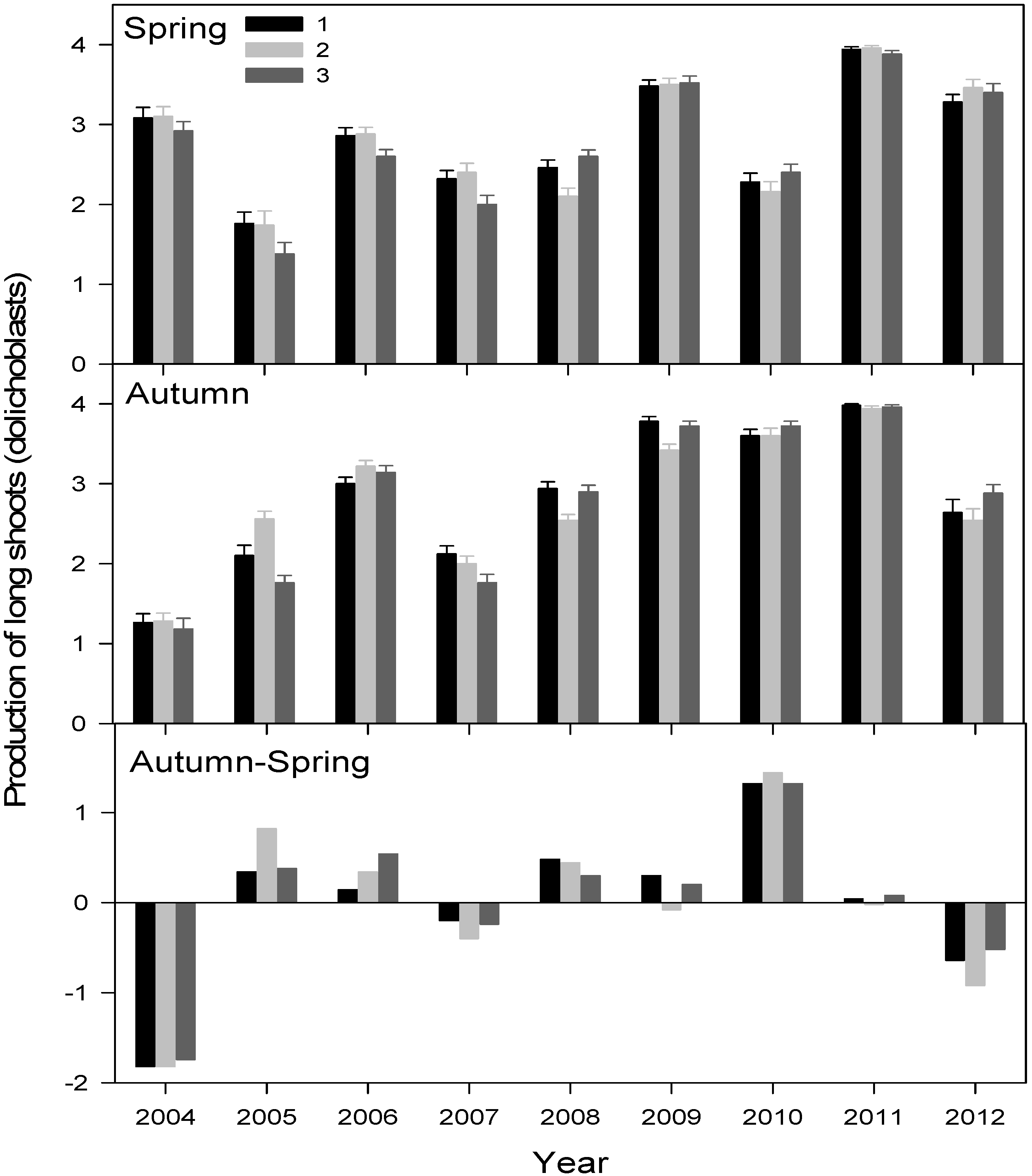
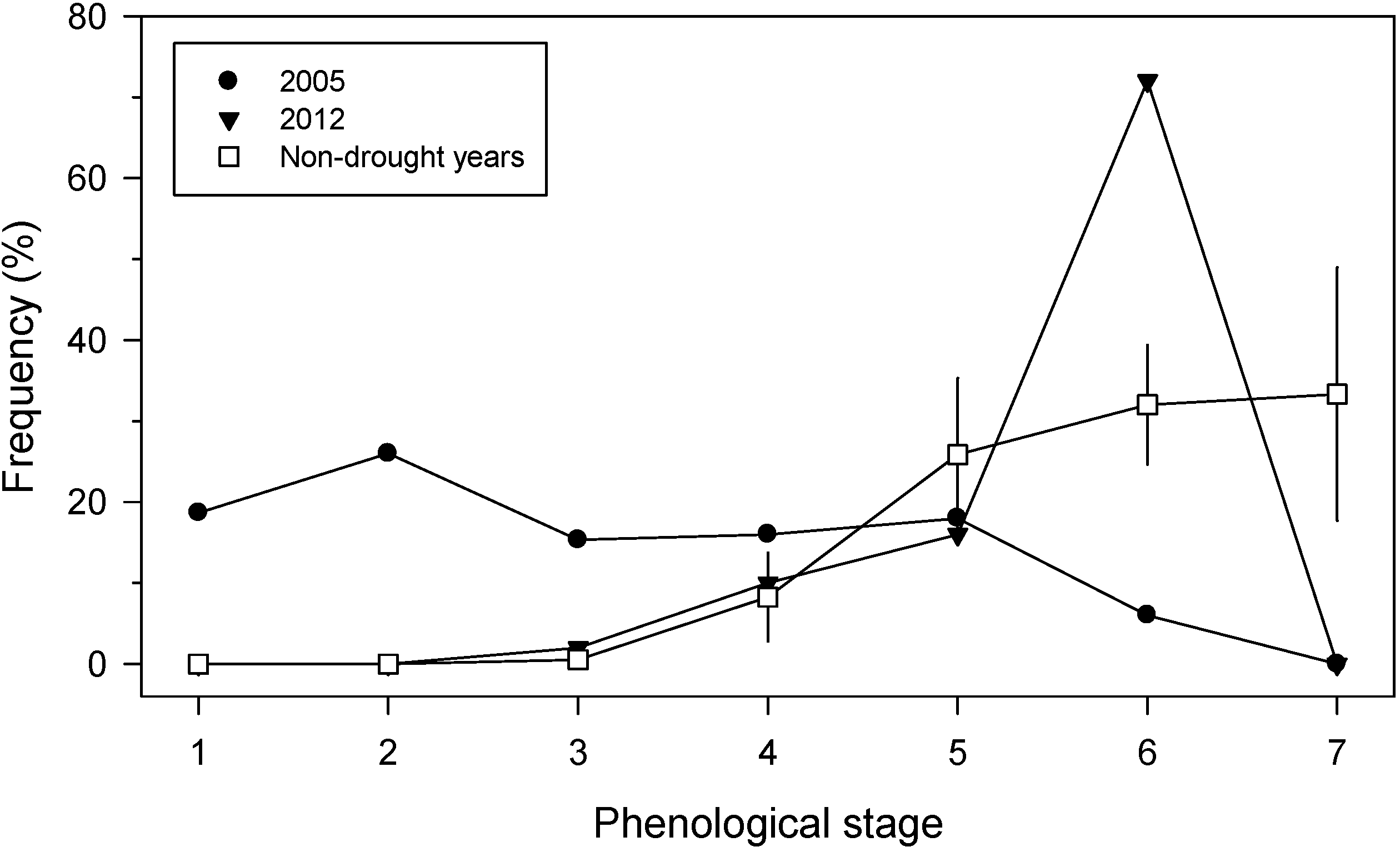
3.3. Canopy-Scale Responses
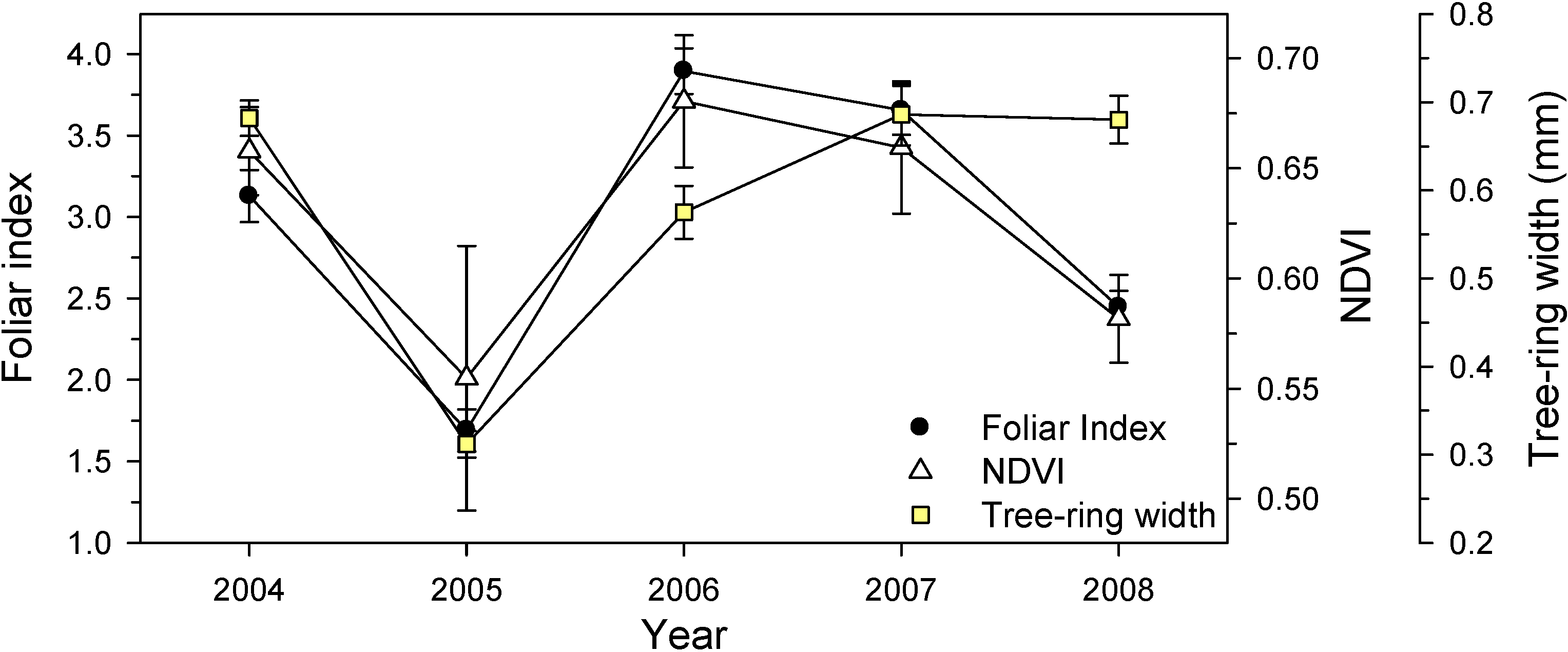
| Year | Sites | Foliar Index | Vegetation Indices | |
|---|---|---|---|---|
| NDII | NDVI | |||
| 2004 | 1–3 | 3.08 ± 0.15 | 0.254 | 0.658 |
| 2 | 3.18 ± 0.18 | 0.252 | 0.657 | |
| 2005 | 1–3 | 2.08 ± 0.11 | 0.121 | 0.570 |
| 2 | 1.83 ± 0.08 | 0.100 | 0.539 | |
| 2006 | 1–3 | 3.82 ± 0.12 | 0.313 | 0.690 |
| 2 | 3.95 ± 0.14 | 0.306 | 0.671 | |
| 2007 | 1–3 | 3.45 ± 0.16 | 0.270 | 0.674 |
| 2 | 3.86 ± 0.15 | 0.242 | 0.644 | |
| 2008 | 1–3 | 2.36 ± 0.08 | 0.254 | 0.584 |
| 2 | 2.53 ± 0.09 | 0.224 | 0.579 | |

3.4. Secondary Growth Responses to Climate and Drought
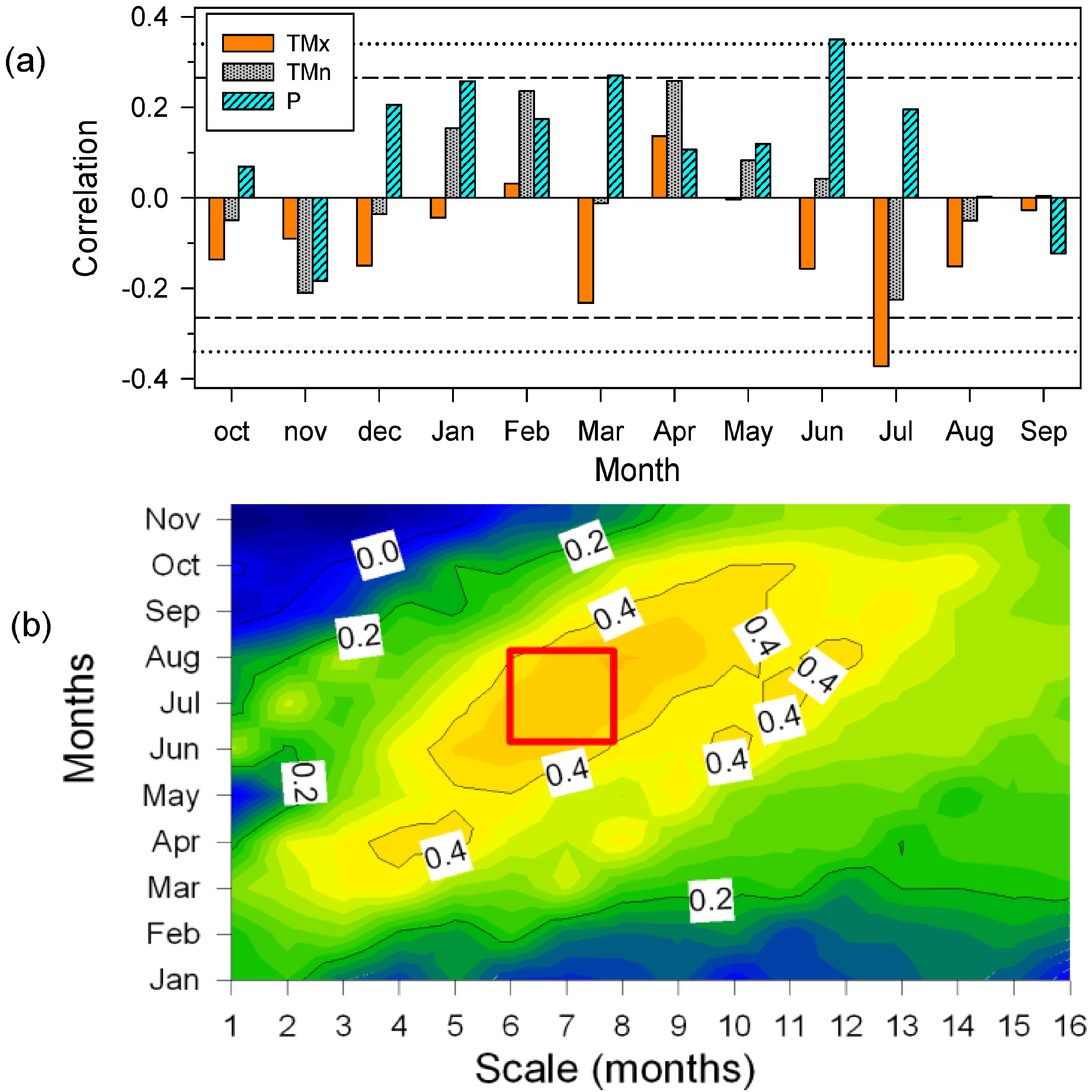
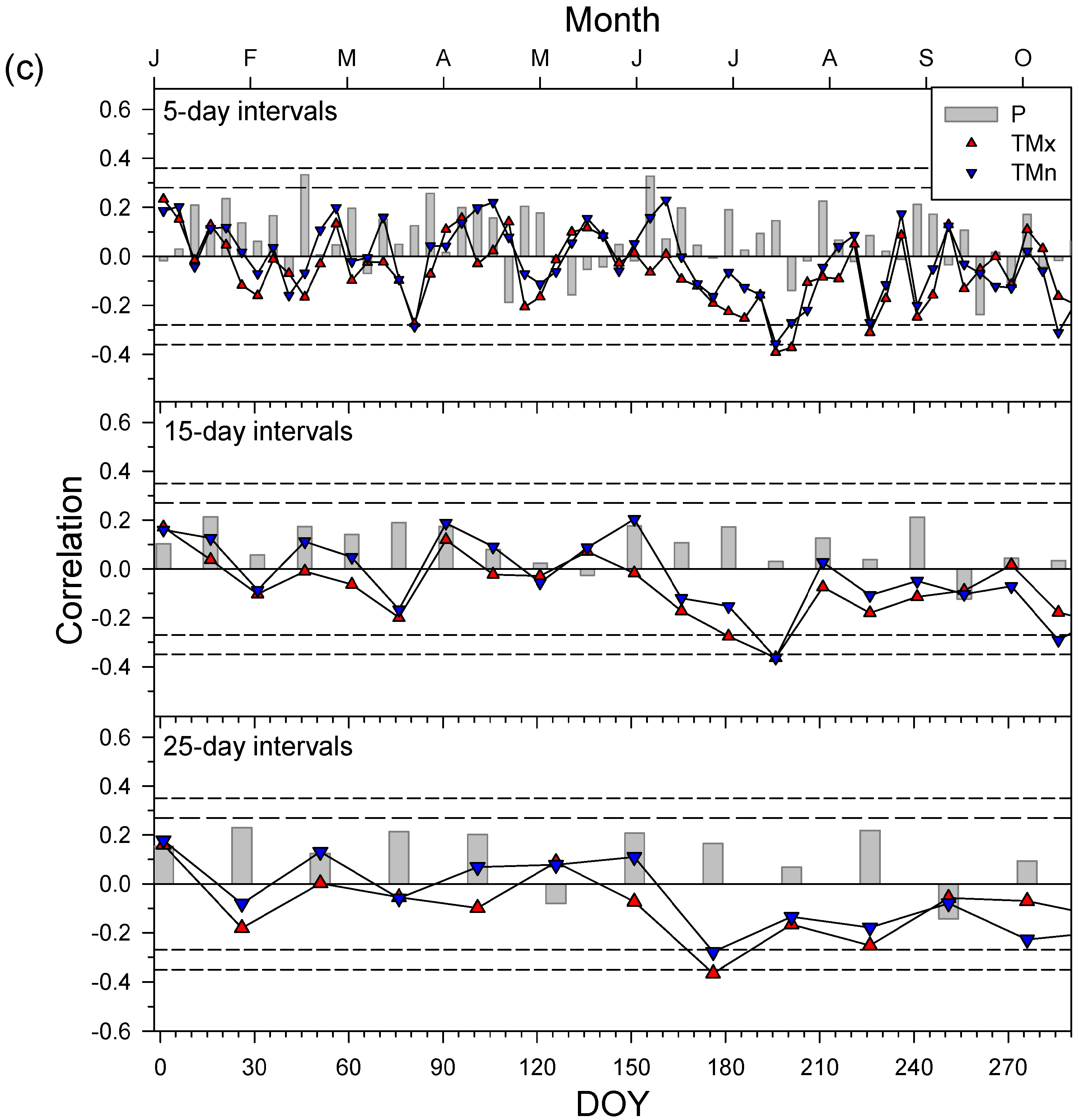
| Data | Statistics | ||||||
|---|---|---|---|---|---|---|---|
| Raw Data | Residual Chronology | ||||||
| No. trees (sites 1, 2, 3) | Mean interval | Age (years) | Tree-ring width (mm) | AC1 | MSx | Correlation between trees | EPS |
| 18 (8, 3, 7) | 1955–2014 | 59 ± 16 | 0.79 ± 0.46 | 0.43 | 0.47 | 0.24 | 0.74 |
3.5. Holm Oak Defoliation at National Level

4. Discussion
4.1. How Drought Reduces Primary Growth and Generates Asynchrony Depends on its Timing
4.2. Drought Diminishes Secondary Growth due to Water Shortage and Elevated Temperatures
4.3. Primary and Secondary Decline in Response to Drought but Show Different Resiliencies
4.4. Implications to Understand how Drought and Temperature Cause Defoliation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gutschick, V.P.; BassiriRad, H. Extreme events as shaping physiology, ecology, and evolution of plants: Toward a unified definition and evaluation of their consequences. New Phytol. 2003, 160, 21–42. [Google Scholar] [CrossRef]
- Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, A.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Chaves, M.M.; Oliveira, M.M. Mechanisms underlying plant resilience to water deficits: Prospects for water-saving agriculture. J. Exp. Bot. 2004, 55, 2365–2384. [Google Scholar] [CrossRef] [PubMed]
- Bréda, N.; Huc, R.; Granier, A.; Dreyer, E. Temperate forest trees and stands under severe drought: A review of ecophysiological responses, adaptation processes and long-term responses. Ann. For. Sci. 2006, 63, 625–644. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G.; et al. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Bigler, C.; Bräker, O.U.; Bugmann, H.; Dobbertin, M.; Rigling, A. Drought as an inciting mortality factor in Scots pine stands of the Valais, Switzerland. Ecosystems 2006, 9, 330–343. [Google Scholar] [CrossRef]
- De Boeck, H.J.; Dreesen, F.E.; Janssens, I.A.; Nijs, I. Climatic characteristics of heat waves and their simulation in plant experiments. Glob. Chang. Biol. 2010, 16, 1992–2000. [Google Scholar]
- Larcher, W. Physiological Plant Ecology, 4th ed.; Springer-Verlag: Berlin, Germany, 2003. [Google Scholar]
- McDowell, N.G.; Beerling, D.J.; Breshears, D.D.; Fisher, R.A.; Raffa, K.F.; Stitt, M. The interdependence of mechanisms underlying climate-driven vegetation mortality. Trends Ecol. Evol. 2011, 26, 523–532. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.P.; Allen, C.D.; Macalady, A.K.; Griffin, D.; Woodhouse, C.A.; Meko, D.M.; Swetnam, T.W.; Rauscher, S.A.; Seager, R.; Grissino-Mayer, H.D.; et al. Temperature as a potent driver of regional forest drought stress and tree mortality. Nat. Clim. Chang. 2012, 3, 292–297. [Google Scholar] [CrossRef]
- Anderegg, W.R.L.; Kanem, J.M.K.; Anderegg, L.D. Consequences of widespread tree mortality triggered by drought and temperature stress. Nat. Clim. Chang. 2013, 3, 30–36. [Google Scholar] [CrossRef]
- Ruffault, J.; Martin-St Paul, N.K.; Rambal, S.; Mouillot, F. Differential regional responses in drought length; intensity and timing to recent climate changes in a Mediterranean forested ecosystem. Clim. Chang. 2013, 117, 103–117. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S. Hot days induced by precipitation deficits at the global scale. Proc. Natl. Acad. Sci. USA 2012, 109, 12398–12403. [Google Scholar] [CrossRef] [PubMed]
- Montserrat-Martí, G.; Camarero, J.J.; Palacio, S.; Pérez-Rontomé, C.; Milla, R.; Albuixech, J.; Maestro, M. Summer-drought constrains the phenology and growth of two co-existing Mediterranean oaks with contrasting leaf habit: Implications for their persistence and reproduction. Trees: Struct. Funct. 2009, 23, 787–799. [Google Scholar] [CrossRef]
- Peñuelas, J.; Lloret, F.; Montoya, R. Severe drought effects on Mediterranean woody flora in Spain. For. Sci. 2001, 47, 214–218. [Google Scholar]
- Lloret, F.; Siscart, D.; Dalmases, C. Canopy recovery after drought dieback in holm-oak Mediterranean forests of Catalonia (NE Spain). Glob. Chang. Biol. 2004, 10, 2092–2099. [Google Scholar] [CrossRef]
- Ogaya, R.; Peñuelas, J. Tree growth, mortality, and above-ground biomass accumulation in a holm oak forest under a five-year experimental field drought. Plant Ecol. 2007, 189, 291–299. [Google Scholar] [CrossRef]
- Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Oliva, J.; Vicente-Serrano, S.M. To die or not to die: Early-warning signals of dieback in response to a severe drought. J. Ecol. 2005, 103, 44–57. [Google Scholar] [CrossRef]
- Anderegg, W.R.L.; Plavcová, L.; Anderegg, L.D.L.; Hacke, U.G.; Berry, J.A.; Field, C.B. Drought’s legacy: Multiyear hydraulic deterioration underlies widespread aspen forest die-off and portends increased future risk. Glob. Chang. Biol. 2013, 19, 1188–1196. [Google Scholar] [CrossRef] [PubMed]
- Carnicer, J.; Coll, M.; Ninyerola, M.; Pons, X.; Sánchez, G.; Peñuelas, J. Widespread crown condition decline, food web disruption, and amplified tree mortality with increased climate change-type drought. Proc. Natl. Acad. Sci. USA 2011, 108, 1474–1478. [Google Scholar] [CrossRef] [PubMed]
- Manzano Serrano, M.J.; Sánchez Peña, G.; San Pedro Santiado, D.; Torres Martínez, B. Vitalidad de Quercus ilex durante los últimos 26 años. Dinámica e identificación de áreas críticas desde el punto de vista sanitario. In Montes, Servicios y Desarrollo Rural, 6º Congreso Forestal Español; SECF: Vitoria, Spain, 2013; pp. 2–11. [Google Scholar]
- De la Cruz, A.C.; Gil, P.M.; Fernández-Cancio, A.; Minaya, M.; Navarro-Cerrillo, R.M.; Sánchez-Salguero, R.; Grau, J.M. Defoliation triggered by climate induced effects in Spanish ICP Forests monitoring plots. For. Ecol. Manag. 2014, 331, 245–255. [Google Scholar] [CrossRef]
- Peguero-Pina, J.J.; Sancho-Knapik, D.; Barrón, E.; Camarero, J.J.; Vilagrosa, A.; Gil-Pelegrín, E. Morphological and physiological divergences within Quercus ilex support the existence of different ecotypes depending on climatic dryness. Ann. Bot. 2014, 114, 301–313. [Google Scholar] [CrossRef] [PubMed]
- Camarero, J.J.; Albuixech, J.; López-Lozano, R.; Casterad, M.A.; Montserrat-Martí, G. An increase in canopy cover leads to masting in Quercus ilex. Trees: Struct. Funct. 2010, 24, 909–918. [Google Scholar] [CrossRef]
- Dobbertin, M. Tree growth as indicator of tree vitality and of tree reaction to environmental stress: A review. Eur. J. For. Res. 2005, 124, 319–333. [Google Scholar] [CrossRef]
- Schomaker, M.E.; Zarnoch, S.J.; Bechtold, W.A.; Latelle, D.J.; Burkman, W.G.; Cox, S.M. Crown-Condition Classification: A Guide to Data Collection and Analysis; General Technical Report; SRS-102; USDA, Forest Service, Southern Research Station: Asheville, NC, USA, 2007.
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Eng. 1982, 108, 225–230. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Camarero, J.J.; Azorín-Molina, C. Diverse responses of forest growth to drought time-scales in the Northern Hemisphere. Glob. Ecol. Biogeogr. 2014, 23, 1019–1030. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Alla, A.Q.; Camarero, J.J.; Palacio, S.; Montserrat-Martí, G. Revisiting the fate of buds: Size and position drive bud mortality and bursting in two coexisting Mediterranean Quercus species with contrasting leaf habit. Trees: Struct. Funct. 2013, 27, 1375–1386. [Google Scholar] [CrossRef]
- Masek, J.G.; Vermote, E.F.; Saleous, N.; Wolfe, R.; Hall, F.G.; Huemmrich, F.; Gao, F.; Kutler, J.; Lim, T.K. LEDAPS Landsat Calibration, Reflectance, Atmospheric Correction Preprocessing Code; Oak Ridge National Laboratory Distributed Active Archive Center: Oak Ridge, TN, USA, 2012.
- Bannari, A.; Morin, D.; Bonn, F.; Huete, A.R. A review of vegetation indices. Remote Sens. Rev. 1995, 13, 95–120. [Google Scholar] [CrossRef]
- Tucker, C.J.; Vanpraet, C.L.; Sharman, M.J.; Vanittersum, G. Satellite remote-sensing of total herbaceous biomass production in the Senegalese Sahel—1980–1984. Remote Sens. Environ. 1985, 17, 233–249. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Klemas, V.; Smart, R.M. The influences of soil salinity, growth form, and leaf moisture on the spectral reflectance of Spartina alterniflora canopies. Photogramm. Eng. Remote Sens. 1983, 49, 77–83. [Google Scholar]
- Fritts, H.C. Tree Rings and Climate, 2nd ed.; Blackburn Press: Caldwell, NJ, USA, 2001. [Google Scholar]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Cook, E.R. A Time Series Analysis Approach to Tree-Ring Standardization. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 5 August 1985. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Appl. Meteorol. Climatol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Cook, E.; Kairiukstis, L. Methods of Dendrochronology: Applications in the Environmental Sciences, 1st ed.; Kluwer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Gutiérrez, E.; Campelo, F.; Camarero, J.J.; Ribas, M.; Muntán, E.; Nabais, C.; Freitas, H. Climate controls act at different scales on the seasonal pattern of Quercus ilex L. stem radial increments in NE Spain. Trees: Struct. Funct. 2011, 25, 637–646. [Google Scholar] [CrossRef]
- International Cooperative Programme on Assessment and Monitoring of Air Pollution Effects on Forests (ICP). Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests Part IV: Visual Assessment of Crown Condition and Damaging Agents; UNECE, ICP Forests: Hamburg, Germany, 2010. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Misson, L.; Degueldre, D.; Collin, C.; Rodriguez, R.; Rocheteau, A.; Ourcival, J.M.; Rambal, S. Phenological responses to extreme droughts in a Mediterranean forest. Glob. Chang. Biol. 2011, 17, 1036–1048. [Google Scholar] [CrossRef]
- Meier, A.R.; Saunders, M.R.; Michler, C.H. Epicormic buds in trees: A review of bud establishment, development and dormancy release. Tree Physiol. 2012, 32, 565–584. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N. Mechanisms linking drought, hydraulics, carbon metabolism, and vegetation mortality. Plant Physiol. 2011, 155, 1051–1059. [Google Scholar] [CrossRef] [PubMed]
- Corcuera, L.; Camarero, J.J.; Gil-Pelegrín, E. Effects of a severe drought on Quercus ilex radial growth and xylem anatomy. Trees: Struct. Funct. 2004, 18, 83–92. [Google Scholar] [CrossRef]
- Colin, F.; Sanjines, A.; Fortin, M.; Bontemps, J.-D.; Nicolini, E. Fagus sylvatica trunk epicormics in relation to primary and secondary growth. Ann. Bot. 2012, 110, 995–1005. [Google Scholar] [CrossRef] [PubMed]
- Ogaya, R.; Barbeta, A.; Başnou, C.; Peñuelas, J. Satellite data as indicators of tree biomass growth and forest dieback in a Mediterranean holm oak forest. Ann. For. Sci. 2015, 72, 135–144. [Google Scholar] [CrossRef]
- Gratani, L.; Bombelli, A. Correlation between leaf age and other leaf traits in three Mediterranean maquis shrub species: Quercus ilex, Phillyrea latifolia and Cistus incanus. Environ. Exp. Bot. 2000, 43, 141–153. [Google Scholar] [CrossRef]
- Bussotti, F.; Bettini, D.; Grossoni, P.; Mansuino, S.; Nibbi, R.; Soda, C.; Tani, C. Structural and functional traits of Quercus ilex in response to water availability. Environ. Exp. Bot. 2002, 47, 11–23. [Google Scholar] [CrossRef]
- Ogaya, R.; Peñuelas, J. Phenological patterns of Quercus ilex, Phyllirea latifolia, and Arbutus unedo growing under a field experimental drought. Écoscience 2004, 11, 263–270. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camarero, J.J.; Franquesa, M.; Sangüesa-Barreda, G. Timing of Drought Triggers Distinct Growth Responses in Holm Oak: Implications to Predict Warming-Induced Forest Defoliation and Growth Decline. Forests 2015, 6, 1576-1597. https://doi.org/10.3390/f6051576
Camarero JJ, Franquesa M, Sangüesa-Barreda G. Timing of Drought Triggers Distinct Growth Responses in Holm Oak: Implications to Predict Warming-Induced Forest Defoliation and Growth Decline. Forests. 2015; 6(5):1576-1597. https://doi.org/10.3390/f6051576
Chicago/Turabian StyleCamarero, J. Julio, Magí Franquesa, and Gabriel Sangüesa-Barreda. 2015. "Timing of Drought Triggers Distinct Growth Responses in Holm Oak: Implications to Predict Warming-Induced Forest Defoliation and Growth Decline" Forests 6, no. 5: 1576-1597. https://doi.org/10.3390/f6051576
APA StyleCamarero, J. J., Franquesa, M., & Sangüesa-Barreda, G. (2015). Timing of Drought Triggers Distinct Growth Responses in Holm Oak: Implications to Predict Warming-Induced Forest Defoliation and Growth Decline. Forests, 6(5), 1576-1597. https://doi.org/10.3390/f6051576







