Estimating Values of Carbon Sequestration and Nutrient Recycling in Forests: An Application to the Stockholm-Mälar Region in Sweden
Abstract
:1. Introduction
2. Conceptual Framework and Cost-Minimizing Model
2.1. Conceptual Framework of the Replacement Cost Method
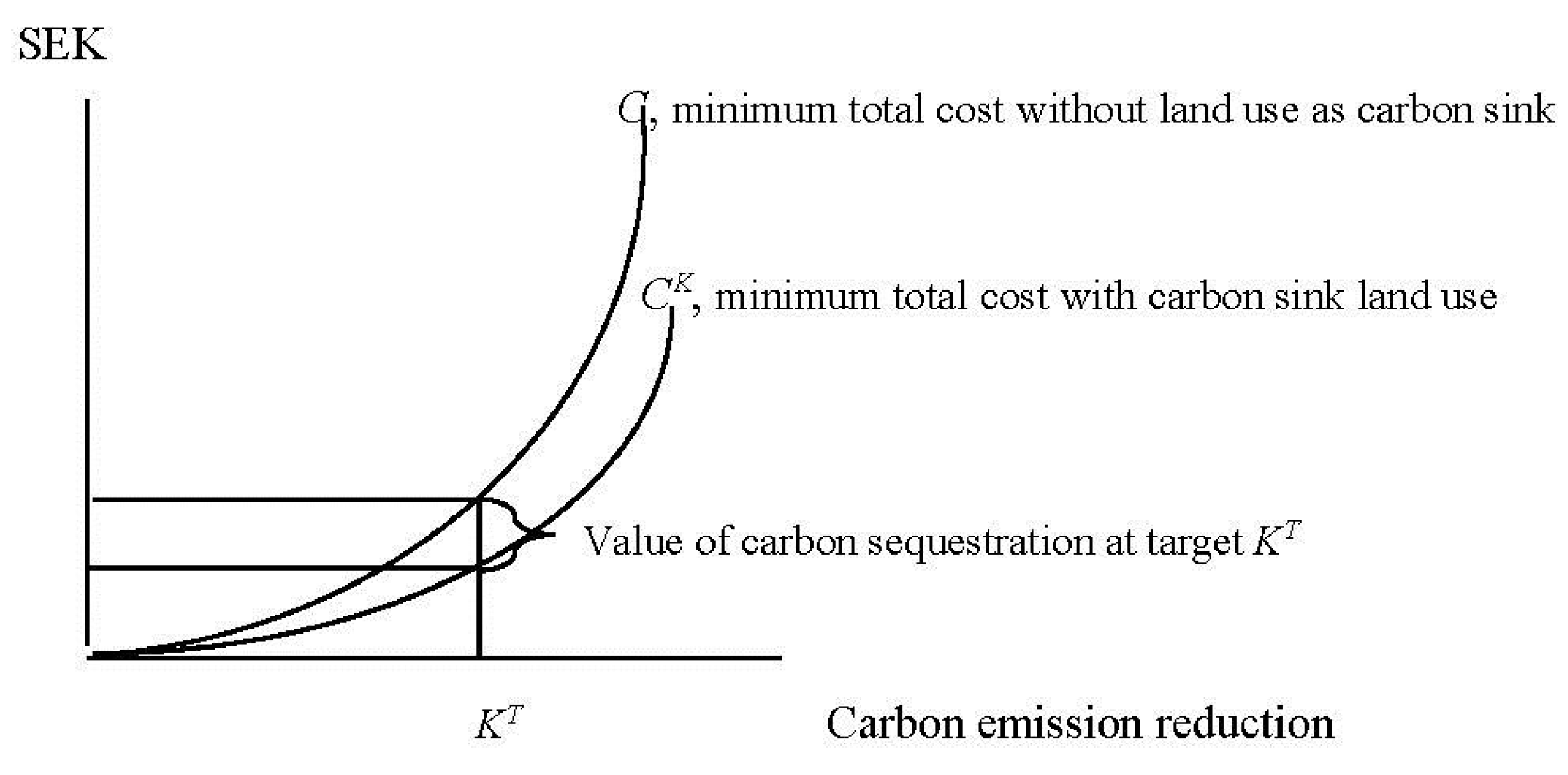
2.2. Description of the Dynamic Cost Minimizing Model
2.3. Determinants of the Value of Carbon and Nutrient Sink in Forests
- -
- the cost of forest plantations is relatively low
- -
- the weighted marginal impact of forest on carbon and nutrient sequestration is high
- -
- the annual growth in sink capacity and depreciation of investment in other technologies are large
- -
- the uncertainty discount of the pollutant sink is low
- -
- the management of all targets occurs simultaneously instead of separately
3. Data Retrieval
3.1. Carbon Emission and Nutrient Leaching
| N, ton a | P, ton a | CO2e Emission , kton b | CO2e Sequestration kton b | |
|---|---|---|---|---|
| Forest land | 773 | 19 | 3531 | |
| Arable land | 1825 | 156 | 840 | |
| Sewage treatment plants | 5613 | 94 | ||
| Transport | 82 | 5451 | ||
| Industry | 23 | 1527 | ||
| Energy production | 70 | 4688 | ||
| Other CO2e sources | 1677 | |||
| Total | 8386 | 269 | 14183 | 3531 |
| Targets c,d | 6457 | 105 | 3438 |
3.2. Abatement Measures and Costs
3.3. Uncertainty, Targets, and Discount Rate
4. Results: Value of the Forest for Provision of Carbon and Nutrient Sequestration
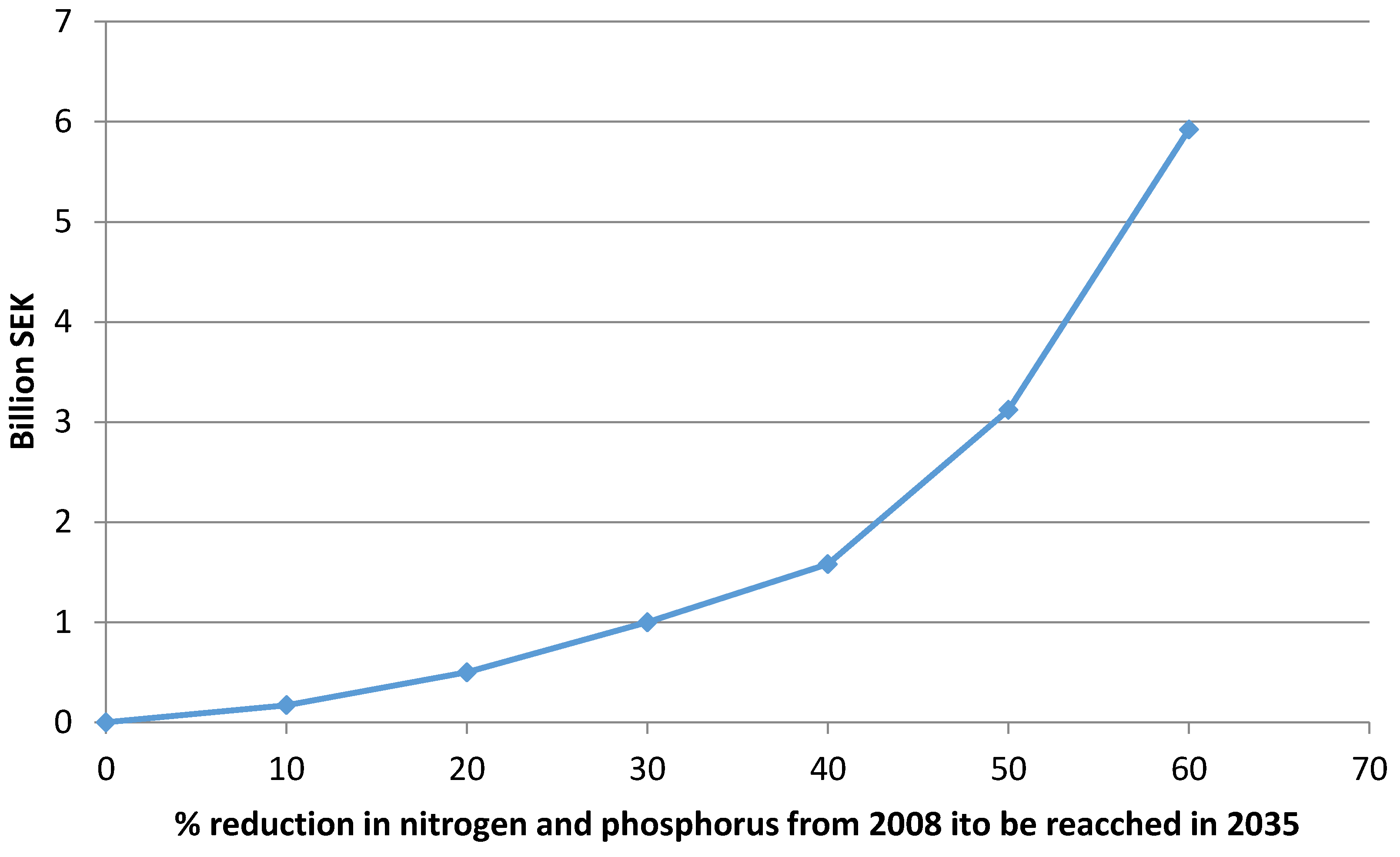
4.1. Value of Pollutant Sink at Different Emission Targets

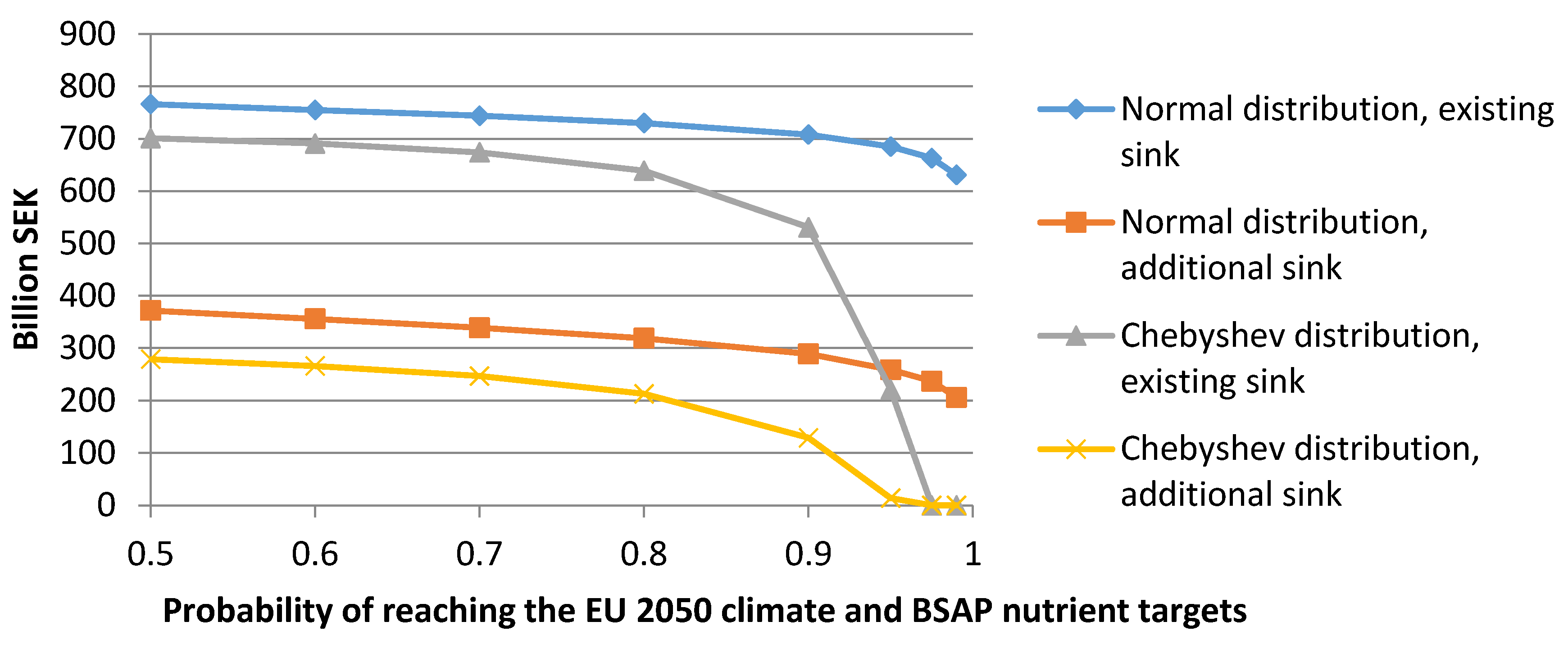
4.2. Uncertainty in Forest Pollutant Sink
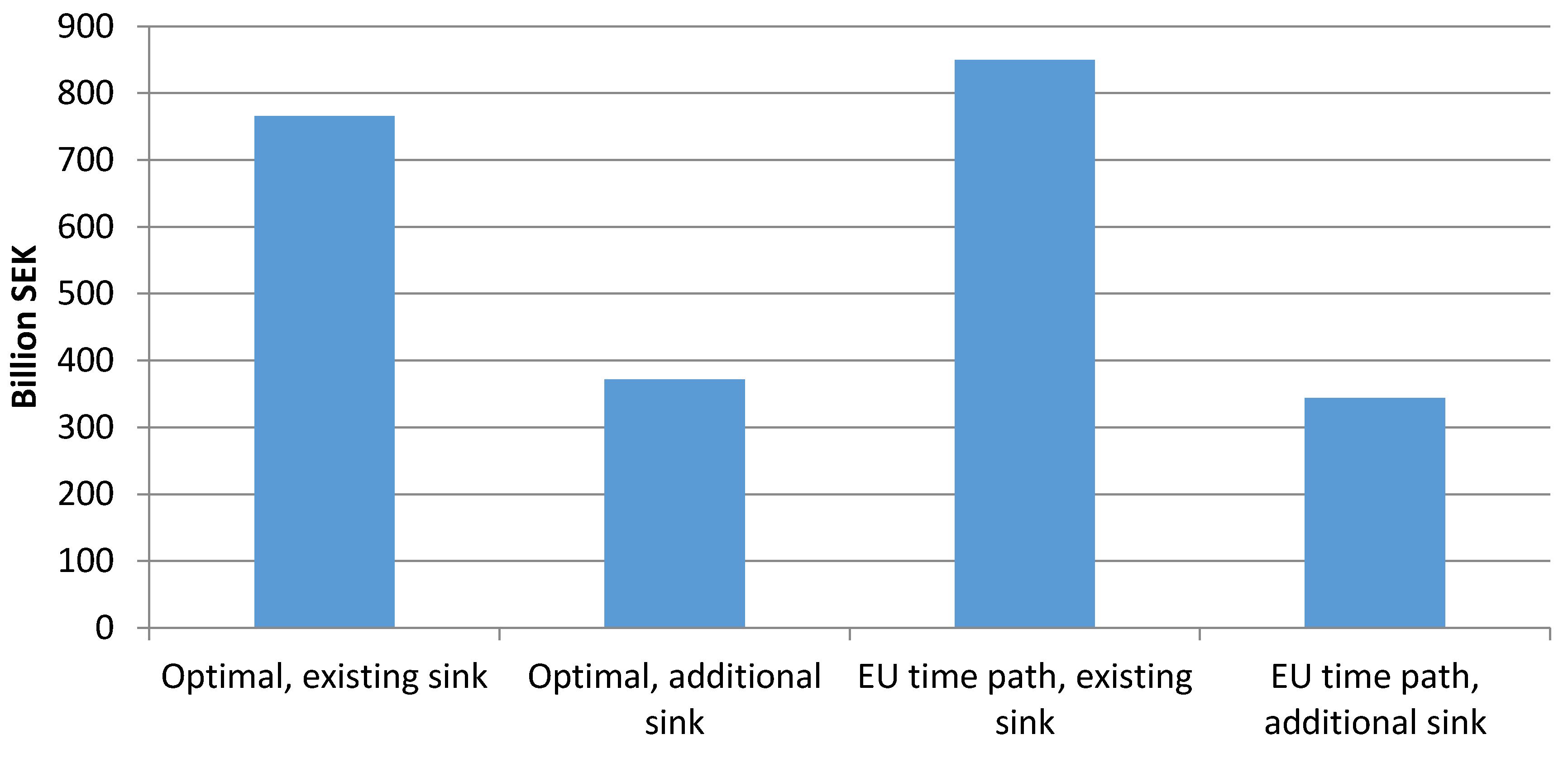
5. Discussion
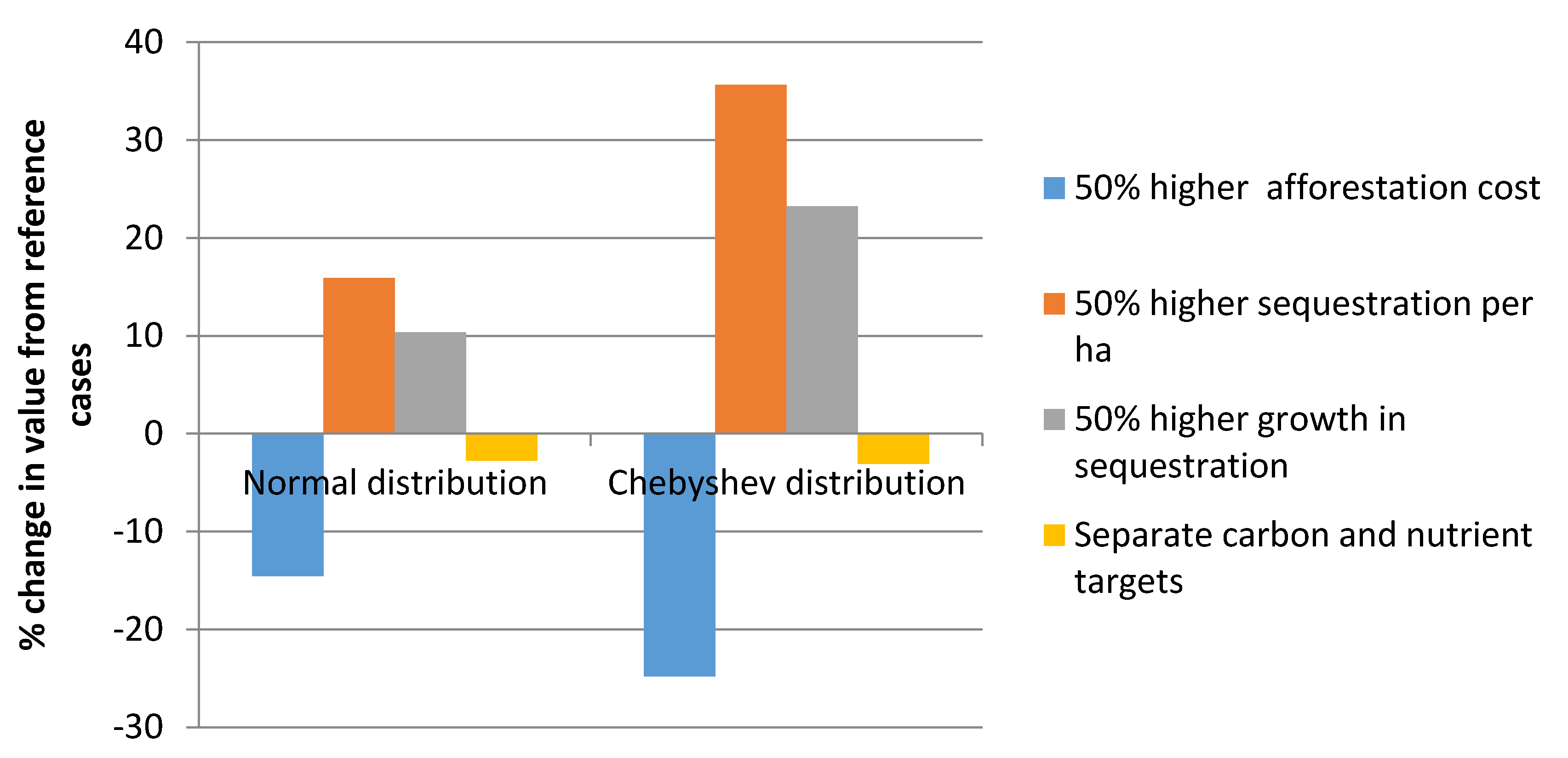
6. Conclusions
| Factor | Increased Calculated Value of Carbon and Nutrient Sinks | Decreased Calculated Value of Carbon and Nutrients |
|---|---|---|
| Uncertainty in all abatement measures and not only carbon sink | × | |
| Inclusion of more forest management option | × | |
| Inclusion of measures reducing uncertainty in the carbon sink | × | |
| Policy implementation of carbon and nutrient sink | × | |
| Consideration of more non-marketed ecosystem services | × | × |
Conflicts of Interest
Acknowledgements
References
- Pearce, D. The economic value of forest ecosystems. Ecosyst. Health 2001, 7, 284–296. [Google Scholar] [CrossRef]
- Lubowski, R.; Plantinga, A.; Stavins, R. Land-use change and carbon sinks: Econometric estimation of the carbon sequestration supply function. J. Environ. Econ. Manag. 2006, 51, 135–152. [Google Scholar] [CrossRef]
- Michetti, M.; Rosa, R.N. Afforestation and Timber Management Compliance Strategies in Climate Policy. A Computable General Equilibrium Analysis. FEEM Working Paper No. 4. 2011. Available online: http://www.feem.it/userfiles/attach/2011118158514NDL2011-004.pdf (accessed on 14 July 2015).
- Gren, I.-M.; Carlsson, M. Economic value of carbon sequestration in forests under multiple sources of uncertainty. J. For. Econ. 2013, 19, 174–189. [Google Scholar] [CrossRef]
- Aklilu, A.; Gren, I.-M. Economic Incentives for Carbon Sequestration: A Review of the Literature. Working Paper 2014: 08; Department of Economics, Swedish University of Agricultural Sciences: Uppsala, Sweden, 2014; Available online: https://ideas.repec.org/p/hhs/slueko/2014_008.html (accessed on 14 July 2015).
- Gilbert, P.M. Eutrophication and harmful algal blooms: A complex global issue, examples from the Arabian Seas and including Kuwait Bay and an introduction to the global ecology and oceanography of harmful algal blooms (GEOHAB) Programme. Int. J. Oceans Oceanogr. 2007, 2, 157–169. [Google Scholar]
- Heisler, J.; Glibert, P.M.; Burkholder, J.M.; Anderson, D.M.; Cochlan, W.; Dennison, W.C.; Dortch, Q.; Goble, C.J.; Heil, C.A.; Humphries, E.; et al. Eutrophication and harmful algal blooms: A scientific consensus. Harmful Algae 2008, 8, 3–13. [Google Scholar] [CrossRef]
- Boberg, J.; Finley, R.; Stenlid, J.; Ekblad, A.; Lindahl, B. Nitrogen and carbon reallocation in fungal mycelia during decomposition of boreal forest litter. PLoS ONE 2014, 9, e92897. [Google Scholar] [CrossRef] [PubMed]
- Gren, I.-M. Climate change and the Water Framework Directive: Cost effectiveness and policy design for water management in the Swedish Stockholm-Mälar region. Clim. Chang. 2010, 100, 463–484. [Google Scholar] [CrossRef]
- Gren, I.-M.; Marbuah, G.; Tafesse, W. Cost-Effective Land Use Dynamics towards a Low Carbon Economy in the Stockholm-Mälar Region; Report for COMPLEX: Newcastle, UK, September 2015; Available online: http://owsgip.itc.utwente.nl/projects/complex/complex_files/D4.2%20land%20use%20simulation%20with%20report.pdf (accessed on 14 July 2015).
- Gosselink, J.G.; Odum, E.P.; Pope, R.M. The Value of the Tidal Marsh. Center for Wetland Resources; Louisiana State University: Baton Rouge, LA, USA, 1972. [Google Scholar]
- Breux, A.; Farber, S.; Day, J. Using natural coastal wetland systems for waste water treatment: An economic benefit analysis. J. Environ. Manag. 1995, 44, 285–291. [Google Scholar] [CrossRef]
- Byström, O. The replacement value of wetlands in Sweden. Environ. Resour. Econ. 2000, 16, 347–362. [Google Scholar] [CrossRef]
- Gren, I.-M. The economic value of coastal waters as nutrient filters for the Baltic Sea. Reg. Environ. Chang. 2013, 13, 695–703. [Google Scholar] [CrossRef]
- Tavoni, M.B.; Sohngen, B. Forestry and the carbon market response to stabilise climate. Energy Policy 2007, 35, 5346–5353. [Google Scholar] [CrossRef]
- Anger, N.; Sathaye, J. Reducing Deforestation and Trading Emissions: Economic Implications for the Post-Kyoto Carbon Market. ZEW-Centre for European Economic Research Discussion Paper (08–016). 2008. Available online: http://ftp.zew.de/pub/zew-docs/dp/dp08016.pdf (accessed on 14 July 2015).
- Byström, O.; Andersson, H.; Gren, I.-M. Economic criteria for restoration of wetlands under uncertainty. Ecol. Econ. 2000, 35, 35–45. [Google Scholar] [CrossRef]
- Kurkalova, L. Carbon sequestration in agricultural soils: Discounting for uncertainty. Can. J. Agric. Econ. 2005, 53, 375–384. [Google Scholar] [CrossRef]
- Kim, M.; McCarl, B. Uncertainty discounting for land based carbon sequestration. J. Agric. Appl. Econ. 2009, 41, 1–11. [Google Scholar]
- Tesler, L.G. Safety-first and hedging. Rev. Econ. Stud. 1955, 23, 1–16. [Google Scholar]
- Gren, I.-M.; Carlsson, M.; Munnich, M.; Elofsson, K. The role of stochastic carbon sink for the EU emission trading system. Energy Econ. 2012, 34, 1523–1531. [Google Scholar] [CrossRef]
- Taha, H.A. Operations Research, an Introduction, 2nd ed.; Macmillan Publishing, Inc.: New York, NY, USA, 1976. [Google Scholar]
- European Commission. Climate Action. Roadmap for Moving to a Low-Carbon Economy in 2050. Available online: http://ec.europa.eu/clima/policies/strategies/2050/faq_en.htm (accessed on 1 October 2015).
- Helcom HELCOM Baltic Sea Action Plan. Nutrient Reduction Scheme. Available online: http://www.helcom.fi/baltic-sea-action-plan/nutrient-reduction-scheme/ (accessed on 7 January 2014).
- SEPA (Swedish Environmental Protection Agency) 2014. Utsläpp av Växthusgaser Från Markanvändning. Available online: http://www.naturvardsverket.se/sa-mar-miljon/statistik.A-O/vaxthusgaser-utslapp-och-upptag-fran-markanvändning/ (accessed on 24 February 2014).
- Munnich Vass, M. Can Renewable Energies with Learning-by-Doing Compete with Forest Sequestration to Cost-Effectively Meet the EU Carbon Target for 2050? Working Paper 2015:04; Department of Economics, SLU: Uppsala, Sweden, 2015; Available online: http://pub.epsilon.slu.se/11905/ (accessed on 14 July 2015).
- Janssens, L.; Freibauer, A.; Schlamadinger, B.; Ceulemans, R.; Ciais, P.; Dolman, A.; Heimann, M.; Nabuurs, G.-J.; Smith, P.; Valentini, R.; et al. The carbon budget of terrestrial ecosystems at country-scale a European case study. Biogeosciences 2005, 2, 15–26. [Google Scholar] [CrossRef]
- McCarl, B.A.; Spreen, T.H. Applied Mathematical Programming Using Algebraic Systems; Texas A&M University: Austin, TX, USA, 2010; pp. 14.1–14.18. Available online: ftp://178.213.241.34/pub/Library/BOOKS/heap/SCI%20BOOKS/books2/_djvu/M_Mathematics/MOc_Optimization%20and%20control/McCarl%20B.A.,%20Spreen%20T.H.%20Applied%20mathematical%20programming%20using%20algebraic%20systems%28567s%29.pdf (accessed on 3 January 2015).
- McSweeny, W.T.; Shortle, J.S. Probabilistic cost effectiveness in agricultural nonpoint pollution control. Southern J. Agric. Econ. 1990, 22, 95–104. [Google Scholar]
- Shortle, J. The allocative efficiency implications of water pollution abatement cost comparisons. Water Resour. Res. 1990, 26, 793–797. [Google Scholar] [CrossRef]
- Weitzman, M. Gamma Discounting. Am. Econ. Rev. 2001, 91, 260–271. [Google Scholar] [CrossRef]
- Newell, R.; Pizer, W. Discounting the distant future. How much do uncertainty increase valuations? J. Environ. Econ. Manag. 2003, 46, 52–71. [Google Scholar] [CrossRef]
- Rosenthal, R. GAMS—A User’s Guide; GAMS Development Corporation: Washington, DC, USA, 2008. [Google Scholar]
- Capros, P.; Paroussos, L.; Fragkos, P.; Tsani, S.; Boitier, B.; Wagner, F.; Busch, S.; Resch, G.; Blesl, M.; Bollen, J. European decarbonisation pathways under alternative technological and policy choices: A multi-model analysis. Energy Strategy Rev. 2013, 2, 231–245. [Google Scholar] [CrossRef]
- Gren, I.-M.; Savchuck, O.; Jansson, T. Cost effective spatial and dynamic management of a eutrophied Baltic Sea. Mar. Resour. Econ. 2013, 28, 263–284. [Google Scholar] [CrossRef]
- Average Assessed Value of Standing Forest and Forest Land by Ownership Class and County, Year 2011. Available online: http://www.skogsstyrelsen.se/Myndigheten/Statistik/Amnesomraden/Ekonomi/Tabeller--figurer/ (accessed on 13 July 2105).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gren, I.-M. Estimating Values of Carbon Sequestration and Nutrient Recycling in Forests: An Application to the Stockholm-Mälar Region in Sweden. Forests 2015, 6, 3594-3613. https://doi.org/10.3390/f6103594
Gren I-M. Estimating Values of Carbon Sequestration and Nutrient Recycling in Forests: An Application to the Stockholm-Mälar Region in Sweden. Forests. 2015; 6(10):3594-3613. https://doi.org/10.3390/f6103594
Chicago/Turabian StyleGren, Ing-Marie. 2015. "Estimating Values of Carbon Sequestration and Nutrient Recycling in Forests: An Application to the Stockholm-Mälar Region in Sweden" Forests 6, no. 10: 3594-3613. https://doi.org/10.3390/f6103594
APA StyleGren, I.-M. (2015). Estimating Values of Carbon Sequestration and Nutrient Recycling in Forests: An Application to the Stockholm-Mälar Region in Sweden. Forests, 6(10), 3594-3613. https://doi.org/10.3390/f6103594





