Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models
Abstract
:1. Introduction
1.1. Context and Problem
1.2. Background of Heuristic Search Methods
2. Materials and Methods
2.1. Materials
2.1.1. Study Area
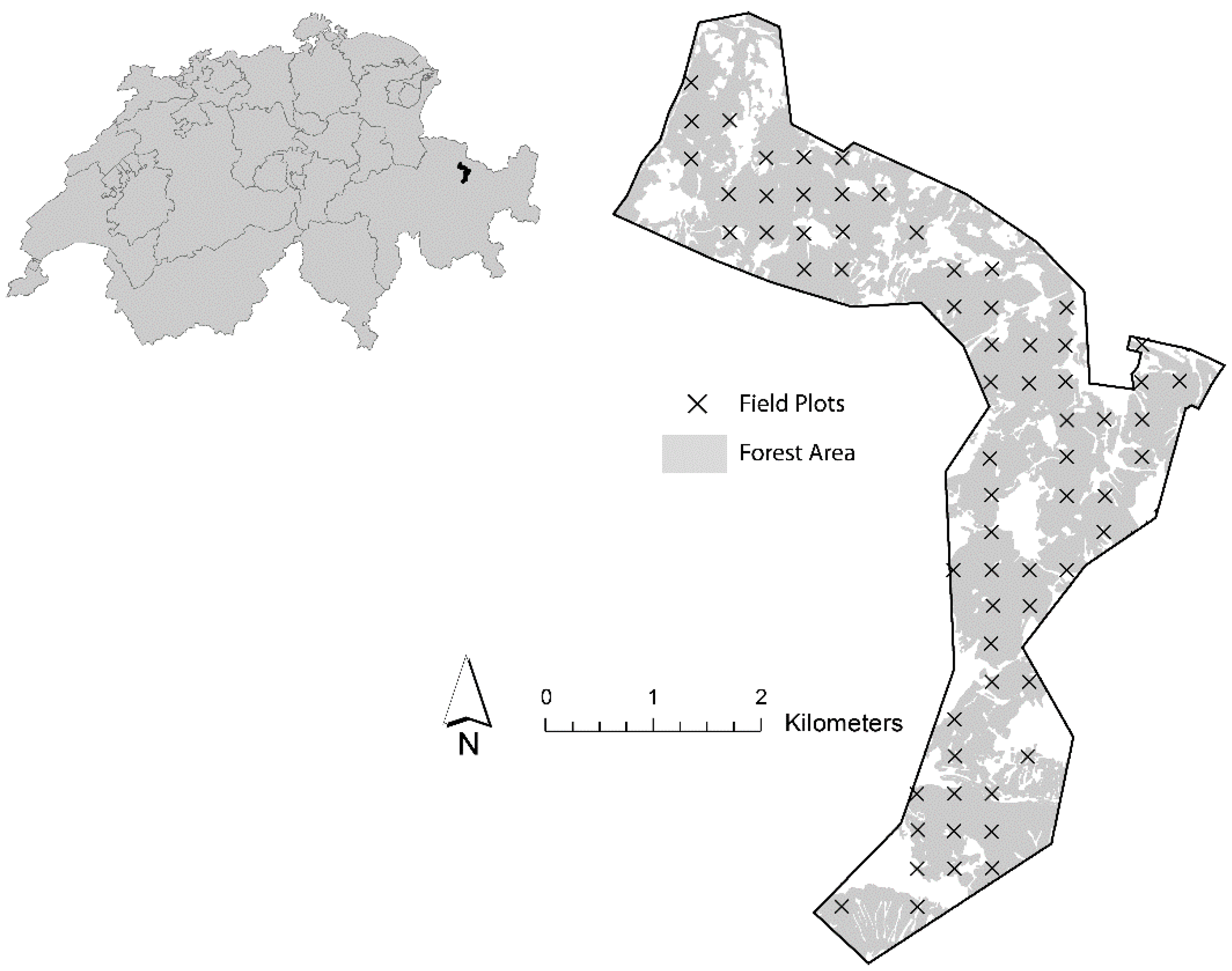
2.1.2. Timber Volume Densities from Field Inventory
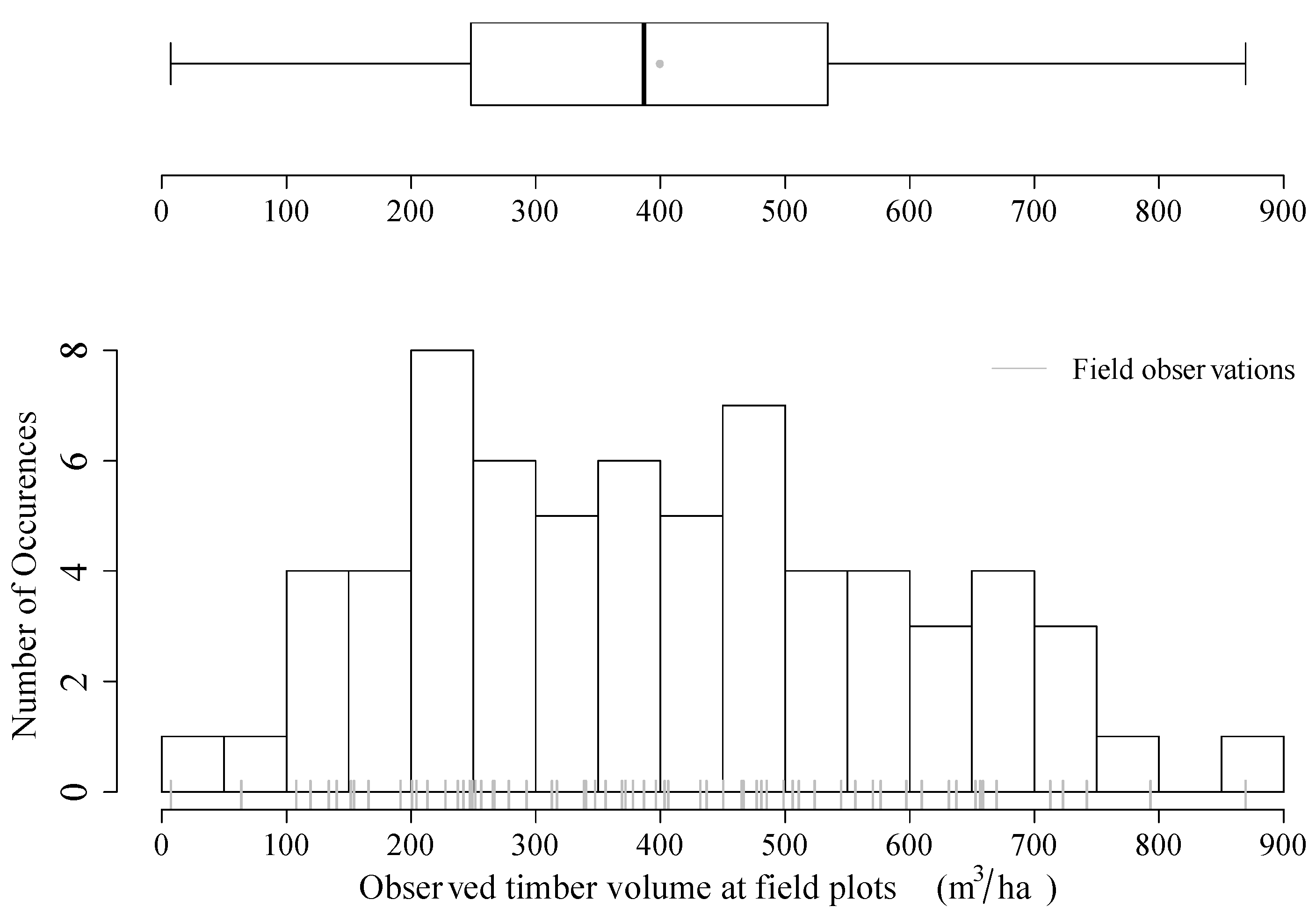
| Range | Mean | Median | SD | n |
|---|---|---|---|---|
| 7.3–869.57 | 399.4 | 386.9 | 194.94 | 67 |
2.1.3. LiDAR Data
| Beam deflection | Rotating mirror |
|---|---|
| Pulse Repetition Frequency (kHz) | 70 |
| Average Flying Altitude (m above ground) | 700 |
| Max. scan angle (°) | ±15 |
| Wavelength (nm) | 1550 |
| Beam divergence (mrad) | ≤0.5 |
| Average echo density (m−2) | 27.4 |
2.2. Methods
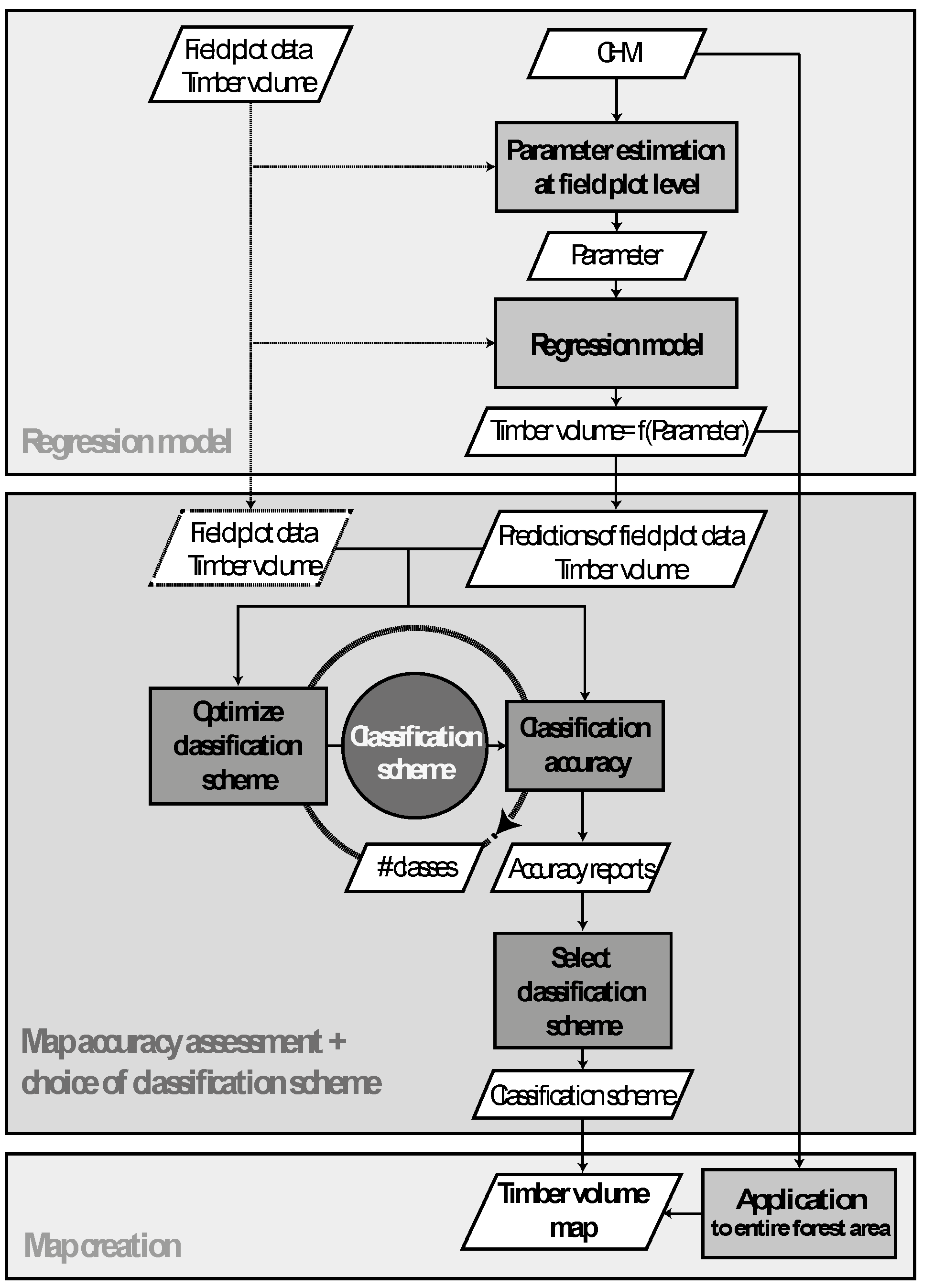
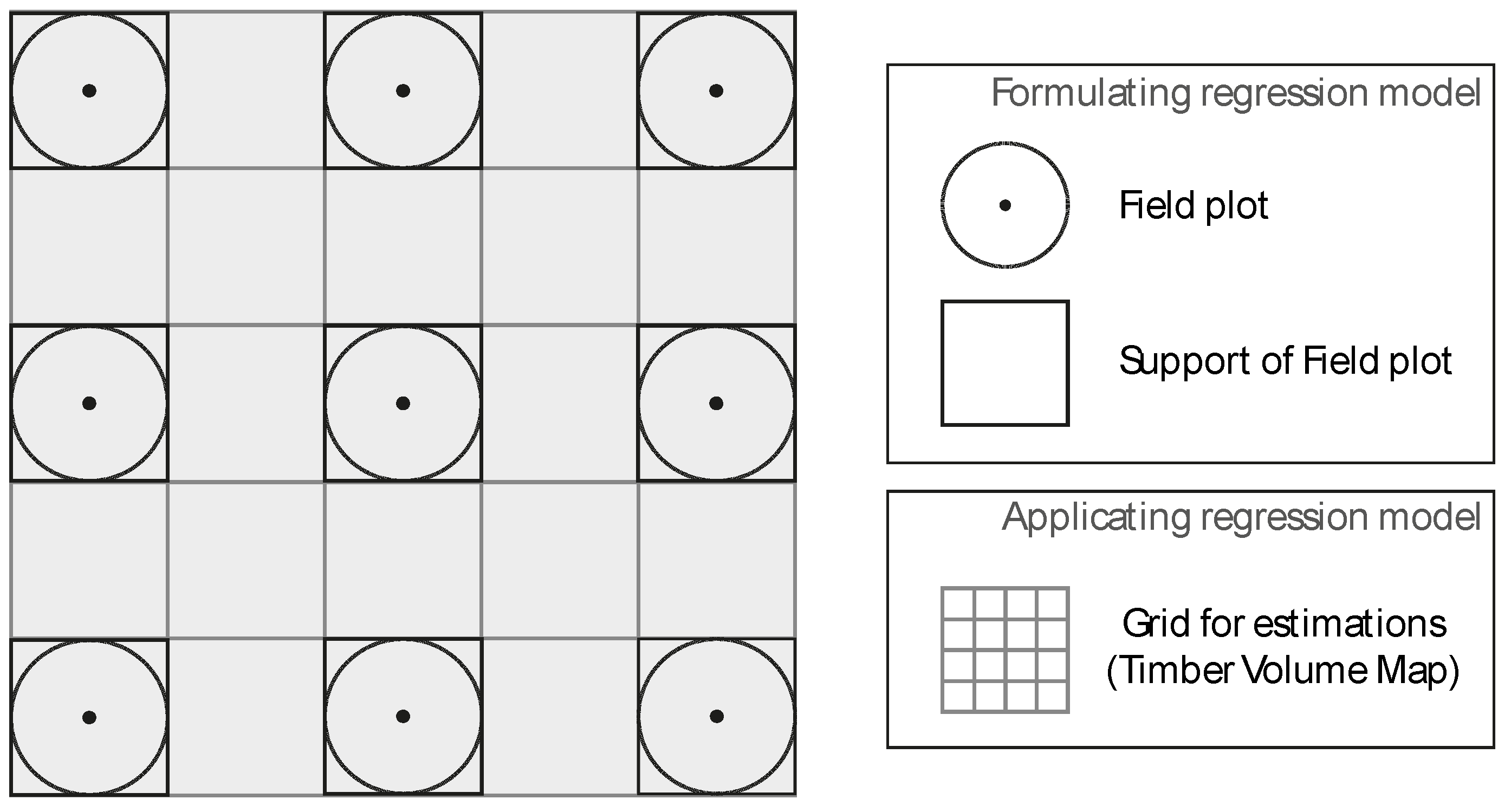
2.2.1. Step I: Computation of Canopy Height Model
2.2.2. Step I: Regression Model
| Metrics | Range | Mean | Median | SD |
|---|---|---|---|---|
| Mean | 2.26–26.03 | 12.07 | 11.31 | 5.89 |
| SD | 3.71–15.97 | 8.93 | 8.64 | 2.73 |
| MAX | 17.03–45.35 | 32.63 | 32.74 | 7.05 |
| Q25 | 0–22.88 | 4.25 | 0.67 | 6.35 |
| Q75 | 1.43–34.21 | 18.92 | 18.81 | 7.96 |
| Q90 | 8.11–37.78 | 23.77 | 23.48 | 7.25 |
2.2.3. Step II: Assessment of Map Accuracy
Prediction Performance
Classification Accuracy
- -
- The overall accuracy (OAA) is the proportion of correctly classified pixels of the entire map. The true overall accuracy of the map is unknown, since we only have references for the classified raster cells at a small subspace of the map. The OAA is therefore estimated by the ratio of the total number of correctly classified pixels and the total number of reference/classified pixels. The 95% confidence interval for the OAA was calculated according to the binomial distribution.
- -
- The producer’s accuracy (PA) is a measure of the classification performance. It indicates the probability that if a ground observation belongs to a certain class, this class will be reflected in the map. The producer’s accuracy can be estimated for each class by dividing the number of correctly classified pixels of a class by the total number of reference pixels in this class.
- -
- The user’s accuracy (UA) of each class is the most interesting information for a user of the map. It indicates the probability that if the map shows a certain class, this class will actually be validated by a terrestrial survey. The producer’s accuracy is estimated by the number of correctly classified pixels in a class divided by the total number of classified data in this class.
- -
- Cohen’s kappa coefficient is a measure to assess to what degree the classification accuracy was realized by a chance agreement. The kappa coefficient ranges between −1 (accuracy was realized under pure chance agreement) and 1 (accuracy was reached by no chance agreement).
Class Selection Problem
Optimization Model
2.2.4. Step III: Computation of the Timber Volume Map
3. Results
3.1. Regression Model
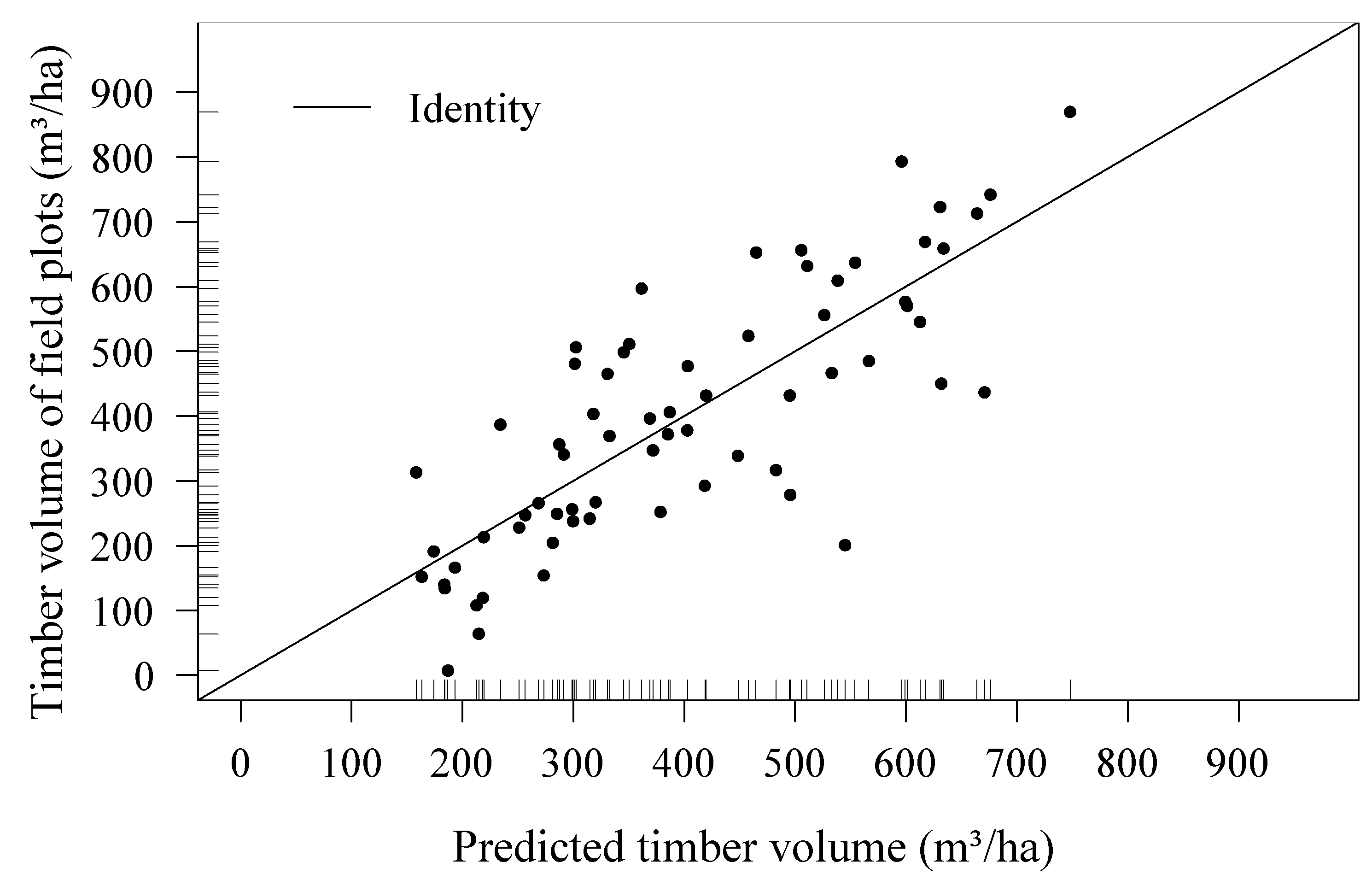
| Predictors | AIC | R2 | Adjusted R2 | Mallow’s Cp | RMSECV | Model Range |
|---|---|---|---|---|---|---|
| Mean *, SD *, Max *, Q75 * | 646.4 | 0.64 | 0.62 | 2.56 | 123.79 | 0–900m3 ha−1 |
3.2. Assessment of Map Classification Accuracy
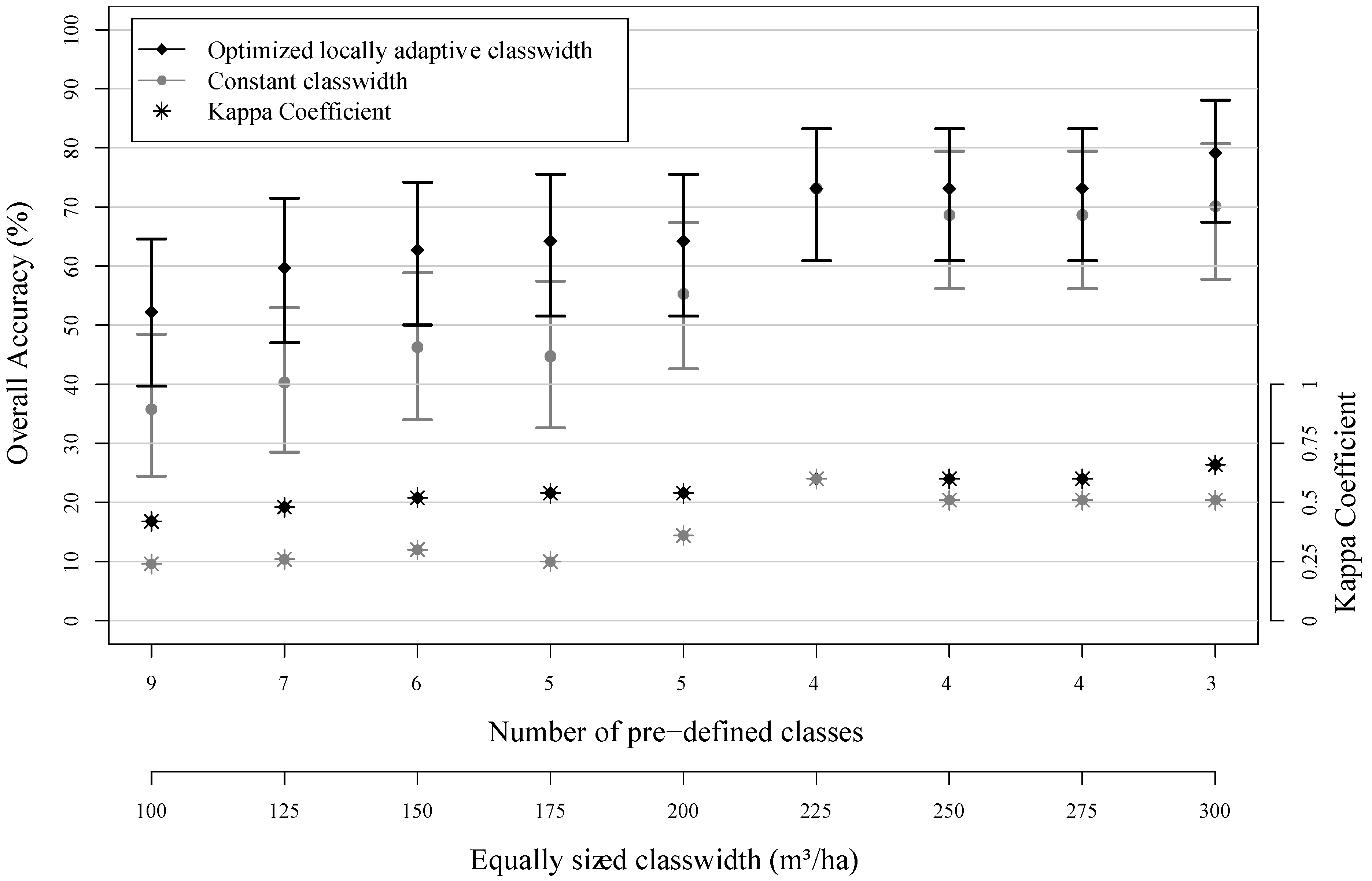
| Classes | Class Width | Producer’s Accuracy | User’s Accuracy | No. of References |
|---|---|---|---|---|
| (0, 200) | 200 | 60 | 85.71 | 10 |
| (200, 400) | 200 | 72 | 60 | 25 |
| (400, 600) | 200 | 40 | 40 | 20 |
| (600, 800) | 200 | 45.45 | 50 | 11 |
| (800, 1000) | 200 | 0 | - | 1 |
| Classes | Class Width | Producer’s Accuracy | User’s Accuracy | No. of References |
|---|---|---|---|---|
| (0, 220) | 220 | 76.92 | 90.91 | 13 |
| (220, 330) | 110 * | 61.54 | 50 | 13 |
| (330, 450) | 120 * | 57.14 | 53.33 | 14 |
| (450, 660) | 210 | 66.67 | 66.67 | 21 |
| (660, 900) | 240 | 50 | 75 | 6 |

3.3. Calculation of the Timber Volume Map
4. Discussion
4.1. Assessment of Map Accuracy
4.2. Class Selection by Optimization Model
4.3. Regression Model
4.4. Availability and Quality of Reference Data
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- McRoberts, R.E.; Tomppo, E.O.; Næsset, E. Advances and emerging issues in national forest inventories. Scand. J. For. Res. 2010, 25, 368–381. [Google Scholar]
- Gregoire, T.G.; Valentine, H.T. Sampling Strategies for Natural Resources and the Environment; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Mandallaz, D. Sampling Techniques for Forest Inventorie; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008; p. 247. [Google Scholar]
- Schreuder, H.T.; Wood, G.B.; Gregoire, T.G. Sampling Methods for Multiresource Forest Inventory; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Cochran, W.G. Sampling Techniques, 2 ed.; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Köhl, M.; Magnussen, S.; Marchetti, M. Sampling Methods, Remote Sensing and Gis Multiresource Forest Inventory; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Holmgren, J. Prediction of tree height, basal area and stem volume in forest stands using airborne laser scanning. Scand. J. For. Res. 2004, 19, 543–553. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
- Saborowski, J.; Marx, A.; Nagel, J.; Böckmann, T. Double sampling for stratification in periodic inventories—Infinite population approach. For. Ecol. Manag. 2010, 260, 1886–1895. [Google Scholar] [CrossRef]
- Von Lüpke, N. Approaches for the Optimisation of Double Sampling for Stratification in Repeated Forest Inventories. Ph.D. Thesis, Georg-August-Universität Göttingen, Göttingen, Germany, 2013. [Google Scholar]
- Mandallaz, D.; Breschan, J.; Hill, A. New regression estimators in forest inventories with two-phase sampling and partially exhaustive information: A design-based monte carlo approach with applications to small-area estimation. Can. J. For. Res. 2013, 43, 1023–1031. [Google Scholar] [CrossRef]
- Breidenbach, J.; Astrup, R. Small area estimation of forest attributes in the norwegian national forest inventory. Eur. J. For. Res. 2012, 131, 1255–1267. [Google Scholar] [CrossRef]
- Mandallaz, D. Design-based properties of some small-area estimators in forest inventory with two-phase sampling. Can. J. For. Res. 2013, 43, 441–449. [Google Scholar] [CrossRef]
- Tonolli, S.; Dalponte, M.; Vescovo, L.; Rodeghiero, M.; Bruzzone, L.; Gianelle, D. Mapping and modeling forest tree volume using forest inventory and airborne laser scanning. Eur. J. For. Res. 2011, 130, 569–577. [Google Scholar] [CrossRef]
- Van Aardt, J.A.; Wynne, R.H.; Scrivani, J.A. Lidar-based mapping of forest volume and biomass by taxonomic group using structurally homogenous segments. Photogramm. Eng. Remote Sens. 2008, 74, 1033–1044. [Google Scholar]
- Franco-Lopez, H.; Ek, A.R.; Bauer, M.E. Estimation and mapping of forest stand density, volume, and cover type using the k-nearest neighbors method. Remote Sens. Environ. 2001, 77, 251–274. [Google Scholar] [CrossRef]
- Latifi, H.; Nothdurft, A.; Koch, B. Non-parametric prediction and mapping of standing timber volume and biomass in a temperate forest: Application of multiple optical/lidar-derived predictors. Forestry 2010, 83, 395–407. [Google Scholar]
- Nothdurft, A.; Saborowski, J.; Breidenbach, J. Spatial prediction of forest stand variables. Eur. J. For. Res. 2009, 128, 241–251. [Google Scholar] [CrossRef]
- Magnussen, S.; Tomppo, E. The k-nearest neighbor technique with local linear regression. Scand. J. For. Res. 2014, 29, 120–131. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Tomppo, E.O.; Finley, A.O.; Heikkinen, J. Estimating areal means and variances of forest attributes using the k-nearest neighbors technique and satellite imagery. Remote Sens. Environ. 2007, 111, 466–480. [Google Scholar] [CrossRef]
- Beaudoin, A.; Bernier, P.Y.; Guindon, L.; Villemaire, P.; Guo, X.J.; Stinson, G.; Bergeron, T.; Magnussen, S.; Hall, R.J. Mapping attributes of canada’s forests at moderate resolution through knn and modis imagery. Can. J. Forest. Res. 2014, 44, 521–532. [Google Scholar] [CrossRef]
- Chirici, G.; Corona, P.; Marchetti, M.; Mastronardi, A.; Maselli, F.; Bottai, L.; Travaglini, D. K-NN forest: A software for the non-parametric prediction and mapping of environmental variables by the k-nearest neighbors algorithm. Eur. J. Remote Sens. 2012, 45. [Google Scholar] [CrossRef]
- Tomppo, E. The finnish multi-source national forest inventory-small area estimationand map production. In Forest Inventory; Springer: Berlin, Germany, 2006; pp. 195–224. [Google Scholar]
- Haara, A.; Kangas, A. Comparing k Nearest Neighbours Methods and Linear Regression—Is There Reason to Select One over the Other? Math. Comput. For. Nat. Res. Sci. 2012, 16, 50–65. [Google Scholar]
- Fehrmann, L.; Lehtonen, A.; Kleinn, C.; Tomppo, E. Comparison of linear and mixed-effect regression models and a k-nearest neighbour approach for estimation of single-tree biomass. Can. J. For. Res. 2008, 38, 1–9. [Google Scholar] [CrossRef]
- Baffetta, F.; Corona, P.; Fattorini, L. Design-based diagnostics for k-nn estimators of forest resourcesthis article is one of a selection of papers from extending forest inventory and monitoring over space and time. Can. J. For. Res. 2010, 41, 59–72. [Google Scholar] [CrossRef]
- Baffetta, F.; Fattorini, L.; Franceschi, S.; Corona, P. Design-based approach to k-nearest neighbours technique for coupling field and remotely sensed data in forest surveys. Remote Sens. Environ. 2009, 113, 463–475. [Google Scholar] [CrossRef]
- Hill, A. Comparison of Small Area Estimators in Forest Inventory Using Airborne Laserscanning Data Vergleich von Kleingebietsschätzern in der Waldinventur Unter Benutzung Von Flugzeugerhobenen Laserscanner Daten. Master Thesis, Georg-August-University, Göttingen, Germany, 2013. [Google Scholar]
- Magnussen, S.; Tomppo, E.; McRoberts, R.E. A model-assisted k-nearest neighbour approach to remove extrapolation bias. Scand. J. For. Res. 2010, 25, 174–184. [Google Scholar] [CrossRef]
- Pirlot, M. General local search methods. Eur. J. Oper. Res. 1996, 92, 493–511. [Google Scholar] [CrossRef]
- Rayward-Smith, V.J. Modern Heuristic Search Methods; Wiley: Chichester, UK, 1996; p. 294. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Ott, E.; Frehner, M.; Frey, H.U.; Lüscher, P. Gebirgsnadelwälder.Ein Praxisorientierter Leitfaden für eine Standortgerechte Waldbehandlung; Paul Haupt: Bern, Switzerland; Stuttgart, Germany; Wien, Austria, 1997. [Google Scholar]
- Brassel, P.; Lischke, H. Swiss National Forest Inventory: Methods and Models of the Second Assessment; Swiss Federal Institute of Forest, Snow and Landscape Research WSL: Birmensdorf, Zurich, Switzerland, 2001. [Google Scholar]
- Keller, M.R. Swiss National Forest Inventory. Manual of the Field Survey 2004–2007; Swiss Federal Institute of Forest, Snow and Landscape Research WSL: Birmensdorf, Zurich, Switzerland, 2011; p. 269. [Google Scholar]
- Hoffmann, C. Die berechnung von tarifen für die waldinventur. Forstwiss. Cent. 1982, 101, 24–36. [Google Scholar] [CrossRef]
- Isaaks, E.; Srivastava, R. Applied Geostatistics; Oxford University: London, UK, 2011. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar remote sensing of the canopy structure and biophysical properties of douglas-fir western hemlock forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Magnussen, S.; Eggermont, P.; LaRiccia, V.N. Recovering tree heights from airborne laser scanner data. For. Sci. 1999, 45, 407–422. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Akaike, H. Information Theory and An Extension of the Maximum Likelihood Principle. In Proceedings of the Second International Symposium on Information Theory, Akademinai Kiado, Budapest, Hungary; 1973; pp. 267–281. [Google Scholar]
- Srivastava, A.K.; Srivastava, V.K.; Ullah, A. The coefficient of determination and its adjusted version in linear regression models. Econom. Rev. 1995, 14, 229–240. [Google Scholar] [CrossRef]
- Mallows, C.L. Some comments on Cp. Technometrics 1973, 15, 661–675. [Google Scholar]
- Clementel, F.; Colle, G.; Farruggia, C.; Floris, A.; Scrinzi, G.; Torresan, C. Estimating forest timber volume by means of “low-cost” lidar data. Ital. J. Remote Sens. Riv. Ital. Di Telerilevamento 2012, 44, 125–140. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; Lewis Publications: Boca Raton, FL, USA, 1999; p. 137. [Google Scholar]
- Richards, J.A. Remote Sensing Digital Image Analysis: An Introduction, 5th ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Beauchamp, J.J.; Olson, J.S. Corrections for bias in regression estimates after logarithmic transformation. Ecology 1973, 54, 1403–1407. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Næsset, E.; Gobakken, T. Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 2013, 128, 268–275. [Google Scholar] [CrossRef]
- Mauro, F.; Valbuena, R.; Manzanera, J.A.; García-Abril, A. Influence of global navigation satellite system errors in positioning inventory plots for tree-height distribution studies. Can. J. For. Res. 2010, 41, 11–23. [Google Scholar] [CrossRef]
- Steinmann, K.; Mandallaz, D.; Ginzler, C.; Lanz, A. Small area estimations of proportion of forest and timber volume combining lidar data and stereo aerial images with terrestrial data. Scand. J. For. Res. 2012, 28, 373–385. [Google Scholar] [CrossRef]
- Fuller, W.A. Measurement Error Models; Wiley: New York, NY, USA, 1987. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hill, A.; Breschan, J.; Mandallaz, D. Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models. Forests 2014, 5, 2253-2275. https://doi.org/10.3390/f5092253
Hill A, Breschan J, Mandallaz D. Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models. Forests. 2014; 5(9):2253-2275. https://doi.org/10.3390/f5092253
Chicago/Turabian StyleHill, Andreas, Jochen Breschan, and Daniel Mandallaz. 2014. "Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models" Forests 5, no. 9: 2253-2275. https://doi.org/10.3390/f5092253
APA StyleHill, A., Breschan, J., & Mandallaz, D. (2014). Accuracy Assessment of Timber Volume Maps Using Forest Inventory Data and LiDAR Canopy Height Models. Forests, 5(9), 2253-2275. https://doi.org/10.3390/f5092253




