Biomass and Carbon Stocks of Sofala Bay Mangrove Forests
Abstract
:1. Introduction
2. Methods and Study Area
2.1. Description of the Study Area
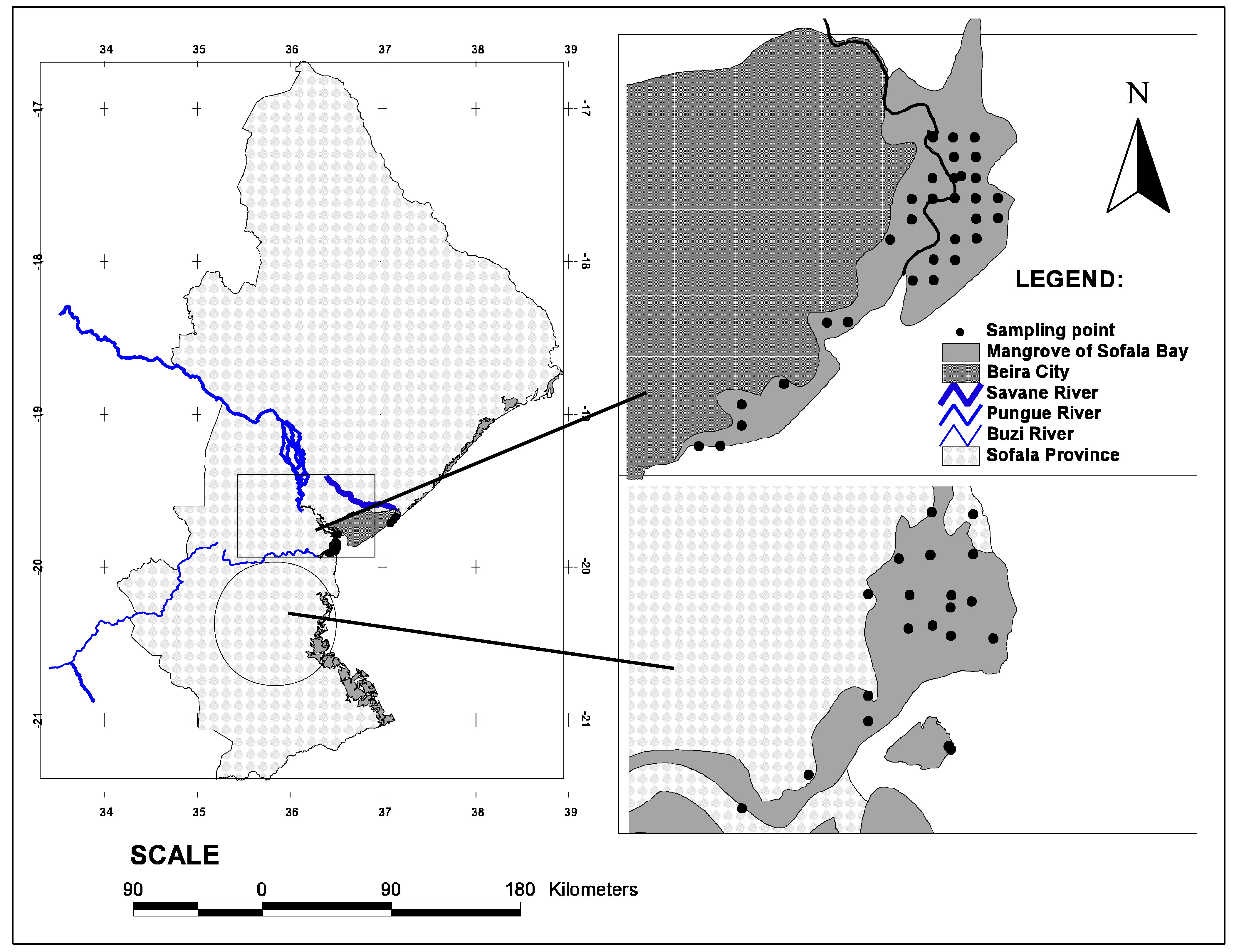
2.2. Study Design
2.2.1. Tree Biomass
2.2.2. Dead Wood, Herbaceous, Litter, and Pneumatophores
2.2.3. Soil Sampling
3. Results and Discussion
3.1. Allometric Equation
| N | DBH Range (cm) | b0 (95% Confidence Limits) | b1 (95% Confidence Limits) | RMSE | AIC | Adjusted R2 |
|---|---|---|---|---|---|---|
| 31 | 0.5–42 | 3.254 (2.214–4.513) | 0.065 (0.055–0.076) | 4.244 | 181.5 | 0.89 |
 ) observed; (
) observed; (  ) fitted line; (B) Scatter plot of the standardized residual against predicted dry weight; (C) Normal Quantile–Quantile plot.
) fitted line; (B) Scatter plot of the standardized residual against predicted dry weight; (C) Normal Quantile–Quantile plot.
 ) observed; (
) observed; (  ) fitted line; (B) Scatter plot of the standardized residual against predicted dry weight; (C) Normal Quantile–Quantile plot.
) fitted line; (B) Scatter plot of the standardized residual against predicted dry weight; (C) Normal Quantile–Quantile plot.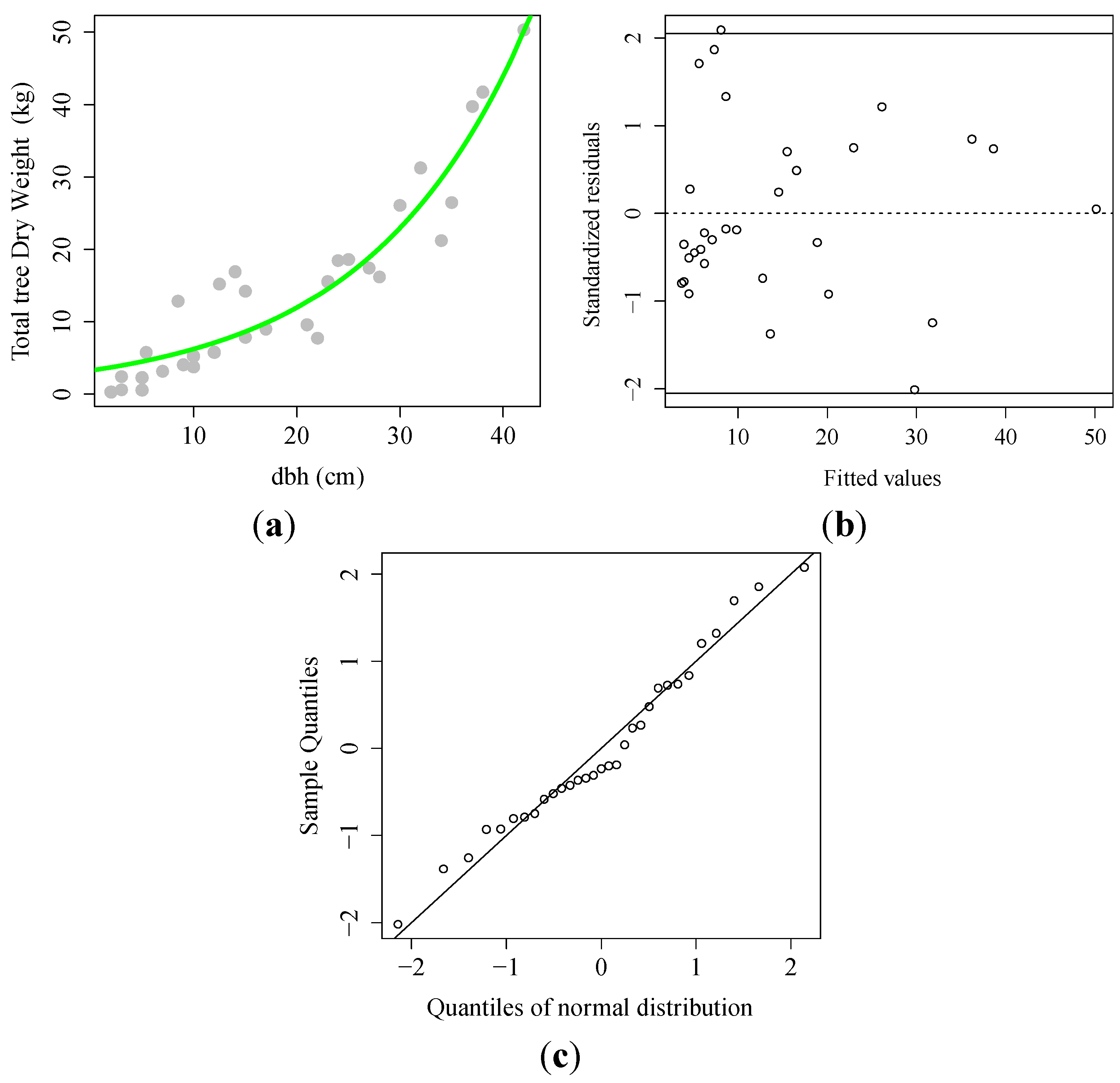
3.2. Above-Ground Biomass and Carbon
| Component | Biomass (Mg·ha−1) | Carbon (Mg·ha−1) | ||
|---|---|---|---|---|
| Average | % | Average | % | |
| Live trees | 58.38 ± 19.1 | 43.4 | 28.02 ± 9.2 | 47.8 |
| Roots * | 64.67 ± 13.4 | 48.0 | 25.22 ± 5.3 | 43.0 |
| Herbaceous | 4.29 ± 2.4 | 3.2 | 1.93 ± 1.1 | 3.3 |
| Litter | 3.08 ± 1.7 | 2.3 | 1.39 ± 0.8 | 2.4 |
| Dead trees | 3.40 ± 1.7 | 2.5 | 1.70 ± 0.9 | 2.9 |
| Wood debris | 0.26 ± 0.2 | 0.2 | 0.13 ± 0.1 | 0.2 |
| Pneumatophores | 0.53 ± 0.3 | 0.4 | 0.21 ± 0.1 | 0.4 |
| Total | 134.61 ± 25.2 | 100 | 58.60 ± 11.5 | 100 |
3.3. Soil Carbon
| Sample Depth (cm) | Bulk Density (g·cm−3) | Mean of % Organic Matter | Mean Soil Carbon | Total Carbon (Mg/ha−1) |
|---|---|---|---|---|
| 0–30 | 1.12 ± 0.23 | 2.73 ± 1.73 | 1.57 ± 1.0 | 53.32 ± 20.8 |
| 30–60 | 1.07 ± 0.26 | 2.35 ± 1.31 | 1.42 ± 0.81 | 45.76 ± 24.43 |
| 60–100 | 1.05 ± 0.26 | 2.49 ± 1.53 | 1.44 ± 0.89 | 60.90 ± 38.04 |
3.4. Total Carbon Stocks
| Component | Carbon (Mg·ha−1) | % of Total |
|---|---|---|
| Total Above-ground carbon (live and dead trees, herbaceous, pneumatophores and litter) | 33.3 | 15.2 |
| Total Below-ground carbon (soil and roots) | 185.2 | 84.8 |
| Total Ecosystem carbon | 218.5 | 100 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Giri, C.O.E.; Tieszen, L.L.; Zhu, Z.; Singh, A. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Spalding, M.; Blasco, F.; Field, C. World Mangrove Atlas; International Society for Mangrove Ecosystems: Okinawa, Japan, 1997; p. 178. [Google Scholar]
- Alongi, D. Present state and future of the world’s mangrove forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
- Alongi, D.S.A.; Chong, V.C.; Pfitzner, J.; Trott, L.A.; Tirendi, F.; Dixon, P.; Brunskill, G.J. Sediment accumulation and organic material flux in a managed mangrove ecosystem: Estimates of land-ocean-atmosphere exchange in peninsular Malaysia. Mar. Geol. 2004, 208, 383–402. [Google Scholar] [CrossRef]
- Ong, E. The Hidden Costs of Mangrove Services: Use of Mangroves for Shrimp Aquaculture; The International Geosphere-Biosphere Program (IGBP): Stockholm, Sweden, 2002. [Google Scholar]
- Tomlinson, C.B. The Botany of Mangroves; Cambridge Tropical Biology Series; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Kauffman, J.B.; Donato, D.C. Protocols for the Measurement, Monitoring and Reporting of Structure, Biomass and Carbon Stocks in Mangrove Forests; Working Paper 86; Center for International Forest Research (CIFOR): Bogor, Indonesia, 2012. [Google Scholar]
- Donato, D.K.J.B.; Murdiyarso, D.; Kurnianto, S.; Stidham, M.; Kanninen, M. Mangroves among the most carbon-rich forests in the tropics. Nat. Geosci. 2011, 4, 293–297. [Google Scholar] [CrossRef]
- Kalk, M.A. A Natural History of Inhaca Island Mozambique, 3rd ed.; Witwatersrand University Press: Capetown, South Africa, 1995. [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). The World’s Mangroves 1980–2005; A Thematic Study Prepared in the Framework of the Global Forest Resources Assessment 2005; FAO: Rome, Italy, 2005. [Google Scholar]
- McLeod, E.; Salm, R.V. Managing Mangroves for Resilience to Climate Change; IUCN: Gland, Switzerland, 2006; p. 64. [Google Scholar]
- Taylor, M.; Ravilious, C.; Green, E.P. Mangroves of East Africa; UNEP and World Conservation Monitoring Center: Cambridge, UK, 2003; p. 25. [Google Scholar]
- Odum, E. Ecologia, 3rd ed.; Guanabara Koogan: Rio de Janeiro, Brazil, 1980; p. 639. [Google Scholar]
- Murdiyarso, D.D.D.; Kauffman, J.B.; Stidham, M.; Kanninen, M. Carbon Storage in Mangrove and Peatland Ecosystems: A Preliminary Account from Plots in Indonesia; Working paper 48; Center for International Forest Research (CIFOR): Bogor, Indonesia, 2011; p. 37. [Google Scholar]
- Barbosa, F.; Cuambe, C.; Bandeira, S. Status and distribution of mangroves in Mozambique. S. Afr. J. Bot. 2001, 67, 393–398. [Google Scholar]
- Relatório do estudo de avaliação da interacção entre a biodiversidade e pobreza em Moçambique; MICOA, Direcção Nacional de Gestão Ambiental: Maputo, Mozambique, 2008; p. 139.
- Marzoli, A. Relatório do Inventário Florestal Nacional; Ministério da Agricultura, Drecção Nacional de Terras e Florestas: Maputo, Mozambique, 2007; p. 82. [Google Scholar]
- Matusse, R.M. Os Mangais de Moçambique e o seu estado de Desmatamento (1990 a 1992); Ministério da Agricultura, Direcção Nacional de Terras e Florestas: Maputo, Mozambique, 1992; p. 18. [Google Scholar]
- De Boer, W. The rise and fall of the mangrove forests in Maputo Bay, Mozambique. Wetl. Ecol. Manag. 2002, 10, 313–322. [Google Scholar]
- Sitoe, A.S.A.; Wertz-Kanounnikoff, S. The Context of REDD+ in Mozambique: Drivers, Agents and Institutions; Occasional Paper; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2012; Volume 79. [Google Scholar]
- Baccini, A.G.S.J.; Walker, W.S.; Lapote, N.T.; Sun, M.; Sulla-Menashe, D.; Hackle, J.; Beck, P.S.A.; Dubayan, M.A.; Friedl, M.A.; Samanta, S.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Harris, N.B.S.; Hagen, S.C.; Saatchi, S.S.; Petrova, S.; Salas, W.; Hansen, M.C.; Potapov, P.V.; Lotsch, A. Baseline map of carbon emissions from deforestation in tropical regions. Science 2012, 336, 1573. [Google Scholar] [CrossRef]
- Harris, N.B.S.; Hagen, S.C.; Baccini, A.; Houghton, R. Progress toward a Consensus on Carbon Emissions from Tropical Deforestation: Policy Brief; Meridian Institute: Washington, DC, USA, 2012. [Google Scholar]
- Angelsen, A. Movind Ahead with REDD: Issues, Options, and Implications; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2008. [Google Scholar]
- Angelsen, A. RealisingREDD+: National Strategy and Policy Options; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2009. [Google Scholar]
- Kanninen, M.M.D.; Seymour, F.; Angelsen, A.; Wunder, S.; German, L. Do Trees Grow Money? The Implications of Deforestation Research and Policies to Promote REDD; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2007. [Google Scholar]
- Williams, M.R.C.M.; Rees, R.M.; Sambane, E.; Fernando, J.; Grace, J. Carbon sequestration and biodiversity of re-growing miombo woodlands in Mozambique. For. Ecol. Manag. 2008, 254, 145–155. [Google Scholar] [CrossRef]
- Ryan, C. Carbon Cycling, Fire and Carbon Cycling, Fire and Phenology in a Tropical Savanna Woodland in Nhambita, Mozambique; University of Edinburgh: Edinburgh, UK, 2009; p. 257. [Google Scholar]
- Fatoyinbo, T.S.M.; Washington-Allen, R.A.; Shugart, H.H. Landscape-scale extent, height, biomass, and carbon estimation of Mozambique’s mangrove forests with Landsat ETM+ and Shuttle Radar Topography Mission elevation data. J. Geophys. Res. 2008, 113, G02S06. [Google Scholar]
- Bosire, J.; Bandeira, S.O.; Rafael, J. Coastal Climate Change Mitigation and Adaptation through REDD+ Carbon Programs in Mangroves in Mozambique: Pilot in the Zambezi Delta. Component: Determination of Carbon Stocks through Localized Allometric Equations; Eduardo Mondlane University: Maputo, Mozambique, 2012; p. 27. [Google Scholar]
- Saket, M.; Matusse, R.M. Estudo da Taxa de Desflorestamento da Vegetação de Mangal em Moçambique; Ministério da Agricultura, Unidade de Inventário Florestal: Maputo, Mozambique; p. 99.
- Sete, C.R.J.; Dove, V. Seasonal Variation of Tides, Currents, Salinity and Temperature along the Coast of Mozambique; Odinafrica, U., Ed.; Centro Nacional de Dados Oceanográficos: Maputo, Mozambique, 2002; p. 72. [Google Scholar]
- Consultec. Estudo Ambiental Simplificado da Dragagem do Canal de Acesso ao Porto da Beira; Consultec: Beira, Mozambique, 2007. [Google Scholar]
- Macamo, C.; Cangy, F.; Bandeira, S. Formas de uso, estrutura e estado de conservação de Mangal de Mieze e Muchara - Baía de Pemba, Cabo Delgado; Universidade Eduardo Mondlane and Instituto Nacional de Investigação: Pesqueira: Maputo, 2008; p. 23. [Google Scholar]
- Brown, S. Estimating Biomass and Biomass Change of Tropical Forests: A Primer; FAO: Rome, Italy, 1997. [Google Scholar]
- R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011.
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Adame, M.K.J.B.; Medina, I.; Gamboa, J.N.; Torres, O. Carbon stocks of tropical coastal wetlands within the karstic landscape of the mexican caribbean. PLoS One 2013, 8. [Google Scholar] [CrossRef]
- Comley, B.W.T.; McGuinness, K.A. Above- and below-ground biomass, and allometry of four common northern Australian mangroves. Austr. J. Bot. 2005, 53, 431–436. [Google Scholar] [CrossRef]
- Arevalo, L.A.; Alegre, J.C.; Vilcahuman, L.J.M. Metodologia para Estimar Estoques de Carbono em Diferentes Sistemas de uso de Terra; Embrapa: São Paulo, Brazil, 2002. [Google Scholar]
- Pearson, T.; Walker, S.M.; Brown, S. Sourcebook for Land Use, Land-Use Change and Forestry Projects; BioCarbon Fund, Winrock International: Washington, DC, USA, 2005; p. 64. [Google Scholar]
- Cerón-Bretón, J.G.; Cerón-Bretón, R.M.; Rangel-Marrón, M.; Muriel-García, M.; Cordova-Quiroz, A.V.; Estrella-Cahuich, A. Determination of carbon Sequestration rate in soil of mangrove forest in Campeche, Mexico. Int. J. Energy Environ. 2011, 5, 328–336. [Google Scholar]
- Kairo, J.L.; Lang’at, J.K.S.; Dahdouh-Guebas, F.; Bosire, J.; Karachi, M. Structural development and productivity of replanted mangrove plantations in Kenya. For. Ecol. Manag. 2008, 255, 2670–2677. [Google Scholar] [CrossRef]
- Kridiborworn, P.C.A.; Yuttitham, M.; Tripetchkul, S. Carbon sequestration by mangrove forest planted specifically for charcoal production in Yeesarn, SamutSongkram. J. Sustain. Energy Environ. 2012, 3, 87–92. [Google Scholar]
- Litton, C.M.; Kauffman, J.B. Allometric models for predicting aboveground biomass in two widespread woody plants in Hawaii. Biotropica 2008, 40, 313–320. [Google Scholar] [CrossRef]
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar]
- Ter-Mikaelian, M.; Korzukhin, M. Biomass equations for sixty-five North American tree species. For. Ecol. Manag. 1997, 97, 1–24. [Google Scholar]
- Raffli, T.P.; Usher, G.; Niles, J.O. Reducing Carbon Emission from Deforestation in the Ulu Masen Ecoystem, Aceh, Indonesia; Provincial Government of Nanggroe Aceh Darussalam: Aceh, Indonesia, 2007. [Google Scholar]
- Wendling, B.J.I.; Mendonça, E.S.; Neves, J.C.L. Carbono organico e estabilidade de agregados de um Latossolo Vermelho Sob diferentes Manejos. Pesquisa Agropecuária 2005, 40, 487–494. [Google Scholar]
- Walker, S.M.; Desanker, P.V. The impact of land use on soil carbon in Miombo Woodlands of Malawi. For. Ecol. Manag. 2004, 203, 345–360. [Google Scholar] [CrossRef]
- Kauffman, J.C.H.; Thomas, G.C.; Kathleen, A.D.; Daniel, C.; Donato, D. Ecosystem carbon stocks of micronesian mangrove forests. Wetlands 2011, 31, 343–352. [Google Scholar] [CrossRef]
- Tomo, F.A. Estimativas de stock de carbono nas florestas de miombo em Gondola. Tese de Licenciatura, DEF, FAEF. In Department of Forestry; Universidade Eduardo Mondlane: Maputo, Mozambique, 2012; p. 63. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sitoe, A.A.; Mandlate, L.J.C.; Guedes, B.S. Biomass and Carbon Stocks of Sofala Bay Mangrove Forests. Forests 2014, 5, 1967-1981. https://doi.org/10.3390/f5081967
Sitoe AA, Mandlate LJC, Guedes BS. Biomass and Carbon Stocks of Sofala Bay Mangrove Forests. Forests. 2014; 5(8):1967-1981. https://doi.org/10.3390/f5081967
Chicago/Turabian StyleSitoe, Almeida A., Luís Júnior Comissário Mandlate, and Benard S. Guedes. 2014. "Biomass and Carbon Stocks of Sofala Bay Mangrove Forests" Forests 5, no. 8: 1967-1981. https://doi.org/10.3390/f5081967
APA StyleSitoe, A. A., Mandlate, L. J. C., & Guedes, B. S. (2014). Biomass and Carbon Stocks of Sofala Bay Mangrove Forests. Forests, 5(8), 1967-1981. https://doi.org/10.3390/f5081967




